commit to user
1
PERAMALAN INDEKS HARGA SAHAM GABUNGAN MENGGUNAKAN
RUNTUN WAKTU FUZZY DENGAN PARTISI INTERVAL
BERDASARKAN FREKUENSI DENSITAS
Sylvia Swidaning Putri, Winita Sulandari dan Muslich
Program Studi Matematika FMIPA UNS
ABSTRAK. Indeks harga saham gabungan merupakan salah satu indikator penting yang perlu diperhatikan sebelum berinvestasi karena perkembangan pasar modal sangat dipengaruhi oleh kegiatan investasi para investor. Dalam penelitian ini, metode runtun waktu fuzzy dengan partisi interval berdasarkan frekuensi densitas orde satu, orde dua, dan orde tiga diterapkan untuk meramalkan data indeks harga saham gabungan dari bulan Januari 2012 sampai dengan Agustus 2015. Hasil pembahasan menunjukkan bahwa orde dua menghasilkan nilai peramalan yang lebih baik dibanding orde satu dan tiga dengan penentuan interval pada runtun waktu fuzzy
berdasarkan frekuensi densitas.
Kata kunci: IHSG, runtun waktu fuzzy, partisi interval berdasarkan frekuensi densitas
1. PENDAHULUAN
Indeks harga saham gabungan (IHSG) merupakan salah satu indikator
penggerak harga saham. Pergerakan indeks sangat dipengaruhi ekspektasi investor
atas kondisi fundamental negara maupun global (Pasaribu dkk., 2008). Peningkatan
IHSG mempengaruhi pasar modal sehingga investor akan mengambil keputusan
menjual saham, sedangkan penurunan IHSG akan menyebabkan investor tidak
menjual saham.
Peramalan perlu dilakukan sehingga investor mempunyai pandangan
tentang keadaan IHSG di masa mendatang. Hansun (2012) menggunakan metode
runtun waktu fuzzy untuk meramalkan IHSG dan menyatakan bahwa metode runtun
waktu fuzzy memberikan hasil peramalan yang cukup baik. Berdasarkan penelitian
yang dilakukan oleh Huarng (2001) dan Huarng dan Yu (2006) diketahui bahwa
penentuan interval mempengaruhi hasil peramalan. Huarng (2001) melakukan
peramalan runtun waktu fuzzy dengan penentuan interval berbasis rata-rata
(average based). Metode ini diterapkan untuk meramalkan pendaftaran Universitas
Alabama dan menghasilkan peramalan yang efektif. Huarng dan Yu (2006)
memperkenalkan metode penentuan interval berbasis rasio pada runtun waktu fuzzy
commit to user
2
(TAIEX). Tahun 2008, Jilani dan Burney mengembangkan metode penentuan
interval dengan mempartisi kembali interval menggunakan frekuensi densitas
disertai pembobot yang digunakan berdasarkan arah tren. Penerapan peramalan
pada TAIEX menghasilkan nilai akurasi lebih baik karena interval dipartisi kembali
sehingga residu yang diperoleh lebih kecil. Pada penelitian berikutnya, Jilani et al.
(2010) menerapkan kembali metode penentuan interval berdasarkan frekuensi
densitas untuk meramalkan pendaftaran di Universitas Alabama tetapi tidak
menggunakan pembobot dalam penentuan nilai peramalan.
IHSG adalah data yang mempunyai pola tren, sehingga metode Jilani dan
Burney (2008) dengan penentuan interval pada runtun waktu fuzzy berdasarkan
frekuensi densitas dapat diterapkan dalam peramalan IHSG. Perhitungan peramalan
pada metode tersebut menggunakan pembobot berdasarkan arah tren. Pada
penelitian ini, peramalan IHSG menggunakan runtun waktu fuzzy orde satu, dua,
dan tiga dalam penentuan interval berdasarkan frekuensi densitas.
2. RUNTUN WAKTU FUZZY
Runtun waktu fuzzy adalah metode peramalan yang menggunakan
prinsip-prinsip fuzzy sebagai dasarnya. Metode runtun waktu fuzzy pertama kali
diperkenalkan oleh Song dan Chissom (1993, 1994) untuk meramalkan pendaftaran
Universitas Alabama. Song dan Chissom (1993, 1994) menyatakan bahwa jika
himpunan semesta � ⊂ �, = , , … , dengan � = , , …, adalah
himpunan fuzzy dan jika � kumpulan dari � , � , … maka � adalah
runtun waktu fuzzy pada � . Runtun waktu fuzzy � dapat disebut sebagai
variabel linguistik dengan � sebagai nilai linguistik yang mungkin dari � . Jika
� = � dipengaruhi oleh � − = �, maka relasi logika fuzzy antara �
dengan � − adalah � → �, sedangkan jika � = � dipengaruhi oleh
� − , � − , … , � − = � , � , … � maka relasi logika fuzzy orde ke-n
commit to user
3
3. RUNTUN WAKTU FUZZY-PARTISI INTERVAL BERDASARKAN
FREKUENSI DENSITAS
Menurut Jilani dan Burney (2008) penentuan interval pada runtun waktu
fuzzy dilakukan dengan mempartisi interval berdasarkan frekuensi densitas. Berikut
ini adalah langkah metode penentuan interval pada runtun waktu fuzzy berdasarkan
frekuensi densitas.
(1) Menentukan himpunan semesta � = [� − � , � � + � ] dengan �
dan � � adalah nilai minimum dan maksimum, sedangkan � dan � adalah
sembarang bilangan positif.
(2) Membagi himpunan semesta U menjadi beberapa interval , , … ,
dengan panjang yang sama.
(3) Menentukan frekuensi data historis pada masing-masing interval.
Mengurutkan interval-interval berdasarkan frekuensinya, dari frekuensi
tertinggi sampai dengan terendah. Menentukan interval yang mempunyai
frekuensi tertinggi dan dibagi dalam n subinterval yang sama panjang.
Kemudian menentukan interval yang mempunyai frekuensi tertinggi kedua dan
dibagi dalam n-1 subinterval yang sama panjang. Interval yang mempunyai
frekuensi terendah tidak dibagi menjadi subinterval. Jika tidak ada frekuensi
data pada sebuah interval, maka interval dihapuskan.
(4) Mendefinisikan himpunan fuzzy � pada himpunan semesta U dengan
menggunakan partisi interval berdasarkan data frekuensi ′ , ′ , … , ′ .
(5) Menentukan relasi logika fuzzy (RLF) dan menentukan grup relasi logika fuzzy
(GRLF) dari semua relasi logika fuzzy.
(6) Menentukan hasil peramalan. Nilai peramalan �̂�, dihitung menggunakan
rumus,
a) untuk =
�̂�, = � + �
( � �+ � �) )
�
commit to user
4 �̂�, =
(
∑= −+ � �−
( − �+ �
( �+
�+
( + � )
�
c) untuk =
�̂�, = � − + �
( � −
− �+ � �)
) �
dengan < � ≤ , adalah nilai tengah dari interval ′ dan � adalah
pembobot. Kriteria untuk pemilihan pembobot pada �̂�, sebagai
berikut.
1. Jika � − − � − − � − − � − > �, maka nilai
tren naik dan pembobot pada �̂�, menjadi � = , � = . , �− =
. , � = , �+ = . , � − = . , dan � =
2. Jika � − − � − − � − − � − < �, maka nilai
tren turun dan pembobot �̂�, menjadi � = , � = . , �− =
. , � = , �+ = . , � − = . , dan � =
3. Jika � − − � − − � − − � − = �, maka nilai
tren tidak berubah dan pembobotpada �̂�, menjadi � = , � = . ,
�− = . , � = , �+ = . , � − = . , dan � =
dengan � adalah suatu konstanta sedemikian hingga nilai akar rata-rata
kuadrat residunya minimum.
4. METODE PENELITIAN
Data yang digunakan dalam penelitian ini merupakan data IHSG dengan
periode bulanan. Terdapat 44 data yang diambil dari bulan Januari 2012 – Agustus
2015. Data dikelompokkan menjadi dua, yaitu 39 data periode Januari 2012 – Maret
2015 sebagai data pelatihan dan 5 data periode April – Agustus 2015 sebagai data
pengujian. Berikut adalah langkah analisis data yang dibutuhkan untuk mencapai
tujuan penelitian.
(1) Menentukan himpunan semesta U pada data IHSG kemudian membagi
commit to user
5
0 1000 2000 3000 4000 5000 6000
1 2 3 4 5 6 7 8 9 1011121314151617181920212223242526272829303132333435363738394041424344
IH
SG
(Poi
n
)
t (Bulan)
(2) Menentukan frekuensi pada data historis masing-masing interval untuk
mempartisi interval kembali.
(3) Menentukan himpunan fuzzy� berdasarkan partisi interval dengan frekuensi
densitas.
(4) Menentukan fuzzifikasi data historis
(5) Menentukan grup relasi logika fuzzy dari hasil fuzzifikasi untuk orde satu, dua,
dan tiga.
(6) Menentukan peramalan data pada waktu ke = , , … , dengan metode
Jilani dan Burney (2008).
(7) Menghitung akurasi hasil peramalan root mean square error (RMSE) dan
meramalkan satu periode ke depan.
5. HASIL PENELITIAN DAN PEMBAHASAN
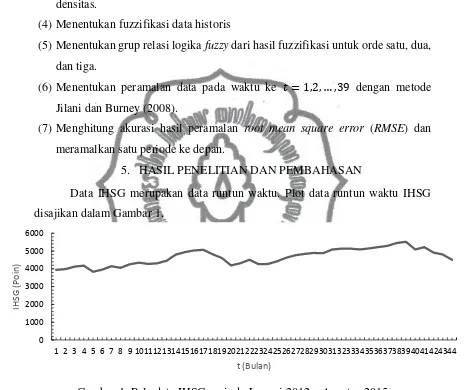
Data IHSG merupakan data runtun waktu. Plot data runtun waktu IHSG
disajikan dalam Gambar 1.
Gambar 1. Pola data IHSG periode Januari 2012 – Agustus 2015
Gambar 1 menunjukkan pola data IHSG terlihat meningkat pada waktu
tertentu sehingga data mengandung pola tren. Berikut adalah langkah metode
runtun waktu fuzzy dengan partisi interval berdasarkan frekuensi densitas untuk
meramalkan IHSG.
(1) Menentukan himpunan semesta menjadi sebuah interval. Data terkecil pada
IHSG adalah 3832,82 dan data terbesar adalah 5518,67, dipilih � = ,
dan � = , sehingga diperoleh himpunan semesta � = [ , ].
� = [ , ] dibagi menjadi 8 interval, dengan = [ , ], =
commit to user
6
(2) Menentukan frekuensi densitas masing-masing interval. Dari Tabel 1 diperoleh
7 frekuensi berbeda. Kemudian interval diurutkan berdasarkan frekuensinya,
dari frekuensi tertinggi sampai dengan terendah. Interval tertinggi dipartisi
menjadi 7 subinterval, interval tertinggi kedua dipartisi menjadi 6 subinterval
dan seterusnya sampai dengan interval terendah tidak dipartisi.
(3) Menentukan himpunan fuzzy � dari masing-masing interval yang diperoleh
pada Langkah 2. Setelah dilakukan partisi didapatkan 27 interval, dengan ,=
[ , ], ,= [ , ], …, ,= [ , ].
Tabel 1. Frekuensi Data pada Interval
Interval Frekuensi Data Interval Frekuensi Data
= [ , ] 1 = [ , ] 6
= [ , ] 6 = [ , ] 8
= [ , ] = [ , ] 2
= [ , ] 5 = [ , ] 2
(4) Menentukan fuzzifikasi data IHSG. Hasil fuzzifikasi data IHSG dinyatakan
pada Tabel
Tabel 2. Fuzzifikasi data IHSG
Tahun t � �
2012 1 3941,69 �
2 3985,21 �
3 4121,55 �
⋮ ⋮ ⋮ ⋮
2015 39 5518,67 �
(5) Membentuk RLF dan GRLF pada orde satu, dua, dan tiga. Sebagai ilustrasi
berikut adalah contoh GRLF pada orde tiga yang ditunjukkan Tabel 3.
Tabel 3. Grup relasi logika fuzzy orde tiga
No Grup Relasi fuzzy
Grup 1 � � � → �
Grup 2 � � � → �
⋮ ⋮
Grup 36 � � � → �
(6) Menentukan nilai peramalan waktu ke t. Hasil peramalan ditunjukkan pada
Tabel 4. Penentuan penggunaan pembobot disesuaikan dengan arah tren.
commit to user
7
minimum. Pada penelitian ini diperoleh � = dengan residu minimum
untuk orde satu, � = − untuk orde dua, dan � = − orde tiga. Sebagai
contoh perhitungan peramalan orde tiga pada bulan April 2012 � =
maka � − − � − − (� − − � − = , > � =
− sehingga tren naik. � = mempunyai grup relasi logika fuzzy
� � � → � , sehingga nilai peramalan waktu � = adalah
�̂ , = ��−�− + �+ �+
��− �+�����+��+ ���+ �
= .
, + , + .,
= ,
Tabel 4. Hasil peramalan orde satu, dua, dan tiga
Tahun � � Orde 1 Orde 2 Orde 3
2012 1 3941,69 � - - -
2 3985,21 � 4069,54 - -
3 4121,55 � 4101,45 4101,45 -
4 4180,73 � 4098,23 4179,73 4179,73
5 3832,82 � 3805,25 3805,25 3840,42
⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮
2015 37 5289,4 � 5304,97 5367,47 5367,47
38 5450,29 � 5429,99 5429,49 5492,49
39 5518,67 � 5429,99 5429,49 5429,49
(7) Menghitung dan membandingkan hasil peramalan IHSG dengan melihat nilai
RMSE. Perbandingan RMSE metode partisi interval pada runtun waktu fuzzy
dengan frekuensi densitas disajikan dalam Tabel 5.
Tabel 5. Hasil perhitungan RMSE untuk orde satu, dua, dan tiga
Orde RMSE
Data Pelatihan Data Pengujian
1 137,50 274,56
2 29,28 313,91
3 28,13 367,55
Tabel 4. menunjukkan bahwa pada orde satu data pengujian
menghasilkan RMSE lebih kecil dibandingkan orde dua dan tiga, maka metode
partisi interval dengan frekuensi densitas pada runtun waktu fuzzy orde satu
digunakan untuk menghitung nilai peramalan satu periode ke depan bulan
September 2015. Pada Gambar 2 terlihat bahwa nilai peramalan data pengujian
commit to user
8
Gambar 2. Perbandingan nilai aktual dengan nilai peramalan
6. KESIMPULAN
Berdasarkan hasil penelitian dan pembahasan, disimpulkan bahwa
penentuan konstanta K pada metode partisi interval runtun waktu fuzzy dengan
frekuensi densitas yang dikembangkan Jilani dan Burney (2008) mempengaruhi
peramalan IHSG. Orde satu pada data pengujian periode April sampai dengan
Agustus 2015 menghasilkan nilai peramalan yang lebih baik dibanding orde satu
dan tiga. Peramalan satu periode ke depan untuk bulan September 2015
menggunakan metode runtun waktu fuzzy dengan partisi interval berdasarkan
frekuensi densitas orde satu adalah , poin.
DAFTAR PUSTAKA
Hansun, S. 2012. Peramalan Data IHSG Menggunakan Fuzzy Time Series. IJJCS,
Vol. 6, pp: 79-88
Huarng, K. 2001. Effective Lengths of Intervals to Improve Forecasting in Fuzzy
Time Series, Fuzzy Sets and System, Vol. 123 , pp: 387-394
Huarng, K., and Yu, H. K. 2006. Ratio-Based Lengths on Intervals to Improve
Fuzzy Time Series Forecasting. IEEE Transactions on Systems, Man and
Cybernetics – Part B: Cybernetics, Vol.36, pp: 328-340
Jilani, T. A., and Burney. S. M. A. 2008. A refined fuzzy time-series model for stock
market forecasting. Physica A, Vol. 387, pp: 2857-2862
Jilani, T. A., Burney, S. M. A., and Ardil, C. 2010. Fuzzy metric approach for fuzzy
time series forecasting based on frequency dencity based partitionin.
International Journal of Computational Intelligence, Vol. 4, pp:39-44.
Pasaribu, P., Tobing, W. R. L., dan Manurung, A. H., 2008. Pengaruh Variabel
Makroekonomi Terhadap IHSG
Song, Q. and Chissom, B. S. 1993. Forecasting Enrollments with Fuzzy Time Series
part I. Fuzzy Sets and System, Vol. 54, pp: 1-9.
Song, Q. and Chissom, B. S. 1994. Forecasting Enrollments with Fuzzy Time Series
part II. Fuzzy Sets and System, Vol. 62, pp: 1-8.
0 1000 2000 3000 4000 5000 6000
IH
SG
BULAN
Data Sebenarnya