MODEL FUNGSI TRANSFER MULTIVARIAT
Skripsi
Disusun untuk melengkapi syarat-syarat
guna memperoleh gelar Sarjana Sains
ANTONI AHMAT
3125102334
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS NEGERI JAKARTA
PERAMALAN RUNTUN WAKTU MENGGUNAKAN MODEL FUNGSI TRANSFER MULTIVARIAT
Nama : Antoni Ahmat No. Registrasi : 3125102334
Nama Tanda Tangan Tanggal
Penanggung Jawab
Dekan : Prof. Dr. Suyono, M.Si. ... ... NIP. 19671218 199303 1 005
Wakil Penanggung Jawab
Pembantu Dekan I : Dr. Muktiningsih, M.Si ... ... NIP. 19600408 199003 2 002
Ketua : Drs. Sudarwanto, M.Si., DEA ... ... NIP. 19650325 199303 1 003
Sekretaris : Drs. Bambang Irawan, M.Si. ... ... NIP. 19681201 200112 1 001
Penguji : Dian Handayani, M.Si. ... ... NIP. 19740415 199803 2 001
Pembimbing I : Dra. Widyanti Rahayu, M.Si. ... ... NIP. 19661103 200112 2 001
Pembimbing II : Vera Maya Santi, M.Si. ... ... NIP. 19790531 200501 2 006
ANTONI AHMAT, 3125102334. Time Series Forecasting Using Multi-variate Transfer Function Model. Thesis. Faculty of Mathematics and Natural Sciences. State University of Jakarta. 2014.
This thesis discusses how to forecast time series data using multivariate transfer function model. Transfer function model is a combination of multiple regression analysis and time series of ARIMA characteristics. Meanwhile, mul-tivariate transfer function model is transfer function model that has more than two input variables of time series. This model is applied to obtain future forecast simultaneous. In this thesis, it will be discuss the procedure to build multivariate transfer function model and its application to forecast real time series data.
Keywords : transfer function model, multivariate, ARIMA, time series.
ANTONI AHMAT, 3125102334. Peramalan Runtun Waktu Menggu-nakan Model Fungsi Transfer Multivariat. Skripsi. Fakultas Matema-tika dan Ilmu Pengetahuan Alam, Universitas Negeri Jakarta. 2014.
Skripsi ini membahas bagaimana meramalkan data runtun waktu dengan model fungsi transfer multivariat. Model fungsi transfer adalah gabungan dari karakteristik analisis regresi berganda dengan karakteristik deret runtun waktu
ARIMA(Autoregressive Integrated Moving Average). Sementara itu model fungsi transfer multivariat merupakan model fungsi transfer yang memiliki variabelinput
lebih dari dua deret runtun waktu. Model ini dapat digunakan untuk menda-patkan ramalan ke depan secara simultan. Di dalam penulisan skripsi ini dije-laskan prosedur pembentukan model fungsi transfer multivariat dan aplikasinya untuk meramalkan data runtun waktu riil.
Kata kunci : model fungsi transfer, multivariat,ARIMA, runtun waktu.
”....Tetapi orang-orang yang ilmunya mendalam di antara mereka, dan orang-orang yang beriman, mereka beriman kepada (Al Qur’an) yang diturunkan
kepadamu (Muhammad) dan kepada (kitab-kitab) yang diturunkan sebelummu
begitu pula mereka yang melaksanakan shalat dan menunaikan zakat dan
beriman kepada Allah dan hari kemudian. Kepada mereka akan Kami berikan
pahala yang besar... ” (QS. Al Nisa’ : 162)
”...Lebih baik menjaga mulut Anda tetap tertutup dan membiarkan orang lain menganggap Anda bodoh daripada membuka mulut Anda
dan menegaskan semua anggapan mereka... ” (Mark Twain)
Skripsi ini kupersembahkan untuk.... kedua orangtuaku Mukrim dan Gusnidar, kakakku Widi Astuti, Hendri, dan adikku Firmanto serta keluarga besarku.
Puji syukur kepada Allah SWT atas pemberian pengetahuan dan kemam-puan sehingga penulis dapat menyelesaikan skripsi yang berjudul ”Peramalan Runtun Waktu Menggunakan Model Fungsi Transfer Multivariat” yang meru-pakan salah satu syarat dalam memperoleh gelar Sarjana Jurusan Matematika Universitas Negeri Jakarta.
Skripsi ini berhasil diselesaikan tak lepas dari bantuan dari berbagai pihak. Oleh karena itu, penulis ingin menyampaikan terima kasih kepada:
1. Dra. Widyanti Rahayu, M.Si. selaku Dosen Pembimbing I dan Vera Maya Santi, M. Si. selaku Dosen Pembimbing II yang telah meluangkan wak-tu, saran, nasehat, serta pengarahan dalam pengerjaan skripsi ini sehingga menjadi lebih baik. Terima kasih banyak bu dan mohon maaf atas segala kekuranganku, semoga kesehatan selalu tercurah kepada Ibu dan keluarga.
2. Drs. Makmuri, M.Si. selaku Ketua Jurusan Matematika FMIPA UNJ dan Ratna Widyanti, S.Si, M.Kom. selaku Ketua Prodi Matematika FMIPA UNJ. Terima kasih atas segala bantuan dan kerja sama Bapak dan Ibu selama masa pengerjaan skripsi ini.
3. Drs. Tri Murdiyanto selaku Pembimbing Akademik atas segala bimbin-gan dan kerja sama Bapak selama perkuliahan penulis dan seluruh Ba-pak/Ibu dosen Jurusan Matematika atas pengajaran yang telah diberikan, serta Mbak Esti dan karyawan/karyawati FMIPA UNJ lainnya atas infor-masi dan bantuan yang diberikan selama masa pengerjaan skripsi ini.
tidak akan mampu menyelesaikan skripsi ini tepat pada waktunya. Terima juga kepada saudara-saudaraku, terima kasih ya Uni, Hendri, Firman atas do’a dan dukungan selama ini.
5. Sahabat-sahabatku tercinta dari prodi Matematika 2010. Terima kasih ku-ucapkan pada Faiz atas persahabatannya selama ini. Terima atas bantuan dan dukungan tulus ikhlas yang telah diberikan selama ini. Terima kasih ju-ga ingin kuucapkan pada rekan sesama satu dosen pembimbingku, Mudita, Annisa dan Dina. Terima ya Mud atas dukungan dan bantuan selama ini. Untuk Anis, terima kasih atas saran dan masukan yang diberikan, dan teri-ma kasih untuk Dina yang memberikan seteri-mangat selateri-ma pengerjaan skripsi ini.
6. Buat Efri, terima kasih sudah menjadi penyelamat keuanganku dengan menyediakan jasa print murah selama penyusunan proposal skripsi hing-ga skripsi ini selesai dikerjakan. Makasih ya pi. Tak lupa juhing-ga kuucapkan terima kasih pada Sandi, Adi, Rayvin, Taufan, Saipulloh, Saget, Jefry dan Fajar atas dukungan, semangat serta persahabatan kalian selama ini. Se-moga persahabatan ini dapat terus terjalin.
7. Teruntuk teman-temanku, Mega, Diesty, Devi, Novilia, Delsi, Dwi, Riska, Arum, Sifa dan Rista, terima kasih atas dukungan serta persahabatan kalian selama ini. Semoga kita dapat tetap menjalin silaturahmi.
8. Kepada Mba Khrisna, terima kasih atas bantuan untuk mengolah data skrip-si saya. Serta tak lupa kepada semua pihak yang telah membantu baik secara
Penulis menyadari skripsi ini masih jauh dari sebuah kesempurnaan. Oleh karena itu masukan dan kritik yang membangun akan sangat berarti. Se-moga skripsi ini dapat bermanfaat bagi pembaca.
Jakarta, September 2014
Antoni Ahmat
KATA PENGANTAR iv
DAFTAR ISI ix
DAFTAR TABEL xi
DAFTAR GAMBAR xiii
I PENDAHULUAN 1
1.1 Latar Belakang Masalah . . . 1
1.2 Perumusan Masalah . . . 3
1.3 Pembatasan Masalah . . . 3
1.4 Tujuan Penulisan . . . 3
1.5 Manfaat Penulisan . . . 4
1.6 Metode Penelitian . . . 4
II LANDASAN TEORI 5 2.1 Pengertian Runtun Waktu . . . 5
2.2 ACF dan PACF . . . 6
2.2.1 ACF(Autocorrelation Function) . . . 6
2.2.2 PACF(Partial Autocorrelation Function) . . . 10
2.3 Proses White Noise . . . 14
2.4 Stasioneritas Data Runtun Waktu . . . 15
2.5 Autoregressive Integrated Moving Average (ARIMA) . . . 18
2.5.1 Model Autoregressive (AR) . . . 18
2.6 Seasonal Autoregressive Integrated Moving Average (SARIMA) . . 27
2.7 Pembentukan Model Runtun Waktu . . . 29
2.7.1 Identifikasi Model . . . 30
2.7.2 Estimasi Parameter dan Uji Hipotesis . . . 30
2.7.3 Uji Diagnostik Model . . . 31
III PEMBAHASAN 35 3.1 Konsep Fungsi Transfer . . . 35
3.2 Model Fungsi Transfer . . . 36
3.3 Prosedur untuk Menentukan Model Fungsi Transfer . . . 38
3.3.1 Identifikasi Bentuk Model Input Tunggal . . . 39
3.3.2 Estimasi Parameter Model Fungsi Transfer . . . 46
3.3.3 Uji Diagnostik Model Fungsi Transfer Input Tunggal . . . . 48
3.3.4 Penentuan Model Fungsi Transfer Multivariat . . . 50
3.4 Penerapan Model Fungsi Transfer pada Peramalan Data Riil . . . 52
3.4.1 Tahap Pertama: Identifikasi Bentuk ModelInput Tunggal . 54 3.4.2 Tahap Kedua: Estimasi Parameter Model Fungsi Transfer . 84 3.4.3 Tahap Ketiga: Uji Diagnostik Model Fungsi Transfer Input Tunggal . . . 86
3.4.4 Tahap Keempat: Pemodelan Fungsi Transfer Multivariat pa-da Curah Hujan . . . 91
3.4.5 Tahap Kelima: Penggunaan Model Fungsi Transfer Multi-variat untuk Peramalan . . . 97
4.2 Saran . . . 100
DAFTAR PUSTAKA 101
LAMPIRAN-LAMPIRAN 102
2.1 Data Sampel Runtun Waktu . . . 8
2.2 Nilai ACF . . . 9
2.3 Nilai PACF . . . 14
2.4 Transformasi Box-Cox . . . 18
3.1 Model Fungsi Transfer r= 0 . . . 44
3.2 Model Fungsi Transfer r= 1 . . . 45
3.3 Model Fungsi Transfer r= 2 . . . 45
3.4 Estimasi Parameter dan Uji Signifikansi ModelARIMAuntuk deret Tekanan Udara . . . 64
3.5 Uji Autokorelasi Residual Model ARIMA (0,0,2)(1,1,0)12 untuk Tekanan Udara . . . 65
3.6 Estimasi Parameter dan Uji Signifikansi ModelARIMAuntuk deret Kelembaban Udara . . . 66
3.7 Uji Autokorelasi Residual Model ARIMA (1,0,0)(0,1,0)12 untuk Kelembaban Udara . . . 67
3.8 Estimasi Parameter dan Uji Signifikansi ModelARIMAuntuk deret Kecepatan Angin . . . 68
3.9 Uji Autokorelasi Residual Model ARIMA (0,0,1)(0,1,0)12 untuk Kecepatan Angin . . . 69
3.10 Estimasi Parameter dan Uji Signifikansi ModelARIMAuntuk deret Suhu Udara . . . 70
3.12 Estimasi Parameter dan Uji Signifikansi ModelARIMAuntuk deret
Intensitas Matahari . . . 73
3.13 Uji Autokorelasi Residual Model ARIMA (1,0,0)(0,1,1)12 untuk Intensitas Matahari . . . 73
3.14 Bobot Respon Impuls yang Mengidentifikasikan Fungsi Transfer . 78 3.15 Estimasi Penentuan (r, s, b) . . . 79
3.16 Estimasi Parameter Deret Noise . . . 81
3.17 Uji Autokorelasi Residual Masing-masing Deret Noise . . . 83
3.18 Estimasi Parameter Variabel InputModel Fungsi Transfer . . . . 85
3.19 Uji Autokorelasi Residual pada Masing-masing Model Fungsi Transfer 87 3.20 Uji Korelasi Silang Residual pada Masing-masing Model Fungsi Transfer . . . 88
3.21 Estimasi Parameter Model Fungsi Transfer Multivariat . . . 93
3.22 Estimasi Parameter Setelah Variabel X4 Dikeluarkan . . . 94
3.23 Estimasi Parameter Setelah Variabel X5 Dikeluarkan . . . 94
3.24 Uji Autokorelasi Residual pada Model Fungsi Transfer Multivariat 95 3.25 Uji Korelasi Silang Residual pada Model Fungsi Transfer Multivariat 96 3.26 Hasil Ramalan Curah Hujan Dengan Model Fungsi Transfer Mul-tivariat . . . 97
2.1 Plot ACF dari Sampel Data Runtun Waktu . . . 9
2.2 Plot ACF dan PACF dari suatu proses white noiseZt=µ+at . . 15
2.3 Plot ACF dan PACF ModelAR(1) . . . 20
2.4 Plot ACF dan PACF ModelAR(2) . . . 21
2.5 Plot ACF dan PACF ModelMA(1) . . . 22
2.6 Plot ACF dan PACF ModelMA(2) . . . 23
2.7 Plot ACF dan PACF ModelARMA(1,1) . . . 25
2.8 Plot Data dan Plot ACF Runtun Waktu Musiman . . . 29
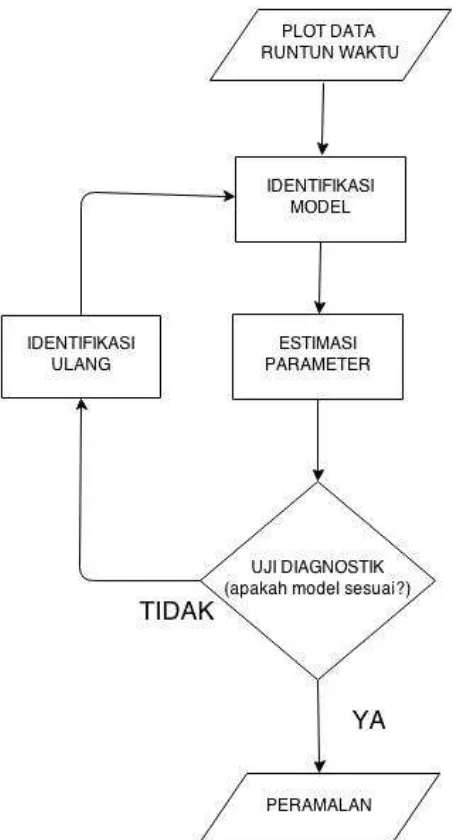
2.9 Diagram Alir Langkah-langkah Pemodelan Runtun Waktu . . . . 34
3.1 Konsep Model Fungsi Transfer . . . 35
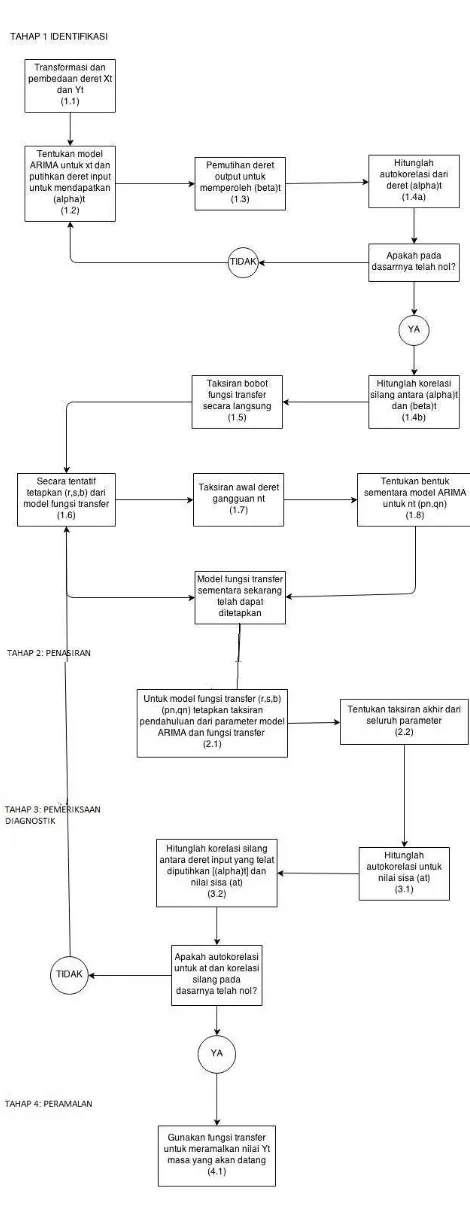
3.2 Diagram Alir Pembentukan Model Fungsi Transfer . . . 53
3.3 Plot Runtun Waktu Data Curah Hujan . . . 54
3.4 Plot ACF dan PACF Data Curah . . . 54
3.5 Plot Transformasi Box Cox Data Curah Hujan . . . 55
3.6 Plot ACF dan PACF Data Curah Hujan Setelah Dilakukan Pem-beda 12 . . . 56
3.7 Plot Runtun Waktu Data Tekanan Udara . . . 56
3.8 Plot ACF dan PACF Data Tekanan Udara . . . 57
3.9 PlotACFdanPACFData Tekanan Udara Setelah Dilakukan Pem-beda 12 . . . 57
3.10 Plot Runtun Waktu Data Kelembaban Udara . . . 58
3.11 Plot ACF dan PACF Data Kelembaban Udara . . . 58
3.13 Plot Runtun Waktu Data Kecepatan Angin . . . 59 3.14 Plot ACF dan PACF Data Kecepatan Angin . . . 60 3.15 Plot ACF dan PACF Data Kecepatan Angin Setelah Dilakukan
Pembeda 12 . . . 60 3.16 Plot Runtun Waktu Data Suhu Udara . . . 61 3.17 Plot ACF dan PACF Data Suhu Udara . . . 61 3.18 PlotACFdanPACFData Suhu Udara Setelah Dilakukan Pembeda
12 . . . 62 3.19 Plot Runtun Waktu Data Intensitas Matahari . . . 62 3.20 Plot ACF dan PACF Data intensitas Matahari . . . 63 3.21 Plot ACF dan PACF Data Intensitas Matahari Setelah Dilakukan
Pembeda 12 . . . 63 3.22 Hasil Ramalan Curah Hujan kota Palembang Periode 2013-2014 . 98
PENDAHULUAN
1.1
Latar Belakang Masalah
Peramalan merupakan suatu cara untuk memprediksi apa yang akan ter-jadi di masa depan. Dengan melakukan peramalan diharapkan suatu keputusan dapat dibuat lebih efektif dan efisien. Ada beberapa cara yang dapat dilakukan untuk meramalkan suatu kemungkinan, salah satunya dengan analisis runtun wak-tu. Analisis runtun waktu merupakan peramalan yang didasarkan pada data kuantitatif di masa lampau. Pada dasarnya, analisis data runtun waktu digu-nakan untuk melakukan analisis data yang mempertimbangkan pengaruh waktu. Data yang dikumpulkan secara periodik berdasarkan urutan waktu seperti hari, minggu, bulan, tahun dan seterusnya dapat dianalisis dengan menggunakan ana-lisis runtun waktu.
Analisis data runtun waktu juga dapat diterapkan pada tipe data satu variabel (univariate) maupun banyak variabel (multivariate) (Makridakis, dkk: 1993). Salah satu model yang sangat penting dan sering digunakan dalam anali-sis runtun waktu univariat adalah model ARIMA (Autoregressive Integrated Mo-ving Average). ModelARIMA cukup fleksibel diterapkan untuk beberapa runtun waktu seperti AR (autoregressive), MA (moving average), dan gabungan kedua nya (ARMA).
Pada dasarnya peramalan data runtun waktu adalah analisis data
variat. Namun dalam kenyataannya sebagian besar pengamatan merupakan data multivariat (lebih dari satu variabel). Misalkan di bidang pemasaran, volume pen-jualan bergantung pada cara pemasaran, bentuk promosi dan daerah pemasaran dimana faktor-faktor tersebut lebih dari satu variabel. Jika analisis peramalan hanya didasarkan pada volume penjualan saja tanpa memperhatikan faktor-faktor yang mempengaruhinya maka informasi untuk pembuatan perencanaan menjadi tidak lengkap, sehingga tujuan peramalan menjadi tidak tercapai secara utuh. Oleh karena itu, diperlukan model-model multivariat untuk memodelkan jenis da-ta tersebut agar diperoleh hasil yang dapat memberikan informasi yang lengkap dan simultan.
Model ARIMA tidak dapat digunakan untuk data multivariat (Makri-dakis, dkk., 1993). Beberapa model untuk penerapan data multivariat diantaranya: model fungsi transfer, analisis intervensi, analisis fourier, analisis spektral, dan model runtun waktu vektor (Wei, 2005). Model fungsi transfer adalah model runtun waktu yang menggambarkan bahwa nilai prediksi masa depan dari suatu runtun waktu yang disebut deret output atau Yt adalah berdasarkan pada nilai-nilai masa lalu dari data runtun waktu itu sendiri dan berdasarkan pula pada satu atau lebih data runtun waktu yang berhubungan dengan deret output yang disebut dengan deret input atau Xt. Selain itu model fungsi transfer menjadi salah satu model runtun waktu yang banyak diterapkan dalam berbagai bidang seperti mekanika, ekonomi dan ilmu manajemen (Liu, 1982).
Model fungsi transfer merupakan pengembangan dari modelARIMA uni-variat. Jika deret runtun waktuYtberhubungan dengan satu atau lebih deret run-tun waktuXtmaka dapat dibuat suatu model berdasarkan informasi deret berkala
dise-but regresi dinamis dengan pendekatan deret waktu (Fathurahman, 2009). Model fungsi transfer multivariat sendiri merupakan gabungan dari analisis regresi lini-er blini-erganda dengan analisis runtun waktu (ARIMA) yang mempertimbangkan pengaruh waktu.
Dalam skripsi ini, penulis ingin mengkaji model peramalan dengan meng-gunakan model fungsi transfer. Dalam hal ini, penulis ingin mengkaji penggunaan model fungsi transfer multivariat. Dengan penggunaan fungsi transfer multivari-at, berbagai faktor-faktor yang menjadi variabel dapat dianalisis sehingga mampu menghasilkan ramalan yang utuh dan akurat.
1.2
Perumusan Masalah
Perumusan masalah yang akan dikaji adalah bagaimana prosedur untuk menentukan model peramalan data runtun waktu multivariat?
1.3
Pembatasan Masalah
Pembatasan masalah dalam skripsi ini adalah:
1. Model yang digunakan untuk peramalan runtun waktu multivariat adalah model fungsi transfer.
2. Data yang digunakan untuk simulasi model adalah data dengan pola musi-man.
1.4
Tujuan Penulisan
1. Mengkaji sifat-sifat statistik model fungsi transfer.
2. Mengkaji model fungsi transfer untuk peramalan data runtun waktu multi-variat.
3. Mengaplikasikan model fungsi transfer pada data riil.
1.5
Manfaat Penulisan
Manfaat yang diharapkan dari skripsi ini adalah dapat memberikan gam-baran mengenai penentuan model peramalan data runtun waktu menggunakan model fungsi transfer multivariat dan contoh penerapannya dalam kehidupan nya-ta.
1.6
Metode Penelitian
LANDASAN TEORI
2.1
Pengertian Runtun Waktu
Runtun waktu adalah himpunan data hasil observasi yang terkumpul dan disusun berdasarkan waktu. Pada analisis data runtun waktu terdapat empat macam pola data, yaitu:
1. Pola Trend: pola yang menggambarkan gerak data runtun waktu dalam jangka waktu yang panjang. Pola ini mencerminkan sifat kontinuitas sela-ma jangka waktu tertentu. Akibat sifat kontinuitas ini, sela-makatrenddianggap pola yang stabil dan menunjukkan arah perkembangan secara umum (ke-cenderungan menaik/menurun).
2. Pola Siklis: pola jangka panjang di sekitar polatrend namun dengan tempo yang lebih pendek. Pola siklis terjadi berulang-ulang namun tidak perlu periodik
3. Pola Musiman: pola yang terjadi lebih teratur dibandingkan pola siklis dan bersifat lengkap dan memiliki pola yang tetap dari waktu ke waktu. Faktor yang menyebabkan pola ini adalah iklim dan kebiasaan.
4. Pola Ireguler (Tidak Teratur): pola ini bersifat sporadis dan sulis dikuasai. Faktor yang mempengaruhi pola ini adalah perang, bencana alam dll.
Data musiman merupakan gerakan suatu data deret runtun waktu yang diklasifikasikan ke dalam periode kurang dari satu tahun seperti kwartalan, bu-lanan, mingguan atau harian dengan periode yang berulang.
Dalam kehidupan nyata, tidak mudah untuk mengetahui pola data secara langsung. Oleh karena itu, perlu dilakukan identifikasi terlebih dahulu untuk mengetahui pola data sebelum dilakukan perhitungan. Metode paling sederhana untuk mengidentifikasi pola suatu data adalah dengan melihat pola yang ada pada plot data runtun waktu.
Dalam skripsi ini pola data yang digunakan adalah pola musiman. Pola musiman memiliki kelebihan yakni mudah diklasifikasikan dalam dua bentuk yakni spesifik dan tipikal. Pola musiman spesifik menunjukkan pola musiman dalam suatu periode seperti bulanan, mingguan atau harian. Sementara pola musiman tipikal menunjukkan rata-rata pola musiman dalam sejumlah periode seperti lima tahunan, sepuluh tahunan dan seterusnya.
2.2
ACF dan PACF
2.2.1
ACF(Autocorrelation Function)
Himpunan data runtun waktu Z1, Z2, ..., Zt yang dianggap sebagai vari-abel acak Zt diasumsikan mempunyai fungsi kepadatan probabilitas bersama
f(Z1, Z2, ..., Zt). Jika struktur probabilitas fkp tidak berubah oleh adanya
Data runtun waktu Zt yang stasioner akan mempunyai nilai rata-rata konstan
E(Zt) = µdan varian konstan E(Zt−µ)2 =σ2. Fungsi autokovariansi antara Zt dan Zt+k adalah
γk =Cov(Zt, Zt+k) = E[(Zt−µ)(Zt+k−µ)] (2.1) Autokorelasi merupakan korelasi atau hubungan antar data pengamatan suatu data runtun waktu. Untuk menghitung autokorelasi antara Zt dan Zt+k adalah
ρk dinamakan fungsi autokorelasi (ACF). Dalam praktiknya ρk tidak diketahui dan dapat diperkirakan dengan ˆρkyang merupakan koefisien korelasi pada sampel dengan rumus
ρk = koefisien autokorelasi
Zt = nilai variabel Z pada periode t
Zt+k = nilai variabel Z pada periode t+k ¯
Z = nilai rata-rata variabel Z
Untuk mengetahui apakah koefisien autokorelasi yang diperoleh signifikan atau tidak, diperlukan pengujian dengan hipotesis (Wei, 2005)
H1 :ρk6= 0 (koefisien autokorelasi signifikan) Statistik uji yang digunakan adalah
t = ρˆk
SE(ˆρk) = standar error untuk autokorelasi pada lag ke-K ˆ
ρi = autokorelasi pada lagi ke-i
k = selisih waktu
n = banyaknya observasi dalam deret waktu Kriteria keputusan H0 ditolak apabila
t <−tα/
2,n−1 atau t > tα/2,n−1
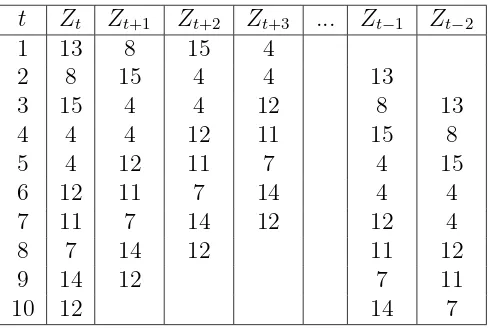
Contoh 2.2.1. Untuk mengilustrasikan perhitungan sampelACF, perhatikanlah sepuluh nilai runtun waktu berikut:
t Zt Zt+1 Zt+2 Zt+3 ... Zt−1 Zt−2
Tabel 2.1: Data Sampel Runtun Waktu
sebagai berikut:
ˆ
ρ1 =
(13−10)(8−10) + (8−10)(15−10) +...+ (14−10)(12−10) (13−10)2+ (8−10)2+...+ (14−10)2+ (12−10)2
= −27
144 =−0,188 ˆ
ρ2 =
(13−10)(15−10) + (8−10)(4−10) +...+ (7−10)(12−10) (13−10)2+ (8−10)2+...+ (14−10)2+ (12−10)2
= −29
144 =−0,201 ˆ
ρ3 =
(13−10)(4−10) + (8−10)(4−10) +...+ (11−10)(12−10) (13−10)2+ (8−10)2+...+ (14−10)2+ (12−10)2
= 26
144 = 0,181
Berikut adalah gambar plot ACF dari data runtun waktu diatas:
Gambar 2.1: PlotACF dari Sampel Data Runtun Waktu
Lag ACF t
1 -0,18750 -0,59 2 -0,201389 -0,62 3 0,180556 0,53
Berdasarkan gambar (2.1) terlihat bahwa tiap lag berada di antara garis signifikan. Dengan membandingkan nilai tiap thit dengan ttab = tα
2,n−1 = 2,26 makathit < ttab sehinggaH0 diterima yang berarti koefisien-koefisien autokorelasi
tidak signifikan.
2.2.2
PACF(Partial Autocorrelation Function)
Partial Autocorrelationadalah tingkat keeratan hubungan antaraZtdan
Zt+ksetelah hubungan linier dengan variabelZt+1, Zt+2, ..., Zt+k−1dipisahkan.
Se-mentara koefisien dari autokorelasi parsial digunakan untuk mengukur derajat hubungan antara nilai-nilai sekarang dengan nilai-nilai sebelumnya dengan pen-garuh nilai variabel waktu lag yang lain dianggap konstan. Fungsi autokorelasi parsial dapat dinyatakan sebagai berikut: (Wei, 2005)
φkk=Corr(Zt, Zt+k|Zt+1, Zt+2, ..., Zt+k−1) (2.4)
Autokorelasi parsial diperoleh melalui model regresi dimana variabel tak bebas
Zt+k dari proses yang stasioner diregresikan pada variabel Zt+k−1, Zt+k−2, ..., Zt berlag k, sebagai berikut:
Zt+k−j(Zt+k) = Zt+k−j(φk1Zt+k−1) +Zt+k−j(φk2Zt+k−2) +...+Zt+k−j(φkkZt+1)
+ Zt+k−j(at+k)
Zt+k−j.Zt+k = Zt+k−1(φk1Zt+k−1) +Zt+k−2(φk2Zt+k−2) +...+Zt+k(φkkZt+1)
+ Zt+k+1(at+k)
E(Zt+k−j.Zt+k) = φk1E(Zt+k−1.Zt+k−1) +φk2E(Zt+k−2.Zt+k−2) +...
+ φkkE(Zt+k.Zt+1) +E(Zt+k+1at+k)
γj = φk1γj−1 +φk2γj−2) +...+φkkγj−1) (2.6)
Akibat persamaan (2.6) maka berdasarkan persamaan (2.2) dan dimisalkanγ0 = 1
diperoleh
ρj =φk1ρj−1+φk2ρj−2+...+φkkρj−kuntukj= 1,2, ..., k (2.7)
Sehingga didapat persamaan berikut:
ρ1 = φk1ρ0+φk2ρ1+...+φkkρk−1
ρ2 = φk1ρ1+φk2ρ0+...+φkkρk−2
...
ρk = φk1ρk−1+φk2ρk−2+...+φkkρ0
dimana ρ0 = 1. Dengan menggunakan aturan Cramer pada persamaan diatas,
φ11 = ρ1
Berdasarkan persamaan (2.3) dan contoh (2.2.1) dapat ditentukan bahwa nilai ρk untuk k = 1,2, ... adalah −1 < ρk < 1. Dengan denikian determinasi pada per-samaan (2.8) dapat dicari determinannya. Walaupun perhitungan determinasinya terlihat rumit namun persamaan (2.8) tetap dapat digunakan karena determinan-nya tidak akan nol. Sama haldeterminan-nya denganρknilai φkk tidak mudah untuk dihitung apalagi dengan determinan serumit itu. Oleh karena itu metode rekursif untuk menghitungφkktelah diberikan oleh Durbin (1960) yang dimulai dengan ˆφ11= ˆφ1
yaitu: Contoh 2.2.2. Dengan menggunakan data di Contoh 2.2.1 akan dihitung nilai dari ˆφ11,φˆ22 dan ˆφ33 sebagai berikut:
Berdasarkan nilaiPACFdan membandingkan nilai tiapthit denganttab =
tα
Lag PACF t
1 -0,18750 -0,59 2 -0,245164 -0,78 3 0,096564 0,31
Tabel 2.3: Nilai PACF
2.3
Proses
White Noise
Menurut Wei (2005) suatu proses at disebut proses white noise jika at merupakan barisan variabel acak yang tidak berkorelasi dari suatu distribusi den-gan rata-rata E(at) = µ0 yang biasa diasumsikan nol, variansi V ar(at) = σ2a dan γk = Cov(at, at+k) = 0 untuk semua k 6= 0. Oleh karena itu, suatu proses
white noise at adalah stasioner dengan fungsi autokovarian
γk = dan fungsi autokorelasi parsial
φkk =
Grafik ACF dan PACF untuk suatu proses white noise ditunjukkan pa-da gambar (2.2). Berpa-dasarkan gambar (2.2) pa-dapat disimpulkan bahwa proses
Gambar 2.2: Plot ACF dan PACF dari suatu proses white noiseZt=µ+at
2.4
Stasioneritas Data Runtun Waktu
Menurut Makridakis dkk. (1993) stasioneritas mempunyai makna bahwa tidak terdapat pertumbuhan atau penurunan pada data. Dengan kata lain, fluk-tuasi data berada di sekitar suatu nilai rata-rata yang konstan, tidak bergantung pada waktu dan variansi dari fluktuasi tersebut.
Data runtun waktu dikatakan stasioner dalam rata-rata jika rata-ratanya tidak mengalami perubahan dari waktu ke waktu (stabil). Untuk melihat apakah suatu data sudah stasioner dalam rata-rata dapat dilihat dari plot data run-tun waktu dan plot ACF. Apabila suatu data runtun waktu tidak stasioner secara rata-rata maka dapat diatasi dengan melakukan pembeda (differencing).
Differencing merupakan pengurangan data tertentu dengan data sebelumnya. Ji-ka differencing orde satu masih belum menghasilkan data yang stasioner, maka dapat dilakukan differencing orde kedua dan seterusnya hingga diperoleh data yang stasioner.
Notasi yang sangat dibutuhkan dalam metode pembeda adalah operator
adalah sebagai berikut:(Makridakis dkk., 1993)
BZt=Zt−1 (2.11)
Notasi B yang dipasangkan pada Zt mempunyai pengaruh menggeser data satu periode ke belakang. Dua penempatan B untuk Zt akan menggeser data dua periode ke belakang sebagai berikut:
B(BZt) = B2Zt =Zt−2
Apabila data runtun waktu belum stasioner, maka data tersebut dapat dibuat stasioner dengan melakukan pembedaan pertama dari deret data dengan persamaan sebagai berikut:
Zt′ =Zt−Zt−1 (2.12)
Dengan menggunakan operatorshiftmundur pada persamaan (2.12) da-pat ditulis kembali menjadi
Zt′ =Zt−BZt = (1−B)Zt (2.13)
Pembedaan pertama dinyatakan oleh (1−B). Sama halnya apabila pembedaan orde kedua (yaitu pembedaan pertama dari pembedaan pertama sebelumnya) harus dihitung, maka
Zt′′ = Zt′ −Zt′−1
= (Zt−2Zt−1−Zt−2)
= (1−2B−B2)Zt = (1−B)2Zt
Pembedaan orde kedua diberi notasi (1−B)2. Secara umum apabila terdapat
pembeda orde ke-d untuk memcapai stasioneritas dapat ditulis sebagai berikut:
Ztd= (1−B)dZt (2.14)
Suatu data runtun waktu stasioner dalam variansi, jika plot data runtun waktunya tidak memperlihatkan adanya perubahan variansi yang signifikan dari waktu ke waktu (Makridakis, 1993). Sama seperti stasioner berdasarkan rata-rata, untuk melihat data runtun waktu sudah stasioner dalam variansi atau belum dapat menggunakan plot data runtun waktu dan plot ACF.
Untuk menstasionerkan data dalam variansi dapat dilakukan dengan proses transformasi. Secara umum, untuk mencapai stasioneritas dalam varian-si dapat dilakukan dengan power transformation (λ) dimana λ adalah parameter transformasi. Secara umum berikut ini nilai dari λ beserta pendekatan transfor-masi yang digunakan yaitu: (Wei, 2005)
T(Zt) =
Zλ t−1
λ , λ6= 0 lnZt, λ= 0
Nilaiλ Estimasi Transformasi
-1 Z1
t
-0,5 √1
Zt
0 lnZt
0,5 √Zt
1 Zt (stasioner)
Tabel 2.4: Transformasi Box-Cox
2.5
Autoregressive Integrated Moving Average
(ARIMA)
Autoregressive Integrated Moving Average (ARIMA) sering disebut juga metode Box-Jenkins. Sedangkan model ARIMA merupakan model yang secara penuh mengabaikan variabel bebas dalam membuat peramalan. ARIMA meng-gunakan nilai masa lalu dan sekarang dari variabel tak bebas untuk menghasilkan peramalan jangka pendek yang akurat. Model ARIMA dibagi dalam tiga kelom-pok yaitu modelautoregressive (AR), modelmoving averge (MA)dan model cam-puran ARMAyang mempunyai karakteristik dari dua model pertama.
2.5.1 Model
Autoregressive (AR)
AR dengan orde ke-pAR(p) dinyatakan sebagai berikut:(Wei, 2005)
Zt =φ1Zt−1+φ2Zt−2+...+φpZt−p+at (2.16) dimana
φp = parameter autoregresif
at = nilai kesalahan pada saat t
Dua kasus yang sering dihadapi apabila p = 1 dan p = 2 yaitu berturut-turut untuk modelAR(1)danAR(2). Dua kasus ini dapat ditulis persamaannya sebagai berikut:
AR(1) atau ARIMA(1,0,0)
Zt=φ1Zt−1+at (2.17) Dengan menggunakan operator shift mundur B, persamaan (2.17) dapat ditulis kembali menjadi:
Zt−φ1Zt−1 =at
atau
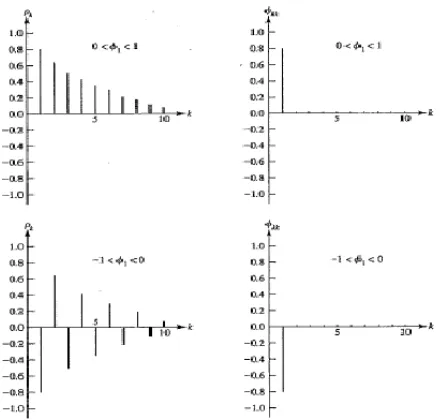
Gambar 2.3: Plot ACFdan PACF Model AR(1)
AR(2) atau ARIMA(2,0,0)
Zt=φ1Zt−1+φ2Zt−2 +at (2.19) Dengan menggunakan operator shift mundur B, persamaan (2.19) dapat ditulis kembali menjadi:
Zt−φ1Zt−1−φ2Zt−2 =at atau
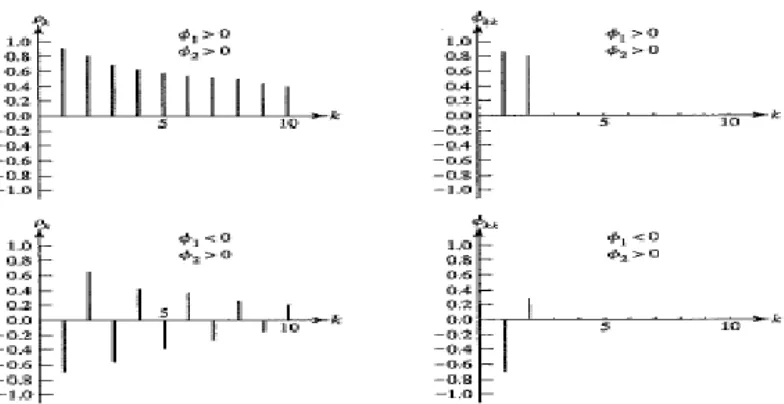
Gambar 2.4: Plot ACFdan PACF Model AR(2)
2.5.2 Model
Moving Average (MA)
Moving Averageadalah rata-rata bergerak yang berarti bahwa nilai run-tun waktu pada waktu t dipengaruhi oleh unsur kesalahan pada saat ini dan mungkin unsur kesalahan pada masa lalu. Suatu data runtun waktu dikatakan sebagai model MA, jika lag-lag pada plot PACF menurun mendekati nol secara eksponensial dan banyaknya lag yang berbeda signifikan dengan nol padaACF di-gunakan sebagai indikasi parameterq. Bentuk umum model MAorde ke-qMA(q)
atau ARIMA(0,0,q) dapat dinyatakan sebagai berikut: (Wei, 2005)
Zt=at−θ1at−1−θ2at−2−...−θqat−q (2.21) dimana
θq = parametermoving average
Dalam praktiknya, dua kasus yang sering dihadapi adalah apabila q= 1 dan q = 2 yaitu berturut-turut untuk model MA(1) dan MA(2). Persamaan untuk dua kasus ini dapat dinyatakan persamaannya sebagai berikut:
MA(1) atau ARIMA(0,0,1)
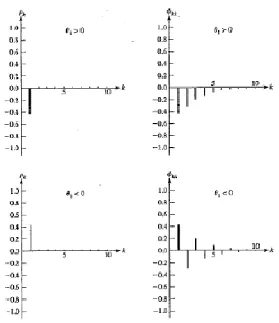
Zt= (1−θ1B)at (2.22) Berikut dibawah ini adalah bentuk plot ACF dan PACF untuk model
MA(1) (Wei, 2005)
Gambar 2.5 menunjukkan bahwa pada kedua plot ACF signifikan pa-da lag pertama pa-dan plot-plot PACF menurun mendekati nol secara eksponensial sehingga orde untuk MA(q) adalah 1.
MA(2) atau ARIMA(0,0,2)
Zt = (1−θ1B−θ2B2)at (2.23) Berikut adalah bentuk plotACF dan PACF model MA(2) (Wei, 2005)
Gambar 2.6: Plot ACF dan PACF ModelMA(2)
dan plot-plot pada PACF menurun mendekati nol secara eksponensial walaupun pergerakannya berbeda-beda sehingga orde untukMA(q) adalah 2.
2.5.3 Model Campuran
Autoregressive Moving Average
(ARMA)
Suatu perluasan yang diperoleh dari model AR dan MA adalah model campuran ARMA. Bentuk umum untuk model campuran ARMA(p,q) dapat di-tulis sebagai berikut:
Zt =φ1Zt−1+φ2Zt−2+...+φpZt−p+at−θ1at−1−θ2at−2−...−θqat−q
Zt−φ1Zt−1−φ2Zt−2−...−φpZt−p =at−θ1at−1−θ2at−2−...−θqat−q
(1−φ1B−φ2B2−...−φpBp)Zt= (1−θ1B−θ2B2−...−θqBq)at dengan
φp(B) = (1−φ1B−φ2B2−...−φpBp)
θq(B) = (1−θ1B −θ2B2−...−θqBq)
Maka model tersebut dapat ditulis sebagai berikut:
φp(B)Zt=θq(B)at (2.24)
Persamaan untuk kasus yang paling sederhana dari proses AR(1) murni dan
ARMA(1,1) atau ARIMA(1,0,1)
Zt = φ1Zt−1+at−θ1at−1
Zt−φ1Zt−1 = at−θ1at−1
(1−φ1B)Zt = (1−θ1B)at
Berikut adalah bentuk plotACF dan PACF model ARMA(1,1) (Wei, 2005)
Gambar 2.7: PlotACF dan PACF ModelARMA(1,1)
Apabila data tidak stasioner (nonstasioneritas), maka pada modelARMA
menjadi model umum ARIMA(p,d,q). Jika dilakukan proses pembedaan deng-an orde ke-d yakni Zd
run-tun waktu yang stasioner. Maka model ARMA(p,q) pada Zt dinamakan model
ARIMA(p,d,q). Suatu prosesARIMAdapat digambarkan dengan dimensi(p,d,q)
dengan:
AR:p= orde dari proses autoregresif
I:d = tingkat perbedaandegree of differencing MA:q = orde dari prosesmoving average
Bentuk umum model ARIMA(p,d,q) adalah sebagai berikut:
φp(B)(1−B)dZt=θq(B)at (2.25)
dengan operator AR(p) dinyatakan dalam bentuk polinomial
φp(B) = (1−φ1B−φ2B2−...−φpBp) dan operator MA(q) adalah
θq(B) = (1−θ1B−θ2B2−...−θqBq)
Parameter d menunjukkan bahwa proses tidak stasioner. Jadi bila parameter
d = 0 maka proses telah stasioner. Namun dalam praktiknya, jarang ditemukan pemakaian nilai p, d, q selain 0, 1, 2. Persamaan kasus paling sederhana dari
ARIMA(1,1,1) adalah sebagai berikut:
2.6
Seasonal Autoregressive Integrated Moving
Average (SARIMA)
Runtun waktu musiman merupakan runtun waktu yang memiliki sifat berulang setelah beberapa periode waktu tertentu, misalnya satu tahun, satu triwulan, satu bulan, dan seterusnya. Sebagai ilustrasi, penjualan es krim di negara-negara Eropa meningkat saat musim panas yakni bulan Juni hingga Agus-tus (triwulan). Kemudian penjualan bendera Merah Putih di Indonesia meningkat setiap bulan Aguatus. Pada contoh pertama, periode deret musimannya adalah 4 sedangkan contoh kedua adalah 12. Pola musiman biasanya dipengaruhi oleh cuaca dan kebiasaan yang berdampak terhadap aktivitas sehari-hari serta dalam pengambilan keputusan.
Pada umumnya komponen musiman diasumsikan bersifat deterministik dan bebas dengan komponen nonmusiman. Namun dalam kenyataannya, kom-ponen musiman seringkali bersifat stokastik dan berkorelasi dengan komkom-ponen nonmusiman. Sebagai contoh, diberikan data tingkat pengangguran suatu negara dalam periode tertentu (tahun). Andaikan akan dilakukan peramalan tingkat pengangguran di bulan ke 7 pada periode selanjutnya. Data pengangguran terse-but mengindikasikan bahwa adanya korelasi antar data, tidak hanya data antar satu bulan dengan bulan lainnya dalam satu tahun tetapi juga korelasi antar satu tahun dengan tahun lainnya. Dengan demikian, untuk meramalkan data pen-gangguran di bulan ke 7, tidak hanya melihat data di bulan ke 5 atau 6 di periode tersebut namun juga harus dilihat data bulan ke 7 pada periode sebelumnya.
sepanjangZt−2s, Zt−s, Zt, Zt+s, Zt+2s, .... Andaikan suatu deret Zt tidak diketahui apakah mengandung periode antara variasi musiman dan membentuk ARIMA
nonmusiman sebagai berikut:
φp(B)(1−B)dZt=θq(B)bt (2.27)
Dari persamaan (2.28) jelas bahwabt tidak memenuhi syaratwhite noise karena mengandung korelasi periode antara yang tidak diketahui. Misalkan
ρj(s)=
E(bt−js−µb)(bt−µb)
σ2
b
(2.28)
adalah fungsi autokorelasi untuk bt yang menjelaskan hubungan periode antara yang tidak diketahui. Dari persamaan (2.29) dapat direpresentasikan modelARIMA
sebagai berikut:
ΦP(Bs)(1−Bs)Dbt= ΘQ(Bs)at (2.29)
dimana
ΦP(Bs) = 1−Φ1(Bs)−Φ2(B2s)−...−ΦP(BPs)
ΘQ(Bs) = 1−Θ1(Bs)−Θ2(B2s)−...−ΘQ(BQs)
adalah persamaan polinomial dalam Bs dan a
t adalah suatu proses white noise dengan rataan nol. Dengan menggabungkan persamaan (2.28) dan (2.30) diper-oleh model SARIMA yang dnotasikan dengan ARIMA(p,d,q)x(P, D, Q)s sebagai berikut:
dimana
˙
Zt=
Zt−µ jika d=D= 0
Zt lainnya dengan
φp(B) = (1−φ1B−φ2B2−....−φpBp) , parameter AR nonseasonal ΦP(BS) = (1−Φ
1BS−Φ2B2S−....−ΦPBP S) , parameter AR seasonal
θq(B) = (1−θ1B −θ2B2−....−θqBq) , parameter MA nonseasonal ΘQ(BS) = (1−Θ
1BS−Φ2B2S−....−ΘqBQS) , parameter MA seasonal
s = banyaknya periode per musim.
Berikut adalah contoh gambar plot data runtun waktu dan plot ACF
yang memiliki pola musiman.
Gambar 2.8: Plot Data dan Plot ACFRuntun Waktu Musiman
2.7
Pembentukan Model Runtun Waktu
2.7.1 Identifikasi Model
Tahap-tahap yang harus dilakukan dalam mengidentifikasikan model adalah sebagai berikut:
1. Menganalisis data runtun waktu dengan membuat plot datanya. Hal ini berguna untuk mengetahui ada tidaknya pengaruh trend ataupun musiman pada data.
2. Menganalisis koefisien autokorelasi dan autokorelasi parsialnya untuk menge-tahui kestasioneran datanya, sehingga dapat dikemenge-tahui perlu tidaknya di-lakukan pembedaan dan transformasi.
3. Dari plot koefisien autokorelasi dan autokorelasi parsial tersebut dapat di-identifikasikan orde untuk model ARIMA nya.
2.7.2 Estimasi Parameter dan Uji Hipotesis
Menurut Makridakis (1993) dalam mendapatkan penaksiran para- meter ada dua cara yang mendasar yaitu:
1. Dengan cara mencoba-coba, yaitu menguji beberapa nilai dari parameter
AR (φ) dan parameter MA (θ) yang berbeda dan memilih satu nilai terse-but (atau lebih apabila lebih dari satu parameter yang akan ditaksir) yang meminimumkan kuadrat nilai sisa.
2. Perbaikan secara iteratif dengan memilih taksiran awal dan menggunakan program komputer untuk memperhalus penaksiran secara iteratif.
model dengan uji hipotesis sebagai berikut:
Autoregressive (AR)
H0 :φi = 0, dimana i= 1,2, ..., k (AR tidak signifikan dalam model)
H1 :φi 6= 0, (AR signifikan dalam model)
Statistik uji yang digunakan adalah sebagai berikut:
thitungAR= ˆ
φk
SE( ˆφk) (2.31)
Moving Average (MA)
H0 :θi = 0, dimanai= 1,2, ..., k (MA tidak signifikan dalam model)
H1 :θi 6= 0, (MAsignifikan dalam model)
Statistik uji yang digunakan adalah sebagai berikut:
thitungM A= ˆ
θk
SE(ˆθk) (2.32)
dengan ˆφk adalah estimator dari φk dan ˆθk adalah estimator dari θk. Kriteria keputusan untuk menolak H0 adalah jika |t| > tα/2,df, df = n−np dengan np adalah banyaknya parameter dan n banyaknya pengamatan atau tolak H0 jika
p-value<0,05
2.7.3 Uji Diagnostik Model
H0 :ρk= 0 (memenuhi syarat white noise)
H1 :ρk6= 0 (tidak memenuhi syarat white noise)
dengan menggunakan statistik uji Ljung-Box (Wei, 2005)
Q=n(n+ 2)
n = banyaknya observasi dalam runtun waktu
k = lag waktu
m = banyaknya lag yang diuji ˆ
ρk = koefisien autokorelasi pada periode ke-k
Namun karena uji hipotesis ini masih dilakukan pada model penduga maka derajat bebas yang digunakan adalah (k −m) dimana m = p+q (p dan
q adalah parameter dari model penduga). Jika ternyata model estimasi yang didapat tidak sesuai (nilai residualnya tidak memenuhi syarat white noise) maka perlu dilakukan identifikasi ulang.
Tahap selanjutnya adalah pemilihan model jika terdapat dua atau lebih model runtun waktu. Tujuannya adalah untuk memilih model mana yang layak digunakan dalam peramalan. Salah satu pendekatan yang dapat digunakan adalah pendekatanAIC (Akaike’s Information Criterion). Semakin kecil nilaiAIC yang didapat, maka semakin baik model tersebut untuk digunakan. Berikut adalah persamaanAIC (Wei, 2005:156):
dengan
n = banyaknya pengamatan residual ˆ
σ2
a = jumlah kuadrat residual dibagi banyaknya pengamtan
M = banyaknya parameter dalam modelARIMA.
PEMBAHASAN
3.1
Konsep Fungsi Transfer
Model fungsi transfer adalah model yang dapat diterapkan pada data multivariat. Model fungsi transfer merupakan gabungan dari analisis regresi linier berganda dengan pendekatan analisis runtun waktu ARIMA. Berikut adalah bagan dari konsep model fungsi transfer:(Makridakis, 1993)
Gambar 3.1: Konsep Model Fungsi Transfer
Berdasarkan konsep fungsi transfer yang ditampilkan di gambar (3.1) pengaruh analisis regresi linier berganda terlihat dari adanya unsur pendekatan kausal (sebab akibat) antara deret input dengan deret output. Deret output yang dinotasikan dengan Yt dipengaruhi oleh deret input yang dinotasikan dengan Xt dan input-input lain yang digabungkan dalam satu kelompok yang disebut gang-guan (noise) Nt. Sementara unsur analisis runtun waktu terdapat pada deret
input dimana deret input dibangun dari ARIMA univariat. Seluruh sistem terse-but adalah sistem yang dinamis. Dengan kata lain, deret input memberikan pen-garuhnya terhadap deret output melalui fungsi transfer.
3.2
Model Fungsi Transfer
Model fungsi transfer ditulis dalam dua bentuk umum yaitu bivariat dan multivariat. Bentuk fungsi transfer bivariat adalah sebagai berikut: (Makridakis dkk., 1993)
Yt = v(B)Xt+Nt (3.1)
= (v0+v1B +v2B2+...+vkBk)Xt+Nt dengan
Yt = deretoutput
Xt= deretinput
Nt= pengaruh kombinasi dari seluruh faktor yang mempengaruhi Yt
v(B) = bobot respon impuls (v0+v1B+v2B2+...+vkBk)
k = orde fungsi transfer.
model fungsi transfer juga dapat dinyatakan sebagai berikut:
yt=nilai Yt yang telah ditransformasi
xt=nilai Xt yang telah ditransformasi
at =nilai gangguan acak
r, s, p, q, b=orde dari parameter-parameter model fungsi transfer
Pada fungsi transfer multivariat terdapat beberapa variabelinputXyang dimasukkan dalam suatu pemodelan. Bentuk umum persamaan model fungsi transfer multivariat adalah sebagai berikut: (Wei, 2005)
xjt dan at diasumsikan saling bebas dengan deret input xjt, untuk j = 1,2, ..., k. Persamaan (3.5) dapat pula ditulis sebagai berikut:
yt= m
X
j=1
[δj(B)]−1ωj(B)Bbjxjt+ [φj(B)]−1θ(B)at (3.6)
yt= variabel tak bebas
xjt = variabel bebas ke j
ωj(B) = operator moving averageorde sj untuk variabel ke-j
δj(B) = operator autoregressive orde rj untuk variabel ke-j
θ(B) = operator moving averageorde q φ(B) = operator autoregressive orde p at = nilai residual
Jika deret input xit dan xjt tidak berkorelasi untuk i 6= j maka analisis dan perhitungan sama seperti model fungsi transfer input tunggal. Sedangkan untuk deret multivariat xit dan xjt dengan i 6= j yang saling berkorelasi maka dilakukan analisis korelasi silang (cross correlation) antar deret runtun waktu untuk mengetahui deret mana yang harus dikeluarkan dari model.
3.3
Prosedur untuk Menentukan Model Fungsi
Transfer
dengan perhitungan korelasi silang untuk deretinputdan deretoutputyang bergu-na untuk menduga bobot-bobot respon impuls. Setelah estimasi bobot-bobot respon impuls diperoleh, akan ditentukan nilai r, s, buntuk model fungsi transfer. Kemudian akan dilakukan identifikasi bentuk model fungsi transfer dan noise -nya. Selanjutnya akan dilakukan estimasi parameter dan uji diagnostik sehing-ga akhirnya didapatkan model fungsi transfernya. Berikut prosedur pemodelan fungsi transfer multivariat.
3.3.1 Identifikasi Bentuk Model Input Tunggal
Mempersiapkan deret input dan output
Pada tahap ini yang perlu dilakukan adalah mengidentifikasikan kesta-sioneran deret input dan output. Untuk menghilangkan ketakstasioneran ma-ka perlu dilakuma-kan pembedaan atau transformasi deret-deret input dan output. Transformasi yang biasanya diterapkan adalah (Makridakis, 1999)
Xt =
(Xt+m)λ , λ6= 0 log(Xt+m) , λ= 0
dimana m adalah faktor penambah yang konstan. Misalkan jika λ = 0.5 maka transformasi yang diterapkan adalah transformasi akar kuadrat, sementara jika
λ= 0 maka transformasi logaritma akan diterapkan pada deret tersebut. Sedang kan untuk pembedaan sama seperti yang diterapkan pada persamaan (2.13).
Pemutihan deret input
ini bertujuan untuk menjadikan deret input dapat lebih diatur dengan menghi-langkan seluruh pola yang diketahui sehingga yang tertinggal hanya white noise. Pemutihan deret input xt dengan proses ARIMA (px,0, qx) adalah:
φx(B)xt=θx(B)αt (3.7)
Sementara untuk mengubah deretinputxtmenjadi deretatadalah sebagai berikut:
φx(B)
θx(B)xt =αt (3.8)
Pemutihan deret output
Apabila suatu proses pemutihan diterapkan untuk xt maka proses yang sama juga harus diterapkan terhadap yt agar fungsi transfer dapat memetakan
xt terhadap yt. Liu (1982) merekomendasikan agar dilakukan juga transformasi pemutihan terhadap deret output terutama dengan deret input yang jumlahnya lebih dari satu (multivariat). Dengan demikian model fungsi transfer dapat diban-gun dengan lebih mudah. Transformasi yt tidak harus mengubah yt menjadi
white noise. Oleh karena itu, makna ”pemutihan” untuk deretytharus dibedakan dengan pemutihan terhadap deret xt. Berikut deret yt yang telah ”diputihkan”:
φx(B)
θx(B)
yt =βt (3.9)
Perhitungan korelasi silang dan autokorelasi deret input dan output
yang telah diputihkan
pe-modelan fungsi transfer, autokorelasi memerankan peranan kedua untuk koefisien korelasi silang. Fungsi korelasi silang adalah ukuran kekuatan hubungan antar dua variabel. Korelasi silang antaraX dan Y menentukan tingkat hubungan an-tar nilaixpada waktutdengan nilaiypada waktut+k. Koefisien korelasi silang dari input xt dan output yt untuk lag ke-k didefinisikan sebagai berikut: (Wei, 2005)
ρxy(k) = γxy(k)
σxσy
k = 0,±1,±2, ... (3.10)
dengan fungsi penduganya adalah
ˆ
Berikut adalah rumus standard error yang berguna untuk memeriksa apakah ˆρxy(k) berbeda nyata dari nol dengan membandingkan nilai ˆρxy(k) dengan kesalahan standarnya. (Wei, 2005:330)
SErxy(k) =
1
√
n−k (3.13)
dari order, s, bpada masing-masinginput maka barulah dilakukan korelasi silang serentak antara nilai y terhadap seluruh variabel input-nya.
Penaksiran langsung bobot respon impuls
Langkah selanjutnya setelah perhitungan korelasi silang adalah penaksi-ran nilai bobot respon impuls. Bobot respon impuls berguna untuk menghitung deret noise. Untuk penaksiran bobot respon impuls secara langsung dibangun dari model fungsi transfer dengan mengamsumsikan b = 0 sebagai berikut:
yt=v(B)xt+nt (3.14)
Kemudian model tersebut ditransformasi denganφx(B)/θk(B) secara keseluruhan maka:
φx(B)
θx(B)yt =v(B)
φx(B)
θx(B)xt+
φx(B)
θx(B)nt (3.15) sehingga
βt=v(B)αt+εt (3.16)
dimana εt adalah deret gangguan yang ditransformasikan dan tidak berhubung-an dengberhubung-an αt. Kemudian akan dikalikan dengan αt−k dan akan diambil nilai
ekspektasinya sehingga diperoleh:
Dengan memsubstitusi nilai sampel pada persamaan (3.11) maka diperoleh:
Sα = standar deviasi deret input yang telah diputihkan
Sβ = standar deviasi deret output yang telah diputihkan
Penetapan orde (r,s,b) untuk model fungsi transfer yang menghubungkan deret input dan output
Tiga orde utama dalam model fungsi transfer adalah (r, b, s) dimana r
menunjukkan orde fungsi δ(B), s menunjukkan orde fungsi ω(B) dan b menun-jukkan keterlambatan sebesar b periode sebelum x mulai mempengaruhi y yang dicatat pada xt−b pada persamaan
yt =
ω(B)
δ(B)xt−b+
θ(B)
φ(B)αt (3.18)
Berikut ini beberapa aturan yang dapat digunakan untuk menduga nilai r, s, b
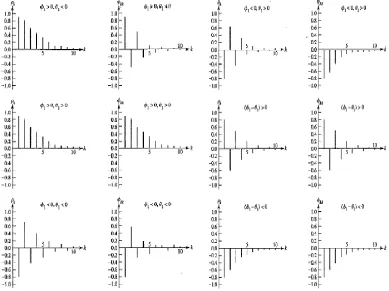
dari suatu fungsi transfer: (Wei, 2005)
se-belum deret berkalainput αyang mulai mempengaruhi deret berkalaoutput
β.
2. Nilaismenyatakan seberapa lama deretytterus dipengaruhixt−b−1, xt−b−2, ...,
xt−b−ssehingga dapat dikatakan bahwa nilaisadalah bilangan pada lag plot korelasi sillang sebelum terjadinya pola menurun.
3. Nilairmenyatakan bahwaytdipengaruhi oleh nilai masa lalunya (yt−1, yt−2, ...,
yt−r, r= 0) bila ada beberapa lag plot pada korelasi silang yang terpotong.
(a) r= 0 bila ada beberapa lag plot pada korelasi yang terpotong.
(b) r= 1 bila plot pada korelasi silang menunjukkan suatu pola eksponen-sial menurun.
(c) r= 2 bila plot pada korelasi silang menunjukkan suatu pola eksponen-sial menurun dan pola sinus.
Orde (r, s, b) ditentukan berdasarkan lag-lag dari perhitungan korelasi silang yang bersesuaian dengan kriteria tersebut diatas. Angka dari orde (r, s, b) tidak terbatas pada 0, 1, 2 saja tetapi bisa lebih besar dari itu. Namun dari berbagai proses perhitungan yang telah dilakukan sebelumnya orde (r, s, b) jarang menyentuh angka-angka besar, terutama orde r dimana orde yang umum dite-mukan hanyalah 0, 1, 2. Berikut beberapa bentuk fungsi transfer yang umum digunakan dalam peramalan:
(r, s, b) Fungsi transfer (0,0,2) v(B)xt=ω0xt−2
(0,1,2) v(B)xt= (ω0 −ω1B)xt−2
(0,2,2) v(B)xt= (ω0−ω1B−ω2B2)xt−2
(r, s, b) Fungsi transfer
Tabel 3.2: Model Fungsi Transfer r = 1 (r, s, b) Fungsi transfer Tabel 3.3: Model Fungsi Transfer r = 2
Penaksiran awal deret gangguan nt
Bobot respon impuls dapat diukur secara langsung sehingga memungkinkan dilakukan perhitungan nilai taksiran dari deret gangguan nt karena,
Penetapan orde (pn, qn) untuk model ARIMA (pn,0, qn) dari deret gang-guan nt
Sesudah menggunakan persamaan deret gangguan nt, nilai-nilai nt di-analisis dengan caraARIMA biasa untuk menentukan model ARIMA yang tepat sehingga diperoleh nilai pn dan qn. Dengan demikian fungsi φn(B) dan θn(B) untuk deret gangguan nt dapat diperoleh untuk mendapatkan persamaan
φn(B)nt=θn(B)at (3.19)
3.3.2 Estimasi Parameter Model Fungsi Transfer
Langkah kedua setelah mengidentifikasikan bentuk model adalah estimasi parameter-parameter model fungsi transfer input tunggal. Model fungsi transfer sementara yang didapatkan pada persamaan (3.18) perlu dilakukan estimasi pa-rameter δ = (δ1, ..., δr)′, ω = (ω1, ..., ωs)′, φ = (φ1, ..., φp)′, θ = (θ1, ..., θq)′ dan σ2a dimana persamaan (3.18) dikalikan dengan δ(B)φ(B) sehingga menjadi
δ(B)φ(B)yt = φ(B)ω(B)xt−b+δ(B)θ(B)at
dimana sikan bahwa at adalah deret white noise berdistribusi normal N(0, σa2), berikut adalah fungsi conditional likelihood:
L(δ, ω, φ, θ, σa2|b, x, y, x0, y0, a0) = (2πσa2)−n/2exp
dimanax0, y0, a0 adalah nilai-nilai awal untuk menghitungat. Nilai awal ini sama halnya dengan nilai awal yang dibutuhkan saat estimasi parameter dari model
ARIMA univariat.
Menurut Wei (2005) secara umum metode estimasiconditional likelihood
dapat digunakan untuk mengestimasiδ, ω, φ, θ, σ2
bersyarat dari nol, maka estimasi kuadrat terkecil nonlinier dari parameter terse-but didapat dengan meminimumkan:
S(δ, ω, φ, θ|b) =
3.3.3 Uji Diagnostik Model Fungsi Transfer
Input
Tunggal
Perhitungan autokorelasi untuk nilai sisa model (r,s,b) yang menghubungkan deret input dan output
Pengujian kelayakan suatu model perlu dilakukan untuk mengetahui ke-sesuaian model yaitu sudah memenuhi syaratwhite noise. Caranya adalah dengan memeriksa autokorelasi dan korelasi residualnya. Pengujian autokorelasi untuk ni-lai sisa dapat menggunakan hipotesis sebagai berikut:
H0 = autokorelasi pada deret sisaat tidak signifikan
H1 = autokorelasi pada deret sisaat signifikan dengan statistik uji
n = banyaknya pengamatan
m= lag terbesar yang diperhatikan (r, s, b) = parameter model fungsi transfer
ˆ
Kemudian hasilnya akan dibandingkan dengan tabel distribusi χ2
de-ngan taraf signifikansi α dan derajat bebas m−pn−qn (pn, qn merupakan nilai
autoregressive dan moving average dari deret noise). Keputusan tolak H0 jika
Q≥χ2
α,df.
Perhitungan korelasi silang antara nilai sisa dengan deret gangguan yang telah diputihkan
Korelasi silang antara deretinputdanoutput yang telah diputihkan akan memberikan gambaran mengenai tingkatan hubungan antar deret. Korelasi silang dapat dikonversikan ke dalam estimasi bobot respon impuls. Susunan dalam bobot-bobot respon impuls mengindikasikan bentuk model fungsi transfer semen-tara. Dengan menggunakan bobot-bobot respon impuls ini dapat membangkitkan suatu deret estimasi noise awal dari model fungsi transfer.
Fungsi respon impuls memiliki peranan untuk mengukur besarnya kore-lasi antara x dan y. Fungsi korelasi silang mirip dengan fungsi autokorelasi dan fungsi autokorelasi parsial dalam menghitung korelasi tetapi korelasi silang mem-punyai nilai tertentu untuk lag ke-0 sedangkan fungsi autokorelasi sendiri adalah satu. Pengujian korelasi silang antara nilai sisa dengan deret gangguan yang telah diputihkan menggunakan statistik uji Q dengan hipotesis:
H0 = Korelasi silang antara deretat dan αt tidak signifikan
H1 = Korelasi silang antara deretat dan αt signifikan dengan statistik uji
n∗ = nilai (s+b+px) p
x adalah banyaknya parameter AR pada model ARIMA dalam deret input (xt)
Hasilnya dibandingkan dengan tabelχ2 derajat bebas m−r−s dengan
kriteria keputusan tolakH0 jika Q≥χ2α,df.
3.3.4 Penentuan Model Fungsi Transfer Multivariat
Pemodelan data runtun waktu menggunakan fungsi transfer multivariat dilakukan dengan cara memodelkan secara serentak seluruh variabel yang su-dah diidentifikasikan sebelumnya. Identifikasi nilai-nilai dari bobot respon impuls dan korelasi silang dijadikan dasar dalam pemodelan serentak yang menghasilkan fungsi transfer multivariat. Cara yang dilakukan dalam model fungsi transfer mul-tivariat sama halnya dengan yang dilakukan pada model input tunggal. Adapun langkah-langkahnya adalah sebagai berikut: (Makridakis, 1993)
1. Mengidentifikasikan deretinputdan outputuntuk mengetahui kestasioneran deret data dan menentukan orde model ARIMA.
2. Melakukan estimasi parameter model-modelARIMAyang sesuai untuk masing-masing deretinput.
3. Kemudian dilakukan uji untuk mengetahui apakah model telah memenuhi syarat white noiseatau belum.
4. Melakukan pemutihan terhadap model ARIMA dari deret input dan deret
output.
6. Korelasi silang berguna untuk menentukan deret noise dan juga menen-tukan orde model fungsi transfer yaitu dengan mengidentifikasi plot korelasi silangnya.
7. Menentukan nilai r, s, b pada masing-masing deret input dan menghitung deret noise (nt).
8. Setelah model deretnoisedidapatkan akan dilakukan penetapan ordeARIMA
dari deret noise-nya sehingga model fungsi transfer input tunggal selesai dibentuk.
9. Mengestimasi parameter dari tiap model fungsi transferinput tunggal.
10. Kemudian lakukan uji diagnostik untuk mengetahui apakah model sudah memenuhi asumsi white noise.
11. Sampai disini adalah tahapan untuk pembentukan model fungsi transfer
input tunggal. Sementara untuk model fungsi transfer multivariat dilan-jutkan dengan;
12. Nilair, s, bpada masing-masing deretinputyang telah didapat kemudian di-estimasi secara serempak dengan metode di-estimasi yaituconditional least squ-are estimation.
13. Sementara untuk menentukan deretnoisegabungannya didapat dari rumus:
nt = yt−yˆt = yt−
k
X
j=1
ˆ
14. Mengestimasi semua parameter yang dimasukan ke dalam model fungsi transfer multivariat.
15. Terakhir lakukan uji diagnostik untuk mengetahui apakah model sudah memenuhi asumsiwhite noise. Dengan demikian model fungsi transfer mul-tivariat dapat digunakan.
Estimasi yang dilakukan dalam model fungsi transfer ini menggunakan alat bantu program SAS. Nilai-nilai r, s, b yang telah diidentifikasi dalam model fungsi transferinputtunggal djumlahkan sehingga model multivariatnya menjadi:
yt = Berikut adalah diagram alir untuk prosedur pembentukan model fungsi transfer yang ditampilkan pada gambar 3.2.
3.4
Penerapan Model Fungsi Transfer pada
Pera-malan Data Riil
3.4.1 Tahap Pertama: Identifikasi Bentuk Model
Input
Tunggal
Mempersiapkan deret input dan output
Pertama-tama akan diidentifkasi terlebih dahulu deret output curah hu-jan. Berikut adalah plot data serta plot ACF dan PACF-nya.
Gambar 3.3: Plot Runtun Waktu Data Curah Hujan
Gambar 3.4: PlotACF dan PACF Data Curah
menye-babkan hal tersebut terjadi karena memang curah hujan merupakan suatu feno-mena musiman.
Hal ini didukung oleh plot data runtun waktu dengan terlihat adanya pe-rubahan nilai pada rataan dan variansi yang tajam sehingga menunjukkan bahwa data curah hujan belum stasioner. Selain itu, pada plotACFterlihat bahwa pada lag 1, 6 dan 12 berbeda nyata dengan nol yang menunjukkan adanya pola musi-man. Untuk menstasionerkan datanya, maka dilakukan transformasi Box Cox.
Gambar 3.5: Plot Transformasi Box Cox Data Curah Hujan
Berdasarkan plot hasil transformasi Box Cox pada gambar 3.5, batas bawah untukλadalah 0,26 dan batas atasnya adalah 0,74 dengan nilai pendekatan
λ terbaik adalah 0,46. Namun nilai λ yang sebaiknya diambil adalah nilai yang memiliki makna, sehingga nilaiλyang terbaik untuk transformasi data adalah 0,5. Selain data belum stasioner dalam variansi, data curah hujan juga belum stasioner dalam rataan. Maka dari itu, perlu dilakukan pembeda terhadap data tersebut dimana pembeda yang dipakai adalah pembeda 12 karena data merupakan pola musiman.
Gambar 3.6: PlotACFdanPACFData Curah Hujan Setelah Dilakukan Pembeda 12
plot ACFdan ACFyang menurun serta adanya pola musiman yang ditunjukkan pada lag 12 yang keluar dari garis signifikan. Bila diidentifikasikan orde model
ARIMA untuk curah hujan maka pada plot PACF menunjukkan AR(1) untuk
pola musimannya, sementara plotACFmemperlihatkan modelM A(2) untuk pola nonmusimannya.
Selanjutnya akan dilakukan identifikasi terhadap tiap deretinput, dimana deret-deretinput-nya adalah tekanan udara, kelembaban udara, kecepatan angin, suhu udara dan intensitas matahari. Pertama akan dilakukan identifikasi terhadap data tekanan udara. Berikut adalah plot data runtun waktu beserta plot ACF
dan PACF dari tekanan udara
Gambar 3.8: Plot ACFdan PACF Data Tekanan Udara
Dari plot data serta plot ACFdan PACF terlihat data belum stasioner, karena masih terjadi perubahan dalam nilai rataan. Oleh karena data tekanan udara berpola musiman maka akan dilakukan pembeda 12 untuk menstasioner-kannya. Berikut adalah plot ACFdan PACF setelah dilakukan pembeda 12.
Gambar 3.9: Plot ACFdan PACF Data Tekanan Udara Setelah Dilakukan Pem-beda 12
penduga awal untuk data tekanan udara adalah (0,0,2)(1,1,0)12. Selanjutnya
akan dilakukan identifikasi terhadap data kelembaban udara. Berikut adalah plot data runtun waktu serta plot ACFdan PACF dari data kelembaban udara.
Gambar 3.10: Plot Runtun Waktu Data Kelembaban Udara
Gambar 3.11: Plot ACFdan PACF Data Kelembaban Udara
Gambar 3.12: Plot ACFdan PACF Data Kelembaban Udara Setelah Dilakukan Pembeda 12
Setelah dilakukan pembeda 12 terhadap data kelembaban udara, terlihat data sudah lebih baik dari sebelumnya dan cenderung staioner terhadap rataannya walaupun masih ada beberapa lag yang keluar dari garis signifikan. Berdasarkan plot ACF dan PACF pada gambar 3.12 dapat diidentifikasikan model ARIMA
nonmusimannya adalah AR(1). Hal ini dikarenakan plot ACF yang menurun se-cara eksponensial sementara plotPACFsignifikan pada lag pertama. Selanjutnya untuk model ARIMA musimannya bila dilihat dari plot ACF dan PACF tidak ada lag signifikan sehingga model penduga awal untuk data kelembaban udara adalah (1,0,0)(0,1,0)12. Selanjutnya deret input yang akan diidentifikasi adalah
kecepatan angin. Berikut adalah plot data beserta plotACFdanPACFdari data kecepatan angin.
Gambar 3.14: Plot ACF dan PACF Data Kecepatan Angin
Berdasarkan plot data dan plot ACF kecepatan angin dapat dikatakan sudah stasioner dalam rataan dan variansi sehingga sudah dapat diidentifikasikan model ARIMA-nya. Namun karena dalam pemodelan fungsi transfer agar meng-hasilkan nilai estimasi yang sesuai dengan model dan memenuhi syaratwhite noise, maka perlu disamakan model yaitu sama-sama distasionerkan. Oleh karena itu, perlu dilakukan pembeda 12 agar data deret kecepatan angin dapat masuk dalam model. Berikut plot ACFdan PACF setelah dilakukan pembeda 12.
Gambar 3.15: Plot ACF dan PACF Data Kecepatan Angin Setelah Dilakukan Pembeda 12
Setelah dilakukan pembeda 12, data kecepatan angin yang sudah stasion-er menjadi lebih baik plotnya, baik dari rataan atau variansinya. Bstasion-erdasarkan plot
nonmusiman-nya yakni AR(1) atau M A(1). Hal ini dikarenakan pada plot ACF maupun plot
PACF sama-sama signifikan pada lag 1. Sementara jika dilihat kembali lag 12 di plotACFtidak signifikan. Begitu juga pada lag 12 di plotPACFtidak signifikan. Dengan demikian dapat diduga modelARIMAuntuk deretinput kecepatan angin adalah (1,0,0)(0,1,0)12 atau (0,0,1)(0,1,0)12.
Selanjutnya akan dilakukan identifikasi terhadap data suhu udara. Berikut adalah plot data dari deret suhu udara beserta plot ACF dan PACF-nya.
Gambar 3.16: Plot Runtun Waktu Data Suhu Udara
Gambar 3.17: Plot ACFdan PACF Data Suhu Udara
Gambar 3.18: PlotACFdanPACFData Suhu Udara Setelah Dilakukan Pembeda 12
Setelah dilakukan pembeda 12, terlihat pada gambar 3.18 data sudah stasioner dalam rataan walaupun masih ada beberapa lag yang keluar dari garis signifikan. Selanjutnya akan diidentifikasikan model penduga untuk suhu udara.
Dari plotPACFterlihat signifikan di lag pertama dan lag-lag di plotACF
menurun mendekati nol sehingga model untuk nonmusimannya adalah AR(1). Sementara untuk pola musiman, modelnya adalahM A(1) atauAR(1) karena pada plotACFdan PACFmasing-masing signifikan di lag 12. Dengan demikian model penduga uhtuk data suhu udara adalah (1,0,0)(0,1,1)12 atau (1,0,0)(1,1,0)12.
Terakhir, akan dilakukan identifikasi terhadap data intensitas matahari. Berikut adalah plot data beserta plot ACFdan PACF dari data intensitas matahari.
Gambar 3.20: Plot ACFdan PACF Data intensitas Matahari
Berdasarkan gambar 3.19 data intensitas matahari belum stasioner kare-na masih terjadi fluktuasi data. Terlihat pula bahwa data intensitas matahari memiliki pola musiman berdasarkan plotACF-nya, sehingga perlu dilakukan pem-beda 12 untuk menstasionerkan data.
Gambar 3.21: Plot ACFdan PACF Data Intensitas Matahari Setelah Dilakukan Pembeda 12
Setelah dilakukan pembeda 12, terlihat plot ACF pada gambar 3.21 su-dah stasioner karena susu-dah tidak terlihat lagi adanya fluktuasi data. Untuk orde model musimannya dapat diduga dengan M A(1). Hal ini dikarenakan plot ACF
signifikan pada lag 12. Sementara untuk nonmusimannya dapat diduga modelnya adalah AR(1), karena plot PACF signifikan pada pertama sedangkan plot ACF
ARIMA untuk data intensitas matahari adalah (1,0,0)(0,1,1)12.
Setelah proses identifikasi deret output dan input selesai maka tahap selanjutnya adalah pemutihan. Namun sebelum melakukan pemutihan, perlu dilakukan penetapan model ARIMA yang sesuai terlebih dahulu. Pada tahap identifikasi telah dilakukan pendugaan orde model ARIMA untuk masing-masing deret input, maka tahap selanjutnya perlu dipilih model mana yang terbaik den-gan melihat nilai p-value untuk mengetahui signifikansi parameter serta memilih nilai AIC yang terkecil apabila terdapat model dugaan lain yang sesuai. Berikut hasil estimasi parameter ARIMA untuk masing-masing deret input dengan ban-tuan program SAS 9.1. Pertama adalah estimasi parameter untuk deret tekanan udara.
ModelARIMA Estimasi Parameter t−value p−value
(0,0,2)(1,1,0)12 θ
2 =−0,34190 -2,44 0,0187
Φ1 =−0,44955 -3,35 0,0016
Tabel 3.4: Estimasi Parameter dan Uji Signifikansi Model ARIMA untuk deret Tekanan Udara
Berikut adalah uji hipotesis untuk mengetahui signifikansi estimasi pa-rameter dari input tekanan udara:
1. Hipotesis
H0 : Estimasi parameter θ2,Θ1 tidak signifikan dalam model
H1 : Estimasi parameter θ2,Θ1 signifikan dalam model
2. Taraf signifikansiα = 0,05
3. Statistik uji
thitung =
4. Kriteria keputusan tolak H0 jika |thi| > tα
2,df atau p-value <0,05 5. Perhitungan ada pada tabel 3.4
6. Kesimpulan
Berdasarkan hasil di tabel 3.4 maka keputusanya adalah tolak H0 karena
kedua parameter memiliki p-value kurang dari α = 0,05 atau nilai |thi| >
tα
2,df sehingga parameter pada ARIMA (0,0,2)(1,1,0)
12 signifikan
Selanjutnya akan dilakukan uji diagnostik model untuk mengetahui ke-sesuaian model yakni residualαtmemenuhi asumsi white noise. Berikut hipotesis yang digunakan untuk mengetahui apakah autokorelasi residualnya berbeda nyata dari nol.
Lag Chi-Square db χ2
α,df p-value
6 5,59 4 9,49 0,2318
12 12,61 10 18,31 0,2462 18 15,35 16 26,30 0,4994 24 28,64 22 33,92 0,1554
Tabel 3.5: Uji Autokorelasi Residual Model ARIMA (0,0,2)(1,1,0)12 untuk
Tekanan Udara
1. Hipotesis
H0 :ρ1 =...=ρk= 0 (autokorelasi residualnya tidak signifikan)
4. Kriteria keputusan tolak H0 jika Q≥χ2α,df atau p-value ≤α
5. Perhitungan menggunakan program SAS dan hasil ada di tabel 3.5
6. Kesimpulan
Berdasarkan tabel 3.5 terlihat nilaip-value untuk semua lag lebih dari 0,05 sehingga dapat disimpulkan bahwa H0 diterima. Ini berarti autokorelasi
residualnnya tidak signifikan atau tidak terdapat korelasi antarlag maka residual memenuhi asumsiwhite noise. Jadi modelARIMA(0,0,2)(1,1,0)12
layak digunakan.
Selanjutnya akan dilakukan estimasi parameter dan uji diagnostik untuk deret kelembaban udara.
ModelARIMA Estimasi Parameter t−value p−value
(1,0,0)(0,1,0)12 φ
1 = 0,69505 6,55 <,0001
Tabel 3.6: Estimasi Parameter dan Uji Signifikansi Model ARIMA untuk deret Kelembaban Udara
Berikut adalah uji hipotesis untuk mengetahui signifikansi estimasi pa-rameter dari input kelembaban udara:
1. Hipotesis
H0 : Estimasi parameter φ1 tidak signifikan dalam model
H1 : Estimasi parameter φ1 signifikan dalam model
2. Taraf signifikansiα = 0,05
3. Statistik uji
thitung =
4. Kriteria keputusan tolak H0 jika |thi| > tα
2,df atau p-value <0,05 5. Perhitungan ada pada tabel 3.6
6. Kesimpulan
Berdasarkan hasil di tabel 3.6 maka keputusannyaa adalah tolakH0 karena
parameter φ1 memiliki p-value kurang dari α= 0,05 atau nilai|thi| > tα
2,df sehingga parameter pada ARIMA (1,0,0)(0,1,0)12 signifikan
Langkah selanjutnya adalah memeriksa apakah autokorelasi residualnya berbeda nyata dari nol atau tidak. Untuk mengetahui maka akan dilakukan uji hipotesis sebagai berikut:
Lag Chi-Square db χ2
α,df p-value 6 4,18 5 11,07 0,5232 12 18,74 11 19,67 0,0659 18 22,07 17 27,59 0,1819 24 23,28 23 35,17 0,4443
Tabel 3.7: Uji Autokorelasi Residual Model ARIMA (1,0,0)(0,1,0)12 untuk
Kelembaban Udara
1. Hipotesis
H0 :ρ1 =...=ρk= 0 (autokorelasi residualnya tidak signifikan)