ESTIMASI TITIK DAN INTERVAL KEPERCAYAAN

(1)

LOGO

ESTIMASI TITIK DAN

INTERVAL KEPERCAYAAN

Elty Sarvia, ST.,MT. Fakultas Teknik Jurusan Teknik Industri

Universitas Kristen Maranatha Bandung

LT Sarvia/Sesi 2

Tujuan

Mendefinisikan suatu estimasi titik (point estimate)

1

Mendefinisikan tingkat kepercayaan (level of confidence)

2

Membuat interval kepercayaan untuk rata-rata populasi apabila diketahui standar deviasi populasinya

3

Membuat interval kepercayaan untuk rata-rata populasi apabila standar deviasi populasinya tidak diketahui

4

Membuat interval kepercayaan untuk suatu proporsi populasi.

5

Menentukan ukuran sampel untuk sampling atribut dan sampling variabel

6

(2)

Estimasi Titik

 Adalah statistik yang dihitung dari informasi sampel yang digunakan untuk memperkirakan parameter populasi.

 Contoh : Best Buy Inc. ingin memperkirakan rata-rata umur pembeli televisi. Mereka memilih sampel berisi 50 pembeli terakhir, menentukan umur masing-masing pembeli, dan memperhitungkan rata-rata umur pembeli dalam sampel tersebut. Rata-rata sampel tersebut adalah estimasi titik dari rata-rata populasi.

 Rata-rata sampel ( ), adalah estimasi titik dari rata-rata populasi m; p (proporsi sampel) adalah estimasi titik dari p

(proporsi populasi); dan s (standar deviasi sampel) adalah

estimasi titik dari s (standar deviasi populasi).

 Secara umum, parameter populasi akan diberi simbol  (baca theta). Jadi  bisa merupakan rata-rata m, simpangan baku s dan proporsi p .

LT Sarvia/2012 x

Karakteristik Sampel dan Populasi

Karakteristik Populasi :

m , s 2 , p

Karakteristik Sampel :

LT Sarvia/2012

x

S 2

p

ˆ

Mengestimasi

(3)

Estimasi Titik

 Estimasi titik hanya menceritakan sebagian dari kisah keseluruhan. Estimasi titik adalah nilai tunggal yang berasal dari suatu sampel dan digunakan untuk memperkirakan nilai populasi. Kita berharap bahwa estimasi titik nilainya sedekat mungkin dengan parameter populasi, karena itu akan kita ukur berapa dekat nilai tersebut sebenarnya. Interval kepercayaan dapat digunakan untuk melakukan pengukuran tersebut.

 Interval Kepercayaan adalah kisaran nilai yang dibuat dari data sampel di mana parameter populasi cenderung terjadi dalam kisaran tersebut dengan probabilitas yang spesifik. Probabilitas spesifik ini disebut tingkat kepercayaan (level of confidence).

 Misalkan, kita memilih sampel yang tdd 50 eksekutif muda untuk mengetahui berapa jam yang mereka habiskan untuk bekerja selama 1 minggu lalu. Hitung rata-rata dari sampel 50 orang ini dan gunakan nilai rata-rata sampel sebagai estimasi titik dari rata-rata populasi yang tidak diketahui. Estimasi adalah nilai tunggal. Pendekatan yang lebih informatif adalah dengan memberikan kisaran nilai yang kita harapkan akan terjadi dalam parameter populasi tertentu yaitu yang kita sebut interval kepercayaan



LT Sarvia/2012

Syarat Estimator

3. Konsisten :

2. Efisien :

1. Tidak Bias

Estimator dikatakan Konsisten, jika Estimator tetap konsisten / berkonsentrasi pada penduga yang dibuat, atau :

Bila s2_{= 0 dan tidak bias, penduga yang secara sempurna nilainya berkonsentrasi di nilai} targetnya bila sampel diperbesar sampai tak terhingga (  ) atau makin besar ukuran sampel, maka statistik penduga makin mendekati parameter  populasi.

Estimator dikatakan Efisien, jika Estimator tersebut memiliki Variansi terkecil

Estimator dikatakan Tidak Bias, jika nilai Statistik sampel = nilai Parameter Populasi

(4)

Gambar 1

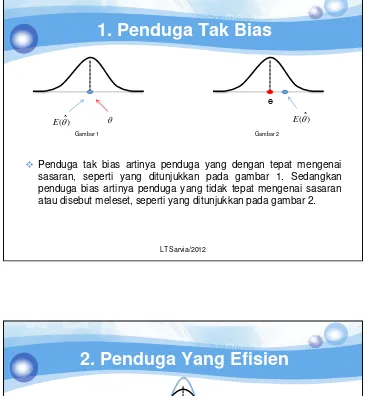
1. Penduga Tak Bias

LT Sarvia/2012

 Penduga tak bias artinya penduga yang dengan tepat mengenai

sasaran, seperti yang ditunjukkan pada gambar 1. Sedangkan penduga bias artinya penduga yang tidak tepat mengenai sasaran atau disebut meleset, seperti yang ditunjukkan pada gambar 2.

ө

Gambar 2 )

ˆ (

E  E(ˆ)

Gambar 3

2. Penduga Yang Efisien

LT Sarvia/2012

 Gambar 3 menunjukkan ada tiga penduga yaitu

yang diperoleh dari 3 sampel, dimana distribusi sampel 1 mempunyai variansi σ12 , sampel 2 mempunyai variansi σ22 , sampel 3 mempunyai variansi σ32 . Oleh karena sampel 1 mempunyai variansi paling kecil, maka dikatakan merupakan penduga yang efisien.

0 ) ˆ (  E

2 1 s

2 2 s s32 2

3 2 2 2

1 s s

s  

3 2 1,ˆ, ˆ

ˆ _ _

 dan

1 ˆ

(5)

Sampel 3, n3

Gambar 4

3. Penduga Yang Konsisten

LT Sarvia/2012

 Gambar 4 ditunjukkan bahwa ukuran sampel 1, yaitu n1, lebih kecil daripada ukuran sampel 2, yaitu n2 dan lebih kecil dari ukuran sampel 3, yaitu n2 . Terlihat bahwa makin besar ukuran sampel, maka statistik penduga makin mendekati parameter dari populasi, dimana distribusi sampel konsisten bergerak ke kiri

ˆ

Sampel 2, n2

Sampel 1, n1



Sifat Estimasi

1

Diketahui statistik sampel (sebagian) dan berbicara tentang parameter (seluruh), estimasi parameter mengandung probabilitas keliru

Makin lebar interval estimasi  makin kecil probabilitas keliru

2

Namun makin lebar interval estimasi  makin kecil ketepatannya sehingga makin rendah kadar informasinya

3

Sebaliknya, makin sempit interval estimasi  makin besar probabilitas keliru, namun makin tinggi kadar informasinya

Interval estimasi  berusaha mencari imbangan terbaik di antara probabilitas keliru dan kadar informasi

(6)

Rumus-rumus Estimasi :



NORMAL

Bila n < 30 dan s tidak diketahui Bila n  30 dan s diketahui

=

Bila n < 30 dan s diketahui

Text

LT Sarvia/2012

I. Estimasi Interval Rata-Rata 1 Populasi ( m )  INGAT FAKTOR KOREKSI !

n Z X n Z

X __/2 s  m   __/2 s

Bila n  30 dan s tidak diketahui n Z X n Z

X __/2 S  m   __/2 S

n t X n t

X /2 /2

S S      

 m ;v = n – 1

Persamaan I.1 Persamaan I.2

Persamaan I.3

Rumus-rumus Estimasi :



NORMAL

LT Sarvia/2012 II. Estimasi Interval Rata-Rata 2 Populasi

1. Bila s1 & s2 diketahui  untuk : n1 & n2 30 dan n1 & n2 < 30









n n Z X X n n Z X X 2 2 2 1 2 1 /2 2 1 2 1 2 2 2 1 2 1 /2 2

1   s s  m m      s s

2. Bila n1 & n2 30 dan s1 & s2 tidak diketahui









n n Z X X n n Z X X 2 2 2 1 2 1 /2 2 1 2 1 2 2 2 1 2 1 /2 2

1   S S  m m      S S

3. Bila n1 & n2 < 30 dan s1 & s2 tidak diketahui  s1  s2  cek dengan Uji F apakah s1  s2









n 1 n 1 Sp t X X n 1 n 1 Sp t X X 2 1 /2 2 1 2 1 2 1 /2 2

1      m m       









2 -n n v ; 2 n n S 1 -n S 1 -n

Sp 1 2

2 1 2 2 2 2 1

1  

(7)

Rumus-rumus Estimasi :



NORMAL

4. Bila n1 & n2 < 30 dan s1 & s2 tidak diketahui  s1s2









n n t X X n n t X X 2 2 2 1 2 1 /2 2 1 2 1 2 2 2 1 2 1 /2 2

1   S S  m m      S S

1 n n 1 n n n n V 2 2 2 2 2 1 2 1 2 1 2 2 2 2 1 2 1                      _  S S S S Persamaan II.4

Rumus-rumus Estimasi :



NORMAL

5. Untuk pengamatan berpasangan :

n Sd t d n Sd t

d _/2  mD   _/2

dimana : v = n – 1

n d

d



i

;

d

_i

=

X1X2





) 1 -n ( n di di n Sd 2 2



 Ciri-ciri pengamatan berpasangan :

1. Jumlah ukuran sampel-nya sama  n₁ = n₂ = n

2. Dilakukan terhadap individu yang sama / identik  mendapat perlakuan yang sama

(8)

Rumus-rumus Estimasi :



NORMAL

Estimasi Interval Proporsi Text Text LT Sarvia/2012 III. Estimasi Interval Proporsi

Untuk 1 Populasi :

n qˆ pˆ Z pˆ n qˆ pˆ Z

pˆ /2 /2

       _  p

Untuk 2 Populasi :













n qˆ pˆ n qˆ pˆ Z pˆ -pˆ n qˆ pˆ n qˆ pˆ Z pˆ -pˆ 2 2 2 1 1 1 /2 2 1 2 1 2 2 2 1 1 1 /2 2 1             _

 p p

Persamaan III.1

Persamaan III.2

Rumus-rumus Estimasi :



NORMAL

Untuk 1 Populasi :

Estimasi Interval Variansi

LT Sarvia/2012 IV. Estimasi Interval Variansi

S ) 1 -n ( S ) 1 -n ( 2 2 / 1 2 2 2 2 / 2    s    

Untuk 2 Populasi :

) , ( f S S ) , ( f 1 S S 1 2 /2 2 2 2 1 2 2 2 1 2 1 /2 2 2 2 1                   

 v v

v

v 

 s

s Lihat Tabel Chi-Square

Lihat Tabel F

Persamaan IV.1

(9)

Uji F :



untuk mengetahui apakah

s

₁

=

s

₂

atau

s

₁

≠

s

₂

LT Sarvia/2012 1. Struktur Hipotesis :

H0 : s2 1 = s2 2 H1 : s2 1 > s2 2

2. Taraf nyata :  = 0,05  uji 1 arah ( sebelah kanan )

3. Statistik Uji :  Uji F

530 , 3 66 , 0

24 , 1 S S

F ₂

2

2 2

2

1  



f 0,05 ( 15 , 9 ) = 3,01 4. Wilayah Kritis

3,01  = 0,05

v1 = 16 – 1 = 15

v2 = 10 – 1 = 9

3,530

Keputusan : Tolak H₀

Kesimpulan : s1≠ s2

Contoh Soal :

1. Sebuah sampel acak tdd 100 mahasiswa telah diambil dari sebuah universitas mengenai nilai-nilai IQ-nya dan menghasilkan nilai rata-rata 112 dan simpangan baku 10. Jika dikehendaki interval taksiran rata-rata dengan tingkat kepercayaan 95%. Hitunglah interval selang kepercayaan tersebut.

LT Sarvia/2012 Jawab

112

x Dist. Z

Diketahui : n = 100

10 S

Tkt. kepercayaan = 95 %   = 1 – 95% = 0,05  _/

(10)

Jawab :

LT Sarvia/2012

Selang kepercayaan 95 % bagi nilai tengah nilai IQ Mahasiswa dari sebuah Universitas adalah :

n Z X n Z

X /2 /2

S

S _ _ _ _

 

 m

100 10 ,96 1 112 100 10 ,96 1

112   m   

110,04 ≤ m ≤ 113,96

Kesimpulan : kita percaya 95 % bahwa IQ rata-rata mahasiswa akan ada dalam interval dengan batas 110,04 – 113,96

Persamaan I.2

Contoh Soal :

2. Idem soal no. 1. Jika dikehendaki interval taksiran rata-rata dengan tingkat kepercayaan 99%. Hitunglah interval selang kepercayaan tersebut.

112

x Dist. Z

Diketahui : n = 100

10 S

Tkt. kepercayaan = 99 %   = 1 – 99% = 0,01  _/

(11)

Jawab :

LT Sarvia/2012

Selang kepercayaan 99 % bagi nilai tengah nilai IQ Mahasiswa dari sebuah Universitas adalah :

n Z X n Z

X /2 /2

S

S _ _ _ _

 

 m

100 10 ,58 2 112 100 10 ,58 2

112   m   

109,42 ≤ m ≤ 114,58

Kesimpulan : kita percaya 99 % bahwa IQ rata-rata mahasiswa akan ada dalam interval dengan batas 109,42 ≤ m ≤ 114,58

Dari contoh diatas, dapat dilihat bahwa makin besar selang kepercayaan makin lebar jarak interval kepercayaan dan sebaliknya. Jika batas-batas selang kepercayaan menjadi satu, kita peroleh titik taksiran dengan derajat kepercayaan paling kecil

Persamaan I.2

Contoh Soal :

3. Isi kaleng asam sulfat adalah 9,8 ; 10,2 ; 10,4 ; 9,8 ; 10,0 ; 10,2 ; & 9,6 liter. Tentukan selang kepercayaan 95% bg nilai tengah isi semua kaleng, bila isi kaleng itu menyebar normal !

10 7

9,9 ... 10,2 9,8

x     Dist. t

Diketahui : n = 7



 







283 , 0 1

7

10 6 , 9 ... 10

2 , 10 10 8 , 9 S

2 2

2

 

(12)

Jawab :

LT Sarvia/2012

Tkt. kepercayaan = 95 %   = 1 – 95% = 0,05

 /2 = 0,025  v = n – 1 = 7 – 1 = 6

t /2 = ± 2,447

Selang kepercayaan 95 % bagi nilai tengah isi semua kaleng

n t X n t

X /2 /2

S

S _ _ _ _

 

 m

7 283 , 0 ,447 2 10,0 7 283 , 0 ,447 2

10,0   m   

9,74 ≤ m ≤ 10,26

Persamaan I.3

Contoh Soal :

4. Misalkan kita ingin menaksir ada berapa persen anggota masyarakat berumur 15 tahun ke atas termasuk ke dalam golongan darah A. Untuk itu sebuah sampel acak berukuran n = 1.200 diambil yang menghasilkan 504 tergolong kategori A. Tentukan selang kepercayaan 95% bagi proporsi anggota masyarakat yang memiliki golongan darah A

LT Sarvia/2012 Diketahui _{x = 504 (gol darah A)}

n = 1.200 _1.200 0,42 42%

504 n x

pˆ    

q = 1-p= 1-0,42 = 0,58

Tkt. kepercayaan = 95 %   = 1 – 95% = 0,05  _/

(13)

Jawab :

LT Sarvia/2012

Selang kepercayaan 95 % bagi bagi proporsi anggota masyarakat yang memiliki golongan darah A adalah :

Kesimpulan : kita percaya 95 % bahwa persentase anggota masyarakat yang termasuk golongan darah A akan ada dalam interval

n qˆ pˆ Z pˆ n

qˆ pˆ Z

pˆ __/2   p   __/2 

1.200 0,58 0,42 ,96

1 0,42 1.200

0,58 0,42 ,96

1

-0,42    p    

0,39 ≤ p ≤ 0,45

0,39 ≤ p ≤ 0,45

Persamaan III.1

Contoh Soal :

5. Ada dua cara pengukuran untuk mengukur kelembaban sesuatu zat. Cara I dilakukan 60 kali yang menghasilkan rata-rata 70, 4 dan s2_{= 37,2. Cara II dilakukan 50 kali yang menghasilkan rata-rata}

60,2 dan s2_{= 24,7. Tentukan selang kepercayaan 95% bagi}

perbedaan rata-rata pengukuran dari kedua cara itu.

LT Sarvia/2012

2 , 60

x2 Dist. Z

Cara I Cara II

n ₁ = 60 n ₂ = 50

4 , 70 x1

s22= 24,7

s12= 37,2

Tkt. kepercayaan = 95 %   = 1 – 95% = 0,05

 /2 = 0,025

(14)

Jawab :

LT Sarvia/2012

Selang kepercayaan 95% bagi perbedaan rata-rata pengukuran dari kedua cara itu adalah :

Kesimpulan : kita percaya 95 % bahwa selisih rata-rata pengukuran kedua cara itu akan ada dalam interval









n n Z X X n n Z X X 2 2 2 1 2 1 /2 2 1 2 1 2 2 2 1 2 1 /2 2

1   S S m m      S S









50 7 , 24 60 2 , 37 ,96 1 2 , 60 4 , 70 50 7 , 24 60 2 , 37 ,96 1 2 , 60 4 ,

70     m₁ m₂     

8,131≤ m 1–m 2 ≤ 18,331

8,131≤ m 1–m 2 ≤ 18,331

Persamaan II.2

Contoh Soal :

6. 20 mahasiswa tingkat satu dibagi ke dalam 10 pasang, dimana setiap pasang kira-kira mempunyai IQ yang sama. Salah seorang dari setiap pasangan diambil secara acak & dimasukkan ke dalam kelas yang hanya menggunakan bahan terprogramkan. Anggota pasangan yang lain dimasukkan ke dalam kelas biasa. Pada akhir semester, ke-2 grup itu diberikan ujian yang sama dan hasilnya adalah sbb :

LT Sarvia/2012

Pasangan Kelas dengan bahan terprogramkan Kelas Biasa

1 76 81

2 60 52

3 85 87

4 58 70

5 91 86

6 75 77

7 82 90

8 64 63

9 79 85

10 88 83

(15)

Jawab No. 6

Kelas dengan bahan terprogramkan

Kelas Biasa

n 1 = 10 n 2 = 10

LT Sarvia/2012

Dist. t - berpasangan

Tkt. kepercayaan = 98 %   = 1 – 98% = 0,02  /2 = 0,01

 v = n – 1 = 10 – 1 = 9

t /2 = ± 2,821

Jawab No. 6 (2)

LT Sarvia/2012 Pasangan Kelas dengan bahan

terprogramkan Kelas Biasa d d 2

1 76 81 -5 25

2 60 52 8 64

3 85 87 -2 4

4 58 70 -12 144

5 91 86 5 25

6 75 77 -2 4

7 82 90 -8 64

8 64 63 1 1

9 79 85 -6 36

10 88 83 5 25

(16)

Jawab No. 6 (3)

LT Sarvia/2012 6

, 1 10

16 n

d

d 



i  

 

) 1 -n ( n

di di n Sd

2 2 



   6,381

) 1 -10 ( 10

16 ) 392 * 10

(  2 _



Selang kepercayaan 98 % bagi selisih sesungguhnya dalam kedua metode pengajaran adalah :

n Sd t d n Sd t

d __/2  m_D   __/2

10 6,381 ,821 2 1,6 10 6,381 ,821 2 1,6

-   mD   

-7,29 ≤ mD ≤ 4,09

Persamaan II.5

Memilih Ukuran Sampel yang Tepat

Tingkat kepercayaan yang diharapkan

Batas Kesalahan yang diterima

Variabilitas populasi yang sedang diteliti

Ukuran

sampel yang

tepat

(17)

Memilih Ukuran Sampel yang

Tepat (2)

Faktor pertama adalah tingkat kepercayaan (level of confidence). Orang yang akan melakukan penelitian harus memilih tingkat kepercayaannya. Tingkat kepercayaan 95 % dan 99 % adalah yang paling lazim, tetapi nilai berapapun antaa 0 dan 100 dapat dipilih. Semakin tinggi tingkat kepercayaan yang dipilih, harus semakin besar ukuran sampelnya.

LT Sarvia/2012 1. Tingkat kepercayaan yang diharapkan

Faktor yang kedua adalah kesalahan yang diizinkan (allowance error). Maksimal kesalahan yang diizinkan, dilambangkan dengan e, adalah jumlah yang ditambahkan pada dan dikurangkan dari rata-rata sampel (atau bagian sampel) untuk menentukan nilai dari interval kepercayaan. Ini adalah jumlah kesalahan yang dapat ditoleransi oleh pihak yang melakukan penelitiannya. Suatu nilai yang kecil untuk kesalahan yang diizinkan akan membutuhkan sebuah sampel yang besar.

2. Batas kesalahan yang dapat diterima

Memilih Ukuran Sampel yang

Tepat (3)

Faktor ketiga dalam menentukan ukuran sampel adalah standar deviasi populasi (population standard deviation). Jika populasi tersebar secara luas, dibutuhkan sampel yang besar. Disisi lain, jika populasinya terkonsentrasi (homogen), ukuran sampel yang dibutuhkan lebih kecil. Sangat penting untuk menggunakan estimasi dalam standar deviasi populasi.

(18)

Beberapa rumus yang sering digunakan untuk mencari ukuran sampel minimum yaitu :

1. Ukuran contoh untuk pendugaan m : 2. Ukuran contoh untuk pendugaan p :

LT Sarvia/2012

2 /2

e

σ

. z

n 

  

 

 

dimana :

e : error / galat

2 2 /2

e qˆ pˆ . z n  

2 2 /2

e 4 z n  

Contoh Soal :

7. Seorang mahasiswa jurusan administrasi negara ingin mengetahui rata-rata dari jumlah pendapatan setiap bulan anggota dewan kota. Kesalahan estimasi rata-ratanya adalah kurang dari $100 dengan tingkat kepercayaan 95 %. Mahasiswa ini menemukan sebuah laporan oleh Departemen Tenaga Kerja yang telah memperkirakan standar deviasinya sebesar $1.000. Berapakah ukuran sampel yang diperlukan?

LT Sarvia/2012

Jawab :

Tingkat kepercayaan = 95%   = 1 – 95% = 0,05  /2 = 0,025

 Z /2 = ± 1,96

e = $ 100

(19)

Sebuah sampel sebanyak 385 dibutuhkan untuk mendapatkan spesifikasinya. Jika mahasiswa ini ingin meningkatkan tingkat kepercayaannya, sebagai contoh 99 %, akan dibutuhkan sampel yang besar, maka :

LT Sarvia/2012

 

19,6 384,16 385 100

1.000 . ,96 1 e

σ . z

n 2

2 2

/2 _   

  

        

 

Jawab :

Ukuran Sampel :



25,75



663,0625 664 100

1.000 . ,575 2 e

σ . z

n 2

2 2

/2 _   

  

        

 

 Z /2 = ± 2,575

Contoh Soal :

8. Sebuah penelitian memperkirakan proporsi kota-kota yang ada kolektor sampah swastanya. Mahasiswa ini ingin batas kesalahannya berada berada dalam 0,10 dari proporsi populasi, tingkat kepercayaan yang diharapkan adaah 90 %, dan estimasi yang tersedia untuk proporsi populasi. Berapakah ukuran sampel yang diperlukan?

LT Sarvia/2012

Jawab :

 Z /2 = ± 1,645

e = 0,10

(20)

Jawab no 8

Mahasiswa ini memerlukan sebuah sampel acak sebanyak 68 kota

LT Sarvia/2012

Jawab :

Ukuran Sampel :

68 65 , 67 1

, 0

5 , 0 5 , 0 645 , 1 e

qˆ pˆ . z

n ₂

2

2 2

/2   

  x x

Soal Latihan

1. Sebuah sampel random terdiri dari 6 orang dan 5 orang dipilih dari

2 buah populasi normal untuk diukur tinggi badannya. Dari hasil observasi diperoleh data sbb :

Buat interval keyakinan sebesar 95 % guna menduga selisih rata-rata ke-2 populasi tsb !

Jawab : Cek dulu apakah s1 = s2 dengan Uji F

LT Sarvia/2012

Sampel 1 157,8 156,2 162,9 154,4 153,6 156,5

(21)

Soal Latihan

2.

Telah ditimbang 10 buah tomat dengan hasil

(dalam gram) : 142, 157, 138, 175, 152, 149,

148, 200, 182, 164.

Jika berat tomat berdistribusi normal, tentukan

interval kepercayaan 95 % untuk rata-rata berat

tomat.

LT Sarvia/2012

Soal Latihan

3. Metode latihan pertama telah digunakan

terhadap 250 orang dan 160 orang dinyatakan

berhasil. Metode latihan kedua dilakukan

terhadap 300 orang dan 225 berhasil. Tentukan

interval kepercayaan 95 % untuk selisih

persentase sebenarnya bagi yang berhasil.

(22)

LOGO