MODEL PERTUMBUHAN POPULASI
TUNGGAL
Makalah
Diajukan Untuk Memenuhi Salah Satu Syarat
Memperoleh Gelar Sarjana Sains
Program Studi Matematika
Oleh:
Maria Etik Damayanti NIM: 093114005
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA
FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA
YOGYAKARTA
MAKALAH
MODEL PERTUMBUHAN POPULASI
TUNGGAL
Oleh:
Maria Etik Damayanti
NIM: 093114005
Telah disetujui oleh:
Pembimbing
Makalah
Model Pertumbuhan Populasi Tunggal
Dipersiapkan dan ditulis oleh:
Maria Etik Damayanti
NIM: 093114005
Telah dipertahankan di depan Panitia Penguji
pada tanggal 24 Juli 2014
dan dinyatakan telah memenuhi syarat
Susunan Panitia penguji
Nama Lengkap TandaTangan
Ketua Lusia Krismiyati Budiasih, M.Si.
Sekretaris Sudi Mungkasi, Ph.D.
Anggota Hartono, Ph.D.
Yogyakarta, 24 Juli 2014
Fakultas Sains dan Teknologi
Universitas sanata Dharma
Dekan,
HALAMAN PERSEMBAHAN
Karya ini adalah tugu peringatan akan kesetiaan Tuhan Yesus dan Bunda Maria dalam hidupku.
“Janganlah hendaknya kamu kuatir tentang
apapun juga, tetapi nyatakanlah dalam segala hal
keinginanmu kepada Allah dalam doa dan
permohonan dengan ucapan syukur.”
(Filipi 4:6)
PERNYATAAN KEASLIAN KARYA
Saya menyatakan dengan sesungguhnya bahwa makalah yang saya tulis ini tidak memuat karya atau bagian karya orang lain, kecuali yang telah disebutkan dalam kutipan dan daftar pustaka, sebagaimana layaknya karya ilmiah.
Yogyakarta, 18 Juli 2014 Penulis
LEMBAR PERNYATAAN PERSETUJUAN
PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS
Yang bertanda tangan di bawah ini, saya mahasiswa Universitas Sanata Dharma :
Nama : Maria Etik Damayanti
Nomor Mahasiswa : 093114005
Demi pengembangan ilmu pengetahuan, saya memberikan kepada Perpustakaan Universitas Sanata Dharma karya ilmiah saya yang berjudul :
MODEL PERTUMBUHAN POPULASI TUNGGAL
beserta perangkat yang diperlukan (bila ada). Dengan demikian saya memberikan kepada Perpustakaan Universitas Sanata Dharma hak untuk menyimpan, me-ngalihkan dalam bentuk media lain, mengelolanya dalam bentuk pangkalan data, mendistribusikan secara terbatas, dan mempublikasikannya di Internet atau media lain untuk kepentingan akademis tanpa perlu meminta ijin dari saya maupun memberikan royalti kepada saya selama tetap mencantumkan nama saya sebagai penulis.
Demikian pernyataan ini yang saya buat dengan sebenarnya.
Dibuat di Yogyakarta
Pada tanggal : 28 Agustus 2014
Yang menyatakan
ABSTRAK
Topik yang dibahas dalam makalah ini adalah model pertumbuhan kontinu. Model ini bertujuan mengadakan pendugaan untuk memperbaiki keadaan pada suatu populasi (disebut model pendugaan). Pertama-tama akan dimodelkan dengan pertumbuhan eksponensial. Kemudian akan diperluas dengan menggunakan pertumbuhan logistik. Pada pertumbuhan logistik, memasukkan batas untuk populasinya sehingga tidak akan tumbuh secara tak berhingga. Maka, jumlah populasinya akan selalu terbatas pada suatu nilai tertentu. Dalam makalah ini, model pertumbuhan populasi yang dibahas hanya dibatasi untuk model pertumbuhan populasi tunggal.
ABSTRACT
Topics covered in this paper is a continuous model of population growth. This model aims to predict the state in a population (called the prediction model). First we will describe the exponential growth model. Then it is expanded to a logistic growth model. In logistic growth model, we put a limit to the population so it will not grow infinitely. Thus, the amount of the population will always be limited to a certain value. In this paper, the population growth model discussed is only limited to a single.
KATA PENGANTAR
Puji syukur penulis panjatkan kepada Tuhan Yesus Kristus yang selalu menyertai dan membimbing penulis sehingga penulis mampu menyelesaikan makalah ini dengan lancar. Makalah ini dimaksudkan untuk memenuhi salah satu syarat dalam menyelesaikan pendidikan Strata 1 (S1) dan memperoleh gelar Sarjana Sains pada Program Studi Matematika di Universitas Sanata Dharma Yogyakarta.
Penulis menyadari bahwa proses penulisan makalah ini melibatkan banyak pihak. Oleh karena itu pada kesempatan ini penulis sudah selayaknya mengucapkan terima kasih kepada:
1. Lusia Krismiyati Budiasih, S.Si., M.Si. selaku Ketua Program Studi Matematika atas dukungannya.
2. Hartono, Ph.D. selaku dosen pembimbing yang telah sabar dalam membimbing, memberi pengetahuan dan memberi saran-saran kepada penulis selama penulisan makalah ini.
3. Romo, Bapak dan Ibu dosen yang telah memberikan pengetahuan kepada penulis selama proses perkuliahan ini.
4. Kedua orang tuaku dan adikku yang senantiasa selalu memberikan doa dan dukungan.
5. Teman-teman Matematika 2009: Yohana, Idut, Ochie, Jojo, Sekar, Erlika, Dimas dan Doweek, terima kasih untuk kebersamaan selama proses kuliah, saling berbagi dalam suka maupun dalam duka dan semangat yang selalu diberikan kepada penulis. Kalian hebat.
6. Mas diko yang selalu memberikan semangat dan sebagai tempat curahan hati.
8. Teman-teman Flater Sarikat Jesus Kolsani: Flater Tama, Flater Heri, Flater Suryadi, Flater Dimas, Flater Eko yang selalu memberikan dukungan beserta doa-doanya.
9. Teman-teman kos Banana: Rosa, Yustin, Rina, Deta, Yani, Nanik dan mbak Icot yang selalu menjadi tempat curahan hati dalam proses penulisan makalah ini
10.Semua pihak yang tidak dapat disebutkan satu persatu yang terlibat dalam proses penulisan makalah ini.
Penulis menyadari bahwa masih banyak kekurangan dalam penulisan makalah ini. Oleh karena itu, penulis mengharapkan saran dan kritik demi penyempurnaan makalah ini. Akhirnya, penulis berharap semoga makalah ini dapat berguna bagi para pembaca.
Yogyakarta, 18 Juli 2014
DAFTAR ISI
BAB III MODEL PERTUMBUHAN POPULASI TUNGGAL ……….… 55
3.1 PENDAHULUAN ……….… 55
3.2 MODEL PERTUMBUHAN EKSPONENSIAL ………...… 56
3.3 MODEL PERTUMBUHAN LOGISTIK ………..… 62
3.4 MODEL PERTUMBUHAN TERBATAS DENGAN PEMANENAN ……… 70
BAB IV APLIKASI MODEL ………...… 80
4.1 PENDAHULUAN……….….. 80
4.2 MEMODELKAN PERKEMBANGAN TEKNOLOGI ……… 80
4.3 KEPADATAN BERGANTUNG PADA KELAHIRAN ……….. 84
4.4 MODEL PANENAN ……….. 86
4.5 MEMANCING DENGAN BATASAN ………. 88
BAB V PENUTUP ………. 92
A. KESIMPULAN ……… 92
B. SARAN ……… 94
DAFTAR GAMBAR
Halaman
Gambar 1.1 Diagram masuk-keluar populasi ……… 2
Gambar 2.1 Grafik nilai-nilai ekstrim yang terjadi pada titik-titik kritis ………….. 21
Gambar 2.2 Grafik naik dan turun ……… 27
Gambar 2.3 Grafik kemiringan ………. 28
Gambar 2.4 Grafik kecekungan ……… 30
Gambar 2.5 Grafik nilai maksimum, minimum dan ekstrim lokal ………... 33
Gambar 3.1 Grafik yang menyatakan laju perubahannya semakin bertambah ……. 59
Gambar 3.2 Grafik yang menyatakan laju perubahannya stabil ………... 60
Gambar 3.3 Grafik yang menyatakan laju perubahannya semakin berkurang …….. 60
Gambar 3.4 Grafik populasi laju pertumbuhan per-kapita ……… 68
Gambar 3.5 Grafik yang menunjukkan solusi kesetimbangan ……….. 69
BAB I
PENDAHULUAN
A. LATAR BELAKANG
Setiap makhluk hidup selalu mengalami perubahan dari waktu ke waktu, dimulai dari kelahiran, pertumbuhan, hingga kematian. Untuk menggambarkan pertumbuhan suatu populasi, diperkenalkan suatu model pertumbuhan yang disebut model pertumbuhan eksponensial. Dalam model pertumbuhan eksponensial ini diasumsikan tidak ada penundaan waktu pada proses pertumbuhan populasi. Selain itu pada model ini dihasilkan solusi yang berbentuk fungsi monoton (naik atau turun), dimana dapat ditafsirkan bahwa jumlah populasi akan terus bertambah (tidak pernah berkurang) atau akan terus berkurang (tidak pernah bertambah).
Model pertumbuhan eksponensial merupakan model pertumbuhan yang sangat sederhana. Pada model ini individu berkembang dengan tidak dibatasi oleh lingkungan seperti kompetisi dan keterbatasan suplai makanan. Laju perubahan populasi dapat dihitung jika banyaknya kelahiran, kematian dan migrasi diketahui. Dinamika populasi dapat dihampiri dengan model ini hanya untuk periode waktu yang pendek saja.
Secara umum model populasi dapat digambarkan sebagai berikut: kelahiran kematian
Gambar 1.1: Diagram masuk-keluar populasi.
Bagan tersebut mengarah ke dalam persamaan yang menggambarkan perubahan populasi,
{ } = ,
- - , -.
Persamaan tersebut akan dikembangkan dengan beberapa asumsi dan kemudian proses kelahiran dan kematian dinyatakan ke dalam simbol.
Asumsi dapat dirumuskan sebagai berikut:
1. Populasi cukup besar sehingga perbedaan antara individu dapat diabaikan. 2. Kelahiran dan kematian kontinu dalam waktu.
3. Laju kelahiran per-kapita dan laju kematian per-kapita konstan dalam waktu.
4. Dalam pengembangan model, pada mulanya imigrasi dan emigrasi diabaikan, selanjutnya akan dimasukkan kemudian.
Dimisalkan jumlah populasi pada saat t adalah X(t) dan populasi awal bernilai , dengan laju kelahiran per-kapita adalah dan laju kematian perkapita adalah . Tujuannya adalah untuk menemukan ukuran populasi pada waktu t. Langkah pertama adalah menentukan persamaan populasi. Diasumsikan bahwa penduduk hanya dapat berubah karena kelahiran atau kematian, imigrasi atau emigrasi diabaikan. Juga, diasumsikan bahwa perubahan populasi setiap saat sebanding dengan jumlah penduduk waktu itu. Karena laju kelahiran per-kapita diasumsikan konstan, maka laju kelahiran adalah laju kelahiran per-kapita dikalikan besarnya populasi saat itu. Demikian juga, untuk laju kematian adalah laju kematian perkapita dikalikan besarnya populasi saat itu. Ini dapat ditulis,
, - = X( t ),
,
- = X( t ).
Dari kedua persamaan di atas dapat diperoleh
dt dX
X - X.
Dengan asumsi bahwa laju kematian per-kapita adalah tidak konstan, maka laju kematian per-kapita akan meningkat seiring dengan peningkatan populasi. Dengan asumsi bahwa laju kematian per-kapita bergantung linear pada suatu populasi, maka dapat dinyatakan sebagai berikut:
{ } ( )
Dimana adalah laju kematian per-kapita dan adalah laju kematian
per-kapita yang bergantung pada suatu populasi. Perhatikan bahwa untuk , laju kematian per-kapita mendekati , sedangkan dengan meningkatnya besarnya populasi maka laju kematian per-kapita akan meningkat. Bentuk linear ini merupakan bentuk yang paling sederhana untuk laju kematian per-kapita yang bergantung pada peningkatan besarnya populasi. Laju kematian adalah laju kematian perkapita dikalikan besarnya populasi saat itu yang dinyatakan sebagai berikut: model pertumbuhan yang bergantung pada kepadatan suatu populasi yang dinyatakan sebagai berikut:
Dengan
Maka secara umum laju pertumbuhan yang bergantung pada suatu populasi dinyatakan sebagai berikut:
Selanjutnya akan dibahas model pertumbuhan populasi terbatas dengan panenan. Pengaruh pemungutan panenan pada suatu populasi secara teratur atau konstan sangatlah penting bagi banyak industri. Salah satu contohnya adalah industri perikanan. Persamaan akan dirumuskan dalam laju panenan yang konstan pada model logistik sehingga dapat ditulis,
{ } = ,
- - , - –
{ } - {
}.
Dengan asumsi laju panenan adalah konstan, maka model di atas dapat dinyatakan ke dalam persamaan diferensial,
Di mana h adalah laju panenan yang dianggap konstan (banyaknya tangkapan per satuan waktu, atau kematian akibat panenan per satuan waktu).
B. RUMUSAN MASALAH
Pokok permasalahan yang akan dibahas dalam tulisan ini yaitu:
2. Bagaimana model pertumbuhan logistik dari suatu populasi tunggal? 3. Bagaimana model pertumbuhan terbatas dengan panenan dari suatu
populasi tunggal?
C. BATASAN MASALAH
Model pertumbuhan populasi yang dibahas dalam tulisan ini yaitu model populasinya tunggal.
D. TUJUAN PENULISAN
Tujuan penulisan ini adalah untuk memperoleh penyelesaian pertumbuhan populasi tunggal dengan beberapa macam model pertumbuhan yaitu: model pertumbuhan eksponensial, model pertumbuhan logistik dan model pertumbuhan terbatas dengan panenan.
E. MANFAAT PENULISAN
F. METODE PENULISAN
Metode yang digunakan penulis adalah metode studi pustaka, yaitu dengan mempelajari buku-buku yang berkaitan dengan model matematika untuk menyelesaikan masalah pertumbuhan populasi tunggal.
G. SISTEMATIKA PENULISAN
BAB I PENDAHULUAN
A. Latar Belakang B. Rumusan Masalah C. Batasan Masalah D. Tujuan Penulisan E. Manfaat Penulisan F. Metode Penulisan G. Sistematika Penulisan
BAB II MODEL MATEMATIKA DAN PERSAMAAN DIFFERENSIAL
A. Pengertian, Tujuan dan Jenis Model B. Limit
C. Kontinuitas D. Turunan E. Integral
BAB III MODEL PERTUMBUHAN POPULASI TUNGGAL
A. Pendahuluan
B. Model Pertumbuhan Eksponensial C. Model Pertumbuhan Logistik
D. Model Pertumbuhan Terbatas dengan Panenan
BAB IV APLIKASI MODEL
A. Pendahuluan
B. Memodelkan Perkembangan Teknologi C. Kepadatan Bergantung pada Kelahiran D. Model Panenan
E. Memancing dengan Batasan
BAB V PENUTUP
A. Kesimpulan B. Saran
BAB II
MODEL MATEMATIKA DAN PERSAMAAN DIFFERENSIAL
Pada Bab sebelumnya telah dibahas gambaran secara umum mengenai pertumbuhan populasi tunggal. Pertumbuhan tersebut berkaitan dengan model matematika untuk menyelesaikan masalah pertumbuhan populasi tunggal. Penyelesaian tersebut antara lain: limit, turunan, integral dan persamaan diferensial biasa. Untuk Subbab 1 pada Bab II ini akan dibahas mengenai pengertian, tujuan dan jenis model.
2.1 Pengertian, Tujuan dan Jenis Model
Definisi 2.1.1
Model adalah gambaran (tiruan, perwakilan) suatu obyek yang disusun berdasarkan tujuan tertentu.
Tujuan penyusunan model dapat dibedakan atas 3 kategori sebagai berikut:
1. Guna mengenali keadaan, sifat, atau perilaku sistem dengan cara mencari keterkaitan antara unsur-unsurnya. Model ini disebut dengan model keterkaitan.
2. Guna mengadakan pendugaan untuk dapat memperbaiki keadaan obyek. Model hasilnya disebut model pendugaan.
3. Guna mengadakan optimisasi bagi obyek. Modelnya disebut model optimisasi.
Pada umumnya penyusunan model kategori kedua dan ketiga harus melalui kategori pertama dulu. Jadi dengan salah satu tujuan di atas sebagai pedoman, model yang disusun akan berfungsi untuk menirukan atau menggambarkan keadaan atau perilaku sistem yang diamati semirip mungkin. Model dapat dibagi menurut jenisnya yaitu sebagai berikut:
1. Model fisis yaitu model yang biasanya cukup mirip dengan obyek dari segi fisis, misalnya bentuknya, atau polanya.
Model fisis dapat dibedakan menjadi 2 bagian, yaitu:
a) Model ikonik yaitu model yang biasanya menekankan keadaan statis obyek atau keadaan dinamis sesaat.
Contoh model ikonik: peta timbul, patung dsb.
Contoh model analog: pola baju, denah rumah dsb.
2. Model simbolik (model matematika) yaitu model yang menggunakan lambang-lambang (simbol) matematika atau logika untuk menyajikan perilaku obyek, maka ini disebut model matematika. Model ini dapat dianggap sebagai usaha abstraksi terhadap obyek lewat cara analisis atau numeris dalam bentuk persamaan-persamaan matematika. Bila penyelesaian ditemukan maka hasil ini dapat digunakan sebagai alat prediksi atau kontrol terhadap obyek. Untuk kerja yang besar proses matematika dapat dibantu oleh perangkat komputer. Model matematika yang dituliskan dalam bahasa komputer disebut
model komputer.
Subbab selanjutnya akan dibahas mengenai limit. Dalam subbab ini akan dibahas mengenai pengertian limit secara intuisi dan limit sepihak yang akan digunakan untuk membahas pada subbab kontinuitas dan turunan.
2.2 Limit
Definisi 2.2.1 (Pengertian Limit Secara Intuisi)
Mengatakan bahwa ( ) berarti bahwa bilamana dekat dengan , tetapi tidak sama dengan , maka ( ) dekat ke .
Contoh 2.2.1
Carilah ( ). Penyelesaian
( )
Definisi 2.2.2 (Definisi Limit secara Formal)
Mengatakan bahwa ( ) berarti bahwa untuk tiap yang
diberikan, terdapat yang berpadanan sedemikian sehingga | ( ) | asalkan bahwa | | ; yaitu
| | | ( ) |
Contoh 2.2.2
Buktikan bahwa
Bukti
Andaikan diberikan . Pilih . Maka | | mengimplikasikan
| | |( )( ) | | | | ( )| | |
●
Limit-limit Sepihak. Bila suatu fungsi mempunyai lompatan, maka limit tidak ada pada setiap titik lompatan. Untuk fungsi-fungsi yang demikian berlaku
Definisi 2.2.3 (Definisi Limit Kanan dan Limit Kiri)
Mengatakan bahwa ( ) berarti bahwa bilamana dekat tetapi pada sebelah kanan , maka ( ) dekat ke . Hal yang serupa, mengatakan bahwa
( ) berarti bahwa bilamana dekat tetapi pada sebelah kiri , maka
( ) adalah dekat ke .
Subbab selanjutnya akan dibahas mengenai kekontinuan pada suatu interval. Pada subbab ini mencakup mengenai kekontinuan itu sendiri.
2.3 Kontinuitas
Definisi 2.3.1
i. ( ) terdefinisi (yaitu berada di daerah asal );
ii. ( ) ada (sehingga haruslah terdefinisi pada suatu selang terbuka yang memuat );
iii. ( ) ( )
Selanjutnya akan dibahas mengenai turunan. Pada subbab ini akan membahas mengenai turunan itu sendiri dan penerapannya seperti, kemonotonan, kecekungan, nilai maksimum, nilai minimum, dan nilai ekstrim.
2.4 Turunan
Definisi 2.4.1
Turunan fungsi adalah fungsi lain ’ (dibaca “ aksen”) yang nilainya pada sebarang bilangan adalah
( ) ( ) ( )
jika limitnya ada.
Contoh 2.4.1
Carilah ( ) jika ( ) √ Penyelesaian
( ) ( ) ( ) √ √
( ) 0√ √ √ √ √ √ 1
(√ √ )
(√ √ )
(√ √ )
√ √
√
Jadi, turunan dari diberikan oleh ( ) ( ⁄ √ ). Daerah asalnya adalah
( ). ●
Definisi 2.4.2
Jika , maka definisi di atas ekivalen dengan
( ) ( ) ( )
Teorema 2.4.1 (Keterdiferensialan Mengimplikasikan Kekontinuan)
Jika ( ) ada, maka kontinu di . Bukti
Perlu diperlihatkan bahwa ( ) ( ).
maka,
( ) 0 ( )
( ) ( )
( )1
( ) ( ) ( ) ( )
( ) ( )
( )
Proses pencarian turunan suatu fungsi langsung dari definisi turunan yakni dengan menyusun hasil bagi dengan selisih
( ) ( )
dan menghitung limitnya dapat memakan waktu yang banyak. Oleh karena itu, akan dikembangkan cara-cara untuk memperpendek proses dan untuk mencari turunan semua fungsi yang tampaknya rumit dengan cepat.
Mengingat kembali bahwa turunan suatu fungsi adalah fungsi lain . Ketika menurunkan , artinya mendiferensialkan . Biasanya menggunakan simbol untuk menandakan operasi diferensial. Simbol menyatakan mengambil turunan (terhadap peubah ). Maka, dapat dituliskan ( ) ( ).
Teorema 2.4.2 (Aturan Fungsi Konstanta)
Jika ( ) dengan suatu konstanta, maka untuk sebarang ( ) ; yakni
( )
( ) ( ) ( )
Teorema 2.4.3 (Aturan Fungsi Identitas)
Jika ( ) , maka ( ) ; yakni
( )
Bukti
( ) ( ) ( )
Teorema 2.4.4 (Aturan Pangkat)
Jika ( ) , dengan bilangan bulat positif, maka ( ) ; yakni
( ) )
Bukti
( ) ( ) ( ) ( )
( )
[
( ) ]
Di dalam kurung, semua suku kecuali yang pertaa mempunyai sebagai faktor,
sehingga masing-masing suku ini mempunyai limit nol bila mendekati nol. Jadi
adalah Operator Linear.
Teorema 2.4.5 (Aturan Kelipatan Konstanta)
Jika suatu konstanta dan suatu fungsi yang terdiferensiasikan, maka ( ) ( )
( ); yakni,
( ) ( )
jika dinyatakan dalam kata-kata, suatu pengali konstanta dapat dikeluarkan dari
operator .
Bukti
Andaikan F(x)=k∙f(x), maka
( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
( )
Teorema 2.4.6 (Aturan Jumlah)
Jika dan adalah fungsi-fungsi yang terdiferensialan, maka ( ) ( )
( ) ( ); yakni,
( ) ( ) ( ) ( )
Jika dinyatakan dalam kata-kata, turunan dari suatu jumlah adalah jumlah dari turunan-turunan.
Bukti
Andaikan ( ) ( ) ( ) maka
0 ( ) ( ) ( ) ( )1
( ) ( ) ( ) ( )
( ) ( )
Sebarang operator disebut linear jika untuk semua fungsi dan :
a. ( ) ( ), untuk setiap konstanta ;
b. ( ) ( ) ( )
Teorema 2.4.7 (Aturan Selisih)
Jika dan adalah fungsi-fungsi yang terdiferensiasikan, maka ( ) ( )
( ) ( ); yakni,
( ) ( ) ( ) ( )
Jika dinyatakan dalam kata-kata, turunan dari suatu selisih adalah selisih dari turunan-turunan.
Bukti
( ) ( ) ( ) ( ) ( )
0 ( ) ( ) ( ) ( )1
( ) ( ) ( ) ( )
Contoh 2.4.2
Tentukan turunan dari . Penyelesaian
( ) ( ) ( ) (Teorema 2.4.7)
( ) ( ) ( ) (Teorema 2.4.6)
( ) ( ) ( ) (Teorema 2.4.5)
(Teorema 2.4.4, 2.4.3, dan 2.4.2) ●
Dalam kehidupan sehari-hari, seringkali dihadapkan masalah untuk mendapatkan cara terbaik dalam melakukan sesuatu. Sebagai contoh, seorang petani ingin memilih kombinasi tanaman yang dapat menghasilkan keuntungan besar. Seringkali dari masalah tersebut dapat dirumuskan sehingga melibatkan pemaksimuman atau peminimuman suatu fungsi pada suatu himpunan. Metode-metode kalkulus menyediakan sarana untuk memecahkan permasalahan tersebut. Dengan demikian, akan ditentukan nilai maksimum dan minimumnya.
Definisi 2.4.3 (Maksimum dan Minimum)
Misalkan , daerah asal , mengandung titik . Dapat dikatakan bahwa
i. ( ) adalah nilai maksimum pada jika ( ) ( ) untuk semua di ;
ii. ( ) adalah nilai minimum pada jika ( ) ( ) untuk semua di ;
iv. Fungsi yang ingin dimaksimumkan atau diminimumkan adalah fungsi obyektif.
Teorema 2.4.8 (Teorema Keberadaan Maks-Min)
Jika kontinu pada interval tertutup , maka mencapai nilai maksimum dan nilai minimum.
Nilai-nilai ekstrim dari fungsi yang didefinisikan pada interval tertutup seringkali terjadi pada titik-titik kritis, seperti pada gambar di bawah ini.
Gambar 2.1: Grafik nilai-nilai ekstrim yang terjadi pada titik-titik kritis
Namun, walaupun Teorema di atas secara intuitif sangat masuk akal, namun sukar dibuktikan sehingga pembuktiannya diabaikan.
Contoh 2.4.3
Penyelesaian
Titik-titik ujung adalah dan 2. Untuk mencari titik stasioner dengan
menyelesaikan ( ) untuk , diperoleh dan . Tidak ada
titik singular. Jadi, titik-titik kritisnya adalah ●
Teorema 2.4.9 (Teorema Titik Kritis)
Misalkan didefinisikan pada interval yang memuat titik . Jika ( ) adalah nilai ekstrim, maka haruslah berupa suatu titik kritis; dengan kata lain, adalah salah satu dari
i. titik ujung dari ;
ii. titik stasioner dari ; yakni titik di mana ( ) ; atau iii. titik singular dari ; yakni titik di mana ( ) tidak ada.
Bukti untuk kasus maksimum
Lihatlah kasus maksimum di mana ( ) adalah nilai maksimum pada dan misalkan bahwa bukan titik ujung atau pun titik singular. Maka harus dibuktikan bahwa adalah titik stasioner.
Karena ( ) adalah nilai maksimum, maka ( ) ( ) untuk semua dalam ; yaitu
( ) ( )
Jadi jika , sehingga , maka
sedangkan jika , maka
( ) ( ) ( )
Tetapi ( ) ada, karena bukan titik singular. Sehingga, diperoleh ( ) dan
( ) . Jadi dapat disimpulkan bahwa ( ) .
Bukti untuk kasus minimum
Pada kasus minimum di mana ( ) adalah nilai minimum pada dan misalkan bahwa bukan titik ujung atau pun titik singular. Maka harus dibuktikan bahwa adalah titik stasioner.
Karena ( ) adalah nilai minimum, maka ( ) ( ) untuk semua dalam ; yaitu
( ) ( )
Jadi jika , sehingga , maka
( ) ( ) ( )
sedangkan jika , maka
( ) ( ) ( )
Tetapi ( ) ada, karena bukan titik singular. Sehingga, diperoleh masing-masing ( ) dan ( ) . Jadi dapat disimpulkan bahwa ( ) .
Contoh 2.4.4
Mencari nilai-nilai maksimum dan minimum dari
pada * +.
Penyelesaian:
1. Langkah pertama mencari tititk-titik kritis yaitu dengan cara mencari turunan dari fungsi tersebut.
( )
( )
( )
( )
Dari perhitungan tersebut, diperoleh titik kritisnya, yaitu .
2. Kemudian dicari nilai fungsi saat sebagai berikut
Saat ( )
Saat ( ) Saat ( ) Saat ( )
Maka, diperoleh nilai maksimumnya, yaitu (dicapai pada dan
) dan nilai minimumnya yaitu (dicapai pada ). ●
Teorema 2.4.10 (Teorema Nilai Rata-rata untuk Turunan)
Jika kontinu pada selang tertutup dan terdiferensialan pada titik-titik dari
( ), maka terdapat paling sedikit satu bilangan dalam ( ) dengan
( ) ( )
( )
Bukti
Pembuktian bersandar pada analisis dari fungsi ( ) ( ) ( ). Di sini
( ) adalah persamaan garis yang melalui ( ( )) dan ( ( )). Karena
garis ini mempunyai kemiringan ( ) ( ) ( ) dan melalui titik
( ( )), bentuk kemiringan titik untuk persamaannya adalah
( ) ( ) ( ) ( ) ( )
Ini kemudian menghasilkan rumus untuk ( ), yaitu
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
Perhatikan bahwa ( ) ( ) dan bahwa untuk dalam ( )
( ) ( ) ( ) ( )
Jika diketahui bahwa terdapat suatu bilangan dalam ( ) yang memenuhi
( ) , pembuktian akan selesai. Karena persamaan yang terakhir mengatakan
( ) ( ) ( )
yang setara dengan kesimpulan teorema tersebut.
kontinu. Jadi, menurut Teorema Keberadaan Maks-Min, harus mencapai baik
nilai maksimum ataupun nilai minimum pada . Jika kedua nilai ini kebetulan adalah , maka ( ) secara identik adalah pada , akibatnya ( ) untuk semua dalam ( ), jauh lebih banyak daripada yang kita perlukan.
Jika satu nilai maksimum atau nilai minimum berlainan dengan , maka nilai tersebut dicapai pada sebuah titik-dalam , karena ( ) ( ) .
Sekarang mempunyai turunan di setiap titik dari ( ), sehingga dengan Teorema Titik Kritis, ( ) .
Contoh 2.4.5
Andaikan ( ) pada . Carilah semua bilangan yang memenuhi kesimpulan Teorema nilai Rata-rata.
Penyelesaian
Dengan menurunkan persamaan, diperoleh ( ) dan ( ) ( )
( )
.
Kemudian diselesaikan dengan atau, secara ekuivalen,
dari persamaan kuadrat. Terdapat dua penyelesaian (
√ ) yang berpadanan dengan dan . kedua bilangan
tersebut dalam selang ( ). ●
membuat beberapa titik dan menghubungkan titik-titik tersebut dengan kurva mulus. Tetapi cara tersebut masih kurang meyakinkan, karena titik-titik tersebut mungkin akan bergoyang di antara titik-titik yang dibuat.
Definisi 2.4.4 (Kemonotonan)
Misalkan terdefinisi pada interval (terbuka, tertutup, atau tak satupun). Dapat dikatakan bahwa:
i. naik pada jika, untuk setiap pasang bilangan dan dalam ,
( ) ( )
ii. turun pada jika, untuk setiap pasang bilangan dan dalam ,
( ) ( )
iii. monoton murni pada jika naik pada atau turun pada .
Definisi di atas diperlihatkan dalam grafik di bawah ini:
Gambar 2.2: Grafik naik dan turun
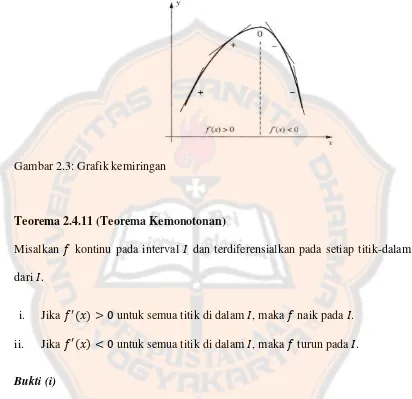
Ingat kembali bahwa turunan pertama ( ) memberi kemiringan dari garis
naik ke kanan. Demikian juga, jika ( ) , maka garis singgung menurun ke kanan. Dapat dilihat pada gambar di bawah ini,
Gambar 2.3: Grafik kemiringan
Teorema 2.4.11 (Teorema Kemonotonan)
Misalkan kontinu pada interval dan terdiferensialkan pada setiap titik-dalam dari .
i. Jika ( ) untuk semua titik di dalam , maka naik pada . ii. Jika ( ) untuk semua titik di dalam , maka turun pada .
Bukti (i)
Andaikan bahwa kontinu pada dan bahwa ( ) di setiap titik di bagian dalam . Tinjaulah dua titik sebarang dan dari dengan . Menurut Teorema Nilai Rata-rata yang diterapkan pada selang , terdapat sebuah
bilangan dalam ( ) yang memenuhi
Karena ( ) , dapat dilihat bahwa ( ) ( ) yakni, ( ) ( ).
Ini yang dimaksud bahwa naik pada . Bukti (ii)
Andaikan bahwa kontinu pada dan bahwa ( ) di setiap titik di bagian dalam . Tinjaulah dua titik sebarang dan dari dengan . Menurut
Teorema Nilai Rata-rata yang diterapkan pada selang , terdapat sebuah bilangan dalam ( ) yang memenuhi
( ) ( ) ( )( )
Karena ( ) , dapat dilihat bahwa ( ) ( ) yakni, ( ) ( ).
Ini yang dimaksud bahwa turun pada .
Contoh 2.4.6
Tentukanlah di mana ( ) ( ⁄ ) naik dan di mana turun. Penyelesaian
Dengan menurunkan persamaan di atas diperoleh
( ) ( ( ) ( )) ( ) ( )( )( )
Karena penyebut selalu positif, ( ) mempunyai tanda sama dengan pembilang
( )( ). Titik-titik pemisah, dan , menentukan tiga selang
( ) ( ) ( ). Bilamana ditemukan bahwa ( ) pada selang
yang pertama dan yang ketiga dan bahwa ( ) pada selang tengah. Dapat disimpulkan dari Teorema Kemonotonan (Teorema 2.4.11) bahwa turun pada
Definisi 2.4.5
Misalkan terdiferensialkan pada interval terbuka . Dapat dikatakan bahwa (dan grafiknya) cekung ke atas pada jika naik pada dan dikatakan bahwa cekung ke bawah pada jika turun pada .
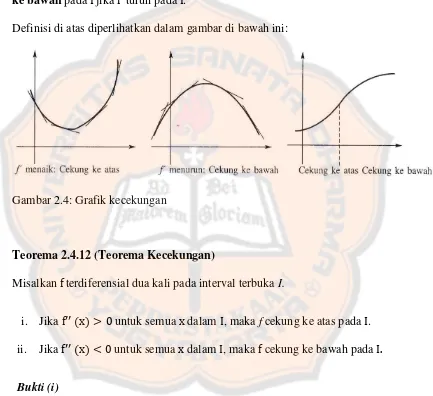
Definisi di atas diperlihatkan dalam gambar di bawah ini:
Gambar 2.4: Grafik kecekungan
Teorema 2.4.12 (Teorema Kecekungan)
Misalkan terdiferensial dua kali pada interval terbuka I.
i. Jika ( ) untuk semua dalam , maka f cekung ke atas pada . ii. Jika ( ) untuk semua dalam , maka cekung ke bawah pada
Bukti (i)
Andaikan bahwa terdiferensialkan dua kali pada dan bahwa ( ) , naik dalam beberapa interval terbuka yang memuat . Tinjaulah dua titik sebarang
dan dari dengan . Menurut Teorema Nilai Rata-rata yang diterapkan
pada selang , terdapat sebuah bilangan c dalam ( ) yang memenuhi
Karena naik, ( ) ( ), maka ( ) ( )( ) ( )
( )( ) ( ). Tetapi, ( ) ( )( ) ( ) adalah persamaan
garis singgung di . Jadi kurva yang terbentang di atas garis singgung adalah cekung ke atas.
Bukti (ii)
Andaikan bahwa terdiferensialkan dua kali pada dan bahwa ( ) , turun dalam beberapa interval terbuka yang memuat . Tinjaulah dua titik sebarang
dan dari dengan . Menurut Teorema Nilai Rata-rata yang diterapkan
pada selang , terdapat sebuah bilangan dalam (a,b) yang memenuhi
( ) ( ) ( )( )
Karena naik, ( ) ( ), maka ( ) ( )( ) ( )
( )( ) ( ). Tetapi, ( ) ( )( ) ( ) adalah persamaan garis
singgung di . Jadi kurva yang terbentang di bawah garis singgung adalah cekung
ke bawah.
Contoh 2.4.7
Di mana ( ) ⁄ (( )) cekung ke atas dan di mana cekung ke bawah? Penyelesaian
Contoh ini sama seperti contoh 2.4.6, bahwa turun pada ( dan )
dan naik pada . Untuk menganalisa kecekungan perlu dihitung .
( ) ( )
( ) ( )( ) ( )( ) ( )
( )
( ) ( )
Karena penyebut selalu positif, maka harus diselesaikan ( ) dan
( ) . Titik-titik pemisah √ dan √ . Tiga titik pemisah itu
menentukan empat selang. Dapat dilihat pada gambar di bawah ini.
Dapat disimpulkan bahwa cekung ke atas pada ( √ ) dan bahwa cekung ke
bawah pada ( √ ) dan ( √ ).
Definisi 2.4.6
Andaikan , daerah asal , memuat titik . Dapat dikatakan bahwa:
i. ( ) nilai maksimum lokal jika terdapat selang ( ) yang memuat sedemikian sehingga ( ) adalah nilai maksimum pada ( ) ;
ii. ( ) nilai minimum lokal jika terdapat selang ( ) yang memuat sedemikian sehingga ( ) adalah nilai minimum pada ( ) ;
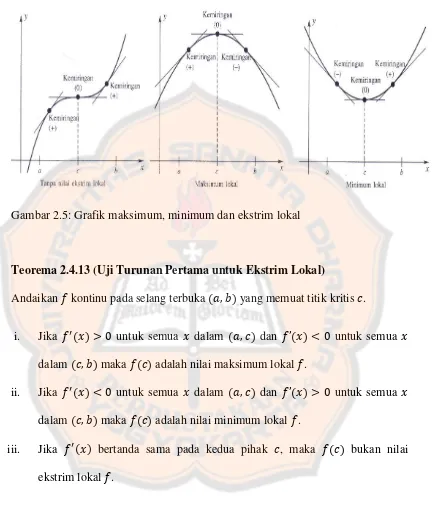
iii. ( ) nilai ekstrim lokal jika ia berupa nilai maksimum lokal atau nilai minimum lokal.
Gambar 2.5: Grafik maksimum, minimum dan ekstrim lokal
Teorema 2.4.13 (Uji Turunan Pertama untuk Ekstrim Lokal)
Andaikan kontinu pada selang terbuka ( ) yang memuat titik kritis .
i. Jika ( ) untuk semua dalam ( ) dan ( ) untuk semua dalam ( ) maka ( ) adalah nilai maksimum lokal .
ii. Jika ( ) untuk semua dalam ( ) dan ( ) untuk semua dalam ( ) maka ( ) adalah nilai minimum lokal .
iii. Jika ( ) bertanda sama pada kedua pihak , maka ( ) bukan nilai ekstrim lokal .
Bukti (i)
Kemonotonan (Teorema 2.4.11) turun pada ( ). Berarti ( ) nilai maksimum
di ( ). Jadi dapat disimpulkan bahwa ( ) adalah maksimum lokal. Bukti (ii)
Karena ( ) untuk semua dalam ( ) maka menurut Teorema kemonotonan (Teorema 2.4.11) turun pada ( ). Berarti ( ) nilai minimum
di ( ). Karena ( ) untuk semua dalam ( ) maka menurut Teorema Kemonotonan (Teorema 2.4.11) naik pada ( ). Berarti ( ) nilai minimum di
( ). Jadi dapat disimpulkan bahwa ( ) adalah minimum lokal.
Bukti (iii)
Karena ( ) untuk semua dalam ( ) maka menurut Teorema Kemonotonan (Teorema 2.4.11) naik pada ( ). Berarti ( ) nilai maksimum di ( ). Karena ( ) untuk semua dalam ( ) maka menurut Teorema kemonotonan (Teorema 2.4.11) naik pada ( ). Berarti ( ) nilai maksimum
di ( ). Sebaliknya, karena ( ) untuk semua dalam ( ) maka menurut Teorema Kemonotonan (Teorema 2.4.11) turun pada ( ). Berarti
( ) nilai minimum di ( ). Karena ( ) untuk semua dalam ( )
maka menurut Teorema kemonotonan (Teorema 2.4.11) turun pada ( ). Berarti ( ) nilai minimum di ( ). Jadi dapat disimpulkan bahwa ( ) bukan
nilai ekstrim lokal .
Contoh 2.4.8
Penyelesaian
Fungsi polinomial kontinu di mana-mana, dan turunannya, ( ) ada untuk semua . Jadi satu-satunya titik kritis untuk adalah penyelesaian tunggal dari ( ) , yakni . Karena ( ) ( ) untuk , turun pada ( dan karena ( ) untuk , naik pada ). Karena
itu, menurut Teorema Uji Turunan Pertama (Teorema 2.4.13), ( ) adalah nilai minimum lokal . Karena 3 adalah satu-satunya bilangan kritis, tidak terdapat nilai ekstrim lain. ●
Teorema 2.4.14 (Uji Turunan Kedua untuk Ekstrim Lokal)
Karena itu, menurut Teorema Uji Turunan Kedua, ( ) adalah nilai minimum
lokal. ●
Pada bab sebelumnya telah dibahas mengenai turunan. Dalam tiap kasus, operasi kedua melepaskan operasi pertama, dan sebaliknya. Oleh karena itu, kasus-kasus pada turunan mempunyai kasus-kasus kebalikannya, balikannya tersebut disebut antiturunan atau integrasi.
2.5Integral
Definisi 2.5.1
Kita sebut suatu antiturunan pada selang jika ( ) ( ) pada yakni, jika ( ) ( ) untuk semua dalam . (Jika suatu titik ujung , ( ) hanya perlu berupa turunan sepihak).
Teorema 2.5.1 (Aturan Pangkat)
Jika adalah sebarang bilangan rasional kecuali , maka
∫
dengan adalah sebarang konstanta. Bukti
Untuk mengembangkan suatu hasil berbentuk
∫ ( ) ( )
( ) ( )
Dalam kasus ini
0 1 ( )
Contoh 2.5.1
Carilah antiturunan yang umum dari ( ) ⁄ . Penyelesaian
∫ ⁄ ⁄
⁄
Integral Tak-tentu adalah Linear. Ingatlah kembali dari Subbab Turunan bahwa adalah suatu operator linear, yaitu
a. ( ) ( )
b. ( ) ( ) ( ) ( )
c. ( ) ( ) ( ) ( )
Ternyata bahwa ∫ juga memiliki sifat operator linear.
Teorema 2.5.2 (Integral Tak-Tentu adalah Operator Linear)
Andaikan dan mempunyai anti turunan (integral tak tentu) dan andaikan suatu konstanta. Maka:
i. ∫ ( ) ∫ ( ) ;
iii. ∫ ( ) ( ) ∫ ( ) ∫ ( ) .
Bukti (i)
Cukup mendiferensialkan ruas kanan, maka akan diperoleh integran dari ruas kiri
[ ∫ ( ) ] ∫ ( ) ( )
Bukti (ii)
Sama seperti cara bukti (i), cukup dengan mendiferensialkan ruas kanan, maka akan diperoleh integran dari ruas kiri
[∫ ( ) ∫ ( ) ] ∫ ( ) ∫ ( )
( ) ( )
Bukti (iii)
Sama seperti cara bukti (i) dan (ii), cukup dengan mendiferensialkan ruas kanan, maka akan diperoleh integran dari ruas kiri
[∫ ( ) ∫ ( ) ] ∫ ( ) ∫ ( )
( ) ( )
Contoh 2.5.2
Hitunglah dengan menggunakan kelinearan integral!
∫( ⁄ )
Penyelesaian
∫( ⁄ ) ∫ ⁄ ∫ ∫ ⁄
Dalam subbab selanjutnya akan dibahas mengenai persamaan diferensial. Persamaan ini mengembangkan metode pemisahan peubah untuk mencari suatu solusi.
2.6Persamaan Diferensial
Definisi 2.6.1
Persamaan diferensial adalah persamaan yang memuat derivatif atau diferensial dari satu atau lebih fungsi.
Persamaan diferensial bermula dari penyelidikan hukum-hukum yang mengatur dunia fisika. Istilah persamaan “diferensial” diperkenalkan oleh Gottfried Leibniz (1646-1716) yang bersama-sama Newton dikenal sebagai penemu kalkulus. Banyak teknik untuk menyelesaikan persamaan diferensial yang dikenal para matematikawan dalam abad ke tujuh belas. Tidak sampai abad ke sembilan belas, Augustin Louis Cauchy (1789-1857) mengembangkan teori umum persamaan diferensial yang bebas dari gejala-gejala fisika.
Seperti yang telah dijelaskan di atas, persamaan diferensial adalah suatu persamaan yang memuat derivatif atau diferensial dari satu atau lebih fungsi.
Contoh 2.6.1
Beberapa contoh persamaan diferensial:
1.
4. ( )
Persamaan diferensial dapat diklasifikasikan dalam banyak cara. Jika fungsi yang belum diketahui dalam persamaan diferensial bergantung pada hanya satu variabel bebas maka persamaan itu disebut persamaan diferensial biasa. Persamaan 1 sampai 6 adalah contoh persamaan diferensial biasa di mana menyatakan fungsi yang belum diketahui (variabel tak bebas) dan menyatakan variabel bebas. Jika fungsi yang belum diketahui bergantung pada dua atau lebih variabel bebas maka persamaan disebut persamaan diferensial parsial. Persamaan 7 dan 8 adalah contoh persamaan diferensial parsial.
Selanjutnya persamaan diferensial dapat juga diklasifikasikan sesuai dengan tingkat derivatif tertinggi yang muncul dalam persamaan itu.
Definisi 2.6.2
Tingkat persamaan diferensial adalah tingkat derivatif tertinggi yang muncul dalam persamaan.
Persamaan diferensial berdasarkan tingkatnya dapat diklasifikasikan menjadi tiga tingkatan, yaitu:
Bentuk umum:
( )
b. Persamaan diferensial tingkat kedua
Bentuk umum:
( )
c. Persamaan diferensial tingkat
ke-Bentuk umum:
( ( ))
Catatan: ( )
.
Di mana adalah suatu fungsi real dengan argumen-argumen ( )
Definisi 2.6.3
Persamaan diferensial biasa tingkat ke- disebut linear dalam jika persamaan diferensial itu dapat ditulis dalam bentuk:
( ) ( ) ( ) ( ) ( )
di mana dan adalah fungsi-fungsi kontinu pada suatu interval yang
Definisi itu menyatakan bahwa persamaan diferensial biasa adalah linear jika syarat-syarat berikut dipenuhi:
1. Fungsi yang belum diketahui dan derivatif-derivatifnya secara aljabar hanya berderajat satu.
2. Tidak ada hasil kali yang berkaitan dengan fungsi yang belum diketahui dan derivatif-derivatifnya atau dua atau lebih derivatif.
3. Tidak ada fungsi transendental dari dan seterusnya.
Persamaan diferensial yang tidak linear disebut nonlinear.
Contoh 2.5.6
a. Persamaan diferensial linear:
,
.
b. Persamaan diferensial biasa tingkat pertama
( ) adalah nonlinear karena derivatif pertama fungsi yang belum
diketahui berderajat tiga.
adalah nonlinear karena berkaitan dengan hasil kali fungsi yang
belum diketahui derivatifnya.
adalah nonlinear dalam fungsi , tetapi persamaan ini
variabel . Persamaan yang diketahui dapat dinyatakan dalam bentuk
yang linear dalam .
c. Persamaan diferensial biasa tingkat kedua
adalah nonlinear karena adalah fungsi transendental dari
fungsi yang belum diketahui. ●
Definisi 2.6.4
Penyelesaian persamaan diferensial tingkat ke- pada interval adalah suatu fungsi yang mempunyai semua turunan yang diperlukan, yang jika
menggantikan ( ) menjadikan persamaan diferensial itu suatu identitas.
Contoh 2.6.2
Buktikan bahwa adalah penyelesaian dari dan tunjukkan batas-batas penyelesaiannya!
Penyelesaian:
Dari diperoleh . Dengan memasukkan dan ke dalam
, diperoleh ( ) . Karena ruas kiri sama
dengan nol untuk semua maka fungsi adalah penyelesaian dari
Definisi 2.6.5
Suatu fungsi real ( ) disebut penyelesaian eksplisit persamaan
diferensial ( ( ) pada , jika
( ( ) ( ) ( ) ( )( )) pada .
Definisi 2.6.6
Suatu relasi ( ) disebut penyelesaian implisit dari persamaan
diferensial ( ( ) pada , jika ( ) menentukan sekurang-kurangnya satu fungsi f pada sedemikian rupa sehingga ( ) adalah penyelesaian eksplisit pada interval ini.
Dalam makalah ini diperlukan beberapa cara dalam menyelesaikan persamaan diferensial, yaitu
1. Persamaan Diferensial Dengan Bentuk ( )
Dalam kalkulus, persamaan diferensial dengan bentuk ( ) dapat
diselesaikan dengan ∫ ( ) Jadi penyelesaian ( ) diperoleh dengan mengintegralkannya, meskipun pengintegralannya belum tentu sederhana.
Contoh 2.6.5
Tentukan penyelesaian umum dari
Penyelesaian:
Penyelesaian dapat ditulis sebagai
∫( )( )
Integral dapat dihitung dengan memecah integran menjadi jumlah dua pecahan parsial yang berbentuk
( )( )
Kedua ruas dikalikan dengan ( )( ) dihasilkan ( )
( )
Untuk menentukan , ambil , sehingga atau Untuk menentukan , ambil , sehingga atau Pecahan parsial yang dimaksud adalah
( )( )
Jadi,
∫ ( *
| | | |
Karena ada suku-suku logaritma, maka konstanta dapat diganti dengan bentuk
( )| | ●
2. Persamaan Diferensial Variabel Terpisah
Perhatikan persamaan diferensial tingkat pertama yang dapat ditulis dalam bentuk derivatif sebagai
( )
Jika ( ) dapat ditulis sebagai
( ) ( ) ( )
maka persamaan diferensial di atas mempunyai bentuk diferensial
( ) ( )
Karena kedua bentuk umum ini dapat dipertukar.
Suatu persamaan diferensial yang dapat dibawa ke dalam bentuk
( ) ( )
atau ekuivalen dengan
( ) ( )
Dapat dilihat bahwa pada persamaan di atas variabel-variabel dan
“dipisahkan” dan bersesuaian dengan diferensial-diferensialnya. Proses
penyesuaian ( ) dengan dan ( ) dengan , disebut pemisahan variabel (separasi variabel). Setelah variabel-variabel dipisahkan, penyelesaian umum persamaan tersebut dapat disajikan dalam bentuk implisit oleh
∫ ( ) ∫ ( )
Contoh 2.6.3
Selesaikan persamaan ( ) . Penyelesaian:
Persamaan di atas belum dalam bentuk terpisah, tetapi, variabel-variabel dapat dipisahkan dengan membagi masing-masing suku dengan ( )
Persamaan tersebut menjadi
Dengan mengintegralkan masing-masing suku diperoleh penyelesaian implisit
| | ( )
Penyelesaian tersebut dapat disederhanakan menggunakan sifat logaritma. Diperoleh
adalah bentuk lain penyelesaian. Penyelesaian di atas dapat disederhanakan lagi dengan mengambil konstanta sebarang dalam bentuk | | sehingga
| | ( ) | |
dan diperoleh penyelesaian implisit yang lebih sederhana, yaitu
( )
3. Persamaan Diferensial Linear Tingkat Pertama
Persamaan diferensial linear tingkat pertama yang didefiniskan pada mempunyai bentuk
( ) ( ) ( ) ( ) (1)
untuk semua dalam .
Dengan membagi persamaan ini dengan ( ) maka diperoleh
( ) ( ) (2)
yang disebut bentuk baku persamaan diferensial linear tingkat pertama.
Untuk menyelesaikan persamaan diferensial linear tingkat pertama, pertama-tama kalikan kedua sisi dengan faktor integrasi, yaitu
∫ ( )
Persamaan diferensial menjadi
∫ ( ) ∫ ( ) ( ) ∫ ( ) ( )
( ∫ ( ) ) ∫ ( ) ( )
Integrasi kedua sisi menghasilkan
∫ ( ) ∫( ( ) ∫ ( ) )
Penyelesaian umumnya menjadi
∫ ( ) ∫( ( ) ∫ ( ) )
Contoh 2.6.4
Selesaikan persamaan linear Penyelesaian:
Ubahlah persamaan dalam bentuk baku maka diperoleh
Dalam persamaan ini ( ) sehingga faktor pengintegral
( ) ∫
Kalikan persamaan diferensial baku dengan maka diperoleh
atau dalam bentuk diferensial
Ruas kiri persamaan ini adalah diferensial dari hasil kali
sehingga persamaan dapat ditulis
( )
atau
●
4. Persamaan Diferensial Bernouli
Persamaan diferensial nonlinear yang dapat diubah menjadi persamaan diferensial linear tingkat pertama dengan menggunakan substitusi yang cocok adalah persamaan diferensial Bernoulli.
Definisi 2.6.7
Suatu persamaan yang berbentuk
( ) ( ) disebut persamaan diferensial Bernoulli.
Jika atau , persamaan diferensial adalah linear. Jika dan , persamaan Bernoulli dapat dibawa ke dalam persamaan diferensial linear dengan menggunakan teorema berikut.
Teorema 2.6.1
Jika dan maka persamaan diferensial ( ) ( ) dapat diubah menjadi persamaan diferensia linear dengan transformasi .
Bukti
Mula-mula kalikan persamaan diferensial dengan , diperoleh
Misalkan , maka
( )
atau
Masukkan nilai-nilai ini ke dalam persamaan diferensial yang diketahui maka diperoleh
( ) ( )
yang merupakan persamaan diferensial linear dalam dan .
Contoh 2.6.6
Selesaikan persamaan diferensial Bernoulli
Penyelesaian:
Dalam persamaan ini sehingga persamaan dikalikan dengan dan diperoleh
Misalkan maka
atau
Dengan memasukkan nilai-nilai ke dalam persamaan diperoleh
Kemudian semua ruas dikalikan dengan dan diperoleh
yang merupakan bentuk baku persamaan diferensial linear dalam x dan v. Faktor pengintegral persamaan ini adalah
∫
Setelah persamaan linear dikalikan dengan , maka diperoleh
atau
atau
( )
Kedua ruas diintegralkan menjadi
∫ ( ) ∫
Kemudian diganti dengan sehingga diperoleh
BAB III
MODEL PERTUMBUHAN POPULASI TUNGGAL
3.1 Pendahuluan
Dalam bab ini, akan dikembangkan model yang menggambarkan pertumbuhan dan penurunan populasi tunggal. Dalam penerapan pemodelan matematika terdapat beberapa model pertumbuhan, namun yang akan dibahas adalah model pertumbuhan kontinu. Model pertumbuhan kontinu meliputi model eksponensial dan model logistik yang masing-masing mempunyai kelemahan dan kelebihan.
Awalnya akan dimodelkan pertumbuhan eksponensial. Pada pertumbuhan eksponensial laju perubahan populasi dapat dihitung jika banyaknya kelahiran, kematian dan migrasi diketahui. Kemudian model pertumbuhan akan diperluas untuk memperhitungkan pertumbuhan bergantung pada kepadatan (pertumbuhan logistik). Model ini memasukkan batas untuk populasinya sehingga jumlah populasi dengan model ini tidak akan tumbuh secara tak berhingga. Laju pertumbuhan populasi terbatas akan ketersediaan makanan, tempat tinggal, dan sumber hidup lainnya. Dengan asumsi tersebut, jumlah populasi dengan model ini akan selalu terbatas pada suatu nilai tertentu.
3.2 Model Pertumbuhan Eksponensial
3.2.1 Model Umum
Secara umum model populasi dapat digambarkan seperti pada persamaan di bawah ini,
{ } = ,
- - , -. (3.1)
Persamaan tersebut akan dikembangkan dengan beberapa asumsi dan kemudian proses kelahiran dan kematian dinyatakan ke dalam simbol.
3.2.2 Model asumsi
Ketika dihadapkan pada populasi yang besar, diasumsikan bahwa setiap individu dalam populasi mempunyai kemungkinan yang sama untuk lahir dan menganggap bahwa setiap individu memiliki kemungkinan yang sama untuk mati dalam interval waktu tertentu. Dengan demikian masuk akal untuk membahas tentang laju kelahiran per-kapita per satuan waktu dan laju kematian per-kapita
per satuan waktu.
Asumsi tersebut dapat dirumuskan sebagai berikut:
1. Populasi cukup besar sehingga perbedaan acak antara individu dapat diabaikan.
2. Kelahiran dan kematian kontinu sepanjang waktu.
3. Laju kelahiran per-kapita dan laju kematian per-kapita konstan sepanjang waktu.
3.2.3 Merumuskan persamaan diferensial
Dimisalkan jumlah populasi pada saat t adalah X(t) dan populasi awal bernilai , dengan laju kelahiran per-kapita adalah dan laju kematian perkapita adalah . Tujuannya adalah untuk menemukan ukuran populasi pada waktu t. Langkah pertama adalah menentukan persamaan populasi. Diasumsikan bahwa penduduk hanya dapat berubah karena kelahiran atau kematian, imigrasi atau emigrasi diabaikan. Juga, diasumsikan bahwa perubahan populasi setiap saat sebanding dengan jumlah penduduk waktu itu.
Karena laju kelahiran perkapita diasumsikan konstan, maka laju kelahiran keseluruhan setiap waktu adalah laju kelahiran per-kapita dikalikan besarnya populasi saat itu. Demikian juga, untuk laju kematian keseluruhan adalah laju kematian perkapita dikalikan besarnya populasi saat itu. Ini dapat ditulis,
, - = X( t ),
, - = X( t ). (3.2)
Dari kedua persamaan di atas diperoleh
Sekarang sudah diperoleh persamaan diferensial yang menyatakan laju perubahan populasi ( ) Maka diperlukan suatu kondisi awal untuk mendapatan penyelesaian tunggal.
3.2.4 Penyelesian persamaan diferensial
Sekarang kita akan menyelesaikan persamaan (3.3) untuk pertumbuhan populasi yang kontinu. Dimisalkan , maka
Kita menyatakan bahwa adalah laju pertumbuhan atau laju reproduksi populasi.
∫ ∫
( )
( )
dengan , maka
( )
Misal , maka
( )
( )
( )
(3.4) Dari persamaan di atas terdapat tiga kasus, yaitu:
1. Untuk
Jika mendekati tak hingga, maka ( ) mendekati tak hingga. Untuk dan , maka gambarnya sebagai berikut:
Gambar 3.1: Grafik yang menyatakan laju perubahannya semakin bertambah.
2. Untuk ( )
Gambar 3.2: Grafik yang menyatakan laju perubahannya stabil.
3. Untuk
Jika mendekati tak hingga, maka ( ) mendekati .
Untuk dan , maka gambarnya sebagai berikut:
Gambar 3.3: Grafik yang menyatakan laju perubahannya semakin berkurang.
3.2.5 Interpretasi dari parameter
Dari laju kematian, dapat dibuat pendekatan angka kematian dengan mengalikan laju kematian dengan panjang interval waktu. Pendekatan ini biasanya lebih baik jika interval waktunya pendek. Maka dapat ditulis
{ } ( )
Dimisalkan bahwa individu akan meninggal setelah waktu , dengan
adalah harapan hidup rata-rata. Kemudian, dimisalkan ( ) dan sedemikian sehingga diperoleh
Oleh karena itu diperoleh
yang memberikan pendekatan untuk sebagai kebalikan pada harapan hidup rata-rata.
3.2.6 Contoh model pertumbuhan eksponensial
Tentukan waktu populasi mempunyai ukuran berganda! Penyelesaian:
( ) ( )
di mana T adalah waktu yang diperlukan untuk ukuran berganda. Maka, digunakan penyelesaian (3.4),
( )
( )
di mana
Maka, waktu yang diperlukan populasi berganda adalah ⁄
3.3 Model Pertumbuhan Logistik 3.3.1 Merumuskan persamaan differensial
{ } = ,
- - , - (3.5)
Diasumsikan laju kelahiran per-kapita konstan pada , maka
, - X( t ).
Dengan asumsi bahwa laju kematian per-kapita adalah tidak konstan, maka laju kematian per-kapita akan meningkat seiring dengan peningkatan populasi. Dengan asumsi bahwa laju kematian per-kapita bergantung linear pada suatu populasi, maka dapat dinyatakan sebagai berikut:
{
} ( ).
Laju kematian adalah laju kematian perkapita dikalikan besarnya populasi saat itu yang dinyatakan sebagai berikut:
, - (3.6)
Jadi,
Dengan menyatakan laju reproduksi, maka diperoleh model pertumbuhan yang bergantung pada kepadatan suatu populasi yang dinyatakan sebagai berikut:
( ) (3.7)
( )
Penyelesaian dapat ditulis
∫ ( )
Integral dapat ditulis dengan memecah integran menjadi jumlah dua pecahan parsial yang berbentuk
( )
Kedua ruas dikalikan ( ) maka dihasilkan
( )
( )
Untuk menentukan A, ambil , sehingga diperoleh .
Untuk menentukan B, ambil – , substitusikan dengan , sehingga
diperoleh .
( )
( )
Kemudian semua ruas diintegralkan
∫ ( ) ∫ ∫ ∫
Terlebih dahulu akan dihitung
∫ ∫
Dengan cara substitusi: Misal :
,
,
Maka:
∫ ∫ ∫
Jadi, dapat diintegralkan untuk memperoleh
| | | |
( | | | |)
.
| |
| |/
.| |/ | |
| |
| |
Dengan , maka
| |
| | | |
| |
| | | |
( )
( )
[ (
*]
Dengan , di mana , maka
( ) ( )
Jika , maka diperoleh
( )
Dengan keadaan awal ( ) diperoleh bahwa ( ) dan
( ) ⁄
Maka dapat ditulis
Untuk laju kelahiran dan laju kematian normal per-kapita, diasumsikan konstan yaitu dan . Jika diberikan ( di mana adalah konstan positif ), maka laju kematian ekstra adalah tlaju kematian ekstra per-kapita dikalikan dengan jumlah populasi pada saat itu. Maka diperoleh
Model ini termasuk ke dalam persamaan diferensial nonlinear. Ini adalah persamaan logistik dan juga sebagai model pertumbuhan terbatas atau model bergantung kepadatan. Untuk dan maka diperoleh nilai populasi yang positif.
3.3.3 Interpretasi dari parameter
Dengan melihat kembali pada bab 3.1 untuk pertumbuhan populasi yang kontinu
Bentuk umum persamaan diferensial untuk pertumbuhan dapat ditulis
( )
dengan ( ) merepresentasikan laju pertumbuhan per-kapita bergantung populasi. Ini adalah persamaan logistik dari laju pertumbuhan per-kapita bergantung populasi, dan dari persamaan (3.8) dapat diidentifikasikan ( ) sebagai
( ) ( )
Dapat dilihat bahwa ( ) suatu fungsi linear dari , dan akan mendekati
Gambar 3.4: Grafik untuk populasi tingkat pertumbuhan per-kapita dinyatakan sebagai garis lurus.
3.3.4 Penyelesaian Equilibrium dan Kestabilan
Dengan melihat persamaan (3.2) sangat tepat untuk memodelkan pertumbuhan populasi dalam kondisi ideal. Namun juga harus dikenali bahwa, sebuah lingkungan memiliki sumber daya yang terbatas. Banyak populasi dimulai dengan bertambah secara eksponensial, tetapi grafik populasi tersebut akan mendatar pada saat populasi tersebut mendekati (kapasitas tampung) atau menurun menuju jika populasi tersebut melampaui .
( *
Ingat bahwa apabila nilai jauh lebih kecil dibandingkan , maka ⁄ mendekati 0 sehingga ⁄ . Jika maka ⁄ bernilai negatif
sehingga ⁄ .
salah satu faktor pada bagian sebelah kanan adalah nol. Jika populasi tersebut adalah 0 atau besarnya sama dengan (kapasitas tampung), maka populasinya akan tetap sama. Dua solusi konstanta ini disebut dengan solusi keseimbangan (ekuilibrium). Jika populasi awal ( ) berada antara dan maka ruas kanan
persamaan di atas bernilai positif, sehingga ⁄ dan populasinya meningkat. Akan tetapi jika populasi tersebut melampaui kapasitas tampungnya ( ), maka ⁄ bernilai negatif, sehingga ⁄ dan populasinya menurun. Ingat bahwa pada kedua kasus ini, jika populasinya mendekati kapasitas tampung ( ), maka ⁄ , sehingga populasinya cenderung tidak akan berubah. Jadi, diperkirakan bahwa solusi persamaan diferensial logistik tersebut memiliki grafik seperti di bawah ini:
Gambar 3.5: Grafik yang menunjukkan solusi kesetimbangan.
Tampak bahwa pada gambar 3.5, untuk grafik bergerak menjauh dari solusi kesetimbangan dan bergerak ke arah solusi kesetimbangan . Untuk mengetahui kecekungan pada grafik fungsi di atas maka diperlukan analisis turunan kedua dari , yaitu
X=K
(
* ( * (
*
Dengan menggunakan Teorema Kecekungan (Teorema 2.4.12) pada kalkulus, maka diperoleh hasil bahwa
1. Jika , maka dan cekung ke atas.
2. Jika , maka dan cekung ke bawah.
Sebagai contoh untuk dan , maka grafiknya menjadi:
Gambar 3.6: Grafik untuk model petumbuhan logistik.
3.4 Model Pertumbuhan Terbatas dengan Pemanenan