BAB 2
LANDASAN TEORI
2.1 Model Transportasi
Menurut Mulyono (2004, p114) persoalan transportasi membahas masalah pendistribusian suatu komoditas atau prouk dari sejumlah sumber (supply) kepada sejumlah tujuan (destination, demand) dengan tujuan meminimumkan ongkos pengangkutan yang terjadi.
Ciri-ciri khusus persoalan transportasi ini adalah: 1. Terdapat sejumlah sumber dan sejumlah tujuan tertentu.
2. Kuantitas komoditas atau barang yang didistribusikan dari setiap sumber dan yang diminta oleh setiap tujuan, besarnya tertentu.
3. Barang yang dikirim atau diangkut dari suatu sumber ke suatu tujuan, besarnya sesuai dengan permintaan dan kapasitas sumber.
4. Ongkos pengangkutan komoditas dari suatu sumber ke suau tujuan, besarnya tertentu.
Secara diagramatik, model transportasi dapat digambarkan sebagai berikut: Misalkan ada m buah sumber dan n buah tujuan.
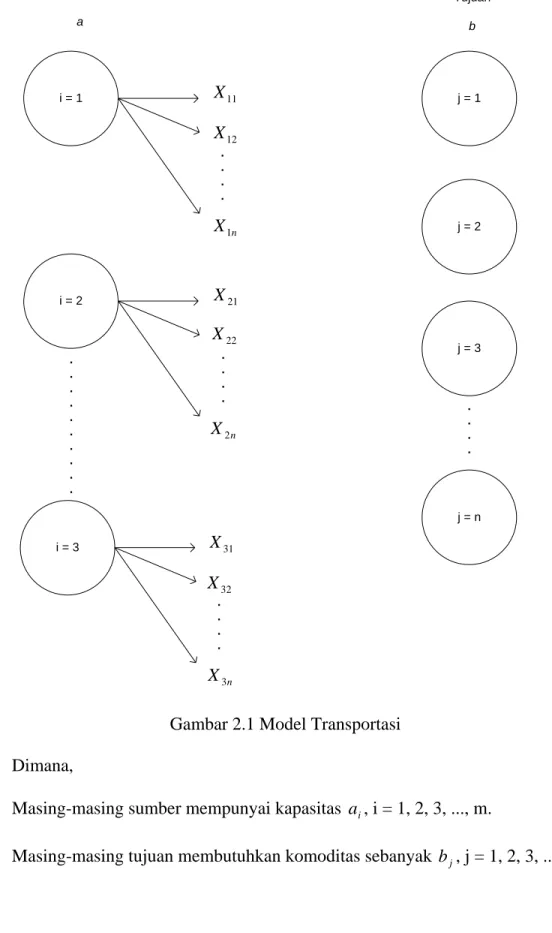
Sumber a Tujuan b i = 1 X11 12 X n X1 . . . . i = 2 X21 22 X n X2 . . . . . . . . . . . . . . i = 3 X31 32 X n X3 . . . . j = 1 j = 2 j = 3 . . . . j = n
Gambar 2.1 Model Transportasi Dimana,
Masing-masing sumber mempunyai kapasitas a , i = 1, 2, 3, ..., m. i
Jumlah satuan (unit) yang dikirimkan dari sumber i ke tujuan j adalah sebanyak
ij X
Ongkos pengiriman per unit dari sumber i ke tujuan j adalah C . ij
Dengan demikian perumusan matematisnya adalah sebagai berikut:
Meminimumkan: z =
∑∑
= = m i n j ij ijX C 1 1 Berdasarkan pembatas: X ai i m n j ij , 1,2,3,..., 1 = =∑
= n j b X i m i ij , 1,2,3,..., 1 = =∑
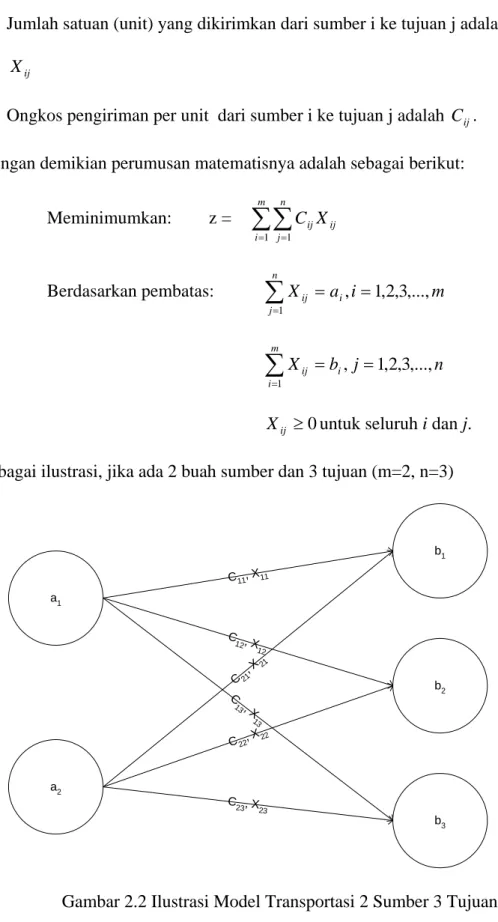
= 0 ≥ ijX untuk seluruh i dan j. Sebagai ilustrasi, jika ada 2 buah sumber dan 3 tujuan (m=2, n=3)
a1 a2 b1 b2 b3 C11, X11 C 12, X 12 C 13, X 13 C21, X 21 C22, X22 C 23, X23
Perumusan matematis: Meminimumkan: 23 23 22 22 21 21 13 13 12 12 11 11X C X C X C X C X C X C z= + + + + + Berdasarkan pembatas: 3 23 13 2 22 12 1 21 11 2 23 22 21 1 13 12 11 b X X b X X b X X a X X X a X X X = + = + = + = + + = + +
Sedangkan matriks berupa tabel dari persamaan tersebut dapat dilihat pada gambar berikut: 1 2 3 Supply 1 C11 X11 C12 X12 C13 X13 a1 2 C21 X21 C22 X22 C23 X23 a2 b1 b3 b3
Gambar 2.3 Matriks Transportasi dalam Tabel 2.2 Model Transshipment
Suatu perluasan dari rumusan transportasi adalah masalah transshipment (pemindahan), dimana setiap sumber dan tujuan dapat juga menjadi titik perantara pengiriman dari sumber-sumber atau tujuan-tujuan lain. Berikut adalah diagram contoh model transshipment.
tujuan pembatas sumber pembatas tujuan sumber (i) demand
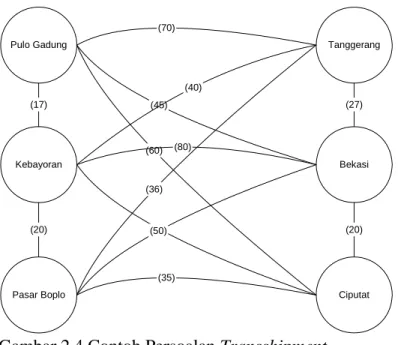
Pulo Gadung Kebayoran Pasar Boplo Sumber ( i ) Supply (bal) (70) (80) (50) Biaya (70) Tanggerang Bekasi Ciputat (45) (60) (40) (80) (36) (50) (35) Demand (bal) (40) (100) (60) (20) (27) (17) (20)
Gambar 2.4 Contoh Persoalan Transshipment
Dalam model ini setiap sumber maupun tujuan dipandang sebagai titik-titik potensial bagi demand maupun supply. Oleh karena itu, untuk menjamin bahwa tiap titik potensial tersebut mampu manampung total barang di samping jumlah barang yang telah ada pada titik-titik itu kuantitas supply dan demand-nya masing-masing sebesar B.
∑
∑
= = = ≥ m j j m i i b a B 1 1dari pemodelan transportasi.
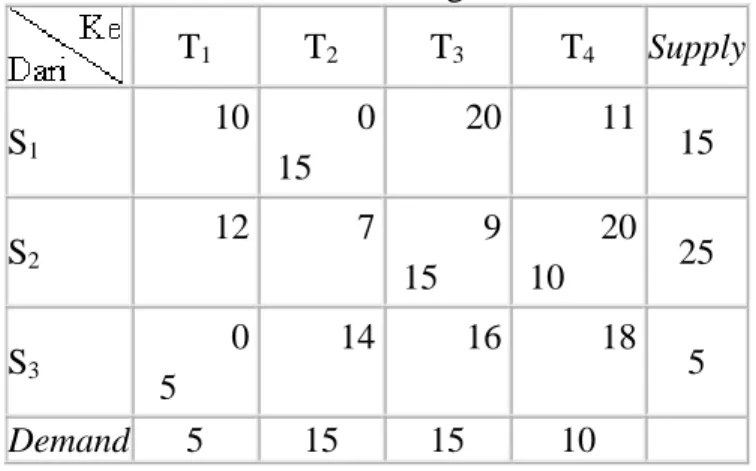
Dengan demikian, bila ada persoalan transportasi sebagai berikut: Tabel 2.1 Contoh Persoalan Transportasi
T1 T2 T3 Supply S1 10 20 30 100 S2 20 50 40 200 Demand 100 100 100
Maka pemodelan transshipment-nya adalah:
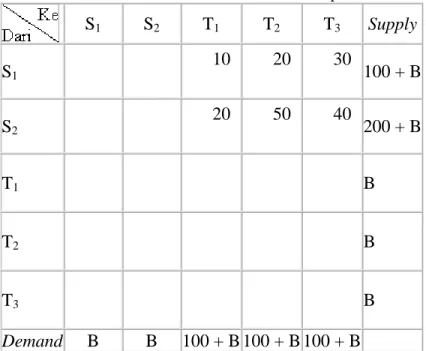
Tabel 2.2 Contoh Persoalan Transshipment
S1 S2 T1 T2 T3 Supply S1 10 20 30 100 + B S2 20 50 40 200 + B T1 B T2 B T3 B Demand B B 100 + B 100 + B 100 + B
Model diatas baru lengkap apabila ongkos per unit pengangkut untuk baris-baris-baris dan kolom-kolom yang lainnya telah ditetapkan. Dalam hal ini perlu diingat bahwa ongkos per unit pada elemen-elemen diagonal adalah nol.
2.3 Metode Northwest-Corner
Metode Northwest-Corner digunakan untuk menentukan solusi awal. Langkah-langkahnya adalah sebagai berikut:
Mulai dari pojok barat laut tabel dan alokasikan sebanyak mungkin pada X11
tanpa menyimpang dari kendala penawaran atau permintaan (artinya X11
ditetapkan sama dengan yang terkecil di antara nilai supply dan demand)
) ,
min( 1 1
11 a b
X = , jika b1 <a1 maka X11 =b1; jika b1 >a1 maka X11 =a1. Kalau 1
11 b
X = , maka yang mendapat giliran untuk dialokasikan adalah X12sebesar
) ,
giliran untuk dialokasikan adalah X12 sebesar min(b1 −a1,a2). Demikian seterusnya.
Contoh:
Tabel 2.3 Tabel Hasil Perhitungan Metode Northwest-Corner
T1 T2 T3 T4 Supply S1 10 5 0 10 20 11 15 S2 12 7 5 9 15 20 5 25 S3 0 14 16 18 5 5 Demand 5 15 15 10 5 ) 5 , 15 min( 5 ; 15 1 11 1 = b = ⎯⎯→X = = a 10a1−b1 =10;b2 =15⎯⎯→X12 =min(10,15)=
Langkah selanjutnya adalah mengisi b2 sampai penuh dengan mengalokasikan sebesar 5 pada X22, yaitu jumlah kekurangan yang terjadi dalam pemenuhan kebutuhan pada b2.
Dengan melanjutkan prosedur di atas, maka akan diperoleh berturut-turut: 5
, 15 24 23 = X =
X dan X34= 5, yang bersama-sama dengan X11, X12, dan X22 membentuk solusi layak basis awal Z = 410.
2.4 Metode Least Cost
Metode Least Cost atau ongkos terkecil berusaha mencapai tujuan minimisasi biaya dengan alokasi sistematik kepada kotak-kotak sesuai dengan besarnya biaya transpor per unit.
Prosedur metode ini adalah:
1. Plih variabel X (kotak) dengan biaya transpor (ij C ) terkecil dan alokasikan ij
sebanyak mungkin. Untuk Cij terkecil, Xij= minumum (Supplyi,Demandj). Ini akan menghabiskan baris i atau kolom j.
2. Dari kotak-kotak sisanya yang layak (yaitu yang tidak terisi atau tidak terhilangkan), pilih nilai Cij terkecil dan alokasikan sebanyak mungkin.
3. Lanjutkan proses ini sampai semua penawaran dan permintaan terpenuhi. Contoh:
Tabel 2.4 Tabel Hasil Perhitungan Metode Least Cost
T1 T2 T3 T4 Supply S1 10 0 15 20 11 15 S2 12 7 9 15 20 10 25 S3 0 5 14 16 18 5 Demand 5 15 15 10
Dengan mengambil contoh diatas, C12 = C31 =0adalah ongkos terkecil dari keseluruhan tabel. Maka X12dan X31 mendapat prioritas pengalokasikan pertama kali. Jumlah unit yang dialokasikan masing-masing adalah X12 = min (Supply1,Demand2) = 15. dan X31 = min (Supply3,Demand1) = 5. Selanjutnya lihat ongkos terkecil berikutnya, yaitu C22= 7. Tetapi, karena tujuan kedua
(Demand2) telah terisi penuh, maka lihat ongkos terkecil berikutnya, diperoleh
23
menjalankan prosedur di atas, diperolah X24=10. Maka X12,X31,X23dan X24
bersama-sama membentuk solusi layak basis awal Z = 335. 2.5 Metode Pendekatan Vogel
Metode Pendekatan Vogel atau Vogel’s Approximation Method (VAM) melakukan alokasi dalam suatu cara yang akan meminimumkan penalty (opportunity cost) dalam memilih kotak yang salah untuk suatu alokasi. Proses Metode Pendekatan Vogel dapat diringkas sebagai berikut:
1. Hitung penalty untuk tiap kolom dan baris dengan jalan mengurangkan elemen ongkos terkecil dari yang kedua terkecil.
2. Selidiki kolom atau baris dengan penalty terbesar. Alokasikan sebanyak mungkin pada variabel dengan ongkos terkecil, sesuaikan supply dan demand, kemudian tandai kolom atau baris yang sudah terpenuhi. Kalau ada 2 buah kolom atau baris yang sudah terpenuhi secara simultan, pilih salah satu untuk ditandai, sehingga supply atau demand sama dengan nol, tidak akan terbawa lagi dalam perhitungan penalty pada iterasi berikutnya.
3. Bila tinggal 1 kolom atau baris yang belum ditandai, stop iterasi.
Bila tinggal 1 kolom atau baris dengan supply atau demand positif yang belum ditandai, tentukan variabel basis pada kolom atau baris dengan cara ongkos terkecil (least cost).
Bila semua baris dan kolom yang belum ditandai mempunyai supply dan
demand sama dengan nol, tentukan variabel-variabel basis yang berharga nol dengan cara ongkos terkecil, kemudian stop.
Jika syarat-syarat diatas tidak terjadi, hitung kembali penalty untuk baris atau kolom yang belum ditandai. Kembali ke nomor 2.
Contoh:
Tabel 2.5 Tabel Perhitungan Iterasi Pertama Vogel
T1 T2 T3 T4 Supply Penalty Baris S1 10 0 20 11 15 10 S2 12 7 9 20 25 2 S3 0 14 16 18 5 14 Demand 5 15 15 10 Penalty Kolom 10 7 7 7
Kerena baris ketiga memiliki penalty terbesar (=14) dan karena C31= 0 merupakan ongkos terkecil di dalam barisnya, maka dialokasikan X31 = 5. Dengan demikian, baris 3 dan kolom 1 sudah terpenuhi secara simultan. Dalam hal ini bisa dipilih baris 3 atau kolom 1 yang akan ditandai. Misalkan dipilih kolom 1 untuk ditandai, maka sisa supply untuk baris 3 menjadi 0.
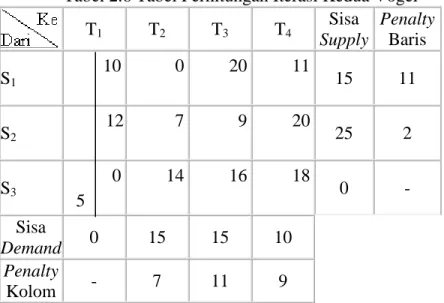
Tabel 2.6 Tabel Perhitungan Iterasi Kedua Vogel T1 T2 T3 T4 Sisa Supply Penalty Baris S1 10 0 20 11 15 11 S2 12 7 9 20 25 2 S3 0 5 14 16 18 0 - Sisa Demand 0 15 15 10 Penalty Kolom - 7 11 9
Selanjutnya ulangi kembali perhitungan penalty. Dapat dilihat bahwa baris 1 dan kolom 3 mempunyai penalty yang sama (=11) sehingga kembali dapat dipilih salah satu untuk ditandai. Misalkan dipilih kolom 3 untuk ditandai, maka alokasikan X23=15. Sisa supply untuk baris 2 sekarang menjadi 10.
Tabel 2.7 Tabel Perhitungan Iterasi Ketiga Vogel
T1 T2 T3 T4 Sisa Supply Penalty Baris S1 10 0 20 11 15 11 S2 12 7 9 15 20 10 13 S3 0 5 14 16 18 0 - Sisa Demand 0 15 0 10 Penalty Kolom - 7 - 9
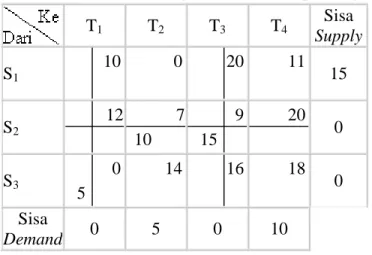
Dengan menghitung penalty yang baru diperoleh penalty terbesar untuk baris 2 (=13) sehingga alokasikan X22= 10. Kemudian tandai baris 2.
Tabel 2.8 Tabel Perhitungan Iterasi Keempat Vogel T1 T2 T3 T4 Sisa Supply S1 10 0 20 11 15 S2 12 7 10 9 15 20 0 S3 0 5 14 16 18 0 Sisa Demand 0 5 0 10
Supply yang masih tersedia adalah 15 (baris 1), sedangkan demand yang belum terpenuhi adalah kolom 2 sebanyak 5 dan kolom 4 sebanyak 10.
Karena tidak ada pilihan lain, maka alokasikan X12= 5 dan X14=10 dengan metode least cost. Pengisian tabel selesai dengan solusi layak basis awal Z = 315:
, 15 , 10 , 10 , 5 14 22 23 12 = X = X = X = X dan X31 = 5.
Tabel 2.9 Hasil Akhir Alokasi dengan Metode Pendekatan Vogel
T1 T2 T3 T4 Supply S1 10 0 5 20 11 10 15 S2 12 7 10 9 15 20 25 S3 0 5 14 16 18 5 Demand 5 15 15 10
2.6 Metode Pendekatan Russell
1. Untuk setiap baris Supplyi yang masih menjadi pertimbangan atau belum terisi, tentukanlah ui yang merupakan biaya per unit (C ) terbesar yang masih ij
ada dalam baris tersebut.
2. Untuk setiap kolomDemandjyang masih menjadi pertimbangan atau belum terisi, tentukanlah vj yang merupakan biaya per unit (Cij) terbesar yang masih ada dalam kolom tersebut.
3. Untuk setiap variabel X yang sebelumnya belum dipilih dalam baris-baris ij
dan kolom-kolom ini, hitunglah Δij =Cij −ui −vj.
4. Pilih variabel yang mempunyai nilai negatif (mutlak) terbesar dari Δ (kalau ij ada yang sama pilih secara arbitrer). Lanjutkan proses ini mulai dari nomor 1 lagi sampai tidak ditemukan nilai negatif (mutlak) terbesar dari Δ . ij
Contoh:
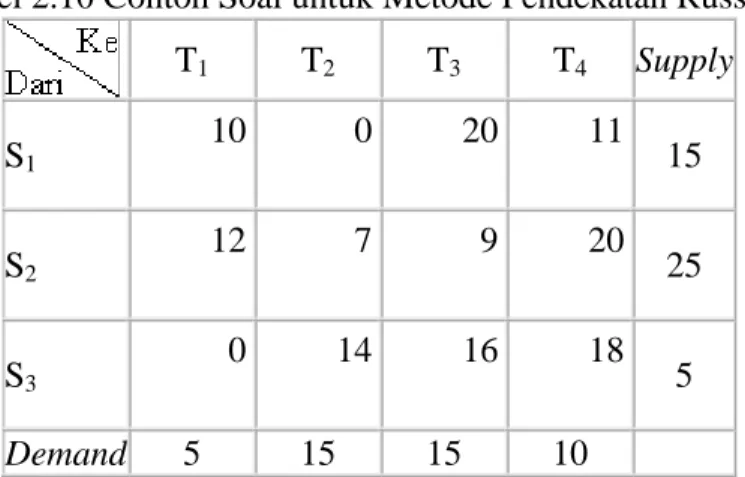
Tabel 2.10 Contoh Soal untuk Metode Pendekatan Russell
T1 T2 T3 T4 Supply S1 10 0 20 11 15 S2 12 7 9 20 25 S3 0 14 16 18 5 Demand 5 15 15 10
Hasil perhitungan iterasi pertama contoh soal dihitung secara berurutan dapat dilihat pada Tabel 2.11 dibawah ini.
Tabel 2.11 Hasil Iterasi Pertama Russell 1 u u2 u3 v1 v2 v3 v4 Δ ij Alokasi 20 20 18 12 14 20 20 Δ11 = -22 = Δ12 -34 * = Δ13 -20 = Δ14 -29 = Δ21 -20 = Δ22 -27 = Δ23 -31 = Δ24 -20 = Δ31 -30 = Δ32 -18 = Δ33 -22 = Δ34 -20 = 12 X 15
Dari tabel 2.11 dapat dilihat nilai Δ negatif terbesar ada pada ij Δ12 sehingga alokasi sebanyak mungkin pada X12 = min(Supply1, Demand2) = 15 sebagai variabel dasar (alokasi) pertama. Karena telah memenuhi Supply1dan Demand2
maka baris 1 dan kolom 2 tidak menjadi pertimbangan lebih lanjut.
Hasil-hasil perhitungan iterasi berikutnya termasuk urutan variabel-variabel dasar (alokasi-alokasi), diperlihatkan dalam Tabel 2.12.
Tabel 2.12 Hasil Perhitungan Semua Iterasi Russell
Iterasi u1 u2 u3 v1 v2 v3 v4 Δ terkecil ij Alokasi
1 2 3 4 20 20 18 - 20 18 - 20 - - 20 - 12 14 20 20 12 - 16 20 - - 9 20 - - - 20 = Δ12 -34 = Δ31 -30 = Δ23 -20 = Δ24 -20 = 12 X 15 = 31 X 5 = 23 X 15 = 24 X 20
Alokasi secara penuh hasil perhitungan metode pendekatan Russell dengan solusi basis awal Z = 335 : X12, X31,X23, dan X24 disajikan dalam Tabel 2.13.
Tabel 2.13 Hasil Akhir Alokasi Metode Pendekatan Russell
T1 T2 T3 T4 Supply S1 10 0 15 20 11 15 S2 12 7 9 15 20 10 25 S3 0 5 14 16 18 5 Demand 5 15 15 10 2.7 Metode Multiplier
Setelah solusi layak dasar awal diperoleh dari masalah transportasi, langkah berikutnya adalah menekan kebawah biaya transpor dengan memasukkan variable nonbasi (yaitu alokasi barang ke kotak kosong ke dalam solusi). Proses evaluasi variable nonbasis yang memungkinkan terjadinya perbaikan solusi dan kemudian mengalokasikan kembali dinamakan Metode multiplier. Cara ini dikembangkan berdasarkan teori dualitas. Untuk tiap basis i dari tabel transformasi dikenal suatu
multiplier ui, dan untuk kolom j disebut multiplier V sehingga untuk tiap variabel j
basis Xij didapat persamaan: ui +vj +Cij.
Dari persamaan di atas dapat dihitung beberapa penurunan ongkos transportasi per unit untuk tiap variabel nonbasisXij sebagai berikut:
j i ij
ij X u v
C = − − .
Sebagai contoh ada solusi awal yang telah didapat dari Metode
Nortwest-Corner
Tabel 2.14 Solusi Awal Hasil Perhitungan Metode Nortwest-Corner
T1 T2 T3 T4 Supply S1 10 5 0 10 20 11 15 S2 12 7 5 9 15 20 5 25 S3 0 14 16 18 5 5 Demand 5 15 15 10 Basis awal: 11 X : u1 +v1 =C11 =10 12 X : u1 +v2 =C12 =0 22 X : u2 +v2 =C22 =7 23 X : u2 +v3 =C23 =9 24 X : u2 +v4 =C24 =20 34 X : u3 +v4 =C34 =18
Dengan menentukan ui =0, maka harga-harga multiplier yang lain dapat dicari sebagai berikut:
10 1 1 + v = u Æ v1 =10 0 2 1 + v = u Æ v2 =0 7 2 2 + v = u Æ u2 =7 9 3 2 + v = u Æ v3= 2 20 4 2 + v = u Æ v4 =13 18 4 3 + v = u Æ u3 = 5
Tabel 2.15 Perhitungan Iterasi Pertama Multiplier
10 v1 = v2 =0 v3 = 2 v4 =13 0 = i u 10 • 0 • 20 +18 11 -2 7 u2 = 12 -5 7 • 9 • 20 • 5 u3 = 0 -15 14 +9 16 +9 18 • 5 15 15 10
Untuk menentukan entering variable, alokasi yang sudah terpenuhi (disimbolkan dengan •) tidak diperhitungkan :
5 2 1 21 21 =C −v −u =− C 15 1 3 31 31 =C −v −u =− C 18 3 1 13 13 =C −v −u = C 2 4 1 14 14 =C −v −u =− C 9 2 3 32 32 =C −v −u = C
9 3 3 33 33 =C −v −u = C
Entering variable adalah X karena memberikan penurunan ongkos per unit 31
yang terbesar, yaitu sebanyak 15 satuan ongkos per unit. Dengan demikian, dapat dibuat sebuah loop yang berawal dan berakhir pada variabel X . 31
Tabel 2.16 Tabel Closed-Loop Iterasi Pertama
T1 T2 T3 T4 Supply S1 10 5 0 10 20 11 15 S2 12 7 5 9 15 20 5 25 S3 10 X 31 14 16 18 5 5 Demand 5 15 15 10 - + - + -+
Tanda - dan + menyatakan bahwa variabel yang bersangkutan (pada
masing-masing kotak) akan bertambah atau berkurang besarnya sebagai akibat perpindahan kolom dan perpindahan baris.
Leaving variable dipilih dari variabel-varibel sudut loop yang bertanda - .
Pada contoh di atas, di mana X telah terpilih sebagai entering variable, calon-31 calon leaving variable-nya adalah X11,X22, dan X34. Dari calon-calon ini, pilihlah salah satu yang nilainya paling kecil.
Pada contoh diatas kebetulan ketiganya bernilai sama (=5) sehingga bisa dipilih salah satu untuk dijadikan leaving variable. Misalkan X34 dipilih sebagai
leaving variable, maka nilai X naik 5 dan nilai-nilai variabel basis yang di sudut 31
Solusi baru ini adalah seperti pada tabel berikut dengan ongkos transportasi sebesar: (0 x 10) + (15 x 0) + (0 x 7) + (15 x 9) + (10 x 20) + (5 x 0) = 335.
Tabel 2.17 Hasil Iterasi Pertama Setelah Perputaran Nilai Pada Closed-Loop
T1 T2 T3 T4 Supply S1 10 0 0 15 20 11 15 S2 12 7 0 9 15 20 10 25 S3 10 5 14 16 18 5 Demand 5 15 15 10
Bandingkan dengan solusi awal pada Tabel 2.4 yang ongkos transportasinya adalah = 410. Selisih ongkos transportasi (410 – 335 = 75) sama dengan hasil perkalian antara: jumlah unit yang ditambahkan pada X x penurunan ongkos per 31
unit Ù (5) x (15).
Perhatikan, angka 0 pada X11danX22 adalah variabel basis yang berharga 0. Jadi, tidak boleh dihilangkan karena ia tidak sama dengan kotak-kotak lain yang tidak ada angkanya (variabel nonbasis).
Sampai tahap ini masih harus memeriksa, barangkali nilai fungsi tujuan masih bisa diperbaiki. Untuk itu lakukanlah kembali langkah-langkah yang sudah dikerjakan sebelumnya, dengan mengunakan Tabel 2.17 sebagai solusi awal (pengganti Tabel 2.14). Sehingga didapat:
Variabel nonbasis Perubahan ongkos per unit 13
X C13 =+18
21 X C21 =−5 32 X C32 =+24 33 X C33 =+24 34 X C34 =+15
Dengan demikian dipilih X21 sebagai entering variable. Tabel 2.18 Tabel Perhitungan Iterasi Kedua Multiplier
T1 T2 T3 Toko4 Supply S1 10 0 0 15 20 11 15 S2 12 X21 7 0 9 15 20 10 25 S3 10 5 14 16 18 5 Demand 5 15 15 10 + -+
Tabel 2.19 Tabel Perhitungan Iterasi Ketiga Multiplier
T1 T2 T3 T4 Supply S1 10 0 15 20 11 14 X 15 S2 12 0 7 0 9 15 20 10 25 S3 10 5 14 16 18 5 Demand 5 15 15 10 + -+
Pada loop yang berasal dan berakhir pada X21 ini, leaving variable-nya ada dua, yaitu X11danX22. Karena keduanya berharga 0, bisa dipilih salah satu untuk dijadikan leaving variable. Misalkan X11 adalah leaving variable, maka X21 = 0
dengan ongkos transportasi tetap 335. Karena itu, dicoba membuat loop dari variabel nonbasis yang lain, yang juga dapat menurunkan ongkos transportasi per unit (yaitu X14). Maka didapat: C11=+5;C32 =+19;C13 =+18;C33 =+19;
2 ;
10
;C34=+ C14 =− .
Dari Tabel 2.10 terlihat bahwa leaving variable adalah X24 sehingga X14= 10; X22 = 10; dan X12 = 5.
Solusi optimal adalah :
Tabel 2.20 Tabel Hasil Akhir Perhitungan dengan Metode Multiplier
T1 T2 T3 T4 Supply S1 10 0 5 20 11 15 S2 12 0 7 10 9 15 20 25 S3 10 5 14 16 18 5 Demand 5 15 15 10
Dengan ongkos transportasi Z = 315. 2.8 Pengetahuan Dasar Algoritma
Dalam konteks matematika dan ilmu komputer, algoritma adalah sebuah prosedur (Suatu himpunan instruksi yang terdeskripsi dengan jelas beserta dengan urutan pengerjaannya) untuk menyelesaikan suatu tugas, dengan diberikan suatu kondisi awal, dan akan berhenti pada kondisi akhir yang telah diketahui. Secara informal, konsep dari algoritma diilustrasikan dengan contoh sebuah resep.
Konsep algoritma berawal pada penggabungan urutan-urutan prosedur menjadi satu untuk menyelesaikan permasalahan matematik, seperti mencari faktor
persekutuan terbesar dari dua bilangan. Konsep tersebut diresmikan pada tahun 1936 melalui Mesin Turing Alan Turing, dan kalkulus lambda Alonzo Church, yang pada akhirnya membentuk fondasi ilmu komputer. Kebanyakan algoritma dapat diimplementasikan secara langsung ke dalam bahasa pemrograman, algoritma lainnya setidaknya dapat disimulasikan secara teoritis oleh program komputer.
2.8.1 Sejarah Singkat Algoritma
Kata algoritma berasal dari nama seorang matematikawan Persia abad ke-9 Abu Abdullah Muhammad bin Musa al-Khwarizmi. Kata algoritma pada awalnya hanya merupakan istilah yang diperuntukkan aturan-aturan dalam melakukan operasi aritmatik menggunakan bilangan Hindu-Arab, namun pada evolusinya melalui terjemahan eropa latin nama al-Khwarizmi diterjemahkan menjadi
algorithm pada abad 18. Definisnya pun mengalami pengembangan sehingga dapat
berarti semua prosedur untuk menyelesaikan suatu masalah atau untuk melakukan suatu tugas.
Pertama kali suatu algoritma ditulis untuk komputer berjudul Ada Byron’s
notes on the analitycal engine pada tahun 1842, di mana nama Ada Byron diterima
secara luas sebagai programmer pertama di dunia. Namun, karena Charles Babbage tidak pernah menyelesaikan analytical engine-nya, algoritma tersebut pun tidak pernah diimplementasikan.
2.8.2 Pseudocode
Algoritma adalah kumpulan langkah-langkah untuk melakukan perhitungan. Kebanyakan algoritma akan diimplementasikan sebagai program komputer. Algoritma dapat ditulis dalam notasi apapun termasuk dalam Bahasa Inggris untuk
tujuan dokumentasi dan penelitian. Namun suatu cara yang lebih disukai untuk menulis algoritma adalah dengan menulisnya dalam bentuk pseudocode. Notasi
pseudocode dapat menghindari ambiguitas dalam bahasa, dan juga dapat
diterjemahkan ke dalam bahasa pemrograman secara langsung.
Salah satu contoh dari algoritma yang paling sederhana adalah untuk menemukan bilangan yang paling besar dari suatu daftar bilangan tidak terurut, yang apabila ditulis dalam Bahasa Inggris adalah sebagai berikut:
1. Let us assume the first item is largest.
2. Look at each of the remaining items in the list and make the following adjustment.
If it is larger than the largest item we gathered so far, make a note of it. 3. The latest noted item is the largest in the list when the process is complete.
Algoritma di atas apabila ditulis menjadi pseudocode menjadi seperti berikut di bawah ini:
Algorithm LargestNumber
Input: A non-empty list of numbers L. Output: The largest number in the list L. largest ← L0
for each item in the list L≥1, do
if the item > largest, then largest ← the item
return largest
Gambar 2.5 Gambar Pseudocode Mencari Nilai Terbesar 2.8.3 Analisis Algoritma
Pada prakteknya, kebanyakan orang yang mengimplementasikan algoritma ingin mengetahui seberapa banyak sumber daya tertentu yang diperlukan untuk algoritma tersebut. Sumber daya yang dimaksud di sini adalah storage (besar memori komputer) dan waktu. Beberapa metode telah dikembangkan untuk
memberikan jawaban yang bersifat kuantitatif untuk pertanyaan di atas; misalnya, algoritma pencarian bilangan terbesar seperti yang pernah disebut sebelumnya memerlukan waktu O(n), menggunakan notasi big O, dengan n sebagai jumlah bilangan yang terdapat pada daftar. Pada setiap satuan waktu, algoritma di atas hanya perlu menyimpan 2 nilai: bilangan terbesar yang telah ditemukan sampai saat tersebut, dan posisi sekarang pada daftar. Oleh karena itu, algoritma tersebut dikatakan memerlukan storage O(1).
Algoritma yang berbeda mungkin dapat menyelesaikan tugas yang sama dengan kumpulan instruksi yang berbeda, yang dapat berakibat pada perbedaan waktu dan/atau storage yang diperlukan.
Waktu proses (computing time) suatu algoritma, dapat dibedakan mejadi dua hal, yaitu:
1. Apriori analysis, yaitu analisis untuk mendapatkan waktu proses dalam bentuk fungsi matematik, yang disebut sebagai fungsi batas waktu proses. Analisis ini dilakukan sebelum algoritma tersebut diproses dengan suatu komputer. Fungsi waktu ini sering disimbolkan dengan notasi Big O.
2. Aposteriortesting, yaitu analisis untuk mendapatkan waktu proses aktual suatu algoritma. Hasil perhitungan waktu didapat pada saat algoritma diproses pada suatu komputer.
2.8.4 Notasi Big O
Dalam membandingkan kecepatan proses algoritma selanjutnya, penulis menggunakan notasi Big O karena notasi ini paling luas digunakan di dunia komputer dibanding notasi-notasi lainnya.
Notasi Big O merupakan suatu notasi matematika untuk menjelaskan batas atas dari magnitude suatu fungsi dalam fungsi yang lebih sederhana. Dalam dunia ilmu komputer, notasi ini sering digunakan dalam analisis kompleksitas algoritma.
Notasi Big O pertama kali diperkenalkan pakar teori bilangan Jerman, Paul Bachman tahun 1894, pada bukunya yang berjudul Analytische Zahlentheorie edisi kedua. Notasi tersebut kemudian dipopulerkan oleh pakar teori bilangan Jerman lainnya, Edmund Landau, dan oleh karena itu, terkadang disebut sebagai symbol Landau.
Notasi Big O sangat berguna saat menganalisis efisiensi suatu algoritma. Sebagai contoh, waktu (atau jumlah langkah) yang diperlukan oleh suatu algoritma untuk menyelesaikan tugas dengan ukuran n adalah T(n) = 4n2-2n+2. Untuk n yang besar, hasil perhitungan n2 menjadi dominan, sehingga perhitungan yang lain dapat diabaikan (misalnya saat n=500, 4n2 1000 kali lebih besar dari 2n, sehingga mengabaikan 2n+2 tidak akan membawa efek yang besar pada tujuan utama pada umumnya). Kemudian koefisien pada polinomial pun dapat dihilangkan dengan alasan yang sama, sehingga dengan notasi big O, dapat disimpulkan: T(n)∈O(n2) bahwa algoritma di atas memiliki kompleksitas waktu dengan orde O(n2).
Untuk membandingkan kompleksitas algoritma yang satu dengan yang lain, dapat digunakan tabel jenis kompleksitas di bawah, yang diurutkan berdasarkan kompleksitas yang paling baik ke yang paling buruk.
Tabel 2.21 Tabel Jenis Kompleksitas Notasi Nama
O(1) Konstan
O(log * n) Logaritma iterative
O(log n) Logaritmik
O([log n]c) Polilogaritmik
O(n) Linier
O(n log n) Linierithmik, loglinier, quasilinier or supralinier
O(n2) Kuadratik
O(nc), c > 1 Polinomial (kadang disebut algebraic)
O(cn) Eksponensial (kadang disebut geometric)
O(n!) Faktorial, kombinatorial