LINEAR QUADRATIC REGULATOR (LQR) UNTUK SISTEM DESKRIPTOR BERINDEKS SATU

LINEAR QUADRATIC REGULATOR (LQR)

UNTUK SISTEM DESKRIPTOR BERINDEKS SATU

Muhammad Wakhid Musthofa

Program Studi Matematika Universitas Islam Negeri Sunan Kalijaga Yogyakarta, mwakhid_m@yahoo.com

Abstrak

Dalam makalah ini dikaji masalah Linear Quadratic Regulator(LQR) pada interval waktu berhingga untuk sistem deskrirptor berindeks satu. Berdasarkan prinsip minimum Pontryagin akan dikonstruksikan persamaan differensial Riccati untuk masalah LQR tersebut yang berperan penting dalam penyelesaiannya.Selanjutnya, akan diturunkan teorema yang menyatakan keberadaan solusi masalah LQR pada sistem linear kuadratik.

Kata kunci: linear quadratic regulator, sistem deskriptor berindeks satu, persamaan

differensial riccati.

1. Pendahuluan

Desain kendali optimal pada suatu sistem bekerja dengan tujuan mengendalikan sistem tersebut dengan biaya seminimal mungkin. Dalam hal sistem disajikan dengan beberapa persamaan diferensial dan fungsi yang menyatakan biaya yang dikeluarkan oleh kendali dinyakatan dalam bentuk fungsi kuadratik maka masalah kendali tersebut disebut kendali linear kuadratik. Pada umumnya kendali didesain untuk membawa state dari sistem yang dikendalikan menuju ke state nol ataupun ke sebuah persekitaran yang sangat dekat dengan nol. Masalah ini disebut sebagai masalah regulator. Sehingga masalah Linear Quadratic Regulator dapat dipandang sebagai masalah mencari kendali pada suatu sistem linear yang akan meminimumkan biaya pengendalian yang disajikan dalam bentuk fungsi kuadratik dengan tujuan pengendalian membawa state dari sistem tersebut menuju ke state nol ataupun ke sebuah persekitaran yang sangat dekat dengan nol. Masalah Linear

Quadratic Regulator merupakan bagian dari masalah kendali optimal yang paling

banyak dikaji dan dikembangkan baik dari sisi pengembangan teori maupun aplikasinya. Referensi dari masalah tersebut untuk sistem nonsingular dapat dilihat pada Bryson dan Ho (1975), Lewis (1995), Kirk (1998) dan Vinter (2000).

Makalah ini akan mengkaji desain kendali optimal pada masalah Linear Quadratic Regulator untuk sistem deskriptor berindeks satu. Sistem deskriptor adalah generalisasi dari sistem biasa (sistem nonsingular). Sistem ini memuat persamaan diferensial dan sekaligus persamaan aljabar. Banyak permasalahan yang disajikan dalam sistem ini, diantaranya adalah proses-proses kimia (Kumar dan Dauotidis 1996), sistem sirkuit listrik (Newcomb 1981, Newcomb dan Dziurla 1989), sistem ekonomi (Luenberger 1977), interkoneksi antar sistem berskala besar (Luenberger dan Arbel 1977, Singh dan Liu 1973), sistem pada teknik mesin (Hemami dan Wyman 1979), sistem pembangkit daya (Scott 1979) dan sistem robot (Mills dan Goldenberg 1989).

Makalah ini disajikan dengan runtutan alur sebagai berikut. Setelah pendahuluan, bagian kedua dari makalah ini menyajikan rumusan masalah yang akan diselesaikan, yaitu mencari kendali optimal pada masalah Linear Quadratic Regulator untuk sistem deskriptor berindeks satu. Pada bagian ini juga dipaparkan transformasi masalah Linear Quadratic Regulator dari sistem deskriptor ke sistem nonsingular. Selanjutnya pada bagian ketiga akan dikonstruksikan persamaan diferensial Riccati yang dibutuhkan dalam mencari kendali optimal dengan memanfaatkan hasil transformasi bada bagian sebelumnya. Bagian keempat adalah bagian inti dari makalah ini. Pada bagian ini disajikan teorema yang memberikan eksistensi solusi dari masalah Linear Quadratic Regulator. Terakhir, bagian kelimamenyajikan contoh numerik yang menggambarkan aplikasi dari sebagian teori yang telah dipaparkan pada bagian-bagian sebelumnya.

2. Rumusan Masalah

Diberikan sistem deskriptor Ex t

 

 Ax t

 

Bu t

 

, x

 

0 x₀(1) dengan

   

,

R

n r n r

E A



   , rank E

 

n,

B



R



n r 



m. Vektor u   

 

_sadalah kendali yang diberikan oleh desainer kendali pada sistem (1). Masalah yang ingin diselesaikan dalam makalah ini adalah masalah Linear Quadratic Regulator yaitu mendesain kendali u   

 

_s pada sistem (1) yang akan meminimalkan fungsi ongkos kuadratik

 

 

 

 

 

 

 

0 , f f t T T T f t f J u 

_

_x t Qx t u t Ru t _ dtx t Q x t (2) dengan matriks-matriks

, dan

f

t

Q R

Q

adalah matriks simetri dan diasumsikan matriks R mempunyai invers. Selanjutnya dikarenakan kendali u   

 

_s yang didesain meminimalkan fungsi ongkos (2) maka kendali

u  

_s disebut kendali optimal dan dilambangkan dengan u   

 

_s.Sistem (1) dikatakan regular jika





det



EA 0. Sistem (1) mempunyai solusi untuk setiap nilai awal yang konsisten jika dan hanya jika sistem (1) regular (Dai 1989). Jika sistem (1) regular maka berlaku teorema transformasi bentuk kanonik Weierstrass berikut.

Teorema 1. (Gantmacher, 1959)Jika sistem deskriptor (1) regular maka terdapat

dua matriks nonsingular X 



X₁ X₂



dan Y 



Y₁ Y₂



sedemikian sehingga

0

0

n T

I

Y EX

N





 







dan 1

0

0

T r

A

Y AX

I





 







(3)

dengan

A

₁ adalah matriks dalam bentuk Jordan yang elemen-elemennya nilai-nilai eigen dari A,

I

_k adalah matriks identitas dan N adalah matriks nilpoten juga dalam bentuk Jordan.

Jika sistem (1) regular, maka solusi dari sistem (1) berbentuk (Engwerda dan Salmah 2009)

 

1 1

 

2 2

 

x t X x t X x t denganX 



X₁ X₂



,

Y





Y

₁T

Y

₂T







,   1, 1 R n r n T X Y    , X₂,Y₂T Rn r  n , dan

 

 

 

 

1 1 1 0

0

t J s t Jt

x t



e x



_

e



Y f s ds

 





1 1 0 n 0 0 x  I X x

 

1

 

2 2 0

,

i k i i i

d

x

t

N Y

f t

dt

 

  

nilai awal bagi persamaan di atas diberikan oleh





1 1

 

0 2 0

0

0

i k i r _i i

d

I

X

x

N Y

f

dt

  

  

.

Bilangan k adalah derajat kenilpotenan matriks N. Yaitu bilangan bulat k dengan sifat

N 

k

0

and

N

k1



0

. Indeks dari sistem deskriptor (1) dinyatakan dengan derajat kenilpotenan k dari matriks N. Jika matriks E nonsingular maka didefinisikan sistem tersebut berindeks nol. Selanjutnya berdasarkan Teorema 1. di atas, dengan

mendefinisikan variabel state yang baru

 

 

 

1 1 2 : x t X x t x t         denganx t ₁

 

Rndan

 

2 Rr

x t  , maka sistem (1) dapat ditulis sebagai

 

 

 

 

 

1 1 1 2 2 0 0 , 0 0 0 n T r x t A x t I Y Bu t x t I x t                        

 

 

1 1 0 2 0 0 x X x x         (4) atau

 

 

 

1 1 1 1 , x t  A x t Y Bu t x₁

_{ }

0 

_

I_n 0

_

X1x₀ (5)

 





 

 

2 2

0

.

T r

x

t

I Y Bu t

Y Bu t

 

 

(6)

Sedangkan fungsi ongkos (2) dapat ditulis sebagai

 

 

 

 

 

 

 

 

 

1 1 2 1 1 2 0 . f f t T T T T T f t f x t J u x t x t X QX u t Ru t dt x t Q x t x t        _{ }   _     



(7)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1 1 1 1 2 2 1 0 2 2 1 2 2 2 2 1 1 1 1 1 1 0

.

f f f f t _{T T} T T T T T T T T T T f t f t T T T f t f T

x t

X QX

X QX Y B

J u

x

t

u

t

u t

B Y X QX

B Y X QX Y B

u

t Ru t

dt

x

t

Q x t

Q

V

x t

x

t

u

t

dt

x

t

Q x t

u t

V

R





_

_{ }

_











_{ }

_









_





_



















 













_



 







 























(8)

Dengan demikian masalah LQR (1,2) ekuivalen dengan masalah LQR (5,8).

3. Persamaan Diferensial Riccati

Pada bagian ini akan dikonstruksikan persamaan diferensial Riccati yang memegang peranan penting dalam menentukan eksistensi solusi dari masalah LQR (1,2) atau LQR (5,8). Transformasi masalah LQR sistem deskriptor (1,2) ke dalam masalah LQR sistem nonsingular (5,8) yang telah berhasil dilakukan mengakibatkan metode pengkonstruksian persamaan diferensial Riccati pada masalah LQR sistem deskriptor dapat menggunakan metode pengkonstruksian persamaan diferensial Riccati pada masalah LQR sistem nonsingular. Untuk kepentingan tersebut, dibentuk fungsi Hamiltonian (Lewis 1995)

 

 

 

 

 



 

 



1 1 1 1 1 1 2 T T T T Q V x t H x t u t t A x t Y Bu t u t V R



       _{   }   _{ }      

 

 

 

 

 

 

 

 

 

 





1 1 1 1 1 1 1 1

2

.

T T T T T T

x

t Qx t

u

t V x t

x

t Vu t

u

t Ru t

A x t

Y Bu t











 













(9)

Berdasarkan prinsip maksimum Pontriagyn (Lewis 2006) syarat perlu penyelesaian optimal masalah di atas adalah

i.

x t

₁

 

H

A x t

_{1 1}

 

Y Bu t

₁

 















ii.

 



₁

 

 

₁

 



 

₁

 

1 2 2 , 2 f T f t f H t Qx t Vu t A t t Q x t x



     





     iii. 0 H 2V x tT ₁

 

2Ru t

 

B YT ₁T

 

t u



       atau

 

1

 

1

 

2Ru t  2V x tT B YT T t .

Dengan mengasumsikan matriks R mempunyai invers diperoleh

 

1 1

 

1₂ 1

 

T T T

Selanjutnya didefinisikan

 

1

 

2

t t







 yang akan menghasilkan persamaanstate and costate

 

 

 

1 1 1 1 x t A x t Y Bu t (11)

 

1

 

 

1

 

,

 

f 1

 

T f t f t Qx t Vu t A t t Q x t



    





 (12) Berikutnya dengan menggunakan metode sweep akan dicari persamaan diferensial Riccati untuk masalah LQR (5,8) sebagai berikut. Diasumsikan

 

t K t x t

   

1



 dengan

 

f

f t

K t Q . (13)

Turunkan persamaan (13) terhadap variabel t dihasilkan

 

t K t x t

   

1 K t x t

   

1



     , (14)

Substitusikan persamaan (10) – (13 )ke dalam persamaan (14) dihasilkan

 



 

   



   

   

 

 

 

   





 

1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

,

_f

.

T T T T T T T f t

Qx t

V

R V x t

B Y K t x t

A K t x t

K t x t

K t A x t

Y B

R V x t

B Y K t x t

K t

Q

 

























(15) Persamaan (15) dapat pula ditulis sebagai

   

   

 

 



 

 

 



   

 





 

 

1 1 1 1 1 1 1 1 1 1 1 1 1

,

.

f T T T T f t

K t x t

A K t x t

K t A x t

K t Y Bx t

Vx t

R

B Y K t x t

V x t

Qx t

K t

Q























(16)

Dikarenakan persamaan (16) berlaku untuk semua nilai awal x₁

 

0 maka diperoleh

 

 

 

 







 



 

1 1 1 1 1

,

_f

.

T T T T f t

K t

A K t

K t A

K t Y B V R



B Y K t

V

Q

K t

Q

 















(17)

Persamaan (17) adalah persamaan diferensial Riccati yang diturunkan dari syarat perlu penyelesaian optimal masalahLQR (5,8).

3.1. Eksistensi Solusi

Setelah berhasil dikonstruksikan persamaan diferensial Riccati pada masalah LQR, berikut disajikan teorema eksistensi solusi dari masalah LQR (1,2) yang ekuivalen dengan (5,8).

Teorema 2.

Diberikan masalah Linear Quadratic Regulator (1,2) yang ekuivalen dengan (5,8). Masalah tersebut mempunyai solusi untuk setiap nilai awal x₁₀ jika dan hanya jika persamaan diferensial Riccati (17) mempunyai solusi simetri K 

 

pada

0,t_f

 

  . Jika masalah LQR tersebut mempunyai solusi maka solusi tersebut adalah tunggal dan kendali optimal feedback tersebut berbentuk

 

 

   

* 1

1 1₂ 1 1

T T T

u t  R V x t  B Y K t x t . (18)

Dalam struktur lingkar terbuka, bentuk kendali (18) adalah

 

 

  



₀

* 1

1 1₂ 1 , 0 1

T T T

u t  R V x t  B Y K t  t x (19) dengan matriks



memenuhi persamaan transisi





1



 











1 1 1

, 0

T T T

, 0 ,

0, 0

t



A

Y BR



V

B Y K t



t

I





















_.

Lebih lanjut, nilai optimal yang diberikan oleh kendali optimal u*

_{ }

t adalah

 

* ₀

 

₀

1

0

1

T

J u



x K

x

. (20)

Pembuktikan dari teorema di atas dilakukan dengan beberapa langkah berikut. Pertama, akan ditunjukkan bahwa jika persamaan diferensial Riccati (17) mempunyai solusi simetri maka masalah LQR (1,2) atau (5,8) mempunyai solusi pada 0,t_f

 .

Bukti Teorema 2, bagian “

 ”

Menggunakan hubungan

     



1 1



1

     

1 1

     

1 0

0

0

0

f t T T T f f f

d

x

t K t x t

dt

x

t

K t

x t

x

K

x

dt







,

maka fungsi ongkos (8) dapat ditulis sebagai

 

 

 

 

 



     



     

 



 



 

1 1 1 1 0 0 1 1 1 1

0

0

0

f f f t t T T T T T T f t f f

Q

V

x t

d

J u

x

t

u

t

dt

x

t K t x t

dt

u t

dt

V

R

x

K

x

x

t

Q

K t

x t





 













_



 







 





























 

 

 

 

 



     



     

 



 



 

1 1 1 1 0 1 1 1 1

0

0

0

.

f f t T T T T T T f t f f

Q

V

x t

d

J u

x

t

u

t

x

t K t x t

dt

u t

dt

V

R

x

K

x

x

t

Q

K t

x t





 













_



 







 



























Kemudian, dengan menggunakan persamaan (5) dan (17), integrand dari persamaan di atas dapat ditulis sebagai (ketergantungan terhadap waktu dihilangkan)



 

 



1 1 1 1 1 1 1 1₂ 1 1 1₂ 1 T T T T T T T T T T T Q V x d x u x Kx u R V x B Y Kx R u R V x B Y Kx u dt V R    _{  }  _{        }  _{    }   .



 



     

1 1 1 1 1 1 0 1 1

1

1

2

2

0

0

0

f T t T T T T T T T

u

R V x

B Y Kx

R u

R V x

B Y Kx

J

x

K

x

 















.

Berdasarkan persamaan di atas didapat J  x₁T

_{     }

0 K 0 x₁ 0 untuk semua u dan kesamaan akan terjadi jika u 

 

dipilih pada persamaan (18).

Untuk membuktikan arah sebaliknya dari Teorema 2 di atas, diasumsikan bahwa masalah LQR (1,2) atau (5,8) mempunyai solusi u*

 

 dengan x*

 

t adalah trayektori dari state yang dihasilkan oleh kendali u*

 

 dan





0

* 1

0,

J x adalah nilai dari ongkos minimum yang dihasilkan oleh kendali u*

 

 . Selanjutnya akan ditunjukkan bahwa jika





0

* 1

0,

J x ada untuk sembarang nilai awal maka terdapat nilai minimum





0

* 1

,

J t x dari masalah optimisasi

 

 

 

 

 

 

 

1 1 1 1 f f t T T T f t f T t Q V x t J u x t u t dt x t Q x t u t V R         _              



(21)

dengan kendala sistem dinamik

 

 

 

1 1 1 1 , x s A x s Y Bu s

 

0 1 1

x t



x

. (22)

Kemudian dengan mengasumsikan bahwa terdapat nilai infimum yang dinyatakan dengan Jinf

_

t x, ₀

_

maka dipenuhi

 



₀



₀

   

₀ inf 1 1 1 , T J t x t x t P t x (23)

dengan tanpa mengurangi keumuman diasumsikan P t

 

adalah matriks simetri. Hal di atas akan ditunjukkan dengan menggunakan bantuan beberapa lemma berikut.

Lemma 1. (Molinari, 1975)

Jika suatu fungsi V memenuhi identitas parallelogram,









2



 

 



V xy V xy  V x V y , untuk semua

x y

,

(24) dan untuk setiap

y, fungsi W x y



,



:V x



y



V x



y



mempunyai sifat W x y



,



adalah fungsi kontinu dalam



pada saat



0(25) Maka V x

 

adalah berbentuk kuadratik.

Lemma berikut berguna untuk menunjukkan bahwa





0 inf 1 , J t x memenuhi identitas parallelogram (24). Lemma 2. (Engwerda, 2005)

Jika





0 inf 1 , J t x ada maka





0 inf 1 ,

J t



x juga ada dan



0





0



inf 2 inf

1 1

, ,

J t



x 



J t x .

Berdasarkan Lemma2 di atas dihasilkan akibat berikut.

Akibat 1.

Diasumsikan terdapat nilai infimum pada persamaan (21) untuk setiap nilai awal

0

1

x . Maka, terdapat matriks simetri P t

 

sedemikian sehingga



₀



₀

   

₀

inf

1 1 1

, T .

J t x x t P t x

Berdasarkan lemma-lemma dan akibat di atas dapat dikonstruksikan bukti arah kanan dari Teorema 2 sebagai berikut.

Bukti Teorema 2, bagian “



”

Diberikan persamaan diferensial Riccati (17). Berdasarkan teorema fundamental eksistensi dan ketunggalan solusi persamaan diferensial terdapat interval waktu maksimal



_{t t 1}, _f dengan persamaan diferensial Riccati (17) mempunyai solusi tunggal. Diasumsikan

t 

₁

0

. Dari Teorema 2 bagian “



” didapat bahwa pada interval waktu



_{t t 1}, _f masalah optimisasi (21,22) mempunyai solusi yang merupakan solusi minimum. Solusi minimum tersebut adalah

   

0 0

1 1

T

x

t P t x

. Dikarenakan hal ini berlaku untuk sembarang nilai awal

0

1

x maka dapat disimpulkan bahwa P t

 

K t

 

pada interval waktu



_{t t 1}, _f . Namun dikarenakan

 

P t terbatas pada 0,t_f 

  maka demikian juga K t

 

juga harus terbatas pada



t t 1, f . Hal ini berakibat bahwa persamaan diferensial Riccati (17) juga mempunyai solusi pada suatu interval waktu



_{t t 2}, _f untuk

t

₂



t

₁. Sehingga keberadaan interval



_{t t 1}, _f bukanlah interval yang maksimal. Hal ini menunjukkan pengasumsian

t 

₁

0

tidaklah tepat dan harusnya

t 

₁

0

.

4. Contoh Numerik

Diberikan masalah Linear Quadratic Regulator

 

 

 

,

 

0 0 Ex t  Ax t Bu t x x (26)

 

 

 

 

 

 

 

1 0 , f T T T f t f J u 

_

_x t Qx t u t Ru t _dtx t Q x t (27)

dengan

0

0

1

1

E

_{ }





_







,

0

1

1

2

A

_{ }





_







,

1

0

B

_{  }

 

 

,

2

0

0

1

Q

_{ }





_





, R 

 

1 dan

1

0

0

1

f t

Q

_{ }





_





, ₀

1

0

x

_{  }

 

 

. Menggunakan transformasi bentuk kanonik Weierstrass,

dapat dicari matriks nonsingular

1 1

1 0

T

Y

_{ }





_





dan

1 1

0 1

X

_{ }





_





sedemikian sehingga masalah LQR (26,27) ekuivalen dengan

 

 

 

1 1 1 1 , x t A x t Y Bu t x₁

_{ }

0 



I_n 0



X1x₀ (28)

 

 

 

 

 

 

 

1 1 1 1 1 0 f T T T f t f T

Q

V

x t

J u

x

t

u

t

dt

x

t

Q x t

u t

V

R





 













_



 







 





















(29) dengan _{1 2}

1

0

T

X



Y

_{  }

 

 

, _{2 1}

1

1

T

X



Y

_{  }

 

 

, A ₁

 

1 , 2 2 2 3 T Q V V R         _{ }        . Substitusikan matriks-matriks di atas ke dalam persamaan (17) menghasilkan persamaan diferensial Riccati

 

7

 

2

2

 

3

K t





K t



K t



, K

 

1 1 (30) yang mempunyai solusi K t

 

t. Selanjutnya, dengan menggunakan persamaan (18) didapat bentuk kendali optimal feedback bagi masalah di atas adalah

 

* 7

5.5 t

u t  e dan trayektori optimalx₁*

 

t diberikan oleh

 

2 7 4 * 1 t t

x

t

e

 _     



.

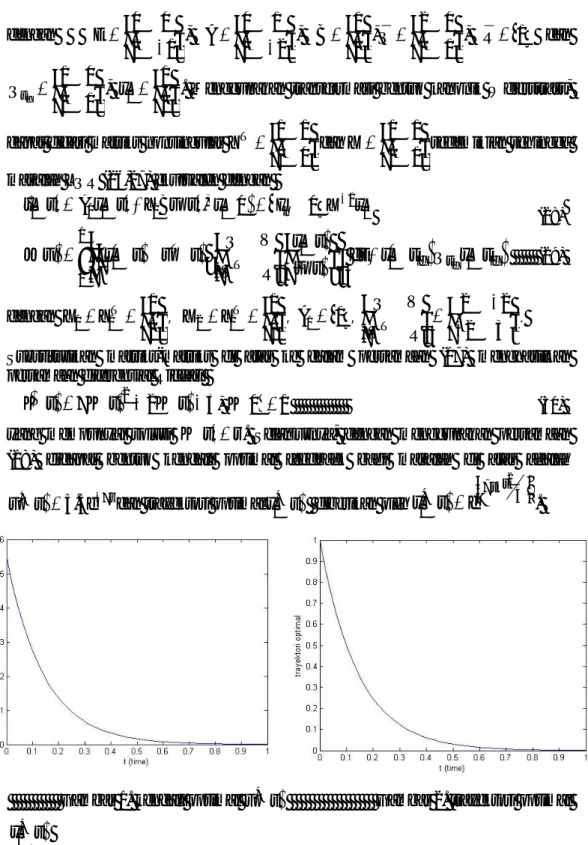
Gambar 1. kendali optimal u*

 

t Gambar 2. trayektori optimal

 

* 1

x t

trayektori optimal pada sistem (28) jika menggunakan kendali u*

 

t untuk mencapai nilai optimal.

5. Kesimpulan

Dalam makalah ini telah dikaji konsep Linear Quadratic Regulator (LQR) untuk sistem deskriptor berindeks satu. Dengan menggunakan bentuk kanonik Weierstrass, masalah LQR untuk sistem deskriptor dapat dibawa ke dalam bentuk LQR sistem nonsingular. Hal tersebut mengakibatkan persamaan diferensial Riccati yang memegang peranan penting dalam mencari eksistensi solusi masalah LQR tersebut dapat dikonstruksikan menggunakan metode pada sistem nonsingular. Selanjutnya telah dibuktikan pula teorema yang menjamin eksistensi solusi dari permasalahan tersebut. Contoh numerik sederhana yang menggambarkan penggunaan teorema yang telah dikonstruksikan telah pula disajikan di akhir makalah ini.

Namun demikian kajian dalam makalah ini masih terbatas pada sistem deskriptor yang berindeks satu. Sehingga pengembangan masalah LQR untuk sistem deskriptor berorde tinggi merupakan obyek penelitian yang masih harus dikaji lebih lanjut.

6. Daftar Pustaka

[1] Bryson, A.E. dan Ho, Y-C., (1975). Applied Optimal Control, Taylor and Francis, New York.

[2] Dai, L. (1989). Singular Control Systems, Springer-Verlag, Berlin.

[3] Engwerda, J.C.(2005) Linear Quadratic Dynamic Optimization and Differential Games, John Wiley & Sons, West Sussex.

[4] Engwerda, J.C. dan Salmah, (2009). The Open-Loop Linear Quadratic Differential Game for Index One Descriptor Systems, Automatica, vol. 45, pp 585-592.

[5] Gantmacher, F., (1959). Theory of Matrices, Chelsea Publishing Company, New York.

[6] Hemami, H. dan Wyman, B. F. (1979). Modeling and Control of Constrained Dynamic Systems with Application to Biped Locomotion in the Frontal Plane, IEEE Transactions on Automatic Control, vol. 24, 526 – 535.

[7] Kirk, D.E., (1998), Optimal Control Theory: An Introduction, Dover Publications, New York.

[8] Kumar, A. danDaoutidis, P. (1996). State-Space Realizations of Linear Differential Algebraic-Equation Systems with Control-Dependent State Space, IEEE Transactions on Automatic Control, vol. 41, 269 – 274.

[9] Lewis, A. D. The Maximum Principle of Pontryaginin Control and in Optimal

Control, catatan kuliah, tersedia dihttp://www.mast.queensu.ca/~andrew/

[10] Lewis, F.L. dan Syrmos, V.L., (1995), Optimal Control, John Wiley and Sons, New York.

[11] Luenberger, D. G., (1977). Dynamic Equation in Descriptor Form, IEEE Transaction on Automatic Control, vol. 22, 312 – 321.

[12] Luenberger, D. G. danArbel. (1977). Singular Dynamic Leontief systems, Econometrica, vol. 45, 991 – 995.

[13] Mills, J. K. dan Goldenberg, A. A., (1989). Force and Position Control of Manipulators During Constrained Motion Tasks, IEEE Transactions on Robotics and Automation, vol. 5, 30 – 46.

[14] Molinari, B.P. (1977). Solving Polynomial Sistem Using Continuation for Scientific and Engineering Problems, Prentice-Hall, New Jersey.

[15] Newcomb, R. W. (1981). The Semistate Description of Nonlinear Time-Variable Circuits, IEEE Transactions on Circuits Systems, vol. vol. 28, 62 – 71. [16] Newcomb, R. W. dan Dziurla, B. (1989). Some Circuits and Systems

Applications of Semistate Theory, Circuits Systems Signal Processes, vol. 8, 235 – 260.

[17] Singh, S. dan Liu, R. W. (1973). Existence of State Equation

Representation of Linear Large-Scale Dynamical Systems, IEEE

Transaction Circuits Systems, vol. 20, 239 – 246.

[18] Scott, B., (1979). Power system Dynamic Response Calculations, IEEE

Proceeding, vol. 67, 219 – 247.