BAB 2 LANDASAN TEORI

BAB 2

LANDASAN TEORI

2.1 Analisis Regresi

Regresi merupakan alat ukur yang digunakan untuk mengukur ada atau tidaknya korelasi antar variabel. Istilah regresi yang berarti ramalan atau taksiran pertama kali diperkenalkan oleh Sir Francis Galton pada tahun 1877, sehubungan dengan penelitiannya terhadap tinggi manusia, yaitu antara tinggi anak dan tinggi orang tua. Dalam penelitiannya, Galton menemukan bahwa tinggi anak dari orang tua yang tingginya cenderung meningkat atau menurun dari berat rata-rata populasi. Garis yang menunjukkan hubungan tersebut disebut garis regresi.

Teknik yang umum digunakan untuk menganalisis hubungan antara dua atau lebih variabel dalam ilmu statistik adalah analisis regresi. Analisis regresi adalah tehnik statistik yang berguna untuk memeriksa dan memodelkan hubungan atara dua variabel atau lebih terutama untuk menyelusuri pola hubungan dua variabel atau lebih dan terutama untuk menelusuri pola hubungan yang modelnya belum diketahui dengan sempurna, sehingga dalam penerepannya lebih bersifat eksploratif.

Analisis regresi setidak-tidaknya memiliki 3 (tiga) kegunaan, yaitu: untuk tujuan deskripsi dari fenomena data atau kasus yang sedang diteliti, untuk tujuan kontrol, serta untuk tujuan prediksi. Regresi mampu mendeskripsikan fenomena data melalui terbentuknya suatu model hubungan yang bersifat numerik. Regresi juga dapat digunakan untuk melakukan pengendalian terhadap suatu kasus atau hal-hal yang sedang diamati melalui penggunaan model regresi yang diperoleh. Selain itu, model regresi juga dapat dimanfaatkan untuk melakukan prediksi untuk variabel

didalam rentang data dari variabel-variabel bebas yang digunakan untuk membentuk model regresi tersebut. Konsep ini disebut sebagai interpolasi.

Di dalam suatu model regresi akan ditemukan koefisien-koefisien. Koefisien pada model regresi sebenarnya adalah nilai duga parameter didalam model regresi untuk kondisi yang sebenarnya, sama halnya dengan statistik mean (rata-rata) pada konsep statistika dasar. Hanya saja, koefisien-koefisien untuk model regresi merupakan nilai rata-rata yang berpeluang terjadi pada variabel Y (variabel terikat) bila suatu nilai X (variabel bebas) diberikan. Koefisien regresi dapat dibedakan menjadi 2 macam, yaitu:

1. Intersep (intercept)

Intersep adalah suatu titik perpotongan antara suatu garis regresi dengan sumbu Y pada diagram/sumbu kartesius saat nilai X = 0. Sedangkan definisi secara statistika adalah nilai rata-rata pada variabel Y apabila nilai pada variabel X bernilai 0. Dengan kata lain, apabila X tidak memberikan kontribusi, maka secara rata-rata, variabel Y akan bernilai sebesar intersep. Perlu diingat, intersep hanyalah suatu konstanta yang memungkinkan munculnya koefisien lain didalam regresi. Intersep tidak selalu dapat atau perlu untuk dinterpretasikan. Apabila data pengamatan pada variabel X tidak mencakup 0 atau mendekati 0, maka intersep tidak memiliki makna yang berarti, sehingga tidak perlu diinterpretasikan.

2. Slope

Secara matematis, slope merupakan ukuran kemiringan dari suatu garis. Slope adalah koefisien regresi untuk variabel X (variabel bebas). Dalam konsep statistika, slope merupakan suatu nilai yang menunjukkan seberapa besar kontribusi (sumbangan) yang diberikan suatu variabel X terhadap Y. Nilai slope dapat pula diartikan sebagai rata-rata pertambahan (pengurangan) yang terjadi pada variabel Y untuk setiap peningkatan satu satuan variabel X.

Persamaan garis regresi adalah merupakan model hubungan antara dua variabel atau lebih, yaitu antara variabel bergantung (dependent variabel) dengan variabel bebasnya (independent variable) sedangkan yang dimaksud garis regresi (regression line/line of the best fit/estimating line) adalah suatu garis yang ditarik di antara titik-titik (scatter diagram) sedemikian rupa sehingga dapat digunakan untuk

menaksir besarnya variabel yang satu berdasarkan besar variabel yang lain, dapat juga dugunakan untuk mengetahui korelasinya (positif atau negatifnya). Apabila dua variabel x dan y mempunyai hubungan atau korelasi, maka perubahan nilai variabel diartikan sebagai variabel yang satu mempengaruhi variabel lainnya.

2.1.1 Regresi Linier Sederhana

Regresi linier sederhana merupakan bagian regresi yang mencakup hubungan linier satu peubah tak bebas Y dengan satu peubah bebas X. Hubungan linier Y dan X dari suatu populasi disebut garis regresi populasi yang dinyatakan persamaan sebagai berikut: X X Y E X Y. ( / ) β0 β1 µ = = + (2.1) Keterangan:

µ = rata-rata Y untuk nilai X tertentu _{Y .X}

β = jarak titik pangkal dengan titik potong garis regresi dengan sumbu Y ₀ (intercept) nilai Y tanpa pengaruh X

β = kemiringan (slope atau gradien) garis regresi 0

Besarnya perubahan Y sebagai akibat perubahan X satu satuan

Kalau ingin menduga rataan µ_{Y .Xi}, maka nilai Y perlu ditentukan untuk satuan Xi tertentu. Nilai Y tersebut untuk Xi dinyatakan dengan Yi. Nilai Yi dan µY .Xi pada

umumnya tidak sama. Perbedaan tersebut tergantung pada ketepatan model untuk menggambarkan keadaan yang sebenarnya dan ketepatan pengukuran peubah Y dan X.

Perbedaan antara Yi dan µY .X_i disebut galat acak (randam error) dan

dinyatakan dengan simbolε . Dengan demikian: _i

i X Y i i Y µ . ε = − atau Yi =µY.Xi +εi

Dari persamaan ini diperoleh model regresi linier sederhana dari suatu populasi sebagai berikut:

I i i

i X

Y =β₀ +β +ε (2.2)

Parameter β dan ₀ β₁ diduga dengan menggunakan garis regresi contoh. Bentuk persamaaan garis regresi contoh adalah sebagai berikut:

X b b

Yˆ = ₀ + ₁ (2.3)

Keterangan:

b0 = intersept, jarak titik pangkal dan titik potong garis regresi dengan sumbu Y b1 = kemiringan atau gradien garis regresi

Keterangan:

b0 merupakan penduga titik bagi β 0

b1 merupakan penduga titik bagi β1 dan

Ŷ merupakan penduga titik bagi µ _{Y .X}

Pendugaan tersebut dilakukan dengan mengambil contoh acak berukuran n dari suatu populasi. Hasil pengamatan berupa pasangan X dan Y sebagai berikut:

(X1 , Y2) , (X2 , Y2) , ….., (Xn , Yn)

Data berpasangan tersebut digambarkan pada sumbu koordinatif siku-siku, akan diperoleh gambar yang disebut diagram pencar (scatter diagram) seperti pada gambar berikut. Nilai-nilai data tersebut dieliminasi dalam persamaan Y =b0 +b1X diperoleh:

X b b Yˆ = ₀ + ₁

Pada umumnya Yi tidak sama dengan Ŷi, perbedaan antara Yi dan Ŷi dinyatakan dengan ei yang disebut sisa (residual). Dalam hal ini:

i i

i Y Y

e = − ˆ atau Y_i = ˆY_i +e_i

Dengan demikian diperoleh model regresi linier sederhana dari contoh sebagai berikut: I i i i b b X e Y = 0 + + (2.4)

Gambar 2.1 Diagram Pencar, Garis Regresi, dan Sisa Untuk Pengamatan Berpasangan (Xi,Yi )

Nilai b0 dan b1 diperoleh dengan menggunakan metode kuadrat terkecil (least-squares method). Metode kuadrat terkecil merupakan satu cara memperoleh b0 dan b1 dengan meminimumkan jumlah kuadrat sisa:

(

)

(

)

2 1 1 0 1 1 2 1

∑

ˆ

∑

∑

− = = − − = − = = n i i i n i i i n i X b b Y Y Y e S (2.5)

Syarat optimum adalah:

(

)

0 2 _{0 1} 0 = − − − = ∂ ∂

_∑

i i b b X Y b S

(

)

0 2 _{0 1} 1 = − − − = ∂ ∂

∑

Xi Yi b b Xi b S

Dari dua persyaratan optimum peroleh persamaan normal sebagai berikut:

∑

∑

= = = + n i i n i i Y X b nb 1 1 1 0

i n i i n i i n i i b X X Y X b

∑

∑

∑

= = = = + 1 1 2 1 1 0 (2.6)

Dari persamaan normal diperoleh:

      −             − =

∑

∑

∑

∑

∑

= = = = = n i i n i i n i i n i i i n i i X n X Y X n Y X b 1 1 2 1 1 1 1 1 1

(

)(

)

(

)

∑

∑

= = − − − = _n i i n i i i X X Y Y X X 1 2 1 (2.7)       −                   −             =

∑

∑

∑

∑

∑

∑

= = = = = = n i i n i i n i i n i i i n i i n i i X n X X Y Y X X b 1 2 2 1 1 2 1 1 1 0 1 = Y −b1X (2.8)

2.1.2 Regresi Linier Ganda

Regresi linier ganda merupakan regresi linier yang melibatkan hubungan fungsional antara sebuah variabel tak bebas dengan dua atau lebih variabel bebas. Semakin banyak variabel bebas yang telibat dalam suatu persamaan regresi semakin rumit menentukan nilai statistik yang diperlukan hingga diperoleh persamaan regresi estimasi. Regresi linier berganda berguna untuk mendapatkan pengaruh dua variabel kriteriumnya atau untuk mencari hubungan fungsional dua variabel prediktor atau lebih dengan variabel kriteriumnya, atau untuk meramalkan dua variabel prediktor atau lebih terhadap variabel kriteriumnya.

Hubungan linier lebih dari dua variabel yang dinyatakan dalam bentuk persamaan matematis adalah:

ε β β β + + + = X_{i k}X_k Y _{0 1} .... (2.9) Keterangan:

Y : variabel tak bebas X ,....₁ X_k : variabel bebas β ,₀ β ,....,₁ β_k : parameter regresi ε : nilai kesalahan (error)

Metode kuadrat terkecil dari estimasi β yang terdiri dari minimum

∑

ε yang i2

berkenaan dengan β, dimana minimum ε'ε = Y −Xβ 2 mengenai β, yaitu:

(

β

) (

β

)

ε

ε' = Y −X ' Y −X

= Y'Y−2β'X'Y +β'X'Xβ

Perbedaan ε'ε mengenai β dan persamaan ' =0 ∂ ∂ β ε ε , diperoleh: 0 ' 2 ' 2 + = − X Y X Xβ atau X'Xβ = X'Y (2.10)

(

X'X

)

X'Y ˆ ₌ −1 β (2.11) Kemudian untuk β:

(

_Y−Xβ

) (

_{' Y −X}β

)

₌

_

_{Y −X}β _+X

(

βˆ₋βˆ

)

_

_'

_

_{Y −X}β _+X

(

βˆ₋βˆ

)

_

=

(

Y −Xβˆ

)(

'Y −Xβˆ

) (

+ βˆ−β

) (

'X'X βˆ−β

)

=

(

Y−Xβˆ

)(

'Y −Xβˆ

)

Minimum dari

(

Y −Xβ

) (

' Y −Xβ

)

adalah

(

Y −Xβˆ

)(

'Y −Xβˆ

)

dicapai pada β = βˆ solusi ini untuk melihat minimum ε'ε.

2.1.3 Regresi Nonlinier Sederhana

Regresi nonliner adalah regresi yang variabel-variabelnya ada yang berpangkat. Bentuk grafik regresi nonlinier adalah berupa lengkungan. Untuk mempelajari peubah respon (Y) berdasarkan peubah lain (X), apabila ada alasan atau dugaan kuat bahwa antara Y dan X terdapat pertautan, maka dapat menggunakan teknik regresi dan korelasi yang bentuk liner. Regresi tersebut dibatasi pada bentuk liner Ŷ= a + bX yang perlu diuji dahulu mengenai bentuk dan keberartiannya sebelum digunakan untuk mengambil kesimpulan.

Untuk mencari regresi Y atas X yang bentuknya nonlinier atau lengkung, beberapa di antaranya adalah:

a. Parabola atau polinom pangkat dua

2

ˆ _{a bX cX}

Y = + +

b. Parabola kubik atau polinom pangkat tiga

3 2 ˆ _{a bX cX dX} Y = + + + c. Polinom pangkat k (k ≥ 2) k kX a X a X a X a a Yˆ = + + + 3 3 +...+ 2 2 1 0 d. Eksponen X ab Yˆ =

e. Eksponen (khusus) atau pertumbuhan

bX ae Yˆ = f. Geometrik b aX Yˆ = g. Logistik X ab Yˆ = 1

h. Hiperbola

bX a Yˆ =

Regresi-regresi model (d), (e), (f), (g), dan (h) dapat diselasaikan dengan menggunakan teknik regresi linier sederhana dan korelasi karena dengan transformasi yang cocok, bentuk-bentuk tersebut dapat menjadi linier. Transformasi yang digunakan adalah logaritma, sehingga:

bentuk (d) menjadi: b X a Yˆ log log log = + ,

yang linier dalam X dan log Y

bentuk (e) menjadi:

bX a Yˆ = ln +

ln , yang linier dalam X dan ln Y, (ln adalah logaritma dengan bilangan pokok e)

bentuk (f) menjadi: X b a Yˆ log log log = + ,

yang linier dalam log X dan log Y

bentuk (g) menjadi: b X a Yˆ log log log =− − , yang linier dalam X dan log Y

bentuk (h) menjadi:

X b

a

Yˆ log log log log = − −

yang linier dalam log X dan log Y

Dengan teknik yang dijelaskan dalam regresi linier sederhana dan korelasi dalam regresi linier sederhana, koefisien-koefisien a dan b melalui log a dan log b dapat ditentukan. Dalam pelaksanaannya harus bekerja dengan data dari X dan Y sudah dibuat logaritmanya terlebih dahulu, untuk (d), (e), (g) tetap masih X.

Regresi-regresi bentuk (a) dan (b) merupakan hal khusus dari bentuk (c) masing-masing untuk k = 2 dan k = 3. Bentuk-bentuk ini tidak dapat dibuat linier seperti untuk (d), (e), (f) dan (g).

2.1.3.1 Model Eksponen

Perkiraan untuk model ini, yang persamaannya:

X

ab

Y

ˆ

=

(2.12)

Keterangan:

Y = variabel tak bebas X = variabel bebas

a, b = konstanta atau penduga

ternyata dapat dikembalikan kepada model linier yang diambil logaritmanya, dalam logaritma persamaannya menjadi :

X b a

Yˆ log (log )

log = + (2.13)

diambil Ŷ = log Ŷ, a´= log a dan b´ = log b, diperoleh model:

X b a Yˆ = ′+ ′

a´ dan b´ dapat dihitung dan selanjutnya karena a´ = log a dan b´ = log b, a dan b juga dapat dihitung. Langsung di dalam logaritma, a dan b dapat dicari dari rumus:

(

)

_       − =

∑

∑

a X b a Y a log i log i log (2.14)

(

) (

)(

)

(

)

∑

∑

∑

∑

∑

− − = ₂ 2 log log log i i i i i i X X n Y X Y X n b

Model eksponen dalam rumus (2.12) sering pula disebut model pertumbuhan karena sering banyak digunakan dalam menganalisis data sebagai hasil pengamatan mengenai fenomena yang sifatnya tumbuh.

Dalam hal ini model persamaannya menjadi:

bX

ae

Y

ˆ

=

(2.15)

Keterangan:

Ŷ = variabel tak bebas X = variabel bebas

a, = konstanta atau penduga b

e = bilangan pokok logaritma asli atau logaritma Napier

harganya hingga empat empat desimal adalah e = 2,7183…..

sekarang harus diambil logaritma Napier dan bukan logaritma biasa. Persamaannya (2.15) sekarang menjadi:

bX a Yˆ = ln +

ln (2.16)

Ini linier dalam X dan lnY sehingga a dan b dapat dicari seperti biasa.

Daftar logaritma Napier tidak tersedia, dapat digunakan daftar logaritma biasa, persamaan (2.16) dalam rumus menjadi:

bX a

Yˆ log 0,4343

log = + (2.17)

Dalam subbab 2.1.2 telah dibahas seperlunya regresi linier ganda dengan k buah (k ≥ 2) variabel bebas X1, X2,…...,Xk, diregresikan terhadap variabel respon Y dalam bentuk linier ganda yang ditaksir berbentuk:

k kX b X b X b b Yˆ = ₀ + _{1 1} + _{2 2} +....+ Keterangan:

Y = variabel tak bebas X1,X2,....Xk = variabel bebas

b₀,b₁,b₂,....b_k = parameter regresi

Jika hanya ada dua variabel bebas X1 dan X2, maka regresinya terhadap Y dalam bentuk kuadratik adalah:

2 2 5 2 1 4 2 1 3 2 2 1 1 0 . ˆ _{b b X b X b X X b X b X} Y = + + + + +

Suatu regresi yang dinamakan regresi nonlinier ganda, tepatnya regresi kuadratik ganda.

Dengan meninjau sepintas tentang regresi nonlinier ganda bersifat multiplikatif. Model multiplikatif yang paling sederhana untuk dua variabel bebas X1 dan X2 misalnya adalah:

C b X aX Yˆ = _{1 2} Keterangan:

Y = variabel tak bebas X = variabel bebas

a ,,b c = konstanta atau penduga

Sebagai taksiran terhadap model regresi dalam populasinya. Pada dasarnya, model nonlinier ini dapat dikembalikan pada model linier dengan jalan mengambil logaritma ke dua ruas persamaan. Hasilnya menjadi:

2 1 log log log ˆ logY = a+b X +c X

Berbentuk model linier ganda dalam log X1, logX2 dan log Y.

Model eksponen untuk regresi nonlinier ganda dengan dua variabel bebas, diambil: 2 2 1 1 0

ˆ

b bX b X

e

Y

=

+ + Keterangan:

Y = variabel tak bebas X1, X2 = variabel bebas

b₀,b₁,b₂ = parameter regresi

Dapat dikembalikan pada bentuk linier ganda dengan mengambil logaritma asli (ln) pada ke dua ruas persamaan. Bentuknya menjadi:

2 2 1 1 0 ˆ lnY =b +b X +b X

Selanjutnya diselesaikan dengan cara regresi linier ganda menggunakan variabel bebas aslinya sedangkan variabel dependennya dalam bentuk logaritma asli dari variabel Y, ialah ln Y.

Model lain yang juga non linier ganda untuk dua prediktor tetapi dapat dikembalikan pada bentuk linier ganda adalah model kebalikan, berbentuk:

2 2 1 1 0 1 ˆ X b X b b Y + + =

Keterangan:

Y = variabel tak bebas X₁, X₂ = variabel bebas b₀,b₁,b₂ = parameter regresi

Dengan mengambil kebalikan ke dua ruas persamaan ini, kita peroleh:

2 2 1 1 0 ˆ 1 X b X b b Y = + +

Linier dalam X1, X2 dan 1/Y. Ini berarti model dapat diselesaikan dengan cara seperti menyelesaikan regresi linier ganda menggunakan data asli X1 dan X2 dan variabel dependennya bukan Y tetapi 1/Y.

Tentu saja masih ada model lain yang non linier ganda dan juga model-model tersebut dapat diperluas untuk tiga, empat, dan seterusnya variabel bebas. Penyelesaiannya, diusahakan dikembalikan pada bentuk linier ganda dengan menggunakan transformasi yang sesuai.

2.2 Metode Kuadrat Terkecil

Metode kuadrat terkecil, yang lebih kenal dengan nama least-squares method adalah salah satu metode pendekatan yang paling penting dalam dunia keteknikan untuk:

a) Regresi ataupun pembentukan persamaan dari titik-titik data diskretnya (dalam pemodelan)

b) Analisis sesatan pengukuran (dalam validasi model)

Metode kuadrat terkecil termasuk dalam keluarga metode-metode pendekatan sesatan terdistribusi (“distributed error” approximation methods), berdasarkan karekteristik kerjanya yang melakukan pengurangan sesatan menyeluruh (global error) yang terukur berdasarkan interval pendekatan keseluruhan (whole approximation

interval) sesuai dengan order pendekatan yang meningkat. Metode ini berbeda dengan metode-metode asimptotis, khususnya yang dikembangkan melalui pendekatan deret ‘Taylor’, karena metode asimptotis memiliki karekteristik kerja yang memperkecil sesatan pada beberapa titik tertentu, sesuai dengan order pendekatan yang meningkat.

Metode kuadrat terkecil ini juga memainkan peranan penting dalam teori statistik, karena metode ini seringkali digunakan dalam penyelesaian problem-problem yang melibatkan kumpulan data yang tersusun secara acak, seperti sesatan-sesatan percobaan.

Andi Supangat (2008) Metode Ordinary Least Square (OLS) atau sering juga dikatakan sebagai metode kuadrat terkecil (least square) pada dasarnya merupakan anggapan-anggapan tertentu, anggapan-anggapan pada metode kuadrat terkecil adalah dimaksudkan sebagai pembentukan model Normal Hesse, yang digunakan untuk menentukan perhitungan besaran intercept dan koefisiensi regresi sampel atau besaran a dan b pada model regresi linier y = a + bx. Begitu pun tentunya pada model-model regresi lainnya, seperti pada model linier multiple, model kudaratis, model semi, model eksponensial.

Metode kuadrat terkecil selain untuk menentukan nilai-nilai intercept dan koefisien regresi, juga berguna untuk membuat pendugaan interval serta menguji hipotesis regresi populasi. Berikut diungkapkan beberapa anggapan penting metode kuadrat terkecil, di antaranya:

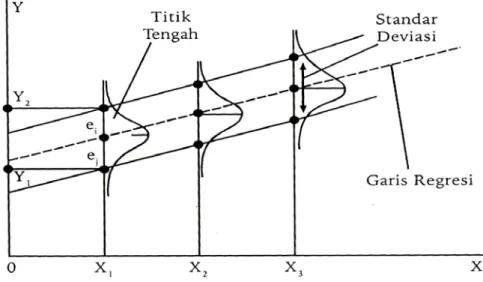
a. Nilai rata-rata dari tingkat kesalahan (error) atau nilai ekspektasi (expected value) dari setiap nilai x sama dengan nol. Anggapan ini dinyatakan seperti pada Gambar 2.5, bahwa untuk setiap x, misalkan x1, x2, dan x3 terdapat beberapa nilai y. nilai Y tersebut terdapat di bawah dan di atas garis regesi, namun nilai rata-rata dari y berada di titik tengah, yaitu pada garis regresi. Karena kurva bersifat simentris, maka nilai di bawah garis regresi sama dengan nilai di atas regresi, sehingga nilai harapan dari Ei untuk setiap x dari x1, samapai xi sama dengan nol.

Gambar 2.2 Nilai rata-rata dari tingkat kesalahan (error) atau nilai ekspektasi (expected value) dari setiap nilai x sama dengan nol

b. Nilai error dari Ei dan Ej dikatakan sebagai covarian yang saling independent (tidak berhubungan), dan oleh karena antara Ei dan Ej tidak ada hubungan, maka dapat diartikan bahwa nilai cov (Ei , Ej) = 0, dimana i ≠ j. berdasarkan uraian di atas, dalam setiap nilai xi akan didapati tingkat kesalahan (error) sebesar Ei demikian pun halnya dengan nilai xj akan didapati tingkat kesalahan (error) sebesar Ej.

c. Varians (σ2

) dari error bernilai: Var

(

E_i /E_j

) (

= Ee_i −e_j

)

2 =σ2. Perhatikan pada gambar sebelumnya, nilai Ei ( yang dilambangkan dengan tanda titik) untuk setiap x yaitu x1, x2, dan x3 tersebar secara tetap sebesar nilai variannya (σ2). Nilai E terbesar di bawah kurva normal sejauh satu standar deviasi dibawah garis reegresi dan satu standar deviasi di atas garis regresinya.

d. Variabel bebas x tidak berhubungan dengan besarnya nilai E (error), untuk kenyataan ini di tuliskan sebagai Covarian atau Cov(Ei , xi ) = 0 . dengan demikian model regresinya ditulis: yˆ=a + b xi + ei , terlihat dari model tersebut bahwa nilai xi dan Ei secara nyata tidak saling mempengaruhi, namun demikian kedua variabel tersebut mempengaruhi variabel y. seandainya antara variabel xi dan variabel Ei saling mempengaruhi, maka pengaruh masing-masing variabel tersebut tidak akan dapat dipisahkan. Secara luas model regresi di atas dapat diartikan, bahwa faktor

yang mempengaruhi y selain x adalah faktor e, maka oleh karenanya variansi dari Ei dan xi saling terpisah atau tidak berhubungan (tidak berkorelasi).

e. Anggapan-anggapan tersebut sangat penting artinya dalam melakukan analisis regresi, sebab apabila anggapan-anggapan tersebut dapat dipenuhi, maka nilai-nilai penduga yaitu a dan b (untuk model regresi linier sederhana), nilai-nilai-nilai-nilai a0, a1, a2 (untuk model regresi linier multiple yˆ= a0 + a1x1 + a2 x2+ ε) ataupun nilai-nilai intercept dan koefisien regresi pada model lainnya akan mempunyai sifat-sifat

seperti berikut: Tidak bias, memiliki variansi yang minimum, hasil perhitungan

(pendugaan) dapat representatif terhadap parameter populasinya walaupun jumlah sampelnya diperbesar, memiliki nilai intercept dan koefisien regresi yang berdistribusi normal dengan dengan nilai rata-rata harapan dari pendugaan sampel E (a) = A dan variansi (a) = σ2a. dan nilai rata-rata harapan dari

pendugaan sampel E (b) = B dan variansi (b) = σ2b.

f. Secara umum metode kuadrat terkecil, ditulis dalam bentuk Normal Hesse, yaitu: Untuk Model Regresi Linier Sederhana yˆ=a + bx+ e

Persamaan Normal Hesse-nya:

∑

y=na+b

∑

x……….1)

∑

=

∑

+

∑

2 x b x a y …………..2)

2.2.1 Persoalan Estimasi Metode Kuadrat Terkecil dalam Model Eksponen Berganda

Metode kuadrat terkecil dapat digunakan untuk memperkirakan koefisien regresi dalam regresi linier berganda. Merupakan metode yang paling populer dan sangat berpengaruh dalam analisis garis regresi. Untuk memperkirakan parameter– parameter

k

β β

β₀, ₁,...., dapat digunakan metode kuadrat terkecil sehingga jumlah kuadrat dari deviasi/simpangan antara observasi- observasi dan garis regresi menjadi minimum.

Hines dan Montgomery (1990) menjelaskan bahwa fungsi kuadrat terkecil adalah: 2 1 1 0 1 2

∑

∑

∑

= = =      − − = = n i n j ij j i n i i Y X L ε β β (2.18)

Fungsi L tersebut dioptimumkan terhadap β₀,β₁,....,β_k. Estimator kuadrat terkecilβ₀,β₁,....,β_k merupakan syarat mutlak harus memenuhi:

0 ˆ ˆ 2 1 1 0 ˆ ˆ ˆ ' 0 0, 1,.... =       − − − = ∂ ∂

_∑

_∑

= = n i k j ij j i X Y L k β β β β β β dan (2.19) 0 ˆ ˆ 2 1 1 0 ˆ ˆ ˆ ' _{0, 1,....}  =      − − − = ∂ ∂

∑

∑

= = ij n i k j ij j i j X X Y L k β β β β β β j = 1, 2,….,k

Penyerdehanaan Persamaan (2.19), diperoleh persamaan-persamaan normal kuadrat terkecil:

∑

∑

∑

∑

= = = = = + + + + n i i n i ik k n i i n i i X X Y X n 1 1 1 2 2 1 1 1 0 ˆ ˆ .... ˆ ˆ _{β β β} β

∑

∑

∑

∑

∑

= = = = = = + + + + n i i i n i ik i k n i i i n i i n i i X X X X X X Y X 1 1 1 1 1 2 1 2 1 1 2 1 1 1 0 ˆ ˆ .... ˆ ˆ _{β β β} β (2.20)     

∑

∑

∑

∑

∑

= = = = = = + + + + n i i ik n i ik k n i i ik i n i ik n i ik X X X X X X Y X 1 1 2 1 2 2 1 1 1 1 0 ˆ ˆ .... ˆ ˆ _{β β β} β

Berdasarkan estimasi pada persamaan (2.20) dalam regresi linier ganda dengan metode kuadrat terkecil, dapat diperoleh rumus estimasi regresi nonlinier ganda untuk model eksponen dengan metode kuadrat terkecil sebagai berikut:

dengan memisalkan:

∑

Y_i =

∑

lnY_i

∑

X_i1y =

∑

X_i1lnY_i

∑

Xi2y =

∑

X12lnYi

bentuk persamaan-persamaan normal kuadrat terkecil yang digunakan untuk model eksponen berganda adalah:

∑

∑

∑

∑

= = = = = + + + + n i i n i ik k n i i n i i X X Y X n 1 1 1 2 2 1 1 1 0 ˆ ˆ .... ˆ ln ˆ _{β β β} β

∑

∑

∑

∑

∑

= = = = = = + + + + n i i i n i ik i k n i i i n i i n i i X X X X X X Y X 1 1 1 1 1 2 1 2 1 1 2 1 1 1 0 ˆ ˆ .... ˆ ln ˆ _{β β β} β (2.21)     

∑

∑

∑

∑

∑

= = = = = = + + + + n i i ik n i ik k n i i ik i n i ik n i ik X X X X X X Y X 1 1 2 1 2 2 1 1 1 1 0 ˆ ˆ .... ˆ ln ˆ _{β β β} β Keterangan:

ln Yi = variabel dependen dalam bentuk logaritma asli dari variabel Y.

Ada p = k + 1 persamaan normal, satu untuk setiap koefisien regresi yang tidak diketahui. Penyelesaian untuk persamaan normal menjadi estimator-estimator kuadrat terkecil dari koefisien-koefisien regresi βˆ₀,βˆ₁,....,βˆ_k

2.2.2 Metode Matriks

Matriks didefinisikan sebagai suatu himpunan angka, variabel atau parameter dalam bentuk suatu persegi panjang, yang tersusun di dalam baris dan kolom. Pada umumnya, matriks di notasikan dalam huruf besar sedangkan elemen-elemennya dalam hurup kecil, sebagai berikut:

di mana: A = Matriks A

[ ] atau ( ) = Notasi matriks

adalah elemen dari matriks A, dimana menyatakan baris dan menyatakan kolom. Misalnya: adalah elemen dari matriks A yang terletak pada baris ke-1 dan kolom ke-1. (PUDJIASTUTI,2006)

Jenis-jenis matriks adalah sebagai berikut: 1. Matriks diagonal

Adalah suatu matriks bujur sangkar yang semua elemen di luar elemen diagonal utama sama dengan nol, dan paling tidak satu elemen pada diagonal utamanya tidak sama dengan nol.

2. Matriks identitas

Adalah suatu matriks bujur sangkar yang elemen-elemen di luar diagonal utamanya sama dengan nol, dan semua elemen pada diagonal utama sama dengan satu. Matriks identitas yang berorde n biasanya diberi simbol In

3. Matriks segitiga atas

Adalah matriks bujur sangkar yang elemen-elemen di bawah diagonal utama bernilai nol. Jadi yang tidak sama dengan nol adalah elemen-elemen pada segitiga atasnya dan paling tidak satu elemen pada diagonal utama tidak sama dengan nol.

4. Matriks segitiga bawah

Adalah matriks bujur sangkar yang elemen-elemen di atas diagonal utama bernilai nol. Jadi yang tidak sama dengan nol adalah elemen-elemen pada segitiga bawahnya dan paling tidak satu elemen pada diagonal utama tidak sama dengan nol.

5. Matriks nol

Adalah suatu matriks yang semua elemnya bernilai nol. Matriks ini biasanya diberi simbol O dan bentuknya tidak selalu bujur sangkar.

Adalah matriks yang hanya terdiri dari satu baris. Matriks ini sering disebut dengan vektor baris.

7. Matriks kolom

Adalah matriks yang hanya terdiri dari satu kolom. Matriks ini sering disebut dengan vektor kolom.

8. Matriks simetris

Adalah suatu matriks bujur sangkar yang memiliki , sehingga transposenya sama dengan matriks semula.

2.2.2.1 Tranpose suatu matrik

Tranpose suatu matriks adalah merubah ordo suatu matriks dari x menjadi x . Jika atau adalah transpose dari matriks , maka baris pada matriks menjadi kolom pada matriks dan sebaliknya kolom pada matriks menjadi baris pada matriks .

2.2.2.2 Determinan

Determinan adalah suatu skalar (angka) yang diperoleh dari suatu matriks bujur sangkar selalui operasi khusus. Disebut operasi khusus karena dalam proses penurunan determinan dilakukan perkalian-perkalian. Determinan dinotasikan dengan tanda | |

2.2.2.3 Invers Matriks

Invers matriks sering disebut dengan matriks kebalikan. Biasanya dituliskan sebagai berikut: jika A adalah suatu matriks bujur sangkar maka merupakan inverst matriksnya.

2.2.3 Persoalan Metode Matriks dalam Model Eksponen Berganda

Dengan menggunakan persamaan matriks

(2.22)

Persamaan regresi dugaan dinyatakan dengan persamaan

(2.23) Dengan

(2.24) Metode kuadrat terkecil merupakan suatu metode untuk mendapatkan nilai-nilai vektor dengan meminimumkan adalah sebagai berikut:

(2.25)

Langkah-langkah untuk menentukan nilai koefisien dari parameter pada regresi linier berganda adalah sebagai berikut:

Langkah 1

(2.26)

Langkah 2

Menghitung nilai determinan matrik dengan cara sebagai berikut:

(2.27) Langkah 3

Mencari Adjoint matriks , di mana:

(2.28)

Langkah 4

Mencari invers matriks dengan cara sebagai berikut:

(2.29)

Langkah 5

Mencari nilai matriks dengan cara sebagai berikut:

(2.30)

Sehingga untuk memperoleh nilai koefisien dari adalah dengan cara sebagai berikut:

(2.31)

Bentuk model eksponen bergandanya menjadi:

dengan memisalkan:

∑

Y_i =

∑

lnY_i

∑

X_i1Y =

∑

X_i1lnY_i

∑

X_i2Y =

∑

X₁₂lnY_i

Sehingga untuk memperoleh nilai koefisien dari adalah dengan cara sebagai berikut:                 ′ =                

∑

∑

∑

∑

i ik i i i i i k X Y Y X Y X Y X X Adj D b b b b ln ln ln ln 1 2 1 2 1 0   (2.32) Keterangan: