Pertemuan 2 Limit dan Kekontinuan 2.1 Pendahuluan - 2 Limit dan Kekontinuan

Pertemuan 2 Limit dan Kekontinuan

2.1 Pendahuluan

Konsep limit digunakan untuk menggambarkan cara sebuah fungsi dapat berbeda. Beberapa fungsi berubah secara kontinu, perubahan kecil pada hanya menghasilkan perubahan kecil pada ( ). Beberapa fungsi lainnya dapat memiliki nilai yang lompat atau berubah secara drastis. Limit memberikan cara yang tepat untuk membedakan sifat-sifat ini. 2.2 Konsep Limit

2.2.1 Rata-rata tingkat perubahan dan garis secant

Diberikan sembarang fungsi ( ), kita dapat menghitung rata-rata tingkat perubahan dari terhadap dalam interval [ ] dengan membagi perubahan nilai ( ) ( ), terhadap panjang interval dimana perubahan tersebut terjadi.

Rata-rata tingkat perubahan dari ( ) terhadap dalam interval [ ] adalah

( ) ( )

( ) ( )

Gambar 2.1 Secant dari grafik fungsi ( ) (Thomas’s Calculus, 11th

ed, p.75) Contoh 2.1 Rata-rata tingkat pertumbuhan

Gambar 2.2 memperlihatkan populasi lalat buah yang berkembangbiak dalam 50 hari. Jumlah lalat dihitung pada interval waktu tertentu dan diplot terhadap waktu, serta dibentuk menjadi kurva. Tentukan rata-rata tingkat pertumbuhan dari hari 23 hingga hari 45!

Gambar 2.2 Pertumbuhan populasi lalat buah dalam suatu eksperimen terkendali (Thomas’s Calculus, 11th

ed, p.76) Jawaban

Terdapat 150 lalat pada hari ke-23 dan 340 lalat pada hari ke-45. Berarti jumlah lalat bertambah dalam hari. Rata-rata tingkat perubahan populasi dari hari ke-23 hingga hari ke-45 adalah

lalat / hari.□ 2.2.2 Limit dari nilai fungsi

( )

yang dibaca “limit dari ( ) saat mendekati adalah .

Contoh 2.2 Karakteristik sebuah fungsi mendekati titik tertentu

Bagaimana karakteristik dari fungsi

b. Jika merupakan fungsi konstan ( ) , maka untuk sembarang nilai

( )

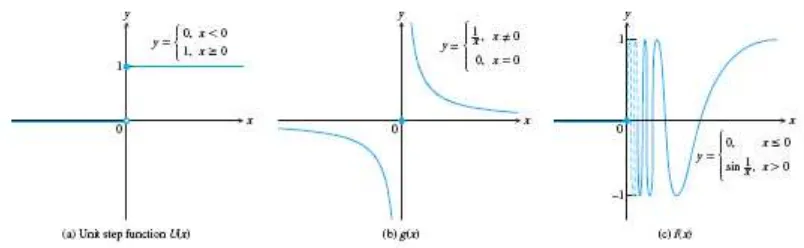
Contoh 2.5 Fungsi yang tidak memiliki limit pada titik tertentu dalam domainnya Tentukan karakteristik fungsi-fungsi berikut saat :

a. ( ) {

b. ( ) {

c. ( ) {

Jawaban

Perhatikan grafik fungsi berikut.

Gambar 2.3 Tidak ada di antara fungsi di atas yang memiliki limit saat (Thomas’s Calculus, 11th ed, p.79)

a. Fungsi tangga ( ) tidak memiliki limit saat karena nilainya melompat saat . Untuk sembarang nilai negatif yang mendekat ke nol, ( ) . Untuk sembarang nilai positif yang mendekat ke nol, ( ) . Tidak ada nilai tunggal yang didekati oleh ( ) saat .

c. ( ) tidak memiliki limit saat karena nilai fungsinya berosilasi antara dan di dalam setiap interval terbuka yang mengandung . Nilai fungsinya tidak mendekati satu bilangan pun saat

2.3 Hukum-Hukum Limit

Teorema di bawah menunjukkan cara untuk menghitung limit fungsi-fungsi yang merupakan kombinasi aritmatika dari fungsi yang limitnya telah diketahui.

Teorema 2.1 Hukum Limit

Jika dan adalah bilangan-bilangan real, dan

( ) ( )

1. Aturan penjumlahan:

( ( ) ( ))

2. Aturan pengurangan:

( ( ) ( ))

3. Aturan perkalian:

( ( ) ( ))

4. Aturan perkalian konstan:

( ( ))

5. Aturan pembagian:

( ) _{( )}

6. Aturan perpangkatan:

Jika dan adalah bilangan bulat yang tidak memiliki faktor yang sama dan ,

maka

( ( )) ⁄ ⁄

dimana ⁄ adalah bilangan real.

a. ( )

Teorema 2.2 Limit polinomial dapat ditemukan dengan substitusi

Jika ( ) , maka

( ) ( )

Teorema 2.3 berlaku hanya jika penyebut dari fungsi rasional tidak nol pada titik limit . Jika penyebutnya nol, maka menghapus faktor umum dalam pembilang dan penyebut sehingga penyebut pecahan tidak lagi nol di merupakan salah satu solusinya.

Contoh 2.8 Menghapus faktor umum

Kita tidak dapat mensubstitusi langsung karena akan membuat penyebutnya menjadi nol. Untuk itu dicari faktor umum untuk pembilang dan penyebut fungsi rasional, sehingga

Dengan menggunakan bentuk pecahan yang lebih sederhana, dapat ditemukan limit fungsi saat dengan substitusi sebagai berikut:

( ) ( )( √ )

( )( √ )

( )( ) ( )( √ )

√

Oleh karena itu,

√

√

( ) √( )

√

Teorema 2.4 Teorema Sandwich

Misal diberikan ( ) ( ) ( ) untuk seluruh dalam beberapa interval terbuka yang

mengandung , kecuali mungkin pada itu sendiri. Misal diketahui pula

( ) ( )

maka

( ) .

Contoh 2.10 Teorema Sandwich Misal diketahui

( ) untu s luruh

tentukan

Jawaban Karena

( ) ( )

maka berdasarkan Teorema Sandwich diketahui bahwa

( ) . Teorema 2.5

Jika ( ) ( ) untuk seluruh dalam beberapa interval terbuka yang mengandung ,

kecuali mungkin pada itu sendiri, dan limit dari fungsi dan keduanya ada saat

mendekati , maka

( ) ( )

2.4 Definisi Formal Limit

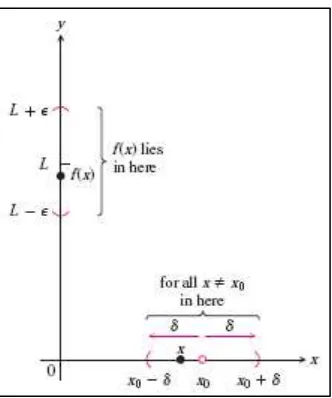
Definisi 2.1 Limit sebuah fungsi

Misal ( ) terdefinisi dalam interval terbuka sekitar , kecuali mungkin pada itu sendiri.

Kita katakan bahwa limit dari ( ) saat mendekati adalah , dan tulis

( )

jika, untuk setiap , terdapat sedemikian sehingga untuk seluruh ,

Gambar 2.4 Hubungan antara dan dalam definisi limit (Thomas’s Calculus, 11th

ed, p.92) Contoh 2.11 Menggunakan definisi

Tunjukkan bahwa

( )

Jawaban

Dari definisi limit diketahui ( ) dan . Untuk sembarang nilai , kita harus menemukan suatu sedemikian sehingga jika dan berada dalam jarak dari , yakni saat

| |

berlaku bahwa ( ) berada dalam jarak dari , sehingga | ( ) |

Kita dapat menemukan dengan langkah mundur dari ketidaksamaan : |( ) | | |

| |

Dengan demikian, kita dapat mengambil . Jika | | maka |( ) | | | | | ( ⁄ )

yang membuktikan bahwa

( )

Contoh 2.12 Menemukan delta dengan aljabar

Untuk limit

√ , temukan yang berlaku untuk . Dengan kata lain, temukan sedemikian sehingga untuk seluruh

| | |√ |

Jawaban

Terdapat dua langkah untuk memecahkan soal di atas.

1. Selesaikan persamaan |√ | untuk menemukan suatu interval yang memiliki dimana ketidaksamaannya berlaku untuk semua .

|√ | √

√

⁄

Ketidaksamaan di atas berlaku untuk seluruh dalam interval terbuka ( ⁄ ), sehingga berlaku pula untuk seluruh dalam interval ini pula.

2. Temukan nilai untuk menempatkan pusat interval di dalam interval ( ⁄ ). Jarak dari 1 ke titik terdekat ujung interval ( ⁄ ) adalah ⁄ . Jika diambil ⁄ atau nilai positif lebih kecil lainnya, maka ketidaksamaan | | akan menempatkan di antara ⁄ dan secara otomatis untuk memenuhi |√ | .

Misal diketahui bahwa ( ) dan ( ) , buktikan bahwa ( ( ) ( ))

Jawaban

Misal diberikan , akan dicari suatu bilangan positif sedemikian sehingga untuk seluruh

| | | ( ) ( ) ( )|

| ( ) ( ) ( )| |( ( ) ) ( ( ) )| | ( ) | |( ( ) )|

Untuk ( ) , terdapat suatu bilangan sedemikian sehingga untuk seluruh

| | | ( ) | ⁄

Demikian pula, untuk ( ) , terdapat suatu bilangan sedemikian sehingga untuk seluruh

| | | ( ) | ⁄

Misal diambil { }. Jika | | maka | | , sehingga | ( ) | ⁄ , dan | | , sehingga | ( ) | ⁄ . Oleh karenanya,

| ( ) ( ) ( )| | ( ) | |( ( ) )| ⁄ ⁄

Terbukti bahwa ( ( ) ( ))

2.5 Limit Kiri dan Limit Kanan

Teorema 2.6

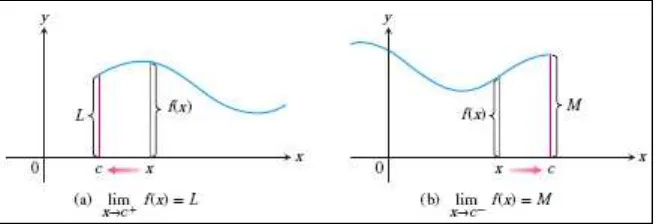
Sebuah fungsi ( ) memiliki limit saat mendekati jika dan hanya jika fungsi tersebut

memiliki limit kiri dan limit kanan dan limit satu sisi tersebut sama:

Gambar 2.5 Limit kanan saat mendekati (a), limit kiri saat mendekati (b) (Thomas’s Calculus, 11th ed, p.102)

Definisi 2.2 Limit kanan dan limit kiri

Kita katakan bahwa ( ) memiliki limit kanan pada , dan ditulis

( )

jika untuk setiap bilangan terdapat sedemikian sehingga untuk seluruh

| ( ) |

Kita katakan bahwa ( ) memiliki limit kiri pada , dan ditulis

( )

jika untuk setiap bilangan terdapat sedemikian sehingga untuk seluruh

| ( ) |

Contoh 2.14 Menentukan delta dengan menggunakan definisi Buktikan bahwa

√

Jawaban

Misal diberikan . Dari soal diketahui dan , sehingga kita ingin mencari suatu sedemikian sehingga untuk seluruh

atau

√

Dengan menguadratkan kedua ruas ketidaksamaan terakhir, diperoleh i a

Jika dipilih , diperoleh

√

atau

|√ |

Menurut definisi 2.2, terbukti bahwa √

Untuk fungsi yang melibatkan , limitnya saat adalah (diukur dalam radian). Perhatikan gambar berikut.

Gambar 2.6 Grafik ( ) (Thomas’s Calculus, 11th

ed, p.105) Teorema 2.7

( )

Definisi 2.3 Fungsi genap dan ganjil

Sebuah fungsi ( ) adalah sebuah

fungsi ganjil dari jika ( ) ( )

jika untuk setiap , terdapat bilangan sedemikian sehingga untuk seluruh

| ( ) |

2. Kita katakan bahwa ( ) memiliki limit saat mendekati minus tak hingga dan

ditulis

( )

jika untuk setiap , terdapat bilangan sedemikian sehingga untuk seluruh

| ( ) | Contoh 2.16 Limit tak hingga

Tunjukkan bahwa

Jawaban

Misal diberikan . Harus ditemukan suatu bilangan sedemikian sehingga untuk seluruh

| _{| | |}

Implikasi ini berlaku jika

Contoh 2.17 Menggunakan teorema 2.8

Definisi 2.6 Limit tak hingga dan negatif tak hingga

2. Kita katakan bahwa ( ) mendekati negatif tak hingga saat mendekati , dan

ditulis

( )

jika untuk setiap bilangan real negatif terdapat sedemikian sehingga

untuk seluruh

| | ( ) Contoh 2.20 Definisi limit tak hingga

Buktikan bahwa

Jawaban

Diberikan , akan dicari sedemikian sehingga

| | b rarti

Sekarang,

atau ekuivalen dengan

| | √

Dengan demikian, dengan memilih

√ (atau sembarang bilangan positif yang lebih kecil), diperoleh

| |

Oleh karenanya, terbukti bahwa

Sebuah garis merupakan suatu vertical asymptote dari grafik fungsi ( ) jika

salah satu pernyataan berikut berlaku

( ) ( )

Contoh 2.21 Mencari asymptote

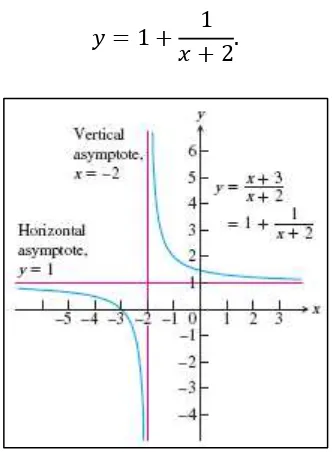
Temukan horizontal dan vertical asymptote dari kurva

Jawaban

Kita tertarik untuk mengetahui karakteristik fungsi saat dan saat , dimana penyebutnya menjadi nol.

Kita dapat menemukan asymptote fungsi tersebut dengan mudah jika fungsi rasional di atas diubah menjadi fungsi polinomial dengan sisa pembagian, yakni dengan membagi ( ) dengan ( ).

Hasilnya

Gambar 2.7 Garis dan merupakan asymptote dari kurva (Thomas’s Calculus, 11th

Sekarang dapat dilihat bahwa kurva tersebut merupakan grafik yang digeser 1 unit ke atas dan 2 unit ke kiri (gambar 2.7). Vertical asymptote kurva adalah garis dan horizontal asymptote kurva adalah .

2.7 Kekontinuan

Untuk memahami kontinuitas, perhatikan gambar di bawah sebagai contoh berikutnya.

Gambar 2.8 Fungsi di atas kontinu pada [ ] kecuali pada dan (Thomas’s Calculus, 11th ed, p.124)

Contoh 2.22 Kontinuitas

Tentukan titik dari fungsi pada gambar 2.8 yang kontinu dan titik dimana diskontinu! Jawaban

Fungsi kontinu di setiap titik dalam domainnya, yakni [ ], kecuali pada dan . Pada titik-titik ini terdapat lompatan dalam grafik fungsi.

Titik-titik dimana kontinu:

Pada

( ) ( )

Pada

( ) ( )

Pada

( ) ( )

Titik-titik dimana diskontinu:

Pada

Pada

( ) t ta i ( ) Pada

( ) t ta i ( )

Pada titi -titi ini tida b rada dalam domain Definisi 2.8 Kontinuitas pada satu titik

Titik interior: Sebuah fungsi ( ) kontinu dalam suatu titik interior dalam domainnya

jika

( ) ( )

Titik ujung: Sebuah fungsi ( ) kontinu dalam suatu titik ujung kiri atau kontinu

dalam suatu titik ujung kanan dalam domainnya jika

( ) ( ) ( ) ( )

Contoh 2.23 Fungsi kontinu dalam domainnya

Fungsi ( ) √ kontinu pada setiap titik dalam domainnya, [ ], termasuk dimana kontinu kanan, dan dimana kontinu kiri.

Uji Kontinuitas

Sebuah fungsi ( ) kontinu pada jika dan hanya jika memenuhi tiga kondisi berikut.

1. ( ) ( )

2. ( ) ( )

3. ( ) ( ) ( )

Contoh 2.24 Fungsi integer terbesar

Gambar 2.9 Fungsi integer terbesar kontinu pada setiap titik noninteger (Thomas’s Calculus, 11th

ed, p.126)

Fungsi di atas diskontinu untuk setiap bilangan bulat karena limitnya tidak ada untuk setiap bilangan bulat :

int int

sehingga limit kiri dan limit kanannya tidak sama saat . Karena int , fungsi integer terbesar kontinu kanan pada tiap integer (tapi tidak kontinu kiri).

Fungsi integer terbesar kontinu pada setiap bilangan real selain bilangan bulat, seperti

int int Umumnya, jika bilangan bulat, maka

int int

Sebuah fungsi dikatakan kontinu pada suatu interval jika dan hanya jika fungsi tersebut kontinu untuk setiap titik dalam interval.

Teorema 2.9 Sifat-sifat fungsi kontinu

Jika fungsi dan kontinu pada , maka kombinasi berikut juga kontinu pada .

1. Penjumlahan:

2. Pengurangan:

3. Perkalian:

4. Perkalian konstan: , untuk sembarang

5. Pembagian: ⁄ , dimana ( )

6. Perpangkatan: ⁄ , dengan catatan fungsi tersebut terdefinisi pada interval terbuka yang mengandung , dimana dan adalah bilangan

bulat.

a. Setiap polinomial ( ) kontinu karena

( ) ( ) menurut Teorema 2.2.

b. Jika ( ) dan ( ) merupakan polinomial, maka fungsi rasional ( ) ( )⁄ kontinu dimanapun, dengan catatan ( ) , berdasarkan Aturan Pembagian Teorema 2.9.

Teorema 2.10 Komposisi fungsi kontinu

Jika kontinu pada dan kontinu pada ( ), maka komposisi kontinu pada .

Contoh 2.26 Menggunakan teorema 2.9 dan 2.10

Tunjukkan bahwa fungsi-fungsi berikut kontinu di setiap titik dalam domainnya.

a. √ b. |

| Jawaban

a. Fungsi akar pangkat dua kontinu pada [ ) karena merupakan fungsi pangkat rasional dari fungsi identitas ( ) . Fungsi yang diberikan merupakan komposisi dari polinomial ( ) dengan fungsi akar ( ) √ .

b. Pembagian

kontinu untuk semua √ , dan fungsi tersebut adalah komposisi dari pembagian dengan fungsi kontinu nilai absolut.

Teorema 2.11 Teorema nilai rata-rata untuk fungsi kontinu

Sebuah fungsi ( ) yang kontinu dalam suatu interval tertutup [ ] memiliki semua

nilai diantara ( ) dan ( ). Dengan kata lain, jika adalah sembarang nilai diantara

( ) dan ( ), maka ( ) untuk dalam [ ].

2.8 Tangen dan Turunan

Definisi 2.9 Slope dan garis tangent

Slope dari kurva ( ) pada titik ( ( )) adalah bilangan

dengan catatan limitnya ada.

Garis tangent dari kurva pada adalah garis yang melalui dengan slope ini.

Contoh 2.27 Menggunakan definisi 2.9

a. Temukan slope dari kurva ⁄ pada . b. Dimanakah slope tersebut sama dengan ⁄ ? Jawaban

a. Diketahui ( ) ⁄ . Slope pada ( ⁄ ) adalah

( ) ( )

( ) _{( )}

_{( )}

_{( )}

Nilai boleh positif atau negatif, tetapi tidak .

b. Slope dari ⁄ pada titik dimana adalah . Nilainya akan jika

atau

Kurva memiliki slope ⁄ pada dua titik ( ⁄ ) dan ( ⁄ ). Rata-rata Perubahan: Turunan pada Satu Titik

Ekspresi

( ) ( )

disebut sebagai difference quotient dari pada dengan increment . Jika difference

quotient memiliki limit saat mendekati nol, limit tersebut dikatakan sebagai turunan dari