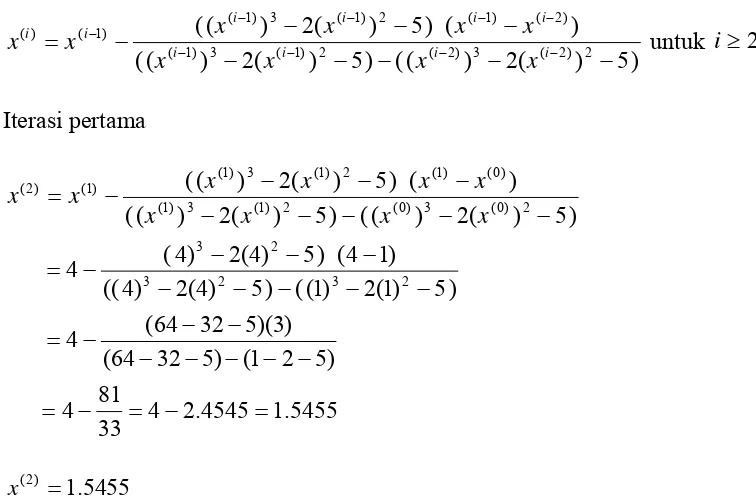Penyelesaian sistem persamaan non-linear dengan metode broyden dan terapannya - USD Repository

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Disusun oleh : Valentina Rian Prastiwi

NIM : 033114008

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA YOGYAKARTA

2007

▸ Baca selengkapnya: pengertian trend non linear

Presented As Partial Fulfillment Of The Requirements To Obtain The Sarjana Sains Degree In Mathematics

By :

Valentina Rian Prastiwi

Student Number : 033114008

STUDY PROGRAM OF MATHEMATICS SCIENCE DEPARTEMANT OF MATHEMATICS

FACULTY OF SCIENCE AND TECHNOLOGY SANATA DHARMA UNIVERSITY

YOGYAKARTA 2007

percobaan-percobaan berat tak akan mencelakakan engkau. Jangan takut sebab Aku melindungi engkau. (Yesaya 43:2,15)

Manfaatkan setiap menit sebagai kunci berharga

yang dapat membuka gerbang kebahagiaan masa depan.

Hidup ini dipenuhi dengan tantangan

yang jika dimanfaatkan secara kreatif, menjadi sebuah kesempatan.

Kegagalan masa lalu adalah semangat

untuk meraih keberhasilan masa depan.

Karya sederhana ini kupersembahkan untuk:

Tuhan Yesus Kristus dengan segala pengorbanan dan limpahan berkatNya Bunda Maria dengan kesetiaanNya mendampingiku Ibu dan Alm. Ayahku tercinta Kakak-kakakku tersayang Teman-teman dan Sahabat-sahabatku Almamaterku

pustaka, sebagaimana layaknya karya ilmiah.

Yogyakarta, September 2007

Penulis

but. Sistem persamaan non-linear dengan persamaan dan variabel dapat dise-lesaikan secara numerik dengan beberapa metode, diantaranya adalah Metode Ti-tik Tetap, Metode Newton, Metode Broyden, dan sebagainya. Dalam penulisan ini hanya akan dibahas penyelesaian sistem persamaan non-linear dengan Metode Broyden.

n n

Metode Broyden merupakan pengembangan dari Metode Secant, yang digunakan untuk menyelesaikan persamaan non-linear. Setiap iterasi dalam perhi-tungan dengan Metode Broyden melibatkan invers dari Matriks Jacobi . Rumus umum untuk mencari penyelesaian sistem persamaan non-linear

dengan menggunakan metode Broyden adalah :

1 − i A

) ( (i)

x F )

( () )

( ) 1

( i

i i i

x F A x

x + = − −1

Penyelesaian sistem persamaan non-linear dengan Metode Broyden mem-punyai sifat konvergen superlinear-q yang terpenuhi bila dan hanya bila kondisi Dennis-Moré terpenuhi, yakni {Ei}≈0, di mana adalah kesalahan dari Ma-triks Jacobi.

i E

Dalam penulisan ini, Metode Broyden akan diterapkan dalam bidang fisika, secara khusus untuk menghitung konsentrasi unsur dalam suatu sampel.

linear equations with the equations and n variables may be solved numerically with some of methods, such as Fixed Points, Newton Method, Broyden’s Method, etc. However, this final project will only discuss about solving systems of non-linear equations with the Broyden’s method.

n

Broyden’s Method is generalization of the Secant Method, which is used to solve the non-linear equations. Every iteration in the calculating with the Broy-den’s Method involve invers from Jacobian Matrix. And the general formula to solve the systems of non-linear equations ( (i)) with Broyden’s method is

x F

) ( () )

( ) 1

( i

i i i

x F A x

x + = − −1

The solution of systems of non-linear equations with Broyden’s Method has q-superlinearly convergence that is hold if and only if Dennis-Moré condition hold, that is{Ei}≈0, which Ei is the error of Jacobian Matrix.

In this final project, Broyden’s Method is applied in the area of physics, particularly to calculate the concentration of elements in a sample.

Segala puji dan syukur penulis haturkan kehadirat Bapa Yang Maha Pe-ngasih atas berkat kasih karunia dan limpahan Roh Kudus yang telah diberikan kepada penulis. Sehingga penulis dapat menyelesaikan Tugas Akhir ini. Sungguh besar berkat dan penyertaan yang penulis rasakan. Tanpa kemurahan dan penyer-taan-Nya penulis tidak akan mampu menyelesaikan tugas akhir ini dan melewati setiap hambatan dan tantangan yang penulis alami selama proses penulisan tugas akhir ini.

Tugas akhir ini disusun untuk memenuhi salah satu syarat guna mencapai gelar Sarjana Sains pada Fakultas Sains dan Teknologi, Universitas Sanata Dharma Yogyakarta. Tugas akhir ini diberi judul “Penyelesaian Sistem Persamaan Non-Linear dengan Metode Broyden dan Terapannya.”

Selesainya penulisan tugas akhir ini tidak lepas dari dukungan dan bantuan dari berbagai pihak, baik bantuan moril maupun materiil, yaitu saran, nasehat, bimbingan, pemikiran, serta waktu dan tenaga yang penulis terima selama ini. Ucapan terima kasih ini penulis haturkan kepada:

1. Ibu Lusia Krismiyati Budiasih, S.Si., M.Si., selaku Kaprodi Mate-matika Fakultas Sains dan Teknologi USD dan dosen pembimbing skripsi yang sabar dan penuh pengertian dalam membimbing, menga-rahkan, serta memberikan saran dan koreksi kepada penulis sehingga dapat menyelesaikan skripsi ini.

2. Bapak Dr. Ign Edi Santosa, S.Si., M.Sc., yang telah menyelenggarakan percobaan kalibrasi untuk mengukur konsentrasi larutan parasetamol dan kafein, sehingga penulis memperoleh data untuk menerapkan Me-tode Broyden, serta atas bimbingan, arahan, koreksi, dan saran yang te-lah diberikan.

4. Ibu Ch. Enny Murwaningtyas, S.Si., M.Si., selaku dosen pembimbing akademik dan seluruh dosen Fakultas Sains dan Teknologi USD yang telah memberikan arahan, petunjuk, dan motivasi kepada penulis se-lama kuliah di USD.

5. Mas Tukijo dan Ibu Linda atas pelayanan yang diberikan selama men-jalani perkuliahan sampai selesai dan selama penulisan skripsi ini. 6. Ayahku (Alm. Ag. Suratman) dan Ibuku (Endang Sulastri) tercinta,

serta kakak-kakakku tersayang, mbak Lisa dan Kak Agung, atas segala cinta, perhatian, pengertian, dukungan, pengorbanan, dan doa yang tiada henti-hentinya untukku.

7. Teman-temanku di prodi Matematika angkatan ’03: Mekar tempatku berkeluh kesah tanpa dukunganmu aku takkan seperti ini, Anin yang selalu setia menemaniku kuliah dan menghadirkan kecerian dengan banyolannya, Dewi sobatku seperjuangan yang lugu tapi baik dan se-lalu kasih semangat, Merry yang asyik dan familiar banget ama orang, Anggi temanku senasib dan seperjuangan, Jegul yang selalu kasih se-mangat dan jadi teman ngobrol yang seru, Septi yang nyantai tapi smart, Sisil yang baik dan selalu kasih semangat, Eko yang baik dan penuh semangat, Koko yang selalu mendoakan dan memberi sema-ngat, dan Ita. Kalian telah mengajariku arti persahabatan. Meski sedikit pokoknya KOMPAK terus.

8. Sobat-sobatku tersayang Wawan, Popeye, kalian selalu ngingetin aku untuk rajin berdoa dan kasih semangat, Cupid yang jadi dokter kom-puterku, Mas Adit thanks bantuan dan semangatnya, Gendrot, Erna, dan teman-teman gerejaku. Kalian semua tempatku berbagi susah dan senang.

9. Buat keluargaku di Jogja, keluarga besar Adi Sumarto dan Kromo Di-meja. Mbah Putri, Pakde, Oom dan tanteku, sepupu-sepupuku Rudy,

yang lain.

11.Buat teman-teman di prodi Matematika, baik kakak angkatan maupun adik angkatanku semua.

12.Semua pihak yang tidak dapat disebutkan satu-persatu yang telah membantu dan mendukung dalam proses penulisan tugas akhir ini.

Penulis menyadari bahwa tugas akhir ini masih jauh dari sempurna, masih banyak kekurangan dan kelemahan. Oleh karena itu penulis terbuka akan segala kritik dan saran yang bersifat membangun dari pembaca demi sempurnanya tugas akhir ini.

Yogyakarta, September 2007 Penulis

Halaman Judul (Inggris)……...……… ii

Halaman Persetujuan Pembimbing………..………….……… iii

Halaman Pengesahan……… iv

Halaman Persembahan………..……… v

Pernyataan Keaslian Karya………...……… vi

Abstrak………..……… vii

Abstract……….……… viii

Kata Pengantar………..……… ix

Daftar Isi………...……… xii

Daftar Tabel……….………. xvi

Bab I PENDAHULUAN……… 1

A. Latar Belakang Masalah………..……… 1

B. Rumusan Masalah ………...……… 3

C. Batasan Masalah………..……… 4

D. Tujuan Penulisan……….……… 4

E. Manfaat Penulisan ………...……… 4

F. Metode Penulisan……….……… 4

G. Sistematika Penulisan………...……… 5

B. Teorema Kalkulus ……… 13

C. Konvergensi………..……… 16

D. Penyelesaian Persamaan Non-Linear dengan Satu Variabel……… 20

Bab III PENYELESAIAN SISTEM PERSAMAAN NON-LINEAR ….. 26

A. Sistem Persamaan Non-Linear………..……… 26

B. Penyelesaian Sistem Persamaan Non-Linear dengan Metode Broyden……… 29

C. Kondisi Dennis-More……….……… 61

D. Analisis Konvergensi Metode Broyden………….……… 71

1. Bounded Deterioration………..……… 75

2. Konvergen Linear Lokal……… 80

3. Pembuktian Kondisi Dennis-More……....……… 84

BAB IV PENERAPAN METODE BROYDEN DALAM MENGHITUNG KONSENTRASI UNSUR DALAM SUATU SAMPEL…….… 86

A. Metode Penyerapan Cahaya………..……… 86

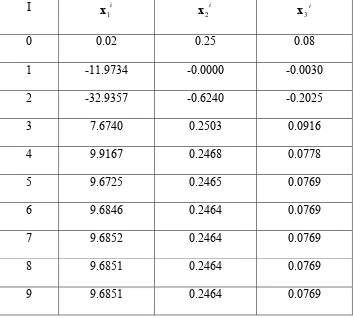
B. Penerapan Metode Broyden untuk Menghitung Konsentrasi Unsur…………..………. 88

2. Pengaruh Nilai Awal pada Hasil………….………….. 93

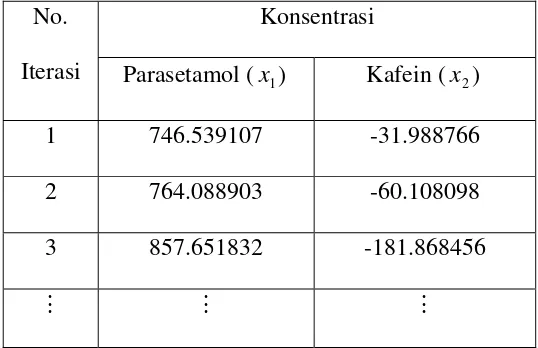
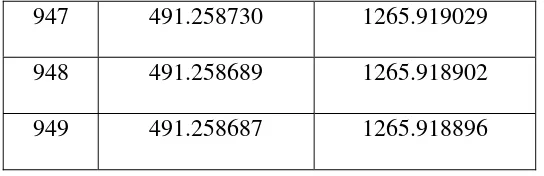
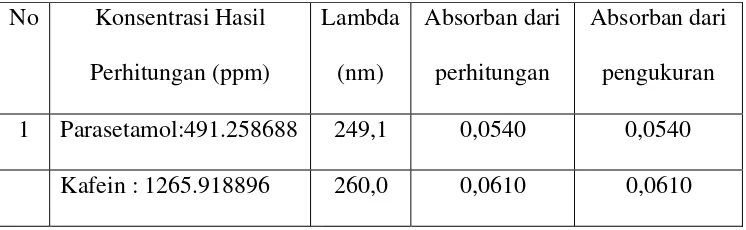
3. Perbandingan Nilai Absorban Hasil Pengukuran dengan Hasil Perhitungan……… 95

4. Konsentrasi Parasetamol dan Kafein yang Memenuhi………..……… 95

BAB V PENUTUP……….. 97

A. Kesimpulan………..………….. 97

B. Saran………...…………... 101

DAFTAR PUSTAKA ……….……… 102

LAMPIRAN……… 104

Lamp.1 Program Metode Broyden………. 105

Lamp.2 Program untuk Fungsi Contoh 3.2.1………. 106

Lamp.3 Program untuk Turunan Fungsi Contoh 3.2.1……….. 107

Lamp.4 Program BroydenMethods………... 108

Lamp.5 Program untuk SPNL Parasetamol dan Kafein 1………. 109

Lamp.6 Program untuk Turunan SPNL Parasetamol dan Kafein 1……. 110

Lamp.7 Program untuk SPNL Parasetamol dan Kafein 2………. 111

Lamp.8 Program untuk Turunan SPNL Parasetamol dan Kafein 2……. 112

Lamp.12 Program untuk Plot Grafik……… 116 Lamp.13 Keluaran SPNL dengan Metode Broyden.………. 117 Lamp.14 Keluaran SPNL dengan Nilai Awal Berbeda………. 118 Lamp.15 Keluaran SPNL dengan Pendekatan Matriks Identitas……….. 119

, 0 5 2 2 3 _{− − =}

x

x dengan metode Secant………...……… 24

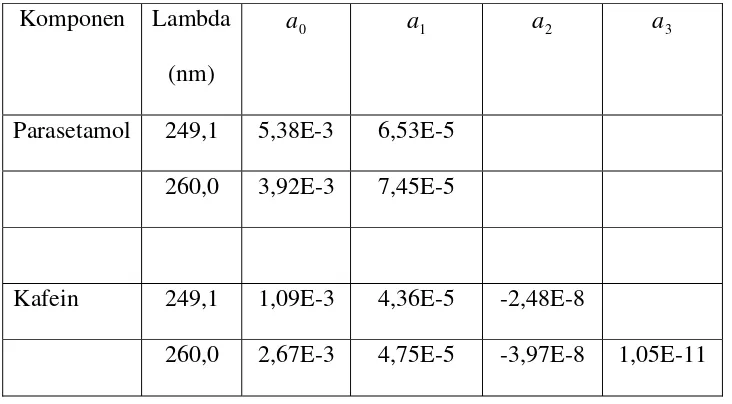
2. Tabel 3.2.1 Hasil Iterasi……… 59 3. Tabel 4.2.1 Koefisien polinomial 3

3 2 2 1

0 ac a c a c a

A= + + +

hubungan antara absorban dan konsentrasi dari parasetamol

dan kafein untuk berbagai panjang gelombang………….………. 89 4. Tabel 4.2.2 Hasil pengukuran absorban dari satu sampel yang

mengandung 500 ppm parasetamol dan 500 ppm kafein……… 89 5. Tabel 4.2.3. Hasil Perhitungan Konsentrasi Parasetamol dan Kafein

antara panjang gelombang 249,1 nm dengan 260,0 nm…..……… 90 6. Tabel 4.2.4. Hasil Perhitungan Konsentrasi

Parasetamol dan Kafein………...……… 91 7. Tabel 4.3.1. Hasil Perhitungan Konsentrasi Parasetamol

dan Kafein pada panjang gelombang 272,2 nm dan 249,1 nm

dengan nilai awal yang berbeda-beda……….……… 93 8. Tabel 4.3.2 Perbandingan nilai absorban

hasil perhitungan dan nilai absorban hasil pengukuran…..……… 95

A. Latar Belakang Masalah

Saat ini matematika banyak diterapkan dalam kehidupan nyata, sehingga tidak heran kalau banyak persoalan yang muncul berkaitan dengan penerapan matematika tersebut. Banyak metode yang digunakan untuk menyelesaikan persoalan-persoalan tersebut. Metode analitis adalah metode yang menggunakan metode-metode aljabar yang sederhana untuk menyelesaikan suatu persoalan. Namun terkadang persoalan-persoalan tersebut sulit atau bahkan tidak bisa diselesaikan secara analitis sehingga diperlukan metode lain yang memformulasikan persoalan matematika sehingga dapat diselesaikan dengan menggunakan operasi-operasi aritmatika. Metode ini sering disebut dengan metode numeris. Metode numeris banyak dipakai untuk menyelesaikan persamaan, baik linear maupun non-linear.

Persamaan non-linear adalah persamaan di mana tiap fungsinya melibatkan bentuk eksponensial, trigonometri, logaritma, rasional, polinomial berderajat dua atau lebih, ada hasil kali antara fungsi yang belum diketahui dengan turunannya, atau fungsi transenden lainnya. Persamaan non-linear sendiri dibagi menjadi persamaan linear dengan satu variabel dan persamaan non-linear dengan variabel, dengan n n>1.

Bentuk umum persamaan non-linear dengan satu variabel adalah 0

) (x =

f .

Sedangkan bentuk umum persamaan non-linear dengan variabel adalah n 0

) ,..., ,

(x1 x2 xn =

f .

Sistem Persamaan non-linear atau sering disingkat SPNL adalah himpunan persamaan non-linear, dengan , yang penyelesaiannya harus memenuhi semua persamaan tersebut.

Bentuk umum sistem persamaan non-linear dengan persamaan dan variabel adalah :

n n>1

n

n n

0 ) ,..., ,

( 1 2 n = j x x x

f untuk j =1,2,3,...n

di mana tiap fungsi merupakan pemetaan vektor x = dari ke , sistem ini dapat ditulis dalam bentuk lain dengan mendefinisikan fungsi F,

etaan dari ke , yakni F

Dengan menggunakan notasi vektor, sistem di atas dapat ditulis dalam bentuk : F(x) = 0

Penyelesaian sistem persamaan non-linear bukan merupakan akar-akar yang merupakan penyelesaian yang eksak, melainkan penyelesaian yang mendekati dengan tingkat konvergensi yang tinggi.

Banyak metode numeris yang telah ditemukan untuk mencari penyelesaian persamaan non-linear, dan yang paling terkenal adalah Metode Newton-Raphson. Meskipun Metode Newton-Raphson telah banyak digunakan, namun metode ini mempunyai beberapa kelemahan, yaitu terkadang turunan fungsi-fungsinya sulit dievaluasi, dan memerlukan pendekatan awal yang baik agar mempunyai tingkat

f (x1,x2,...,xn)t

n ℜ

ℜ

suatu pem ℜn ℜn

t n n

n n

n f x x x f x x x f x x x

x x

x , ,...., ) ( ( , ,...., ), ( , ,...., ),...., ( , ,...., ))

konvergensi yang tinggi. Untuk mengatasi kelemahan itu muncul metode baru, yaitu Metode Secant. Metode Secant adalah pengembangan Metode Newton-Raphson untuk menyelesaikan persamaan non-liear yang tidak harus menghitung turunan di setiap iterasi. Sedangkan pengembangan Metode Secant untuk menyelesaikan sistem persamaan dengan n persamaan dan n variabel disebut Metode Broyden atau sering disebut juga Metode Quasi-Newton.

Bidang lain di luar matematika, khususnya bidang fisika, juga membutuhkan analisis matematis untuk menyelidiki suatu persoalan yang sulit atau bahkan tidak dapat diselesaikan hanya dengan menggunakan rumus atau teori fisika saja. Dalam hal ini Metode Broyden dapat digunakan untuk menyelesaikan sistem persamaan non-linear yang muncul dalam persoalan di bidang fisika, seperti untuk menghitung konsentrasi unsur dalam sampel yang menggunakan metode penyerapan cahaya oleh atom.

B. Rumusan Masalah

Dari uraian yang dikemukakan dalam latar belakang, dapat dirumuskan beberapa masalah :

1.Bagaimana mencari penyelesaian sistem persamaan non-linear secara numeris dengan menggunakan Metode Broyden?

C. Batasan Masalah

1.Sistem persamaan non-linear yang akan diselesaikan adalah sistem dengan n persamaan dan n variabel.

2.Bahasa pemrograman yang digunakan untuk membantu mencari pe-nyelesaian sistem persamaan non-linear adalah Matlab.

D. Tujuan Penulisan

Tujuan penulisan skripsi ini adalah untuk menyelesaikan sistem persamaan non-linear secara numeris dengan menggunakan Metode Broyden dan menerapkan Metode Broyden untuk menyelesaikan sistem persamaan non-linear yang dimodelkan dari persoalan dalam bidang fisika, khususnya untuk menghitung konsentrasi unsur dalam suatu sampel.

E. Manfaat Penulisan

Manfaat penulisan skripsi ini adalah agar pembaca mengetahui dan mendalami Metode Broyden untuk menyelesaikan sistem persamaan non-linear, serta untuk mengetahui penerapan Metode Broyden dalam bidang fisika terutama untuk menghitung konsentrasi unsur dalam suatu sampel.

F. Metode Penulisan

G. Sistematika Penulisan BAB I PENDAHULUAN

(Bagian ini berisi tentang latar belakang, rumusan masalah, batasan masalah, tujuan penulisan, manfaat penulisan, metode penulisan, dan sistematika penulisan).

BAB II MATRIKS, RUANG VEKTOR, NORMA, KONVERGENSI DAN PENYELESAIAN PERSAMAAN NON-LINEAR

(Penjelasan tentang matriks, ruang vektor, norma, dan proyeksi orthogonal, serta teorema-teorema kalkulus, konvergensi, dan penyelesaian persamaan non-linear dengan satu variabel terdapat pada bagian ini).

BAB III PENYELESAIAN SISTEM PERSAMAAN NON-LINEAR

(Pengertian sistem persamaan non-linear, penyelesaian sistem persamaan non-linear dengan Metode Broyden, Kondisi Dennis-Moré, serta analisis konvergensi Metode Broyden disajikan pada bagian ini).

BAB IV MENGHITUNG KONSENTRASI UNSUR DALAM SUATU SAMPEL DENGAN METODE BROYDEN

(Penerapan Metode Broyden untuk menghitung konsentrasi unsur dalam suatu sampel, dan analisis perhitungan konsentrasi unsur dengan Metode Broyden disajikan pada bagian ini).

BAB V PENUTUP

Dalam Bab II ini akan dibahas tentang matriks, konvergensi, dan penyelesaian persamaan non-linear yang akan digunakan sebagai dasar untuk membahas bab-bab selanjutnya.

A. Matriks, Ruang Vektor, dan Norma

Pada subbab ini akan dibahas mengenai sifat-sifat matriks, vektor, norma dan proyeksi orthogonal.

Definisi 2.1.1

Jika A adalah sebarang matriks mxn, maka transposA dinyatakan dengan T, didefinisikan sebagai matriks

A nxm yang didapatkan dengan

mempertukarkan baris dan kolom dari A; yaitu kolom pertama dari adalah baris pertama dari

T A A, kolom kedua dari T adalah baris kedua dari

A A, dan

seterusnya.

Jika T dan

A BT berturut-turut adalah transpos matriks A dan B, maka berlaku sifat : T T T

A B AB) = (

Bukti :

Misalkan A=(aij)mxp, B=(bij)pxn,dan C = A.B=(cij)mxn

Maka elemen baris ke-i, kolom ke- j dari C = A.B adalah yang

merupakan elemen baris

ke-∑

=

= p

k

kj ik ij a b c

1 .

j, kolom ke- dari i

T T

B A

C =( . ) (2.1.1)

Elemen-elemen kolom ke- dari i AT adalah elemen baris ke-i dari A,

⎥ ⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢ ⎢

⎣ ⎡

ip i i

a a a

M 2 1

dan baris ke- j dari T

B adalah

[

b1_j b2_j Lb_pj

]

Maka elemen baris ke-j kolom ke- dari i BTAT adalah

[

]

∑

=

= =

+ + +

=

+ + +

=

⎥ ⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢ ⎢

⎣ ⎡

p k

ij kj ik

pj ip j

i j i

ip pj i

j i j ip i i pj j j

c b a

b a b

a b a

a b a

b a b a a a b b

b

1

2 2 1 1

2 2 1 1 2 1

2 1

L L M

L

(2.1.2)

Dari persamaan (2.1.1) dan persamaan (2.1.2)

T T T

A B AB) = (

■

Definisi 2.1.2

Suatu matriks bujursangkar A=a_ij disebut matriks simetri jika atau

T A A=

j i ji ij a

Definisi 2.1.3

Suatu matriks bujursangkar A dikatakan invertibel atau non singular jika terdapat matriks B sedemikian sehingga AB=BA=I. Matriks B tersebut

dinamakan invers dari A, dan biasanya ditulis A−1.

Teorema 2.1.1

Invers dariA adalah tunggal.

Bukti:

Misalkan B dan C invers dariA, Maka AB=BA= I dan AC =CA=I Di lain pihak B=BI =B(AC)= IC=C, yaitu B=C

Jadi terbukti bahwa invers dari A adalah tunggal.

■

Teorema 2.1.2 1 −

A invertibel dan (A−1)−1 = A

Bukti :

Misalkan A−1 merupakan invers dari matriksA maka berlaku I

A A AA−1 = −1 =

Jadi, A merupakan invers dari A−1, yaitu (A−1)−1 = A

Definisi 2.1.4

Grup adalah suatu himpunan dengan operasi * pada G yang memenuhi setiap aksioma berikut ini:

G

1. Bersifat asosiatif

c b a c b

a*( * )=( * )* , ∀a,b,c∈G

2. Terdapat Elemen Identitas

Terdapat elemen e∈G sedemikian sehingga a*e=e*a =a, ∀a∈G 3. Terdapat Invers

, , sedemikian sehingga G

a∈

∀ ∃b∈G a*b=b*a=e

Definisi 2.1.5

Grup Komutatif adalah grup yang operasi perkaliannya bersifat komutatif, yaitu

, a b b

a* = * ∀a,b∈G

Definisi 2.1.6

Lapangan adalah himpunan tak kosong dengan dua operasi yang disebut penjumlahan dan perkalian, dengan sifat:

F

i. Himpunan F dengan operasi penjumlahan membentuk Grup

ii. Himpunan F−{0} dengan operasi perkalian membentuk Grup Komutatif

iii. Berlaku sifat Distributif :

ac ab c b

Definisi 2.1.7

Andaikan V merupakan suatu himpunan yang dilengkapi dengan dua operasi, yakni penjumlahan dan perkalian dengan skalar dalam lapangan F. Didefinisikan

V

V + ∈

∈

∀x ,x y yang disebut penjumlahan dan ∀x∈Vdan ∀a∈F, ax∈Vyang

disebut dengan perkalian skalar, maka V dinamakan dengan ruang vektor atas bila memenuhi syarat-syarat sebagai berikut:

F

1. ∀x,y∈V, x+y=y+x

2. ∀x,y,z∈V, (x+y)+z =x+(y+z)

3. ∃0∈V,∀x∈V, x+0=x

4. ∀x∈V, ∃y∈V, x+y=0

5. ∀x∈V, 1x=x

6. ∀x∈V, ∀a,b∈F, (a+b)x=ax+bx

7. ∀x∈V, ∀a∈F, a(x+y)=ax+ay

8. ∀x∈V, ∀a,b∈F,(ab)x=a(bx)

Definisi 2.1.8

Vektor-vektor dan di dalam x y ℜ2 (atau ℜ3) dikatakan orthogonal jika 0

=

Definisi 2.1.9

Hasil kali dalam untuk ℜn adalah sebuah pemetaan dari n n ke xℜ

ℜ ℜ

yang menunjuk setiap pasang vektor-vektor x dan y di dalam dengan sebuah

bilangan real yang memenuhi syarat sebagai berikut:

n ℜ

(i) <x,x> ≥0 dan <x,x> =0⇔ x=0

(ii) <x,y>=< y,x> untuk semua dan di dalam x y ℜn

(iii) <αx+βy,z>=α <x,z>+β <y,z> untuk semua x,y,z di dalam

ℜndan semua skalar α β dan .

Definisi 2.1.10

Hasil kali dalam untuk ℜn adalah hasil kali skalar <x,y>=xTy.

Definisi 2.1.11 (Norma Vektor)

Sebuah ruang vektor dikatakan ruang linear bernorma jika untuk setiap

dikaitkan dengan sebuah bilangan real yang disebut norma dari yang memenuhi:

n ℜ

n ℜ ∈

x ||x|| x

(i) ||x|| ≥0 dan ||x||=0 ⇔ x =0

(ii) ||α x|| = |α |||x|| untuk setiap skalar α

Definisi 2.1.12

Jika adalah sebuah vektor dalam sebuah ruang hasil kali dalam ,

panjang atau norma dari diberikan oleh

x ℜn

x

> < =

= x x,x

x|| || ||₂

|| (2.1.5)

Definisi 2.1.13

ℜ → ℜ

⋅ mxn

: ||

|| adalah suatu norma matriks jika memenuhi :

(i) ||A|| ≥0 untuk semua A∈ℜmxn dan ||A||=0⇔ A =0 (ii) ||α A|| = |α ||| A|| untuk semua A∈ℜmxn dan α∈ℜ (iii) || A+B|| ≤ ||A||+||B|| untuk semua ∈ℜmxn

B A,

(iv) || AB || ≤ ||A||||B|| untuk semua matriks yang sesuai

Definisi 2.1.14

Jika ∈ℜmxn dan , panjang atau norma dari diberikan oleh :

A x∈ℜnx1 A

maks

λ

= =

=1 2

|| ||

2 max || || ||

|| A Ax

x

di mana λ_maksadalah nilai λ terbesar sedemikian sehingga A−λI bersifat singular.

Definisi 2.1.15

Sifat-sifat norma matriks-2 adalah sebagai berikut:

(i) || || max max | * | 1

|| || 1 || ||

2 y Ax

A

x= =

=

(ii) ||A||₂=||A*||₂ (iii) ||A*A||₂=||A||₂

(iv) max{|| || ,|| || } 0

0

2 2 2

B A

= ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛

B A

(v) ||U*AV||₂=||A||₂ di mana U*U=I dan V*V =I

Definisi 2.1.16

Misalkan ∈ℜnxn adalah suatu proyeksi,

P P2 =P. Pernyataan-pernyataan

berikut ini ekuivalen dengan P adalah suatu Proyeksi Orthogonal, yaitu : (i) R(P)⊥ N(P)

(ii) PT =P (Proyeksi Orthogonal ⇔ P2 =P=PT) (iii) ||P||₂=1

B. Teorema Kalkulus

Dalam subbab ini akan dibahas tentang teorema-teorema dalam kalkulus,

terutama yang berkaitan dengan integral, yaitu Teorema Dasar Kalkulus, yang

akan digunakan dalam pembahasan bab-bab selanjutnya.

Teorema 2.2.1 (Teorema Nilai Rata-rata untuk Turunan)

Jika f kontinu pada selang tertutup

[ ]

a,b dan terdiferensial pada titik-titik

dalam dari , maka terdapat paling sedikit satu bilangan c dalam

dimana :

) ,

) ( ) ( )

( '

c f a

b a f b

f ₌

− −

(2.2.1)

atau ekuivalen dengan

) ( ) ( ) ( )

(b f a f ' c b a

f − = − (2.2.2)

Bukti:

Pembuktian ini didasarkan pada analisis dari fungsi

sedangkan adalah persamaan garis yang melalui dan

. Karena garis ini mempunyai kemiringan

), ( ) ( )

(x f x g x

s = −

) (x g

y= (a, f(a))

)) ( ,

(b f b [f(b)− f(a)]/(b−a) dan

melalui (a, f(a)), bentuk titik kemiringan untuk persamaannya adalah

) ( ) ( ) ( ) ( )

( x a

a b

a f b f a f x

g −

− − =

−

Kemudian menghasilkan rumus untuk s(x), yaitu,

) ( ) ( ) ( ) ( ) ( )

( x a

a b

a f b f a f x f x

s −

− − −

− =

Perhatikan bahwa s(b)=s(a)=0 dan untuk x dalam (a,b)

a b

a f b f x f x s

− − −

= '( ) ( ) ( ) )

( '

Jika diketahui bahwa terdapat suatu bilangan dalam yang memenuhi

, pembuktian selesai. Karena persamaan terakhir mengatakan c (a,b)

0 ) ( ' c = s

a b

a f b f c f

− − −

= '( ) ( ) ( ) 0

Untuk melihat bahwa s'(c)=0 untuk suatu dalam , alasannya

adalah jelas kontinu pada , karena merupakan selisih dua fungsi kontinu. c (a,b)

Jadi harus mencapai baik nilai maksimum maupun nilai minimum pada .

Jika kedua nilai ini kebetulan adalah 0, maka secara identik adalah 0 pada

, akibatnya untuk semua

s [a,b]

) (x s

] ,

[a b s'(x)=0 x dalam (a,b).

Jika salah satu nilai maksimum atau nilai minimum berlainan dengan 0, maka

nilai tersebut dicapai sebuah titik dalam , karena c s(a)=s(b)=0. Sekarang

mempunyai turunan di setiap titik dari , sehingga

s

) ,

(a b s'(c)=0.

■

Teorema 2.2.2 (Teorema Dasar Kalkulus)

Misalkan f kontinu (karenanya terintegralkan) pada

[ ]

a,b dan andaikan

sebarang anti turunan dari di sana. Maka,

F f

) ( ) ( )

(x dx F b F a f

b a

− =

∫

(2.2.3)

Bukti:

Andaikan p:a=x₀ <x₁ < x₂ <L< x_n−1 <x_n =b adalah partisi sebarang dari

[

a,b

]

, maka dengan mengurangkan dan menambahkan secara baku diperoleh:

∑

= −

− −

− − =

− +

+ −

+ −

= −

n i

i i

n n

n n

x F x F

x F x F x

F x

F x

F x F a F b F

1

1

0 1

2 1

1

)] ( ) ( [

) ( ) ( )

( ) ( ) ( ) ( ) ( )

( L

Menurut Teorema 2.2.1 untuk turunan yang diterapkan pada F pada selang

] , [x_i−1 x_i

i i

i i i i

i

x x f

x x x F x

F x F

Δ =

− =

− _{− −}

) (

) )(

( ) ( )

( 1

untuk suatu pilihan xi dalam selang terbuka (x_i−1,x_i). Jadi,

∑

=

Δ =

− n

i

i i x x f a

F b F

1 ) ( )

( ) (

pada ruas kiri merupakan konstanta, sedangkan ruas kanan merupakan jumlah

Riemann untuk pada . Bila kedua ruas diambil limitnya untuk ,

diperoleh

f [a,b] | p|→0

∫

∑

Δ =

= −

= →

b a n

i

i i

p f x x f x dx a

F b

F( ) ( ) lim ( ) ( )

1 0 | |

■

C. Konvergensi

Dalam subbab ini dibahas konsep konvergensi yang nantinya akan

digunakan untuk menganalisis Metode Broyden untuk menyelesaikan sistem

persamaan non-linear.

Definisi 2.3.1

Suatu barisan (atau barisan tak hingga) adalah suatu fungsi yang daerah

asalnya adalah himpunan bilangan bulat positif.

Barisan ditulis dengan menggunakan notasi kurawal atau dapat juga

dengan menuliskan

+∞ =1 } {a_{n n} ,...

,..., ,

, 2 3

Definisi 2.3.2

Suatu barisan {a_n}∞_n=1 disebut mempunyai limit L bila untuk sebarang 0

>

ε terdapat bilangan bulat positif N sedemikian sehingga an −L <ε bila

. Bila barisan mempunyai limit L, maka barisan dikatakan

konvergen ke-L dan ditulis N

n≥ {a_n}∞_n=1

L an n→∞ =

lim .

Suatu barisan yang tidak mempunyai limit dikatakan divergen.

Definisi 2.3.3

Suatu deret tak hingga adalah suatu ungkapan bentuk

... ...

3 2

1 +u +u + +un + u

atau dengan notasi sigma ; ₁, ₂, ₃,... disebut suku-suku deret. 1

u u u u k

k

∑

∞

=

Secara informal, bentuk

∑

adalah jumlah suku-suku ∞

=1 k

k

u u₁,u₂,u₃,...

Misalkan S_n menyatakan jumlah suku pertama dari deret. Dengan demikian, n

∑

∞ =

= + + + =

+ + =

+ = =

1 2

1

3 2 1 3

2 1 2

1 1

, , ,

k k n

n u u u u

S

u u u S

u u S

u S

L K K K K K K K K K

Bilangan disebut jumlah parsial ke- dari deret dan barisan disebut

barisan jumlah parsial. n

Definisi 2.3.4

Misalkan adalah barisan jumlah parsial deret {Sn}

∑

∞

=1 . k

k u

Jika barisan konvergen ke limit maka deret itu disebut konvergen dan

disebut jumlah deret. Dapat dituliskan }

{S_n S S

∑

∞ = =

1 k

k u S

Jika barisan jumlah parsial dari deret adalah divergen maka deret disebut

divergen. Suatu deret yang divergen tidak mempunyai jumlah.

Contoh 2.3.1

Tentukan apakah deret 1−1+1−1+1−1+L konvergen atau divergen ?

Penyelesaian:

Jumlah parsialnya adalah

. seterusnya dan

, 0 1 1 1 1

, 1 1 1 1

, 0 1 1

, 1

4 3 2 1

= − + − =

= + − =

= − = =

S S S S

Jadi barisan jumlah parsial adalah 1,0,1,0,… yang divergen. Karena barisan

jumlah parsialnya divergen maka deretnya juga divergen dan akibatnya tidak

Teorema 2.3.1

Suatu deret geometri

0 , 1 3

2 + + + + ≠

+

+ −

a ar

ar ar ar

a L k L

konvergen jika |r|<1 dan divergen jka |r|≥1

Jika deret konvergen, jumlah deret itu adalah

L

L+ +

+ + + + = −

−1 3

2 1

k ar ar

ar ar a r a

Bukti:

Misalkan |r|=1.

Jika r=1, deretnya adalah a+a+a+L+a+L sehingga jumlah parsial ke- adalah dan

n na

S_n = =±∞

∞ → na n

lim (tanda bergantung pada apakah a positif atau

negatif). Bukti ini membuktikan divergensi.

Jika r =−1, deretnya adalah a−a+a−a+L sehingga barisan jumlah parsialnya adalah a,0,a,0,K yang divergen.

Sekarang perhatikan kasus jika |r|≠1

Jumlah parsial dari deret adalah

n

n a a a a

S = ₁ + ₂ + ₃ +L+

1 2+ + − +

+

= n

n a ar ar ar

S L (2.3.1)

Gandakan kedua ruas dengan r, diperoleh

n n ar ar ar ar

rS = + 2 + 3 +L+

(2.3.2)

atau r)S

-(1

atau

n

n n n

n

ar a

ar a rS S

− =

− = −

(2.3.3)

r ar r a S

n n

− − − =

1

1 (2.3.4)

Jika maka sehingga barisan konvergen. Dari

persamaan (2.3.4) diperoleh 1

|

|r < lim =0 +∞ →

n

n r {Sn}

r a S_n nlim→+∞ =₁−

Jika |r|>1 maka r>1 atau r<−1. Dalam kasus r >1 maka

dan dalam kasus

+∞ =

+∞ →

n

nlim r r <−1 maka

n

r berosilasi antara bernilai positif

dan negatif sehingga {S_n}divergen.

■

Contoh 2.3.2

Deret + + ₂ +L+ ₋₁ +L 4

5 4

5 4 5

5 _k adalah deret geometri dengan a=5 dan 4 1 =

r .

Karena 1

4 1 |

|r = < maka deret konvergen dengan jumlah

3 20

4 1 1

5 1−r = ₋ =

a

.

D. Penyelesaian Persamaan Non-linear dengan satu variabel

Persamaan non-linear dengan satu variabel dapat diselesaikan secara

numerik dengan beberapa metode. Dalam subbab ini pembahasan lebih

karena Metode Secant yang akan digunakan sebagai dasar untuk menyelesaikan

sistem persamaan non-linear dengan Metode Broyden. Metode Secant adalah

salah satu metode yang muncul untuk mengatasi kelemahan dari Metode

Newton-Raphson.

Salah satu metode yang sangat terkenal adalah Metode Newton-Raphson.

Pada Metode Newton-Raphson untuk menemukan akar digunakan turunan

pertama dari fungsi yaitu . Misalkan dan misalkan

adalah suatu pendekatan ke- sedemikian sehingga dan

adalah kecil. Dengan mempertimbangkan Polinomial Taylor pertama

untuk ekspansi , diperoleh:

f f' 2[ , ]

b a C f ∈ ] , [ ) ( b a

xi ∈ p f'(x(i))≠0

| |x(i)− p

) (x

f x(i)

)) ( ( " 2 ) ( ) ( ' ) ( ) ( ) ( 2 ) ( ) ( ) ( ) ( x f x x x f x x x f x f i i i

i + − + − ξ

= (2.4.1)

di mana ξ(x) terletak antara x dan x(i)

Karena f(p)=0 dan diberikan x= p, maka persamaan (2.4.1) menjadi

)) ( ( " 2 ) ( ) ( ' ) ( ) ( 0 )) ( ( " 2 ) ( ) ( ' ) ( ) ( ) ( 2 ) ( ) ( ) ( ) ( 2 ) ( ) ( ) ( ) ( p f x p x f x p x f p f x p x f x p x f p f i i i i i i i i ξ ξ − + − + = − + − + = (2.4.2)

Dalam Metode Newton diasumsikan bahwa kecil, sehingga

suku yang mengandung mendekati nol, maka persamaan (2.4.2)

menjadi sebagai berikut:

| | p−x(i) 2

) (

| | p−x i

) ( ' ) ( ) (

) ( '

) (

) (

) ( )

(

i i i

x f

x f x

p ≈ − (2.4.4)

Apabila adalah nilai awal yang diberikan, maka secara umum

didefinisikan dengan: ) 0 (

x {x(i+1)}

) ( '

) (

) (

) ( )

( ) 1 (

i i i

i

x f

x f x

x + = − (2.4.5)

Iterasi dimulai dengan menentukan suatu nilai awal (0) dan suatu nilai

x ε >0,

kemudian substitusikan ke persamaan (2.4.5).

Langkah diulangi sampai ditemukan suatu nilai

ε

< −

+

| |x(i 1) x(i)

Metode Newton-Raphson mempunyai kemungkinan divergen, biasanya

disebabkan karena kesalahan menentukan nilai awal. Jadi Metode

Newton-Raphson mempunyai beberapa kelemahan, yaitu nilai awalnya harus baik dan

harus dapat mengetahui nilai turunan fungsi (atau dapat ditulis dengan ) di

setiap iterasinya. Seringkali mencari sangat sulit dan membutuhkan

perhitungan aritmatika yang sangat rumit, bahkan sering tidak dapat ditentukan

nilainya.

f f'

) ( ' x f

Untuk mengatasi masalah perhitungan turunan dalam Metode

Newton-Raphson diturunkan suatu variasi, yaitu perhitungan turunan persamaan

didekati dengan menggunakan limit sebagai berikut:

f

) 1 (

) 1 ( )

1

( ( ) ( )

lim )

( '

) 1

( −

− →

−

− −

= _{− i} i

x x i

x x

x f x f x

f

i (2.4.6)

) 2 ( ) 1 ( ) 2 ( ) 1 ( ) 1 ( ) 2 ( ) 1 ( ) 2 ( ) 1 ( ) ( ) ( ) ( ) ( ) ( ' − − − − − − − − − − − = − − = i i i i i i i i i x x x f x f x x x f x f x f (2.4.7)

Dengan menggunakan pendekatan dari dalam perhitungan dengan

Metode Newton-Raphson, yaitu sebagai berikut: ) ( ' x(i−1) f ) ( ) ( ) )( ( ) 2 ( ) 1 ( ) 2 ( ) 1 ( ) 1 ( ) 1 ( ) ( − − − − − − − − −

= i i _i i _i i

i x f x f x x x f x

x (2.4.8)

Teknik yang digunakan dalam formulasi sehingga diperoleh persamaan (2.4.8) di

atas disebut dengan Metode Secant.

Metode Secant dimulai dengan dua pendekatan awal dan ,

sedangkan pendekatan adalah titik potong

sumbu-) 0 (

x x(1)

) 2 (

x x dari persamaan garis

yang melalui dan dan pendekatan adalah titik

potong dari persamaan garis yang melalui dan , dan

seterusnya.

)) ( ,

(x(0) f x(0) (x(1),f(x(1))) (3) x

)) ( ,

(x(1) f x(1) (x(2),f(x(2)))

Contoh 2.4.1

Selesaikan persamaan non-linear dengan pendekatan

awal [1,4] dengan mengunakan Metode Secant dengan tingkat kesalahannya ,

0 5 2 2 3 − − =

x x

4 10−

Jawab:

Diketahui , dan ,

sehingga , 0 5 2 )

(x = x3 − x2 − =

f (0) =1

x (1) =4

) 5 ) ( 2 ) ( ( ) 5 ) ( 2 ) ( ( ) ( ) 5 ) ( 2 ) ( ( 2 ) 2 ( 3 ) 2 ( 2 ) 1 ( 3 ) 1 ( ) 2 ( ) 1 ( 2 ) 1 ( 3 ) 1 ( ) 1 ( ) ( − − − − − − − − − = − ₋ − ₋ − ₋ − −₋ i i i i i i i i i i x x x x x x x x x

x untuk i≥2

Iterasi pertama 5455 . 1 4545 . 2 4 33 81 4 ) 5 2 1 ( ) 5 32 64 ( ) 3 )( 5 32 64 ( 4 ) 5 ) 1 ( 2 ) 1 ( ( ) 5 ) 4 ( 2 ) 4 (( ) 1 4 ( ) 5 ) 4 ( 2 ) 4 ( 4 ) 5 ) ( 2 ) ( ( ) 5 ) ( 2 ) ( ( ) ( ) 5 ) ( 2 ) ( ( 2 3 2 3 2 3 2 ) 0 ( 3 ) 0 ( 2 ) 1 ( 3 ) 1 ( ) 0 ( ) 1 ( 2 ) 1 ( 3 ) 1 ( ) 1 ( ) 2 ( = − = − = − − − − − − − − = − − − − − − − − − = − − − − − − − − − = x x x x x x x x x x 5455 . 1 ) 2 ( ₌ x

Dengan menggunakan langkah yang sama seperti iterasi pertama dapat

diperoleh nilai x untuk iterasi selanjutnya seperti pada tabel berikut:

Tabel 2.4.1 Hasil Perhitungan persamaan non-linear x3 −2x2 −5=0,

dengan Metode Secant

i (i)

8 2.7014

9 2.6909

10 2.6909

Karena kesalahan dari nilai x pada iterasi kesembilan dan kesepuluh lebih kecil

dari , maka penyelesaian persamaan non-linear adalah

2.6909. 4

Persamaan non-linear adalah persamaan yang tiap suku-sukunya melibatkan bentuk eksponensial, trigonometri, logaritma, rasional, polinomial berderajat dua atau lebih, ada hasil kali antara fungsi yang belum diketahui dengan turunannya, atau fungsi transenden lainnya. Berikut diberikan beberapa contoh persamaan non-linear

0

2 1 2 3

2 1 2

1 + =

+ x x

x

e x x e x

e (3.1.1)

0 ) cos( 2 ) 2

sin( x + x = (3.1.2)

0 5 . 0 ) cos(

3x₁− x₁x₂ − = (3.1.3)

0 10 3

2 _{+ − =} x

x (3.1.4)

Persamaan-persamaan non-linear di atas dapat dibedakan menjadi persamaan non-linear dengan satu variabel, seperti persamaan (3.1.2) dan persamaan (3.1.4), dan persamaan non-linear dengan variabel, dengan , seperti persamaan (3.1.1) dan persamaan (3.1.3).

n n>1

Bentuk umum persamaan non-linear dengan satu variabel adalah 0

) (x =

f . (3.1.5)

dengan x adalah variabel tunggal yang dapat mempunyai beberapa nilai yang disebut sebagai akar-akar persamaan tersebut. Akar dari persamaan tersebut bisa real dan berlainan, real dan berulang, serta kompleks.

Sedangkan bentuk umum persamaan non-linear dengan variabel adalah n 0

) ,..., ,

(x1 x2 xn =

f . (3.1.6)

Definisi 3.1.1

Sistem Persamaan non-linear adalah himpunan n persamaan non-linear, dengan , yang penyelesaiannya harus memenuhi semua persamaan

tersebut. 1

>

n n

Bentuk umum sistem persamaan non-linear dengan persamaan dan

variabel adalah :

m n

0 ) ,..., ,

(

0 ) ,..., ,

(

0 ) ,..., ,

(

2 1

2 1 2

2 1 1

= = =

n m

n n

x x

x f

x x

x f

x x

x f

M M

M (3.1.7)

Setiap fungsi merupakan pemetaan vektor x = dari

ke . Sistem persamaan (3.1.7) dapat ditulis dalam bentuk lain, yakni dengan

mendefinisikan fungsi F, yang merupakan pemetaan dari ke , yaitu f (x1,x2,...,xn)t

n ℜ

ℜ

n

ℜ ℜm

F(x₁,....,x_n)=(f₁(x₁,....,x_n), f₂(x₁,....,x_n),....,f_m(x₁,....,x_n))t (3.1.8) Dengan menggunakan notasi vektor, sistem di atas dapat ditulis dalam bentuk :

F(x) = 0 (3.1.9)

Fungsi f₁,f₂,...,f_n disebut fungsi koordinat dariF.

Dalam penulisan ini masalah hanya difokuskan pada sistem persamaan non-linear

Contoh 3.1.1

Perhatikan sistem persamaan non-linear

0 ) cos (sin 2 0 3 5 2 1 2 2 2 2 1 = − + = − x x x x x (3.1.10)

Sistem persamaan (3.1.10) adalah contoh sistem persamaan non-linear

dengan dua persamaan dan dua variabel. Dalam sistem tersebut dapat

didefinisikan menjadi dua fungsi f₁:ℜ2 →ℜ dan f₂ :ℜ2 →ℜ, yakni

dan (3.1.11)

), cos (sin 2 ) , ( , 3 5 ) , ( 2 1 2 2 1 2 2 2 2 1 2 1 1 x x x x x f x x x x f − + = − =

Dengan demikian dapat didefinisikan fungsi F pemetaan dari

dengan

2 2 →ℜ ℜ t t x x x x x x x f x x f x x ) ) cos (sin 2 , 3 5 ( ) ) , ( ), , ( ( ) , ( ) ( 2 1 2 2 2 2 1 2 1 2 2 1 1 2 1 − + − = = =F x F (3.1.12) Contoh 3.1.2

Perhatikan sistem persamaan non-linear

0 3 1 10 0 6 3 0 1 ) cos 2 ) (sin( 2 1 3 3 2 2 1 3 2 1 2

1 + − =

= + − = − + − x e x x x x x x x x (3.1.13)

Sistem persamaan (3.1.13) adalah contoh sistem persamaan non-linear

dengan tiga persamaan dan tiga variabel yang dapat didefinisikan menjadi tiga

, 3 1 10 ) , , ( , 6 3 ) , , ( , 1 ) cos 2 ) (sin( 2 1 ) , , ( 3 3 2 1 3 3 2 2 1 3 2 1 2 3 2 1 3 2 1 1 2

1 + −

= + − = − + = − x e x x x f x x x x x x f x x x x x x f x x (3.1.14)

Dengan demikian dapat didefinisikan fungsi F pemetaan dari

dengan

3 3 →ℜ ℜ t x x t x e x x x x x x x x x f x x x f x x x f x x x ) 3 1 10 , 6 3 , 1 ) cos 2 ) (sin( 2 1 ( ) ) , , ( ), , , ( ), , , ( ( ) , , ( ) ( 3 3 2 2 1 3 2 1 3 2 1 3 3 2 1 2 3 2 1 1 3 2 1 2

1 + −

+ − − + = = = − F x F (3.1.15)

Untuk mencari penyelesaian persamaan atau sistem persamaan non-linear

lebih sering digunakan metode numeris daripada metode analitis. Hal ini

disebabkan karena sistem persamaan non-linear melibatkan banyak persamaan

dengan banyak variabel. Metode numeris digunakan untuk menemukan

pendekatan dari penyelesaian persamaan atau sistem persamaan non-linear,

apabila penyelesaian eksak tidak dapat ditemukan secara analitik.

B. Penyelesaian Sistem Persamaan Non-Linear dengan Metode Broyden

Metode Broyden merupakan pengembangan dari Metode Secant untuk

menyelesaikan sistem persamaan dengan fungsi dan variabel yang tidak

diketahui.

n n

Definisi 3.2.1

Metode Secant adalah metode untuk menyelesaikan persamaan dengan

satu variabel dimana dalam menghitung turunannya dengan menggunakan

) 1 ( ) 1 ( ) 1 ( ' ( ) ( ) lim ) ( ) 1 ( − − → − − −

= _{− i} i

x x i x x x f x f x f

i (3.2.1)

Misalkan diketahui = (i−1) , x x

Maka turunannya dapat dihitung dengan rumus :

) 2 ( ) 1 ( ) 2 ( ) 1 ( ) 1 ( ) 2 ( ) 1 ( ) 2 ( ) 1 ( ' ( ) ( ) ( ) ( ) ) ( _{− −} − − − − − − − − − = − −

= i_{i i} i i_{i i} i

i x x x f x f x x x f x f x

f (3.2.2)

dengan menggunakan pendekatan seperti pada persamaan (3.2.2), maka

penyelesaian persamaan dengan Metode Secant adalah )

( ( 1) ' i−

x f ) ( ) ( ) )( ( ) 2 ( ) 1 ( ) 2 ( ) 1 ( ) 1 ( ) 2 ( ) 1 ( − − − − − − − − − −

= i i _i i _i i

i x f x f x x x f x

x (3.2.3)

Penyelesaian sistem persamaan dengan Metode Broyden dapat dilakukan

dengan langkah-langkah, misalkan bahwa suatu pendekatan awal diberikan

untuk solusi pdari F(x) = 0. Untuk menghitung pendekatan berikutnya terlebih dahulu dibentuk Matriks Jacobi .

) 0 ( x ) 1 ( x ) (x J Definisi 3.2.2

Matriks Jacobi adalah matriks yang dibentuk dengan mencari turunan

parsial masing-masing persamaan terhadap masing-masing variabel. )

(x J

Bentuk umum Matriks Jacobi untuk sistem persamaan dengan

persamaan dan n variabel adalah sebagai berikut: ) (x

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ = n n n n n n x f x f x f x f x f x f x f x f x f ) ( ... ) ( ) ( ) ( ... ) ( ) ( ) ( ... ) ( ) ( ) ( 2 1 2 2 2 1 2 1 2 1 1 1 x x x x x x x x x x J M M M (3.2.4)

Dari persamaan (3.2.4) Matriks Jacobi dapat dinyatakan dengan

persamaan sebagai berikut:

(3.2.5)

) ( )

(x F' x

J =

Atau dapat juga ditulis dalam bentuk

k j x f ∂ ∂ = ( ) )

(x x

J , (3.2.6)

untuk j dan k masing-masing menunjukkan baris dan kolom, dengan 1≤ j,k ≤n

dan turunan parsial pada iterasi ke- adalah i

) 1 ( ) ( ) 1 ( ) ( ) ( ) ( ) ( ) ( − − − − ≈ ∂ ∂ i k i k i j i j k i j x x f f x

f x x x

, (3.2.7)

Setelah diperoleh Matriks Jacobi , substitusikan ke dan

, sehingga diperoleh Matriks Jacobi dan . Matriks Jacobi

pada iterasi awal dinotasikan sebagai matriks . Kemudian analog

dengan persamaan (3.2.3) maka penyelesaian sistem persamaan non-linear (3.1.9)

adalah:

) (x

J x(0) J(x)

) (x

F J(x(0)) F(x(0))

) (x(0)

J A₀

) ( (0) 1 0 ) 0 ( ) 1 ( x F A x

Setelah perhitungan dari , kemudian Matriks Jacobi didekati

dengan matriks yang harus memenuhi persamaan (3.2.2), yaitu )

1 (

x J(x(1))

1 A (3.2.9) ) ( ) ( )

( (1) (0) (1) (0) 1 x x F x F x

A − = −

Supaya vektor orthogonal x(1) −x(0) tidak terpengaruh oleh , maka

diperlukan syarat tambahan, yaitu

) (x(0) J (3.2.10) z x J z

A₁ = ( (0)))

meskipun (x(1) −x(0))tz=0

Kondisi ini menjelaskan bahwa vektor orthogonal akan

digantikan dengan perbaikan dari yang menggunakan perhitungan

menjadi , yang selanjutnya akan digunakan untuk menghitung .

Menggunakan persamaan (3.2.9) dan persamaan (3.2.10) diperoleh:

) ( (1) (0)

x

x −

) (x(0)

J x(1)

1

A x(2)

t t ) )( ( ) )]( )( ( ) ( ) ( [ ) ( ) ( ) ( ) ( ) ( ) ( ) 0 ( ) 1 ( ) 0 ( ) 1 ( ) 0 ( ) 1 ( ) 0 ( ) 1 ( ) 0 ( ) 0 ( ) 1 ( ) 0 ( ) 0 ( ) 1 ( ) 0 ( ) 1 ( ) 0 ( 1 ) 0 ( ) 1 ( ) 0 ( ) 1 ( 1 x x x x x x x x x J x F x F x J x x x F x F x J A ε x x x F x F A − − − − − − = − − − = − = − − = 2 2 ) 0 ( ) 1 ( ) 0 ( ) 1 ( ) 0 ( ) 1 ( ) 0 ( ) 0 ( ) 1 ( ) ( ) )]( )( ( ) ( ) ( [ x x x x x x x J x F x F ε − − − − −

= t (3.2.11)

ε x J

A₁ = ( (0))+ dengan persamaan (3.2.11) dapat diperoleh matriks sebagai

berikut:

1

2 2 ) 0 ( ) 1 ( ) 0 ( ) 1 ( ) 0 ( ) 1 ( ) 0 ( ) 0 ( ) 1 ( ) 0 ( 1 || || ) )]( )( ( ) ( ) ( [ ) ( x x x x x x x J x F x F x J A − − − − − +

= t (3.2.12)

Kemudian matriks mensubstitusikan untuk menghitung

yang ekuivalen dengan persamaan (3.2.8), yaitu: 1

A J(x(1)) (x(2))

(3.2.13) )

( (1) 1 1 ) 1 ( ) 2 ( x F A x

x = − −

Sedangkan untuk menghitung dapat dilakukan dengan metode yang

sama dengan menggunakan menggantikan dan

menggantikan dan menggantikan . Sehingga pendekatan Matriks

Jacobi untuk iterasi kedua adalah

) 3 (

x

1

A A₀ ≡J(x(0)) x(2)

) 1 (

x x(1) x(0)

2 2 ) 1 ( ) 2 ( ) 1 ( ) 2 ( ) 1 ( ) 2 ( ) 1 ( ) 1 ( ) 2 ( ) 1 ( 2 || || ) )]( )( ( ) ( ) ( [ ) ( x x x x x x x J x F x F x J A − − − − − +

= t (3.2.14)

Berdasarkan persamaan (3.2.8), (3.2.12), (3.2.13) dan (3.2.14), dengan

t i i i i i i i s s s A y A A 2 2 1 1 || || ) ( ₋ − − +

= (3.2.15)

) ( )

( () − (−1)

= i i

i F x F x

y ) 1 ( ) ( − −

= i i

i x x

s

secara umum (i) dipakai untuk menghitung yakni

x x(i+1)

(3.2.16) ) ( () 1 ) ( ) 1 ( i i i i x F A x

x + = − −

Setelah perhitungan dari , maka akan diperbaharui menjadi ,

dalam proses Matriks Jacobi yang didekati dengan matriks akan

menentukan berhasil atau tidaknya Metode Quasi-Newton. Keuntungan dari )

1 (i+

x A_i A_i+1

) (x(0)

metode ini adalah penyelesaian persamaan (3.2.16) lebih mudah daripada

menggunakan koefisien matriks '( (i)).

x F

Definisi 3.2.3

Suatu barisan {x(i)} dikatakan konvergen superlinear-q ke jika x

0 || ||

|| ||

lim ₍₎ ) 1 (

= −

−

+ ∞

→ _{x x}

x x

i i

i (3.2.17)

Metode Quasi-Newton yang dipakai dalam Metode Broyden ini

mempunyai sifat konvergen superlinear yang dapat mempertahankan sifat simetri

atau definit positif. Sifat ini menjamin bahwa determinan dari matriks bernilai

positif sehingga akan selalu ada. Sehingga Metode Broyden ini merupakan

salah satu alternatif yang sangat baik untuk menggantikan Metode Newton. i

A

1 − i

A

Preposisi 3.2.1

Misalkan A adalah sebuah matriks nonsingular yang berukuran n x n dan misalkan , maka adalah invertibel jika dan hanya jika

atau n

ℜ ∈ v

u, A+uvt

0 1+vtA−1u≠

1 1 1 1

1 ) ( )

( ₋ −

− −

⎟⎟ ⎠ ⎞ ⎜⎜

⎝ ⎛

+ − =

+ A

u A v

v u A I uv

A _t

t t

(3.2.24)

Ekspresi pada persamaan (3.2.24) sering disebut dengan formula

Bukti:

Suatu matriks nonsingular apabila dikalikan dengan inversnya, maka akan

menghasilkan matriks identitas . Jika dari persamaan (3.2.24) ruas kiri dan

kanan dikalikan dengan matriks , maka harus dibuktikan bahwa:

I

) (A+uvt

I A u A v v u A I uv

A _⎟⎟ =

⎠ ⎞ ⎜⎜ ⎝ ⎛ + − + − − − 1 1 1 1 ) ( ) ( _t t t

Perhatikan bahwa

(

)

(

)

I A v u I A v u A v u A v u I A v u A v u A v u A v u I A v u A v u A v u A v u I A v u A v u A uv A uv A v u A v u I A v u A v u A A uv A A v u A v u A A uv A A u A v v u A I uv A = − − = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − + + − = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + − + − = + + − + − = + − + + − = + − + = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − + = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − + − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ) 1 1 ( 1 1 1 1 1 1 1 ) 1 ( 1 ) 1 ( ) 1 ( ) 1 ( ) 1 )( ( ) ( 1 ) ( ) ( 1 ) ( ) ( t t t t t t t t t t t t t t t t t t t t t t t t t t t

Jadi terbukti bahwa ₁ 1

1 1 1 ) ( ) ( ₋ − − − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − = + A u A v v u A I uv A _t t t ■ Teorema 3.2.4

Misalkan A adalah matriks nonsingular yang berukuran nxn serta adalah vektor maka adalah matriks nonsingular yang berukuran

y

n x

n jika dan hanya jika 1+ytA−1x adalah matriks nonsingular yang berukuran n

x

n dan ytA−1x≠−1 atau dapat dituliskan:

x A y

A xy A A xy

A ₁

1 1

1 1

1 )

( ₋

− −

− −

+ − =

+ t _t t

Bukti:

)

(⇒ Diketahui:A adalah matriks nonsingular yang berukuran nxn adalah vektor

y xdan

adalah matriks nonsingular yang berukuran t

xy

A+ nxn

Akan dibuktikan: 1+ytA−1x≠0

Karena adalah matriks nonsingular yang berukuran A+xyt nxn, berarti mempunyai invers atau ada.

t

xy

A+ ( + t)−1

xy A

Menurut sifat invers matriks dari Sherman dan Morrison [Matrix

Analysis:1984].

1 1

1 1

1 1 1 1

1 1

1

) 1

( )

(

− −

− −

− − − −

− −

+ − =

+ −

= +

A y x A y

x A A

A y x A y x A A xy

A

t t

t t

t

x A y

A xy A A xy

A ₁

1 1

1 1

1 )

( ₋

− −

− −

+ − =

+ t _t t

(3.2.20)

Dari sifat invers matriks di atas berarti 1 1 ada, maka )

1

( +ytA−x −

)

(⇐ Diketahui: A adalah matriks nonsingular yang berukuran nxn adalah vektor

y xdan

0 1+ytA−1x≠

Akan dibuktikan: A+xyt adalah matriks nonsingular yang berukuran nxn

Bukti :

Karena berarti 1+ytA−1x≠0 1 1 ada. Sehingga, )

1

( +ytA−x −

Karena , maka menurut sifat invers matriks dari Sherman dan

Morrison [Matrix Analysis:1984], berlaku 0

1+ytA−1x≠

1 1

1 1 1

1 1

1 1

1 1 1 1

1

) (

1 1 )

1 (

− −

− − −

− −

− −

− − − −

−

+ =

+ − =

+ − = +

−

t t

t t t

t t

xy A

x A y

A xy A A

A y x A y

x A A

A y x A y x A A

Karena ada berarti bahwa adalah matriks

non-singular yang berukuran 1 )

(A+xyt − (A+xyt)

n x n .

■

Formula bisa dihitung langsung dari eliminasi membutuhkan

invers matriks pada setiap iterasi. 1

− i

A A_i−1−1

2 2 1 || || ) ( i i i i s s A y

x= − − dan y=s_i, dengan persamaan (3.2.15) dan

(3.2.20) diperoleh

2 2 1 1 2 2 1 1 1 1 1 1 2 2 1 1 1 1 1 2 2 1 1 1 1 1 1 2 2 1 1 1 || || || || ) ( ) || || ) ( ( 1 ) || || ) ( ( ) || || ) ( ( i i i t i i i t i i i i i<