BAB 2
LANDASAN TEORI
Peramalan adalah kegiatan umtuk memperkirakan apa yang akan terjadi pada masa yang akan datang berdasarkan pengalaman di masa lalu. Metode peramalan yang sering digunakan dalam ekonomi dan dunia usaha adalah deret waktu (time series).
2.1 Beberapa Uji Yang Digunakan 2.1.1 Uji Kecukupan Sampel
Sebelum melakukan analisa terhadap data, langkah awal yang harus dilakukan adalah pengujian terhadap anggota sampel. Pengujian ini dimaksudkan untuk mengetahui apakah data yang diperoleh dapat diterima sebagai sampel. Dengan tingkat keyakinan 95% (
α
=0,05) rumus yang digunakan untuk menentukan jumlah anggota sampel adalah:2 1 2 1 1 2 20 ' − =
∑
∑
∑
= = = N t t N t t N t t Y Y Y N N (2-1) Dengan : = 'N Ukuran sampel yang dibutuhkan =
N Ukuran sampel percobaan
=
tY
Data aktualApabila N' < N, maka sampel percobaan dapat diterima sebagai sampel.
2.1.2 Uji Musiman
o
H
: Data tidak dipengaruhi musiman1
H
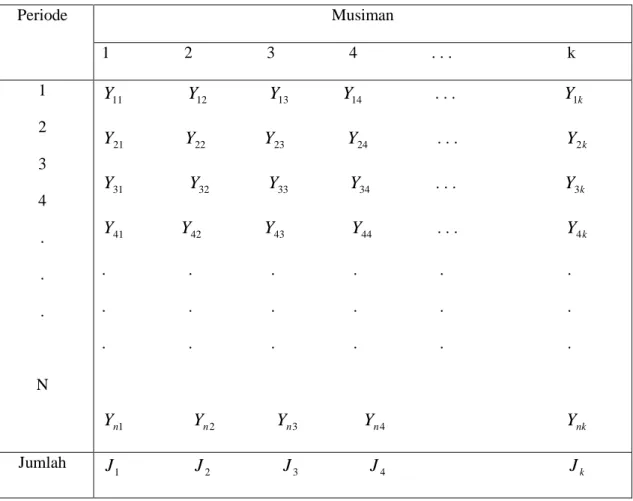
: Data dipengaruhi musimanTabel 2.1 Perhitungan Uji Musiman
Periode Musiman 1 2 3 4 . . . k 1 2 3 4 . . . N 11
Y
Y
12Y
13Y
14 . . .Y
1k 21Y
Y
22Y
23Y
24 . . .Y
2k 31Y
Y
32Y
33Y
34 . . .Y
3k 41Y
Y
42Y
43Y
44 . . .Y
4k . . . . . . . . . . . . . . . . . . 1 nY
Y
n2Y
n3Y
n4Y
nk Jumlah 1J
J
2J
3J
4J
kUntuk perhitungan digunakan notasi :
∑
∑
= =
=
k i i k i i yn
J
R
1 2 1 (2-2) Dengan : yR = Jumlah kuadrat-kuadrat (JK) untuk rata-rata
i
i
n
= Ukuran sampel percobaany k i i i y
R
n
J
A
=
∑
−
=1 2 (2-3) Dengan : yA = Jumlah kuadrat-kuadrat (JK) antar kelompok
y
R = Jumlah kuadrat-kuadrat (JK) untuk rata-rata
i
J
= Jumlah nilai pengamatani
n
= Ukuran sampel percobaan2 2 12 2 11 2
...
Y
nkY
Y
Y
=
+
+
+
∑
(2-4) Dengan :Y = Jumlah data aktual
y y
y
Y
R
A
D
=
∑
2−
−
(2-5)Dengan :
Y = Jumlah data aktual
y
D = Jumlah kuadrat-kuadrat (JK) dalam kelompok
y
R = Jumlah kuadrat-kuadrat (JK) untuk rata-rata
y
A = Jumlah kuadrat-kuadrat (JK) antar kelompok
Sehingga F hitung = y D
A
Dengan :
y
A = Jumlah kuadrat-kuadrat (JK) antar kelompok
y
D = Jumlah kuadrat-kuadrat (JK) dalam kelompok
Kemudian akan disusun dalam tabel ANAVA.
Tabel 2.2 Perhitungan Anava Uji Musiman
Sumber Variasi Derajat Bebas Jumlah Kuadrat Jumlah Kuadrat Rata-rata Statistik Uji Antar Musim Dalam Musim 1 − k
∑
n
− k
y A yD
1
−
=
k
A
A
yk
n
D
D
y−
=
D A F = Total∑
n
-1∑
2Y
Dengan k = Menyatakan musiman n = Periode musimanMaka kriteria pengujiannya adalah :
0
H
: Diterima jika F hitung > F (k-1, n-k)1
2.1.3 Uji Trend
Tujuan dari uji trend adalah untuk melihat apakah ada pengaruh komponen trend terhadap data. Hipotesis ujinya adalah :
0
H
: frekuensi naik dan turun dalam data adalah sama, artinya tidak ada trend1
H
: frekuensi naik lebih besar dari frekuensi turun, artinya trend menaikStatistik penguji :
σ
µ)
(
−
=
m
Z
(2-7) 2 1 − = nµ
(2-8)2
1
+
=
n
σ
(2-9) Dengan :=
m
frekuensi naik=
n
jumlah data=
µ
frekuensi naik yang diharapkan=
σ
standar error antara naik dan turunKriteria penguji :
Dengan taraf signifikan
α
maka :0
H
: Diterima jika Z hitung > Z tabel1
2.2 Jenis-jenis Peramalan
Berdasarkan sifat ramalan yang telah disusun, ramalan dapat dibedakan atas dua macam, yaitu :
1. Peramalan Kualitatif
Peramalan kualitatif adalah peramalan yang didasarkan atas data kualitatif pada masa lalu. Hasil peramalan yang dibuat sangat tergantung pada orang yang menyusunnya. Hal ini penting karena hasil peramalan tersebut ditentukan berdasarkan pemikiran yang bersifat intuisi, pendapat, dan pengetahuan serta pengalaman dari penyusunnya.
2. Peramalan Kuantitatif
Peramalan kuantitatif adalah peramalan yang didasarkan atas data kuantitatif pada masa lalu. Hasil peramalan yang dibuat sangat tergantung pada metode yang digunakan dalam peramalan tersebut. Dengan metode yang berbeda akan diperoleh hasil peramalan yang berbeda. Metode yang baik adalah metode yang memberikan nila-nilai perbedaan atau penyimpangan yang kecil antara hasil ramalan dengan kenyataan yang terjadi.
Peramalan kuantitatif hanya dapat digunakan apabila tiga kondisi sebagai berikut dipenuhi :
a. Adanya informasi tentang keadaan yang lalu
b. Informasi tersebut dapat dikuantitatifkan dalam bentuk data
c. Dapat diasumsikan bahwa pola yang lalu akan berkelanjutan pada masa yang akan datang.
2.3 Metode Peramalan
2.3.1 Pengertian Metode Peramalan
Metode peramalan adalah cara memperkirakan secara kuantitatif apa yang akan terjadi pada masa depan, berdasarkan data yang relevan pada masa lalu. Oleh karena metode peramalan ini didasarkan pada data yang relevan pada masa lalu, maka metode peramalan ini dipergunakan dalam peramalan yang objektif.
Disamping itu, metode peramalan juga merupakan cara memperkirakan secara kuantitatif, oleh karena itu metode peramalan termasuk dalam metode peramalan kuantitatif.
2.3.2 Jenis-Jenis Metode Peramalan
Peramalan dapat dibedakan atas peramalan kuantitatif dan kualitatif. Pada dasarnya metode peramalan kuantitatif dapat dibedakan atas :
a. Metode Regresi (kausal)
Metode peramalan kausal ini didasarkan atas penggunaan analisa pola hubungan antara variabel yang akan diperkirakan dengan variabel lain yang mempengaruhinya, yang bukan waktu. Metode ini mengasumsikan bahwa faktor yang diramalkan menunjukkan suatu hubungan sebab akibat dengan satu atau lebih variabel bebas.
Metode regresi ini terdiri dari :
1. Metode regresi dan korelasi 2. Metode ekonometrika 3. Metode input output b. Deret waktu
Metode peramalan deret berkala (time series) didasarkan atas penggunaan analisa pola hubungan antar variabel yang diperkirakan dengan variabel waktu, yang merupakan deret waktu (time series). Metode peramalan deret waktu data historis dianalisa untuk mengidentifikasi pola data dan diasumsikan bahwa pola data tersebut akan terus berlanjut pada masa yang akan datang. Pola data yang diperoleh kemudian dianalisa untuk memperoleh nilai peramalan pada masa yang akan datang. Dalam model peramalan deret waktu tidak ada usaha menemukan faktor yang mempengaruhi terhadap data historis yang dianalisa.
Metode peramalan deret waktu ini terdiri dari :
1. Metode Smoothing 2. Metode Box-Jenkins
3. Metode Proyeksi Trend dengan Regresi
2.4 Klasifikasi Model Box-Jenkins
Model Box-Jenkins dikelompokkan ke dalam tiga kelompok yaitu :
1. Model Autoregressive (AR)
2. Model Rataan Bergerak / Moving Average (MA) 3. Model Campuran
Model campuran ini dapat berupa model campuran model Autoregressive Moving Average (ARMA) dan model Autoregressive Integrated Moving Average (ARIMA).
2.4.1 Model Autoregressive Persamaan umum dari model AR(p) :
(
)
t t p pB
Y
e
B
B
−
−
−
=
+
−
φ
φ
...
φ
δ
1
1 2 2 (2-10) Dengan :B = operator penggerak mundur (backward shift operator)
1
φ
= parameter autoregressive ke-i (dengan i = 1,2,3,…,p)=
tY
Data aktualδ
= suatu konstanta te
= sisaan (residu) ke – t2.4.2 Model Rataan Bergerak (Moving Average)
Bentuk umum dari model rataan bergerak dengan ordo q atau biasa ditulis MA(q).
2.4.3 Model Campuran Autoregressive – Rataan Bergerak
Secara singkat bentuk umum model campuran autoregressive rataan bergerak berordo (p,q) yang mengkombinasikan proses autoregressive ordo p dan proses rataan bergerak ordo q atau biasa ditulis dengan ARMA(p,q).
2.4.4 Model Integrasi Autoregressive – Moving Average (ARIMA)
Untuk deret waktu yang tidak stasioner, model Box-Jenkins dapat diterapkan dengan jalan mentransformasikannya menjadi deret yang stasioner dengan pembedaan ordo pertama atau lebih. Box-Jenkins menyatakan model tersebut Integrasi Autoregressive-Rataan Bergerak (Autoregressive-Integrated-Moving Average / ARIMA).
Bentuk umum model ARIMA berordo (p,d,q) yang mengkombinasikan proses autoregressive berodo p, dan proses rataan bergerak berordo q pada deret waktu yang sudah di transformasikan dengan pembedaan ordo ke-d atau biasa ditulis dengan ARIMA(p,d,q) adalah sebagai berikut :
(
)
(
)
t q q t p pB
W
B
B
e
B
φ
δ
θ
θ
φ
−
−
=
+
−
−
−
−
...
1
...
1
1 1 (2-11) Dengan : 1φ
= parameter autoregressive ke-iB = operator penggerak mundur (backward shift operator)
t
W
= deret yang sudah dideferensi dengan ordo dδ
= konstanta te
= sisaan (residu) ke – tDalam praktek, nilai p,d,q yang biasa digunakan adalah 0,1,2. Meskipun demikian dengan nilai p,d,q yang seperti itu dapat dibuat banyak variasi model yang cukup berguna. Persamaan model yang sederhana, ARIMA (1,1,1) adalah sebagai berikut :
(
1
−
1)
−1−
1 −2+
+
−
1 −1=
t t t t tY
Y
e
e
Y
φ
φ
δ
θ
(2-12) Dengan :=
tY
Data aktual 1φ
= parameter autoregressive ke-iδ
= konstantat
e
= sisaan (residu) ke – t2.5 Kestasioneran dan Faktor Musiman 2.5.1 Kestasioneran
Parsial. Data yang dianalisa dalam model ARIMA adalah data yang bersifat stasioner, yaitu data yang rata-rata dan variansinya relative konstan dari satu periode ke periode selanjutnya.
Autokorelasi-autokorelasi dari data yang tidak stasioner berbeda secara signifikan dari nol dan mengecil secara perlahan membentuk garis lurus sedangkan autokorelasi-autokorelasi dari data stasioner mengecil secara drastis membentuk garis lengkung ke arah nol setelah periode kedua atau ketiga. Jadi bila autokorelasi pada periode satu, dua maupun periode ketiga tergolong signifikan sedangkan autokorelasi-autokorelasi pada periode lainnya tergolong tidak signifikan, maka datanya bersifat stasioner.
Menurut Box-Jenkins deret data yang tidak stasioner dapat ditransformasikan menjadi deret data yang stasioner dengan melakukan pembedaan (diferensi) pada data aktual. Pembedaan ordo pertama dari data aktual dapat dinyatakan sebagai berikut :
1 −
−
=
t t tY
Y
W
(2-13) Dengan : tW
= deret yang sudah dideferensi dengan ordo d=
tY
Data aktualBiasanya dengan melakukan pembedaan pertama dan kedua data akan menjadi data yang stasioner dengan melihat koefisien autokorelasi data pembedaan akan turun mendekati nol setelah lag ke-2 atau lag ke-3.
2.5.2 Faktor Musiman
Makridakis (1991) dan Assauri (1984) mendefenisikan musiman sebagai suatu
pola yang berulang-ulang dalam selang waktu yang tetap. Pola musiman dapat berupa musiman triwulan (3 bulanan), kuartal (4 bulanan), semesteran (6 bulanan) atau tahunan (12 bulanan). Notasi ARIMA yang digunakan untuk mengatasi aspek musiman, secara umum ditulis sebagai berikut :
s
Q
D
P
q
d
p
ARIMA
(
,
,
)(
,
,
)
Komponen (p,d,q) adalah bagian tidak musiman dari model (P,D,Q) adalah bagian musiman dari model dan S adalah jumlah periode per musim.
Model ARIMA yang mengandung faktor musiman, ARIMA (1,1,1,)
(
1
,
1
,
1
)
12 mempunyai persamaan sebagai berikut :(
B)
(
B)
B B Yt(
B)
(
B)
et 12 1 1 12 12 1 1 1 (1 )(1 ) 1 1 1−φ
−Φ − − =δ
+ −θ
−Θ (2-14) Dengan : 1φ
= Parameter autoregressive ke-1B = Operator penggerak mundur (backward shift operator)
1
Φ
= Sudut fase (dalam radian) tY
= Data aktualδ
= Konstanta1
θ
= Nilai rata – rata bergerak MA1
Θ
= Nilai SMA te
= Sisaan (residu) ke – tDalam hal ini :
(
1
−
φ
1B
)
= proses AR (1) bukan musiman(
12)
1
1
−
Φ
B
= proses AR (1) musiman(
1
−
B
)
= pembedaan ordo pertama bukan musiman(
12)
1 B
−
= pembedaan ordo pertama musiman(
1
−
θ
1B
)
= proses MA (1) bukan musiman(
12)
1
1
−
Θ
B
= proses MA (1) musiman2.5.3 White Noise
White noise maksudnya residu tersebut berdistribusi normal dengan nilai tengah nol dan varians konstan. Jika residu bersifat white noise maka residu hanya merupakan suatu proses gangguan kecil yang tidak perlu diperhatikan. Hal ini dapat dilihat dari nilai Q Box-Pierce <
2
χ
tabel dan koefisien autokorelasi dan autokorelasi parsial residu yang tidak berbeda nyata dari nol.2.6 Fungsi Autokorelasi dan Fungsi Autokorelasi Parsial
Fungsi autokorelasi dan fungsi autokorelasi parsial populasi dapat di estimasi
dengan menghitung fungsi autokorelasi dan fungsi autokorelasi parsial sampel yang biasa disebut dengan fungsi autokorelasi dan fungsi autokorelasi parsial contoh. Fungsi autokorelasi dan fungsi autokorelasi parsial dapat digunakan untuk mengidentifikasi model box-jenkins dengan melihat prilaku dari kedua fungsi tersebut.
2.6.1 Fungsi Autokorelasi
Koefisien autokorelasi merupakan derajat hubungan antara
Y
t danY
t−k. Menurut Spyros Makridakis, Steven C. Wheelwright dan Victor E. McGee dengan persamaan :(
)(
)
(
)
∑
∑
= − = +−
−
−
=
n t t k n t k t t kY
Y
Y
Y
Y
Y
r
1 2 1 (2-15) Dengan : kr
= Koefisien autokorelasi tY
= Data actual pada periode tY = Nilai tengah (mean) dari data aktual
k t
Y
+ = Data aktual pada periode t dengan time lag (ketertinggalan) k( )
n
r
SE
k1
=
(2-16) Dengan : kr
= Koefisien autokorelasi n = Periode musimanKoefisien autokorelasi dari data acak mempunyai distribusi sampling yang mendekati kurva
normal baku dengan nilai tengah (mean) nol dan kesalahan standar
n
1
. Suatu deret bersifat
acak apabila koefisien korelasinya berada dalam batas interval -
( )
r
kr
kZ
SE
( )
r
kSE
Z
2 2 α α≤
≤
.Fungsi autokorelasi dapat digunakan untuk pendugaan parameter model ARIMA. Makridakis (1991) menyatakan bahwa persamaan autokorelasi untuk proses MA(q) adalah sebagai berikut : k
ρ
=k
q
q q k q k k,...,
2
,
1
;
...
1
...
2 2 2 2 1 1 1=
+
+
+
+
+
+
+
−
+ −θ
θ
θ
θ
θ
θ
θ
θ
(2-17) 0 ; k = q Dengan : kρ
= Nilai teoritisk = q = ketertinggalan waktu (time lag)
Proses rataan bergerak berordo q mempunyai nilai nol untuk lag lebih dari q. Karena nilai teoritis
ρ
k tidak diketahui, maka nilai taksiran pendahuluan dari koefisienq
θ
θ
θ
θ
1, 2, 3,..., dapat diperoleh dengan mensubstitusi autokorelasi empirisr
k.2.6.2 Fungsi Autokorelasi Parsial
Koefisien autokorelasi parsial digunakan untuk mengukur tingkat keeratan antara
Y
t danY
− , apabila pengaruh dari time lag 1,2,3,…,k-1 dianggap terpisah. Dalam analisa deretberkala koefisien autokorelasi parsial berguna untuk membantu menetapkan model ARIMA yang tepat untuk peramalan.
Koefisien autokorelasi parsial berorde m didefenisikan sebagai koefisien autoregressive terakhir dari model AR(m).
Nilai koefisien autokorelasi parsial dapat dihitung dengan menggunakan persamaan berikut : t k t kk k t k t
Y
Y
e
Y
=
φ
1 −+
...
+
φ
−+
(2-18) Dengan : tY
= Data aktual kφ
= Parameter autoregressive ke-k kt
Y
− = Nilai keterlambatan pada saat k periodet
e
= Kesalahan ramalan2.7 Pemeriksaan Ketepatan Model
Setelah berhasil menaksir nilai-nilai parameter, langkah selanjutnya adalah menguji apakah model yang didefenisikan telah tepat. Untuk itu dilakukan pemeriksaan terhadap :
2.7.1 Nilai Sisaan (Residu)
Model yang telah ditetapkan akan memperlihatkan perbedaan residu atau kesalahan antara nilai-nilai data deret waktu dan nilai-nilai estimasi dari model sangat kecil atau tidak berarti. Kesalahan ramalan dapat diperoleh dari persamaan berikut :
)
(h
Y
Y
e
t=
t−
t (2-19) Dengan : te
= Kesalahan ramalan tY
= Data aktual)
(h
Y
= Nilai ramalant
e
= Kesalahan ramalanDari nilai-nilai kesalahan dapat diperoleh koefisien autokorelasi residu. Jika tidak terdapat pola data yang secara nyata berbeda dari nol, sehingga kesalahan diasumsikan menjadi acakan atau tidak perlu diperhatikan maka model dianggap cukup tepat.
2.7.1.1 Pemeriksaan Kesalahan Standar Residu
Rumus kesalahan standar untuk memeriksa apakah
r
k(e
)
tertentu secara nyata berbeda dari nol adalah :[
]
n
k
r
SE
e(
)
=
1
(2-20) Dengan : kr
= Koefisien autokorelasi n = Periode musimanKoefisien autokorelasi dari data random akan mempunyai distribusi sampling yang
mendekati kurva normal baku dengan nilai tengah nol dan kesalahan standar
n
1
, sehingga
untuk menetapkan apakah
r
k(e
)
berasal dari populasi yang mempunyai nilai autokorelasi kesalahan nol pada time lag k, dilakukan pengujian apakahr
k(e
)
dengan tingkat kepercayaan 95% terletak dalam batas interval yang telah ditentukan dengan menggunakan persamaan :
≤
≤
−
n
r
n
k1
96
,
1
1
96
,
1
(2-21) Dengan : n = Jumlah sampel=
kr
koefisien autokorelasi2.7.1.2 Statistik Box-Pierce
Untuk memeriksa apakah autokorelasi nilai-nilai sisaan (residu) berpola acakan (bersifat white noise), digunakan statistik Box-Pierce Sebagai berikut :
∑
==
m k ke
r
n
Q
1 2)
(
(2-22) Dengan :Q
= Hasil perhitungan statistik Box-Piercem
= Jumlah autokorelasi residu (jumlah lag)n
= N – d – SDN = Jumlah anggota sampel
d = Ordo pembedaan bukan musiman
D = Ordo pembedaan musiman
S = Jumlah periode per musim
)
(e
r
k = Koefisien autokorelasi residu pada lag – kJika model cukup tepat, maka statistik Q akan berdistribusi
χ
2 dengan m-p-q-P-Q derajat kebebasan, dengan p,q adalah jumlah koefisien autoregressive serta moving-average (rataan-bergerak) bukan musiman sedangkan P , Q adalah jumlah koefisien autoregressive serta moving-average (rataan-bergerak) musiman. Pengujian hipotesis adalah tolakH
0. Bahwa residu bersifat white noise jika nilai statistik Qχ
2 yang diperoleh dari tabel.2.7.2 Overfitting Model ARIMA
Langkah pemeriksaan ketepatan model selanjutnya adalah overfitting model ARIMA yang telah ditetapkan. Overfitting dilakukan dengan menambahkan parameter yang diestimasi pada model yang telah ditetapkan. Nilai-nilai statistic yang telah ditetapkan untuk melihat kcocokan dari model yang sedang dipelajari. Perbandingan ini dimaksudkan untuk meyakini bahwa model yang ditetapkan adalah model yang tepat.
2.8 Peramalan Dengan Model ARIMA Box-Jenkins
Setelah parameter-parameter model ARIMA diestimasi, maka langkah selanjutnya adalah menggunkana model tersebut untuk peramalan. Untuk tujuan ilustrasi, tetapkan model ARIMA (1,1,1). Agar dapat digunakan, maka model tersebut dikembangkan dalam bentuk persamaan regresi biasa, yaitu :
1 1 2 1 1 1 1 − − − −
+
−
+
+
−
=
t t t t t tY
Y
Y
e
e
Y
φ
φ
δ
θ
(2-23) Dengan : tY
= Data aktual 1 − tY
= Nilai keterlambatan pertama1
φ
= Parameter autoregressive ke-iδ
= Konstantat
e
= Sisaan (residu) ke – t1
θ
= Nilai rata – rata bergerak MA1 −
t
e
= Sisaan (residu) ke-1Untuk meramalkan satu periode kedepan yaitu
Y
t(
1
)
, maka ditambahkan satu angka indeks yang menunjukkan waktu, yaitu :t t t t t t
Y
Y
Y
e
e
Y
+1=
+
φ
1−
φ
1 −1+
δ
+
+1−
θ
1 (2-24) Dengan : 1 + tY
= Nilai peramalan satu periode ke depant
Y
= Data aktual1 −
t
Y
= Nilai keterlambatan pertama1
φ
= Parameter autoregressive ke-iδ
= Konstantat
e
= Sisaan (residu) ke – t1
θ
= Nilai rata – rata bergerak MA1 +
t
e
= Sisaan (residu) satu periode kedepanUntuk meramalkan h periode kedepan yaitu
Y
t(h
)
maka persamaan menjadi :h t h t h t h t h t h t
Y
Y
Y
e
e
Y
+=
−1++
φ
1 −1+−
φ
1 −2++
δ
+
+−
θ
1 −1+ (2-25) Dengan : h tY
+ = Nilai peramalan h periode kedepanh t
Y
−1+ = Nilai periode keterlambatan pertama saat h periode kedepan1
φ
= Parameter autoregressive ke-iδ
= Konstantah t
e
+ = Nilai sisaan (residu) peramalan h periode kedepanh t
e
−1+ = Nilai sisaan (residu) keterlambatan pertama saat h periode kedepanUntuk mengetahui ketepatan ramalan ini dapat dihitung nilai MSE dan MAPE yang merupakan ukuran ketepatan ramalan.
1. MSE (Mean Square Error)
[
]
2 1)
(
1
∑
=−
=
t t t tY
h
Y
T
MSE
(2-26) Dengan : tY
= Data aktual)
(h
Y
t = Data hasil ramalanT = Banyak sistem (residu)
% 100 ) ( 1 1 × − =