Algoritma Expectation-Maximization(EM) Untuk Estimasi Distribusi Mixture

(1)

Algoritma Expectation-Maximization(EM) Untuk Estimasi Distribusi Mixture

Tomy Angga Kusuma¹⁾, Suparman²⁾

1)Program Studi Matematika FMIPA UAD ²⁾Program Studi Pend. Matematika UAD

Abstrak

Distribusi mixture merupakan distribusi yang dapat digunakan untuk memodelkan data yang populasinya tersusun dari beberapa sub populasi. Setiap sub populasi memiliki karakteristik yang berbeda. Namun kendala umum yang dihadapi adalah mengestimasi parameter pada distribusi mixture. Sehingga penelitian ini bertujuan untuk mengestimasi parameter pada distribusi mixture. Pendugaan parameter pada distribusi mixture dapat menggunakan metode algoritma Expectation-Maximization (EM). Algoritma EM memiliki kelebihan yaitu dapat menyelesaikan beberapa permasalahan pada bidang statistik seperti menduga parameter bagi gabungan fungsi-fungsi serta parameter dari data yang tidak lengkap. Kinerja Algoritma EM diuji dengan menggunakan data simulasi.

Keywords— Distribusi Mixture, Algoritma Expectation-Maximization (EM)

1. Pendahuluan

Statistika inferensia mencakup semua metode yang berhubungan dengan analisis sebagian data atau juga sering disebut sampel untuk kemudian sampai pada peramalan atau penarikan kesimpulan mengenai keseluruhan data induknya (populasi). Salah satu cara penarikan kesimpulan mengenai karakteristik populasi tersebut yaitu penaksiran parameter. Penaksiran parameter ini bertujuan untuk mendapatkan taksiran dari suatu nilai parameter populasi yang tak diketahui berdasarkan sampel.

Dalam statistika terdapat dua jenis penaksiran parameter, yaitu penaksiran paramater titik dan penaksiran parameter interval. Penaksiran titik berupa sebuah nilai dari parameter populasi, sedangkan penaksiran interval berupa selang di mana parameter populasi terletak pada interval tersebut. Penentuan penaksiran parameter titik dapat ditempuh dengan menggunakan beberapa metode yaitu Metode Kemungkinan Maksimum, Metode Momen, Metode Kuadrat terkecil, dan sebagainya.

Namun dalam beberapa kasus metode-metode tersebut tidak dapat memberikan solusi atas parameter yang ingin diketahui. Salah satu masalah yang tidak dapat diselesaikan mengenai distribusi mixture.

Distribusi mixture menggabungkan sejumlah komponen yang kemungkinan berasal dari distribusi yang sama atau bahkan berbeda-beda sehingga dapat memberikan gambaran mengenai sifat-sifat data. Hasil distribusi mixture dapat memfasilitasi deskripsi suatu sistem yang kompleks dengan lebih teliti. Mixture beberapa distribusi tersebut menghasilkan distribusi baru yang mempunyai beberapa parameter. Sehingga

(2)

diharuskan mengestimasi parameternya. Pendugaan parameter dapat menggunakan beberapa metode salah satu metode terbaik yaitu algoritma Expectation-Maximization (EM).

Algoritma EM memiliki kelebihan dimana mampu menyelesaikan beberapa permasalahan pada bidang statistik seperti menduga parameter bagi gabungan fungsi- fungsi serta parameter dari data yang tidak lengkap.

2. Tinjauan Pustaka

2.1 Distribusi Mixture

Salah satu model khusus yang dapat digunakan untuk memodelkan data yang populasinya merupakan susunan dari beberapa sub populasi atau kelompok. Setiap sub populasi merupakan komponen penyusun dari model mixture serta mempunyai proporsi yang bervariasi untuk masing-masing komponennya (McLachlan dan Basford, 1988) dan (Gelman, Carlin, Stren, dan Rubin, 1995). Mixture distribution menggabungkan sejumlah komponen yang kemungkinan berasal dari distribusi yang sama atau berbeda-beda sehingga dapat memberikan gambaran mengenai sifat-sifat dari data. Hasil dari distribusi mixture dapat memfasilitasi deskripsi dari suatu sistem yang kompleks dengan lebih teliti. Distribusi mixture menyediakan kerangka parametrik yang fleksibel dalam permodelan dan analisis statistik (Marin, Mengersen, dan Robert, 2005).

McLahlan dan Krishnan (2008) menjabarkan suatu model mixture merupakan sebuah model probabilistik yang digambarkan dengan densitas

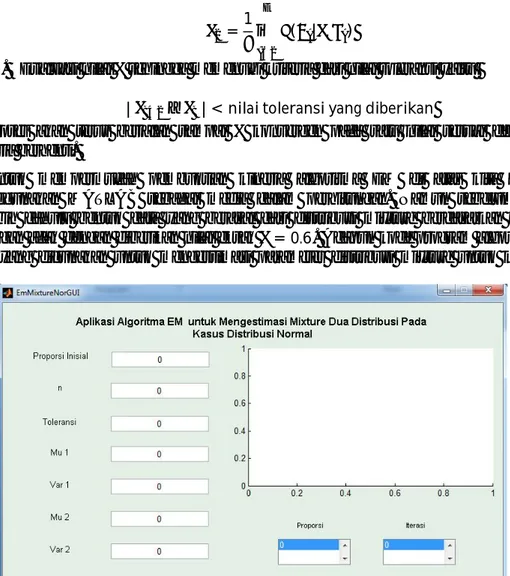
( ; ) = ( ) Eq. 1 Dimana

0 ≤ ≤ 1, ∑ = 1 Keterangan

: Probabilitas atau proporsi dari komponen mixture.

( ) : Fungsi densitas yang menggambarkan mekanisme probabilistik untuk membangkitkan data di dalam populasi yang secara lengkap dapat dikenali dari parameter .

: Melambangkan banyaknya komponen dalam mixture.

Model yang dijabarkan pada Eq. 1 disebut sebagai finite mixture model yang berlaku untuk model dengan jumlah komponen tertentu.

2.2 Maximum Likelihood Estimation

Maximum Likelihood Estimation (MLE) diperkenalkan oleh R. A Fisher pada tahun 1912. MLE merupakan salah satu metode penduga yang banyak sekali digunakan.

MLE biasanya digunakan untuk menduga nilai-nilai parameter yang dimiliki suatu fungsi, seperti mean, variansi, dan sebagainya.

(3)

Bain dan Engelhardt (1992) mendefinisikan MLE sebagai berikut :

Misalkan , , … , adalah sampel random dari populasi dengan densitas ( ; ) fungsi likelihood didefinisikan dengan :

( , , … , ) = ( ; ) Eq. 2

Bila fungsi likelihood ini terdiferensikan dalam maka calon estimator likelihood yang mungkin adalah sedemikian sehingga

( )= 0

Untuk membuktikan bahwa benar-benar memaksimumkan fungsi likelihood ( ) harus ditunjukkan bahwa :

( )< 0

Dalam banyak kasus dimana diferensi digunakan, akan lebih mudah bekerja pada logaritma dari ( )yaitu log ( ). Hal ini dimungkinkan karena fungsi logaritma naik tegas pada (0, ∞) yang berarti bahwa ( ) mempunyai ekstrem yang sama.

Sehingga untuk menentukan estimator maksimum likelihood dari sebagai berikut : 1. Tentukan fungsi likelihood

( , , … , ) = ( ; ) 2. Bentuk log likelihood = log ( )

3. Tentukan turunan dari = log ( ) terhadap log [ ]

= 0

Penyelesaian dari persamaan poin 3 merupakan estimator maksimum likelihood untuk .

4. Tentukan turunan kedua dari = log ( )terhadap . Jika ^{( )}< 0, maka akan membuktikan bahwa benar-benar memaksimumkan fungsi likelihood.

2.3 Algoritma Expectation-Maximization (EM) Definisi (Hogg, McKean dan Craig, 2005)

Algoritma EM pertama kali diperkenalkan oleh Dempster, Laird, dan Rubin pada tahun 1977. Secara garis besar, algoritma EM adalah algoritma untuk menduga suatu parameter dalam suatu fungsi dengan menggunakan MLE, di mana fungsi tersebut mengandung data yang tidak lengkap. Algoritma EM merupakan proses yang terbagi atas dua langkah yaitu :

 Langkah Expectation (E-step)

Pencarian nilai ekspektasi untuk fungsi likelihood berdasarkan variabel yang diamati.

 Langkah Maximization (M-Step)

(4)

Pencarian MLE dari parameter-parameter dengan memaksimumkan ekspektasi likelihood yang dihasilkan dari E-step.

Parameter-parameter yang dihasilkan dari M-step akan digunakan kembali untuk E- step yang berikutnya, dan langkah ini akan diulang terus sampai memberikan nilai yang konvergen serta merupakan penduga dari suatu parameter.

Misalkan kita anggap ada sampel dari item dimana dari item tersebut teramati sementara = − item tidak teramati. Item yang teramati dilambangkan dengan

= ( , , … , ) dan item yang tidak teramati dilambangkan dengan = ( , , … , ). Asumsikan S adalah variable saling bebas dan berdistribusi identik (independent and identically distribution) dengan fungsi kepadatan peluang ( | ),dimana ∈ Ω. Asumsikan S dan S adalah saling bebas. Mari kita lambangkan fungsi kepadatan peluang gabungan dari dengan ( | ). Kemudian ℎ( , | ) untuk fungsi kepadatan peluang gabungan untuk data yang teramati dan tidak teramati. Sedangkan ( | , ) melambangkan notasi fungsi kepadatan peluang bersyarat dari data yang hilang untuk memberikan data yang teramati. Maka dapat kita peroleh

( | , ) =ℎ( , | ) ( | ) Eq. 5 Fungsi Likelihood data yang teramati yaitu

( | ) = ( | )Eq. 6

Kemudian fungsi likelihood untuk data lengkap didefinisikan dengan ( | , ) = ℎ( , | )Eq. 7

Tujuan kita adalah memaksimalkan fungsi likelihood ( | ) dengan menggunakan fungsi likelihood lengkap ( | , ) didalam proses. Gunakan persamaan ( | , ), kita peroleh

log ( | ) = log ( | ) ∙ ( | , ) log ( | ) = log ( | ) ∙ ( | , )

log ( | ) = [log ℎ( , | ) − log ( | , )] ∙ ( | , )

log ( | ) = log ℎ( , | ) ∙ ( | , ) − log ( | , ) ∙ ( | , ) log ( | ) = [log ( | , )| , ] − [log ( | , )| , ]

Dimana ekspektasi diambil di bawah fungsi kepadatan peluang bersyarat dari ( | , ). Kemudian mendefinisikan bagian pertama di sisi kanan pada fungsi di atas

( | , ) = [log ( | , )| , ]

Ekspektasi yang didefinisikan fungsi dinamakan E-Step dari Algoritma EM.

Ingat kita ingin memaksimalkan log ( | ). Dilambangkan ^{( )} inisial estimasi dari , berdasarkan pada fungsi likelihood teramati. Kemudian ^{( )} menjadi argumen yang memaksimalkan ^{( )}, . Ini adalah langkah pertama untuk mengestimasi kemudian kita definisikan algoritma EM sebagai berikut.

(5)

Dilambangkan ^{( )} dalam mengestimasi langkah ke-m. Kemudian untuk mengestimasi langkah ke ( + 1) :

 Langkah Expectation (E-step)

( ), = ( ) log ( | , )| ^{( )},

Dimana ekspektasi diambil dari fungsi kepadatan peluang bersyarat ( | ^{( )}, )

 Langkah Maximization (M-step)

( )= Arg max ^{( )}, Dimana

( ) ( ), ≥ ^{( )} ^{( )},

3. Metode Penelitian

Metodologi penelitian merupakan cara berfikir dan berbuat yang dipersiapkan secara matang dalam rangka untuk mencapai tujuan penelitian, yaitu menemukan, mengembangkan atau mengkaji kebenaran suatu pengetahuan secara ilmiah.

Salah satu unsur terpenting dalam metodologi penelitian adalah penggunaan metode ilmiah tertentu yang digunakan sebagai sarana yang bertujuan untuk mengidentifikasi besar kecilnya objek atau gejala dan mencari pemecahan masalah yang sedang diteliti, sehingga hasil yang diperoleh dapat dipertanggung jawabkan kebenarannya secara ilmiah. Pada dasarnya fakta-fakta tidak tergeletak disekitar begitu saja tetapi butuh suatu metode untuk mengetahui dan mengambil masalah tersebut.

Penelitian dilakukan dengan mempelajari literatur-literatur yang memuat dan membahas tentang MLE, Distribusi Mixture, Algoritma EM, dan beberapa teori – teori pendukung.

Tahap – tahap penelitiannya adalah sebagai berikut : 3.1 Pengumpulan Literatur

Penulis mencari dan mengumpulkan literatur-literatur yang berhubungan dengan teori-teori probabilitas, variabel random, ekspektasi, estimasi parameter dan berbagai metode-metode lain yang relevan untuk sampai pada pembahasan tentang estimasi distribusi mixture menggunakan algoritma EM. Pengumpulan berasal dari berbagai sumber seperti dari buku, skripsi, jurnal, artikel, dan situs-situs internet yang menunjang materi yang diperlukan.

3.2 Pengkajian Literatur

Penulis membaca dan mengkaji literatur-literatur yang telah terkumpul, kemudian mengelompokkan dan mencatat literatur-literatur tersebut sesuai dengan masalah yang akan dibahas.

(6)

Sebagai langkah pertama penulis mempelajari teori probabilitas, teori estimasi parameter dan teori mengenai distribusi-distribusi dalam statistika pada buku Ilmu Peluang dan Statistika untuk Insinyur dan Ilmuwan (Walpole dan Myers, 1995).

Dilanjutkan dengan memahami maksud Distribusi Mixture dalam buku Introduction to Mathematical Statistics (Hogg, McKean dan Craig, 2005), Finite Mixture Models (McLachlan dan Peel, 2000). Selanjutnya mempelajari maksud dan teori Algoritma EM dalam buku The EM Algorithm and Extensions (McLachlan dan Krishnan, 2008),

3.3 Pengembangan Literatur

Pada tahap ini penulis pengelompokan dan mencatat literatur-literatur tersebut maka akan dilanjutkan dengan melakukan pengembangan-pengembangan dengan memberi uraian-uraian, yang diharapkan dapat lebih memahami konsep-konsep, sifat- sifat, dan teorema-teorema yang sudah ada.

3.4 Pembuatan Program MATLAB

Pembuatan program digunakan untuk aplikasi algoritma EM untuk mengestimasi distribusi mixture sehingga memudahkan perhitungan yang rumit. Selanjutnya mempelajari hasil praktek program aplikasi algoritma EM untuk mengestimasi distribusi mixture sesuai dengan tujuan dari penulisan skripsi ini. Program aplikasi algoritma EM untuk mengestimasi distribusi mixture ditulis dalam bahasa pemrograman Matlab2010. Hasil penelitan yang diperoleh kemudian akan dikaji dan dianalisa.

3.5 Penyusunan Hasil Penelitian

Penyusunan hasil penelitian digunakan sebagai langkah awal untuk memberi gambaran secara menyeluruh tentang topik yang akan dibahas.

4. Algoritma EM untuk Estimasi Distribusi Mixture

Algoritma EM adalah metode umum untuk mencari MLE ketika ada data yang hilang atau variabel tersembunyi. Dalam konteks mixture model, data yang hilang direpresentasikan dengan himpunan pengamatan Z dari variabel random diskrit dimana ∈ {1, … , } menunjukkan komponen mixture yang dihasilkan dari pengamatan .

Adapun fungsi likelihood dari data lengkap ( , ) mengambil bentuk multinomial berikut

ℎ( , | ) = (Ψ| , ) = ( | , Ψ) ( |Ψ)

= ( ( )) ⁽ ⁾Eq. 8

Dimana 1 adalah fungsi indikator 1( = ) = 1 jika = dan 1( = ) = 0 untuk yang lain.

(7)

Sebelum itu, kita perlu mendefinisikan posterior probabiltas dari = dengan aturan Bayes kita dapat mendefinisikan sebagai berikut misalkan ( = | , Ψ) =

( = | , Ψ) kemudian kita dapat tuliskan ( | = , Ψ) = ( |ψ ), ( = |Ψ) = dan ( |Ψ) = ∑ ( |ψ )

( = | , Ψ) = ( , = , Ψ)

( , Ψ)

= ( = , Ψ) ( | = , Ψ) ( , Ψ)

= ( = |Ψ) (Ψ) ( | = , Ψ) ( |Ψ) (Ψ)

= ( = |Ψ) ( | = , Ψ) ( |Ψ)

= ( |ψ )

∑ ( |ψ ) Eq. 9

Dalam kasus mixture model maka kita dapat memanipulasi algoritma EM sebagai berikut ;

(Ψ, Ψ ) = [log (Ψ | , )| , Ψ ]

= ∑ _∈ log (Ψ|X, Z) ( | , Ψ )

= ∑ _∈ ∑ log ( |ψ ) ∏ ( | , Ψ )

= ∑ _∈ ∑ ∑ _, log[ ( |ψ )] ∏ ( | , Ψ )

= ∑ ∑ log[ ( |ψ )] ∑ _∈ _, ∏ ( | , Ψ )

= ∑ ∑ log[ ( |ψ )] ∑ … ∑ … ∑ _, ∏ ( | , Ψ )

= ∑ ∑ log[ ( |ψ )]

∑ … ∑ ∑ … ∑ ∏ , Ψ ( | , Ψ )

= ∑ ∑ log[ ( |ψ )] ∏ ∑ , Ψ

1

( | , Ψ )

= ∑ ∑ log[ ( |ψ )] ( | , Ψ )

Berdasarkan penjabaran di atas maka persamaan dapat kita tuliskan sebagai berikut

(Ψ, Ψ ) = log( ) ( | , Ψ ) +

log[ ( |ψ )] ( | , Ψ ) Eq. 10

Kita perlu mencari nilai ekspektasi atau E-step dari (Ψ|X, Z) denagn diberikan dan parameter. Dimana log (Ψ|X, Z) adalah linier di langkah ini mengurangi untuk menghitung nilai ekspektasi = dengan diberikan dan parameter Ψ sehingga dapat dituliskan

[ = | , Ψ ] = ( = | , Ψ )Eq. 11

(8)

Kemudian untuk mengestimasi parameter proporsi dari Eq.10 kita akan menggunakan sebagai pengali Lagrange, kemudian kita atur = − maka kita dapatkan

log( ) ( | , Ψ ) + − 1

= 0 1

( | , Ψ ) + = 0

Sehingga diperoleh

= 1

( | , Ψ ) Eq. 12

Untuk mencari ( | , Ψ ) telah dijabarkan pada Eq. 9 untuk selanjutnya persamaan Eq.12 kita sebut M-step untuk mecari proporsi.

5. Estimasi Distribusi Mixture untuk Dua Distribusi

Pada bagian ini, penulis menggunakan mixture yang terdiri dari dua distribusi kemudian akan ditaksir menggunakan algoritma EM. Adapun distribusi yang digunakan yaitu distribusi normal atau gaussian yang dijabarkan sebagai berikut

Andaikan variabel random adalah disitribusi mixture dengan adalah distribusi independen kemudian = dan = 1 − kita tuliskan

~ ( ) + (1 − )ℎ( ) = 1, … ,

Dimana (. ) dan ℎ(. ) diketahui. Algoritma EM dapat digunakan untuk mencari estimator maksimum likelihood dari . Misalkan , … , dimana menunjukkan dari mana distribusi digambarkan sebagai berikut

| = 1~ ( )

| = 0~ℎ( ) Maka dari permasalahan di atas dapat diketahui bahwa

( | ) = [ ( ) + (1 − )ℎ( )] Eq. 13

Kemudian kita akan menuliskan ( | , ) dengan memperhatikan Eq. 8 sebagai berikut

( | , ) = [ ( ) + (1 − )ℎ( )] (1 − ) Eq. 14

Untuk E-step dari penjabaran pada persamaan Eq. 9 dan Eq. 11 dimana kita dapatkan

(9)

[ | , ] = ( | , )

= ( )

[ ( ) + (1 − )ℎ( )]Eq. 15 Maka diperoleh M-step berdasarkan pada persamaan (12) yaitu

=1 ( )

[ ( ) + 1 − ℎ( )]Eq. 16 6. Perhitungan Numerik

Pengujian akan difokuskan pada distribusi normal dan distribusi poisson yang dibatasi atas mixture dua distribusi. Agar perhitungan lebih akurat dan efisien penelitian akan menggunakan Matlab2010. Adapun pembahasan tertera seperti berikut 6.1 Estimasi Parameter Distribusi Mixture Menggunakan Algoritma EM untuk

Kasus Distribusi Normal

Penelitian pada kasus ini bertujuan mengukur kinerja algoritma EM dalam mengestimasi distribusi mixture dengan dibatasi dua distribusi yang diketahui berdistribusi normal yang merupakan distribusi kontinu. Dimana diketahui

| = 1~ ( , )

| = 0~ ( , )

Berdasarkan persamaan (4.7) maka fungsi likelihood yang diperoleh yaitu

( | ) = [ 1

√2

( )

+ (1 − ) 1

√2

( )

]

Kemudian untuk data fungsi likelihood lengkap dari persamaan (4.8)

( | , ) = 1

√2

( )

+ (1 − ) 1

√2

( )

(1 − ) Sehingga dapat kita tuliskan algoritma EM untuk mencari parameter distribusi mixture pada kasus distribusi normal sebagai berikut

1. Inisialisasi nilai untuk , , , , dan banyaknya data atau serta nilai toleransi untuk kriteria berhenti.

2. E-Step Evaluasi nilai parameter [ | , ] = ( | , )

= ^√

exp −⁽ ⁾

[ √ exp −⁽ ⁾ + (1 − )

√ exp −⁽ ⁾ ] 3. M-Step untuk mendapatkan nilai

(10)

= 1

( | , )

4. Evaluasi nilai sehingga memenuhi kriteria dari nilai toleransi yaitu

| − | < nilai toleransi yang diberikan

Proses akan terus berjalan sampai konvergen pada satu nilai sesuai dengan kriteria berhenti.

Untuk mempermudah pembuktian kinerja algoritma EM di atas kita akan menggunakan MATLAB sebagai media dalam perhitungan. Namun sebelum itu terlebih dahulu bentuk data yang berasal dari distribusi mixture berdasarkan teori bilangan acak dengan diberikan nilai eksak = 0.6. Adapun kode program algoritma EM yang digunakan untuk mengestimasi parameter distribusi mixture untuk kasus

distribusi normal sebagai berikut.

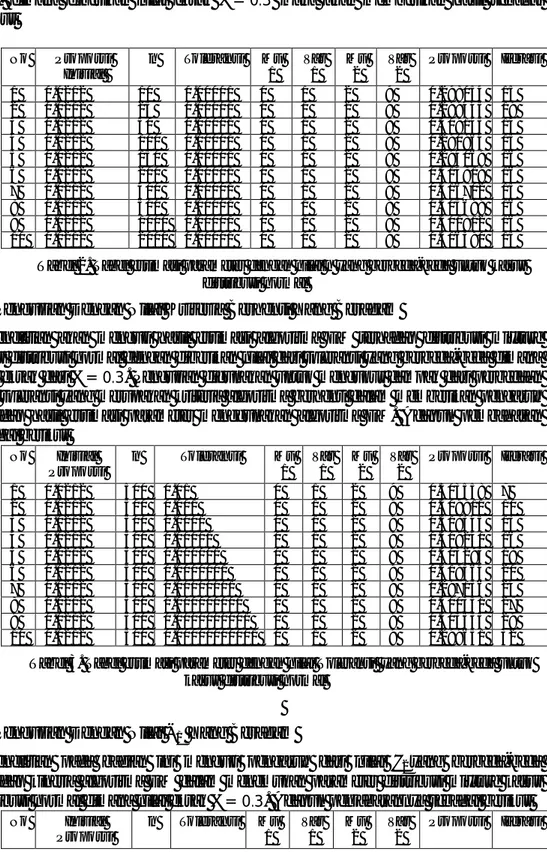
Selanjutnya Graphical User Interface (GUI) dari program algoritma EM untuk mengestimasi parameter distribusi mixture berdasarkan kode program 1 diperlihatkan pada gambar 1 berikut

Gambar 1. GUI program algoritma EM untuk estimasi parameter distribusi mixture kasus distribusi normal

Adapun keterangan mengenai aplikasi pada Gambar 1 yaitu

 Proporsi Inisial : Sebagai nilai awal inisialisai dengan range 0 < < 1.

 : Banyaknya jumlah data yang ingin diestimasi.

 Toleransi : Nilai toleransi yang digunakan sebagai kriteria berhenti.

(11)

 Mu 1 : Nilai yang berasal dari distribusi normal pertama.

 Var 1 : Nilai yang berasal dari distribusi normal pertama.

 Mu 2 : Nilai yang berasal dari distribusi normal kedua.

 Var 2 : Nilai yang berasal dari distribusi normal kedua.

 Proporsi : Nilai proporsi estimasi yang dihasilkan dari algoritma EM.

 Iterasi : Banyaknya iterasi dalam mengestimasi niali proporsi.

Kemudian penelitian akan dilanjutkan dengan menguji lebih dalam kemampuan algoritma EM dengan mengganti nilai masukkan baik itu Proporsi Inisial, , Mu 1, Var 1, Mu 2, dan Var 2. Sehingga dapat terlihat keakuratan dan kecepatan algoritma EM dalam mengestimasi nilai parameter distribusi mixture untuk kasus distribusi normal.

6.2 Pengujian Dengan Nilai Proporsi Awal Yang Beragam

Pada bagian ini penelitian akan menguji kinerja algoritma EM dalam mengestimasi parameter distribusi mixture dengan diberikan nilai proporsi awal yang berbeda-beda.

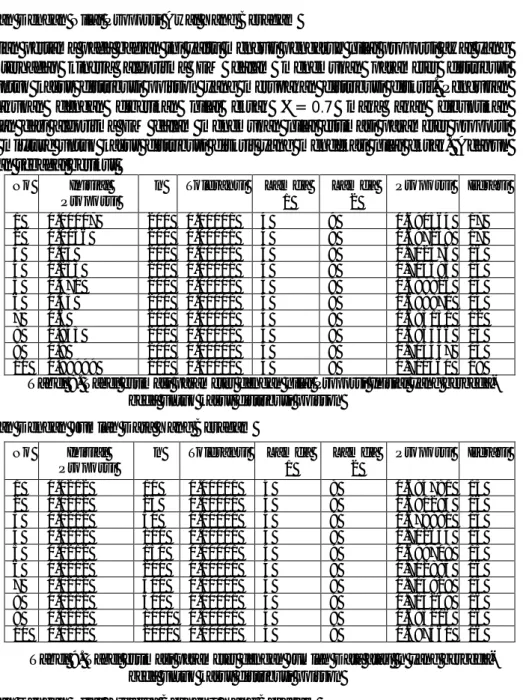
Pengujian yang dilakukan dengan diberikan nilai eksak = 0.3 maka akan dibuktikan kemampuan dari algoritma EM dalam menemukan nilai estimasi parameter proporsi distribusi mixture untuk kasus distribusi normal yang mendekati nilai eksak. Adapun pembuktian sebagai berikut

No Proporsi Inisial

n Toleransi Mu 1

Var 1

Mu 2

Var 2

Proporsi Iterasi

1 0.00007 200 0.00001 0 1 2 9 0.292268 22

2 0.0056 200 0.00001 0 1 2 9 0.297329 17

3 0.03 200 0.00001 0 1 2 9 0.302134 15

4 0.253 200 0.00001 0 1 2 9 0.304313 11

5 0.471 200 0.00001 0 1 2 9 0.297588 12

6 0.55 200 0.00001 0 1 2 9 0.313308 11

7 0.7 200 0.00001 0 1 2 9 0.311657 12

8 0.843 200 0.00001 0 1 2 9 0.316331 13

9 0.9 200 0.00001 0 1 2 9 0.310555 12

10 0.99999 200 0.00001 0 1 2 9 0.303344 13 Tabel 1. Tabel estimasi parameter dengan nilai Proporsi Awal yang berbeda-beda

untuk kasus distribusi normal 6.3 Pengujian Dengan Jumlah Data Yang Beragam

(12)

Pada pengujian dengan nilai masukkan dari banyaknya data atau n yang berbeda- beda, dimana diberikan nilai eksak = 0.3 maka akan memberikan hasil sebagai berikut

No Proporsi Inisial

Var 1

Mu 2

Var 2

1 0.0212 10 0.00001 0 1 2 9 0.298054 15

2 0.0212 25 0.00001 0 1 2 9 0.299445 19

3 0.0212 50 0.00001 0 1 2 9 0.309145 14

4 0.0212 100 0.00001 0 1 2 9 0.290964 15

5 0.0212 150 0.00001 0 1 2 9 0.294069 16

6 0.0212 200 0.00001 0 1 2 9 0.314819 16

7 0.0212 400 0.00001 0 1 2 9 0.316702 15

8 0.0212 500 0.00001 0 1 2 9 0.305699 16

9 0.0212 1000 0.00001 0 1 2 9 0.301812 16 10 0.0212 2000 0.00001 0 1 2 9 0.316390 15 Tabel 2. Tabel estimasi parameter dengan nilai n yang berbeda-beda untuk kasus

distribusi normal

6.4 Pengujian Dengan Nilai Kriteria Berhenti Yang Beragam

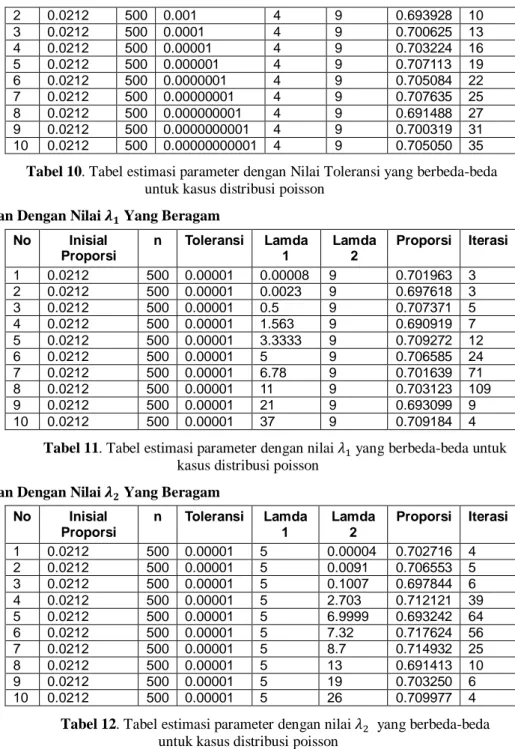
Penelitian akan menguji hasil estimasi algoritma EM terhadap distribusi mixture kasus distribusi normal dengan diberikan nilai dari toleransi yang berbeda-beda dimana nilai eksak dari = 0.3. Pengujian digunakan untuk mengukur dampak dari perbedaan nilai toleransi yang merupakan kriteria algoritma berhenti dalam memberikan pengaruh terhadap hasil estimasi parameter menggunakan algoritma EM. Adapun pembahasan sebagai berikut

No Inisial Proporsi

Var 1

Mu 2

Var 2

1 0.0212 500 0.01 0 1 2 9 0.303558 7

2 0.0212 500 0.001 0 1 2 9 0.309911 10

3 0.0212 500 0.0001 0 1 2 9 0.318345 13

4 0.0212 500 0.00001 0 1 2 9 0.309240 16

5 0.0212 500 0.000001 0 1 2 9 0.303293 18 6 0.0212 500 0.0000001 0 1 2 9 0.319364 20 7 0.0212 500 0.00000001 0 1 2 9 0.297156 24 8 0.0212 500 0.000000001 0 1 2 9 0.300351 27 9 0.0212 500 0.0000000001 0 1 2 9 0.305555 29 10 0.0212 500 0.00000000001 0 1 2 9 0.299651 32

Tabel 3. Tabel estimasi parameter dengan nilai Toleransi yang berbeda-beda untuk kasus distribusi normal

6.5 Pengujian Dengan Nilai Yang Beragam

Penelitian pada bagian ini menguji pengaruh dari nilai yang berbeda-beda terhadap kinerja algoritma EM dalam menemukan parameter distribusi mixture kasus distribusi normal dimana nilai eksak = 0.3. Adapun penjabarannya sebagai berikut

Var 1

Mu 2

Var 2

(13)

1 0.0212 500 0.00001 3 7 2 9 0.313940 350

2 0.0212 500 0.00001 5 7 2 9 0.299999 210

3 0.0212 500 0.00001 8 7 2 9 0.314602 89

4 0.0212 500 0.00001 17 7 2 9 0.313564 19 5 0.0212 500 0.00001 20 7 2 9 0.316423 14

6 0.0212 500 0.00001 40 7 2 9 0.300614 5

7 0.0212 500 0.00001 50 7 2 9 0.316192 3

8 0.0212 500 0.00001 65 7 2 9 0.293950 3

9 0.0212 500 0.00001 80 7 2 9 0.314000 2

10 0.0212 500 0.00001 100 7 2 9 0.290000 2 Tabel 4. Tabel estimasi parameter dengan nilai yang berbeda-beda untuk kasus

distribusi normal 6.6 Pengujian Dengan Nilai Yang Beragam

Sedangkan pada pengujian bagian ini kita akan melihat pengaruh dari nilai yang berbeda-beda dalam menemukan parameter distribusi mixture menggunakan algoritma EM kasus distribusi normal dengan diketahui nilai eksak = 0.3. Pemaparan akan disajikan sebagai berikut

Var 1

Mu 2

Var 2

1 0.0212 500 0.00001 8 1 2 9 0.312998 14

2 0.0212 500 0.00001 8 5 2 9 0.318148 58

3 0.0212 500 0.00001 8 6 2 9 0.309211 74

4 0.0212 500 0.00001 8 11 2 9 0.295012 91 5 0.0212 500 0.00001 8 14 2 9 0.295712 66 6 0.0212 500 0.00001 8 21 2 9 0.289930 29 7 0.0212 500 0.00001 8 27 2 9 0.289205 22 8 0.0212 500 0.00001 8 33 2 9 0.285089 19 9 0.0212 500 0.00001 8 37 2 9 0.281883 16 10 0.0212 500 0.00001 8 40 2 9 0.315565 15 Tabel 5. Tabel estimasi parameter dengan nilai ₁²yang berbeda-beda untuk kasus

distribusi normal 6.7 Pengujian Dengan Nilai Yang Beragam

Penelitian dilanjutkan untuk menguji pengaruh dari nilai yang berbeda-beda terhadap kinerja algoritma EM dalam menemukan parameter distribusi mixture kasus distribusi normal dimana nilai eksak = 0.3. Adapun penjelasan sebagai berikut

Var 1

Mu 2 Var 2

1 0.0212 500 0.00001 3 7 0.004 4 0.310074 47 2 0.0212 500 0.00001 3 7 0.05 4 0.305825 47 3 0.0212 500 0.00001 3 7 0.156 4 0.303526 48 4 0.0212 500 0.00001 3 7 1.97 4 0.300357 64

5 0.0212 500 0.00001 3 7 5 4 0.303805 62

6 0.0212 500 0.00001 3 7 8 4 0.322921 35

7 0.0212 500 0.00001 3 7 14 4 0.293525 13

8 0.0212 500 0.00001 3 7 23 4 0.295491 6

9 0.0212 500 0.00001 3 7 49 4 0.306000 2

10 0.0212 500 0.00001 3 7 80 4 0.304000 2

(14)

Tabel 6. Tabel estimasi parameter dengan nilai yang berbeda-beda untuk kasus distribusi normal

6.8 Pengujian Dengan Nilai Yang Beragam

Pengujian terakhir akan dilihat pengaruh dari nilai yang berbeda-beda dalam menemukan parameter distribusi mixture menggunakan algoritma EM kasus distribusi normal dengan diketahui nilai eksak = 0.3. Adapun penjabaran akan disajikan sebagai berikut

Var 1

Mu 2

Var 2

1 0.0212 500 0.00001 3 7 2 0.5 0.308025 8 2 0.0212 500 0.00001 3 7 2 1.5 0.317198 15 3 0.0212 500 0.00001 3 7 2 1.7 0.298112 16 4 0.0212 500 0.00001 3 7 2 2.87 0.304377 29 5 0.0212 500 0.00001 3 7 2 13 0.312603 101 6 0.0212 500 0.00001 3 7 2 17 0.290055 59 7 0.0212 500 0.00001 3 7 2 19 0.310588 49 8 0.0212 500 0.00001 3 7 2 27 0.289886 33 9 0.0212 500 0.00001 3 7 2 64 0.305481 15 10 0.0212 500 0.00001 3 7 2 100 0.311352 12 Tabel 7. Tabel estimasi parameter dengan nilai ₂²yang berbeda-beda untuk kasus

distribusi normal

7. Estimasi Parameter Distribusi Mixture Menggunakan Algoritma EM untuk Kasus Distribusi Poisson

Pada kasus distribusi poisson penelitian juga bertujuan untuk menguji kinerja algoritma EM dalam menghasilkan nilai estimasi parameter distribusi mixture khususnya untuk masalah diskrit. Dimana diketahui

| = 1~ ( )

| = 0~ ( )

Berdasarkan persamaan (4.7) maka fungsi likelihood yang diperoleh yaitu ( | ) = [

! + (1 − )

! ] Kemudian untuk data fungsi likelihood lengkap dari persamaan (4.8)

( | , ) =

! + (1 − )

! (1 − )

Maka dapat kita tuliskan algoritma EM untuk mencari parameter distribusi mixture untuk kasus distribusi poisson sebagai berikut

1. Inisialisasi nilai untuk , , dan banyaknya data atau serta nilai toleransi untuk kriteria berhenti.

2. E-Step Evaluasi nilai parameter

(15)

[ | , ] = ( | , )

= ^!

[ ! + (1 − )

! ] 3. M-Step untuk mendapatkan nilai

= 1

( | , )

4. Evaluasi nilai sehingga memenuhi kriteria dari nilai toleransi yaitu

| − | < nilai toleransi yang diberikan

Proses akan terus berjalan sampai konvergen pada satu nilai sesuai dengan kriteria berhenti.

Pembuktian kinerja algoritma EM di atas akan menggunakan MATLAB sebagai media dalam perhitungan. Namun sebelum itu terlebih dahulu bentuk data yang berasal dari distribusi mixture yang dijabarkan berdasarkan teori bilangan acak dengan diberikan nilai eksak = 0.6. Adapun kode program untuk menghasilkan bilangan acak pada distribusi poisson sebagai berikut

Selanjutnya GUI program algoritma EM untuk mengestimasi parameter distribusi mixture berdasarkan kode program 3 diperlihatkan pada Gambar 2 berikut

Gambar 2. GUI program algoritma EM untuk estimasi parameter distribusi mixturekasus distribusi poisson

Adapun keterangan mengenai aplikasi pada Gambar 2 yaitu

 Proporsi Inisial : Sebagai nilai awal inisialisai dengan range 0 < < 1.

 : Banyaknya jumlah data yang ingin diestimasi.

(16)

 Toleransi : Nilai toleransi yang digunakan sebagai kriteria berhenti.

 Lamda 1 : Nilai yang berasal dari distribusi poisson pertama.

 Lamda 2 : Nilai yang berasal dari distribusi poisson kedua.

Pengujian Dengan Nilai Proporsi Awal Yang Beragam

Penelitian pertama pada bagian ini yaitu menguji pengaruh nilai proporsi awal yang beragam terhadap kinerja algoritma EM dalam menemukan parameter distribusi mixture untuk kasus distribusi poisson yang merupakan distribusi diskrit. Pengujian yang dilakukan dengan diberikan nilai eksak = 0.7 maka akan dibuktikan kemampuan dari algoritma EM dalam menemukan nilai estimasi parameter proporsi distribusi mixture untuk kasus distribusi diskrit yang mendekati nilai eksak. Adapun pembuktian sebagai berikut

n Toleransi Lamda 1

Lamda 2

1 0.00007 200 0.00001 4 9 0.690564 17

2 0.0056 200 0.00001 4 9 0.697258 17

3 0.03 200 0.00001 4 9 0.702376 16

4 0.253 200 0.00001 4 9 0.704595 14

5 0.471 200 0.00001 4 9 0.698826 13

6 0.55 200 0.00001 4 9 0.699871 14

7 0.6 200 0.00001 4 9 0.695151 12

8 0.843 200 0.00001 4 9 0.696366 13

9 0.9 200 0.00001 4 9 0.703447 13

10 0.99999 200 0.00001 4 9 0.711360 18

Tabel 8. Tabel estimasi parameter dengan nilai Proporsi Inisial yang berbeda- beda untuk kasus distribusi poisson

Pengujian Dengan Jumlah Data Yang Beragam No Inisial

Proporsi

Lamda 2

1 0.0212 10 0.00001 4 9 0.694791 15

2 0.0212 25 0.00001 4 9 0.691294 16

3 0.0212 50 0.00001 4 9 0.679881 15

4 0.0212 100 0.00001 4 9 0.702634 15

5 0.0212 150 0.00001 4 9 0.699708 15

6 0.0212 200 0.00001 4 9 0.702885 16

7 0.0212 400 0.00001 4 9 0.714829 15

8 0.0212 500 0.00001 4 9 0.713269 16

9 0.0212 1000 0.00001 4 9 0.695216 16

10 0.0212 2000 0.00001 4 9 0.697561 16

Tabel 9. Tabel estimasi parameter dengan Jumlah Data atau n yang berbeda- beda untuk kasus distribusi poisson

Pengujian Dengan Nilai Kriteria Berhenti Yang Beragam No Inisial

Proporsi

Lamda 2

1 0.0212 500 0.01 4 9 0.692151 7

(17)

2 0.0212 500 0.001 4 9 0.693928 10

3 0.0212 500 0.0001 4 9 0.700625 13

4 0.0212 500 0.00001 4 9 0.703224 16

5 0.0212 500 0.000001 4 9 0.707113 19

6 0.0212 500 0.0000001 4 9 0.705084 22

7 0.0212 500 0.00000001 4 9 0.707635 25

8 0.0212 500 0.000000001 4 9 0.691488 27 9 0.0212 500 0.0000000001 4 9 0.700319 31 10 0.0212 500 0.00000000001 4 9 0.705050 35

Tabel 10. Tabel estimasi parameter dengan Nilai Toleransi yang berbeda-beda untuk kasus distribusi poisson

Pengujian Dengan Nilai Yang Beragam No Inisial

Proporsi

Lamda 2

1 0.0212 500 0.00001 0.00008 9 0.701963 3 2 0.0212 500 0.00001 0.0023 9 0.697618 3

3 0.0212 500 0.00001 0.5 9 0.707371 5

4 0.0212 500 0.00001 1.563 9 0.690919 7 5 0.0212 500 0.00001 3.3333 9 0.709272 12

6 0.0212 500 0.00001 5 9 0.706585 24

7 0.0212 500 0.00001 6.78 9 0.701639 71

8 0.0212 500 0.00001 11 9 0.703123 109

9 0.0212 500 0.00001 21 9 0.693099 9

10 0.0212 500 0.00001 37 9 0.709184 4

Tabel 11. Tabel estimasi parameter dengan nilai yang berbeda-beda untuk kasus distribusi poisson

Pengujian Dengan Nilai Yang Beragam No Inisial

Proporsi

Lamda 2

1 0.0212 500 0.00001 5 0.00004 0.702716 4 2 0.0212 500 0.00001 5 0.0091 0.706553 5 3 0.0212 500 0.00001 5 0.1007 0.697844 6 4 0.0212 500 0.00001 5 2.703 0.712121 39 5 0.0212 500 0.00001 5 6.9999 0.693242 64

6 0.0212 500 0.00001 5 7.32 0.717624 56

7 0.0212 500 0.00001 5 8.7 0.714932 25

8 0.0212 500 0.00001 5 13 0.691413 10

9 0.0212 500 0.00001 5 19 0.703250 6

10 0.0212 500 0.00001 5 26 0.709977 4

Tabel 12. Tabel estimasi parameter dengan nilai yang berbeda-beda untuk kasus distribusi poisson

8. Kesimpulan

Adapun kesimpulan yang diperoleh dari penilitian mengenai kinerja algoritma EM dalam mengestimasi parameter distribusi mixture sebagai berikut

1. Algoritma EM menunjukkan kinerja yang baik dalam menemukan nilai parameter distribusi mixture untuk kasus distribusi normal yang merupakan distribusi kontinu dengan diberikan sembarang nilai inisialisasi proporsi,

(18)

banyaknya jumlah data atau n, nilai toleransi kriteria berhenti, nilai , , , dan yang berbeda-beda dimana nilai proporsi estimasi yang dihasilkan mendekati nilai proporsi eksak serta memenuhi sifat-sifat estimator yang baik.

Pengaruh yang signifikan hanya terlihat pada kecepatan iterasi atau kecepatan kekonvergenan yang beragam dalam menemukan nilai parameter proporsi yang ingin diestimasi.

2. Algoritma EM menunjukkan kinerja yang baik dalam menemukan nilai parameter distribusi mixture untuk kasus distribusi poisson yang merupakan distribusi diskrit dengan diberikan sembarang nilai inisialisasi proporsi, banyaknya jumlah data atau n, nilai toleransi kriteria berhenti, nilai dan yang berbeda-beda dimana nilai proporsi estimasi yang dihasilkan mendekati nilai proporsi eksak serta memenuhi sifat-sifat estimator yang baik. Pengaruh yang signifikan hanya terlihat pada kecepatan iterasi atau kecepatan kekonvergenan yang beragam dalam menemukan nilai parameter proporsi yang ingin diestimasi

(19)

D

AFTAR

P

USTAKA

[1] Bain, L., & Engelhardt. 1992. Introduction to Probability and Mathematical Statistics (2 ed.). California, USA : Duxbury Press.

[2] DeGroot, M. H. &Schervish, M. J. 2012. Probability and Statistics (4 ed.). Addison- Wesley.

[3] Dempster, A. P., Laird, N. M., & Rubin, D. B. 1977. Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society B, 39 (1), 1-38.

[4] Gelman, A, Carlin, J.B, Stren, H.S, dan Rubin, D.B. (1995). Bayesian Analysis Theory and Methods. New York : Springer.

[5] Hogg, R. V., McKean J. W., & Craig, A. T. 2005. Introduction to Mathematical Statistics (6 ed.). United States of America : Pearson Education.

[6] Marin, J.M, Mengersen, K, dan Robert, C.P. 2005. Bayesian Modelling and Inference on Mixtures of Distribution. Handbook of Statistics. Vol. 25, hal 50.

[7] McLachlan, G.J. and Basford, K.E. (1988). Mixture Models: Inference and Applications to Clustering. New York: Marcel Dekker.

[8] McLahlan, G. J., & Krishnan, T. 2008. The EM Algorithm and Extensions (2 ed.).United States of America : John Wiley & Sons.