Model regresi poisson bivariat untuk memprediksi peringkat klub sepak bola - USD Repository

(1)

i

MODEL REGRESI POISSON BIVARIAT

UNTUK MEMPREDIKSI PERINGKAT KLUB SEPAK BOLA

SKRIPSI

Diajukan untuk Memenuhi Salah Satu Syarat

Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Oleh :

Arga Sari Ardhi Rahayu NIM : 103114002

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA

FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA

YOGYAKARTA

(2)

(3)

(4)

iv

HALAMAN PERSEMBAHAN

Karya ini sebagai bukti kasih setia Tuhan Yesus dalam hidupku.

Segala perkara dapat kutanggung di dalam Dia yang memberi kekuatan kepadaku. ( Filipi 4: 13 )

….KAKI yang akan berjalan lebih jauh dari biasanya, TANGAN yang akan berbuat lebih banyak dari biasanya, MATA yang akan menatap lebih lama dari biasanya, LEHER yang akan lebih sering melihat ke atas, lapisan TEKAD yang 1000 kali lebih keras dari baja, HATI yang akan bekerja lebih keras dari biasanya,

serta MULUT yang akan selalu berdoa….. ( 5 cm )

Karya ini aku persembahkan untuk :

Orang-orang terkasih: bapak, ibu, Milano, dan Tian

Orang-orang terhebat: sahabat-sahabat matematika 2010

(5)

(6)

vi ABSTRAK

Arga Sari Ardhi Rahayu. 2014. Model Regresi Poisson Bivariat untuk Memprediksi Peringkat Klub Sepak Bola. Skripsi. Program Studi Matematika, Jurusan Matematika, Fakultas Sains dan Teknologi, Universitas Sanata Dharma, Yogyakarta.

Topik yang dibahas dalam skripsi ini adalah aplikasi model regresi Poisson bivariat dalam sepak bola. Hasil pertandingan sepak bola tidak mudah untuk diketahui secara pasti, sehingga membuat para penggemar sepak bola lebih sering hanya menebak-nebak tim mana yang akan menang dan berada di peringkat teratas. Namun, dalam proses memprediksi peringkat dapat digunakan model regresi Poisson bivariat, sebagai berikut :

untuk i = 1,2,…,n dimana i adalah banyaknya percobaan atau pertandingan, menyatakan banyaknya gol yang dicetak sebagai tim tuan rumah, menyatakan banyaknya kemasukan gol yang dialami sebagai klub tamu, menyatakan banyaknya gol yang dicetak sebagai klub tamu, menyatakan banyaknya kemasukan gol yang dialami sebagai klub tuan rumah, dan menyatakan total poin sebagai klub tuan rumah dan klub tamu, dan

menyatakan rata-rata, merupakan parameter konstan, dan merupakan parameter home effect ( HE ).

Untuk menduga parameter regresi, digunakan metode kemungkinan maksimum dan diselesaikan dengan metode Newton. Persamaan parameter yang diselesaikan menggunakan metode Newton, yaitu

di mana t = 0,1,2,…; j = 1,2; merupakan vektor gradien dan merupakan matriks Hessian.

(7)

vii ABSTRACT

Arga Sari Ardhi Rahayu. 2014. Bivariate Poisson Regression Model for Predicting Football Club Rating. A Thesis. Mathematics Study Program, Departement of Mathematics, Faculty of Science and Technology, Sanata Dharma University, Yogyakarta.

The topic that is covered in this thesis is the application of bivariate Poisson regression models in football. It is not easy to know the result of a football match; therefore, it makes the football fans only guess which club will win and be on the top rank. However, the process can be used to predict ratings bivariate Poisson regression model, as follows:

for i = 1,2,…,n where i is the number of trials or the matches, is the number of goals scored by the home club, is a number of experienced club conceded guest, is a number of goals scored by the guest club, is a number of goals conceded experienced by the home club, and is the total point of the home and the guest club, and is a mean, is a constant parameter, and

is the home effect parameter ( HE ).

The regression parameters is estimated by using the maximum likelihood method and it would be solved by Newton’s method. The equation parameters that were solved by using Newton’s method:

where t = 0,1,2,…; j = 1,2; is a gradient vector, and is a Hessian matrix.

(8)

viii

KATA PENGANTAR

Puji dan syukur penulis panjatkan kepada Tuhan Yesus Kristus yang telah

melimpahkan berkat dan kasihNya sehingga penulis dapat menyelesaikan skripsi

ini dengan baik.

Dalam penulisan skripsi ini penulis mendapatkan bantuan baik moril

maupun materiil dari berbagai pihak. Oleh karena itu, penulis ingin mengucapkan

terima kasih kepada :

1. YG. Hartono, S.Si., M.Sc., Ph.D, selaku Ketua Program Studi

Matematika.

2. Ir. Ig. Aris Dwiatmoko, M.Sc., selaku dosen pembimbing skripsi dan

pembimbing akademik yang telah meluangkan banyak waktu dan

membimbing penulis dengan penuh kesabaran.

3. Bapak, Ibu, dan Romo, dosen-dosen yang telah memberikan ilmu yang

berguna kepada penulis.

4. Kedua orang tua, Bapak Sukardi dan Ibu Tri Rahayu, yang selalu

mendukung penulis dengan doa, semangat, dan materi.

5. Milano Yuda Pramuktya (adik) dan Kristian Wijanarko yang selalu

memberikan canda tawa, semangat, dan doa.

6. Astri, Celly, Ayu, Tika, Ratri, Yohan, Pandu, Roy, Marsel, Yosi, Dini,

Agnes, Sari, dan Leni, terima kasih untuk canda tawa, kebersamaan,

(9)

ix

7. Teman-teman sepelayanan GKJ Wonosari yang senantiasa memberikan

doa dan semangatnya.

8. Semua pihak yang telah ikut membantu penulis dalam menyelesaikan

skripsi ini.

Penulis menyadari bahwa skripsi ini masih jauh dari sempurna. Oleh karena

itu, penulis mengharapkan kritik dan saran yang dapat membangun serta

menyempurnakan skripsi ini. Akhirnya, penulis berharap semoga skripsi ini dapat

memberikan wawasan dan pengetahuan bagi pembaca.

Yogyakarta, 4 Agustus 2014

(10)

(11)

xi DAFTAR ISI

Halaman

HALAMAN JUDUL ... i

HALAMAN PERSETUJUAN PEMBIMBING ... ii

HALAMAN PENGESAHAN ... iii

HALAMAN PERSEMBAHAN ... iv

PERNYATAAN KEASLIAN KARYA ... v

ABSTRAK ... vi

ABSTRACT ... vii

KATA PENGANTAR ... viii

PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH ... x

DAFTAR ISI ... xi

DAFTAR TABEL ... xiii

DAFTAR LAMPIRAN ... xv

BAB I PENDAHULUAN ... 1

A. Latar Belakang ... 1

B. Rumusan Masalah ... 7

C. Batasan Masalah ... 7

D. Tujuan Penulisan ... 7

E. Metode Penulisan ... 8

F. Manfaat Penulisan ... 8

G. Sistematika Penulisan ... 8

BAB II DASAR TEORI PROBABILISTAS DAN REGRESI ... 10

(12)

xii

B. Distribusi Probabilitas Bersama ... 13

C. Distribusi Poisson ... 18

D. Metode Kemungkinan Maksimum (Maximum Likelihood Estimation) ... 20

E. Analisis Regresi ... 22

1. Model Regresi Linear ... 23

2. Penduga Parameter Regresi ... 25

F. Model Regresi Poisson ... 27

1. Penduga Parameter Regresi Poisson ... 29

G. Metode Newton ... 33

BAB III MODEL REGRESI POISSON BIVARIAT ... 49

A. Model Regresi Poisson Bivariat ... 49

B. Penduga Parameter Regresi Poisson Bivariat ... 50

BAB IV APLIKASI MODEL REGRESI POISSON BIVARIAT UNTUK MEMPREDIKSI PERINGKAT KLUB SEPAK BOLA ... 61

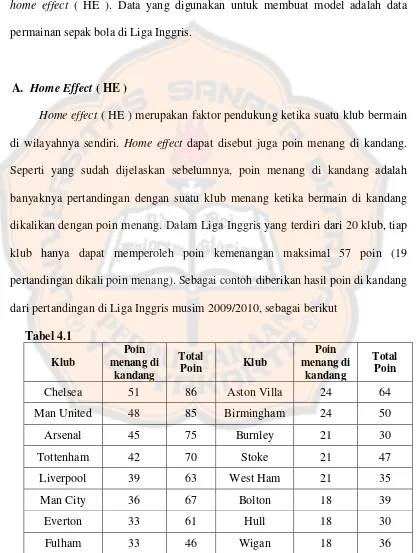
A. Home Effect ... 68

B. Aplikasi Model Regresi Poisson Bivariat untuk Memprediksi Peringkat Klub Sepak Bola ... 69

BAB V PENUTUP ... 89

A. Kesimpulan ... 89

B. Saran ... 91

(13)

xiii

DAFTAR TABEL

Halaman

Tabel 3.2 Iterasi Contoh Penerapan Penduga Parameter Regresi Poisson

Bivariat ... 58

Tabel 3.3 Iterasi Contoh Penerapan Penduga Parameter Regresi Poisson

Bivariat ... 59

Tabel 4.1 Contoh Data Hasil Pertandingan Sepak Bola ... 68

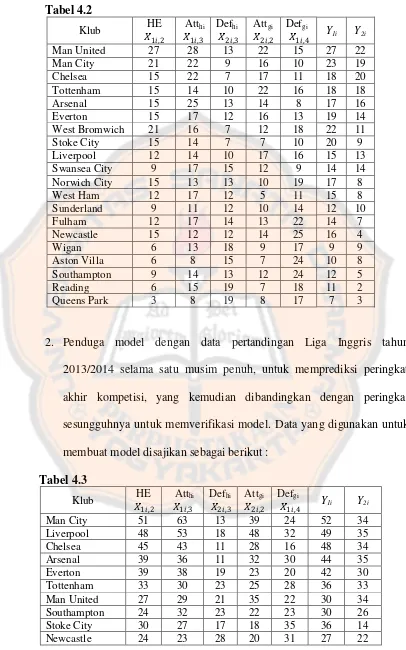
Tabel 4.2 Data Hasil Pertandingan Sepak Bola di Liga Inggris Musim

Pertama Tahun 2012/2013 ... 72

Tabel 4.3 Data Hasil Pertandingan Sepak Bola di Liga Inggris Tahun

2013/2014 ... 72

Tabel 4.4 Data Hasil Pertandingan Sepak Bola di Liga Inggris Musim

Pertama Tahun 2013/2014 ... 73

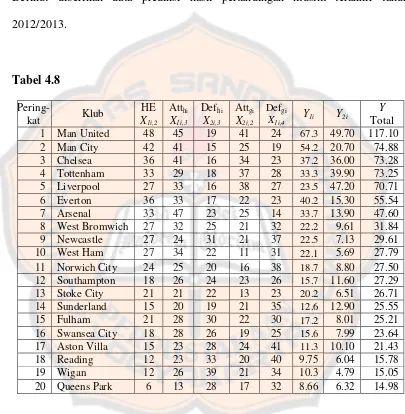
Tabel 4.8 Data Prediksi Hasil Pertandingan Musim Terakhir Tahun

2012/2013 ... 77

Tabel 4.9 Data Nyata Hasil Pertandingan Musim Terakhir tahun

2012/2013 ... 77

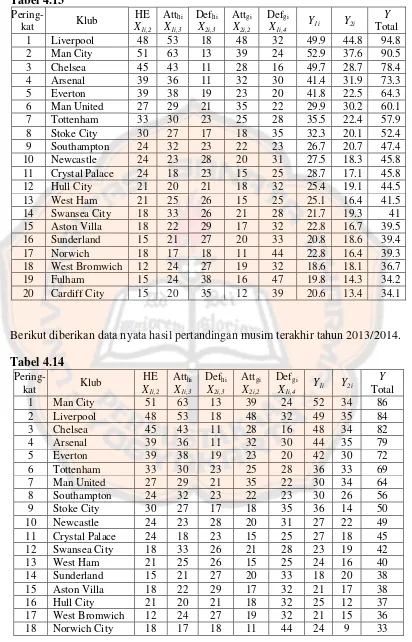
Tabel 4.13 Data Prediksi Hasil Pertandingan Akhir Kompetisi Tahun

2013/2014 ... 82

Tabel 4.14 Data Nyata Hasil Pertandingan Akhir Kompetisi Tahun

(14)

xiv

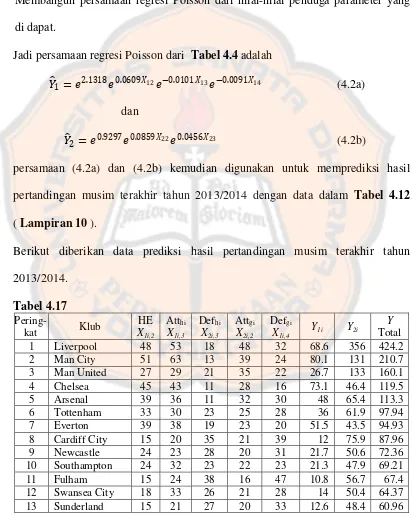
Tabel 4.17 Data Prediksi Hasil Pertandingan Musim Terakhir Tahun

2013/2014 ... 86

Tabel 4.18 Data Nyata Hasil Pertandingan Musim Terakhir Tahun

(15)

xv DAFTAR LAMPIRAN

Halaman

Lampiran 1 Uji Sampel Tunggal Kolmogorov-Smirnov ... 93

Lampiran 2 Tabel 3.1 Contoh Data ... 98

Lampiran 3 Uji Distribusi Poisson Tabel 3.1 Menggunakan SPSS ... 99

Lampiran 4 Program Matlab untuk Menduga Parameter Regresi

Poisson Bivariat Tabel 3.1 ... 100

Lampiran 5 Uji Distribusi Poisson Tabel 4.2, Tabel 4.3, dan Tabel 4.4

Menggunakan SPSS ... 102

Lampiran 6 Program Matlab untuk Menduga Parameter Regresi

Poisson Bivariat Data Hasil Pertandingan Sepak Bola di

Liga Inggris ... 104

Lampiran 7 Tabel 4.5 dan Tabel 4.6 Iterasi Data Hasil Pertandingan

Sepak Bola untuk Menduga Parameter Regresi Poisson

Bivariat ... 106

Lampiran 8 Tabel 4.7 Data Hasil Pertandingan Sepak Bola Musim

Terakhir Tahun 2012/2013 ... 108

Bivariat ... 109

Lampiran 10 Tabel 4.12 Data Hasil Pertandingan Sepak Bola Musim

(16)

xvi

(17)

1 BAB I PENDAHULUAN

A. Latar Belakang Masalah

Sepak bola merupakan olah raga yang sangat populer di dunia, karena

permainan sepak bola mudah dilakukan dan peraturan permainannya cukup

sederhana dibandingkan dengan olah raga lainnya. Karena sangat populer dan

diminati banyak orang, maka dibentuklah organisasi sepak bola dunia bernama

Federation of International Football Association ( FIFA ) yang beranggotakan

negara-negara di seluruh dunia. FIFA berhak membuat peraturan-peraturan yang

harus dipatuhi oleh negara anggota FIFA agar pertandingan sepak bola dapat

berjalan dengan tertib. Salah satu kesepakatan yang dibuat FIFA adalah dalam

menentukan poin saat menang, kalah, dan seri. Jika menang akan mendapat 3 poin,

seri mendapat 1 poin, dan kalah mendapat 0 poin. FIFA juga membuat

kesepakatan tentang pertandingan kandang dan tandang dalam sebuah kompetisi,

misalnya dalam Liga Inggris juga menggunakan sistem kandang dan tandang.

Tiap negara mempunyai divisi yang berbeda-beda, karena jumlah klub yang

dimiliki tiap negara tidaklah sama. Divisi adalah tingkatan dalam pertandingan

sepak bola. Setiap klub di tiap divisi berusaha untuk meningkatkan kualitas

permainan agar mampu mencapai divisi tertinggi, misalnya dalam Liga Inggris,

merupakan liga paling atas di negara Inggris. Tiap klub yang berada di bawah liga

utama di suatu negara, akan berlomba-lomba untuk mencapai peringkat teratas di

liga tersebut agar di musim kompetisi berikutnya dapat dipromosikan ke dalam

(18)

liga utama berlomba-lomba untuk mencapai peringkat tiga terbaik, agar dapat

dipromosikan ke liga utama untuk menggantikan klub-klub yang terdegradasi. Ini

berarti tidak semua klub dapat masuk dalam liga utama, hanya klub yang memiliki

peringkat tinggi yang dapat bertanding di liga utama.

Saat ini, cara memeringkat klub sepak bola hanya didasarkan pada jumlah

poin yang didapat dari klub-klub yang bertanding. Jika suatu klub menang dalam

suatu kompetisi, maka klub tersebut akan mendapat poin 3, jika kalah akan

mendapat poin 0, dan jika seri akan mendapat poin 1. Dari poin tersebut biasanya

dibuat peringkat agar dapat diketahui posisi klub tersebut dibanding dengan

klub-klub lainnya.

Kata “peringkat” menurut Kamus Besar Bahasa Indonesia (KBBI) berarti

tingkat, pangkat, sedangkan “pemeringkatan” berasal dari kata “peringkat” yang

mendapat imbuhan pe-an yang berarti proses memeringkat. Secara umum,

pemeringkatan dapat digunakan untuk mengetahui juara dalam suatu kompetisi

dan mengukur kualitas klub yang bersangkutan, selain itu klub yang mendapat

peringkat terbaik juga akan memperoleh keuntungan finansial.

Dalam permainan sepak bola, pemeringkatan memiliki manfaat yang cukup

besar. Misalnya, jika sebuah klub mengikuti kompetisi di divisi utama dan dapat

berada di peringkat teratas, maka klub tersebut berhak untuk mengikuti kompetisi

yang lebih besar dari kompetisi sebelumnya, sehingga rating klub tersebut akan

naik.

Dari manfaat tersebut, tidak heran jika memprediksi peringkat dalam

(19)

untuk dapat masuk dalam liga yang lebih besar, namun peringkat yang dimiliki

tidak memungkinkan klub tersebut untuk mengambil bagian dalam liga tersebut,

maka klub tersebut dapat mengubah strategi atau mengambil tindakan lain agar

klub tersebut dapat meraih poin yang ditargetkan sehingga peringkat klub itu

dapat naik.

Adapun salah satu contoh konkrit yang berkaitan dengan pemeringkatan

adalah sebagai berikut, di pertandingan Liga Inggris musim 2012/2013 ada 20

klub yang berada di divisi utama.

POS Klub P W D L GF GA GD PTS

1 Manchester United 38 28 5 5 86 43 43 89

2 Manchester City 38 23 9 6 66 34 32 78

3 Chelsea 38 22 9 7 75 39 36 75

4 Arsenal 38 21 10 7 72 37 35 73

5 Tottenham Hotspur 38 21 9 8 66 46 20 72

6 Everton 38 16 15 7 55 40 15 63

7 Liverpool 38 16 13 9 71 43 28 61

8 West Bromwich 38 14 7 17 53 57 -4 49

9 Swansea City 38 11 13 14 47 51 -4 46

10 West Ham United 38 12 10 16 45 53 -8 46

11 Norwich City 38 10 14 14 41 58 -17 44

12 Fulham 38 11 10 17 50 60 -10 43

13 Stoke City 38 9 15 14 34 45 -11 42

14 Southampton 38 9 14 15 49 60 -11 41

15 Aston Villa 38 10 11 17 47 69 -22 41

16 Newcastle United 38 11 8 19 45 68 -23 41

17 Sunderland 38 9 12 17 41 54 -13 39

18 Wigan Athletic 38 9 9 20 47 73 -26 36

19 Reading 38 6 10 22 43 73 -30 28

20 Queens Park Rangers 38 4 13 21 30 60 -30 25 sumber :

http://www.premierleague.com/en-gb/matchday/league-table.html?season=2012-2013&month=MAY&timelineView=date&toDate=1368918000000&tableView=CURRENT_STANDINGS

Keterangan:  POS: peringkat

 P : jumlah pertandingan  W : menang

(20)

 D : seri  L : kalah

 PTS: total poin

Wigan, Reading dan QPR adalah tiga klub terbawah di divisi utama, maka

tiga klub paling bawah itu akan terdegradasi. Dan tiga klub yang berada di bawah

liga utama inggris, seperti Cardiff, Hullcity, dan Crystal Palace akan

dipromosikan ke divisi utama Liga Inggris.

Hasil dari pertandingan sepak bola sampai saat ini belum dapat diketahui

secara pasti, sehingga para penggemar sepak bola lebih sering hanya

menebak-nebak klub mana yang akan menang di antara kedua klub yang bertanding. Secara

umum, ada dua cara memeringkat, yaitu memeringkat secara intuitif dan

memeringkat menggunakan data. Memeringkat secara intuitif adalah menetapkan

peringkat yang diperoleh dari feeling, menebak-nebak, atau bahkan berdasarkan

keegoisan masing-masing orang yang menjadi penggemar dari klub yang akan

bertanding dalam memprediksi hasil pertandingan di suatu kompetisi. Sedangkan

memeringkat dengan data adalah menetapkan peringkat yang diperoleh dengan

memprediksi hasil pertandingan sebelumnya. Memprediksi hasil pertandingan

sepak bola cukup sulit, karena perlu menentukan nilai kemungkinan yang tepat,

untuk itu diperlukan suatu model matematika untuk menyelesaikan permasalahan

tersebut.

Dalam memodelkan permasalahan tersebut diperlukan pengamatan hasil

pertandingan. Saat mengamati hasil pertandingan suatu klub, banyaknya gol yang

didapat oleh klub tersebut tidak tergantung dengan gol yang telah diraih di

(21)

pertandingan, maka peluang klub tersebut untuk mencetak gol semakin besar.

Mempertimbangkan hal-hal tersebut maka data yang didapat dari hasil

pertandingan memiliki ciri yang sama dengan ciri-ciri percobaan Poisson.

Percobaan Poisson adalah percobaan yang menghasilkan nilai-nilai bagi

suatu peubah acak Y, yaitu banyaknya hasil percobaan yang terjadi selama suatu

selang waktu tertentu. Adapun ciri-ciri percobaan Poisson, yaitu

1. Kejadian satu peristiwa dengan peristiwa lain pada selang waktu

tertentu adalah independen. Dalam pertandingan sepak bola, poin

yang didapat dalam interval 15-21 dalam total poin tidak tergantung

pada poin dalam interval 0 – 3 dalam total poin.

2. Suatu peristiwa dapat terjadi secara acak dan pada selang waktu

tertentu. Dalam suatu kompetisi sepak bola, kemungkinan terjadinya

menang ( 3 poin ), kalah ( 0 poin ), atau seri ( 1 poin ) hanya pada

interval 0-57 dalam total poin ( 19 kali pertandingan ) dan belum

dapat diprediksi kapan kemungkinan itu terjadi.

3. Peluang kejadian suatu peristiwa sebanding dengan panjang selang

waktu dan luas tempat peristiwa terjadi. Dalam sepak bola, peluang

terjadinya menang ( 3 poin ), kalah ( 0 poin ), atau seri ( 1 poin ) pada

selang 0-36 dalam total poin lebih besar dari selang 48-57 dalam total

poin.

Karena kemiripan sifat hasil pertandingan sepak bola dengan sifat

percobaan Poisson, maka proses memeringkat dapat didekati dengan distribusi

(22)

Distribusi Poisson menjadi salah satu alat untuk memprediksi hasil dalam

suatu pertandingan sepak bola. Distribusi tersebut digunakan untuk mengetahui

peluang suatu kejadian acak pada selang waktu tertentu. Peluang banyaknya gol

yang akan diciptakan oleh masing-masing klub dapat ditentukan menggunakan

distribusi Poisson. Selain itu, distribusi Poisson dapat digunakan untuk

memprediksi peringkat klub dalam suatu pertandingan. Namun, dalam skripsi ini

hanya akan dibahas tentang distribusi Poisson untuk memprediksi peringkat klub

sepak bola. Distribusi Poisson diklasifikasikan menjadi dua, yaitu distribusi

Poisson univariat dan distribusi Poisson multivariat. Pengklasifikasian ini

didasarkan pada banyaknya variabel tak bebas yang digunakan.

Dalam memodelkan hasil pertandingan, akan digunakan dua variabel tak

bebas, yaitu Y1 yang menyatakan total poin sebagai klub tuan rumah dan Y2

menyatakan total poin sebagai klub tamu, sehingga distribusi Poisson yang

digunakan adalah distribusi Poisson bivariat. Proses untuk mendapatkan peringkat

klub sepak bola didapat dari membuat model regresi Poisson.

Model regresi adalah model hubungan antara variabel yang mengikuti suatu

distribusi tertentu. Sedangkan model regresi Poisson adalah model regresi yang

variabel tak bebasnya mengikuti distribusi Poisson. Dengan asumsi variabel tak

bebas dalam konteks sepak bola ini mengikuti distribusi Poisson bivariat, maka

untuk memprediksi peringkat menggunakan model regresi Poisson bivariat.

Peringkat klub sepak bola dapat diprediksi dengan menghitung total poin

(23)

satu musim dan dituangkan dalam bentuk tabel, kemudian digunakan model

regresi Poisson bivariat untuk menyelesaikannya.

A. Rumusan Masalah

Pokok permasalahan yang akan dibahas dalam tulisan ini yaitu :

1. Apa yang dimaksud dengan regresi Poisson bivariat ?

2. Bagaimana memprediksi peringkat klub sepak bola menggunakan

model regresi Poisson bivariat ?

B. Batasan Masalah

1. Dalam skripsi ini, penulis akan membahas model regresi Poisson bivariat.

2. Dasar – dasar teori yang dibahas hanya yang berkaitan langsung dengan

model regresi Poisson bivariat.

3. Dalam skripsi ini hanya akan dibahas tentang distribusi Poisson untuk

memprediksi peringkat klub sepak bola.

4. Data yang digunakan adalah data pertandingan sepak bola di Liga Inggris.

C. Tujuan Penulisan

Tujuan yang akan dicapai dalam tulisan ini adalah

1. Memahami model regresi Poisson bivariat dan cara mendapatkan

parameter-parameternya.

2. Memperoleh model regresi Poisson bivariat untuk memprediksi

(24)

D. Metode Penulisan

Metode penulisan yang digunakan penulis adalah metode studi

pustaka, yaitu dengan membaca referensi buku – buku pendukung dan jurnal

ilmiah yang berkaitan dengan model regresi Poisson bivariat untuk memprediksi

peringkat hasil sepak bola. Data diolah menggunakan software Matlab dan SPSS.

E. Manfaat Penulisan

Manfaat penulisan ini adalah untuk memperoleh pengetahuan tentang

regresi Poisson bivariat, membahas dasar-dasar teori yang terkain, dapat

menentukan parameter-parameter dari model regresi Poisson bivariat, serta dapat

memprediksi peringkat klub sepak bola menggunakan model regresi Poisson

bivariat.

F. Sistematika Penulisan

BAB I : PENDAHULUAN

Bab ini menjelaskan tentang latar belakang masalah, rumusan

masalah, batasan masalah, tujuan penulisan, metode penulisan,

manfaat penulisan, dan sistematika penulisan.

BAB II : DASAR TEORI PROBABILITAS DAN REGRESI

Bab ini menjelaskan tentang variabel random dan distribusi

probabilitas, distribusi probabilitas bersama, distribusi Poisson,

metode kemungkinan maksimum (MLE), analisis regresi, model

(25)

BAB III : MODEL REGRESI POISSON BIVARIAT

Bab ini menjelaskan tentang model regresi Poisson bivariat,

pendugaan parameter regresi Poisson bivariat.

BAB IV : APLIKASI MODEL REGRESI POISSON BIVARIAT UNTUK MEMPREDIKSI PERINGKAT KLUB SEPAK BOLA

Bab ini menjelaskan tentang home effect, aplikasi model regresi

Poisson bivariat untuk memprediksi peringkat klub sepak bola.

BAB V : PENUTUP

(26)

10

BAB II

DASAR TEORI PROBABILITAS DAN REGRESI

A. Variabel Random Teorema 2.1

Untuk setiap fungsi distribusi probabilitas diskret p(x), harus memenuhi :

1. p(x_i)0 , untuk setiap xi

2.



( )1

xi i x p

dengan i =1,2,…

Bukti :

1. Sifat p(x)0berasal dari fakta bahwa nilai fungsi probabilitas diskret

yang harus tidak negatif.

2. Nilai x₁,x₂,... menggambarkan semua kemungkinan nilai X, kejadian



X  x₁



X  x₂



...merupakan partisi lengkap dari ruang sampel, sehingga



 

  

i i

x x

i

i P X x

x

p( ) ( ) 1 ∎

Definisi 2.1

Misal X adalah variabel random diskret dengan fungsi probabilitas p(x). Maka

nilai harapan dari X , E(X), didefinisikan sebagai berikut :





x

xp

X

(27)

Definisi 2.2

Misal X adalah variabel random kontinu dengan fungsi densitas f(x), maka nilai

harapan dari X , E(X), didefinisikan sebagai berikut :





 

 xf x dx X

E( ) ( )

Teorema 2.2

Jika X variabel random dan c adalah konstanta, maka E(cX)cE(X).

Bukti :

Pembuktian untuk variabel random diskret.

) (cX

E =



 n

i

x cxp

1

) (

=



 n

i x xp c

1 ) (

= cE(X)

Pembuktian untuk variabel random kontinu.

) (cX

E =





 

dx x cxf( )

=





 

dx x xf c ( )

= cE(X) ∎

Definisi 2.3

Andaikan X variabel random dan g(x) adalah fungsi dari variabel random X ,

nilai harapan dari fungsi variabel random X yang dinotasikan dengan E



g

 

X



(28)

(i)



 





p dan nilai sigmanya konvergen absolut.

(ii)



 





f dan nilai integralnya ada.

Teorema 2.3

Pembuktian untuk variabel random diskret

   

Pembuktian untuk variabel random kontinu

(29)

=





 

dy y f y h dx x f x

g( ) ( ) ( ) ( )

= E



g

 

X



E

 

h

 

Y ∎

Definisi 2.4

Bila X adalah variabel random dengan nilai harapan E(X), variansi dari variabel

random X didefinisikan sebagai nilai harapan dari (X E(X))2. Sehingga

2 )] ( [

)

(X E X E X

Var  

Definisi 2.5

Misal X adalah variabel random diskret dengan fungsi probabilitas p(x)dan nilai

harapan E(X), maka







x

x p X E x X

Var( ) ( ( ))2 ( )

Definisi 2.6

Misal X adalah variabel random kontinu dengan fungsi densitas f(x)dan nilai

harapan E(X), maka





 



 x E X f x dx

X

Var( ) ( ( ))2 ( )

A. Distribusi Probabilitas Bersama

Di banyak aplikasi akan ditemukan lebih dari satu variabel random,

(30)

dianggap sebagai komponen dari sebuah vektor k-dimensi,



X X Xk



X  1, 2,..., ,yang mempunyai nilai x



x1,x2,...,xk



.

Definisi 2.7

Distribusi probabilitas bersama dari variabel random diskret berdimensi k ,



X X Xk



random dikatakan independen jika dan hanya jika

(31)

Definisi 2.10

Jika X1,X2,...,Xk adalah variabel random yang berdistribusi bersama, maka

fungsi distribusi probabilitas bersama dari X1,X2,...,X_kadalah

)

sedemikian sehingga fungsi distribusi kumulatifnya dapat dinyatakan dengan





_{  }





Akibat dari definisi di atas, fungsi densitas bersama dapat diperoleh dari

fungsi distribusi kumulatif melalui diferensiasi, yaitu :

(32)

 



_





Andaikan X₁dan X₂variabel random diskret dengan fungsi probabilitas bersama

(33)

Definisi 2.15

Andaikan X₁dan X₂variabel random diskret dengan fungsi probabilitas bersama

) , (x₁ x₂

p dan fungsi probabilitas marginal p₁(x₁) dan p₂(x₂) secara

berturut-turut :

(i) Fungsi probabilitas bersyarat dari X₁dengan diketahui X₂ x₂ adalah

sebagai berikut



_{ }



2 2

2 1,

x p

x x p

,p₂

 

x₂ 0

 ) | (x₁ x₂ p

0 ,selainnya

(ii) Fungsi probabilitas bersyarat dari X₂ dengan diketahui X₁  x₁ adalah

sebagai berikut



_{ }



1 1

2 1,

x p

x x p

,p₁

 

x₁ 0

 ) | (x₂ x₁ p

0 ,selainnya

Definisi 2.16

Andaikan variabel random X dan Yberdistribusi bersama, nilai harapan bersyarat

dari Y jika diketahui X x dinotasikan dengan E(Y |x) didefinisikan sebagai

berikut

(i) 



_

yyp y x X

Y

E( | ) ( | ) , jika X dan Y diskret dengan fungsi

(34)

(ii)





 

 yf y x dy X

Y

E( | ) ( | ) , jika X dan Y kontinu dengan fungsi densitas

bersyarat f(y|x).

B. Distribusi Poisson

Percobaan Poisson adalah percobaan yang menghasilkan nilai-nilai bagi

suatu variabel random Y, yaitu banyaknya hasil percobaan yang terjadi selama

suatu selang waktu tertentu atau di suatu daerah tertentu. Selang waktu tertentu

dapat berupa semenit, sehari, seminggu, sebulan, setahun, dan seterusnya.

Sedangkan daerah tertentu dapat berupa satu meter, satu meter kubik, dan

lain-lain.

Percobaan Poisson memiliki ciri-ciri sebagai berikut :

1. Kejadian satu peristiwa dengan peristiwa lain pada selang waktu

tertentu adalah independen.

2. Suatu peristiwa dapat terjadi secara acak dan pada selang waktu

tertentu.

3. Peluang kejadian suatu peristiwa sebanding dengan panjang selang

waktu dan luas tempat peristiwa terjadi.

Definisi 2.17

Variabel random diskret Y dikatakan berdistribusi probabilitas Poisson jika dan

hanya jika

,... 2 , 1 , 0 , ! )

(  e y

y y p

y 



(35)

Variabel Y yang menyatakan banyaknya hasil percobaan dalam suatu

percobaan Poisson disebut variabel random Poisson.

Teorema 2.4

Jika Y adalah variabel berdistribusi Poisson dengan parameter , maka



 E(Y) dan 2 V(Y)

Bukti :

(i) Bukti untuk nilai harapan

Dari definisi nilai harapan,

)

 adalah fungsi probabilitas untuk variabel

(36)

(ii) Bukti untuk variansi

Dari definisi variansi,





C. Metode Kemungkinan Maksimum (Maximum Likelihood Estimation) Metode kemungkinan maksimum (maximum likelihood estimation) adalah

metode yang digunakan untuk menentukan penduga yang memaksimumkan

fungsi kemungkinan. Ide dasar dari metode ini adalah mencari nilai parameter

(37)

suatu data yang terobservasi sebagai suatu penduga dari parameter yang tak

diketahui.

Definisi 2.18

Andaikan X₁,X₂,...,X_n adalah variabel random kontinu dan  adalah sebuah

vektor parameter dari X1,X2,...,Xn. Fungsi densitas gabungan dari X1,X2,...,Xn

dapat ditulis sebagai hasil kali dari fungsi densitas bersyarat sebagai berikut :



Bila X₁,X₂,...,X_nadalah variabel random yang memiliki fungsi densitas bersama

)

merupakan kemungkinan dari sebagai suatu fungsi dari x1,x2,...,xndidefinisikan





Logaritma dari fungsi kemungkinan (likelihood function), yang disebut

kemungkinan log (log-likelihood) didefinisikan sebagai berikut

(38)

Penduga maksimum likelihood  didapat dari turunan pertama fungsi log

likelihood kemudian menyamakan turunan pertama tersebut ke nol.

D. Analisis Regresi

Analisis regresi merupakan analisis untuk menjelaskan tentang hubungan

antara dua variabel atau lebih.

Dalam analisis regresi, dikenal dua jenis variabel, yaitu :

1) Variabel dependent ( variabel tak bebas ), yaitu variabel yang

dipengaruhi oleh variabel lainnya. Variabel dependent biasanya

dinotasikan dengan Y.

2) Variabel independent ( variabel bebas ), yaitu variabel yang tidak

dipengaruhi oleh variabel lainnya. Variabel independent biasanya

dinotasikan dengan X.

Analisis regresi bertujuan menganalisis hubungan antara Y dan X.

Dalam analisis regresi linear, ada beberapa asumsi yang harus dipenuhi.

Asumsi dalam analisis regresi linear adalah sebagai berikut :

1. Model regresi harus linear dalam parameter.

2. Nilai X tetap disetiap percobaan, dengan kata lain nilainya bersifat

nonstochastic.

3. Nilai i yang diharapkan adalah nol dan secara simbolik dinyatakan

dengan E



_i |X_i



0. 0

ln _

 



(39)

4. Variansi dari _i adalah sama atau bersifat homoskedastisitas, dan

secara simbolik dinyatakan dengan var





2

| 

i Xi  .

5. Tidak ada autokorelasi antara _i dan j pada setiap nilai Xi dan Xj.

Secara simbolik dinyatakan dengan

cov



_i,_j |X_i,X_j



E



_i |X_i





_j |X_j



0.

6. Tidak ada korelasi antara _i dan X_i.

7. Banyaknya observasi n harus lebih besar daripada banyaknya

parameter yang diduga.

8. Variabel X harus bervariasi.

9. Model regresi ditetapkan dengan tepat.

10. Tidak ada multikolinearitas sempurna antar variabel bebas.

1. Model Regresi Linear Definisi 2.21

Model regresi linear k-variabel yang meliputi variabel tak bebas Y dan k

variabel bebas X2,X3,...,Xkdapat ditulis sebagai berikut

i ki k i

i

i X X X

Y ₁₂ ₂ ₃ ₃ ...  _(2.1)

di mana :

i

Y = variabel tak bebas

1

 = intersep

j

(40)

ji

X = nilai variabel bebas ke-j pada pengamatan ke-i

i

 = galat (error)

i = 1,2,3,…,n

j = 2,3,…,k

n = ukuran populasi

Persamaan dalam Definisi 2.21 ,dapat dinyatakan dalam bentuk matriks menjadi

Matriks tersebut dapat dinyatakan sebagai berikut

y = Xβ + ε

matriks, yaitu :

a. Nilai harapan dari vektor galat ε adalah nol, sehingga E(ε) = 0, di

(41)

b. Vektor galat ε tidak berkorelasi dengan vektor galat ε’, tetapi memiliki

variansi yang sama.

E(ε ε’) =



n



n

E   

  



 1 2

2 1

   

 

   

 

Secara ringkas dapat dinyatakan dengan E(ε ε’) = σ2I, di mana ε’

adalah transpose dari vektor kolom ε dan I adalah matriks identitas

berordo



nn



.

c. Matriks X berordo



nk



.terdiri dari bilangan - bilangan tetap ( tak

stokastik ).

d. Matriks X mempunyai derajat kolom sama dengan k ( = banyaknya

kolom dalam X ), dan k lebih kecil dari n.

e. Vektor galat ε memiliki distribusi normal multivariat ε ~ N(0,σ2I).

2. Pendugaan Parameter Regresi

Parameter β dalam model regresi dapat diduga dengan salah satu

metode pendugaan yaitu metode penduga kemungkinan maksimum

(Maximun Likelihood Estimation). Misalkan dari persamaan model regresi

pada persamaan (2.1), Yi berdistribusi normal, dan karena asumsi bahwa galat

𝛆 berdistribisi normal, ε ~ N(0,σ2I), dengan E(ε)=0, rata-rata E(Y) =μ=Xβ,

dan var(𝛆)=σ2 ,sehingga fungsi probabilitas gabungan dari Y1,Y2,…,Yn dapat

(42)





_





f merupakan fungsi densitas

dari variabel yang berdistribusi normal, sehingga fungsi probabilitas

gabungannya menjadi

Untuk mendapatkan penduga kemungkinan maksimum dari β,

digunakan fungsi log-likelihood sebagai berikut :

(43)

= −𝑛

2𝑙𝑛 2𝜋𝜎

2₋ 1

2𝜎2 𝒀′− 𝜷′𝑿′ 𝒀 − 𝑿𝜷

= −𝑛

2𝑙𝑛 2𝜋𝜎

2₋ 1 2𝜎2 𝒀

′_{𝒀 − 𝒀}′_{𝑿𝜷 − 𝜷}′_𝑿′_𝒀₊_𝜷_′_𝑿_′_𝑿𝜷

= −𝑛

2𝑙𝑛 2𝜋𝜎

2₋ 1

2𝜎2 𝒀′𝒀 − 𝒀′𝑿𝜷 ′− 𝜷′𝑿′𝒀+𝜷′𝑿′𝑿𝜷

= −𝑛

2𝑙𝑛 2𝜋𝜎

2₋ 1

2𝜎2 𝒀′𝒀 − 𝜷′𝑿′𝒀 − 𝜷′𝑿′𝒀+𝜷′𝑿′𝑿𝜷

= −𝑛

2𝑙𝑛 2𝜋𝜎

2₋ 1 2𝜎2 𝒀

′_{𝒀 −}₂_𝜷′_𝑿′_𝒀₊_𝜷_′_𝑿_′_𝑿𝜷

Pendugaan untuk parameter 𝜷 adalah sebagai berikut

𝜕

𝜕𝜷ln𝐿 𝜷 = 0

𝜕 𝜕𝜷 −

𝑛

2𝑙𝑛 2𝜋𝜎

2₋ 1 2𝜎2 𝒀

′_{𝒀 −}₂_𝜷′_𝑿′_𝒀₊_𝜷_′_𝑿_′_𝑿𝜷_{= 0}

−₂_𝜎12 −2𝑿

′_𝒀_{+ 2}_𝜷_′_𝑿_′_𝑿_{= 0}

𝑿′𝒀 𝜎2

−

𝜷 𝑿′𝑿

𝜎2

= 0

−

𝜷 𝑿_𝜎2′𝑿

=

−

𝑿′𝒀

𝜎2

𝜷 𝑿′_𝑿 ₌_𝑿′_𝒀

𝜷 = 𝑿′𝑿 −1_𝑿′𝒀

E. Model Regresi Poisson

Model regresi Poisson merupakan regresi yang menggambarkan hubungan

antara variabel tak bebas (Y) dengan variabel bebas (X), dimana variabel tak bebas

(Y) bersifat diskret yang bernilai bulat tak negatif dan berdistribusi Poisson.

Sehingga dapat disimpulkan bahwa regresi Poisson terbentuk dari distribusi

(44)

diskret yang variabel tak bebasnya berdistribusi Poisson, yang memiliki rata-rata

(mean) dan variansi sama yaitu 0.

Bila diberikan variabel tak bebas Yi berdistribusi Poisson dengan k variabel

bebas X2,X3,...,Xk , persamaan regresi Yi dengan X2,X3,...,Xk dinyatakan

seperti persamaan (2.1), maka nilai harapan bersyarat Yi dengan X2i = x2i , X3i =

0

2

1       

  E X _i X _i x_i X_ki x_ki _kE X_ki X _i x_i X_ki x_ki

ki k i

i x x

x  



    

 ₁ ₂ ₂ ₃ ₃ ...

Dikarenakan Yi|Xki berdistribusi Poisson, maka nilai rata-ratanya E(Yi|Xki) =

ki k i

i x x

x  



₁ ₂ ₂  ₃ ₃ ... _{= λ h}_{arus tak negatif ( dalam interval (0,})),

padahal telah diketahui bahwa nilai regresi ₁₂x₂_i ₃x₃_i..._kx_ki tak

berhingga (,). Untuk itu, diperlukan fungsi penghubung ( link function ) g

yang dapat membuat memiliki nilai dalam interval (0,), yaitu dengan fungsi

penghubung logaritma (logarithmic link), sehingga



) (

g 1 2x2i 3x3i ...kxki

gmerupakan fungsi logaritma, sehingga model regresi Poisson menjadi

 

   x _i  x _i ..._kx_ki

(45)

atau dapat juga dinyatakan dengan



 exp (x β)

Definisi 2.22

Model regresi Poisson dinyatakan dalam bentuk



 ln x β

di mana  adalah rata-rata yang bergantung pada vektor variabel x dan vektor koefisien β.

Model regresi Poisson merupakan regresi non-linear yang termasuk

keluarga eksponensial.

1. Penduga Parameter Regresi Poisson

Parameter β dalam model regresi Poisson dapat diduga dengan salah

satu metode penduga yaitu metode penduga kemungkinan maksimum

(Maximun Likelihood Estimation).

Fungsi probabilitas bersyarat Y bila diberikan X = x untuk  0adalah

,... 2 , 1 , 0 , ! ) ; |

(  

 y y e x

y p

y



  di mana  exp (xβ), sehingga

p(y|x) =

exp(-exp(xβ))(exp(xβ)y

)

= exp(-exp(xβ))(exp(yxβ))

Fungsi probabilitas gabungannya sebagai berikut

p(y1,…,yn|x21,…,xki;β)= 𝑛_𝑖=1𝑝 𝑦_𝑖|𝒙_𝑘𝑖;𝜷

(46)

L(β) = 𝑒𝑥𝑝 −𝑒𝑥𝑝 𝒙𝒌𝒊_𝑦𝜷 𝑒𝑥𝑝 𝑦! 𝑖𝒙𝒌𝒊𝜷 𝑛

𝑖=1

Untuk mendapatkan penduga kemungkinan maksimum dari β,

digunakan fungsi log-likelihood sebagai berikut :

ln L(β) = ln 𝑛𝑖=1𝑝 𝑦𝑖|𝒙𝑘𝑖;𝜷

= ln 𝑒𝑥𝑝 −𝑒𝑥𝑝 𝒙𝒌𝒊𝜷 𝑒𝑥𝑝 𝑦𝑖𝒙𝒌𝒊𝜷

𝑦! 𝑛

𝑖=1

= ln _𝑖𝑛₌₁𝑒𝑥𝑝 −𝑒𝑥𝑝 𝒙_𝒌𝒊𝜷 +𝑙𝑛 _𝑖𝑛₌₁𝑒𝑥𝑝 𝑦_𝑖𝒙_𝒌𝒊𝜷 − 𝑙𝑛 𝑛_𝑖₌₁𝑦_𝑖!

= 𝑛𝑖=1−𝑒𝑥𝑝 𝒙𝒌𝒊𝜷 + 𝑦𝑖𝑛=1 𝑖𝒙𝒌𝒊𝜷 − 𝑛𝑖=1𝑙𝑛 𝑦𝑖!

= −𝑒𝑥𝑝 𝒙𝑛_𝑖₌₁ _𝒌𝒊𝜷 +𝑦_𝑖𝒙_𝒌𝒊𝜷 − 𝑙𝑛𝑦_𝑖! (2.2)

Memaksimalkan nilai untuk 𝜷, biasa dinotasikan dengan 𝜷 , dapat

ditentukan dari k turunan pertama dari fungsi log-likelihood dan menyama

dengankan nol.

Misal diberikan persamaan regresi Poisson dengan variabel sebanyak

k=2, maka



) (

g 12x2

 

1 2 2

ln    x

Sehingga  exp



₁₂x₂



Bila diketahui , 0,1,2,...

! )

; |

(  

 y y e x

y p

y



 

Maka,

 









! exp exp

exp 1 2 2 1 2 2

y

x y

x

(47)

=





 



untuk mendapatkan ₂



 , maka digunakan metode Newton.

Misal diberikan persamaan regresi Poisson dengan variabel sebanyak k =3,

(48)

(49)

Persamaan (2.2), (2.3), dan (2.4) bila dinyatakan dengan matriks, maka

Penduga parameter _{dari persamaan (2.2) dapat diperoleh dengan}

 

Karena persamaan (2.6) tidak linear, maka persamaan tersebut dapat

diselesaikan dengan pendekatan yang disebut metode numeris. Salah satu

metode numeris yang digunakan adalah metode Newton.

F. Metode Newton

Metode Newton adalah salah satu metode numeris yang digunakan untuk

(50)

Bila diketahui f C2

 

a,b. Misal 𝑥 ∈ 𝑎,𝑏 adalah aproksimasi untuk p

sedemikian hingga 𝑓′ 𝑥 ≠0 dan |𝑥 − 𝑝|‘kecil’. Polinomial Taylor berderajat 1

untuk 𝑓 𝑥 di sekitar 𝑥 dinyatakan sebagai berikut

𝑓 𝑥 = 𝑓 𝑥 + 𝑥 − 𝑥 𝑓′ 𝑥 + 𝑥−𝑥 2

2 𝑓′′ 𝜉 𝑥 (2.7)

di mana 𝜉 𝑥 merupakan variabel yang menyatakan suku sisa dari deret Taylor,

karena 𝑓 𝑝 = 0 dan x p , persamaan (2.7) menjadi

0 =𝑓 𝑥 + 𝑝 − 𝑥 𝑓′ 𝑥 + 𝑝 − 𝑥 2

2 𝑓′′ 𝜉 𝑝

Metode Newton sederhana dapat ditentukan dengan asumsi bahwa suku yang

memuat (𝑝 − 𝑥 )2 diabaikan, sehingga

0≈ 𝑓 𝑥 + 𝑝 − 𝑥 𝑓′ 𝑥 (2.8)

maka penyelesaian untuk p pada persamaan (2.8) adalah

𝑝 ≈ 𝑥 −_{𝑓′ 𝑥}𝑓 𝑥

bila didekati dengan titik awal p₀, maka menjadi







 

, '



0, 1

' ₁ 1

1

1  

 _

 

 f p n

p f

p f p

p _n

n n n

n

Misalkan diberikan dua persamaan tidak linear yang tidak diketahui dalam

variabel x₁dan x₂.



₁, ₂



0 1 x x 

f



₁, ₂



0 2 x x 

(51)

Kedua fungsi tersebut dapat diperluas ke dalam deret Taylor di sekitar titik

superscript (1) digunakan untuk menunjukkan banyaknya iterasi pendugaan.

Misalkan ruas kiri dari persamaan (2.9a) dan (2.9b) disama dengankan nol dan

dipangkas pada turunan kedua pada deret Taylor, sehingga menjadi

 

bila dinyatakan dalam bentuk matrik, persamaan (2.10a) dan (2.10b) menjadi

(52)

 

kemudian akar persamaan didapat dari rumus

 

Diberikan fungsi berdimensi n yang dinyatakan dalam bentuk matriks sebagai

berikut

memberikan kekonvergenan secara kuadratik untuk penyelesaian dari 𝑭 𝒙 =𝟎 ,

(53)

Definisi 2.24

Misal 𝑝_𝑛 _𝑛∞₌₀ konvergen ke p dan himpinan En = p – pn untuk . Jika konstanta

positif A ada, dan

lim_𝑛→∞ 𝑝−𝑝𝑛+1

𝑝−𝑝𝑛 2 = lim𝑛→∞

𝐸𝑛+1 𝐸𝑛 2 =𝐴

sehingga barisan tersebut dikatakan konvergen ke p dengan derajat

kekonvergenan 2 ( konvergen secara kuadratik ) dan A adalah konstanta eror

asimtotik.

Teorema 2.5

Misalkan 𝒑 adalah penyelesaian dari 𝑮 𝒙 =𝒙untuk fungsi 𝑮= 𝑔₁,𝑔₂,…,𝑔_𝑛 𝑇

yang memetakan ℝ𝑛 ke ℝ𝑛. Andaikan 𝛿 > 0 ada dengan

(i) 𝜕𝑔𝑖

𝜕𝑥𝑗 kontinu di 𝑁𝛿(𝒑) = 𝒙| 𝒙 − 𝒑 < 𝛿 , untuk setiap 𝑖= 1,2,…,𝑛

dan 𝑗= 1,2,…,𝑛 ;

(ii) 𝜕

2_𝑔 𝑖(𝒙)

(𝜕𝑥_𝑗𝜕𝑥_𝑘) kontinu, dan 𝜕2

𝑔_𝑖(𝒙)

(𝜕𝑥_𝑗𝜕𝑥_𝑘) ≤ 𝑀 untuk suatu konstanta M, saat

𝒙 ∈ 𝑁𝛿 , untuk setiap 𝑖= 1,2,…,𝑛, 𝑗 = 1,2,…,𝑛, dan 𝑘 = 1,2,…,𝑛 ;

(iii) 𝜕𝑔𝑖(𝒑)

𝜕𝑥𝑘

= 0

, untuk setiap 𝑖= 1,2,…,𝑛 dan 𝑘= 1,2,…,𝑛.

Maka ada 𝛿 ≤ 𝛿 sedemikian hingga barisan yang dibangkitkan oleh 𝒙(𝑘) ₌

𝑮(𝒙 𝑘−1 ) konvergen secara kuadratik ke 𝒑 untuk setiap pilihan 𝒙(0)_,dengan

syarat 𝒙(0)_{− 𝒑}_< _𝛿_{. Selain itu}

𝒙(𝑘)_{− 𝒑} ∞ ≤

𝑛2_𝑀 2 𝒙

(𝑘−1)_{− 𝒑} ∞ 2

(54)

Bukti :

Tanpa mengurangi perumuman bukti, diasumsikan 𝒙 = 𝑥_𝑦, 𝒑= 𝑝_𝑝1

2 , 𝑮 𝒙 =

𝑔1(𝑥,𝑦)

𝑔2(𝑥,𝑦) .

Ambil 0 < w < 1 dan 𝛿> 0 sedemikian hingga di 𝑁_𝛿(𝒑) berlaku ∇𝒈 𝒙 _∞ ≤ 𝑤,

dengan ∇𝒈 𝒙 =

𝑔1(𝑥,𝑦) 𝜕𝑥

𝑔1 (𝑥,𝑦) 𝜕𝑦 𝑔2(𝑥,𝑦)

𝜕𝑥

𝑔2 (𝑥,𝑦) 𝜕𝑦

= 𝑔1 𝑋(𝑥,𝑦) 𝑔1 𝑌(𝑥,𝑦)

𝑔2 𝑋(𝑥,𝑦) 𝑔2 𝑌(𝑥,𝑦) dan

𝜕2_𝑔 𝑖(𝒙)

(𝜕𝑥_𝑗𝜕𝑥_𝑘) kontinu untuk setiap 𝑖= 1,2 , 𝑗 = 1,2 , dan 𝑘 = 1,2 . Karena

∇𝒈 𝒙 ∞ ≤ 𝑤< 1, maka 𝒑𝑛 ∞𝑛=0 termuat di 𝑁𝛿(𝒑) dengan n adalah banyaknya

barisan. Sehingga, perluasan 𝒈 𝑥,𝑦 dalam polynomial Taylor untuk 𝑥,𝑦 ∈

𝑁𝛿(𝒑) adalah

𝑔1 𝑥,𝑦 = 𝑔1 𝑝1,𝑝2 +𝑔1 𝑋 𝑝1,𝑝2 𝑥 − 𝑝1 +𝑔1 𝑌 𝑝1,𝑝2 𝑦 − 𝑝2

+1

2! 𝑔1 𝑋𝑋 𝜉 (𝑥 − 𝑝1) 2_{+ 2}_𝑔

1 𝑋𝑌 𝜉 𝑥 − 𝑝1 𝑦 − 𝑝2 +𝑔 1 𝑌𝑌 𝜉 (𝑦 − 𝑝2)2

𝑔2 𝑥,𝑦 = 𝑔2 𝑝1,𝑝2 +𝑔2 𝑋 𝑝1,𝑝2 𝑥 − 𝑝1 +𝑔2 𝑌 𝑝1,𝑝2 𝑦 − 𝑝2

+1

2! 𝑔2 𝑋𝑋 𝜉 (𝑥 − 𝑝1) 2_{+ 2}_𝑔

2 𝑋𝑌 𝜉 𝑥 − 𝑝1 𝑦 − 𝑝2 +𝑔 2 𝑌𝑌 𝜉 (𝑦 − 𝑝2)2

di mana 𝜉 berada di antara 𝒙 dan 𝒑.

Bila 𝒈 𝒑 =𝒑 dan ∇𝒈 𝒑 =𝟎, maka

𝑔1 𝑥,𝑦 =𝑝1+ 1

2! 𝑔 1 𝑋𝑋 𝜉 (𝑥 − 𝑝1) 2_{+ 2}_𝑔

1 𝑋𝑌 𝜉 𝑥 − 𝑝1 𝑦 − 𝑝2

(55)

𝑔2 𝑥,𝑦 =𝑝2+

bila dinyatakan dalam bentuk matriks, menjadi

(56)

(57)

Untuk n variabel, menjadi

𝒙(𝑘)− 𝒑 _∞ ≤𝑛2

2 𝑴 𝒙

(𝑘−1)_{− 𝒑} ∞

2

,𝑘 ≥1 ∎

Andaikan 𝐴 𝒙 adalah matriks n x n dari fungsi di ℝ𝑛 ke ℝ pada persamaan

(2.11). Diasumsikan 𝐴 𝒙 tak singular mendekati penyelesaian 𝒑 dari 𝑭 𝒙 = 0

dan misalkan 𝑏_𝑖𝑗(𝒙) menyatakan elemen dari 𝐴 𝒙 −1_{di baris ke-}_i_{dan kolom ke-}_j_.

Karena 𝑮 𝒙 =𝒙 − 𝐴(𝒙)−1𝑭(𝒙), sehingga 𝑔𝑖 𝒙 =𝑥𝑖− 𝑛𝑗=1𝑏𝑖𝑗 𝒙 𝑓𝑗(𝒙) dan

𝜕𝑔𝑖

𝜕𝑥𝑘 𝒙 =

1− 𝑏_𝑖𝑗(𝒙)_𝜕𝑥𝜕𝑓𝑗

𝑘 𝒙 +

𝜕𝑏𝑖𝑗

𝜕𝑥𝑘 𝒙 𝑓𝑗(𝒙) ,𝑢𝑛𝑡𝑢𝑘𝑖 =𝑘

𝑛 𝑗=1

− 𝑏𝑖𝑗(𝒙)_𝜕𝑥𝜕𝑓𝑗

𝑘 𝒙 +

𝜕𝑏𝑖𝑗

𝜕𝑥𝑘 𝒙 𝑓𝑗(𝒙)

𝑛

𝑗=1 ,𝑢𝑛𝑡𝑢𝑘𝑖 ≠ 𝑘

Dalam Teorema 2.5 diketahui bahwa 𝜕𝑔𝑖(𝒑)

𝜕𝑥𝑘

= 0

, untuk setiap 𝑖=

1,2,…,𝑛 dan 𝑘 = 1,2,…,𝑛. Ini berarti untuk i = k,

0 = 1− 𝑏_𝑖𝑗(𝒑)_𝜕𝑥𝜕𝑓𝑗

𝑘𝑓𝑗(𝒑)

𝑛

𝑗=1 , sehingga

𝑏𝑖𝑗(𝒑)_𝜕𝑥𝜕𝑓𝑗

𝑘𝑓𝑗(𝒑)

𝑛

𝑗=1 = 1 (2.12)

ketika 𝑘 ≠ 𝑖,

0 =− 𝑏_𝑖𝑗(𝒑)_𝜕𝑥𝜕𝑓𝑗

𝑘𝑓𝑗(𝒑)

𝑛

𝑗=1 , sehingga

𝑏𝑖𝑗(𝒑)_𝜕𝑥𝜕𝑓𝑗

𝑘𝑓𝑗(𝒑)

𝑛

𝑗=1 = 0 (2.13)

(58)

𝐽 𝒙 = 𝜕𝑓1

𝜕𝑥1(𝒙) ⋯ 𝜕𝑓1 𝜕𝑥𝑛(𝒙)

⋮ ⋱ ⋮

𝜕𝑓𝑛

𝜕𝑥1(𝒙) ⋯ 𝜕𝑓𝑛

𝜕𝑥𝑛(𝒙)

(2.14)

dari persamaan (2.12) dan (2.13) menghendaki

𝐴 𝒑 −1_{𝐽 𝒑}₌ _𝐼_{, merupakan matriks identitas}

sehingga

𝐴 𝒑 = 𝐽 𝒑 .

Pilihan yang tepat untuk 𝐴 𝒙 adalah 𝐴 𝒙 =𝐽 𝒙 karena memenuhi

kondisi (iii) dalam Teorema 2.5. Fungsi G didefinisikan sebagai berikut

𝑮 𝒙 = 𝒙 − 𝐽 𝒙 −1𝑭(𝒙),

dan langkah iterasi fungsi berkembang dari pemilihan 𝒙 0 _{dan membangkitkan}

untuk 𝑘 ≥1,

𝒙(𝑘) ₌_{𝑮 𝒙} 𝑘−1 ₌_𝒙(𝑘−1)_{− 𝑱 𝒙} 𝑘−1 −1_{𝑭 𝒙} 𝑘−1

𝐽 𝑥 merupakan matriks Jacobi yang memuat turunan parsial dari persamaan tidak

linear.

Definisi 2.25

Metode Newton untuk sistem persamaan yang tidak linear didefinisikan sebagai

berikut

𝒙(𝑘) ₌_{𝑮 𝒙} 𝑘−1 ₌_𝒙(𝑘−1)_{− 𝑱 𝒙} 𝑘−1 −1_{𝑭 𝒙} 𝑘−1

(59)

Contoh 2.1

Diberikan dua persamaan tak linear sebagai berikut

0

Cari akar persamaan di atas!

Penyelesaian :

 Untuk persamaan pertama







   





 





 1



 Untuk persamaan kedua

(60)

misal   1 1

bila dinyatakan dalam bentuk matriks menjadi

(61)

 

Akar persamaan dapat diperoleh dari

 

(n-1)

)

Proses ini dilakukan berulang sampai 1 1

 n

x dan 2 1

 n

x konvergen ke suatu nilai.

Setelah melakukan 6 kali iterasi ternyata x₁dan x₂ konvergen ke 0,5000dan

8660 .

0 , seperti dinyatakan dalam tabel berikut

(62)

Bila Definisi 2.25 dikaitan dengan model regresi Poisson, maka 𝑭 𝒙 𝑘−1

diperoleh dengan metode Newton sebagai berikut

(63)

𝑦 − 𝑒𝑥𝑝 𝛽1+𝛽2𝑥2+𝛽3𝑥3 𝑥2

𝑦 − 𝑒𝑥𝑝 𝛽1+𝛽2𝑥2+𝛽3𝑥3 𝑥3

dengan k = 1,2,…

Untuk membahas tentang penduga bagi  , yaitu  , diperlukan definisi

matriks Hessian sebagai berikut

Definisi 2.25

Matriks Hessian merupakan matriks n x n yang berisi turunan parsial kedua dari

suatu fungsi. Misalkan f(x)adalah fungsi dengan n variabel yang turunan parsial

keduanya ada dan kontinu, maka matriks Hessian dari f adalah

 

metode Newton adalah sebagai berikut

𝛽 𝑡+1 = 𝛽 𝑡− 𝐻 𝛽 𝑡 −1

𝑔 𝛽 𝑡

dimana 𝑔 menyatakan gradien persamaan (2.6), H adalah matriks Hessian, yaitu

matriks turunan kedua dari fungsi log-likelihood, dan 𝛽 1 menyatakan nilai awal.

(64)

𝐻 𝜷 =𝜕

2_{𝑙𝑛𝐿 𝜷}

𝜕𝜷𝜕𝜷′

= 𝜕

𝜕𝜷 𝑦𝑛𝑖=1 𝑖− 𝑒𝑥𝑝 𝒙𝒌𝒊𝜷 𝒙𝒌𝒊

= − 𝑛_𝑖₌₁𝑒𝑥𝑝 𝒙_𝒌𝒊𝜷 𝒙_𝒌𝒊𝒙_𝒌𝒊′ (2.15)

Secara umum model regresi Poisson ada dua jenis, yaitu model regresi

Poisson univariat dan model regresi Poisson multivariat. Pengklasifikasian ini

didasarkan pada banyaknya variabel tak bebas yang digunakan. Pada skripsi ini

akan dibahas mengenai model regresi Poisson bivariat. Untuk menguji distribusi

Poisson digunakan uji sampel tunggal Kolmogorov-Smirnov yang terdapat pada

(65)

49

BAB III

MODEL REGRESI POISSON BIVARIAT

A. Model Regresi Poisson Bivariat

Bila diberikan dua variabel tak bebas Y₁_i dan Y₂_i berdistribusi Poisson

dengan variabel bebas X₁₁,X₁₂,...,X₁_k dan X₂₁,X₂₂,...,X₂_k , maka persamaan

regresinya dinyatakan sebagai berikut

 

i k ki i

i

i x x x

Y₁ ₀1  ₁₁₁₁ ₁₂₁₂... ₁ ₁ ₁ (3.1a)

 

i k ki i

i

i x x x

Y₂ ₀2  ₂₁₂₁ ₂₂₂₂... ₂ ₂ ₂ (3.1b)

di mana :

i = 1,2,…,n

j = 1,2

m = 1,2,…,k

ji

Y = variabel tak bebas ke-j pengamatan ke-i

 j

0

 = intersep

jm

 = koefisien regresi dari variabel bebas ke-m variabel tak bebas ke-j

jmi

x = nilai variabel bebas ke-m pada pengamatan ke-i

ji

 = galat

n = ukuran populasi

seperti pada pembahasan regresi Poisson di bab sebelumnya, dikarenakan

ki i X

Y₁ | ₁ dan Y₂_i |X₂_ki berdistribusi Poisson, maka nilai rata-ratanya





 

1 1 1 12

12 11 11 1 0 1

1i |X ki  x i x i ...xki k  Y

(66)

 

2 2 2 22

22 21 21 2

0   ...  

 x _i x _i  x _ki _k  harus tak negatif. Untuk itu diperlukan

fungsi penghubung ( link function ) g₁dan g₂ yaitu dengan fungsi penghubung

logaritma ( logarithmic link ), sehingga menjadi

 

k ki i

i x x

x

g₁ ₁ ₀1  ₁₁₁₁ ₁₂₁₂... ₁ ₁

 

k ki i

i x x

x

g₂ ₂ ₀ 2  ₂₁₂₁ ₂₂₂₂... ₂ ₂

g merupakan fungsi logaritma, sehingga model regresi Poisson bivariat menjadi

 

k ki i

i x x

x₁₁ ₁₁ ₁₂ ₁₂ ₁ ₁

1 0

1 ...

ln         

 

k ki i

i x x

x₂₁ ₂₁ ₂₂ ₂₂ ₂ ₂

2 0

2 ...

ln         

atau dapat juga dinyatakan dengan

𝜆1 = exp (𝒙𝟏𝜷1)

𝜆2 = exp (𝒙𝟐𝜷2)

Definisi 3.1

Model regresi Poisson bivariat adalah

𝑙𝑛 𝜆1 = 𝒙𝟏𝜷𝟏

𝑙𝑛 𝜆2 =𝒙𝟐𝜷𝟐

di mana  adalah rata-rata yang bergantung pada vektor variabel x dan vektor koefisien β.

A. Penduga Model Regresi Poisson Bivariat

Parameter β dalam model regresi Poisson bivariat dapat diduga dengan

(67)

Fungsi probabilitas bersyarat Yj bila diberikan Xj = xj untuk j 0adalah

Fungsi probabilitas gabungannya sebagai berikut

p(y11,…,y1n|x111,…,x1ki;β1)= 𝑛_𝑖=1𝑝 𝑦1𝑖|𝒙1𝑘𝑖;𝜷𝟏

Untuk mendapatkan penduga kemungkinan maksimum dari β, digunakan

fungsi log-likelihood sebagai berikut :