Pengantar Analisis dan Komputasi Metode Numerik

(1)

Numerik

4.1 Rasionalisasi

Persamaan Diferensial adalah sutu persamaan yang memuat turunan. Sebagai contoh berikut ini

y dx

dy dx

y d

  3 4 2

2

. Penyelesaian secara analitik dapat

dengan mudah dilakukan jika bentuk suatu persamaan diferensial berbentuk khusus atau sederhana. Bentuk-bentuk yang kompleks umumnya tidak dapat diselesaikan secara analitik. Cara numerik menjadi alternatif yang efektif dan efesien. Beberapa metode yang dapat diterapkan dalam penyelesaian persamaan diferensial secara numerik adalah metode Deret Taylor, Euler, Beda Hingga, Multi Step dan lainnya. Penyelesaian dari suatu persamaan diferensial adalah formula atau nilai dari fungsi asal y = f(x). Penyelesana secara analitik diperoleh berupa nilai y = f(x) dalam bentuk analitik. Sedangkan penyelesaian secara numerik berupan nilai y = f(x) dalam bentuk bilangan atau grafk.

4.2 Klasifiasi Persamaan Diferensial

Secara umum Persamaan Diferenail dapat dibedakan menjadi dua, yaitu persamaan diferensial biasa dan parsial. persamaan diferensial biasa merupakan persamaan diferensial yang hanya memuat satu variable

bebas. Sebagai contoh adalah y dx

dy dx

y d

 

3 4

2 2

.

Ripai, S.Pd., M.Si

BAB

4.

PERSAMAAN DIPERENSIAL

(2)

Numerik

Sedangkan persamaan diferensial parsial merupakan persamaan diferensial yang memuat lebih dari satu variable bebas. Sebagai contoh adalah

0 2 2 2 2 2

     

 _xy

y f x

f

Tingiatan atau orde dari Persamaan diferensial merupakan ukuran yang menyatakan turunan tertinggi yang ada pada suatu persamaan diferensial. Persamaan

Diferenail y

dx dy dx

y d

 

3 4

2 2

disebut berorde 2 (dua), karena dalam persamaan diferensial tersebut memuat paling tinggi turunan tingkat 2 (dua). Sedangkan

Persamaan 1

2 4

       

dx dy x d

y

d _{disebut berorde 4 (empat)}

karena dalam persamaan diferensial tersebut memuat paling tinggi turunan tingkat 4 (empat).

Derajat atau degree dari Persamaan Diferenail adalah pangkat tertinggi yang dimiliki oleh turunan tertinggi yang ada pada persamaan diferensial tersebut.

Persmaan diferensial y

dx dy dx

y d

 

3 4

2 2

disebut berderajat 1, karena pangkat tertinggi dari turunan tertinggi yang termuat dalam persamaan diferensial tersebut adalah 1 (satu). Sedangkan

3 2

2 3 3 4 2 2

                  

y dx

y d dx

y d

adalah disebut persamaan diferensial berderajat 2 (dua) karena pangkat tertinggi dari turunan tertinggi persamaan diferensial tersebut adalah 2 (dua).

Linieritas suatu persamaan diferensial adalah ukuran yang menyatakan ketergantungan dari variabel persamaan diferensila tersebut. persamaan diferensial

3 2

2 3 3 4 2 2

              

y dx

y d dx

y

(3)

Numerik

tertinggi dari variabelnya adalah 1 (satu). Sedangkan

persamaan diferensial 2 4 3

2 3 3 4 2 2

                  

y dx

y d dx

y d

disebut tidai linier, karena varibelnya memuat pangkat 4 (empat).

4.3 Masalah Nilai Awal ( Initial Value Problem ) Masalah nilai awal adalah suatu permasalahan persamaan diferensial yang memuat informasi tambahan dimana informasi tambahan itu memuat nilai variabel bebas yang sama.

Contoh :

y" = y + x +1 , y(0) = 0 , y’(0) = 0 y’ = y + x , y(0) = 0

4.4 Masalah Nilai Batas ( Bundary Value Problem ) Masalah nilai batas adalah persamaan diferensial yang memuat informasi tambahan dimana informasi tambahan itu memuat nilai variabel bebas yang tidak sama.

Contoh :

2 2

6 1

1

x y x y x

y   , y(1) = 1 dan y’(1.5) = -1 Bandingkan dengan :

y x y u x x u

     

 ₃ 2

dengan syarat awal ( initial condition ) u(x,0) = x2

4.5 Penyelesaian Numerii Persamaan Diferensial Biasa

Beberapa metode yang dapat digunakan untuk menyelesaikan persamaan diferensial biasa secara numerik adalah metode Euler, Multi Step dan Beda hingga.

4.5.1 Penyelesaian Diferensial Biasa Orde 1 (satu) 4.5.1.1 Metode Euler

Misalkan dimiliki fungsi y = f(x) dengan bentuk persamaan diferensial y’ = f(x,y) maka berdasarkan

(4)

Numerik

defnisi turunan fungsi beda maju tingkat pertama diperoleh formula metode Euler sebagai berikut:

h x f h x f x

f

h

) ( ) ( lim ) (

0

  



 (bentuk analitik)

0 , 1

  

  _h

h f f

f i i

i (bentuk numerik)

Karena y = f(x), maka

h y y y h

f f

f i i

i i i

i 1   1 ==> yi1  yi h yi

==> y_i₁ y_i h f(x_i,y_i)(karena y’=f(x,y)) )

, (

1 i i i

i y h f x y

y   disebut sebagai bentuk iteratif

metode Euler.

Teladan 4.1

Misalkan dimiliki Persamaan diferensial 2 0

  x y

dx dy

dengan y(0) = 2, maka tentukan nilai dari y(0.5) a) dengan secara numerik mengunakan metode Euler b) dengan cara analitik mengunakan metode integral

atau operator D

Solusi

a) Solusi numerik dengan metode Euler

Diketahui : PD. 2 ₀ _y _x2

dx dy y

x dx dy

     

Nilai awal y(0) = 2 ==> x0 = 0

dan y0 = 2

Ditanyakan : y(1,1) = …? ==> x = 1,2

a. Solusi Numerik

Jika h = 0.1, maka x=[0 0.1 0.2 0.3 0.4 0.5 0.5 0.7 0.8 0.9 1.0 1.1]. Persamaan Euler

) , (

1 i i i

i y h f x y

y   , maka

)

( 2

1 i i i

i y h y x

y   

y(0.1) = y1 = y0 + h(y0 – x02)

= 2 + 0.1(2-0.12_{) = 2.2}

y(0.2) = y2 = y1 + h(y1 – x12)

= 2.2 + 0.1(2.2 – 0.22_{) = 2.421}

y(0.3) = y3 = y2 + h(y2 – x22)

= 2.421 + 0.1 (2.421 – 0.32_{) = 2.6671}

(5)

Numerik

= 2.6671 + 0.1 (2.6671 – 0.42_{) = 2.9428}

y(0.5) = y5 = y4 + h(y4 – x42)

= 2.9428+ 0.1 (2.9428– 0.52_{) = 3.2531}

Jadi nilai y(0.5) = 3.2531

b. Solusi Analitik

2 2

2 _y _x _p₍_x₎ ₁_dan_q₍_x₎ _x

dx dy x

y dx dy

  

 

    

Maka  

_



 

e e vy vq x dx e x dx

v dx x ₍ ₎ x 2

Misal _u _x _du _xdx_dan_dv _ex_dx _v _ex    

 

 2 2

Akibatnya



_{ }



  

    

uv vdu x e e xdx

dx x

e x 2 2 x x₂



_



 

 x2e x ₂ xe xdx

Misal u = x ==> du = dx dan dv = e-x_{dx ==> v = -e}-x

) 1 (

2

 

  

 

   

     



xe xdx uv



vdu xe x



e xdx x e x e x e x x

ye-x _{= - (-x}2_e-x_{+ 2(-e}-x_(x+1)))

= e-x_(x2_{+ 2x + 2)}

y = x2_{+ 2x + 2}

Jadi y = x2_{+ 2x + 2}

Atau dengan cara lain mengunakan operator D

2 2

2 _x

dx dy y x y dx dy x y dx dy

        

2 ) 1

( D yx 



2



2

2 ₁ 1

1

x D D x

D

y    

  

 y = x2_{+ 2x + 2}

Jadi y = x2_{+ 2x + 2}

Pengujian apakah solusi analitik ini benar dilakukan sebagai berikut:

y = x2 _{+ 2x + 2} _ _₂_x_₂

dx dy





2 2



2



2 2 2



0

2

       

x y x x x x

dx dy

. Bentuk

0

2_ _

x y dx

dy _{sesuai dengan persamaan diferensial}

yang diberikan. Untuk x = 0, maka y(0) = 2 sesui dengan nilai awal yang diketahui. Jadi y = x2_{+ 2x + 2}

merupakan solusi analitik persamaan diferensial

(6)

Numerik

0

2_ _

x y dx

dy _{. Dengan demikian dapat diperoleh nilai}

sejati dari y(0.5) = (0.5)2_{+ 2(0.5) + 2 = 3.25.}

Kode komputasi metode Euler yang dapat digunakan untuk membandingkan solusi numerik dan analitik serat tingkat error relatif dari PD x2y0

dx

dy _.

h=0.1; x=[0:h:0.5]; y=2;

for i=1:length(x)-1

y(i+1)=y(i)+h*(y(i)+x(i)^2);

end

f=inline('x.^2+2.*x+2','x');

Tabel=[x;y;f(x);abs(100*(y-f(x))./f(x))]' xlswrite('hasil',Tabel)

plot(x,y,x,f(x)) grid on

x yNumerik yAnalitik Error Relatif

0 2 2 0 %

0.1 2.2 2.21 0.452488688 %

0.2 2.421 2.44 0.778688525 %

0.3 2.6671 2.69 0.851301115 %

(7)

Numerik

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 2

2.5 3 3.5

Gambar 4.1 Solusi Numerik PD x2y0

dx dy Teladan 4.2

Dapatkan model numerik dan nilai dari y(10) jika y(0) = 0 dari persamaan diferensial 3 xy2

dx dy Solusi:

Akan di tunjukkan bentuk numeriknya dengan menggunakan metode Euler sebagai berikut :

 

 2

3 xy

dx dy

xy dx

dy

 2 3

3

2 xy

dx dy 

 

Karena xi ih, maka Bentuk umum persamaan numerik

motode Euler



i i



i

i y hf x y

y₁  ,



3

2 _i _i

i

y x h

y  



3 2 3yi h xiyi 

3 . . 2

3y_i  hhihy_i



3 . 2

3y_i  hih2 y_i



3 2

3 _ih2 _y _h

i 

 



3 2 3

2 3

:

2 1

h y ih y

xy dx dy

PDB i

i   

  

 

(8)

Numerik

Dengan mengambil h = 0.1, maka kode komputasi yang

dapat diterapkan untuk mengevaluasi nilai dari y(10)

sebagaimana di bawah dengan hasil komputasi

x f(x) x f(x) x f(x) x f(x)

0.1 0.066666667 2.6

0.8578896 21

5. 1

0.4521328 84

7. 6

0.275393 421

0.2

0.132888

889 2.7

0.8473462 22

5. 2

0.4404298 51

7. 7

0.271375 776

0.3 0.198226667 2.8 0.834927241 5.3 0.429287244 7.8 0.267484741

0.4 0.262250311 2.9 0.820884274 5.4 0.418682207 7.9 0.263713759

0.5 0.324546139 3 0.805462513 5.5 0.408590469 8 0.260056757

0.6

0.384721

883 3.1

0.7888980 54

5. 6

0.3989869 15

8. 1

0.256508 099

0.7

0.442411

706 3.2

0.7714155 95

5. 7

0.3898460 67

8. 2

0.253062 552

0.8 0.497280727 3.3 0.753226546 5.8 0.381142494 8.3 0.249715246

0.9 0.549028972 3.4 0.734527537 5.9 0.372851137 8.4 0.246461644

1 0.597394673 3.5 0.715499325 6 0.364947576 8.5 0.243297511

1.1

0.642156

868 3.6

0.6963060 72

6. 1

0.3574082 36

8. 6

0.240218 891

1.2

0.683137

26 3.7

0.6770949 9

6. 2

0.3502105 34

8. 7

0.237222 08

1.3 0.720201312 3.8 0.657996291 6.3 0.343332988 8.8 0.234303603

1.4 0.753258584 3.9 0.63912344 6.4 0.336755284 8.9 0.231460201

1.5 0.782262322 4 0.620573648 6.5 0.330458306 9 0.228688807

1.6

0.807208

331 4.1

0.6024285 83

6. 6

0.3244241 45

9. 1

0.225986 536

1.7

0.828133

192 4.2

0.5847552 48

6. 7

0.3186360 86

9. 2

0.223350 665

1.8 0.845111868 4.3 0.567606996 6.8 0.313078573 9.3 0.220778625

1.9 0.858254783 4.4 0.551024636 6.9 0.307737168 9.4 0.218267989

2 0.867704464 4.5 0.535037608 7 0.302598496 9.5 0.215816459

2.1

0.873631

818 4.6

0.5196651 74

7. 1

0.2976501 85

9. 6

0.213421 859

2.2

0.876232

151 4.7

0.5049176 3

7. 2

0.2928808 07

9. 7

0.211082 125

(9)

Numerik

x f(x) x f(x) x f(x) x f(x)

005 55 4 57 9 516

2.5 0.866302504 5 0.464417129 7.5 0.27954476 10 0.204373011

0 1 2 3 4 5 6 7 8 9 10

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

x

f

(

x

)

Solusi PD: 3(dy/dx )+xy =2

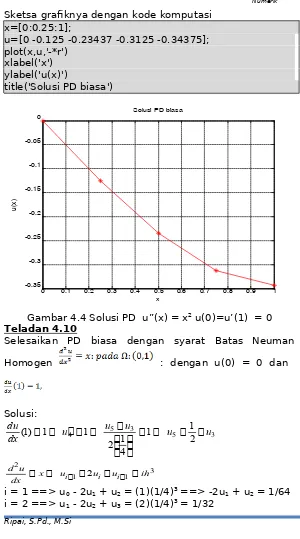
Gambar 4.2 Solusi numerik PD 3 xy2

dx dy

x0=0; f(1)=0; x=10; h=0.1 x=[x0:h:x];

[n,m]=size(x); for i=1:m-1

f(i+1)=((3-i.*h.^2).*f(i)+2.*h)./3; end

disp([x;f]') plot(x,f) xlabel('x') ylabel('f(x)')

title('Solusi PD: 3(dy/dx)+xy=2') grid on

4.5.2 Metode Multi Step

Multi step merupakan metode integrasi yang didasari dari pendekatan poliniam Newton Gregori dengan batas integral dari [xn xx+1]. Tinjau kembali polynomial Newton

Gregori Mundur sebagai berikut:

 



 

    



  







  

! 3

2 1 !

1

3 3 2

2 1

0 s f s s f s s s f

f x P x f

Untuk x0 = xn , maka

(10)

Numerik sebagai berikut:

x ydx P x dx berdasarkan polynomial Newton Mundur adalah



1 2



(11)

Numerik

Diketahui persamaan diferensial: x y dx

dy



 dengan nilai awal y(0) = 1; y(0,2) = 1,242 dan y(0,4) = 1,5836. Dapatkan nilai dari y(0,6).

Solusi:

Misalkan f(x,y) dx

dy

 , maka menurut metode Multi Step nilai y(x) dapat ditentukan secara iteratif dengan



1 2



1 23 16 5

12  

  n n  n  n

n y h f f f

y .

xn yn fn

0 1 0 + 1 = 1

0.2 1.242 0.2 + 1.242 = 1.442 0.4 1.5836 0.4 + 1.536 = 1.9836 0.6 ..?



23



1,9836



16



1,4428



5

 

1



2,0426 12

2 , 0 36 8 5 , 1 6 , 0

5 16

23

12 1 2

1

  

 



  



y

f f

f h y

yn n n n n

4.5.3 Metode Adam Multon

Tentukan rumus penyelesaian metode Adam Multon untuk penyelesaian PERSAMAAN DIFERENSIAL

Solusi:

Teladan 4.4

(12)

Numerik

Diketahui Persamaan Diferensial 2_;

Dengan y(0.2) = 1.2186, y(0.4) =1.4682, y(0.6) = 1.7379. Gunakan metode Adam Multon yang cocok untuk empat nilai terakhir (x,y) dan cari y(1,2) serta bandingkan penyelesain analitiknya.

Solusi:

h=0,2

N xn Y(xn) f(x,y) ket

0 0 1 1 Dik

1 0,2 1.2186 1.1786 Dik

2 0,4 1.4682 1.3082 Dik

3 0,6 1.7379 1.3779 Dik

4 0,8 2.014641 1.374641 Predikato r

0,8 2.014479 1.374479 Korektor

5 1 2.282184 1.282184 Predikato

r

1 2.281945 1.281945 Korektor

6 1,2 2.520724 1.080724 Predikato r

1,2 2.520456 1.080456 Korektor

Predicator :

Korektor :

4.5.4 Metode Deret Taylor

Tinjau kembali persamaan deret Taylor, dimana persamaan tersebut memuat turunan.

!

) ( ) ( !

3

) ( ) ( !

2

) ( ) ( ) ( ) ( ) ( )

( 0

) ( 0 0

3 0 0

2 0 0

0 0

n x f x x x

f x x x f x x x f x x x f x f

n n

      

   

 

(13)

Numerik

memahami metode penerapannya, berikut diberikan teladan.

Teladan 4.5

Diketahui persamaan difrensial y’ + y = sin x dengan y(0) = 0. Tentukan nilai y(1).

Solusi:

Teladan 4.6

Diketahui persamaan difrensial tingkat satu:

.

Tentukan y(0.50) dengan metode Deret Taylor untuk h= 0.25.

Solusi:

(14)

Numerik

Diketahui y(x0) = y(0) = 1, maka dapat ditentukan

Sehingga menurut Deret Taylor

= ?

Sehingga,

Jadi, y(0.50) ≈ 0.8364682

4.5.2 PERSAMAAN DIFERENSIAL Orde Dua 4.5.2.1 Metode Deret Taylor

Tinjau kembali persamaan deret Taylor, dimana persamaan tersebut memuat turunan.

!

) ( ) ( !

3

) ( ) ( !

2

) ( ) ( ) ( ) ( ) ( )

( 0

) ( 0 0

3 0 0

2 0 0

0 0

n x f x x x

f x x x f x x x f x x x f x f

n n

      

   

 

(15)

Numerik

pemahaman konsep penyelesaian persamaan diferensial dengan mengunakan deret taylor

Teladan 4.7

Tentukan sampai suku dengan metode deret Taylor dari persamaan diferensial

Solusi:

= 0 

Untuk

(16)

Numerik

Teladan 4.8

Dapatkan penylesaikan n Polynomial derajat 3 dari PDB 2

2 2

3 xy

dx y d dx dy



 dengan pendekatan Deret

Maclaurin, jika nilai awal y 0 0_dan y' 0 1_.

Solusi:

2 2 2

3 xy

dx y d dx dy

 

  3 "   2 

' x f x xy

f

x xy f x

f " '

3 2

 



  00 1

"

3 2

 



 f x

 3 f "x1

  1₃

" 

 f x

Selanjutnya mencari f'''

 

x _{dengan cara}

menurunkan persamaan pertama terhadap x, diperoleh :

  ₃ _"  2

' x f x xy

f  

x f x  y  yy x

f " 3 '''  1 2  2 

3f ''' x  y2 2xyf  x  f" x 3f' ''

 

x 02 

    

2 0 0 1 1₃

 

9 1 ' '

' x 

f

bentuk dari persamaan maclaurinnya adalah :



2



3

! 3

0 ' ' ' !

2 0 " !

1 0 '

0 f x f x f x

f x

(17)

Numerik

2 3

6 9 1

2 3 1 1 1

0 x x  x



2 3

54 1 6

1_x _x

x 



4.1.2.1 Metode Beda Hingga

Jika u = u(x) maka menurut defnisi turunan dapat diperoleh

a. Menurut beda maju

b. Menurut beda mundur

c. Menurut beda tengah

Tinjaun terhadap deret Taylor

   

    

   

 

! 3

) )( ( !

2 ) )( ( ) )( ( ) ( ) (

3 0 0

2 0 0

0 0

0 u x x x u x x x u x x x

x u x u

Menurut metode Deret Taylor

(18)

Numerik

ada 3 syarat batas Syarat batas Direchlet

Syarat batas Neumanat

Syarat batas Robbins

Persamaan Paisson

Persamaan diferensial Poisson adalah persamaan

diferensial derajat dua yang berbentuk

Misalkan PDB tersebut diselesaikan pada domain [0 1] dengan nilai awal u(0) = 0 dan u(1) = 0, maka diperoleh formula numerik sebagai berikut:

=0

(19)

Numerik

Teladan 4.9

Tentukan solusi numerik dan sketsa grafknya dari persamaan diferensial berikut

dengan syarat batas

Syarat Batas Dirichet Homogen

Syarat Batas Dirichet Non Homogen

Solusi:

Dengan mengambil h = ¼ , maka x= [0 0.25 0.5 0.75 1], maka diperoleh i = 0, 1, 2, 3, 4 dengan x0 = 0, x1 = 0.25,

x2 = 0.5, x3 = 0.75 dan x4 = 1.

Dari nilai awal yang diketahui u(0) = 0  u0 = 0 dan u(1)

= u4 = 100.

Dengan defnisi turuna kedua maka diperoleh: 3 1 1

2 1

1 2

2

2 2

ih u u u ih h

u u u x dx

u d

i i i i

i

i   _ _ _ _ _



   _ _

i = 1 ==> u0 – 2u1 + u2 = (1)(1/4)3 = 1/64 ==> -2u1 + u2

= (1/64) – 0 = 1/64

i = 2 ==> u1 – 2u2 + u3 = (2)(1/4)3 = 1/32

i = 3 ==> u2 – 2u3 + u4 = (3)(1/4)3 = 3/64 ==> u2 – 2u3

= (3/64) - 100

Disajikan dalam bentuk matriks

    

 

    

  

100 ) 64 / 3 (

32 / 1

64 / 1

2 1 0

1 2 1

0 1 2

3 2 1

u u u

Penyelesaian untuk nilai ui dengan metode Eliminasi

Gauss Jordan dengan kode komputasi pada bagian terakhir pembahasan diperoleh

Program : Solusi SPL dengan Eliminasi Gauss Jordan ---A = [-2 1 0;1 -2 1;0 1 -2];

(20)

Numerik

B = [1/64;1/32;(3/64)-100];

Augmented Matriks Koefesien Sistem Persamaan Linier -2.0000 1.0000 0 0.0156

1.0000 -2.0000 1.0000 0.0313 0 1.0000 -2.0000 -99.9531

Proses Eliminasi Gauss Jordan B2 - (1/-2)B1

-2.0000 1.0000 0 0.0156 0 -1.5000 1.0000 0.0391 0 1.0000 -2.0000 -99.9531

B3 - (1/-1.5)B2

-2.0000 1.0000 0 0.0156 0 -1.5000 1.0000 0.0391 0 0 -1.3333 -99.9271

B2 - (1/-1.3333)B3

-2.0000 1.0000 0 0.0156 0 -1.5000 0 -74.9062 0 0 -1.3333 -99.9271

B1 - (0/-1.3333)B3

-2.0000 1.0000 0 0.0156 0 -1.5000 0 -74.9062 0 0 -1.3333 -99.9271

B1 - (1/-1.5)B2

-2.0000 0 0 -49.9219 0 -1.5000 0 -74.9062 0 0 -1.3333 -99.9271 (1/-2)B1

1.0000 0 0 24.9609 0 -1.5000 0 -74.9062 0 0 -1.3333 -99.9271

(1/-1.5)B2

1.0000 0 0 24.9609 0 1.0000 0 49.9375 0 0 -1.3333 -99.9271 (1/-1.3333)B3

(21)

Numerik

0 0 1.0000 74.9453

Solusi dari SPL adalah u1 = 24.9609

u2 = 49.9375 u3 = 74.9453

Karena nilai h = ¼ dan dari hasil komutasi serta nilai awal di atas, maka diperoleh solusi numeri

U(0) = 0

U1 = 24.9609 ==> U(0.25) = 24.9609

U2 = 49.9375 ==> U(0.50) = 49.9375

U3 = 74.9453 ==> U(0.75) = 74.9453.

U(1) = 100

Jika solusi tersebut disajikan dalam bentuk grafk, maka diperoleh

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0

10 20 30 40 50 60 70 80 90 100

x

u

(

x

)

Solusi PD biasa

Gambar 4.3 Solusi PD

Kode komputasi unutk mengambar grafk fungsi solusi dari Persamaan diferensial.

x=[0:0.25:1];

u=[0 24.9609 49.9375 74.9453 100]; plot(x,u,'*-r')

grid on xlabel('x'); ylabel('u(x)')

title('Solusi PD biasa')

Teladan 4.9

(22)

Numerik

Selesaikan persamaan diferensial berikut dan sketsa grafknya.

:

Solusi:

Dari persamaan PD yang diketahui, maka diperoleh persamaan numeriknya sebagai berikut:

Dari syarat batas yang diketahui dan mengunakan turunan beda tengah diperoleh

3 5 3

5

4 0

4 1 2 0 0

) 1

( u u u u u

dx du

              

u(0) = 0 ==> u0 = 0

Dari PD yang diketahui, maka

3 1 1

2 1

1 2

2

2 _ih _u _u _u _ih

h u u u x dx

u d

i i i i

i

i   _ _ _ _ _



    

i = 1 ==> u0 – 2u1 + u2 = (1)(1/4)3 ==> -2u1 + u2 = 1/64

i = 2 ==> u1 – 2u2 + u3 = (2)(1/4)3 ==> u1 – 2u2 + u3 =

1/32

i = 3 ==> u2 – 2u3 + u4 = (3)(1/4)3 ==> u2 – 2u3 + u4 =

3/64

i = 4 ==> u3 – 2u4 + u5 = (4)(1/4)3 ==> 2u3 – 2u4 = 1/16

Bentuk Augmented Matriksnya diperoleh

    

 

    

       

 

    

 

    

 

    

 

   

16 / 1

64 / 3

32 / 1

64 / 1

2 2 0 0

1 2 1 0

0 1 2 1

0 0 1 2

4 3 2 1

u u u u

Program : Solusi SPL dengan Eliminasi Gauss Jordan

---A = [-2 1 0 0;1 -2 1 0;0 1 -2 1;0 0 2 -2]; B = [1/64;1/32;3/64;1/16];

(23)

Numerik

0 0 2.0000 -2.0000 0.0625 Proses Eliminasi Gauss Jordan

B2 - (1/-2)B1

-2.0000 1.0000 0 0 0.0156 0 -1.5000 1.0000 0 0.0391 0 1.0000 -2.0000 1.0000 0.0469 0 0 2.0000 -2.0000 0.0625

B3 - (1/-1.5)B2

-2.0000 1.0000 0 0 0.0156 0 -1.5000 1.0000 0 0.0391 0 0 -1.3333 1.0000 0.0729 0 0 2.0000 -2.0000 0.0625

B4 - (2/-1.3333)B3

-2.0000 1.0000 0 0 0.0156 0 -1.5000 1.0000 0 0.0391 0 0 -1.3333 1.0000 0.0729 0 0 0 -0.5000 0.1719

B3 - (1/-0.5)B4

-2.0000 1.0000 0 0 0.0156 0 -1.5000 1.0000 0 0.0391 0 0 -1.3333 0 0.4167 0 0 0 -0.5000 0.1719

B2 - (0/-0.5)B4

-2.0000 1.0000 0 0 0.0156 0 -1.5000 1.0000 0 0.0391 0 0 -1.3333 0 0.4167 0 0 0 -0.5000 0.1719 B1 - (0/-0.5)B4

-2.0000 1.0000 0 0 0.0156 0 -1.5000 1.0000 0 0.0391 0 0 -1.3333 0 0.4167 0 0 0 -0.5000 0.1719

B2 - (1/-1.3333)B3

-2.0000 1.0000 0 0 0.0156 0 -1.5000 0 0 0.3516 0 0 -1.3333 0 0.4167 0 0 0 -0.5000 0.1719 B1 - (0/-1.3333)B3

(24)

Numerik

-2.0000 1.0000 0 0 0.0156 0 -1.5000 0 0 0.3516 0 0 -1.3333 0 0.4167 0 0 0 -0.5000 0.1719

B1 - (1/-1.5)B2

-2.0000 0 0 0 0.2500 0 -1.5000 0 0 0.3516 0 0 -1.3333 0 0.4167 0 0 0 -0.5000 0.1719

(1/-2)B1

1.0000 0 0 0 -0.1250 0 -1.5000 0 0 0.3516 0 0 -1.3333 0 0.4167 0 0 0 -0.5000 0.1719

(1/-1.5)B2

1.0000 0 0 0 -0.1250 0 1.0000 0 0 -0.2344 0 0 -1.3333 0 0.4167 0 0 0 -0.5000 0.1719

(1/-1.3333)B3

1.0000 0 0 0 -0.1250 0 1.0000 0 0 -0.2344 0 0 1.0000 0 -0.3125 0 0 0 -0.5000 0.1719 (1/-0.5)B4

1.0000 0 0 0 -0.1250 0 1.0000 0 0 -0.2344 0 0 1.0000 0 -0.3125 0 0 0 1.0000 -0.3437 Solusi dari SPL adalah

u1 = -0.125 u2 = -0.23437 u3 = -0.3125 u4 = -0.34375

Berdasarkan nilai awal dan hasil komputasi tersebut, maka diperoleh solusi numerik pada interval [0 1] dengan h = ¼ adalah

u(0) = 0; u(0.25) = u1 = -0.125; u(0.5) = u2 = -0.23437;

(25)

Numerik

Sketsa grafknya dengan kode komputasi x=[0:0.25:1];

u=[0 -0.125 -0.23437 -0.3125 -0.34375]; plot(x,u,'-*r')

xlabel('x') ylabel('u(x)')

title('Solusi PD biasa')

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 -0.35

-0. 3 -0.25 -0. 2 -0.15 -0. 1 -0.05 0

x

u

(

x

)

Solusi PD bias a

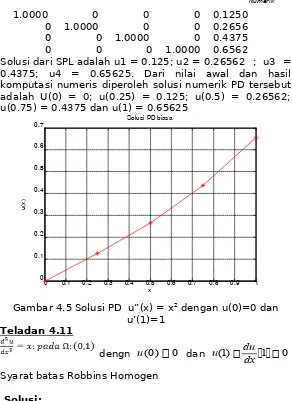
Gambar 4.4 Solusi PD u”(x) = x2_{u(0)=u’(1) = 0}

Teladan 4.10

Selesaikan PD biasa dengan syarat Batas Neuman

Homogen : dengan u(0) = 0 dan

Solusi:

3 5

4 1 1₂

4 1 2 1 1

) 1

( u u u u u

dx du

               

3 1 1

2

2u u ih

u x dx

u d

i i

i   



  

i = 1 ==> u0 - 2u1 + u2 = (1)(1/4)3 ==> -2u1 + u2 = 1/64

(26)

Numerik

i = 3 ==> u2 - 2u3 + u4 = (3)(1/4)3 = 3/64

i = 4 ==> u3 – 2u4 + u5 = (4)(1/4)3 ==> 2u3 – 2u4 =

(1/16)-(1/2) =-7/16

    

 

    

 

      

 

    

 

    

 

    

 

   

16 / 7

64 / 3

32 / 1

64 / 1

2 2 0 0

1 2 1 0

0 1 2 1

0 0 1 2

4 3 2 1

u u u u

Program : Solusi SPL dengan Eliminasi Gauss Jordan ---A = [-2 1 0 0;1 -2 1 0;0 1 -2 1;0 0 2 -2];

B = [1/64;1/32;3/64;-7/16];

Augmented Matriks Koefesien Sistem Persamaan Linier -2.0000 1.0000 0 0 0.0156 1.0000 -2.0000 1.0000 0 0.0313 0 1.0000 -2.0000 1.0000 0.0469 0 0 2.0000 -2.0000 -0.4375

Proses Eliminasi Gauss Jordan B2 - (1/-2)B1

-2.0000 1.0000 0 0 0.0156 0 -1.5000 1.0000 0 0.0391 0 1.0000 -2.0000 1.0000 0.0469 0 0 2.0000 -2.0000 -0.4375

B3 - (1/-1.5)B2

-2.0000 1.0000 0 0 0.0156 0 -1.5000 1.0000 0 0.0391 0 0 -1.3333 1.0000 0.0729 0 0 2.0000 -2.0000 -0.4375 B4 - (2/-1.3333)B3

-2.0000 1.0000 0 0 0.0156 0 -1.5000 1.0000 0 0.0391 0 0 -1.3333 1.0000 0.0729 0 0 0 -0.5000 -0.3281

B3 - (1/-0.5)B4

-2.0000 1.0000 0 0 0.0156 0 -1.5000 1.0000 0 0.0391 0 0 -1.3333 0 -0.5833 0 0 0 -0.5000 -0.3281

(27)

Numerik

-2.0000 1.0000 0 0 0.0156 0 -1.5000 1.0000 0 0.0391 0 0 -1.3333 0 -0.5833 0 0 0 -0.5000 -0.3281

B1 - (0/-0.5)B4

-2.0000 1.0000 0 0 0.0156 0 -1.5000 1.0000 0 0.0391 0 0 -1.3333 0 -0.5833 0 0 0 -0.5000 -0.3281

B2 - (1/-1.3333)B3

-2.0000 1.0000 0 0 0.0156 0 -1.5000 0 0 -0.3984 0 0 -1.3333 0 -0.5833 0 0 0 -0.5000 -0.3281

B1 - (0/-1.3333)B3

-2.0000 1.0000 0 0 0.0156 0 -1.5000 0 0 -0.3984 0 0 -1.3333 0 -0.5833 0 0 0 -0.5000 -0.3281 B1 - (1/-1.5)B2

-2.0000 0 0 0 -0.2500 0 -1.5000 0 0 -0.3984 0 0 -1.3333 0 -0.5833 0 0 0 -0.5000 -0.3281 (1/-2)B1

1.0000 0 0 0 0.1250 0 -1.5000 0 0 -0.3984 0 0 -1.3333 0 -0.5833 0 0 0 -0.5000 -0.3281 (1/-1.5)B2

1.0000 0 0 0 0.1250 0 1.0000 0 0 0.2656 0 0 -1.3333 0 -0.5833 0 0 0 -0.5000 -0.3281 (1/-1.3333)B3

1.0000 0 0 0 0.1250 0 1.0000 0 0 0.2656 0 0 1.0000 0 0.4375 0 0 0 -0.5000 -0.3281 (1/-0.5)B4

(28)

Numerik

1.0000 0 0 0 0.1250 0 1.0000 0 0 0.2656 0 0 1.0000 0 0.4375 0 0 0 1.0000 0.6562

Solusi dari SPL adalah u1 = 0.125; u2 = 0.26562 ; u3 = 0.4375; u4 = 0.65625. Dari nilai awal dan hasil komputasi numeris diperoleh solusi numerik PD tersebut adalah U(0) = 0; u(0.25) = 0.125; u(0.5) = 0.26562; u(0.75) = 0.4375 dan u(1) = 0.65625

0 0.1 0.2 0.3 0. 4 0.5 0.6 0.7 0. 8 0.9 1 0

0.1 0.2 0.3 0.4 0.5 0.6 0.7

x

u

(

x

)

Solus i PD bias a

Gambar 4.5 Solusi PD u”(x) = x2_{dengan u(0)=0 dan}

u’(1)=1 Teladan 4.11

dengn u(0) 0 dan (1)

 

1 0

dx du u

Syarat batas Robbins Homogen

Solusi:

Pada domain [0 1] dengan h = ¼ , maka u(1) = u4 dan

4

) 1

( u

dx du



 sehingga dari syarat batas Robbins

Homogen diperoleh

4 3 5 3

5 4 4

4 0 1₂

4 1 2 0

0 ) 1 ( ) 1

( u u u u u u u u

dx du

u    

              

(29)

Numerik

3 1 1

2 1

1 2

2

2 _ih _u _u _u _ih

h u u u x dx

u d

i i i i

i

i   _ _ _ _ _



    

i = 1 ==> u0 – 2u1 + u2 = (1)(1/4)3 ==> -2u1 + u2 =

1/64

i = 2 ==> u1 – 2u2 + u3 = (2)(1/4)3 ==> u1 -2u2 + u3 =

1/32

i = 3 ==> u2 – 2u3 + u4 = (3)(1/4)3 ==> u2 – 2u3 + u4 =

3/64

i = 4 ==> u3 – 2u4 + u5 = (4)(1/4)3 ==> 2u3 – 2½ u4 =

1/16

Bentuk Augmented Matriksnya adalah

    

 

    

       

 

    

 

    

 

    

 

   

16 / 1

64 / 3

32 / 1

64 / 1

5 . 2 1 0 0

1 2 1 0

0 1 2 1

0 0 1 2

4 3 2 1

u u u u

Program : Solusi SPL dengan Eliminasi Gauss Jordan ---A = [-2 1 0 0;1 -2 1 0;0 1 -2 1;0 0 1 -2.5];

B = [1/64;1/32;3/64;1/16];

Augmented Matriks Koefesien Sistem Persamaan Linier -2.0000 1.0000 0 0 0.0156 1.0000 -2.0000 1.0000 0 0.0313 0 1.0000 -2.0000 1.0000 0.0469 0 0 1.0000 -2.5000 0.0625 Proses Eliminasi Gauss Jordan

B2 - (1/-2)B1

-2.0000 1.0000 0 0 0.0156 0 -1.5000 1.0000 0 0.0391 0 1.0000 -2.0000 1.0000 0.0469 0 0 1.0000 -2.5000 0.0625 B3 - (1/-1.5)B2

-2.0000 1.0000 0 0 0.0156 0 -1.5000 1.0000 0 0.0391 0 0 -1.3333 1.0000 0.0729 0 0 1.0000 -2.5000 0.0625

B4 - (1/-1.3333)B3

-2.0000 1.0000 0 0 0.0156 0 -1.5000 1.0000 0 0.0391 0 0 -1.3333 1.0000 0.0729 0 0 0 -1.7500 0.1172

(30)

Numerik

B3 - (1/-1.75)B4

-2.0000 1.0000 0 0 0.0156 0 -1.5000 1.0000 0 0.0391 0 0 -1.3333 0 0.1399 0 0 0 -1.7500 0.1172

B2 - (0/-1.75)B4

-2.0000 1.0000 0 0 0.0156 0 -1.5000 1.0000 0 0.0391 0 0 -1.3333 0 0.1399 0 0 0 -1.7500 0.1172

B1 - (0/-1.75)B4

-2.0000 1.0000 0 0 0.0156 0 -1.5000 1.0000 0 0.0391 0 0 -1.3333 0 0.1399 0 0 0 -1.7500 0.1172 B2 - (1/-1.3333)B3

-2.0000 1.0000 0 0 0.0156 0 -1.5000 0 0 0.1440 0 0 -1.3333 0 0.1399 0 0 0 -1.7500 0.1172

B1 - (0/-1.3333)B3

-2.0000 1.0000 0 0 0.0156 0 -1.5000 0 0 0.1440 0 0 -1.3333 0 0.1399 0 0 0 -1.7500 0.1172 B1 - (1/-1.5)B2

-2.0000 0 0 0 0.1116 0 -1.5000 0 0 0.1440 0 0 -1.3333 0 0.1399 0 0 0 -1.7500 0.1172

(1/-2)B1

1.0000 0 0 0 -0.0558 0 -1.5000 0 0 0.1440 0 0 -1.3333 0 0.1399 0 0 0 -1.7500 0.1172

(1/-1.5)B2

(31)

Numerik

0 0 -1.3333 0 0.1399 0 0 0 -1.7500 0.1172 (1/-1.3333)B3

1.0000 0 0 0 -0.0558 0 1.0000 0 0 -0.0960 0 0 1.0000 0 -0.1049 0 0 0 -1.7500 0.1172 (1/-1.75)B4

1.0000 0 0 0 -0.0558 0 1.0000 0 0 -0.0960 0 0 1.0000 0 -0.1049 0 0 0 1.0000 -0.0670

Solusi dari SPL adalah u1 = -0.055804 u2 = -0.095982 u3 = -0.10491 u4 = -0.066964

Berdasarkan nilai awal dan perolehan hasil komputasi di atas, maka diperoleh solusi numerik unutk PDB tersebut adalah

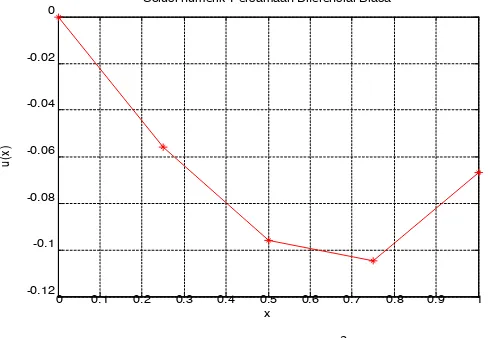
U(0) = 0; U(0.25) = -0.055804; u(0.5) = -0.095982; u(0.75) = -0.10491 dan u(1) = -0.066964

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 -0.12

-0. 1 -0.08 -0.06 -0.04 -0.02 0

x

u

(

x

)

Solusi numerik Pers amaan Diferens ial Bias a

Gambar 4.6 Solusi PD u”(x) = x2_{dg u(0)=0 dan}

u(1)+u’(1)=0

(32)

Numerik

x=[0:0.25:1];

y=[0 -0.055804 -0.095982 -0.10491 -0.066964]; plot(x,y,'*-r');

grid xlabel('x'); ylabel('u(x)')

title('Solusi numerik Persamaan Diferensial Biasa')

Kode Komputasi Eliminasi Gauss Jordan clc;

clear all;

disp('Program : Eliminasi Gauss Jordan ') disp('---') A=input('A = ');

B=input('B = '); M=[A B];

n=length(B);

disp('Augmented Matriks Koefesien Sistem Persamaan Linier')

disp(M)

disp('Proses Eliminasi Gauss Jordan')

for i=1:n-1 if M(i,i)==0 c=i;

while M(c,i)==0 c=c+1; end

T=M(i,:); M(i,:)=M(c,:); M(c,:)=T;

disp(['B' num2str(i) '<--> B' num2str(a)]) disp(M)

end

for j=i+1:n if M(j,i)~=0

disp(['B' num2str(j) ' - (' num2str(M(j,i)) '/'

num2str(M(i,i)) ')B' num2str(i)])

M(j,:)=M(j,:)-(M(j,i)./M(i,i)*M(i,:)); disp(M)

end

(33)

Numerik

if M(n,n)==0&M(n,n+1)~=0

disp('SPL tidak memiliki solusi')

else

for i=n:-1:2

for j=i-1:-1:1

disp(['B' num2str(j) ' - (' num2str(M(j,i)) '/'

num2str(M(i,i)) ')B' num2str(i)])

M(j,:)=M(j,:)-(M(j,i)./M(i,i)*M(i,:)); disp(M)

end

for i=1:n

disp(['(1/' num2str(M(i,i)) ')B' num2str(i)]) M(i,:)=(1/M(i,i)*M(i,:));

disp(M) end

end

disp('Solusi dari SPL adalah') for i=1:n

disp(['u' num2str(i) ' = '

num2str(M(i,n+1))]) end

4.6 Persamaan Diperensial Parsial 4.6.1 Metode Beda Hingga

Telah dibahas Defnisi Turunan pertama: Beda Maju:

h x f h x f dx

dy (  ) ( )



Beda Mundur :

h h x f x f dx

dy ( ) (  )

 Beda Tengah :

h h x f h x f dx dy

2

) ( )

(   

 dan

2 2

2 ₍ ₎ ₍ ₎ ₂ ₍ ₎

h

x f h x f h x f dx

y

d    



Berdasarkan defnisi tersebut, maka dapat diketahui

defnisi dari turunan parsial sebagai berikut:

(34)

Numerik

Dan defnisi turunan Parsial Tingkat Dua.

2

Teladan 4.12

Dimiliki persamaan diferensial parsial: xy

persamaan diferensial parsial tersebut dengan mengambil

(35)

Numerik

Untuk h=0,25 dan domain 0 ≤ x ≤ 1 dan 0 ≤ y ≤ 1, maka diperoleh

x = 0, 0.25, 0.5, 0.75 dan 1 serta y = 0, 0.25, 0.5, 0.75

dan 1

Dari persamaan diferensial parsial diperoleh j

Variabel-variabel tersebut adalah f

1,0

Selanjutnya SPL perlu direduksi agar menjadi SPL dengan

banyaknya variable sama dengan banyaknya

persamaan. Untuk mereduksi SPL tersebut menjadi 16

(36)

Numerik

variabel, maka ditentukan nilai dari 4 (empat) variable

lainnya dengan menganalisis dari nilai awal dan syarat

batas yang digunakan sebagai beikut:



Berdasarkan perolehan dari nilai awal dan syarat batas tersebut, disubtitusikan ke SPL yang telah diperoleh sebelumnya sehingga SPL menjadi 16 persamaan dan 16 variabel sebagai beikut:

(37)

Numerik

(38)

Numerik

(39)

Numerik

Hasil komputasi dengan kode program di bawah A=[-4 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0;...

B=[0.25^4-20; 2*0.25^4-10;3*0.25^4-10; 0.25^3-11;2*0.25^4-10;...

(40)

Numerik

4*0.25^4; 6*0.25^4;2*0.25^3-1;3*0.25^4-10;6*0.25^4;9*0.25^4;...

3*0.25^3-1;0.25^3-10;2*0.25^3;3*0.25^3; 0.25^2-1];

f=inv(A)*B;

f1,1 = 9.7195  f(0.25, 0.25) = 9.7195

f1,2 = 9.3793  f(0.25, 0.50) = 9.3793

f1,3 = 8.8783  f(0.25, 0.75) = 8.8783

f

1,4

= 7.9684  f(0.25, 1,00) = 7.9684

f

2,1

= 9.5024  f(0.50, 0.25) = 9.5024

f

2,2

= 8.9273  f(0.50, 0.50) = 8.9273

f

2,3

= 8.1771  f(0.50, 0.75) = 8.1771

f2,4 = 7.1170  f(0.50, 1,00) = 7.1170

f3,1 = 9.3708  f(0.75,0.25) = 9.3708

f3,2 = 8.6659  f(0.75, 0.50) = 8.6659

f3,3 = 7.8091  f(0.75, 0.75) = 7.8091

f3,4 = 6.7354  f(0.75, 1.00) = 6.7354

f4,1 = 9.3265  f(1.00, 0.25) = 9.3265

f4,2 = 8.5801  f(1.00, 0.50) = 8.5801

f4,3, = 7.6931 f(1.00, 0.75) = 7.6931

f4,4 = 6.6210  f(1.00, 1.00) = 6.6210

(41)

Numerik

f0,0 = 10  f(0, 0.00) = 10

f

0,1

= 10  f(0, 0.25) = 10 dan f

1,0

= 10  f(0.25, 0) =

10

f

0,2

= 10  f(0, 0.50) = 10 dan f

2,0

= 10  f(0.50, 0) =

10

f0,3 = 10  f(0, 0.75) = 10 dan f3,0 = 10  f(0.75, 0) =

10

f0,4 = 10  f(0, 1.00) = 10 dan f4,0 = 10  f(1.00, 0) =

10

f5,0 = f3,0 = 10  f(1.25, 0.00) = 10

f5,1 = f3,1 = 9.3708  f(1.25, 0.25) = 9.3708

f5,2 = f3,2 = 8.6659  f(1.25, 0.50) = 8.6659

f

5,3

= f

3,3

= 7.8091  f(1.25, 0.75) = 7.8091

f

5,4

= f

3,4

= 6.7354  f(1.25, 1.00) = 6.7354

f0,5 = 1 + f0,3 – 0.5f0.4 = 1 + 10 -0.5(10) = 6

 f(0, 1.25) = 6

f1,5 = 1 + f1,3 – 0.5f1,4 = 1 + 8.8783 – 0.5(7.9684) = 6.8941

 f(0.25, 1.25) = 6.8941

f2,5 = 1 + f2,3 – 0.5f2,4 = 1 + 8.1771 – 0.5(7.1170) = 5.6186

 f(0.50, 1.25) = 5.6186

f3,5 = 1 + f3,3 – 0.5f3,4 = 1 + 7.8091 – 0.5(6.7354) = 5.4414

(42)

Numerik

 f(0.75, 1.25) = 5.4414

f4,5 = 1 + f4,3 – 0.5f4,4 = 1 + 7.6931 – 0.5(6.6210) = 5.3826

 f(1.00, 1.25) = 5.3826

Hasil analisis tersebut di atas, jika diringkas dalam

sebuah table, maka akan diperoleh sebagai berikut

i j x y f(x,y) i j x y f(x,y)

0 0 0 0 10 3 0 0.75 0 10

0 1 0 0.2

5 10 3 1 0.75 0.25 9.3708

0 2 0 0.5 10 3 2 0.75 0.5 8.6659

0 3 0 0.7

5 10 3 3 0.75 0.75 7.8091

0 4 0 1 10 3 4 0.75 1 6.7354

0 5 0 1.2

5 6 3 5 0.75 1.25 5.4414

1 0 0.2

5 0 10 4 0 1 0 10

1 1 0.2

5 0.25 9.7195 4 1 1 0.25 9.3265

1 2 0.2

5 0.5 9.3793 4 2 1 0.5 8.5801

1 3 0.2

5 0.75 8.8783 4 3 1 0.75 7.6931

1 4 0.2

5 1 7.9684 4 4 1 1 6.6210

1 5 0.2

5 1.25 6.8941 4 5 1 1.25 5.3826

2 0 0.5 0 10 5 0 1.25 0 10

2 1 0.5 0.2

5 9.5024 5 1 1.25 0.25 9.3708

2 2 0.5 0.5 8.9273 5 2 1.25 0.5 8.6659

2 3 0.5 0.7

5 8.1771 5 3 1.25 0.75 7.8091

2 4 0.5 1 7.1170 5 4 1.25 1 6.7354

2 5 0.5 1.2

(43)

Numerik

0

0.5

1

1.5

0 0.5 1 1.5

5 6 7 8 9 10

x y

f

(

x

,

y

)

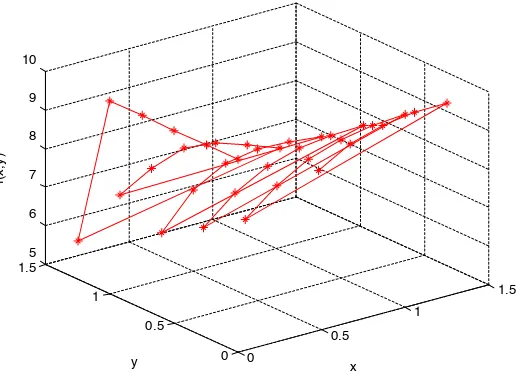
Gambar 4.6 Solusi Numerik PDP: _xy

y f x

f

     

2 2 2 2

x=[0 0 0 0 0 0 0.25 0.25 0.25 0.25 0.25 0.25,...

0.5 0.5 0.5 0.5 0.5 0.5 0.75 0.75 0.75 0.75 0.75 0.75,...

1 1 1 1 1 1 1.25 1.25 1.25 1.25 1.25];

y=[0 0.25 0.5 0.75 1 1.25 0 0.25 0.5 0.75 1 1.25,...

0 0.25 0.5 0.75 1 1.25 0 0.25 0.5 0.75 1 1.25,...

0 0.25 0.5 0.75 1 1.25 0 0.25 0.5 0.75 1];

f=[10 10 10 10 10 6 10 9.7195 9.3793 8.8783 7.9684 6.8941,...

10 9.5024 8.9273 8.1771 7.1170 5.6186 10 9.3708 8.6659,...

7.8091 6.7354 5.4414 10 9.3265 8.5801 7.6931 6.6210,...

5.3826 10 9.3708 8.6659 7.8091 6.7354]; plot3(x,y,f,'-*r')

grid on; xlabel('x'); ylabel('y'); zlabel('f(x,y)')

4.6.2 Siema Beda Hingga

Suatu cara lain unutk mendapatkan Augmented matriks dari permasalahan PDP pada teladan di atas adalah

(44)

Numerik

dengan mengunakan skema beda hingga. Dari syarat batas PDP yang diketahui

10 10

) 0 ,

(x   f_i_,₀

f _dan f(0,y)10 f₀_,_j 10

j j j

f f f

f f

f y

x f

, 3 , 5 ,

3 , 5 , 1 4 , 1 4

0 5

, 0 )

25 , 0 ( 2 0

) , 1

(        



  

4 , 3

, 5

, 4

, 1 4 , 1 4

, ₂ ₁ ₀_,₅

) 25 , 0 ( 2 2

) 1 , ( ) 1 ,

(x f x fi fi f_i f_i f_i f_i

y f

   

  



  

serta dengan h = ¼ , maka terjemahan syarat batas PDP tersebut dalam skema beda hingga diberikan pada gambar di bawah.

Persamaan diferensial yang akan diselesaikan dengan skema beda hingga tersebut adalah xy

y f x

f

     

2 2 2 2

dengan nilai awal dan syarat

4 2

2 , 1 , 1 , , 1 ,

1 f f f 4f h xy h (ih)(jh) ijh f_i_ _j  _i_ _j _i _j_  _i _j_  _i _j  _i _j  

4 1 , 1 , , 1 , 1 ,

4f_i _j f_i _j f_i _jf_i _j  f_i _j ijh

    

(45)

Numerik

Gambar 4.7 Skema beda hingga PDP xy y

f x

f

     

2 2 2 2

(1,1) ==> -4f1,1 + f2,1 + 10 + f1,2 + 10 = (1)(1)(1/4)4 =

1/256

 -4f1,1 + f1,2 + f2,1 = 1/256 – 20

(1,2) ==> -4f1,2 + f2,2 + 10 + f1,3 + f1,1 = (1)(2)(1/4)4 =

1/128

 f1,1 - 4f1,2 + f1,3 + f2,2 = 1/128 - 10

(1,3) ==> -4f1,3 + f2,3 + 10 + f1,4 +f1,2 = (1)(3)(1/4)4 =

3/256

 -4f1,3 + f1,2 + f1,4 + f2,3 = 3/256 – 10

(1,4) ==> -4f1,4 + f2,4 + 10 + f1,3 + (1+f1,3 – 0.5f1,4) = (1)

(4)(1/4)4_{= 1/64}

 2f1,3 – 4.5f1,4 + f2,4 = 1/64 -11

(2,1) ==> -4f2,1 + f3,1 + f1,1 + f2,2 + 10 = (2)(1)(1/4)4 =

1/128

 f1,1 – 4f2,1 + f2,2 + f3,1 = 1/128 – 10

(2,2) ==> -4f2,2 + f3,2 + f1,2 + f2,3 + f2,1 = (2)(2)(1/4)4 =

1/64

(46)

Numerik

(2,3) ==> -4f2,3 + f3,3 + f1,3 + f2,4 + f2,2 = (2)(3)(1/4)4 =

3/128

 f2,2 -4f2,3 + f2,4 + f1,3 + f3,3 = 3/128

(2,4) ==> -4f2,4 + f3,4 + f1,4 + f2,3 + (1+f2,3 – 0.5f2,4) = (2)

(4)(1/4)4

 f1,4 + 2f2,3 – 4.5f2,4 + f3,4 = 1/32 – 1 = (132)/32 =

-31/32

(3,1) ==> -4f3,1 + f4,1 + f2,1 + f3,2 + 10 = (3)(1)(1/4)4  f2,1 – 4f3,1 + f3,2 + f4,1 = 3/256 – 10

(3,2) ==> -4f3,2 + f4,2 + f2,2 + f3,3 + f3,1 = (3)(2)(1/4)4  f2,2 + f3,1 – 4f3,2 + f3,3 + f4,2 = 3/128

(3,3) ==> -4f3,3 + f4,3 + f2,3 + f3,4 + f3,2 = (3)(3)(1/4)4  f2,3 + f3,2 -4f3,3 + f3,4 + f4,3 = 9/256

(3,4) ==> -4f3,4 + f4,4 + f2,4 + f3,3 + (1+f3,3 – 0.5f3,4) = (3)

(4)(1/4)4

==> f2,4 + 2f3,3 – 4.5f3,4 + f4,4 = (3/64)-1

(4,1) ==> -4f4,1 + f3,1 + f3,1 + f4,2 + 10 = (4)(1)(1/4)4 =

1/64

 2f3,1 – 4f4,1 + f4,2 = (1/64)-10

(4,2) ==> -4f4,2 + f3,2 + f3,2 + f4,3 + f4,1 = (4)(2)(1/4)4 =

1/32

 2f3,2 + f4,1 – 4f4,2 + f4,3 = 1/32

(4,3) ==> -4f4,3 + f3,3 + f3,3 + f4,4 + f4,2 = (4)(3)(1/4)4 =

(3/64)

 2f3,3 + f4,2 – 4f4,3 + f4,4 = 3/64

(4,4) ==> -4f4,4 + f3,4 + f3,4 + f4,3 + (1+ f4,3 – 0.5f4,4) = (4)

(4)(1/4)4_{= 1/16}

 2f3,4 + 2f4,3 – 4.5f4,4 = (1/16) – 1 

(47)

Numerik

Bentuk augmented matriks yang diperoleh sama dengan hasil yang diperoleh sebelumnya.

Teladan 4.13

Selesaikan persamaan diferensial Parsial 0 2

Solusi:

Model skema beda hingga dari permasalahan di atas adalah

(48)

0

2 2 2 2

     

y T x

T

Numerik

Gambar 4.8 Skema beda hingga PDP:

Dari PDP yang diketahui diperoleh

0

2 2 2 2

     

y T x

T

0 2

2

, 1 , 1 , 2

, ,

1 ,

1

 

    

h

T T

T h

T T

Ti j i j i j i j i j i j

0 2

2 , , 1 , 1 ,

, 1 ,

1      

 Ti j Ti j Ti j Ti j Ti j Ti j

0 4 ,  1,  1,  , 1  , 1 



 Ti j Ti j Ti j Ti j Ti j

Menurut PDP numerik di atas, maka nilai Tk pada tiap titik adalah

T1 ==> -4T1 + T2 +25 + T5 + 25 = 0 ==> -4T1 +

T2 + T5 = -50

T2 ==> -4T2 + T3 + T1 + T6 + 25 = 0 ==> T1 – 4T2 + T3 + T6 = -25

(49)

Numerik

T4 ==> -4T4 + (12.5+T3) + T3 + T8 + 25 = 0

==> 2T3 – 4T4 + T8 = -12.5

T5 ==> -4T5 + T6 + 25 + T9 + T1 = 0 ==> T1 – 4T5 + T6 + T9 = -25

T6 ==> -4T6 + T7 + T5 + T10 + T2 = 0 ==> T2 + T5

- 4T6 + T7 + T10 = 0

T7 ==> -4T7 + T8 + T6 + T11 + T3 = 0 ==> T3 + T6 – 4T7 + T8 + T11 = 0

T8 ==> -4T8 + (12.5+T7) + T7 + T12 + T4 = 0 ==> T4 + 2T7 – 4T8 + T12 = -12.5

T9 ==> -4T9 + T10 + 25 + T13 + T5 = 0 ==> T5 – 4T9 + T10 + T13 = -25

T10 ==> -4T10 + T11 + T9 + T14 + T6 = 0 ==> T6 + T9 – 4T10 + T11 + T14 = 0 T11 ==> -4T11 + T12 + T10 + T15 + T7 = 0

==> T7 + T10 – 4T11 + T12 + T15 = 0

T12 ==> - 4T12 + (12.5 + T11) + T11 + T16 + T8 = 0

==> T8 + 2T11 – 4T12 + T16 = -12.5

T13 ==> -4T13 + T14 + 25 + (12.5+T9) + T9 = 0

==> 2T9 – 4T13 + T14 = -37.5

T14 ==> -4T14 + T15 + T13 + (12.5+T10) + T10 = 0

==> 2T10 + T13 – 4T14 + T15 = -12.5

T15 ==> -4T15 + T16 + T14 + (12.4 + T11) + T11 = 0

==> 2T11 + T14 – 4T15 + T16 = -12.5

T16 ==> -4T16 + (12.5+T15) + T15 + (12.5+T12) + T12

= 0

==> 2T12 + 2T15 – 4T16 = -25

(50)

Numerik

Penyelesaian SPL tersebut dengan invers matriks diperoleh sebagai berikut:

(51)

Numerik

T1 = 26.3032; T2 = 28.3518; T3 = 28.8280; T4 =

26.8593;

T5 = 28.3518; T6 = 33.2759; T7 = 42.7902; T8 =

49.0017

T9 = 28.8280; T10 = 35.1008; T11 = 41.0183; T12 =

46.1187

T13 = 26.8593; T14 =37.2811; T15 =40.0635; T16 =

40.9364

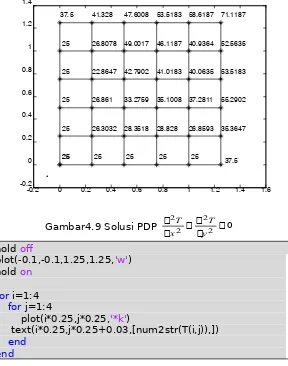
Berdasarkan nilai syarat batas yang diberikan, maka sketsa penyelesaian dari PDP tersebut diberikan oleh gambar di bawah ini.

-0.2 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6

-0.2 0 0.2 0.4 0.6 0.8 1 1.2 1.4

26.3032 26.861 22.8647 26.8078

28.3518 33.2759 42.7902 49.0017

28.828 35.1008 41.0183 46.1187

26.8593 37.2811 40.0635 40.9364

25 25 25

25 25

25

35.3647 55.2902 53.5183 52.5635 41.328 47.6008 53.5183 58.6187

37.5 71.1187 37.5

Gambar4.9 Solusi PDP 0 2 2 2 2

     

y T x

T

hold of

plot(-0.1,-0.1,1.25,1.25,'w') hold on

for i=1:4 for j=1:4

plot(i*0.25,j*0.25,'*k')

text(i*0.25,j*0.25+0.03,[num2str(T(i,j)),]) end

end

(52)

Numerik

for i=0:0.25:1.25 hold on

plot([i,i],[0,1.25],'k') hold on

plot([0,1.25],[i,i],'k')

end

for i=0:0.25:1 plot(0,i,'*k')

text(0,i+0.03,' 25') plot(i,0,'*k')

text(i,0.03,' 25')

end

for i=1:4

plot(1.25,i*0.25,'*k')

text(1.25,i*0.25+0.03,[num2str(12.5+T(i,3))])

end

for i=1:4

plot(i*0.25,1.25,'*k');

text(i*0.25,1.28,[num2str(12.5+T(3,i))])

end

plot(1.25,0,'*k')

text(1.28,0,[num2str(12.5+25)]) plot(1.25,1.25,'*k')

text(1.25,1.28,[num2str(12.5+58.6187)]) plot(0,1.25,'*k')

text(0,1.28,[num2str(12.5+25)]) 4.7 Rangiuman

1. Persamaan Diferensial adalah sutu persamaan yang memuat turunan dibedakan menjadi dua, yaitu persamaan diferensial biasa dan parsial.

2. Persamaan diferensial biasa merupakan persamaan diferensial yang hanya memuat satu variable bebas. Sedangkan persamaan diferensial parsial merupakan persamaan diferensial yang memuat lebih dari satu variable bebas

(53)

Numerik

4. Derajat atau degree dari Persamaan Diferenail adalah pangkat tertinggi yang dimiliki oleh turunan tertinggi yang ada pada persamaan diferensial tersebut

5. Linieritas suatu persamaan diferensial adalah ukuran yang menyatakan ketergantungan dari variabel persamaan diferensila tersebut

6. Masalah nilai awal adalah suatu permasalahan persamaan diferensial yang memuat informasi tambahan dimana informasi tambahan itu memuat nilai variabel bebas yang sama.

7. Masalah nilai batas adalah persamaan diferensial yang memuat informasi tambahan dimana informasi tambahan itu memuat nilai variabel bebas yang tidak sama.

8. Persamaan diferensial biasa yang dapat dinyatakan sebagai y’ = f(x,y) dapat diselesaikan dengan metode Euler dengan formula iterasi

) , (

1 i i i

i y h f x y

y   .

9. Penyelesaian dari persamaan diferensial dengan metode multi step hingga beda ke-2 dari polinomial newton Gregory dinyatakan secara iteratif sebagai



1 2



1 23 16 5

12  

  n  n n  n

n y h f f f

y

10. Penyelesaian Persamaan diferensial biasa dengan metode Adam Multon dinyatakan secara iteratif

dengan formula prediktor

dan

formula korektor

r

11. Formula iteratif penyelesaian persamaan diferensial biasa (PDB) dengan metode beda hingga diberikan oleh formula beda maju

h f f dx

df _i  _i

 1 , formula beda

(54)

Numerik

mundur

h f f dx

df _i  _i_₁

 dan beda tengah

h f f dx

df _i _i

2

1 1    

12. Formula iteratif untukk penyelesaian secara numerik persamaan diferensial Parsial tingkat orde 1 (satu) Beda Maju :

h

y x f y h x f x

f (  , ) ( , )

  

dan

h

y x f h y x f y

f ( ,  ) ( , )

  

Beda Mundur :

h

y h x f y x f x

f ( , ) (  , )

  

dan

h

h y x f y x f y

f ( , ) ( ,  )

  

Beda Tengah :

h

y h x f y h x f x f

2

) , ( ) ,

(   

 

 _dan

h

h y x f h y x f y f

2

) , ( ) ,

(   

  

13. Formula iteratif penyelesaian Persamaan diferensial

parsial Tingkat 2 (dua) adalah

2 2

2 ₍ _, ₎ ₍ _, ₎ ₂ ₍ _, ₎

h

y x f y h x f y h x f x

f    

 

 _dan

2 2

2 ₍ _, ₎ ₍ _, ₎ ₂ ₍ _, ₎

h

y x f h y x f h y x f y

f    

  

4.8 Latihan 4.

1.Dengan menggunakan metode Euler, tentukan nilai y(1,5) dari PDB

Dengan h = 0,25 dan h = 0,1

2. Lakukan sama seperti no.1 namun menggunakan metode Multi Step 3. Lakukan dengan metode Adam Multon untuk mendapatkan y(0,5)

(55)

Numerik

a. y’= y, y(0) = 1 dan cari y(0.2) dengan menggunakan h = 0.05.

b. y’= x+ y, y(0) = 0 dan cari y(0.5) dengan menggunakan h = 0.1

c. y’=3x-y y, y(1) =0 dan cari y(0.5) dengan menggunakan h= -0.1.

5. Bandingkan penyelesaian anlitik dan numerik dari PDP y’’ + xy’ – 3x = 4.2 x dengan y(0) = 0, y(1) = 1.9 dan h = 0.25.

6. dapatkan solusi numerik dengan metode yang cocok untuk mendapatkan nilai dari y’’’ + 10y’ – 5y3_{– x}2_{– xy}

dengan y(0) = 0; y(2) = -1 dan y”(2) = 0. 7. Selesaika Persamaan diferensial parsial berikut

0

2 2 2 2

     

y u x u

dengan u(x,0)=u(x,10) = u(0,y) = 0 dan u(20,y) = 100.

8. Suatu benda dimodelkan dalam bidang dinemsi 2 dipanaskan dengan kondisi awal hasil pengukuran tiap pinggir bidang tersebut sebagai berikut:

Dengan mengunakan persamaan energi, dapatkan temperatur pada titik-titik yang di dibutuhkan sebagaimana pada gambar di atas.

(56)