HUBUNGAN FUNGSI NON-LINEAR DALAM PENERAPAN EKONOMI
Disusun Guna Memenuhi Tugas Matematika Ekonomi
Dosen Pengampu : Wardono
Rombel 1 Oleh:
1. Farah Anisah Zahra 4101413064
2. Rizky Rahman 4101413066
3. Hana Mufti Aulia 4101413086
4. Jihan Dzulfikar 4101413164
5. Nur Said 4101413186
JURUSAN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS NEGERI SEMARANG
2015
Pendahuluan
Fungsi non linier merupakan model yang tidak kalah pentingnya dibandingkan dengan fungsi linier dalam penerapan ekonomi, karena sebagian dari model ekonomi linier yang ada, sesungguhnya merupakan linierisasi dari model non linier.
Ada 4 macam bentuk fungsi non linier yang paling sering dijumpai dalam analisis ekonomi, yaitu : - Fungsi Kuadrat
- Fungsi Kubik
- Fungsi Eksponensial - Fungsi Logaritma
Diantara ke empat fungsi nonlinier tersebut yang paling sering digunakan adalah fungsi kuadrat.
FUNGSI KUADRAT
Fungsi Kuadrat adalah fungsi yang mempunyai pangkat tertinggi dari variabelnya adalah pangkat dua.
Gambar fungsi kuadrat bisa berupa : a. Lingkaran
b. Ellips c. Hiperbola d. Parabola
Tetapi dalam penerapan ekonomi, yang paling sering digunakan adalah fungsi kuadrat yang berbentuk Parabola.
Bentuk yang lebih umum dari fungsi kuadrat : a X 2 + b Y 2 + c X + d Y + p X Y + e = 0 dimana a atau b 0
sebuah fungsi kuadrat jika mempunyai ciri-ciri berikut ini maka :
Jika p = 0 dan a = b 0 bentuk kurvanya Lingkaran p 2 – 4 a b < 0 ; a b dan tanda sama bentuk kurvanya Elips p 2 – 4 a b > 0 ; a & b tanda berlawanan bentuk kurvanya Hiperbola
berati jika salah satu saja yaitu jika a = 0 atau b = 0 tetapi tidak keduanya, maka kurvanya akan berbentuk Parabola
A. LINGKARAN
Lingkaran adalah tempat kedudukan titik-titik yang berjarak tetap terhadap sebuah titik tertentu yang disebut pusat.
Bentuk umum persamaan lingkaran : a X 2 + b Y 2 + c X + d Y + e = 0
Lalu ubah bentuk persamaan menjadi ( X – i ) 2 + ( Y – j ) 2 = r 2
Dimana : i = a c 2 ; j = a d 2 dan r = a e j i2 2
Maka i = jarak pusat lingkaran terhadap sumbu Y j = jarak pusat lingkaran terhadap sumbu X r = jari-jari lingkaran
Lingkaran bisa digambarkan jika nilai r 2 > 0
Titik potong lingkaran pada sumbu koordinat dapat dicari dengan memisalkan masing-masing X = 0 dan Y = 0 secara bergantian.
Jika i > r lingkaran tidak memotong sumbu Y j > r lingkaran tidak memotong sumbu X Contoh : 3 X 2 + 3 Y 2 – 24 X – 18 Y = 33 : 3 X 2 + Y 2 – 8 X – 6 Y = 11
i =
a c 2 =
1 2 8 = 4 j = a d 2 =
1 2 6 = 3 dan r = a e j i2 2 = 1 11 3 42 2 = 36 = 6jadi lingkaran tersebut mempunyai titik pusat pada sumbu koordinat ( 4 ; 3 ) dengan jari-jari lingkaran = 6
A. ELLIPS
Elips adalah tempat kedudukan titik-titik yang jumlah jaraknya terhadap dua fokus Elips adalah tempat kedudukan titik-titik yang jumlah jaraknya terhadap dua fokus selalu konstan. Elips mempunyai dua sumbu simetri yang saling tegak lurus. Sumbu yang selalu konstan. Elips mempunyai dua sumbu simetri yang saling tegak lurus. Sumbu yang panjang disebut Sumbu Mayor. Dan yang pendek disebut Sumbu Minor. Titik potong antara panjang disebut Sumbu Mayor. Dan yang pendek disebut Sumbu Minor. Titik potong antara kedua sumbu elips tersebut merupakan pusat elips ybs.
kedua sumbu elips tersebut merupakan pusat elips ybs. Bentuk Umum Persamaan Elips :
Bentuk Umum Persamaan Elips : a X
a X 22 + b Y + b Y 22 + c X + d Y + e = 0 + c X + d Y + e = 0
dimana : a tandanya sama dengan b tetapi nilai a dimana : a tandanya sama dengan b tetapi nilai a b b Pusat dan jari-jari elips dirumuskan sebagai berikut : Pusat dan jari-jari elips dirumuskan sebagai berikut :
1
)
(
)
(
2
2
2
2
1
2
r
j
Y
r
i
X
jika r1
= r2
maka akan menjadi lingkaran
Contoh :
Tentukan pusat , jari-jari dan perpotongan kurva elips dengan masing-masing sumbu koordinatnya ( sumbu X dan Y ) dari persamaan elips berikut :
8 X 2 + 2 Y 2 - 32 X - 12 Y + 18 = 0 : 2 4 X 2 + Y 2 - 16 X - 6 Y = - 9 Y 3X 2 + 3Y 2 - 24X – 18Y = 33 7,47 r =6 (4,3) i=4 j=3 -1,47 X -1,19 0 9,19
4 X 2 - 16 X + Y 2 - 6 Y = - 9 4 X 2 - 16 X + k1 + Y 2 - 6 Y + k2 = - 9 + k1 + k2 (4 X 2 - 16 X + 16) + (Y 2 - 6 Y + 9) = - 9 + 16 + 9 4 (X – 2) 2 + (Y – 3) 2 = 16 : 16 4 ) 2 (X 2 + 16 ) 3 (Y 2 = 1 2 2 2 ) 2 (X + 2 2 4 ) 3 (Y = 1 Dengan demikian : i = 2 dan j = 3 r1 = 2 dan r2= 4 Berarti : pusat elips ada pada titik ( 2 ; 3 )
Karena r1 < r2 maka sumbu mayor elips // sumbu vertikal Y
r1 adalah jari-jari pendek dan r2adalah jari-jari panjang
Hitunglah : pada titik koordinat berapakah terjadi perpotongan kurva elips dengan sumbu X dan sumbu Y.
B. HIPERBOLA
Hiperbola adalah tempat kedudukan titik-titik yang perbedaan jaraknya terhadap dua Hiperbola adalah tempat kedudukan titik-titik yang perbedaan jaraknya terhadap dua fokus selalu konstan. Hiperbola mempunyai dua sumbu simetri yang saling tegak lurus dan fokus selalu konstan. Hiperbola mempunyai dua sumbu simetri yang saling tegak lurus dan sepasang asimtot. Perpotongan antara sumbu-sumbu simetri (antara asimtot-asimtot) sepasang asimtot. Perpotongan antara sumbu-sumbu simetri (antara asimtot-asimtot) merupakan pusat hiperbola.
merupakan pusat hiperbola.
Bentuk umum persamaan hiperbola : Bentuk umum persamaan hiperbola : a X
a X 22 + b Y + b Y 22 + c X + d Y + e = 0 ; dimana a dan b berlawanan tanda + c X + d Y + e = 0 ; dimana a dan b berlawanan tanda
y 7 8x2+2y2+32x-12y+18=0 2,3 3 x -1 3,32
Pusat hiperbola dapat dicari dengan cara : Pusat hiperbola dapat dicari dengan cara :
1 ) ( ) ( 2 2 2 2 n j Y m i X
dimana sumbu lintang // sumbu X dimana sumbu lintang // sumbu X
atau atau 1 ) ( ) ( 2 2 2 2 m j Y n i X
dimana sumbu lintang // sumbu Y dimana sumbu lintang // sumbu Y dimana ( i , j ) adalah koordinat titik pusat hiperbola
dimana ( i , j ) adalah koordinat titik pusat hiperbola
Jika nilai m = n maka asimtotnya akan saling tegak lurus, dan sumbu lintangnya tidak lagi Jika nilai m = n maka asimtotnya akan saling tegak lurus, dan sumbu lintangnya tidak lagi sejajar salah satu sumbu koordinat, dan hiperbolanya disebut hiperbola sama sisi
sejajar salah satu sumbu koordinat, dan hiperbolanya disebut hiperbola sama sisi .
.
C. PARABOLA
Parabola adalah tempat kedudukan titik-titik yang berjarak sama terhadap sebuah titik Parabola adalah tempat kedudukan titik-titik yang berjarak sama terhadap sebuah titik fokus dan sebuah garis lurus yang disebut direktriks. Setiap parabola mempunyai sebuah fokus dan sebuah garis lurus yang disebut direktriks. Setiap parabola mempunyai sebuah sumbu simetri dan sebuah titik ekstrim.
sumbu simetri dan sebuah titik ekstrim.
Persamaan parabola : Persamaan parabola :
y = a X y = a X 22 + b X + c jika sumbu simetri // sumbu vertikal (sumbu y) + b X + c jika sumbu simetri // sumbu vertikal (sumbu y)
X = a Y X = a Y 22 + b Y + c jika sumbu simetri // sumbu horisontal (sumbu x) + b Y + c jika sumbu simetri // sumbu horisontal (sumbu x)
X X Y Y Titik Ekstrim : Titik Ekstrim : a ac b a b 4 4 ; 2 2
Jarak titik ekstrim
Jarak titik ekstrim Jarak titik ekstrim Jarak titik ekstrim Pada sumbu Y
Pada sumbu Y pada sumbu X pada sumbu X
y y y y x x x x a > 0 a < 0 a > 0 a < 0
Contoh : Tentukan titik ekstrim dan perpotongannya dengan sumbu-sumbu koordinat (sumbu x dan y) dari parabola berikut :
Y = - X 2 + 6 X – 2
Sumbu simetri sejajar sumbu Y
Karena nilai a = - 1 < 0 ; maka parabolanya menghadap ke bawah. Titik ekstrimnya terletak di atas atau titik maksimum, dengan titik koordinat : a ac b a b 4 4 ; 2 2 = ) 1 ( 4 ) 2 )( 1 ( 4 6 ; ) 1 ( 2 6 2 = 4 8 36 ; 2 6 = ( 3 , 7 ) Perpotongan dengan sumbu Y terjadi pada saat X = 0 Y = - 2
Perpotongan dengan sumbu X terjadi pada saat Y = 0 0 = - X 2 + 6 X – 2
Dengan menggunakan rumus a b c diperoleh X1 = 5,65 dan X2 = 0,35
y
(3,7)
7
y = -x2 + 6x - 22
x = 3
sumbu simetri
x
0 0,35 3 5,65
-2
FUNGSI KUBIK
Fungsi kubik atau fungsi berderajat tiga ialah fungsi yang pangkat tertinggi dari variabelnya adalah pangkat tiga. Setiap fungsi kubik setidak - tidaknya mempunyai sebuah titik belok (inflextion point), yaitu titik peralihan bentuk kurva dari cekung menjadi cembung atau cembung menjadi cekung. Selain titik belok, sebuah fungsi kubik mungkin pula mempunyai satu titik ekstrim (maksimum atau minimum) atau titik dua ekstrim (maksimum atau minimum). Ada tidaknya titik ekstrim dalam suatu fungsi kubik tergantung pada besarnya nilai-nilai b, c, dan d di dalam persamaannya. Dengan demikian terdapat beberapa kemungkinan mengenai bentuk kurva suatu fungsi kubik. Fungsi-fungsi kubik hanya mempunyai titik belok, tanpa titik ekstrim.
Persamaan parabola : y = a X 3 + b X 2 + c X + d Fungsi Kubik Mencari : 1. Titik Ekstrims 2. Titik Belok
HUBUNGAN NON LINEAR 1. Permintaan, Penawaran, dan Keseimbangan Pasar
Selain berbentuk fungsi linier, permintaan dan penawaran dapat pula berbentuk fungsi non linier. Fungsi permintaan dan fungsi penawaran yang kuadratik dapat berupa potongan lingkaran, potongan elips, potongan hiperbola maupun potongan parabola. Cara menganalisis keseimbangan pasar untuk permintaan dan penawaran yang non linier sama seperti halnya dalam kasus yang linier. Keseimbangan pasar ditunjukkan oleh kesamaan
Qd=Qs , pada perpotongan kurva permintaan dan kurva penawaran.
Qd=Qs Qd=¿ jumlah permintaan Qs=¿ jumlah penawaran E=¿ titik keseimbangan Pe=¿ harga keseimbangan Qe=¿ jumlah keseimbangan
Analisis pengaruh pajak dan subsidi terhadap keseimbangan pasar juga sama seperti pada kondisi linier. Pajak atau subsidi menyebabkan harga jual yang ditawarkan oleh produsen berubah, tercermin oleh berubahnya persamaan penawaran, sehingga harga keseimbangan dan jumlah keseimbangan yang tercipta di pasarpun berubah. Pajak menyebabkan harga keseimbangan menjadi lebih tinggi dan jumlah keseimbangan menjadi lebih sedikit. Sebaliknya subsidi menyebabkan harga keseimbangan menjadi lebih rendah dan jumlah keseimbangan menjadi lebih banyak.
Contoh Soal
Fungsi permintaan akan suatu barang ditunjukan oleh persamaan Qd = 19 – P2 , sedangkan fungsi penawarannya adalah Qs = –8 + 2P2 . Berapakah harga dan jumlah keseimbangan yang tercipta di pasar ?
Penyelesaian Keseimbangan Pasar Qd=Qs ↔19 – P2 =– 8+2 P2 ↔27=3 P2 ↔ P2=9 ↔ P=3 Q=19 – P2 ¿19−(3 )2 ¿19−9 ¿10 Jadi, Pe=3 dan Qe=10
Jika misalnya terhadap barang yang bersangkutan dikenakan pajak spesifik sebesar 1 (rupiah) per unit, maka persamaan penawaran sesudah pengenaan pajak menjadi :
Q's=– 8+2(P – 1)2=– 8+2(P2– 2 P+1)=– 6 – 4 P+2 P2
Keseimbangan pasar yang baru : Q d=Q ' s
19 – P2=– 6 – 4 P+2 P2
3 P2– 4 P – 25=0
Selanjutnya dengan rumus abc diperoleh P1=3,63 dan P2=– 2,30 . P2 tidak dipakai karena harga negative adalah irrasional.
Dengan memasukkan P=3,63 ke dalam persamaan Q d atau Q' s diperoleh Q=5,82 .
Jadi, dengan adanya pajak : P'e=3,63 atau Q'e=5,82 .
Selanjutnya dapat dihitung beban pajak yang menjadi tanggungan konsumen dan produsen per unit barang, serta jumlah pajak yang diterima oleh pemerintah, masing-masing adalah sebagai berikut.
t k =P 'e−P=3,63 – 3=0,63 t p=t – t k=1 – 0,63=0,37 T =Q'e× t=5,82×1=5,82
2. Fungsi Biaya
Selain pengertian biaya tetap, biaya variabel dan biaya total, dalam konsep biaya dikenal pula pengertian biaya rata-rata (average cost) dan biaya marjinal (marginal cost). Biaya rata-rata adalah biaya yang dikeluarkan untuk menghasilkan tiap unit produk atau keluaran, merupakan hasil bagi biaya total terhadap jumlah keluaran yang dihasilkan. Adapun biaya marjinal ialah biaya tambahan yang dikeluarkan untuk menghsilkan satu unit tambahan produk.
Biaya tetap : FC=k (k: konstanta) Biaya variabel : VC=J (Q)
Biaya total : C=FC+VC=k +f(Q)=c (Q)
Biaya variabel rata-rata : AVC=VCQ
Biaya rata-rata : AC=CQ=AFC + AVC Biaya marjinal : MC=∆ C∆ Q
Bentuk non linier dari fungsi biaya pada umumnya berupa fungsi kuadrat parabolik dan fungsi kubik. Hubungan antara biaya total dan bagian-bagiannya secara grafik dapat dilihat sebagai berikut :
a. Biaya total merupakan fungsi kuadrat parabolik Andaikan C=aQ 2 – bQ
⏟
VC +c⏟
FC maka: AC =C Q=aQ−b+ c Q AVC=VC Q =aQ−b AFC =FC Q = c QBiaya total (C) maupun biaya variabel (VC) sama-sama berbentuk parabola. Perbedaan antara keduanya terletak pada konstanta c, yang mencerminkan biaya tetap (FC). Secara grafik, kurva C dan kurva VC adalah sebangun, dengan perbedaan sejarak c.
Karena C dan VC berbentuk parabola, maka dengan memanfaatkan rumus titik ekstrim parabola, dapat dihitung tingkat produksi (Q) pada C minimum dan VC minimum serta besarnya C minimum dan VC minimumnya. C dan VC yang berbentuk parabola membawa konsekuensi AC dan AVC berbentuk linear; sementara AFC asimtotik terhadap kedua sumbu C dan sumbu Q, sebab F linear.
b. Biaya total merupakan fungsi kubik Andaikan C=aQ 3 – bQ2+cQ
⏟
VC +d⏟
FC maka: AC=C Q=aQ 2 −bQ+c+ d Q AVC=VC Q =aQ 2 −bQ+cAFC =FC
Q =
d Q
Biaya total berfungsi kubik seperti di atas selalu membuahkan AC dan AVC berbentuk parabola terbuka ke atas. Sedangkan AFC tetap asimtotik terhadap sumbu C dan sumbu Q, sebab FC selalu berupa konstanta yang kurvanya sejajar sumbu Q.
Contoh Soal
Biaya total yang dikeluarkan oleh sebuah perusahaan ditunjukkan oleh persamaan
C=2Q2
– 24 Q+102 . Pada tingkat produksi berapa unit biaya total ini minimum?
Hitunglah besarnya biaya total minimum tersebut. Hitung pula besarnya biaya tetap, biaya variabel, biaya rata-rata, biaya tetap rata-rata dan biaya variabel rata-rata pada tingkat produksi tadi. Seandainya dari kedudukan ini produksi dinaikkan dengan 1 unit, berapa besarnya biaya marjinal?
Penyelesaian
Berdasarkan rumus titik ekstrim parabola, C minimum terjadi pada kedudukan
Q=−b 2 a= 24 4 =6 unit. Besarnya C minimum ¿2Q2– 24 Q+102 ¿2(6 )2– 24 (6)+102=30
C minimum dapat juga dicari dengan rumus ordinat titik ekstrim parabola, yaitu (b2−4 ac) −4 a ; hasilnya C minimum ¿ (242−4 × 2× 102) −4 ×2 = −240 −8 =30 , tidak berbeda.
Selanjutnya, pada Q=6 ini: FC=102 VC=2Q2– 24 Q=2(6 )2– 24 (6)=−72 AC=C Q= 30 6 =5 AFC =FC Q = 102 6 =17 AVC=VC Q = −72 6 =−12
Jika Q=7 , C=2(7)2– 24(7)+102=32
MC=∆ C ∆ Q=
32−30 7−6 =2
Berarti untuk menaikkan produksi dari 6 unit menjadi 7 unit diperlukan biaya tambahan (biaya marjinal) sebesar 2.
3. Fungsi Penerimaan
Bentuk fungsi penerimaan total (total revenue, R) yang non-linear pada umumnya berupa sebuah persamaan parabola terbuka ke bawah. Ini merupakan bentuk fungsi penerimaan yang lazim dihadapi oleh seorang produsen yang beroperasi di pasar monopoli. Sedangkan fungsi penerimaan total yang linear merupakan fungsi penerimaan yang dihadapi oleh seorang produsen yang beroperasi di pasar persaingan sempurna.
Penerimaan total merupakan fungsi dari jumlah barang, juga merupakan hasil kali jumlah barang dengan harga barang per unit. Seperti halnya dalam konsep biaya, dalam konsep penerimaanpun dikenal pengertian rata-rata dan marjinal. Penerimaan rata-rata (average revenue, AR) ialah penerimaan yang diperoleh per unit barang, merupakan hasilbagi penerimaan total terhadap jumlah barang. Penerimaan marjinal (marginal revenue, MR) ialah penerimaan tambahan yang diperoleh dari setiap tambahan satu unit barang yang dihasilkan atau terjual.
Penerimaan total : R=Q × P=f (Q)
Penerimaan rata-rata : AR=QR Penerimaan marjinal : MR=∆ R∆ Q Contoh
Fungsi permintaan yang dihadapi oleh seorang produsen monopolis ditunjukkan oleh P=900 – 1,5Q . Bagaimana persamaan penerimaan totalnya? Berapa besarnya penerimaan total jika terjual barang sebanyak 200 unit, dan berapa harga jual perunit? Hitunglah penerimaan marjinal dari penjualan sebanyak 200 unit menjadi 250 unit. Tentukan tingkat penjualan yang menghasilkan penerimaan total maksimum, dan besarnya penerimaan maksimum tersebut.
Penyelesaian
P=900 – 1,5Q → R=Q × P=900 Q – 1,5Q2 Jika Q=200, R=900(200 ) – 1,5(200 )2=120.000
P=900 – 1,5(200 )=600 atau P=QR=120000200 =600 Jika Q=250, R=900(250)– 1,5(250)2=131.250 MR=∆ R ∆ Q= 131.250−120.000 250−200 =225 R=−1,5 Q2+900 Q R maksimum pada Q=−2 ab=−900−3 =300 Besarnya R maksimum ¿1,5(300)2+900(300)=135.000
Dalam membentuk fungsi peneriman melalui fungsi permintaan, persamaan permintaannya harus dalam bentuk P=f (Q) . Jika persamaan permintaan berbentuk
Q=f (P) maka harus dibalik dulu menjadi bentuk P=f (Q) , mengingat
penerimaan merupakan fungsi dari jumlah barang [ R=r (Q)¿ dan bukan fungsi dari
harga [bukan R=r (P) ].
4. Keuntungan, Kerugian, dan Pulang Pokok
Tingkat produksi yang menghasilkan keuntungan, kerugian, dan keadaan pulang-pokok secara grafik dapat dilihat sebagai berikut:
Analisis pulang pokok (break-even) yaitu suatu konsep yang digunakan untuk menganalisis jumlah minimum produk yang harus dihasilkan atau terjual agar perusahaan tidak mengalami kerugian. Keadaan pulang pokok (profit nol, π = 0 ) terjadi apabila R=C ; perusahaan tidak memperoleh keuntungan tetapi tidak pula menderita
kerugian. Secara grafik hal ini ditunjukkan oleh perpotongan antara kurva R dan kurva C .
Tingkat produksi Q1 dan Q4 mencerminkan keadaan pulang pokok, sebab
Q1 dan sebelah kanan Q4 mencerminkan keadaan rugi, sebab penerimaan total
lebih kecil dari pengeluaran total, R<C . Sedangkan area diantara Q1 dan Q4 mencerminkan keadaan untung, sebab penerimaan total lebih besar dari pengeluaran total,
R>C . Tingkat produksi Q3 mencerminkan tingkat produksi yang memberikan penerimaan total maksimum. Besar kecilnya keuntungan dicerminkan oleh besar kecilnya selisih positif antara R dan C .
Besar kecilnya keuntangan dicerminkan oleh besar kecilnya selisih positif antara R dan C . Secara grafik, hal ini ditunjukkan oleh jarak antara kurva R dan kurva
C . Semakin lebar lebar jarak positif tersebut semakin besar keuntungan yang
diperoleh. Jarak positif terlebar antara kurva R dan kurva C terjadi pada posisi di mana lereng (slope) dari kedua kurva itu sama besar, dan ini mencerminkan keuntungan terbesar atau maksimum.
Satu hal yang penting dicatat ialah bahwa jarak positif terlebar antara kurva R dan kurva C tidak selalu terjadi pada saat kurva R mencapai maksimum, juga tidak mesti terjadi pada saat kurva C mencapai minimum. Keuntungan maksimum tidak selalu terjadi saat R maksimum atau C minimum.
Contoh soal
Penerimaan total yang diperoleh sebuah perusahaan ditunjukkan oleh persamaan
R=−0,1 Q2+20Q , sedangkan biaya total yang dikeluarkan
C=0,25 Q3– 3Q2+7 Q+20 . Hitunglah profit perusahaan ini jika dihasilkan dan terjual barang sebanyak 10 dan 20 unit?
Penyelesaian π =R – C=−0,1 Q2 +20Q – 0,25Q3+3 Q2– 7 Q – 20 π =– 0,25Q3+2,9 Q2+13 Q – 20 Q=10 → π =– 0,25 (1000)+2,9(100)+13(10) – 20 ¿– 250+290+130 – 20=150 (keuntungan)
Q=20 → π =– 0,25 (8000)+2,9(400)+13(20) – 20
¿– 2000+1160+260 – 20=– 600 (kerugian)
7.3.5 Fungsi Utilitas
Fungsi utilitas menjelaskan besarnya utilitas (kepuasan, kegunaan) yang diperoleh seseorang dari mengkonsumsi suatu barang atau jasa. Pada umumnya semakin banyak jumlah suatu barang dikonsumsi semakin besar utilitas yang diperoleh, kemudian mencapai puncaknya (titik jenuh) pada jumlah konsumsi tertentu, sesudah itu justru menjadi berkurang atau bahkan negatif bila jumlah barang yang dikonsumsi terus menerus ditambah.
Utilitas total merupakan fungsi dari jumlah barang yang dikonsumsi. Persamaan utilitas total (total utility, U) dari mengkonsumsi suatu jenis barang berupa fungsi kuadrat parabolik, dengan kurva berbentuk parabola terbuka ke bawah. Utilitas marjinal (marginal
utility, MU) ialah utilitas tambahan yang diperoleh dari setiap tambahan satu unit barang yang
dikonsumsi.
Utilitas total mencapai puncaknya ketika utilitas marginal nol, dan berkurang ketika utilitas masrjinal negatif. 7.3.6 Fungsi Produksi Utilitas total : U=f (Q) Utilitas marjinal : MU =ΔU ΔQ U=f (Q) MU Q 0
Bentuk fungsi produksi toal (total product, P) yang nonlinear pada umumnya berupa sebuah persamaan kubik yang mempunyai titik belo dan sebuah titik puncak. Produk total merupakan fungsi dari jumlah masukan (input faktor produksi) yang digunakan. Dalam konsep produksi juga dikenal pengertian rata-rata dan marjinal.Produk rata-rata (average
product, AP) ialah jumlah keluaran atau produk yang dihasilkan dari setiap unit masukan
yang digunkana, merupakan hasil bagu produk total terhadap jumlah masukan. Sedangkan produk marjinal (marginal product, MP) ialah produk tambahan yang dihasilkan dari setiap tambahan satu unit masukan yang digunakan.
Jika dalam suatu kegiatan produksi dianggap hanya terdapat satu masukan variabel, katakanlah X , sementara masukan-masukan lainnya merupakan masukan tetap, maka fungsi produksinya dapat dinyatakan dengan notasi P=f ( X )
Produk total : P=f ( X ) Produk rata-rata : AP=PX
Produk marjinal : MP=ΔXΔP
Secara gravik, kurva produk total P mencapai puncaknya tepat ketika kurva produk marjinal MP=0 . Sedangkan MP mencapai puncaknya tepat pada posisi titik belok
kurva P . Di samping itu, kurva MP memotong kurva AP pada posisi maksimum AP . Penjelasan mengenai hal ini akan dibahas pada bab 9.
I : Titik Belok (Inflection Point)
0
y
x
0
y
x
Kasus 27Fungsi produksi yang dihadapi oleh seorang produsen ditunjukkan oleh P=9 X2−X3 . Bentuklah persamaan produk rata-ratanya serta hitunglah produk total dan produk rata-rata tersebut jika digunakan masukan sebanyak 6 unit. Berapa produk marjinalnya jika masukan yang digunakan ditambah 1 unit?
Diketahui P=9 X2−X3 sehingga AP=PX=9 X 2 −X3 X =9 X−X 2 Untuk X =6 , maka P=9 X2−X3=9 (6)2−(6 )3=108 AP=9 X −X2=9.6−(6 )2=18 Jika X =7 , maka P=9 X2−X3=9 (7)2−(7 )3=98 MP=ΔXΔP=98−1087−6 =−101 =−10
Produk marjinal negatif berarti masukan tambahan yang digunakan justru mengurangi hasil produksi.
7.3.7 Kurva Transformasi Produk
Kurva transformasi produk (product transformation curve) ialah kurva yang menunjukkan pilihan kombinsai jumlah produksi dua macam barang dengan menggunakan masukan yang sama sejumlah tertentu. Kurva ini dikenal juga dengan sebutan kurva kemungkinan produksi (product possibility curve). Kurva transformasi produk yang kuadratik dapat berupa potongan –potongan lingkaran, elips, hipernola maupun potongan parabola.
(a) (b)
Pada gambar di atas, x dan y masing-masing melambangkan jumlah produk X dan jumlah produk Y . Karena kurva transformasi produk mencerminkan pilihan kombinasi produksi, maka penambahan jumlah produk yang satu akan mengurangi jumlah produk yang lain. Patut dicatat : kurva transformasi produk dapat pula berupa garis lurus berlereng negatif. Kasus 28
Sebuah pabrik yang menggunakan bahan baku kulit menghasilkan sepatu dan tas. Kurva transformasi produk yang dihadapinya ditunjukkan oleh persamaan 4 s2+6,25 t2=40.000. Berapa pasang sepatu dan berapa buah tas paling banyak yang dapat diproduksi? Berapa pasang sepatu dapat dibuat jika pabrik ini memproduksi 60 buah tas?
Jumlah sepatu terbanyak yang dapat dibuat adalah jika pabrik tidak memproduksi tas (t=0) . Dengan perkataan lain, seluruh kulit yang tersedia (40.000unit) dialokasikan untuk membuat sepatu.
t=0 → 4 s2
=40.000 ↔ s2=10.000 ↔ s=100 pasang Jumlah tas terbanyak dapat dibuat :
s=0 → 6,25t2
=40.000 ↔t2=6.400 ↔ t=80 pasang
Kurva transformasi produk Berupa potongan elips Kurva transformasi produk
Jika t=60 , maka 4 s2+6,25 (60 )2=40.000 4 s2+6,25 (3600)=40.000 4 s2+22.500=40.000 4 s2=17.500 s2=4.375 s=66,14 = 66 pasang
7.3.8 Model Distribusi Pendapatan Pareto
Menurut Vilfredo Pareto, jumlah penduduk dari suatu populasi a yang berpendapat melebihi x adalah dimana b merupakan suatu parameter atau besaran populasi
tertentu, pada umunya berkisar 1,5. Kecuali ditentukan lain nilai b=1,5 . Model distribusi pendapatan versi Pareto ini mencerminkan sebuah hiperbola sama sisi untuk rentang 0<N <a dan 0<x <¿ pendapatan maksimum dalam populasi. Karena model ini
diterapkan secara universal, variabel pendapatan x dinyatakan dalam mata uang yang umum digunakan oleh negara-negara di seluruh dunia, yakni dollar Amerika Serikat (US $). Dengan demikian untuk untuk diterapkan pada kasus Indonesia, pendapatan dalam rupiah harus dikonversikan dulu ke dalam satuan US $.
Kasus 29
Hitunglah berapa dari 8 juta penduduk DKI Jakarta yang berpendapatan melebihi Rp 800 ribu. Berapa orang yang berpendapatan antara Rp 480 ribu dan Rp 640 ribu? (Kurs yang berlaku US$ 1= 2.000,00)
Untuk pendapatan > Rp 800 ribu X =Rp 800.000,00=US $ 400 N= a xb= 8.000 .000 400 3 2 =8.000 .000 8.000 =1.000
Untuk pendapatan antara Rp 480 ribu dan Rp 640 ribu X =Rp 480.000,00=US $ 240 N= a xb= 8.000 .000 240 3 2 =8.000 .000 ❑ =2.152 X =Rp 640.000,00=U S $ 320 N= a xb= 8.000 .000 320 3 2 =8.000 .000 5.724 =1.398
Jadi, terdapat 100 orang yang berpendapatan melebihi Rp 800 ribu. Sedangkan pendudukyang berpendapatan antara Rp 480 ribu dan Rp 640 ribu ada 2.152−1.398=754 orang (angka-angka di belakang koma dalam perhitungan ini dibulatkan).
Bentuk an disebuat sebagai bentuk eksponensial atau perpangkatan, dengan a disebut basis atau bilangan pokok dan n disebut eksponen atau pangkat. Sifat – sifat yang berlaku dalam bilangan berpangkat rasional diantaranya adalah sebagai berikut :
Perhatikan contoh soal berikut :
Hitunglah hasil perpangkatan (0,008)⋅² jawab : (0,008)⋅² = (1/125)⋅² = (1/5³)⋅² = (5⋅³)⋅² = 5^6 = 15.625 2. Persamaan Eksponen
Persamaan eksponen adalah suatu persamaan yang pangkatnya (eksponen), bilangan pokoknya, atau bilangan pokok dan eksponennya memuat suatu variabel.
Bentuk-bentuk persamaan eksponen yang akan kita bahas yaitu a. Bentuk persamaan a^f(x)=1
Misal terdapat persamaan a^f(x)=1 dengan a>0 dan a≠1, untuk menentukan himpunan penyelesaian bentuk persamaan tersebut gunakan sifat bahwa :
a^f(x) = 1 ⇔f(x)=0 b. Bentuk persamaan a^f(x) = a^p
Misalkan terdapat persamaan a^f(x) = a^p, dengan a>0 dan a≠1. Himpunan penyelesaian bentuk persamaan eksponen diatas ditentukan dengan cara menyamakan pangkat ruas kiri dengan ruas kanan.
a^f(x)= a^p ⇔ f(x) = p c. Bentuk persamaan a^f(x) = a^g(x)
Misalkan terdapat persamaan a^f(x) = a^g(x) dengan a>0 dan a≠1. Himpunan penyelesaian persamaan diatas dapat ditentukan dengan cara menyamakan persamaan pangkatnya. Jadi dapat kita katakan sebagai berikut :
a^f(x) = a^g(x) ⇔ f(x) = g(x) d. Bentuk Persamaan a^f(x) = b^f(x)
Misalkan terdapat persamaan a^f(x) = b^f(x), dengan a≠b ;a,b >0 ; a,b ≠1. Himpunan penyelesaian persamaan eksponen tersebut dapat ditentukan dengan cara menyamakan f(x0 dengan nol. Jadi dapat disimpulkan sebagai berikut :
a^f(x) = b^f(x) ⇔ f(x) = 0 e. Bentuk persamaan a^f(x) = b^g(x)
Misalkan diberikan persamaan a^f(x) = b^g(x) dengan a≤b ; a,b >0 ; a,b ≠1, dan f(x) ≠ g(x). Himpunan penyelesaian untuk bentuk persamaan eksponen tersebut dengan melogaritmakan kedua ruas, yaitu :
log a^f(x) = log b^g(x) f. Bentuk Persamaan A{a^f(x)}² + B{a^f(x)}+ C = 0
Untuk menentukan penyelesaian persamaan eksponen yang berbentuk persamaan kuadrat dapat dikerjakan dengan cara memfaktorkan, melengkapkan kuadrat sempurna atau rumus abc.
g. Bntuk persamaan f(x)^g(x) =1 ; f(x)≠g(x)
Untuk menyelesaikan persamaan eksponen dengan bentuk tersebut, lakukanlah langkah-langkah berikut :
1). g(x)=0 karena ruas kanan nilainya 1 berarti g(x) harus sama dengan nol. 2). f(x)=1 karena jika f(x)=1 maka bilangan 1 dipangkatkan berapapun nilainya 1. 3). f(x)=-1, dengan syarat g(x) harus genap.
h. Bentuk persamaan f(x)^g(x) = f(x)^h(x)
Untuk nilai g(x) ≠ h(x). Himpunan penyelesaian bentuk eksponen tersebut diperoleh dari empat kemungkinan berikut :
1). g(x)=h(x0 karena bilangan pokok sudah sama maka pangkatnya harus sama.
2). f(x)=1 karena g9x) ≠ h(x) maka bilangan pokok harus bernilai 1 (satu) agar persamaan bernilai benar.
3). f(x)=-1, bewrakibat g(x) dan h(x) harus sama-sama bernilai genap atau sama-sama bernilai ganjil.
4). f(x)=0, dengan g(x) dan h(x) masing-masing bernilai positif dituliskan g(x)>0 atau h(x)>0. i. Bnetuk persamaan g(x)^f(x) = h(x)^f(x)
persamaan diatas akan bernilai benar jika a. f(x)=0 untuk g(x)≠0 dan h(x)≠0 ; b. g(x)=h(x)
FUNGSI LOGARITMA
Bentuk eksponen atau perpangkatan dapat kita tulis dalam bentuk logaritma. Secara umum dapat ditulis sebagai berikut :
Jika ab = c dengan a > 0 dan a ≠ 1 maka alog c = b dalam hal ini a disebut basis atau pokok logaritma dan c merupakan bilangan yang dilogaritmakan. Logaritma memuliki sifat-sifat sebagai berikut :
3.1 Bentuk umum dari fungsi logaritma yaitu Jika ay = x dengan a ≥0 dan a ≠ 1 maka y =alog x
mempunyai sifat-sifat :
1. semua x > 0 terdefinisi
2. jika x mendekati no maka nilai y besar sekali dan positif 3. untuk x=1 maka y=o
4. untuk x > 1 maka y negatif sehingga jika nilai x semakin besar maka nilai y semakin kecil.
3.2. Grafik Fungsi y =alog x untuk a >0 mempunyai sifat – sifat sebagai berikut :
1. untuk semua x > 0 terdefinisi
3. untuk x=1 maka y=0
4. untuk x > 1 maka y positif sehingga jika x semakin besar maka y semakin besar. Berikut ini gambar grafiknya :
Fungsi pertumbuhan merupakan salah satu contoh aplikasi fungsi eksponen dalam bidang ekonomi. Sifat utama fungsi ini adalah meningkat secara monoton. Fungsi pertumbuhan mempunyai beberapa bentuk, dengan atau tanpa asimtut yang merupakan batas atas.
Dalam karya tulis ini fungsi pertumbuhan yang dimaksud hanya terbatas pada fungsi bunga majemuk, pertumbuhan penduduk atau biologis, kurva (fungsi) Gompertz, dan kurva (fungsi) pengajaran.
1. Fungsi Bunga Majemuk
Besarnya modal yang dibungakan tergantung dari waktu lamanya modal dibungakan asal tingkat bunga konstan. Jika modal (pokok) sebesar dibungakan kali per tahun dengan bunga sebesar 100 % (atau r) per tahun maka setelah tahun, modal tersebut akan menjadi:
Apabila sangat besar yaitu , maksudnya bunga yang dibayarkan secara kontinyu atau bunga ditambahkan terus menerus terhadap modal, maka persamaannya akan menjadi:
Dengan,
= Modal awal atau besar modal pada tahu yang ke nol. = Modal akhir atau besar modal pada tahun yang ke = Bilangan basis dalam logaritma natural
= Kelipatan bunga yang dibayar per tahun = Waktu lamanya modal (pokok) dibungakan = Besarnya bunga per tahun
Jikan fungsi dibuat grafiknya, secara umum bentuknya sebagai berikut:
Gambar 02 Grafik Fungsi Bunga Majemuk Dengan Contoh:
Seorang petani membutuhkan uang sebesar 5 juta rupiah pada 10 tahun yang akan datang. Berapa jumlah uang yang harus ditabung mulai sekarang dengan bunga 24% per tahun untuk memperoleh jumlah uang yang diharapkan?
Penyelesaian: Diketahui: = 5000000 = 10 tahun = 24 % = 0,24 = 1 Ditanyakan: = ...? Jawab:
2. Pertumbuhan Penduduk
Bila penduduk suatu negara (daerah) pada suatu saat mengalami pertumbuhan sebesar 100 % per tahun (atau per tahun), maka setelah t tahun, jumlah penduduk menjadi:
Bila suatu negara (daerah) dengan jumlah penduduk yang besar, maka pertumbuhan penduduk berlangsung hampir kontinyu, jumlah penduduk setelah t tahun menjadi:
Misalkan pada persamaan sama dengan yaitu , maka
persamaan di atas dapat dinyatakan sebagai berikut.
= jumlah penduduk pada tahun yang ke t
= jumlah penduduk pada tahun awal yaitu tahun yang ke nol = tingkat pertumbuhan
= = tingkat pertumbuhan ditambah 1 Contoh:
Pada tahun 2001 penduduk sebuah kota adalah 629039 jiwa. Sedangkan pada tahun 2006 jumlah penduduknya adalah 771186 jiwa.
a. Berapa tingkat pertumbuhan penduduk kota tersebut? b. Perkirakan jumlah penduduk kota tersebut pada tahun 2016! Penyelesaian:
Diketahui: = 629039
= 771186 (tahun 2006)
t = 5 (dari 2001 sampai dengan 2006) Ditanyakan:
a. = ...?
b. = ...? (tahun 2016) Jawab:
b. t = 15 (dari 2001 sampai dengan 2016)
Karena t cukup besar maka untuk mempermudah perhitungan kita gunakan logaritma, sehingga:
3. Fungsi Gompertz
Fungsi ini menggambarkan perkembangan yang lambat waktu mulai tumbuh, dan waktu mendekati asimtut batas pertumbuhan. Fungsi ini dinyatakan sebagai berikut.
Keterangan:
= jumlah penduduk pada tahun ke
= tingkat pertumbuhan (dengan ) = proporsi pertumbuhan awal
= tingkat pertumbuhan dewasa (yaitu asimtut tertinggi) = indeks waktu
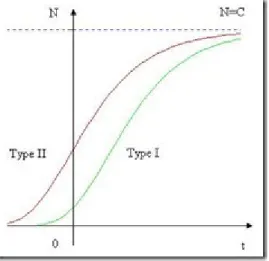
Sifat utama dari fungsi Gompertz digambarkan dengan dua jenis kurva di bawah ini. Tipe I:
Tipe II:
Gambar 03 Kurva Gompertz
Kurva I, untuk nilai kecil yang positif kurva cembung tehadap sumbu t (berakselerasi positif) dan untuk nilai besar yang positif, kurva cekung tehadap sumbu (berakselerasi negatif). Sedangkan kurva II, untuk semua nilai positif, kurva cekung terhadap sumbu (berakselerasi negatif).
Kurva yang ditemukan Gompertz ini dalam bidang ekonomi digunakan untuk fungsi pendapatan total dan produksi.
Contoh:
Penjualan setiap bulan dari sebuah perusahaan memenuhi fungsi
p adalah jumlah pengeluaran untuk promosi dan advertensi. adalah penjumlahan atau omzet setiap bulan.
a. Berapa besar penjualan bila pengeluaran untuk promosi dan advertensi sama dengan nol atau berapa besar penjualan awalnya?
b. Berapa penjualan maksimumnya?
c. Berapa besar penjualannya bila pengeluaran untukpromosi dan avertensi 5? Penyelesaian: Diketahui: Ditanyakan: a. jika b. maksimum =...? ( ) c. jika Jawab:
a. Jika , maka adalah:
Jadi penjualan awalnya adalah 100
b. Penjualan maksimum terjadi saat tingkat pertumbuhannya nol
Jadi, penjualan maksimunya adalah 1000 c. Jika , maka adalah:
Jadi, besar penjualannya bila pengeluaran untuk promosi dan advertensi 5 adalah
4. Fungsi Pengajaran
Fungsi pengajaran umumnya dipakai oleh psikolog untuk menggambarkan taraf pertumbuhan pendidikan manusia, yang sifatnya meningkat cepat pada awalnya dan semakin lambat ketika mendekati asimtut batas pertumbuhan. Fungsi ini dinyatakan sebagai berikut.
, , dan adalah konstanta positif = keaktifan belajar
= variabel pendorong
Bentuk grafiknya secara umum adalah sebagai berikut.
Gambar 04 Grafik Fungsi Pengajaran
Fungsi pengajaran dalam ewkonomi dapat digunakan untuk menjelaskan fungsi biaya dan produksi.
Contoh:
Biaya produksi total (dalam jutaan rupiah) dari sebuah perusahaan dapat dinyatakan sebagai berikut.
a. Berapa besar biaya tetapnya?
b. Bila berproduksi 100 unit, berapa besar proporsi biaya produksi tetapnya terhadap biaya produksi totalnya?
Penyelesaian: Diketahui: Ditanyakan: a. =...? jika
b. Besar proporsi biaya produksi tetapnya terhadap biaya produksi totalnya =...? jika
Jawab:
a. Jika , maka adalah
Jadi biaya tetapnya adalah 50 juta rupiah b. Jika , maka total adalah
Jadi, besar proporsi biaya produksi tetapnya terhadap biaya produksi totalnya ( ) adalah: