TIGA DIMENSI
01. MA-75-08
Banyaknya garis lurus yang memotong tiga buah garis yang saling bersilangan ada …
A. nol buah B. dua buah
C. lebih dari dua buah D. satu buah
02. MA-95-01
Garis g tegak lurus pada bidang V dan bidang W mem-bentuk sudut lancip dengan bidang V. Jika W memo-tong V menurut suatu garis s, maka proyeksi g pada W A. tegak lurus pada V
B. tegak lurus pada s
C. berselang tegak lurus dengan g D. sejajar dengan V
E. sejajar dengan s 03. MA-96-10
Garis-garis h dan k pada bidang V dengan h ⊥ k. Garis g tegak lurus V, maka …
(1) ada bidang melalui g dan sejajar h
(2) ada garis memotong g, sejajar V dan tegak lurus h (3) g ⊥ h dan g ⊥ k
(4) ada bidang yang tegak lurus g dan tegak lurus h. 04. MA-87-02
a dan b adalah dua buah garis yang bersilang. Titik-titik P, Q, R terletak pada a dan Titik-titik-Titik-titik K, L, M terletak pada b. Bidang yang melalui P, Q, dan K dan bidang yang melalui R, L , M …
A. berhimpit B. sejajar C. berpotongan sepanjang QL D. berpotongan sepanjang PM E. berpotongan sepanjang RK 05. MA-79-42
Garis g dan h bersinggungan. Bidang V melalui g sejajar dengan garis h berpotongan dengan bidang V. Jika k adalah garis potong kedua bidang tersebut, maka
A. k sejajar dengan g dan memotong h
B. k memotong g dan h
C. k dan h bersilangan
D. k sejajar h memotong g
E. k berimpit dengan g
06. MA-85-30
Bila garis a tegak lurus bidang A, garis b tegak lurus pa da bidang B, bidang A berpotongan dengan bidang B pada garis h, maka …
(1) a tegak lurus pada h (2) a tegak lurus pada B (3) b tegak lurus pada h (4) b tegak lurus pada A
07. MA-80-43
Bila garis a tegak lurus pada bidang A, garis b tegak lurus pada bidang B, dan bidang A berpotongan dengan bidang B pada garis h, maka … (1) a tegak lurus pada h
(2) a tegak lurus pada B (3) b tegak lurus pada h (4) b tegak lurus pada A 08. MA-78-12
Bidang V dan bidang W saling berpotongan pada garis a. Jika garis g tegak lurus bidang V, maka …
A. g tegak lurus bidang W
B. g sejajar a
C. g selalu sejajar bidang W
D. g selalu memotong bidang W
E. g tegak lurus a 09. MA-83-32
Bidang V dan bidang W berpotongan sepanjang garis a. Bidang U tegak lurus pada garis a. Dengan demikian …
(1) bidang U ⊥ bidang V (2) bidang U ⊥ bidang W
(3) garis potong bidang U dan bidang W ⊥ a (4) garis potong bidang U dan bidang V ⊥ a 10. MA-82-32
Diketahui tiga bidang U, V dan W, maka yang benar adalah
(1) Jika U dan W berpotongan, V dan W berpo-tongan, maka U sejajar V
(2) Jika W tegak lurus U dan V tegak lurus U maka V sejajar W
(3) Jika U dan V berpotongan dan W tegak lurus U maka V tidak akan memotong W
(4) Jika U sejajar V dan W tegak lurus U, maka W tegak lurus V
11. ITB-76-33
Garis g dan h bersinggungan. Bidang V melalui g dan sejajar dengan garis h, bidang W melalui h dan berpotongan dengan bidang V. Jika k adalah garis potong kedua bidang tersebut, maka …
A. k memotong g dan h
B. k dan h bersilangan C. k sejajar h dan memotong g
12. MA-02-08
Bidang V dan W berpotongan tegak lurus sepanjang garis g. Garis l membentuk sudut 45o dengan V dan 30o
dengan W. Sinus sudut antara l dan g adalah … A. 2 1 B. 22 C. 23 D. 31 3 E. 32 13. MA-82-20
ABCD adalah empat persegi panjang pada bidang horisontal, dan ADEF empat persegi panjang pula pada bidang vertikal. Panjang AF = 3 m, BC = 4 m dan CE = 7 m. Jika α dan β berturut-turut sudut antara BE dengan bidang ABCD dan bidang ADEF, maka tan α tan β= … A. 5 3 3 B. 5 3 4 C. 5 3 5 D. 214 E. 215 14. MA-78-33
Kubus ABCD.EFGH berusuk a cm. P, Q dan R adalah titik-titik tengah dari AD, AB dan BF. Penampang bidang PQR dengan kubus berupa …
A. bujur sangkar B. segi tiga sama sisi C. segi lima beraturan D. trapesium sama kaki E. segi enam beraturan 15. MA-78-42
Perbandingan panjang rusuk kubus ABCD.EFGH dan panjang rusuk kubus KLMN.PQRS adalah sebagai 3 : 4 sedangkan jumlah isi kedua kubus itu sama dengan 728 cm2, maka … A. KL = 6 cm B. KL = 4 cm C. AB = 8 cm D. AB = 6 cm E. AB = 3 cm 16. MA-77-25
Dalam kubus ABCD.EFGH garis-garis AF dan BH bersilangan dengan sudut …
A. 300
B. 450
C. 600
17. MA-77-38
B1 ialah bola luar kubus K, sedangkan B2 ialah bola
dalam kubus K. Maka perbandingan (isi B1) : (isi B2)
sama dengan A. 3√3 : 1 B. 2√2 : 1 C. 27 : 1 D. 3 : 1 E. 2 : 1 18. ITB-76-36
Perbandingan antara isi bola dalam dan isi bola luar kubus adalah …
A. 1 : 2√2 B. 1 : 3√3 C. 1 : 5√5
D. tergantung dari panjang rusuk kubus. 19. MA-79-36
Dalam sebuah kubus ABCD.EFGH dengan panjang rusuk sama dengan 2 dibuat bola dengan titik pusat berhimpit dengan titik pusat kubus sedemikian sehingga rusuk-rusuk AB, CD, EF dan GH menyinggung bola tersebut. Maka luas permukaan bola tersebut sama dengan …
A. 12π B. 4π C. 38π√2 D. 8π√2 E. 8π 20. MA-01-09
Panjang rusuk kubus ABCD.EFGH adalah a. Jarak A ke diagonal BH adalah … A. a2 6 B. a3 6 C. a4 6 D. a5 6 E. a6 6 21. MA–99–03
Diketahui kubus ABCD.EFGH dengan rusuk 4. Titik T pada perpanjangan CG sehingga CG = GT. Jika sudut antara TC dan bidang BDT adalah α maka tan α = … A. √2
B. 21√2 C. 31√2 D. 41√2 E. 61√2
22. MA–99–03
Diketahui kubus ABCD.EFGH dengan rusuk 4. Titik T pada perpanjangan CG sehingga CG = GT. Jika sudut antara TC dan bidang BDT adalah α maka tan α = …
A. √2 B. 21√2 C. 31√2 D. 41√2 E. 61√2 23. MA-06-03
Diketahui kubus ABCD.EFGH dengan panjang rusuk 4 cm. Jika titik P pada CG dan titik Q pada DH dan CP = DQ = 1 cm. maka bidang PQEF mengiris kubus tersebut menjadi dua bagian. Volume bagian yang lebih besar adalah …
A. 36 cm3 B. 38 cm3 C. 40 cm3 D. 42 cm3 E. 44 cm3 24. MA-00-04
Dalam kubus ABCD.EFGH titik S adalah titik tengah sisi CD dan P adalah titik tengah diagonal ruang BH. Perbandingan antara volume limas P.BCS dan volume kubus ABCD.EFGH adalah …
A. 1 : 4 B. 1 : 6 C. 1 : 8 D. 1 : 12 E. 1 : 24 25. MA-94-01
Titik P, Q, R masing-masing terletak rusuk rusuk BC, FG, dan EH sebuah kubus ABCD.EFGH.
Jika BP = 31BC, FQ= 32FG dan ER = 32EH, perban-dingan luas irisan bidang P,Q dan R dan luas permu-kaan kubus adalah …
H G A. 1 : 6 R Q B. √8 : 6 E F C. √10 : 6 D. √8 : 18 D C E. √10 : 18 A B P 26. MA-87-07
H G Diketahui kubus ABCD.EFGH dengan rusuk a. Melalui diagonal E F DF dan titik tengah rusuk AE di
buat bidang datar. Luas bagian bi- D C dang di dalam kubus sama dengan
… A B A. 23a2 B. 2 a2 C. a2 √6 D. 12a2 √6 E. 31a 27. MA-86-12
Diketahui kubus ABCD.EFGH dengan sisi a. T adalah suatu ririk pada perpanjangan AE sehingga TE = 21a.
Jika bidang TBD memotong bidang alas EFGH sepan-jang PQ, maka PQ = … A. a3 T H G B. a3√2 E F C. a2 D C D. a2√2 A B E. 23a√2 28. MA-03-05
Diketahui kubus ABCD.EFGH dengan panjang rusuk a cm. Jika S merupakan proyeksi titik C pada bidang AFH, maka jarak titik A ke titik S adalah …
A. 13a 3 cm B. 13a 6 cm C. 32a 6 cm D. a√2 cm E. a√3 cm 29. MA-80-40
Pada suatu kubus ABCD.EFGH, sudut antara garis AH dan bidang diagonal BFHD sama dengan …
A. 150
B. 300
C. 450
D. 600
30. MA-88-03
H G Diketahui kubus ABCD.EFGH P pertengahan AE, Q
pertengah
E F Q an CG. Bidang yang melalui H, P dan Q membagi kubus atas P D C dua bagian dengan perbanding-
an volumenya … A B A. 3 : 4 B. 3 : 2 C. 3 : 1 D. 2 : 1 E. 1 : 1 31. MA-80-24
Jarak antara titik C dengan bidang BDG dalam kubus ABCD.EFGH yang panjang rusuknya 6 cm , adalah … A. 3√2 cm B. 2√6 cm C. √6 cm D. √3 cm E. 2√3 cm 32. MA-84-16
Ditentukan kubus ABCD.EFGH. Tangen sudut antara CG dengan bidang BDG ialah
A. 21√3 H G B. √2 E F C. 21√2 D. √3 D C E. √6 A B 33. MA-04-09
Diketahui kubus ABCD.EFGH dengan panjang rusuk a. P dan Q masing-masing merupakan titik tengah AB dan CD, sedangkan R merupakan titik perpotongan EG dan FH. Jarak titik R ke bidang EPQH adalah … A. 5 a B. 3 a C.
2
a
D. 5 5 a E. 2 2 a 34. MA-05-03Diketahui kubus ABCD.EFGH dengan panjang rusuk 2. Jika P titik tengah HG, Q titik tengah FG, R titik tengah PQ dan BS adalah proyeksi BR pada bidang AMCD, maka panjang BS = …
A. 12√14 B. 12√10 C. 12√6 D. 1 E. 12√2 35. MA-81-22 H G E F D C A B
ABCD.EFGH suatu kubus dengan rusuk a. Di antara pernyataan-pernyataan di bawah ini
1.AF memotong BG 2.AC ⊥ BH
3.Jarak BD dan CE sama dengan 61a√6 4.BD ⊥ CH
5.Jarak AE dan DF sama dengan 12a√2 yang benar ialah pernyataan …
A. 1, 2 dan 4 B. 2, 3 dan 5 C. 2, 4 dan 5 D. 1, 3 dan 5 E. 1, 4 dan 5 36. MA-81-32
Tinggi suatu bidang empat beraturan, dengan rusuk-rusuk sama dengan a cm, adalah …
A. 21a√6 cm B. 13a√6 cm C. 32a√6 cm D. 41a√3 cm E. 13a√3 cm
37. MA–98–06
Pada bidang empat T.ABCD, bidang alas ABC merupa-kan segitiga sama sisi, TA tegak lurus pada bidang alas, panjang TA sama dengan 1 dan besar sudut TBA ada-lah 30o. Jika α adalah sudut antara
bidang TBC dan bidang alas, maka tan α = … A. 3 2 B. 3 3 C. 3 3 2 D. √3 E. 2 3 38. MA-93-05
T Pada limas beraturan T.ABCD, AT = 3a√2, AB = 3a. Luas irisan bidang datar melalui D C A dan tegak lurus TC A B dengan limas … A. a2√3 B. 3a2√2 C. 3a2√6 D. 6a2√3 E. 6a2√6 39. MA-91-06
Panjang setiap rusuk bidang empat beraturan T.ABC sa ma dengan 16 cm. Jika P pertengahan AT dan Q perte-ngahan BC, maka PQ sama dengan …
A. 8 √2 cm B. 8 √3 cm C. 8 √6 cm D. 12 √2 cm E. 12 √3 cm 40. MA-97-09
Pada bidang empat T.ABC, bidang TAB, TAC dan ABC saling tegak lurus. Jika TA = 3, AB = AC = √3 dan α adalah sudut antara bidang TBC dan ABC, maka sin α adalah … 7 42 7 7 2 7 21 7 14 7 7 E. D. C. . B A. 41. MA-81-20
Dari sebuah bidang-empat ABCD diketahui BC ⊥ BD dan AB tegak lurus bidang BCD. BC = BD = a√2 dan AB = a , maka sudut antara bidang ACD dan bidang BCD sama dengan … A. 6 π B. 5 π C. 4 π D. 3 π E. 2 π 42. MA-90-05
Rusuk TA, TB TC pada bidang empat T.ABC saling te-gak lurus pada T. AB = AC = 2√2 dan AT = 2. Jika α adalah sudut antara bidang ABC dan bidang TBC, ma-ka tan α = … A. √2 B. √3 C. 21√2 D. 21√3 E. 31√6 43. MA–98–06
Pada bidang empat T.ABCD, bidang alas ABC merupa-kan segitiga sama sisi, TA tegak lurus pada bidang alas, panjang TA sama dengan 1 dan besar sudut TBA ada-lah 30o. Jika α adalah sudut antara
bidang TBC dan bidang alas, maka tan α = … A. 3 2 B. 3 3 C. 3 3 2 D. √3 E. 2 3 44. MA-83-19
Pada limas beraturan T.ABCD , TA = TB = TC = TD = √3 dm dan ABCD bujur sangkar dengan sisi 2 dm. Besar sudut antara bidang TAB dan TCD ialah … A. 90 0
B. 75 0
C. 60 0
D. 45 0
45. MA-92-10
Diketahui bidang empat T.ABC. TA = TB = 5 ; TC = 2 ; CA = CB = 4 ; AB = 6. Jika α sudut antara TC dan bi-dang TAB, maka cos α adalah …
A. 1615 B. 1613 C. 1611 D. 169 E. 167 46. MA-89-07
Diketahui ABCD sebuah siku empat. ∆TAB sama kaki dengan alas AB. ∆TAB tegak lurus pada ABCD. Jika AB = 12, AD = 7 dan TD = 25 maka jarak T ke bidang ABCD adalah … C D A. 12√2111 B. 6√15 B C. 15√6 A D. 17 E. √612 T 47. MA-86-34
Diketahui ABC segitiga D sembarang dan E pada BC.
Jika DA ⊥ ABC dan AE ⊥ BC, maka …
(1) DA ⊥ BC A C
(2) BC ⊥ ADE
(3) DE ⊥ BC E
(4) ∠ AED = sudut antara
bidang ABC dan bidang BCD B 48. MA-85-13
Dari limas beraturan T.PQRS diketahui TP = TQ = TR = TS = 2 dan PQ = QR = RS = SP = 2. Jika α adalah su-dut antara bidang TPQ dan bidang TRS, maka cos α sama dengan … A. 21 B. 31 C. 32 D. 21√3 E. 31√3 49. MA-85-15
D Pada bangun DABC diketahui bahwa segitiga ABC sama sisi A DC ⊥ bidang ABC, panjang
DC = 1, dan sudut DBC = 300
C Bila α menyatakan sudut anta- ra bidang DAB dengan CAB, B maka tg α adalah … A. √3 B. 31√3 C. 32√3 D. 32 E. 23 50. MA-79-15
Pada bangun DABC, diketahui bidang ABC sama sisi, DC tegak lurus ABC, panjang DC = 1 , dan sudut DBC = 300. Bila α adalah sudut antara bidang DAB dan
CAB, maka tan α adalah … D A. √3 B. 31√3 A C. 32√3 C D. 23 B E. 32 51. MA-79-22
Dari sebuah kerucut lingkaran tegak diketahui bahwa : penambahan volum karena bertambahnya jari-jari dengan 24 cm sama dengan penambahan volum karena bertambahnya tinggi kerucut itu dengan 24 cm. Jika ting gi semula kerucut tersebut 3 cm, maka jari-jari semula … A. 18 cm B. 12 cm C. 8 cm D. 6 cm E. 3 cm 52. MA-75-31
Dari suatu bidang empat tegak OABC, diketahui OA tegak lurus bidang ABC, OA = 6 cm, segitiga ABC sama sisi dengan AB = 8 cm. Maka luas segitiga OBC adalah …
A. 4√42 cm2
B. 6√21 cm2
C. 16√5 cm2
53. MA-75-39
Jika dari suatu limas beraturan T.ABCD diketahui TA = AB = 4 cm, maka tinggi dan isinya berturut-turut adalah … A. 2√2 cm dan 16√2 cm3 B. 2√2 cm dan 32 32 cm3 C. 3√2 cm dan 16√3 cm3 D. 3√2 cm dan 32 32 cm3 54. MA-84-28
Bidang empat (tetrahedron) T.ABC mempunyai alas segitiga siku-siku ABC, dengan sisi AB = AC. TA = 5√3 dan tegak lurus pada alas. Jika BC = 10, maka sudut an-tara bidang TBC dan bidang alas adalah … A. 300 B. 450 C. 600 D. 750 E. 900 55. ITB-76-34
Tinggi sebuah kerucut lingkaran tegak 16 cm, sedangkan jejari (radius) lingkaran alasnya 12 cm. Perbandingan antara isi bola dalam kerucut dan isi kerucut itu sendiri adalah …
A. 3 : 5 B. 3 : 8 C. 5 : 3 D. 5 : 8 56. ITB-76-35
Diketahui limas T.ABC, pada rusuk TA dipilih titik P pada TB titik Q dan pada TC titik R sehingga:
TP : PA = 1 : 2 TQ : QB = 2 : 3 TR : RC = 3 : 4
Maka perbandingan isi limas T.ABC dan T.PQR adalah …
A. 35 : 2 B. 35 : 98 C. 5 : 1 D. 4 : 1
Eksponen
01. MA-77-48
Jika n bilangan asli, maka 10 2n – 1 habis dibagi oleh
… (1) 3 (2) 9 (3) 99 (4) 11 02. MA-80-30
Harga x yang memenuhi persamaan 4 x + 3 = 48x+5
ialah … A. 2 B. 5 C. 59 D. –59 E. 52 03. MD-93-09
Nilai x yang memenuhi persamaan
( )
41 x−1=323x+1adalah … A. x = 92 B. x = 94 C. x = 95 D. x = 52 E. x = 54 04. MA-78-02
Akar dari persamaan 3 5x – 1 = 27 x + 3 adalah …
A. 1 B. 2 C. 3 D. 4 E. 5 05. MA-86-35
Jika diketahui 3x2- 1=27 x+3 , maka x = …
(1) 5 (2) –5 (3) –2 (4) 2 06. MD-92-13
Penyelesaian persamaan 32x+1= 9x-2 ialah …
A. 0 B. 1 2 1 C. 2 07. MD-04-01
Nilai x yang memenuhi persamaan
( )
3 2 1 1 . 3 2 2 1 − − = + x adalah … A. 4 B. 2 C. 0 D. –2 E. –4 08. MA-89-06Nilai x yang memenuhi pertaksamaan
3 2 9 1 x > 8127 2 2 x- ) x ( adalah … A. x >−125 B. x <−125 C. x >54 D. x >−54 E. x <−54 09. MD-89-14 Persamaan 93x+2 = 2 5 81 1 x - mempunyai penyelesaian x = ... A. 261 B. 1 7 6 C. 1 7 1 D. 1 12 1 E. 1141 10. MA-83-23
Nilai x dari persamaan 3 2 2 9 1 3 3 = x- ⎟⎠ ⎞ ⎜ ⎝ ⎛ adalah … A. 32 B. 421 C. –331 D. 331 E. –421
11. MD-05-02
Nilai x yang memenuhi persamaan :
(
)
( )
0,2 1 008 , 0 5 4 3 7 2 = + − − x x adalah … A. –3 B. –2 C. –1 D. 0 E. 1 12. MA-06-13 Jika xy 2 8 = 32 dan 4x . 2y = 322 , maka x + y = … A. 1 B. 5 C. 6 D. 7 E. 8 13. MD-95-20 Jika 3x- 2y = 811 dan 2x – y – 16 = 0, maka nilai x + y = …
A. 21 B. 20 C. 18 D. 16 E. 14 14. MD-96-23
Untuk x dan y yang memenuhi sistem persamaan 5x – 2y + 1 = 25x – 2y dan 4x – y + 2 = 32x – 2y + 1 , maka nilai
x . y = … A. 6 B. 8 C. 10 D. 15 E. 20 15. MD-83-16
Nilai x yang memenuhi persamaan 3x 0,4 = 9
( )
0,6 3 1 adalah … A. 3 1 B. 1 C. 3 D. √3 E. 91 16. MA-77-22 Jika 4 3 1 2 - x - x = 0 maka haruslah … A. x = 1 B. x = + 2 C. x = 31 D. x = 0 E. x = –31 17. MD-85-17Dari fungsi eksponen f (x) = 2x2-x-2 harga x yang memenuhi f (x) = 1 adalah … A. 0 B. 14 C. –1 atau 2 D. 0 atau 4 1 E. –2 atau 1 18. MD-00-21 Diberikan persamaan : 9 1 3 3 243 1 2 2 3 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − x x
Jika xo memenuhi persamaan, maka nilai 1 – 43xo = …
A. 1163 B. 1 41 C. 143 D. 2 41 E. 243 19. MD-06-19
Jika x1 dan x2 solusi persamaan 3.9x + 91 – x = 28, maka
x1 + x2 = … A. –12 B. 0 C. 2 1 D. 1 E. 112 20. MD-83-15
Himpunan jawab persamaan 32x + 2 + 8 3x – 1 = 0 adalah
A. (12) B. (12 , 3 1 ) C. (–2 , 3 1 ) D. (–2) E. (–2 , –31) 21. MD-84-17 Bila 4 5 (2 3x - 2) + 20 8x = 1 , maka x = … A. 2 3 B. 32 C. –32 D. –23 E. 1
22. MA-92-05 Diketahui f (x) = 25–x + 2x – 12. Jika f (x1) = f (x2) = 0 maka x1 . x2 = … A. 6 B. 5 C. 4 D. –5 E. –6 23. MD-90-20
Jumlah-jumlah akar persamaan 3 (4x) – 5 (2x) + 2 = 0
adalah … A. –2 B. –1 C. 0 D. 1 E. 2 24. MD-98-19
Jumlah akar-akar persamaan 5x+1 + 51–x = 11 adalah …
A. 6 B. 5 C. 0 D. –2 E. –4 25. MA-03-04
Jarak kedua titik potong kurva y = 22x+1 – 5.2x + 2
dengan sumbu x adalah … A. 2 B. 3 C. 4 D. 5 E. 6 26. MD-94-23
Nilai-nilai x yang memenuhi persamaan 1000 (x2 – 3x – 4) = 10 (x2 – 2x – 3) adalah … A. x1 = 1 ; x2 = 29 B. x1 = –1 ; x2 = 29 C. x1 = –1 ; x2 = 27 D. x1 = 1 ; x2 = – 27 E. x1 = –12 , x2 = 9 27. MD-89-10
Himpunan penyelesaian
( )
x2 x =x4x−x2adalah ... A. {1} B. {2} C. {0 , 2} D. {1 , 2} E. {0, 1 , 2} 28. MD-85-06 Jika f = x → x - x) ( ) x ( 1 67 2 2 maka f (3) adalah … A. 256 B. 64 C. 32 D. 16 E. 8 29. MA-04-06 Kurva x x y ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = + 9 13 1 berada di bawah kurva y = 3x + 1 pada saat … A. x < 2 B. x > 1 C. x < 1 D. x > 0 E. x < 0 30. MD-05-16
Jika grafik fungsi y = N (3–ax) melalui titik (1,
27 1 ) dan
(21,91), maka nilai a yang memenuhi adalah … A. –2 B. –1 C. 2 1 D. 1 E. 2 31. MD-05-01
Jika f(n) = 2n +2 6n – 4 dan g(n) = 12n – 1 , n bilangan asli,
maka ) ( ) ( n g n f = … A. 32 1 B. 271 C. 181 D. 91 E. 92 32. MA-87-09
Jika f (x) = 4x dan g (x) = 4 –x , maka …
(1) grafik f (x) dan grafik g (x) berpotongan di (0,1) (2) g (x) adalah fungsi invers dari f (x)
(3) grafik g (x) adalah cermin grafik f (x) terhadap sumbu y
33. MA-77-24
Bila rumus pertumbuhan suatu kecambah adalah y = 1 – 2 – t, maka garis batas pertumbuhannya adalah … A. y = 0 B. y = 1 C. y = 12 D. y = 43 E. y = 2 34. MA-05-07
Suatu populasi hewan mengikuti hukum pertumbuhan yang berbunyi :
N(t) = 100.000 . 2t – 2
N(t) : besar populasi pada saat t t : waktu dalam satuan tahun
Agar besar populasi menjadi 3 kali lipat populasi awal (saat t = 0) maka t = … A. 10log 3 B. 10log 3 – 2 C. 2log 3 – 4 D. 2log 3 – 2 E. 2log 3 35. MA-84-23
Jika x1 dan x2 akar-akar dari persamaan
3x + 33 - x – 28 =0 maka jumlah kedua akar tersebut adalah … A. 0 B. 3 C. log 3 D. 3 log 3 E. 3 log 14
Logaritma
01. MA-80-03
Jika diketahui: a, b dan c bilangan-bilangan nyata, a > 0, a ≠ 1 dan b > 0 maka hubungan ac = b dapat dituliskan
juga sebagai … A. a log b = c B. b log a = c C. c log a = b D. a log c = b E. b log c = a 02. MD-81-47 p b
cclog = dapat dinyatakan dengan (1) c log b . log c = log p
(2) c log b . clog c = clog p
(3) log b . log c = log p . log c (4) b = p 03. MD-82-15 (b+c) alog = … A. alog b + alog c B. a (b+c) log log C. a c b + log log log D. alog b . alog c E. log (b+c)a 04. MD-94-17
Untuk a > 0 dan b > 0 , amlog bn = … A. mn alog b B. m an log b C.
(
)
m n alog b D. n m alog b E. mn blog a 05. MD-83-29Manakah di antara yang berikut ini ekivalen dengan
2log x2 y4 ? (1) 4log x4 y8 (2) 2log x2 + 2log y4 (3) √2log x + √2log y4 (4) log xy2 06. MA-78-03
Harga dari alog b . blog c . clog d ialah …
A. alog d 07. MA-77-13 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ b a 1 log . ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ c b 1 log . ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ a c 1 log = … A. 1 – abc B. 1 + abc C. 1 D. –1 E. abc 1 08. MA-81-05 Bila x > 1, maka x
mlog1 + nlog1 x sama dengan … A. mn log x B. (m + n) log x C. (m + n) log2 x D. x2 log (m + n) E. x log mn 09. MA-86-32
Jika m = alog x dan n = blog x , maka …
(1) b n m=alog (2) b a n m xlog 1 1 − = (3) a m n=blog (4) ab n m xlog 1 1 + = 10. MA-81-41
Bila a > 1, b > 1 dan alog b = p, maka a2 log b2 sama
dengan … A. 21p B. p C. p2 D. √p E. 2p 11. MA-78-05
Jika 2 log (a2 – b2) = 2 log (a – b) dan a > b, maka …
A. (a – b) = 1 B. (a – b) = 2 C. (a + b) = 1 D. (a + b) = 2 E. (a + b) = 21 12. MA-77-05
Bila g dan a masing-masing bilangan nyata positif, maka g log a berharga negatif bila …
A. a tidak negatif
B. a lebih besar daripada 1 C. a lebih kecil daripada 1
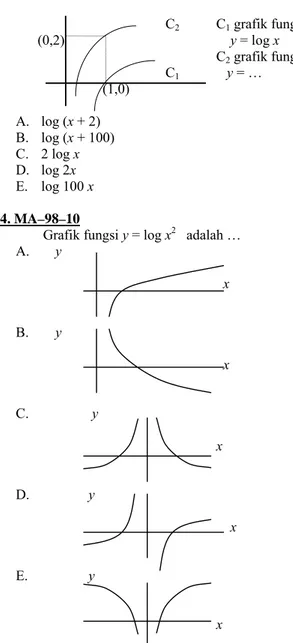
13. MA-88-04 C2 C1 grafik fungsi (0,2) y = log x C2 grafik fungsi C1 y = … (1,0) A. log (x + 2) B. log (x + 100) C. 2 log x D. log 2x E. log 100 x 14. MA–98–10
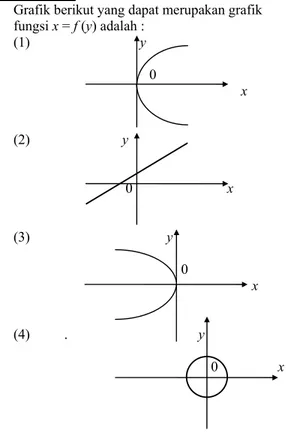
Grafik fungsi y = log x2 adalah …
A. y x B. y x C. y x D. y x E. y x 15. ITB-75-09
Grafik fungsi y = alog |x| , a > 0 dan a ≠ 1 , simetris
terhadap … A. garis y = |x| B. garis y = x C. sumbu y D. sumbu x 16. MA-78-14
Grafik fungsi y = 2 log x berada di bawah sumbu x jika
A. 0 < x < 2 B. 0 < x < 1 C. 0 ≤ x < 1 D. x < 1 E. x < 0 17. MD-82-34
Jika log 2 = 0,30103 , maka … (1) log 50 = 1,69897 (2) log 160 = 2,20412 (3) log 20 = 1,30103 (4) log 2 1= 0,69897 18. MD-83-35
Bila log 5 = 0,69897, maka … (1) log 500 = 10,69897 (2) log 50 = 1,69897 (3) log 0,05 = –2,69897 (4) log 2 = 0,30103 19. MD-88-23
Jika a = 0,1666 … maka alog 36 = … A. –21 B. 21 C. 1 D. –2 E. 2 20. MD-99-20
Diketahui log 2 = 0,3010 dan log 3 = 0,4771 maka log
(
32× 3)
= … A. 0,1505 B. 0,1590 C. 0,2007 D. 0,3389 E. 0,3891 21. MD-86-20 27 log . 3 log 3 9 adalah … A. 6 B. 32 C. 1 2 1 D. 6 1 E. 3 22. MD-93-105 log √27 . 9 log 125 + 16 log 32 = …
A. 3661 B. 49 C. 2061 D. 1241 E. 27
23. MD-87-30 = 12 log 4) log ( 36) log ( 3 2 3 2 3 − … A. 2 B. 4 C. 8 D. 12 E. 18 24. MD-97-17
Jika b = a4 , a dan b positif, maka alog b – blog a
adalah … A. 0 B. 1 C. 2 D. 3 4 3 E. 441 25. MD-98-20 a . c . b c b a = 3 2 1 log 1 log 1 log … A. –6 B. 6 C. c a b 2 D. b c a2 E. 61 26. MD-02-24
Jika a > 1, b > 1, dan c > 1, maka
b log √a . c log b2 . a log √c = …
A. 14 B. 21 C. 1 D. 2 E. 3 27. MA-82-27
Diketahui y = log x dan x2 + ax + (a – 1) = 0. Agar y
ada nilainya untuk semua x tersebut di atas, haruslah …
A. a ≠ 0 B. a ≠ 1 C. a > 0 D. a < 0 E. 0 < a < 1 28. ITB-75-15
Fungsi log x hanya didefinisikan untuk x positif, bilangan-bilangan asli yang terkandung didalam daerah
definisi fungsi
( )
⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + − − = 1 3 2 25 log 2 2 x x x x f adalah … A. 2, 3, 4 29. MA-82-10Penyelesaian persamaan ( 2 log x )2 = 1
A. x = 2 dan x = 12 B. x = 2 dan x = √2 C. x = 2 D. x = 1 dan x = –1 E. x = 1 30. MD-94-24
Jika (alog (3x – 1)) (5log a) = 3 , maka x = …
A. 42 B. 48 C. 50 D. 36 E. 35 31. MD-81-24
Jika diketahui log log x + log 2 = 0, maka ...
A. x = 4 B. x = 2 C. x = 21 D. x = 100 E. x = 10 32. MD-89-20
Penyelesaian dari 2log x=1 ialah ... A. 0 B. 1 C. 2 D. 10 E. 10 1 33. MD-04-16
Jika kurva F(x) = log (x2 – 3x + 3) memotong sumbu x
di titik (a, 0) dan (b, 0), maka (a + b) = … A. –2 B. –1 C. 1 D. 2 E. 3 34. MD-89-23
Jika 2log a = 3, maka
(
)
2 1 3 2) (a − = ... A. 64 1 B. 81 1 C. 729 1 D. 512 1 E. 4096 135. MD-91-27
Nilai x yang memenuhi sistem persamaan linear : 2 log x – log y = 1 log x + log y = 8 adalah … A. 2 B. 100 C. 200 D. 1000 E. 2000 36. MD-97-18 log x = 3 1 log 8 + log 9 – 3
1 log 27 dipenuhi untuk x
sama dengan … A. 8 B. 6 C. 4 D. 2 E. 1 37. MD-96-24
Jika 4 log (4x . 4) = 2 – x , maka x = …
A. –1 B. –12 C. 12 D. 1 E. 2 38. MD-88-18 (x y) ) (x y ) + y ( ) + x (x log 2 log log log = … A. 2 1 B. 1 C. 2 3 D. 2 E. 2 5 39. MD-01-18
Jumlah akar-akar persamaan log 2+16=1 x x sama dengan ... A. 10 B. 6 C. 2 D. 0 E. –2 40. MD-89-22
Himpunan penyelesaian persamaan 93log(2x−1)=25 adalah ... A. { 2 1} B. {–2 } C. {3 } D. { 2 1 , 3 } E. {–2 , 3 } 41. MD-85-29
Karena operasi logaritma hanya dapat dilakukan kepada bilangan positif, maka
4log (x – 3) + 4log (x – 4) = 2 1 untuk x = … (1) 3 (2) 2 (3) 4 (4) 5 42. MD-87-28
Jika x1 dan x2 akar-akar persamaan
log (2x2 – 11x + 22) = 1 , maka x 1 x2 = … A. 11 B. 6 C. –521 D. –2 E. – 2 1 43. MD-87-36
Persamaan 104 log x - 3(102 log x) - 4 = 0 dipenuhi oleh … (1) –1 (2) 1 (3) –2 (4) 2 44. MD-88-28
Himpunan penyelesaian persamaan 106 log x – 4(10)3 log x = 12 adalah … A.
{ }
3 6 B.{
36 ,−32}
C. {2} D. {6 , –2} E. {216 , –8} 45. MD-90-27Persamaan 42logx−5.2logx+6=0 dipenuhi oleh … (1) 6
(2) 5 (3) 4 (4) 3 46. MD-94-27
Jika a dan b adalah akar-akar persamaan 3 3 log (4x2 + 3) + 4 2 log (x2 – 1) = 39 maka a + b = … A. 3 B. 2 C. 1 D. 0 E. –1
47. MD-87-25
Jika x1 dan x2 memenuhi (1 + 2 log x) log x = log 10
maka x1 x2 = … A. 2√10 B. √10 C. 21 D. 10 1 E. –21 48. MD-87-27
Penyelesaian dari ( 2 log x )2 + 2 2 log (
x 2 ) = 1 adalah A. x = 1 B. x = 2 1 C. x = 2 D. x = 4 E. x =√2 49. MD-91-28 Jika 2 5log100 10 5 2 log ⎟= + ⎠ ⎞ ⎜ ⎝ ⎛ x+ x , maka x = … (1) –52,5 (2) –2,45 (3) 2,55 (4) 4,75 50. MA-80-19
Jika x > 0 dan x ≠ 1 , maka nilai x yang memenuhi persamaan xlog (x + 12) – 3 xlog 4 + 1 = 0 adalah …
A. 2 B. 4 C. 8 D. 16 E. 12 51. MA-84-21
Jika {a log (3x – 1) } (5 log a ) = 3, maka x = …
A. 36 B. 39 C. 42 D. 45 E. 48 52. MA-97-03
Jika 2 log a + 2 log b = 12
2 log a – 2 log b = 4 maka a + b = … A. 144 B. 272 C. 528 D. 1024 E. 1040 53. MD-90-25
Nilai maksimum fungsi f (x) = 2 log (x+5) + 2 log (3–x)
adalah … A. 4 B. 8 C. 12 D. 15 E. 16 54. MD-95-21 Jika f (x) = x x log 3 2 1 log 3 − maka f (x) + f
( )
x 3 sama dengan … A. 3 B. 2 C. 1 D. –1 E. –3 55. MD-90-22 Supaya 4x 3x log5 2⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −ada nilainya, maka … A. 0 < x < 34 B. x < 0 atau x > 34 C. x ≠ 31 atau x ≠ 1 D. 0 < x < 34 dan x ≠ 31 dan x ≠ 1 E. x > 0 dan x ≠ 1 56. MD-92-15
Jika (x+1) log (x3 + 3x2 + 2x + 4) = 3 maka x adalah …
A. 0 B. 1 C. 3 D. 5 E. 9 57. MD-98-29
Jika 2x + y = 8 dan log (x + y) = 23 log 2 . 8 log 36
maka x2 + 3y = … A. 28 B. 22 C. 20 D. 16 E. 12 58. MD-00-17
Jika x1 dan x2 memenuhi persamaan:
(
)
log10 10 log 1 1 log 2 x− 2 = x1 . x2 = … A. 5√10 B. 4√10 C. 3√10 D. 2√10 E. √1059. MD-00-18
Nilai x yang memenuhi:
log x = 4log (a+b) + 2log (a–b) – 3log (a2–b2) – log
b a b a − + adalah … A. (a + b) B. (a – b) C. (a + b)2 D. 10 E. 1 60. MD-03-14
Jika 2 3 log (x – 2y) = 3 log x + 3 log y, maka
y x = … A. 4 atau 41 B. 1 atau 4 1 C. 1 atau 4 D. 3 atau 4 1 E. 4 atau 31 61. MD-06-23
Jika y = log x dan x2 + ax + (3 – a) = 0, maka yang
bernilai real untuk a yang memenuhi … A. a > 3 B. a < 3 C. a < –6 D. a > –6 E. -6 < a < 3 62. MD-84-22 Diketahui 3 log 4 = 3 2x , maka 0,25 log 9 = … A. –3x B. – x 3 C. x D. x3 E. 3x 63. MD-04-14
Jika 3 log 4 = a dan 3 log 5 = b , maka 8 log 20 = …
A. a b a 2 + B. a b a 3 + C. a b a 3 2 2 + D. a b a 2 3 3 + E. a b a 3 2 + 64. MD-95- MD-95-12
Jika 9log8=3m, nilai4log3=… A. m 4 1 B. m 4 3 C. m 2 3 D. 4 m E. 3 4m 65. MD-06-15
Jika 4 log 6 = m + 1, maka 9 log 8 = …
A. 4 2 3 + m B. 2 4 3 + m C. 2 4 3 − m D. 4 2 3 − m E. 2 2 3 + m 66. MD-03-16
Jika 3 log 5 = p dan 3 log 11 = q , maka 15 log 275 = …
A. 1 2 + + p q p B. 1 2 + + p q p C. p q 1 2 + D.
(
2p+q)(
p+1)
E.(
p+2q)(
q+1)
67. MA-77-114 log 39 ada diantara …
A. 3 dan 4 B. 1 dan 2 C. 2 dan 3 D. 4 dan 5 E. 5 dan 6 68. MA-85-22 Jika log 42 b a = – 24, maka log 3 2 a b sama dengan … A. –8 B. –4 C. 2 D. 4 E. 8
69. MA-81-17 Jika 3 2 2 log maka , 12 = log a b b a sama dengan … A. –2 B. –1 C. 0 D. 1 E. 2 70. MA-80-29
Bila 7 log 2 = a dan 2 log 3 = b, maka 6 log 98 sama
dengan … ) b(a + a + b + a + ) a (b + a + b + a + a + b a 1 2 E. 2 1 D. 1 2 C. 1 2 B. A. 71. MA-03-03
Jika 2log x + 4log √y = 4log z2, maka z2 = …
A. x√y B. x2√y C. xy D. x4 y E. x24 y 72. MA-94-05
Hasil kali semua x yang memenuhi persamaan
(
)
24 2 40 2 64 log x − x = 0 adalah … A. 144 B. 100 C. 72 D. 50 E. 36 73. MA-05-10Diketahui 2 (4log x)2 – 2 4log √x = 1.
Jika akar-akar persamaan di atas adalah x1 dan x2, maka
x1 + x2 = … A. 5 B. 412 C. 4 D. 212 E. 214 74. MA-93-04
Jika x1 dan x2 memenuhi persamaan :
x x x x log 5 log log log 10 10 10 10 5 10 = − ; maka x1 + x2 = . . . A. 5 B. 6 C. 60 D. 110 E. 1100 75. MA-85-21
Jika x ≠ 1 dan x > 0, maka nilai x yang memenuhi per-samaan x log (x + 12) – 3x log 4 + 1 = 0 adalah …
A. 21 B. 2 C. 4 D. 8 E. 16 76. MA-93-08 Jika t = 7 3 3 2 x - - x
; maka log (1 – | t |) dapat ditentukan untuk … A. 2 < x < 6 B. –2 < x < 5 C. –2 ≤ x ≤ 6 D. x ≤ –2 atau x > 6 E. x < –2 atau x > 3 77. MA-00-01
Nilai x yang memenuhi persamaan
2 log 2 log (2x + 1 + 3) = 1 + 2 log x adalah …
A. log 3 2 B. 2 log 3 C. 3 log 2 D. –1 atau 3 E. 8 atau 2 1 78. MA-00-08
Jumlah semua akar-akar persamaan
(
2 12) (
log 2 12)
(
4) (
2 3)
2 10x −x− x −x− = x− x+ adalah … A. –2 B. –1 C. 0 D. 1 E. 279. MA-01-05 Jika b a log log 3 2 = m dan b a log log 2 3 = n, a > 1 dan b > 1, maka n m = … A. 2 log 3 B. 3 log 2 C. 4 log 9 D. (3 log 2)2 E. (2 log 3)2 80. MA-06-07 Jika 81 log x 1 = x log y 1 = y log 81 1 , maka 2x – 3y = … A. –162 B. –81 C. 0 D. 81 E. 162 81. MA-97-10
Diketahui deret geometri : a1 + a2 + a3 + …
Jika a6 = 162 dan
log a2 + log a3 + log a4 + log a5 = 4 log 2 + 6 log 3 ,
maka a3 = … A. 2 B. 3 C. 6 D. 8 E. 9 82. MA-91-05 Perhatikan deret :
1 + log cos x + log2 cos x + log3 cos x + …
Jumlah deret ini, yaitu S, dapat mengambil setiap nilai… A. 21< S < 1 B. 21< S < 2 C. S <12 D. S >12 E. S > 1 83. MA-89-10
Jumlah deret geometri tak hingga
2log x + 4log x + 16log x + . . . adalah …
A. 21log x B. 2 log x C. 21 2log x D. 2log x E. 2 2log x 84. MA–99–10
Himpunan jawab pertidaksamaan
3log x + 3log (2x – 3) < 3 adalah …
A. { x | x >23} B. {x | x > 29} C. {x | 0 < x < 29} D. { x | 23 < x < 92} E. {x | –3 < x < 29} 85. MA-96-04
Himpunan penyelesaian pertaksamaan 2 log x ≤ log (x + 3) + log 4 adalah …
A. { x | –2 ≤ x ≤ 6 } B. { x | x ≥ 6 } C. { x | 0 < x ≤ 6 } D. { x | 0 < x ≤ 2 } E. { x | 0 < x ≤ 2 atau x ≥ 6 } 86. MA-02-11
Himpunan penyelesaian pertaksamaan 3 12 log 2 ⎟≥ ⎠ ⎞ ⎜ ⎝ ⎛ + x x adalah … A. {x ∈ R | x ≤ 2 atau x ≥ 6} B. {x ∈ R | 0 < x ≤ 2 atau x ≥ 6} C. {x ∈ R | x < 0 atau 2 ≤ x ≤ 6} D. {x ∈ R | 1 ≤ x ≤ 2 atau x ≥ 6} E. {x ∈ R | 2 ≤ x ≤ 6} 87. MA-86-27
Jawab pertaksamaan logaritma : 2log (x2 – x) ≤ 1 ialah
… A. –1 < 0 atau x > 1 B. –1 ≤ x ≤ 2, x ≠ 0 dan x ≠ 1 C. –1 ≤ x ≤ 0 atau 1 < x ≤ 2 D. –1 < x ≤ 0 atau 1 ≤ x ≤ 2 E. –1 ≤ x ≤ 0 atau 1 ≤ x ≤ 2 88. MA-83-20
Himpunan penyelesaian persamaan
xlog (5x3 – 4x) = xlog x5 ialah …
A. {2} B. {1 , 2} C. {–2 , –1 , 2} D. {–2 , –1 , 1 , 2} E. {–2 , –1 , 0 , 1 , 2}
89. MA-04-01 Penyelesaian pertaksamaan 0 1 log 2 log 2 2 2x+ − x+ ≤ adalah … A. x ≤ −43 atau −21 < x ≤ 1 B. –1 < x ≤ −43 atau −21 < x ≤ 1 C. −43 ≤ x ≤ −12 atau x ≥ 1 D. −43 ≤ x < −21 atau x ≥ 1 E. –1 < x < −21 atau x ≥ 1 90. MA-95-04
Himpunan jawab pertaksamaan
log ( x+3) + 2 log 2 > log x2 adalah …
A. { x | –3 < x < 0} B. { x | –2 < x < 0} ∪{ x | 0 < x < 6} C. { x | –2 < x < 6} D. { x | –3 < x < –2}∪{ x | x > 6} E. { x | x < –2}∪{ x | x > 6} 91. MA-77-29
Nilai-nilai yang memenuhi 2log
(
2 3)
1 − x > 0 adalah … A. –√3 < x < √3 B. –2 < x < –√3 atau √3 < x < 2 C. –2 < x < 2 D. x ≥ 2 atau x ≤ –2 E. x > 2 atau x < √3
Fungsi komposisi & Fungsi Invers
01. MD-92-06 Fungsi f (x) = - x x - x 1 5 2terdefinisi dalam daerah … A. x ≤ 0 atau 1 < x ≤ 5 B. x < 0 atau 1 < x < 5 C. x ≤ 0 atau 1 ≤ x ≤ 5 D. 0 ≤ x < 1 atau x ≥ 5 E. 0 < x < 1 atau x > 5 02. MD-93-07
Fungsi f dengan rumus f (x) = 1 2 + − x x x terdefinisikan pada himpunan … A. { x | x ≥ –1 } B. { x | x ≥ 0 } C. { x | x ≥ 1 } D. { x | –1 ≤ x ≤ 0 atau x ≥ 1 } E. { x | –1 < x ≤ 0 atau x ≥ 1 } 03. MD-87-13
Bila Df menyatakan daerah asal dan Rf daerah hasil
fungsi y = x - 1 maka … A. Df ={x | x ∈ R} , Rf = {y | y ∈ R} B. Df ={x | x ∈ R , x > 0} , Rf ={y | y ∈ R , y > 0} C. Df ={x | x ∈ R , x > 1} , Rf ={y | y ∈ R} D. Df ={x | x ∈ R , x ≥ 1} , Rf ={y | y ∈ R , y ≥ 0} E. Df ={x | x ∈ R , x ≥ 0} , Rf ={y | y ∈ R , y ≥ 0} 04. MA-81-14
Bila f : R → R ditentukan oleh f(x) = x2 dan f –1 invers f
maka f –1 ({4, 25}) ialah himpunan …
A. { x | 2 ≤ x ≤ 5} B. { x | –5 ≤ x ≤ 2} C. { x | 2 ≤ x ≤ 5 atau –5 ≤ x ≤ –2} D. { x | 2 < x ≤ 5} E. { x | 2 < x < 5} 05. MA-82-11
Jika A = { x : x < –1 }, B dan C adalah himpunan bilangan real, f : A → B dengan f(x) = –x + 1 : g: B → C dengan g(x) = x2 dan h = g o f : A → C, bilangan x
di A dipetakan ke 64 di C, maka x sama dengan … A. 7 B. 8 C. –9 D. –8 E. –7 06. MA-83-26
Fungsi yang mempunyai invers adalah …
(1) y = x + 1
(2) y = x3
(3) y = log x
(4) y = x2 – 1
07. MD-89-26
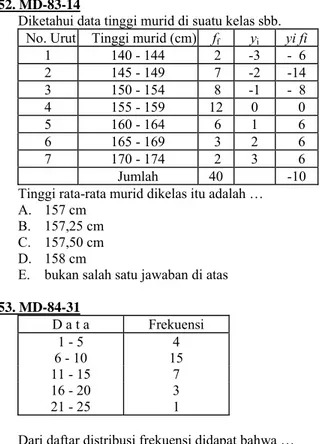
Grafik berikut yang dapat merupakan grafik fungsi x = f (y) adalah :
(1) y 0 x (2) y 0 x (3) y 0 x (4) . y 0 x 08. MA-80-48
Di antara gambar-gambar berikut, yang kurvanya merupakan grafik dari fungsi yang punya invers ialah …
(1) (2)
(3) (4)
09. MD-90-02
Bila f : R → R dan g : R → R ditentukan oleh f(x) = 2x2 + 5x dan g(x) = x 1 , maka (f o g)(2) adalah A. 4 B. 3 C. 2 D. 2 1 E. 13
10 MD-81-41
Diketahui fungsi f : x → x + 3 dan g : x → x + 1 untuk setiap x ∈ R. Maka dapat disimpulkan bahwa ... (1) f o g : x → x + 4 (2) f + g : x → 2x + 4 (3) g o f : x → x + 4 (4) f – g : x → 2 11. MD-97-03 Jika (g o f) (x) = 4 x2 + 4x , g(x) = x2 – 1 , maka f (x – 2) adalah … A. 2x + 1 B. 2x – 1 C. 2x – 3 D. 2x + 3 E. 2x – 5 12. MA-80-09
Jika f(x) = x2 – 2 dan g(x) = 2x + 1 maka komposisi
f{g(x)} = … A. 4x2 – 2 B. 1x2 – 3 C. x2 + 2x – 1 D. 4x2 + 4x + 1 E. 4x2 + 4x – 1 13. MD-02-20
Jika f(x) = ax , maka untuk setiap x dan y berlaku
A. f(x) f(y) = f(xy) B. f(x) f(y) = f(x + y) C. f(x) f(y) = f(x) + f(y) D. f(x) + f(y) = f(xy) E. f(x) + f(y) = f(x + y) 14. MA-81-44
Jika f –1 dan g –1 berturut-turut adalah invers fungsi f
dan fungsi g, dengan f(x) = x + 1 dan g(x) = x 1 , x ≠ 0, maka … (1) (f o f) (x) = f (f(x)) = x + 2 (2) (f o f –1) (x) = f (f –1 ) (x) = x (3) (g –1 o g) (x) = g –1 (g(x)) = x (4) (f o g) (x) = f (g(x)) = 1 1 + x 15. MD-00-06 Diketahui f (x) = 2x + 5 dan g (x) = 4 1 + − x x . Jika (f o g) (a) = 5, maka a = …
A. –2 B. –1 C. 0 D. 1 E. 2 16. MA-84-07 Jika f(x) = x + 1 x dan g (x) = x - 1 x maka g {f(x)} adalah … A. 2 12 x x − B. 1 1 2 2 + − + x x x x C. 1 1 2 2 − − − x x x x D. 2x E. 1 1 2 2 2 + − + x x x x 17. MD-90-16
Jika f(x) = 3x dan g(x) = 3x , maka 3 log [g o f (x)] = …
A. f (x) B. g (x) C. x D. 3 f (x) E. 3 log x 18. MA-84-12
Bila f : x → 5 2x, maka f –1 adalah …
A. 5 log 2x B. 5 log √x C. 2x log 5 D. 5 log 2x E. 2 log 5x 19. MA-85-07
Jika f (x) = 53x dan f –1 (x) invers dari f (x), maka nilai
f –1 (5√5) adalah … A. –21 B. 61 C. 21 D. 1 E. 23 20. MD-93-08 Invers dari f(x) =
( )
3 1 3 1−x + 2 adalah … A.(
)
3 5 2 − x B. 1 –(
)
3 5 2 − x C. 1 +(
)
3 5 2 − x D.{
(
)
}
3 1 5 2 1− x− E.{
(
)
}
3 1 5 2 1+ x−21. MD-91-03
Jika diketahui bahwa f (x) = 2x , g(x) = 3 – 5x , maka (g o f)–1 (x) = … A. 113 (6 + x B. 116 (3 + x) C. 101 (3 – x) D. 101 (6 – x) E. 116 (6 – x) 22. MD-92-10
Fungsi f : R → R dan g : R → ditentukan oleh F (x) = 2x + 5 dan g(x) = x + 2, maka (f o g)-1 (x)
me-metakan x ke … A. 2 9 x - B. x – 9 C. 2 9 x + D. x + 9 E. 2 6 x - 23. MD-95-03
Fungsi f : R → R dan g : R → R dirumuskan dengan : f(x) = 2 1x – 1 dan g(x) = 2x + 4 , maka (g o f)–1(10) = … A. 4 B. 8 C. 9 D. 12 E. 16 24. MD-98-02
Jika g(x) = (x + 1) dan (f o g)(x) = x2 + 3x + 1, maka
f (x) = … A. x2 + 5x + 5 B. x2 + x – 1 C. x2 + 4x + 3 D. x2 + 6x + 1 E. x2 + 3x – 1 25. MD-89-03 Diketahui f (x) = x + 1 dan f o g (x) = 3x2 + 4.
Rumus g (x) yang benar adalah ... A. g (x) = 3x + 4 B. g (x) = 3x + 3 C. g (x) = 3x2 + 4 D. g (x) = 3(x2 + 1) E. g (x) = 3(x2 + 3) 26. MD-01-07
Jika (f o g) (x) = 4x2 + 8x – 3 dan g(x) = 2x + 4 , maka
f–1 (x) = ... A. x + 9 B. 2 + √x C. x2 – 4x – 3 D. 2 + x+1 E. 2 + x+7 27. MA-84-26
Fungsi invers dari f (x) = 1 2 4 3 − + x x adalah … A. 4 3 1 2 + − x x B. 3 2 4 − + x x C. 1 2 4 3 + − x x D. 4 3 2 + − x x E. 3 2 4 + + x x 28. MA-80-38 Jika F(x) = 1 x -
x ; maka fungsi inversnya F -1(x) adalah
x x + x x - x x x + x ) (x - 1 E. 1 D. 1 C. 1 B. 1 A. 29. MD-94-03
Fungsi f : R → R dan g : R → R dirumuskan dengan f(x) = x x−1 , x ≠ 0 dan g(x) = x + 3, maka {g(f(x))}–1 = … A. 1 3 2 − − x x B. 1 3 2 + + x x C. x x−2 D. x x 1 4 − E. x − 4 1
30. MD-96-03 Jika f (x) = x 1 dan g(x) = 2x – 1 , maka (f o g)–1(x) = … A. x x 1 2 − B. 1 2x− x C. x x 2 1 − D. x x 2 1 + E. 1 2 − x x 31. MD-97-15 Jika f (x) = 4 2 3 x x -
+ , maka turunan dari f
–1(x) adalah … 2 2 2 2 2 ) 3 ( 14 E. ) 3 ( 8 14 D. ) 3 ( 8 C. ) 3 ( 10 B. 3 10 8 A. x x x x x x ) (x-x - − − − − − 32. MA-86-15 Jika f (x) = 1 1 x - , g –1 (x) = x - x 1 dan h (x) = g [f(x)], maka h –1 (x) = … A. + x -1 1 B. - x -1 1 C. + x 1 1 D. - x 1 1 E. x – 1 33. MD-99-03 Jika f(x) = √x , x ≥ 0 dan g(x) = 1 + x x , x ≠ – 1, maka (g o f) –1 (2) = … A. 14 B. 12 C. 1 D. 2 E. 4 34. MD-00-27 Diketahui fungsi f (x) = x x+1, x ≠ 0 dan f–1 adalah
invers f. jika k adalah banyaknya faktor prima dari 210, maka f–1(k) = … A. 5 1 B. 4 1 C. 3 1 D. 3 E. 4 35. MD-99-02 Jikaf
( )
x = x2+1 dan(
)( )
4 5 2 1 2− + − = ο x x x x g f maka g(x – 3) = … A. 5 1 − x B. 1 1 + x C. 1 1 − x D. 3 1 − x E. 3 1 + x 36. MA-82-02Diketahui fungsi f dan h, dengan f(x) = 10x dan h(x) = x2 + 2 untuk setiap bilangan x real. Untuk x ≠0
maka f –1 {h (x2) – 2} = … A. log x2 B. log x4 C. log ( x2 + 2 ) D. log ( x2 – 2 ) E. log ( x4 + 2 ) 37. MA-86-28
Jika f (x) = x2 – 8x + 16 dan g (x) = 5x untuk x > 0,
maka f –1 { g (x)} = … A. 2x 1 5 + 4 B.
(
)
2 1 4 5x+ C. 5 x D. 5 x+ 4 E. tidak ada38. MA-83-15
Misalkan f(x) = x + 2 untuk x > 0 dan g(x) = x 15
untuk x > 0. Dengan demikian (f –1 o g–1) (x) = 1 untuk x
sama dengan … A. 1 B. 3 C. 5 D. 8 E. 10 39. ITB-75-40
Diketahui grafik-grafik dari fungsi-fungsi y = f(x) dan y = g(x) seperti pada gambar di bawah
g(x) (a,0) (b,0) (c,0) f(x) maka y = ) ( ) ( x g x f > 0 bila … A. a < x < 0 atau b < x < c B. a ≤ x ≤ 0 atau b ≤ x ≤ c C. x < a , 0 < x < b , x > c D. a < x < c
Hitung Keuangan
01. MD-82-07
Pada saat yang sama Sri mulai menabung Rp. 100.000,- dan Atik Rp. 80.000,-. Kemudian tiap bulan Sri menabung Rp. 1.000,- dan Atik menabung Rp. 1.500,-. Setelah berapa bulan tabungan Sri dan Atik tepat sama ?
A. 80 bulan B. 60 bulan C. 50 bulan D. 40 bulan
E. tidak pernah tepat sama 02. MD-85-23
Modal Rp. 20.000,00 dibungakan secara bunga tunggal dengan bunga 5 % setahun. Sesudah n tahun modal men-jadi Rp. 27.000,00 maka n adalah …
A. 5 B. 6 C. 7 D. 14 E. 35 03. MD-84-19
Seorang pedagang meminjam modal x rupiah di Bank dengan bunga tunggal 2 % sebulan. Ternyata setelah satu tahun dia mengembalikan pinjaman dan bunga semuanya Rp. 310.000,00. Berapa modal yang dipinjam ? A. Rp. 200.000,00 B. Rp. 225.000,00 C. Rp. 250.000,00 D. Rp. 275.000,00 E. Rp. 300.000,00 04. MD-81-35
B meminjam uang sebanyak Rp. 500.000,00 dengan bunga tunggal. Setelah 15 bulan ia mengembalikan uang itu seluruhnya ditambah dengan bunga, sehingga jumlahnya menjadi Rp. 537.500,00, maka bunganya tiap tahun adalah ...
A. 7,5 % B. 6 % C. 5 % D. 3 % E. 2 % 05. MD-81-34
Modal sebesar Rp. 50.000,00 dibungakan secara tung-gal dengan dasar bunga p % per bulan. Setelah 10 tahun bunga yang diterima Rp. 120.000,00. Berapakah p ? A. 2,4 B. 2 C. 0,24 D. 0,2 E. 0,02 06. MD-81-33
Suatu modal sebesar M rupiah dibungakan dengan bunga p % per tahun. Jika dengan bunga majemuk maka sesudah n tahun modal tersebut menjadi ... A. n p M ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + 100 B.
(
M+p%.M)
n C. n M2 . p % D. M (1 – p %) n E. M (1 + p %)n 07. MD-86-24Bi Neneng memiliki modal sebesar Rp. 1.000.000,- di-bungakan 5 %. Modal sesudah 20 tahun adalah … A. Rp. 26.532.969,00 B. Rp. 2.653.296,90 C. Rp. 1.653.296,00 D. Rp. 1.100.000,00 E. Rp. 1.753.000,00 08. MD-89-15
Pada 1 Januari ′80 Budi menabung di bank Rp.20.000,- dengan suku bunga 20 % pertahun. Demikian pula pada 1 Januari tahun-tahun berikutnya sampai 10 kali. Tabungan Budi pada tahun ′90 menjadi ...
A. (1,210 – 1,2 ) (100.000) rupiah B. (1,211 – 1 ) (100.000) rupiah C. (1,210 – 1 ) (100.000) rupiah D. (1,210 – 1 ) (120.000) rupiah E. (1,211 – 1,2 ) (120.000) rupiah 09. MD-85-24
Ali menyerahkan modal pada bank sebesar Rp.1.000,00. Selama 3 tahun dengan dasar bunga majemuk sebesar 30 % setahun. Maka uang yang diterima Ali setelah 3 tahun adalah …
A. Rp. 1.297,00 B. Rp. 1.397,00 C. Rp. 2.197,00 D. Rp. 3.197,00 E. (103 . 133 ) rupiah 10. MD-83-30
Pada tiap awal tahun, Jono menabung Rp.100,- di se-buah bank dengan bunga 4% per tahun. Setelah 20 tahun, tabungan Jono menjadi (dalam rupiah) :
(1) 104 x (1,04) - 1 0,04 20 (2) 100 (1 + 0,04)20 (3) 100 (1,04) n n=
∑
1 20 (4) 100 + 100 (1,04) n n=∑
1 2011. MD-84-15
Harga sebuah mesin semula Rp. 3.125.000,00. Jika harganya setiap tahun menyusut 20 % dari harga yang ditaksir pada akhir tahun sebelumnya, maka harga taksiran mesin tersebut pada akhir tahun ke lima adalah A. Rp. 209.600,00 B. Rp. 204.800,00 C. Rp. 200.000,00 D. Rp. 195.200,00 E. Rp. 190.400,00 12. MD-86-25
Suatu perusahaan memiliki utang Rp. 5.000.000,- harus dibayar dengan 10 anuitet tiap tahun. Pembayaran perta ma dilakukan sesudah 1 tahun. Jika bunga 4 %, besar anuitet adalah … A. Rp. 61.645,47 B. Rp. 6.164,54 C. Rp. 616.454,78 D. Rp. 616,45 E. Rp. 616.400,00 13. MD-88-06
Untuk produk suatu merek sabun, hukum penawarannya berbunyi bahwa harga (p) berbanding langsung dengan kuadrat besar permintaan (n). Untuk n = 3 ternyata p = 3. Grafik fungsi penawaran di atas adalah … A. p 3 0 3 n B. p –1 0 1 n C . p 3 –3 0 3 n D. p 13 1 n E. p 1 0 1 n 14. MD-90-05
Harga suatu barang berbanding lurus dengan logaritma permintaan. Bila h = harga dan d = permintaan maka grafik hubungan h dan d dapat digambarkan sebagai berikut … A. D B. D C. D D. d E. d
Permutasi & Kombinasi
01. MD-99-26
Jika Crn menyatakan banyaknya kombinasi r elemen
dari n elemen dan C3n= 2n , maka C72n = …
A. 160 B. 120 C. 116 D. 90 E. 80 02. MD-85-25
Pada suatu konferensi hadir 7 negara, yaitu A, B, C, D, E, F, dan G. Bendera masing-masing negara akan di-kibarkan pada tiang yang diatur menjadi satu baris (7 tiang ). Ada berapa macam cara mengatur 7 bendera itu agar bendera negara A dan B terletak di ujung ? A. 5 ! 2 B. 5 ! C. 7 ! 2 D. 2 ( 5 ! ) E. 2 ( 6 ! ) 03. MD-81-36
Ada lima orang dalam ruangan yang belum saling mengenal. Apabila mereka ingin berkenalan dengan berjabat tangan sekali dengan setiap orang, maka jabatan tangan yang akan terjadi sebanyak ... A. 5 kali B. 10 kali C. 15 kali D. 20 kali E. 24 kali 04. MD-06-17
Dalam babak penyisihan suatu turnamen, 25 pecatur satu sama lain bertanding satu kali. Banyaknya pertandingan yang terjadi adalah …
A. 150 B. 180 C. 200 D. 270 E. 300 05. MD-82-23
Ali, Bagong, Candra dan Dadang akan bekerja secara bergilir. Banyaknya urutan bekerja yang dapat disusun dengan Ali selalu pada giliran terakhir adalah … A. 3 B. 6 C. 12 D. 18 E. 24 06. MD-01-26
Dari 12 orang yang terdiri atas 8 pria dan 4 wanita akan dibentuk kelompok kerja beranggotakan 4 orang. Jika dalam kelompok kerja ini terdapat paling sedikit 2 pria, maka banyaknya cara membentuknya ada ... A. 442 B. 448 C. 456 D. 462 E. 468 07. MD-01-27
Dari angka-angka 2, 3, 5, 6, 7 dan 9 dibuat bilangan yang terdiri atas tiga angka yang berlainan. Banyaknya bilangan yang dapat dibuat yang lebih kecil dari 400 adalah ... A. 10 B. 20 C. 40 D. 80 E. 120 08. MD-00-29
Bilangan terdiri dari tiga angka disusun dari angka-angka 2, 3, 5, 6, 7 dan 9. Banyaknya bilangan dengan angka-angka yang berlainan dan yang lebih kecil dari 400 adalah … A. 20 B. 35 C. 40 D. 80 E. 120 09. MD-97-21
Dari angka 3, 5, 6, 7 dan 9 dibuat bilangan yang terdiri atas tiga angka yang berbeda. Di antara bilangan-bilang an tersebut yang kurang dari 400, banyaknya adalah … A. 16 B. 12 C. 10 D. 8 E. 6 10. MD-98-27
Seorang murid diminta mengerjakan 9 dari 10 soal ulangan, tetapi soal nomor 1 sampai dengan nomor 5 harus dikerjakan. Banyaknya pilihan yang dapat di-ambil murid tersebut adalah …
A. 4 B. 5 C. 6 D. 9 E. 10
11. MA-04-10
Seatu sekolah membentuk team delegasi yang terdiri dari 4 anak kelas I, 5 anak kelas II dan 6 anak kelas III. Kemudian akan ditentukan pimpinan yang terdiri dari Ketua, Wakil Ketua dan Skretaris. Jika kelas asal Ketua harus lebih tinggi dari kelas asal Wakil Ketua dan Sekretaris, maka banyaknya kemungkinan susunan pimpinan adalah … A. 156 B. 492 C. 546 D. 600 E. 720 12. MA-03-14
Tono beserta 9 temannya bermaksud membentuk tim bola volley terdiri 6 orang. Apabila Tono harus men-jadi anggota tim tersebut maka tim yang mungkin dibentuk adalah … A. 126 B. 162 C. 210 D. 216 E. 252 13. MA-05-14
Suatu delegasi terdiri atas 3 pria dan 3 wanita yang dipilih dari himpunan 5 pria yang berbeda usia dan 5 wanita yang juga berbeda usia. Delegasi itu boleh mencakup paling panyak hanya satu anggota termuda dari kalangan wanita atau anggota termuda dari kalang-an pria. Dengkalang-an persyaratkalang-an ini, bkalang-anyak cara menyusun keanggotaan delegasi ini adalah …
A. 52 B. 56 C. 60 D. 64 E. 68 14. MA-02-05
Dari 10 orang siswa yang terdiri 7 orang putra dan 3 orang putri akan dibentuk tim yang beranggotakan 5 orang. Jika disyaratkan anggota tim tersebut paling banyak 2 orang putri, maka banyaknya tim yang dibentuk adalah … A. 168 B. 189 C. 210 D. 231 E. 252
Peluang
01. MD-85-26Jika tiga mata uang dilempar bersama-sama maka pelu-ang untuk memperoleh dua sisi muka dan satu sisi belakang adalah … A. 61 B. 62 C. 81 D. 82 E. 83 02. MD-81-37
Sebuah kotak berisi lima bola merah dan tiga bola putih. Kita ambil dua bola sekaligus dari kotak itu. Berapa peluang (probabilitas) bahwa bola yang terambil bola merah dan putih ?
A. 151 B. 14 C. 1028 D. 2 1 E. 31 03. MD-83-23
Sebuah kotak berisi 3 buah kelereng putih dan 2 buah kelereng hitam. Pada pengambilan dua kali berurutan, peluang untuk mendapatkan sebuah kelereng hitam pada pengambilan pertama dan sebuah kelereng hitam lagi pada pengambilan yang kedua adalah :
A. 0,08 B. 0,10 C. 0,16 D. 0,20 E. 0,30
Statistika
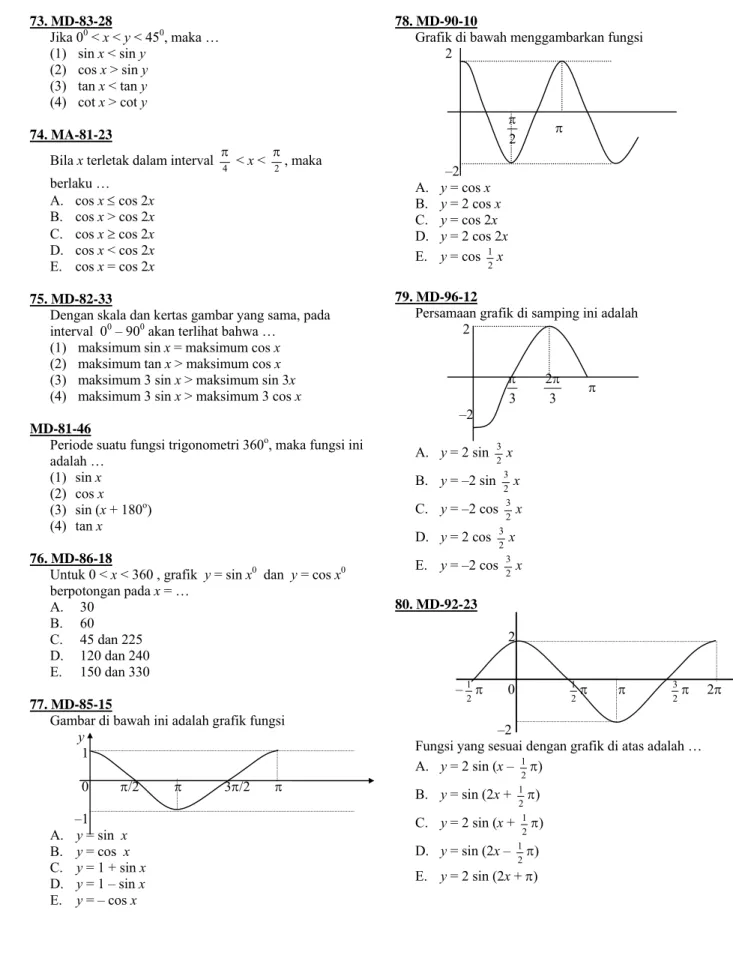
01. MA-83-34
Dari sepotong pipa peralon yang panjangnya (30,0 + 0,5) dm diperlukan 4 potongan dengan panjang masing-masing (6,0 + 0,1) dm. Dengan demikian panjang pipa yang tersisa …
(1) antara 5,1 dm dan 6,1 dm (2) mempunyai toleransi 1,8 dm (3) mempunyai toleransi 0,6 dm (4) antara 5,1 dm dan 6,9 dm 02. MA-86-13
Jika jangkauan batang masing-masing (6 + 0,5) m dan (4 + 0,5) m maka salah satu mutlak selisihnya adalah …
A. 2 m B. 1 m C. 0,1 m D. 0,2 m E. 0,3 m 03. MA-84-09
Panjang satu blok bahan pakaian seragam adalah (40 + 1) m. Jika bahan tersebut dipotong menjadi potong-an-potongan yang berukuran 1,5 m dengan salah mutlak 0,05 m, maka banyaknya potongan bahan pa-kaian seragam yang diperoleh berada di antara …
A. 25 dan 26 B. 25 dan 27 C. 25 dan 28 D. 26 dan 28 E. 26 dan 29 04. MA-85-24
Suatu keluarga mempunyai persediaan beras sebanyak 2000,0 gram. Jika setiap hari keluarga itu
menggunakan 237,5 gram, maka dalam seminggu sisanya adalah anta-ra …
A. 337,35 gram dan 337,65 gram B. 336,65 gram dan 338,35 gram C. 337,65 gram dan 338,35 gram D. 336,65 gram dan 337,65 gram E. 337,10 gram dan 337,90 gram 05. MD-92-01
Nilai rata-rata ujian dari 39 orang siswa adalah 45. Jika ada Upik, seorang siswa lainnya, digabungkan dengan kelompok tersebut maka nilai rata-rata ke-40 orang sis-wa menjadi 46. Ini berarti nilai ujian Upik adalah … A. 47 B. 51 C. 85 D. 90 E. 91 06. MD-93-18
Jika uang lelah 220 rupiah diberikan kepada 4 orang tukang kebun dan 2 orang pembersih ruangan, dan 140 rupiah diberikan kepada 3 orang tukang kebun dan seorang pembersih ruangan, maka masing-masing tukang kebun dan pembersih ruangan berturut-turut menerima uang lelah sebesar …
A. Rp. 50,- dan Rp. 10,- B. Rp. 50,- dan Rp. 30,- C. Rp. 40,- dan Rp. 30,- D. Rp. 30,- dan Rp. 50,- E. Rp. 20,- dan Rp. 70,- 07. MD-83-02
Sejumlah murid di suatu sekolah mengumpulkan uang sebanyak Rp. 960,00. Setiap murid harus memberi iuran yang sama. Kemudian ternyata bahwa 4 orang tidak membayar iurannya. Untuk menutup kekurangan-nya, murid-murid lainnya harus menambah iurannya masing-masing Rp. 20,00. Jadi jumlah murid yang membayar ada … A. 8 orang B. 12 orang C. 16 orang D. 24 orang E. 32 orang 08. MA-80-10
Ali, Badu dan Carli memancing ikan. Ternyata bahwa jumlah ikan Ali dan ikan Badu lebih banyak dari pada dua kali ikan Carli, sedangkan ikan Badu lebih sedikit dari pada ikan Carli. Yang memiliki ikan terbanyak ialah …
A. Carli B. Badu C. Ali
D. Ali dan Badu E. Ali dan Carli 09. MA-86-21
Dalam suatu kelas terdapat siswa sebanyak 21 orang. Nilai rata-rata matematikanya adalah 6. Bila seorang siswa yang paling rendah nilainya tidak diikut sertakan, maka nilai rata-ratanya berubah menjadi 6,2. Dengan demikian, nilai siswa yang paling rendah itu …
A. 4 B. 3 C. 2 D. 1 E. 0 10. MA-85-01
Nilai rata-rata 11 buah bilangan sama dengan 13. Nilai rata-rata 13 bilangan yang lain sama dengan 11. Dengan demikian nilai rata-rata 24 bilangan tersebut sama dengan …
A. 11 B. 111211 C. 12
11. MA-84-03
Nilai rata-rata ujian sekelompok siswa yang berjumlah 40 orang adalah 51. Jika seorang siswa dari kelompok ini yang mendapat nilai 90 tidak dimasukkan dalam perhitungan rata-rata tersebut, maka nilai rata-rata ujian akan menjadi … A. 50 B. 49 C. 48 D. 47 E. 46 12. MA-79-30
Nilai rata-rata ujian matematika dari 39 orang siswa adalah 45. Jika nilai dari seorang siswa lainnya yang bernama Kasdi digabungkan dengan kelompok itu, maka nilai rata-rata ujian matematika dari 40 orang siswa sekarang menjadi 46. Ini berarti bahwa dalam ujian tersebut Kasdi mendapat nilai …
A. 47 B. 51 C. 85 D. 90 E. 92 13. MA-86-08
Untuk dapat diterima di suatu pendidikan, harus lulus test matematika dengan nilai tidak kurang dari 7, dan test biologi dengan nilai tidak kurang dari 5, sedangkan jumlah nilai matematika dan biologi tidak boleh kurang dari 13. Seorang calon dengan jumlah dua kali nilai ma tematika dan 3 kali nilai biologinya sama dengan 30 …
A. pasti ditolak B. pasti diterima
C. diterima asal nilai matematika tidak lebih dari 9 D. diterima asal nilai biologi tidak kurang dari 5 E. diterima hanya bila nilai biologi 6
14. MD-06-25
Berat rata-rata 10 siswa adalah 60 kg. Salah seorang di antaranya diganti oleh Andi sehingga berat rata-ratanya menjadi 60,5 kg. Jika berat Andi 62 kg, maka berat siswa yang digantikan adalah …
A. 57 B. 56 C. 55 D. 54 E. 53 15. MD-03-23
Nilai rata dari 9 bilangan adalah 15 dan nilai rata-rata 11 bilangan yang lain adalah 10. Nilai rata-rata-rata-rata dari 20 bilangan tersebut adalah …
A. 11 2 1 B. 1143 C. 12 D. 12 4 1 E. 12 2 1 16. MD-95-29
Tes matematika diberikan kepada tiga kelas siswa ber-jumlah 100 orang. Nilai rata-rata kelas pertama, kedua dan ketiga adalah 7, 8, 7
2
1. Jika banyaknya siswa kelas
pertama 25 orang dan kelas ketiga 5 orang lebih ba-nyak dari kelas kedua, maka nilai rata-rata seluruh siswa tersebut adalah …
A. 7,60 B. 7,55 C. 7,50 D. 7,45 E. 7,40 17. MD-90-14
Nilai rata-rata pada tes matematika dari 10 siswa ada-lah 55 dan jika digabung lagi dengan 5 siswa, nilai rata-rata menjadi 53. Nilai rata-rata dari 5 siswa tersebut adalah … A. 49 B. 50 C. 51 D. 52 E. 54 18. MD-97-22
Jika 30 siswa kelas IIIA1 mempunyai nilai rata-rata 6,5;
25 siswa kelas IIIA2 mempunyai nilai rata-rata 7 dan
20 siswa kelas IIIA3 mempunyai nilai rata-rata 8, maka
nilai rata-rata ke 75 siswa kelas III tersebut adalah … A. 7,16 B. 7,10 C. 7,07 D. 7,04 E. 7,01 19. MD-94-18
Kelas A terdiri atas 35 murid sedangkan kelas B terdiri atas 40 murid. Nilai statistika rata-rata kelas B adalah 5 lebih baik dari nilai-rata-rata kelas A. Apabila nilai rata-rata gabungan kelas A dan kelas B adalah 5732 maka nilai statistika rata-rata untuk kelas A adalah … A. 50 B. 55 C. 60 D. 65 E. 75 20. MD-93-14
Empat kelompok siswa yang masing-masing terdiri dari 5, 8, 10 dan 17 orang menyumbang korban bencana alam. Rata-rata sumbangan masing-masing kelompok adalah Rp. 4.000,-, Rp. 2.500,-, Rp. 2.000,-, Rp. 1.000,-Maka rata-rata sumbangan tiap siswa seluruh kelompok adalah …
A. Rp. 1.050,- B. Rp. 1.255,- C. Rp. 1.925,- D. Rp. 2.015,- E. Rp. 2.275,-