PERAN TRANSFORMASI TUSTIN PADA RUANG KONTINU DAN RUANG DISKRET SAMSURIZAL

PERAN TRANSFORMASI TUSTIN PADA RUANG

KONTINU DAN RUANG DISKRET

SAMSURIZAL

SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR

BOGOR 2009

PERNYATAAN MENGENAI TESIS DAN

SUMBER INFORMASI

Dengan ini saya menyatakan bahwa tesis Peran Transformasi Tustin pada Ruang Kontinu dan Ruang Diskret adalah karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.

Bogor, Agustus 2009 Samsurizal NIM G551070131

ABSTRACT

SAMSURIZAL. The Role of Tustin Transformation in Continuous and Discrete-Time Systems. Under supervision of TONI BAKHTIAR and NUR ALIATININGTYAS.

This thesis studies the role of the so-called Tustin transformation. The continuous-time system can be discretized into that discrete-time system, and viceversa. Tustin transformation is one of the methods that can be used to change continuous into a discrete-time system. It is well-known that the stability region of continuous-time system is located in the left-hand-side of the complex space, while that of the discrete-time system is laid in the unit circle. In this thesis, we demonstrate that Tustin transformation can be exploited in analyzing both of the stability regions. We also derive several corresponding properties of the continuous and discrete-time domain by exploiting Tustin transformation.

Keywords: continuous-time systems, discrete-time systems, Tustin transformation, stability region.

RINGKASAN

SAMSURIZAL. Peran Transformasi Tustin pada Ruang Kontinu dan Ruang Diskret. Dibimbing oleh TONI BAKHTIAR dan NUR ALIATININGTYAS.

Sistem ruang waktu terdiri dari dua bagian, yaitu: sistem ruang kontinu dan sistem ruang diskret. Sistem ruang kontinu dinyatakan dalam persamaan diferensial, sedangkan sistem ruang diskret dinyatakan dalam persamaan beda. Secara umum, solusi dari persamaan diferensial dan persamaan beda lebih sulit ditemukan daripada solusi persamaan aljabar. Oleh karena itu, biasanya persamaan diferensial dan persamaan beda ditransformasikan menjadi fungsi rasional yang merupakan bentuk khusus dari fungsi aljabar.

Transformasi Laplace adalah suatu metode yang bermanfaat untuk menemukan penyelesaian dari suatu persamaan diferensial secara lebih mudah, yaitu dengan cara mengubah bentuk suatu persamaan diferensial dalam peubah waktu kontinu menjadi suatu persamaan aljabar dalam peubah kompleks. Persamaan aljabar ini selanjutnya dinyatakan dalam ekspresi fungsi rasional. Sehingga ekspresi fungsi hasil transformasi Laplace disebut juga fungsi transfer atau fungsi alih. Fungsi alih sistem persamaan linear parameter konstan didefinisikan sebagai perbandingan dari transformasi Laplace keluaran (fungsi respon) dan transformasi Laplace masukan (fungsi penggerak) dengan menganggap semua nilai awal adalah nol. Dari fungsi alih tersebut didefinisikan

zeros sebagai akar-akar dari persamaan transformasi Laplace keluaran dan poles

sebagai akar-akar dari persamaan transformasi Laplace masukan. Poles dikatakan stabil, jika terletak di sebelah kiri sumbu khayal pada bidang s dan selainnya poles dikatakan takstabil. Demikian juga dengan zeros, jika terletak di sebelah kiri sumbu khayal pada bidang s, maka mempunyai fase minimum, selainnya zeros mempunyai fase tidak minimum.

Metode lainnya yang bermanfaat untuk mengubah suatu persamaan adalah transformasi–Z. Transformasi–Z dapat mengubah suatu persamaan beda dalam peubah waktu diskret menjadi suatu persamaan aljabar dalam peubah kompleks. Ekspresi hasil fungsi transformasi–Z juga sering dinyatakan dalam bentuk fungsi rasional. Pada fungsi tersebut akar dari pembilang dinamakan zeros dan akar-akar dari penyebut disebut poles. Sistem diskret dikatakan stabil, jika poles terletak di dalam lingkaran satuan terbuka dengan pusat titik asal pada bidang z dan selainnya poles dikatakan takstabil.

Suatu sistem kontinu dapat didiskretkan sehingga menjadi suatu sistem diskret, demikian juga sebaliknya. Transformasi Tustin adalah salah satu metode yang digunakan untuk mengubah sistem kontinu menjadi sistem diskret. Penelitian ini mengkaji peran transformasi Tustin dalam proses transformasi dari sistem kontinu ke sistem diskret. Dua topik yang menjadi pusat perhatian adalah masalah transformasi daerah kestabilan sistem dan transformasi beberapa sifat yang berlaku di ruang kontinu dan diskret.

Hasil penelitian menunjukkan bahwa daerah kestabilan sistem ruang kontinu terletak di sebelah kiri sumbu khayal pada bidang s, sedangkan daerah kestabilan sistem ruang diskret terletak di dalam lingkaran satuan terbuka pada bidang z. Dari penelitian ini pun diperoleh hasil bahwa transformasi Tustin dapat mentransformasikan daerah kestabilan sistem ruang kontinu yang terletak di

sebelah kiri sumbu khayal pada bidang s kepada daerah kestabilan sistem ruang diskret yang terletak di dalam lingkaran satuan terbuka dengan pusat titik asal pada bidang z. Peran transformasi Tustin yang lain adalah diperoleh hasil padanan Teorema Redaman Integral Bode, Akibat Redaman Integral Bode, dan Teorema Integral Bode di ruang diskret. Sedangkan di ruang kontinu diperoleh padanan Teorema Poisson–Jensen.

Kata-kata kunci: sistem waktu kontinu, sistem waktu diskret, transformasi Tustin, daerah kestabilan.

© Hak Cipta milik IPB, tahun 2009 Hak Cipta dilindungi Undang-Undang

1. Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumbernya.

a. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik atau tinjauan suatu masalah.

b. Pengutipan tidak merugikan kepentingan yang wajar IPB.

2. Dilarang mengumumkan dan memperbanyak sebagian atau seluruh karya tulis dalam bentuk apa pun tanpa izin IPB.

PERAN TRANSFORMASI TUSTIN PADA RUANG

KONTINU DAN RUANG DISKRET

SAMSURIZAL

Tesis

sebagai salah satu syarat untuk memperoleh gelar Magister Sains

pada Program Studi Matematika Terapan

SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR

BOGOR 2009

Judul Tesis : Peran Transformasi Tustin pada Ruang Kontinu dan Ruang Diskret Nama : Samsurizal NIM : G551070131 Disetujui Komisi Pembimbing Dr. Toni Bakhtiar, M.Sc. Ketua

Dra. Nur Aliatiningtyas, M.Si. Anggota

Diketahui

Ketua Program Studi Matematika Terapan

Dr. Ir. Endar H. Nugrahani, M.S.

Dekan Sekolah Pascasarjana

Prof. Dr. Ir. Khairil A. Notodiputro, M.S.

Kupersembahkan untuk

yang tercinta Rima Susiana dan

yang tersayang Athiyyah Riri Syahfitri

PRAKATA

Segala puji dan syukur penulis panjatkan ke hadirat Allah Swt. yang telah memberikan nikmat, rahmat dan karunia sehingga tesis yang berjudul Peran Transformasi Tustin pada Ruang Kontinu dan Ruang Diskret dapat diselesaikan pada waktunya.

Pada kesempatan ini, penulis mengucapkan terima kasih kepada yang terhormat:

(1) Departemen Agama RI yang telah memberikan tugas belajar di Sekolah Pascasarjana pada Institut Pertanian Bogor periode 2007-2009;

(2) Prof. Dr. Ir. Khairil A. Notodiputro, M.S. selaku Dekan Sekolah Pascasarjana IPB;

(3) Dr. Berlian Setiawaty, M.S. dan Dr. Ir. Endar H. Nugrahani, M.S. berturut-turut selaku Ketua Departemen Matematika FMIPA IPB dan Ketua Program Studi Matematika Terapan Sekolah Pascasarjana IPB;

(4) Dr. Toni Bakhtiar, M.Sc., dan Dra. Nur Aliatiningtyas, M.Si. selaku penguji dan komisi pembimbing yang telah memberikan bimbingan dan saran; (5) Dr. Jaharuddin, M.Si. selaku penguji di luar komisi pembimbing; (6) Dosen-dosen dan staf administrasi Departemen Matematika FMIPA IPB; (7) Kepala MAN 1 Bandar Lampung beserta pendidik dan tenaga kependidikan; (8) Rekan-rekan BUD Departemen Agama RI pada Sekolah Pascasarjana IPB

periode 2007-2009;

Ungkapan terima kasih juga disampaikan kepada yang mulia kedua ibunda, yang tercinta isteri dan anak-anak yang senantiasa memberikan dukungan serta do’a untuk keberhasilan penulis.

Semoga tesis ini dapat bermanfaat. Amin.

Bogor, Agustus 2009 Samsurizal

RIWAYAT HIDUP

Penulis dilahirkan di Medan Sumatera Utara pada tanggal 7 November 1968, merupakan anak pertama dari lima bersaudara pasangan ayahanda Raffiudin dan ibunda Natilah.

Pendidikan yang pernah ditempuh penulis: SDN 40 Inpres Tanjungkarang, lulus tahun 1982; SMPN 5 Tanjungkarang, lulus tahun 1985; SMAN 2 Tanjungkarang, lulus tahun 1988. Pendidikan tingkat sarjana ditempuh di program studi Pendidikan Matematika jurusan Pendidikan MIPA Fakultas Keguruan dan Ilmu Pendidikan Universitas Lampung, lulus tahun 1993. Dan sejak tahun 2007, penulis memperoleh kesempatan untuk melanjutkan studi Program Magister pada program studi Matematika Terapan Sekolah Pascasarjana IPB melalui beasiswa Departemen Pendidikan Agama Republik Indonesia.

Penulis pernah bekerja sebagai staf pendidik di SMTI Tanjungkarang mengajar bidang studi Aljabar dan Kalkulus (tahun 1990–1994), staf pengajar Matematika di Lembaga Pendidikan Primagama Cabang Bandar Lampung (tahun 1994–2002), staf pengajar Matematika di Lembaga Pendidikan Prima Quantum (tahun 2002–sekarang) dan staf pendidik di MAN 1 Bandar Lampung mengajar bidang studi Matematika (tahun 1997–sekarang). Penulis pernah mengikuti pelatihan, antara lain: Pelatihan Aktualisasi Guru Bidang Studi Matematika Provinsi Lampung (tahun 2002), pelatihan Komputer EMIS dalam rangka Mendukung Pengajaran Kreatif (tahun 2003), Pelatihan Sosialisai Kurikulum Berbasis Kompetensi Mata Pelajaran Eksakta (tahun 2004), pelatihan Guru Bina MAN Model Se-Indonesia (tahun 2004), dan Workshop Penyusunan Madrasah Development and Investment Plan (tahun 2006).

DAFTAR ISI

Halaman

DAFTAR GAMBAR ... xiii

DAFTAR LAMPIRAN ... xiv

I PENDAHULUAN ... 1

1.1 Latar Belakang ... 1

1.2 Tujuan Penelitian ... 1

1.3 Metode Penelitian ... 2

II LANDASAN TEORI ... 3

2.1 Peubah Kompleks dan Fungsi Kompleks ... 3

2.2 Fungsi Analitik ... 3

2.3 Transformasi Laplace ... 4

2.4 Fungsi Alih, Zeros, dan Poles Sistem Kontinu ... 5

2.5 Kestabilan Sistem Kontinu ... 6

2.6 Transformasi–Z ... ... 7

2.7 Fungsi Alih, Zero dan Pole Sistem Diskret ... 8

2.8 Kestabilan Sistem Diskret ... 8

2.3 Transformasi Möbius ... 9

III TRANSFORMASI ... 10

3.1 Transformasi Bilinear ... 10

3.2 Transformasi Tustin ... 13

IV DAERAH KESTABILAN SISTEM ... 14

4.1 Fungsi Alih Sistem Kontinu ... 14

4.2 Kestabilan Sistem Kontinu ... 20

4.3 Fungsi Alih Sistem Diskret ... 21

4.4 Kestabilan Sistem Diskret ... 23

4.5 Transformasi Daerah Kestabilan Sistem ... 24

V PADANAN TEOREMA ... 26

5.1. Padanan Teorema di Ruang Diskret ... 26

5.2. Padanan Teorema di Ruang Kontinu ... 34

VI SIMPULAN ... 37

DAFTAR PUSTAKA ... 38

LAMPIRAN ... 39

DAFTAR GAMBAR

Halaman

1 Daerah pada bidang z dengan |z| < 1 ... 11

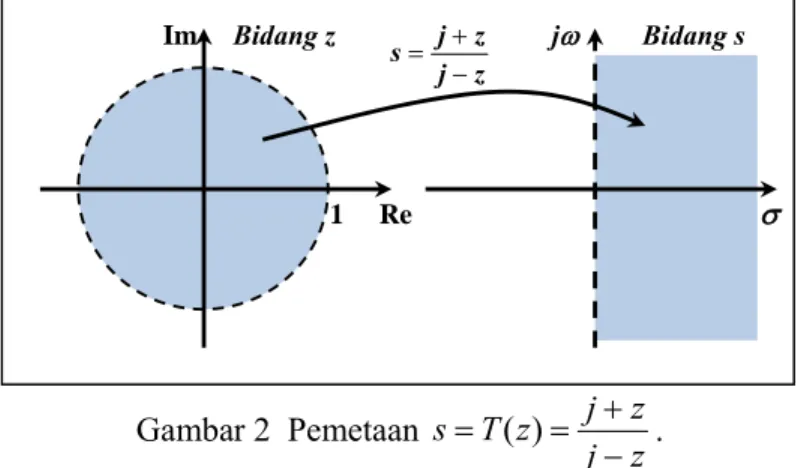
2 Pemetaan z j z j z T s − + = = ( ) ... 11

3 Daerah pada bidang s dengan Im(s) > 0 ... 12 4 Pemetaan s j s j s T z + − = = ( ) ... 13

5 Daerah pada bidang z dengan |z| > 1 ... 14

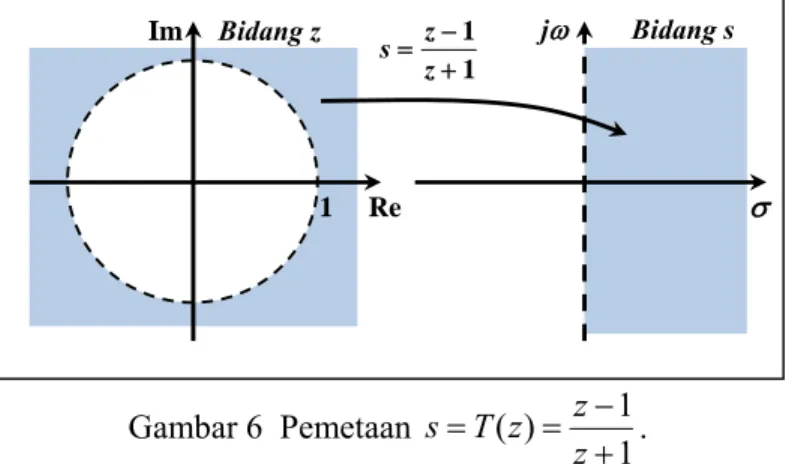
6 Pemetaan 1 1 ) ( + − = = z z z T s ... 14

7 Daerah kestabilan sistem kontinu ... 21

8 Daerah kestabilan sistem diskret ... 23

9 Daerah pada bidang s dengan Re(s) < 0 ... 24

10 Transformasi daerah kestabilan ... 25

11 Grafik fungsi LHS1 (o) dan RHS1 (x) ... 29

DAFTAR LAMPIRAN

Halaman

1 Transformasi Laplace beberapa fungsi sederhana ... 40

2 Transformasi –Z beberapa fungsi sederhana ... 41

3 Notasi dan makna suatu domain ... 42

4 Bukti Teorema 1 ... 43

5 Bukti Teorema 2 ... 45

6 Penurunan padanan Teorema Redaman Integral Bode di ruang diskret 48

7 Penurunan padanan Akibat Redaman Integral Bode di ruang diskret .. 51

8 Penurunan padanan Teorema Integral Bode di ruang diskret ... 54

9 Penurunan padanan Teorema Poisson-Jensen di ruang kontinu ... 57

10 Beberapa ilustrasi penggunaan padanan Teorema ... 61

11 Beberapa program perhitungan dan pembuatan grafik dengan software Mathematica ... 67

1.1 Latar Belakang

Sistem ruang waktu terdiri dari dua bagian, yaitu: sistem ruang kontinu dan sistem ruang diskret. Sistem ruang kontinu dinyatakan dalam persamaan diferensial, sedangkan sistem ruang diskret dinyatakan dalam persamaan beda. Secara umum, solusi dari persamaan diferensial dan persamaan beda lebih sulit ditemukan daripada solusi persamaan aljabar. Analisis kualitatif terhadap persamaan diferensial dan persamaan beda pun sulit dilakukan. Oleh karena itu, biasanya persamaan diferensial dan persamaan beda ditransformasikan menjadi fungsi rasional yang merupakan bentuk khusus dari fungsi aljabar. Transformasi Laplace adalah suatu metode yang mentransformasikan persamaan diferensial menjadi fungsi rasional, sedangkan untuk mentransformasikan persamaan beda menjadi fungsi rasional digunakan transformasi–Z.

Suatu sistem kontinu dapat didiskretkan sehingga menjadi sistem diskret, demikian juga sebaliknya. Beberapa metode yang dapat digunakan dalam proses diskretisasi, antara lain: zero order hold (ZOH), first order hold (FOH), matched

pole-zero, backward difference, atau bilinear transformation (Adam et al. 2003).

Transformasi bilinear yang sering disebut transformasi Tustin adalah salah satu metode yang akan diteliti perannya dalam proses diskretisasi. Dalam desain IIR (Infinite Impulse Response), pendekatan transformasi Tustin sering sekali digunakan. Desain ini dimulai dengan fungsi transfer analog filter dan menyajikannya dalam pemetaan domain s ke domain z (Tung 2003). Dalam optimisasi, meskipun metode yang digunakan dalam pembahasan-pembahasan sering disajikan untuk sistem waktu kontinu tetapi dengan transformasi Tustin (bilinear) dapat juga diterapkan suatu algoritma optimisasi H2 untuk sistem waktu diskret (Megretski 2004).

Penelitian ini akan mengkaji sejauh mana peran transformasi Tustin dalam proses transformasi dari sistem kontinu ke sistem diskret. Dua topik yang menjadi pusat perhatian adalah masalah transformasi daerah kestabilan sistem dan transformasi beberapa sifat yang berlaku di ruang kontinu dan diskret.

1.2 Tujuan Penelitian

Berdasarkan latar belakang di atas, maka dirumuskan tujuan penelitian sebagai berikut:

(1) menunjukkan daerah kestabilan sistem ruang kontinu dan daerah kestabilan sistem ruang diskret;

(2) menunjukkan peran transformasi Tustin dalam mentransformasikan daerah kestabilan dari sistem ruang kontinu kepada sistem ruang diskret;

(3) menurunkan beberapa sifat yang berlaku di ruang kontinu ke ruang diskret dengan menggunakan transformasi Tustin, dan sebaliknya.

1.3 Metode Penelitian

Metode yang digunakan pada penelitian ini adalah studi pustaka dengan langkah-langkah yang dilakukan sebagai berikut:

(1) akan ditunjukkan bahwa daerah kestabilan sistem ruang kontinu terletak di sebelah kiri sumbu khayal pada bidang s;

(2) akan ditunjukkan bahwa pada sistem ruang diskret, daerah kestabilannya terletak di dalam lingkaran satuan terbuka dengan pusat titik asal bidang z; (3) akan diperiksa apakah transformasi Tustin dapat mentransformasikan daerah

kestabilan sistem ruang kontinu kepada daerah kestabilan sistem ruang diskret;

(4) akan diturunkan padanan beberapa sifat yang berlaku di ruang diskret dari sifat-sifat yang berlaku di ruang kontinu dengan menggunakan transformasi Tustin, dan sebaliknya. Adapun sifat-sifat yang akan dicari padanannya adalah Teorema Redaman Integral Bode, Akibat Redaman Integral Bode, Teorema Integral Bode, dan Teorema Poisson–Jensen.

II LANDASAN TEORI

2.1 Peubah Kompleks dan Fungsi Kompleks

Sebuah bilangan kompleks dapat dinyatakan dalam bentuk

z = x + jy, (2.1)

dengan x dan y adalah bilangan-bilangan real dan j= −1. Bilangan x disebut bagian real dari z dan ditulis

x = Re(z), (2.2)

dan bilangan y disebut bagian imajiner dari z dan ditulis

y = Im(z). (2.3)

Konjugat dari bilangan kompleks z = x + jy adalah

jy x

z= − . (2.4)

Dalam bentuk polar, z = x + jy dapat dinyatakan sebagai

z = |z| (cos θ + sin θ) = |z| e jθ. (2.5) (Fisher 1990).

Jika bagian real dan/atau bagian imajiner dari bilangan kompleks terdiri dari peubah-peubah, maka bilangan kompleks disebut suatu peubah kompleks. Pada transformasi Laplace, notasi s menyatakan sebuah peubah kompleks, yaitu

s = σ + jω (2.6)

dengan σ bagian real, ω bagian imajiner (Ogata 1997).

Sebuah fungsi kompleks F(s) adalah suatu fungsi dari s yang mempunyai bagian real dan bagian imajiner, atau

y

x jF

F s

F( )= + (2.7)

dengan Fx dan Fy adalah kuantitas-kuantitas real (Ogata 1997).

2.2 Fungsi Analitik

Definisi 1 Suatu fungsi dari peubah kompleks z adalah analitik pada titik z0, jika fungsi tersebut turunannya ada, tidak hanya pada titik z0, tetapi pada setiap titik z di sekitar z0. Suatu fungsi adalah analitik di daerah R, jika fungsi tersebut analitik pada setiap titik di dalam R (Curchill & Brown 1990).

2.3 Transformasi Laplace

Transformasi Laplace adalah suatu metode yang bermanfaat untuk menemukan penyelesaian dari suatu persamaan diferensial dengan lebih mudah, yaitu dengan cara mengubah bentuk suatu persamaan diferensial menjadi suatu persamaan aljabar dalam peubah kompleks.

Definisi 2 Misalkan f adalah suatu fungsi dari waktu t sedemikian sehingga

f(t) = 0 untuk t < 0, dan s adalah suatu peubah kompleks, maka transformasi Laplace dari f(t) didefinisikan:

{ }

_{= =}

_∫

∞ − 0 ) ( ) ( ) (t F s e f t dt f st L . (2.8)

Transformasi Laplace suatu fungsi f(t) dikatakan ada, jika integral (2.8) konvergen untuk suatu nilai s, jika tidak demikian maka transformasi Laplace dikatakan tidak ada (Ogata 1997).

Definisi 3 (Kontinuitas Sebagian-Sebagian)

Suatu fungsi f dari t dikatakan kontinu sebagian-sebagian pada interval

[ ]

a,b , jika:

(i) interval

[ ]

a,b dapat dibagi menjadi subinterval-subinterval berhingga banyaknya yang menyebabkan f

( )

t kontinu pada subinterval-subinterval tersebut,

(ii) limit kiri dan limit kanan dari f

( )

t pada setiap ujung subinterval bernilai hingga (Andrews 1991).

Definisi 4 (Terbatas Eksponensial)

Suatu fungsi f mempunyai eksponen berorder α, jika terdapat konstanta M > 0 dan α sedemikian sehingga untuk beberapa t₀≥0, berlaku f

( )

t ≤Meαt; t≥ . t₀

Sifat-sifat transformasi Laplace (1) Sifat linear.

Jika L {f₁(t)}=F₁(s) dan L {f₂(t)}=F₂(s), maka untuk suatu konstanta c1 dan c2 berlaku: ) ( ) ( )} ( ) ( {c₁f₁ t +c₂f₂ t =c₁F₁ s +c₂F₂ s L . (2.9) (2) Sifat pergeseran.

Jika L

{

f(t)

}

= F(s), maka berlaku:

) ( )} ( {eatf t =F s−a L . (2.10)

(3) Transformasi Laplace dari turunan fungsi.

Jika f(t),f&(t),f&&(t) adalah fungsi-fungsi yang kontinu dan terbatas eksponensial, maka berlaku:

) 0 ( ) ( )} ( {f& t =sF s − f L _{, (2.11)}

dan L {f&&(t)}=s2F(s)−sf(0)− f&(0)_. (2.12)

Secara umum, jika n _n n _n

dt t f d dt t f d dt t f d dt t df t f(), (), 2 ₂(),_K, ( −₍1)₋₁₎(), () adalah fungsi-fungsi yang kontinu dan terbatas eksponensial, maka berlaku:

1 1 2 2 2 1 ₍₀₎ (0) (0) (0) ) ( ) ( − − − − − − _{− − − −} − = ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ n n n n n n n n n dt f d dt f d s dt df s f s s F s dt t f d L L (2.13) dengan F(s)=L

{

f(t)

}

.

(4) Transformasi Laplace dari integral fungsi. Jika L

{

f(t)

}

=F(s), maka: s s F du u f t ) ( ) ( 0 = ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧

∫

L . (2.14) (Ogata 1997).

2.4 Fungsi Alih, Zeros, dan Poles Sistem Kontinu

Kegunaan dari transformasi Laplace adalah mengubah suatu persamaan diferensial menjadi suatu persamaan aljabar. Persamaan aljabar ini selanjutnya dinyatakan dalam ekspresi fungsi rasional. Sehingga ekspresi fungsi hasil

transformasi Laplace disebut juga fungsi transfer atau fungsi alih. Fungsi alih sistem persamaan linear parameter konstan didefinisikan sebagai perbandingan dari transformasi Laplace keluaran (fungsi respon) dan transformasi Laplace masukan (fungsi penggerak) dengan menganggap semua nilai awal adalah nol, dinyatakan dalam bentuk:

m n a s a s a s b s b s b s b s U s Y s H n n n n m m m m ≥ + + + + + + + + = = − − − − ; ) ( ) ( ) ( 1 1 1 1 1 1 0 L L (2.15)

dengan Y(s) dan U(s) tidak memiliki faktor persekutuan (Ogata 1997).

Jika pembilang (numerator) dan penyebut (denominator) dari H(s) pada persamaan (2.15) masing-masing difaktorkan, serta keduanya tidak memiliki faktor persekutuan (coprime), maka persamaan tersebut dapat diubah menjadi

m n p s p s p s z s z s z s K s U s Y s H n m _≥ − − − − − − = = ;dengan ) ( ) )( ( ) ( ) )( ( ) ( ) ( ) ( 2 1 2 1 L L _{. (2.16)}

Zeros dan poles berturut-turut didefinisikan sebagai akar-akar dari

persama-an Y(s) = 0 dpersama-an U(s) = 0. Sehingga s = zi dengan i = 1,2, …, m disebut zeros dari H(s), dan s = pi dengan i = 1,2, …, n disebut poles dari H(s). Jika Re(pi) < 0, maka poles dikatakan stabil, dan selainnya poles dikatakan takstabil. Jika Re(zi) < 0,

maka zeros mempunyai fase minimum, dan selainnya zeros mempunyai fase tidak minimum (Seron et al. 1997).

2.5 Kestabilan Sistem Kontinu

Diberikan sistem persamaan linear fungsi masukan dan fungsi keluaran sebagai berikut: ) ( ) ( ) (t Axt Bu t x_& = + (2.17)

( )

t Cx(t) Du(t) y = + . (2.18)

Sistem persamaan (2.16) dan (2.17) dapat ditulis dalam simbol

∑

=(A,B,C,D)

dengan A∈Rnxn, B∈Rnxm, C∈Rrxn, dan D∈Rrxm. Adapun

x

∈

R

nadalah

state dari sistem,

u

∈

R

m adalah fungsi masukan (input), dan y∈Rr adalah fungsi keluaran (output).

Definisi 5 Suatu sistem persamaan linear

∑

=(A,B,C,D) adalah (1) stabil, jika <∞ ∞ → sup () lim xt t

untuk setiap penyelesaian x(t) dari

x

_&

(

t

)

=

Ax

(

t

)

; (2) stabil asimtotik, jika lim ( ) <0

→∞ xt

t

untuk setiap penyelesaian x(t) dari x&(t)= Ax(t); (3) takstabil, jika sistem tidak stabil (Lewis 2004).

Sistem

∑

=(A,B,C,D) _{dapat dinyatakan dalam bentuk fungsi alih berikut}

D B A sI C s U s Y s H = = ( − )−1 + ) ( ) ( ) ( (2.19) dengan U(s) menyatakan fungsi masukan dan Y(s) menyatakan fungsi keluaran.

2.6 Transformasi–Z

Seperti halnya transformasi Laplace, transformasi–Z pun merupakan suatu metode yang bermanfaat untuk mengubah suatu persamaan. Transformasi–Z mengubah suatu persamaan beda dalam peubah waktu diskret menjadi suatu persamaan aljabar dalam peubah kompleks.

Definisi 6 (Transformasi–Z Dua Sisi).

Transformasi–Z dari barisan bilangan x(k) dengan k = 0, ±1, ±2, ... didefinisikan:

(

)

k k z k x k x z X ∞ − −∞ =

∑

= = ( ) ( ) ) (

Z

. (2.20) (Ogata 1995). Sifat-sifat transformasi–Z

Misalkan x(k) dapat ditransformasi–Z kan dan x(k) = 0 untuk k = –1, –2, …. (1) Sifat linear.

Misalkan x(k) dapat dibentuk oleh kombinasi linear x(k) = c1 f1 (k) + c2 f2(k). Jika F1(z) dan F2(z) berturut-turut adalah transformasi–Z dari f1(k) dan f2(k), serta c1 dan c2 adalah skalar, maka transformasi–Z dari x(k) adalah

(2) Perkalian dengan ak.

Jika X(z) adalah transformasi–Z dari x(k), maka:

(

)

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = a z X k x ak ( ) Z . (2.22) (3) Teorema pergeseran.

Jika X(z) adalah transformasi–Z dari x(k) dan k=0,1,2,_L, maka:

(

x(k−n)

)

= z−nX(z) Z _(2.23) dan

(

)

_⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = +

_∑

− = − 1 0 ) ( ) ( ) ( n k k n _{X z x k z} z n k x Z . (2.24) (Ogata 1995).

2.7 Fungsi Alih, Zeros, dan Poles Sistem Diskret

Seperti hasil fungsi pada transformasi Laplace, ekspresi hasil fungsi transformasi–Z juga sering dinyatakan dalam bentuk fungsi rasional berikut:

m n a z a z a z b z b z b z b z H n n n n m m m m d ≥ + + + + + + + + = − − − − ; ) ( 1 1 1 1 1 1 0 L L (2.25) (Seron et al. 1997).

Pada persamaan (2.25) akar dari pembilang dinamakan zeros dan akar-akar dari penyebut disebut poles.

2.8 Kestabilan Sistem Diskret Diberikan suatu persamaan beda

L , 2 , 1 , 0 , 0 0 = =

∑

∑

= + = + B u n y A P k n k Q k k n k k . (2.26)

P dan Q adalah bilangan-bilangan bulat tak negatif; A0, …, AP dan B0, …, BQ

adalah bilangan-bilangan real atau kompleks. Barisan-barisan bilangan {uk} dan

{yk} berturut-turut disebut fungsi masukan (input) dan fungsi keluaran (output)

sistem. Adapun y0, …, yP–1 adalah syarat awal yang ditentukan (Fisher 1990). Dengan asumsi bahwa syarat awal adalah nol, yaitu y0, …, yP–1 = 0,

masukan (input) untuk u0, …, uQ–1 = 0, dan P ≥ Q maka bentuk eksplisit

Yd(z) = Hd(z)Ud(z) _(2.27) dengan

( )

_∑

∑

∑

∞ = = = ₌ = 0 0 0 k k k P k k k Q k k k d z f z A z B z H . (2.28) (Fisher 1990).

Definisi 7 Diberikan sistem persamaan linear fungsi masukan {uj} dan fungsi

keluaran {yn} sebagai berikut:

∑

= − = n k k n k n f u y 0 . (2.29)

Sistem persamaan linear ini adalah stabil, jika diberikan fungsi masukan yang terbatas menghasilkan fungsi keluaran yang terbatas juga (Fisher 1990).

2.9 Transformasi Möbius

Definisi 8 Suatu transformasi

; ) ( d cz b az z T s + + = = (ad ≠ bc) (2.30)

dengan a, b, c, dan d adalah bilangan-bilangan kompleks disebut transformasi pecahan linear atau dikenal dengan transformasi Möbius (Churchill & Brown 1990).

III TRANSFORMASI

3.1 Transformasi Bilinear

Dari persamaan (2.30), yaitu ( ) ;

d cz b az z T s + + = = (ad ≠ bc). Jika c d z≠− , maka persamaan tersebut dapat dikalikan dengan cz + d, sehingga diperoleh

czs + ds = az + b.

Selanjutnya persamaan di atas, dikurangkan dengan az + b, maka diperoleh

czs – az + ds – b = 0.

Dengan memisalkan A = c, B = –a, C = d, dan D = –b, maka persamaan (2.30) dapat ditulis dalam bentuk

Azs + Bz + Cs + D = 0; (AD ≠ BC). (3.1)

Jadi persamaan (2.30) dapat ditulis dalam bentuk persamaan (3.1), demikian juga sebaliknya. Karena bentuk persamaan (3.1) adalah linear dalam z dan s, maka transformasi pecahan linear atau transformasi Möbius disebut juga transformasi bilinear.

Sebagai ilustrasi akan ditunjukkan bahwa

z j z j z T s − + = = ( ) memetakan

daerah = {z ∈  : |z| < 1} pada daerah + = {s ∈  : Re(s) > 0}. Transformasi

z j z j z T s − + =

= ( ) adalah transformasi Möbius dengan a = 1, b = j, c = –1, dan

d = j. Untuk menunjukkan bahwa daerah = {z ∈  : |z| < 1} dipetakan pada daerah + _{= {s ∈  : Re(s) > 0} oleh}

z j z j z T s − + =

= ( ) , maka terlebih dahulu dicari

invers dari s=T(z), yaitu

1 ) 1 ( ) ( 1 + − = = − s s j s T z .

Pada Gambar 1, andaikan z adalah sembarang titik di dalam lingkaran satuan pada bidang z, maka |z| < 1. Dengan mensubstitusikan

1 ) 1 ( + − = s s j z , maka 1 1 ) 1 ( _< + − s s j sehingga diperoleh 1 ) 1 (s− < s+ j . (3.2)

Gambar 1 Daerah pada bidang z dengan |z| < 1.

Dengan mensubstitusikan s = σ + jω ke persamaan (3.2), kemudian bagian real dan bagian imajinernya dikelompokkan, maka diperoleh

ω

σ

σ

ω

+ j − < + + j

− ( 1) ( 1) . (3.3)

Selanjutnya dengan menghitung jaraknya, maka

2 2 2 2 ₍

_σ

_{1) (}

_σ

₁₎

_ω

ω

+ − < + + , sehingga diperoleh 0 >

σ

atau Re(s) > 0. (3.4)

Dengan demikian dapat ditunjukkan bahwa

z j z j z T s − + = = ( ) memetakan daerah di dalam lingkaran satuan terbuka dengan pusat titik asal; = {z ∈  : |z| < 1} pada daerah di sebelah kanan sumbu khayal; + = {s ∈  : Re(s) > 0}, seperti yang dapat dilihat pada Gambar 2.

Gambar 2 Pemetaan z j z j z T s − + = = ( ) . Im 1 Re Bidang z ● z jω Bidang s Im Bidang z 1 Re σ z j z j s − + =

Ilustrasi di atas menunjukkan pemetaan dari bidang z ke bidang s dari suatu transformasi Möbius. Berikut ini akan diberikan pula ilustrasi dari bidang s ke bidang z dari transformasi Möbius lainnya.

Akan ditunjukkan bahwa

s j s j s T z + − =

= ( ) memetakan daerah Im(s) > 0 pada

daerah di dalam lingkaran satuan |z| < 1.

s j s j s T z + − = = ( ) adalah transformasi Möbius dengan a = –1, b = j, c = 1, d = j. Untuk menunjukkan bahwa daerah Im(s) > 0 dipetakan pada daerah di dalam lingkaran satuan |z| < 1 oleh

s j s j s T z + − =

= ( ) , maka terlebih dahulu dicari invers dari z=T(s), yaitu

z z j z T s + − = = − 1 ) (1 ) ( 1 _.

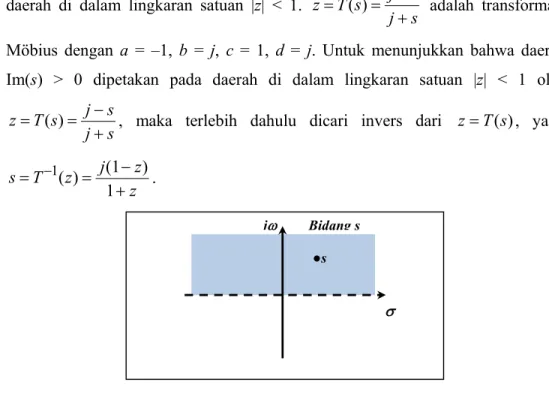
Gambar 3 Daerah pada bidang s dengan Im(s) > 0.

Pada Gambar 3, andaikan s adalah sembarang titik di daerah Im(s) > 0, maka 0

>

ω , sehingga 2ω>−2ω. Dengan menambahkan σ2+ω2+1 _{pada kedua sisi,} maka diperoleh σ2+(ω+1)2>σ2+(ω−1)2. _(3.5) Persamaan (3.5) merupakan representasi jarak dari

) 1 ( ) 1 ( + > + − + ω σ ω σ j j . (3.6) atau (σ+ jω)+ j > (σ+ jω)− j _(3.7) Dengan mensubstitusi z z j j s + − = + = 1 ) (1

ω

σ

ke dalam persamaan (3.7), maka

j z z j j z z j ₋ + − > + + − 1 ) 1 ( 1 ) 1 ( , sehingga diperoleh z <1_{. (3.8)} σ jω Bidang s ●s

Dengan demikian dapat ditunjukkan bahwa s j s j s T z + − = = ( ) memetakan daerah di atas sumbu real; Im(s) > 0 pada daerah di dalam lingkaran satuan terbuka

denganpusat titik asal; z <1, seperti yang dapat dilihat pada Gambar 4.

Gambar 4 Pemetaan s j s j s T z + − = = ( ) . 3.2 Transformasi Tustin

Dari persamaan 2.30, yaitu ( ) ;

d cz b az z T s + + = = (ad ≠ bc). Jika dipilih b = –1

dan a = c = d = 1, maka transformasi Möbius menjadi

1 1 ) ( + − = = z z z T s . (3.9)

Bentuk transformasi pada persamaan (3.9) ini disebut dengan transformasi Tustin. Dengan demikian, transformasi Tustin merupakan bentuk khusus dari transformasi Möbius.

Berikut ini akan diberikan ilustrasi dari transformasi Tustin, yaitu akan ditunjukkan bahwa 1 1 ) ( + − = = z z z T

s memetakan daerah C = {z ∈  : |z| > 1} pada daerah   + _{= {s ∈  : Re(s) > 0}. Untuk menunjukkan bahwa daerah} C _{= {z ∈  :}

|z| > 1} dipetakan pada daerah   + _{= {s ∈  : Re(s) > 0} oleh}

1 1 ) ( + − = = z z z T s ,

maka terlebih dahulu dicari invers dari z=T(s), yaitu

s s s T z − + = = − 1 1 ) ( 1 _. jω Bidang s σ Im Bidang z 1 Re s j s j z + − =

Gambar 5 Daerah pada bidang z dengan |z| > 1.

Pada Gambar 5, andaikan z adalah sembarang titik di daerah |z| > 1.Dengan

mensubstitusikan s s z − + = 1 1 , maka 1 1 1 _> − + s s sehingga diperoleh 1+s >1−s. (3.10) Dengan mensubstitusi s=

σ

+ j

ω

ke dalam persamaan (3.10), maka

1 1 1 1 1 1 + − − > + − + z z z z , (3.11) sehingga diperoleh z >1_{. (3.12)}

Dengan demikian dapat ditunjukkan bahwa

1 1 ) ( + − = = z z s T z memetakan daerah di

luar lingkaran satuan terbuka dengan pusat titik asal; C _{= {z ∈  : |z| > 1} pada}

daerah di sebelah kanan sumbu khayal;  + _{= {s ∈  : Re(s) > 0}, seperti yang} dapat dilihat pada Gambar 6.

Gambar 6 Pemetaan 1 1 ) ( + − = = z z z T s . Im 1 Re Bidang z ● z 1 Re σ jω Bidang s 1 1 + − = z z s Im Bidang z

IV DAERAH KESTABILAN SISTEM

4.1 Fungsi Alih Sistem Kontinu

Diberikan sistem persamaan linear masukan dan keluaran sebagai berikut:

) ( ) ( ) (t Axt Bu t x& = + _(4.1) ) ( ) ( ) (t Cxt Dut y = + . (4.2)

Persamaan–persamaan (4.1) dan (4.2) dapat ditulis dalam simbol

∑

=(A,B,C,D)

dengan A∈Rnxn, B∈Rnxm, C∈Rrxn, dan D∈Rrxm. Adapun

x

∈

R

nadalah

state dari sistem,

u

∈

R

m adalah masukan (input), dan y∈Rr adalah keluaran (output). Selanjutnya akan ditunjukkan hubungan antara sistem

∑

=(A,B,C,D)

dengan fungsi alih hasil transformasi dengan menggunakan transformasi Laplace. Dengan menggunakan sifat (1) dan sifat (3) dari transformasi Laplace, maka persamaan (4.1) dapat ditransformasi menjadi

) ( ) ( ) 0 ( ) (s x AX s BU s sX − = + .

Diasumsikan bahwa syarat awal fungsi masukan, yaitu x(0) = 0, maka

) ( ) ( ) (s AX s BU s sX = + .

Kemudian kita kelompokkan X(s), sehingga diperoleh

) ( ) ( ) (s AX s BU s sX − = .

Agar peubah kompleks s dengan matriks A dapat dioperasikan, maka s harus

dikalikan terlebih dahulu dengan matriks identitas, kemudian hasilnya dapat dikurangkan dengan matriks A, sehingga

) ( ) ( ) (sI−A X s =BU s _.

Selanjutnya untuk memperoleh X(s), maka invers dari sI – A dikalikan dari kiri

dengan _{BU(s) sehingga diperoleh}

) ( ) ( ) (_{s sI A} 1_{BU s} X _{= −} − (4.3) Adapun persamaan (4.2) dengan menggunakan sifat (1) dari transformasi Laplace dapat ditransformasi menjadi

) ( ) ( ) (s CX s DU s Y = + (4.4)

) ( ) ( ) ( ) (s C sI A 1BU s DU s Y = − − + .

Kemudian _{U(s) dikelompokkan, maka}

) ( ] ) ( [ ) (s C sI A 1B D U s Y = − − + sehingga diperoleh D B A sI C s U s Y _{= − −1 +} ) ( ) ( ) ( Misalkan ) ( ) ( ) ( s U s Y s

H = , dengan U(s) menyatakan fungsi masukan (input) dan Y(s)

menyatakan fungsi keluaran (output). Maka sistem

∑

=(A,B,C,D) _dapat

dinyatakan dalam bentuk fungsi alih berikut

D B A sI C s H( )= ( − )−1 + (4.5)

Sebagai ilustrasi untuk memperoleh fungsi alih dari suatu sistem ruang kontinu, misalkan suatu sistem translasi mekanik memenuhi persamaan diferensial berikut: ) ( ) ( ) ( ) (t f y t kyt x t y m && + & + = _(4.6)

dengan m = massa benda, f = koefisien gesekan viskos, k = konstanta pegas.

Andaikan gaya x(t) sebagai masukan dan perpindahan y(t) dari massa sebagai

keluaran, serta ditentukan bahwa syarat awal sama dengan nol, sedemikian rupa sehinggay(0)= y_&(0)=0, maka dengan menggunakan sifat (1) dan sifat (3) dari transformasi Laplace persamaan diferensial (4.6) dapat diubah menjadi persamaan aljabar berikut ) ( ) ( )] 0 ( ) ( [ )] 0 ( ) 0 ( ) ( [s2Y s sy y f sY s y kY s X s m − − _& + − + = .

Kemudian dengan mensubstitusikan syarat awal, yaitu y(0)= y_&(0)=0, maka

) ( ) ( ) ( ) ( 2_{Y s fsY s kY s X s} ms + + = . ) ( ) ( ) (_ms2_{+ fs+k Y s =X s}

sehingga diperoleh fungsi alih berikut

k fs ms s X s Y + + = ₂ 1 ) ( ) ( . _(4.7)

Selanjutnya akan ditunjukkan bahwa persamaan (4.6) dapat diubah menjadi persamaan (4.7) dengan menggunakan sistem

∑

=(A,B,C,D).

Pertama kita misalkan y₁=y dan y₂= y_&, maka

2 1 y y_& = dan x m y m f y m k y y&₂ = &&=− ₁− ₂+ 1 . Kemudian diubah ke dalam bentuk matriks, maka

x y y y y m m f mk ⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 1 2 1 2 1 0 1 0 & & _.

Persamaan ini dapat ditulis y&=Ay+Bx

dengan _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − = m f m k A 0 1 dan _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = m B 0₁ .

Selanjutnya kita misalkan bahwa fungsi keluarannya adalah: (1) jika u = y = y1, maka

(

)

x y y u 1 0 (0) 2 1 ₊ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ,

sehingga u = Cy + Dx dengan C = (1 0) dan D = (0).

Jika A, B, C, dan D disubstitusi ke persamaan (4.5), maka fungsi alih dari

fungsi masukan X(s) dan fungsi keluaran U(s) adalah

(

1 0

)

1 0 (0) ) ( ) ( 1 1 + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + − = − m m f mk s s s X s U

(

)

1 0 (0) ) 1 ( ) ( 1 0 1 _1⎟⎟+ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + − − + = m mk m f mk m f _s s s s

(

1 0

)

1 1 0₁ (0) 2 ⎟⎟_⎠+ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + + + = m mk m f mk m f _s s s s

(

1 0

)

₂ 1 0_1⎟⎟+(0) ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + + + = m mk m f s s k fs ms m

(

1 0

)

0₁ (0) 2 2 2 2 + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = + + + + − + + + + + m k fs ms ms k fs ms k k fs ms m k fs ms f ms ) 0 ( 0 1 2 2 ⎟⎟+ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + + + + + = m k fs ms m k fs ms f ms k fs ms s X s U + + = ₂ 1 ) ( ) ( .

Karena dimisalkan u= y, maka U(s) = Y(s) sehingga diperoleh fungsi alih

k fs ms s X s Y + + = ₂ 1 ) ( ) ( . (2) jika u= &y= y₂, maka

(

)

x y y u 0 1 (0) 2 1 ₊ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ,

sehingga u = Cy + Dx dengan C = (0 1) dan D = (0).

Jika A, B, C, dan D disubstitusi ke persamaan (4.5), maka fungsi alih dari

fungsi masukan X(s) dan fungsi keluaran U(s) adalah

(

0 1

)

1 0 (0) ) ( ) ( 1 1 + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − = − m m f mk s s s X s U

(

)

1 0 (0) ) 1 ( ) ( 1 1 0 _1⎟⎟+ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + − − + = m mk m f mk m f _s s s s

(

0 1

)

1 1 0₁ (0) 2 ⎟⎟_⎠+ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + + + = m mk m f mk m f _s s s s

(

0 1

)

₂ 1 0_1⎟⎟+(0) ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + + + = m mk m f s s k fs ms m

(

0 1

)

0₁ (0) 2 2 2 2 + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = + + + + − + + + + + m k fs ms ms k fs ms k k fs ms m k fs ms f ms ) 0 ( 0 1 2 2 ⎟⎟+ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + + + + − = m k fs ms ms k fs ms k

. ) ( ) ( 2 _{fs k} ms s s X s U + + =

Karena dimisalkan u=y&, maka U(s) = sY(s), maka

k fs ms s s X s sY + + = ₂ ) ( ) (

sehingga diperoleh fungsi alih k fs ms s X s Y + + = ₂ 1 ) ( ) ( . (3) jika x m y m f y m k y u= &&=− ₁− ₂+ 1 , maka x m y y m f m k u ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛_{− −} = 1 2 1 Sehingga u = Cy + Dx dengan ⎟ ⎠ ⎞ ⎜ ⎝ ⎛_{− −} = m f m k C , dan ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = m D 1

Jika A, B, C, dan D disubstitusi ke persamaan (4.5), maka fungsi alih dari

fungsi masukan X(s) dan fungsi keluaran U(s) adalah

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛_{− −} = − m s s m f m k s X s U m m f mk 1 0 1 ) ( ) ( 1 1 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + − − + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛_{− −} = m s s s s m f m k m mk m f mk m f 1 0 1 ) 1 ( ) ( 1 1 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + + + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛_{− −} = m s s s s m f m k m mk m f mk m f 1 0 1 1 1 2 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + + + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛_{− −} = m s s k fs ms m m f m k m mk m f 1 0 1 1 2 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛_{− −} = + + + + −+ + + + + m m f m k m k fs ms ms k fs ms k k fs ms m k fs ms f ms 1 0 1 2 2 2 2

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _{+ +} = + + − + + − + + + + + − m m k fs ms m fms k fs ms m km k fs ms m kf k fs ms m f ms k 0 1 1 ) ( ) ( ) ( ) ( ) ( 2 2 2 2 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + + − + + + − = m k fs ms m fs k fs ms m k 1 ) ( ) ( 2 2 ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + + + + + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + + − − = ) ( ) ( 2 2 2 _{m ms fs k} k fs ms k fs ms m k fs ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + + = ) ( 2 2 k fs ms m ms k fs ms s s X s U + + = ₂ 2 ) ( ) ( .

Karena dimisalkan u=y&&, maka U(s) = s2Y(s), maka

k fs ms s s X s Y s + + = ₂ 2 2 ) ( ) (

sehingga diperoleh fungsi alih k fs ms s X s Y + + = ₂ 1 ) ( ) ( .

Dari hasil di atas, maka dapat ditunjukkan bahwa dengan menggunakan sistem

∑

=(A,B,C,D) persamaan diferensial ) ( ) ( ) ( ) (t f y t ky t xt y m && + & + =

dapat diubah menjadi fungsi alih

k fs ms s X s Y + + = ₂ 1 ) ( ) ( .

Dari ilustrasi di atas dapat dilihat bahwa untuk memperoleh fungsi alih yang merupakan bentuk khusus dari persamaan aljabar dapat menggunakan sistem

∑

=(A,B,C,D) _{atau dapat juga dengan menggunakan transformasi Laplace.}

4.2 Kestabilan Sistem Kontinu

Daerah kestabilan sistem ruang kontinu, akan lebih mudah dicari dengan menentukan letak poles fungsi alih yang diperoleh dari hasil transformasi Laplace

Teorema 1 Diberikan sistem H(s) yang memiliki poles p1, p2, …, pn, maka

pernyataan-pernyataan berikut berlaku:

(1) sistem H(s) stabil, jika dan hanya jika Re(pi) ≤ 0 untuk semua i = 1, 2, …, n;

(2) sistem H(s) stabil asimtotik, jika dan hanya jika Re(pi) < 0 untuk semua i = 1,2,…, n;

(3) sistem H(s) takstabil, jika dan hanya jika Re(pi) > 0 untuk semua i = 1, 2, …, n.

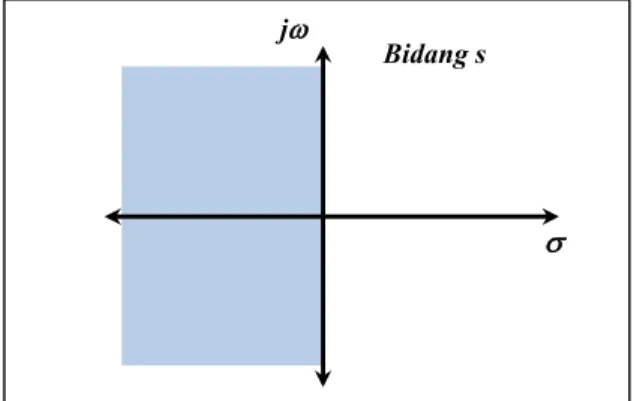
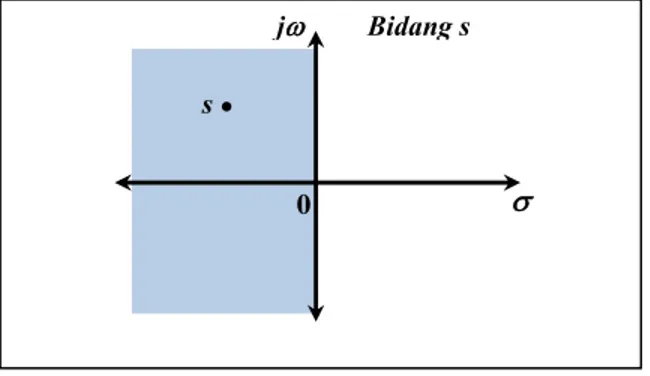
Berikut ini adalah daerah kestabilan sistem pada ruang kontinu. Pada Gambar 7, dapat dilihat bahwa daerah yang diarsir merupakan daerah kestabilan sistem ruang kontinu. Daerah tersebut terletak di sebelah kiri sumbu khayal pada bidang s.

Gambar 7 Daerah kestabilan sistem kontinu.

4.3 Fungsi Alih Sistem Diskret Diberikan suatu persamaan beda

L , 2 , 1 , 0 , 0 0 = =

∑

∑

= + = + B u n y A P k n k Q k k n k k . (4.8)

P dan Q adalah bilangan-bilangan bulat tak negatif; A0, …, AP dan B0, …, BQ

adalah bilangan-bilangan real atau kompleks. Barisan bilangan {uk} dan {yk}

berturut-turut disebut fungsi masukan (input) dan fungsi keluaran (output) sistem.

Dengan menggunakan sifat (1) dan sifat (2) dari transformasi–Z, maka persamaan (4.8) dapat diubah menjadi

L , 2 , 1 , 0 , ) ( ) ( 0 0 = =

∑

∑

= + = + n u Z B y Z A P k n k Q k k n k k jω σ Bidang s

sehingga diperoleh

∑

∑

∑

∑

= − = − = − = − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − = ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − P k Q k k k k Q k k P k k k k kz Y z y z B z U z u z A 0 1 0 0 1 0 ) ( ) ( .

Diasumsikan bahwa syarat awal y0, …, yP–1 = 0, input u0, …, uQ–1 = 0, dan P ≥ Q,

maka

∑

∑

= = = P k k Q k k k kz Y z B z U z A 0 0 ) ( ) ( ) ( ) ( 0 0 _{U z} z Y k P k k k Q k k z A z B ∑ ∑ = = = . Misalkan k P k k k Q k k z A z B d z H ∑ ∑ = = = 0 0 )

( , maka bentuk eksplisit transformasi–Z dari persamaan

(4.8) adalah Y(z) = Hd (z)U(z), sehingga

) ( ) ( ) ( z U z Y z H_d = . (4.9)

Sebagai ilustrasi untuk memperoleh fungsi alih dari suatu sistem ruang diskret, disajikan dua contoh berikut:

(1) Jika diberikan persamaan beda linear

0 , , 2 , 1 , 0 , 2 ₁= = ₀ = + y ₊ u n y y_{n n n L} , (4.10)

dengan un fungsi masukan (input) dan yn fungsi keluaran (output), maka

transformasi–Z persamaan di atas adalah

Y(z) +2(zY(z) – zy0) = U(z). Karena y0 = 0, maka diperoleh

(1 + 2z)Y(z) = U(z)

sehingga diperoleh fungsi alih sistem ruang diskret sebagai berikut:

z z U z Y 2 1 1 ) ( ) ( + = . (4.11)

Dari persamaan (4.11) dapat kita lihat bahwa sistem hanya memiliki satu

(2) Diberikan persamaan beda berikut:

x(k+2) + 3x(k+1) + 2x(k) = 0; x(0) = 0, x(1) = 1, (4.12) maka dengan metode transformasi–Z persamaan tersebut dapat diubah menjadi:

(

z2X(z)−z2x(0)−zx(1)

)

+3

(

zX(z)−zx(0)

)

+2X(z)=0. Karena x(0) = 0 dan x(1) = 1, maka diperoleh

z z X z z +3 +2) ( )= ( 2

sehingga diperoleh fungsi alih sebagai berikut:

) 1 )( 2 ( ) ( + + = z z z z X . (4.13)

Dari persamaan (4.13) dapat dilihat bahwa sistem sistem memiliki satu zero,

yaitu z = 0 dan dua pole, yaitu p1 = –1 dan p2 = –2.

4.4 Kestabilan Sistem Diskret

Untuk menentukan daerah kestabilan pada sistem ruang diskret akan digunakan poles fungsi alih yang diperoleh dari hasil transformasi–Z.

Teorema 2 Suatu persamaan beda linear pada persamaan (4.8) dengan fungsi alih sistem Hd yang diberikan pada persamaan (4.9) adalah stabil jika dan hanya jika

semua pole-nya terletak di dalam cakram terbuka {z : |z| < 1} (Fisher 1990).

Berikut ini adalah daerah kestabilan sistem pada ruang diskret. Pada Gambar 8, dapat dilihat, bahwa daerah yang diarsir merupakan daerah kestabilan sistem ruang diskret terletak di dalam lingkaran satuan terbuka dengan pusat titik asal pada bidang z.

Gambar 8 Daerah kestabilan sistem diskret.

Im

1 Re Bidang z

4.5 Transformasi Daerah Kestabilan Sistem

Sudah ditunjukkan bahwa daerah kestabilan pada sistem ruang kontinu terletak pada daerah di sebelah kiri sumbu khayal bidang s. Demikian pula daerah

kestabilan sistem ruang diskret sudah ditunjukkan terletak di dalam lingkaran satuan pada bidang z. Selanjutnya akan ditunjukkan bahwa transformasi Tustin

dapat membawa daerah kestabilan pada sistem ruang kontinu kepada daerah kestabilan sistem ruang diskret.

Untuk menunjukkan bahwa transformasi Tustin dapat membawa daerah kestabilan pada sistem ruang kontinu kepada daerah kestabilan sistem ruang diskret, lihat Gambar 9.

Gambar 9 Daerah pada bidang s dengan Re(s) < 0.

Andaikan s adalah sembarang titik di daerah Re(s) < 0, maka σ <0, sehingga

σ

σ 2

2 <− . Dengan menambahkan σ2+ω2+1 _{pada kedua sisi, maka diperoleh} 2 2 2 2 _{( 1)} ) 1 (σ+ +ω < σ− +ω . (4.14)

Persamaan (4.14) merupakan representasi jarak dari

ω σ ω σ +1)+ j <( −1)+ j ( . (4.15) atau (σ+ jω)+1< (σ+ jω)−1 _(4.16) Dengan mensubstitusi 1 1 + − = + = z z j

s

σ

ω

ke dalam persamaan (4.16), maka

1 1 1 1 1 1 ₋ + − < + + − z z z z , sehingga diperoleh z <1. _(4.17) σ jω Bidang s s ● 0

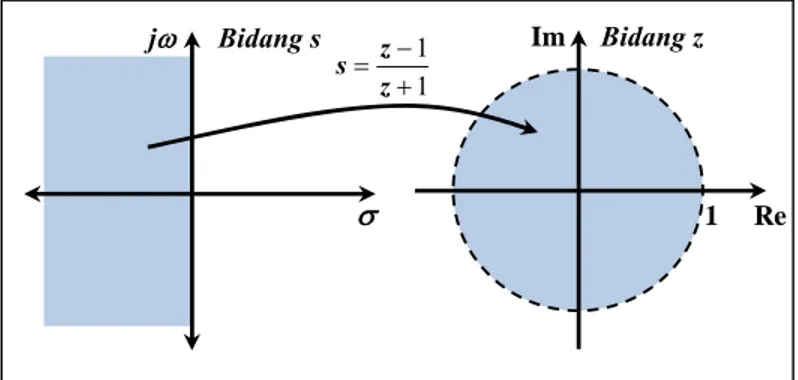
Dengan demikian, dapat ditunjukkan bahwa transformasi Tustin dapat membawa daerah kestabilan pada sistem ruang kontinu kepada daerah kestabilan sistem ruang diskret, seperti yang terlihat pada gambar 10.

Gambar 10 Transformasi daerah kestabilan dari kontinu ke diskret. σ 1 1 + − = z z s jω Bidang s Im Bidang z 1 Re

V PADANAN TEOREMA

Pada bab IV sudah ditunjukkan peran transformasi Tustin dalam mentransformasikan daerah kestabilan dari sistem kontinu ke sistem diskret. Pada bab V akan ditunjukkan peranan transformasi Tustin yang lain, yaitu peranannya dalam menurunkan padanan beberapa sifat yang berlaku di ruang diskret dari sifat-sifat yang berlaku di ruang kontinu, dan sebaliknya.

5.1 Padanan Teorema di Ruang Diskret

Teorema 3 (Redaman Integral Bode)

Andaikan g(s) adalah fungsi analitik di + _{memenuhi g(jω) = g}

1(ω) + jg2(ω) dan )

( ) (s g s

g = (simetrik konjugat), maka

(

)

(

ω

)

ω π g g d g s g s s

∫

∞ ∞ − ∞ → − ∞ = ( )− (∞) 1 ) ( ) ( lim _{1 1} . (5.1)

Teorema ini sudah dibuktikan benar (lihat Seron et al. 1997). Selanjutnya dengan menggunakan transformasi Tustin akan dicari padanannya di ruang diskret.

Untuk memperoleh padanan g(s), transformasi Tustin

1 1 + − = z z s disubstitusi ke dalam g(s), maka ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − = 1 1 ) ( z z g z

f sehingga padanan g(s) adalah f (z), dan akibatnya padanan g(s)=g(s) _adalah f(z)= f(z). Karena g(s) adalah fungsi analitik di +, maka f (z) adalah fungsi yang analitik di C.

Kemudian untuk memperoleh padanan g(jω) = g1(ω) + jg2(ω), maka digunakan fungsi alih. Misalkan H(s) adalah fungsi alih sistem kontinu dan Hd(z)

adalah fungsi alih sistem diskret. Dengan menggunakan transformasi Tustin

1 1 + − = z z s , maka ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − = 1 1 ) ( z z H z

H_d . Kemudian dengan mensubstitusikan z=ejθ ,

maka _⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + − = 1 1 ) ( jθ _jj_θθ d e e H e

H =H(jtanθ₂) =H(jω) _dengan ω=tanθ₂ , sehingga

Selanjutnya untuk memperoleh padanan

(

)

(

ω

)

ω π g g d g s g s s

∫

∞ ∞ − ∞ → − ∞ = ( )− (∞) 1 ) ( ) ( lim _{1 1} ,

dari transformasi Tustin

1 1 + − = z z

s , jika s→∞, maka z→−1 sehingga θ→π.

Kemudian ω=tanθ₂ didiferensialkan terhadap θ, maka θ

θ ω d d ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + = cos 1 1 .

Untuk batas-batas integral ditentukan dari ω=tanθ₂. Jika ω = –∞, maka θ = –π dan jika ω = ∞, maka θ = π. Dengan demikian, padanan dari

(

)

(

ω

)

ω π g g d g s g s s

∫

∞ ∞ − ∞ → − ∞ = ( )− (∞) 1 ) ( ) ( lim _{1 1} adalah

(

)

(

)

θ θ π θ π π π d f f f z f z z z ⎟⎠ ⎞ ⎜ ⎝ ⎛ + − = − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + −

∫

− − → 1 cos 1 ) ( ) ( 1 ) 1 ( ) ( 1 1 lim _{1 1} 1 θ θ π θ π π π d f f z f z f z

∫

− − → ⎟⎠ ⎞ ⎜ ⎝ ⎛ + − = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − − − cos 1 ) ( ) ( 1 1 ) 1 ( ) ( lim 2 1 1 1 .

Dengan menggunakan dalil L’Hospital, maka

θ θ π θ π π π d f f z f z

∫

− − → ⎟⎠ ⎞ ⎜ ⎝ ⎛ + − = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ′ − − cos 1 ) ( ) ( 1 1 0 ) ( lim 2 1 1 1 sehingga diperoleh θ θ π θ π π π d f f f

∫

− ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − − = − ′ cos 1 ) ( ) ( 2 1 ) 1 ( 1 1 .

Jadi, padanan Teorema 3 di ruang diskret adalah

Andaikan f (z) adalah fungsi analitik di C _{memenuhi f (e} jθ_{) = f}

1(θ) + jf2(θ) dan )

( ) (z f z

f = (simetrik konjugat), maka

θ θ π θ π π π d f f f

∫

− ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − − = − ′ cos 1 ) ( ) ( 2 1 ) 1 ( 1 1 . (5.2)

Sebagai ilustrasi akan ditunjukkan bahwa

( )

p z z z f − + =3 1; p ∈ (–1, 1) analitik di C memenuhi θ θ π θ π π π d f f f

∫

− ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − − = − ′ cos 1 ) ( ) ( 2 1 ) 1 ( 1 1 .

Pertama, dihitung nilai dari f′(−1). Dari fungsi

( )

p z z z f − + = 3 1 , maka

( )

₂ ) ( 1 3 p z p z f − + − = ′ , sehingga diperoleh

( )

₂ ) 1 ( 3 1 1 p p f + + − = − ′ . Misalkan LHS₁= f′

( )

−1 , maka _{1 2} ) 1 ( 3 1 p p LHS + + − = ; p ∈ (–1, 1).

Berikutnya, dihitung nilai dari θ

θ θ π π π d f f

∫

− ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − − cos 1 ) 0 ( ) ( 2 1 _{1 1} . Untuk keperluan

itu, substitusikan z=ejθ =cosθ + jsinθ ke dalam fungsi

( )

p z z z f − + =3 1, maka p e e e f j _jj − + = _θθ θ₎ 3 1 ( p j j − + + + = ) sin (cos 1 ) sin (cos 3 θ θ θ θ 2 2 _{1 2 cos} sin ) 3 1 ( cos 2 1 cos ) 3 1 ( ) 3 ( ) ( p p p j p p p p e f j + − + − + + − − + − = θ θ θ θ θ _,

sehingga diperoleh bentuk f(ejθ)= f₁(θ)+ jf₂(θ)

dengan _{1 2} cos 2 1 cos ) 3 1 ( ) 3 ( ) ( p p p p f + − − + − = θ θ θ dan _{2 2} cos 2 1 sin ) 3 1 ( ) ( p p p f + − + − = θ θ θ . Jika θ = π, maka 2 1 2 1 3 1 3 ) π ( p p p p f + + + − − = p + = 12 . Misalkan θ θ π θ π π π d f f RHS

∫

− ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − − = cos 1 ) ( ) ( 2 1 _{1 1} 1 , maka θ θ π π π d p p p p p RHS

∫

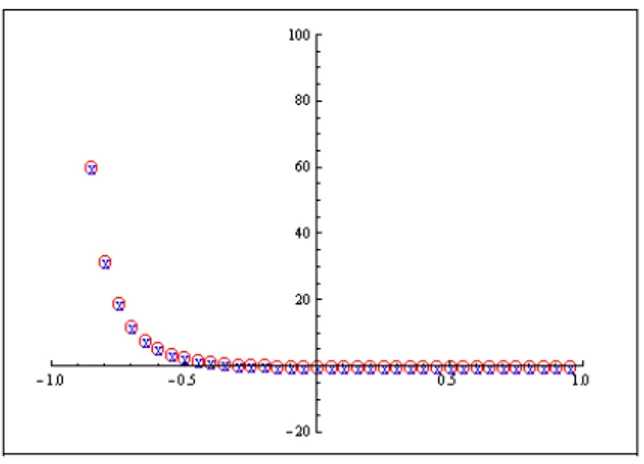
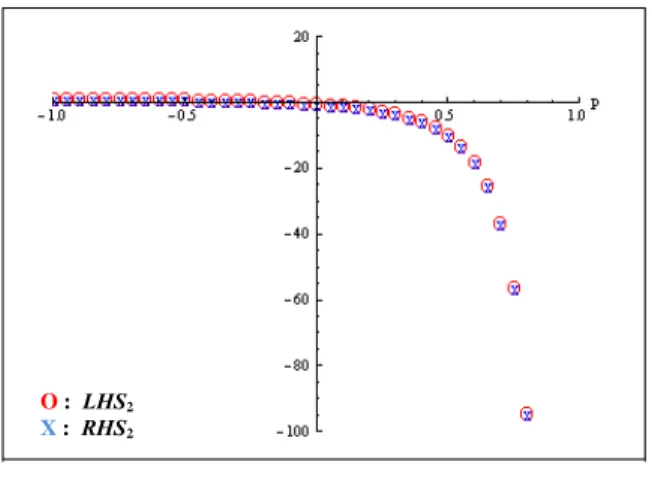
− ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + − + − − = 2 2 1 cos 2 1 1 ) 1 ( 2 1 2 3 _{; p ∈ (–1, 1).}

Nilai-nilai dari LHS1 dan RHS1 masing-masing dihitung secara terpisah dengan menggunakan software Mathematica 7. Selanjutnya hasil keduanya dinyatakan dalam bentuk grafik, seperti yang dapat dilihat pada Gambar 11.

Gambar 11 Grafik LHS1 (o) dan RHS1 (x).

Pada gambar 11, dapat dilihat bahwa nilai-nilai LHS1 yang dilambangkan dengan “o” dan nilai-nilai dari RHS1 yang dilambangkan dengan “x” keduanya saling berhimpit. Hal ini menunjukkkan bahwa

θ θ θ π π π d f f f

∫

− ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − − = − ′ cos 1 ) 0 ( ) ( 2 1 ) 1 ( 1 1 untuk

( )

p z z z f − + =3 1; p ∈ (–1, 1).

Akibat 1 (Redaman Integral Bode)

Andaikan g(s) adalah fungsi analitik di + _{memenuhi g(jω) = g}

1(ω) + jg2(ω) dan )

( ) (s g s

g = (simetrik konjugat), maka

( )

( )

ω ω ω π d g g g

∫

∞ ∞ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = ′ 2 1 1( ) 0 1 0 . (5.3)

Teorema ini sudah dibuktikan benar (lihat Seron et al. 1997). Selanjutnya dengan menggunakan transformasi Tustin akan dicari padanannya di ruang diskret.

Untuk memperoleh padanan g(s), transformasi Tustin

1 1 + − = z z s disubstitusi ke dalam g(s), maka ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − = 1 1 ) ( z z g z

f sehingga padanan g(s) adalah f (z), dan

akibatnya padanan g(s)=g(s) _adalah f(z)= f(z). Karena g(s) adalah fungsi analitik di +, maka f (z) adalah fungsi yang analitik di C.

Kemudian untuk memperoleh padanan g(jω) = g1(ω) + jg2(ω), maka digunakan fungsi alih. Misalkan H(s) adalah fungsi alih sistem kontinu dan Hd(z)