Bab 7 NILAI DAN VEKTOR EIGEN

Bab 7

NILAI DAN

VEKTOR EIGEN

7.1 Motivasi

Dimotivasi bab ini dengan mendiskusikan persamaan

ax2 + 2hxy + by2 = c,

dengan tidak semua dari a, b, dan c adalah nol. Pernyataan ax2 _{+ 2hxy + by}2 _disebut bentuk kuadratik dalam x dan y, serta terdapat identitas

ax2 + 2hxy + by2 =

[

x y

]

_ú û ù ê ë é b h h a ú û ù ê ë é y x = XTAX , dengan _ú û ù ê ë é = y x X dan _ú û ù ê ë é = b h h a

A . Matriks A disebut matriks dari bentuk kuadratik. Selanjutnya sumbu x dan sumbu y dirotasikan berlawanan arah jarum jam sebesar

q radian ke sumbu baru x1 dan y1. Persamaan yang dihasilkan dari rotasi sumbu diturunkan sebagai berikut.

Diambil X yang mempunyai koordinat (x, y) relatif terhadap sumbu x dan sumbu

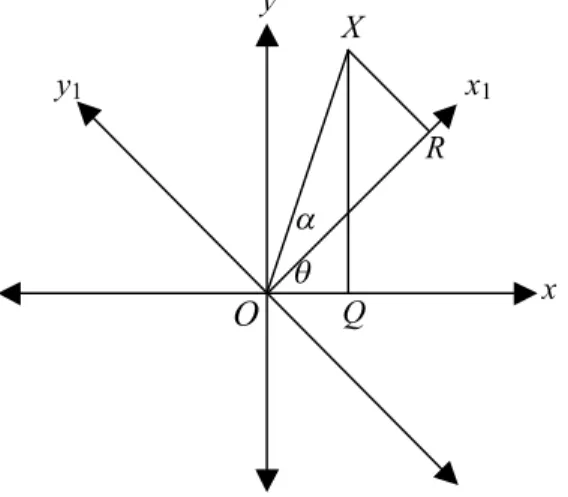
y, serta koordinat (x1, y1) relatif terhadap sumbu x1 dan sumbu y1. Diperhatikan Gambar 7.1.

Gambar 7.1: Rotasi sumbu

X R x1 x y y1 Q a q

O

© 2010 Didit B. Nugroho

x = OQ = OPcos(q + a)

= OP(cos(q).cos(a) – sin(q).sin(a)) = (OP.cos(a))cos(q) – (OP.sin(a))sin(q) = OR.cos(q)– PR.sin(q)

= x1 cos(q)– y1 sin(q). Sejalan dengan itu, diperoleh y = x1 sin(q) + y1 cos(q)

Dinyatakan persamaan di atas ke persamaan matriks tunggal:

ú û ù ê ë é ú û ù ê ë é -= ú û ù ê ë é 1 1 ) cos( ) sin( ) sin( ) cos( y x θ θ θ θ y x , atau X = PY, dengan _ú û ù ê ë é = y x X , _ú û ù ê ë é = 1 1 y x Y dan _ú û ù ê ë é -= ) cos( ) sin( ) sin( ) cos( θ θ θ θ P . Dicatat bahwa

kolom-kolom dari P memberikan arah sumbu positif x1 dan y1. P adalah matriks ortogonal, karena itu PPT = I2 atau P–1 = PT. Selain itu, matriks P mempunyai sifat khusus yaitu det(P) = 1.

Suatu matriks berjenis _ú

û ù ê ë é -= ) cos( ) sin( ) sin( ) cos( θ θ θ θ

P disebut matriks rotasi. Dapat

ditunjukkan dengan mudah bahwa suatu matriks ortogonal real 2´2 dengan determinan sama dengan 1 adalah suatu matriks rotasi.

Dapat juga diselesaikan untuk koordinat-koordinat baru dalam koordinat lama:

ú û ù ê ë é ú û ù ê ë é -= = = ú û ù ê ë é y x θ θ θ θ X P Y y x _T ) cos( ) sin( ) sin( ) cos( 1 1 _,

karena itu x1 = x.cos(q) + y.sin(q) dan y1 = –x.sin(q) + y.cos(q). Jadi

XTAX = (PY)TA(PY) = YT(PTAP)Y.

Selanjutnya diandaikan bahwa bisa dipilih suatu sudut q sehingga PTAP adalah matriks diagonal, misalnya diag(l1, l2), maka

[

]

2 1 2 2 1 1 1 1 2 1 1 1 ₀ 0 y λ x λ y x λ λ y x AX XT _ú= + û ù ê ë é ú û ù ê ë é = (7.1)

dan relatif terhadap sumbu baru. Persamaan ax2 _{+ 2hxy + by}2 _{= c menjadi}

c y λ x λ + 2 = 1 2 2 1

1 yang mudah dibuat sketsa kurvanya. Kurva ini simetris terhadap sumbu x1 dan y1, dengan P1 dan P2 adalah kolom-kolom dari P, yang memberikan arah sumbu simetri.

Dapat diperiksa juga bahwa P1 dan P2 memenuhi persamaan

AP1 = l1P1 dan AP2 = l2P2. Persamaan tersebut dibatasi pada l1 dan l2. Jika ú

û ù ê ë é = 1 1 1 _v u

P , maka persamaan pertama menjadi ú û ù ê ë é = ú û ù ê ë é ú û ù ê ë é 1 1 1 1 1 v u λ v u b h h a atau _ú û ù ê ë é = ú û ù ê ë é ú û ù ê ë é -0 0 1 1 1 1 v u λ b h h λ a .

Karena itu, sistem homogen dari dua persamaan linear dalam dua variabel tersebut mempunyai suatu penyelesaian nontrivial (u1, v1). Karena itu

0 1 1 ₌ -λ b h h λ a .

Sejalan dengan itu, l2 memenuhi persamaan yang sama. Dalam bentuk yang diperluas, l1 dan l2 memenuhi

l2 _{– (a + b)l + ab – h}2 _{= 0.} Persamaan tersebut mempunyai akar real

(

)

(

)

(

)

2 4 2 4 2 2 2 _{ab h a b a b h} b a b a λ= + ± + - - = + ± - + (7.2)

(Akar-akar ini adalah berbeda jika a ¹b atau h ¹ 0. Untuk kasus a = b dan h = 0 tidak perlu dilakukan penyelidikan karena memberikan suatu persamaan lingkaran.)

Persamaan l2 _{– (a + b)l + ab – h}2 _{= 0 disebut persamaan nilai eigen dari} matriks A.

7.2 Menghitung Nilai dan Vektor Eigen

Pada bagian ini akan dipelajari dasar-dasar mencari nilai eigen (eigenvalue) dan vektor eigen (eigenvector) dari suatu matriks persegi.

DEFINISI 7.2.1 (Nilai eigen, vektor eigen)

Diambil T : V®V sebagai operator linear pada ruang vektor V atas fieldF. Suatu vektor tak nol v Î V dinamakan suatu vektor eigen dari T jika terdapat suatu skalar l Î F

sehingga

T(v) = lv.

Skalar l disebut nilai eigen dari T yang berkorespondensi dengan vektor eigen v. Pasangan (l, v) dinamakan suatu pasangan eigen (eigenpair) dari T.

Untuk AÎMn(F), suatu vektor tak nol vÎFn dinamakan suatu vektor eigen dari A jika terdapat suatu skalar lÎF sehingga

Av = lv.

Skalar l disebut nilai eigen dari A yang berkorespondensi dengan vektor eigen v. Pasangan (l, v) dinamakan suatu pasangan eigen dari A.

Syarat Av = lv dapat dituliskan kembali menjadi

lInv – Av = (lIn – A)v = 0

dengan I adalah matriks identitas yang berukuran sama dengan matriks A. Jika diandaikan bahwa det(lI – A) ¹ 0 maka lI – A mempunyai invers, karena itu

(lI – A)–1(lI – A)v = (lI – A)–10 v = 0.

Padahal diberikan vektor v tidak sama nol, sehingga haruslah det(lI – A) = 0.

Gambar 7.2: (a) Dilatasi l > 1. (b) Kontraksi 0<l < 1. (c) Pembalikan arah (l < 0)

v

Av =

l

v

(

l

> 1)

v

Av =

l

v (

l

< 0)

v

Av =

l

v

(0<

l

< 1)

(a)

(b)

(c)

© 2010 Didit B. Nugroho

DEFINISI 7.2.2 (Persamaan dan polinomial karakteristik)

Untuk A ÎMn(F), persamaan det(lI – A) = 0 disebut persamaan karakteristik dari A,

sedangkan polinomial det(lI – A) disebut polinomial karakteristik dari A dan seringkali dinotasikan dengan ch_A

( )

λ atau pA(l).

Karena itu, nilai eigen dari A tidak lain adalah akar-akar persamaan karakteristik dari A. Sedangkan vektor eigen

ú ú ú û ù ê ê ê ë é = n v v v ! 1

yang bersesuaian dengan nilai eigen l dicari dengan cara menyelesaikan sistem persamaan linear

(lI – A)v = 0.

CONTOH 7.2.1 Selesaikan masalah nilai eigen untuk

ú û ù ê ë é = 2 1 1 2 A jika diberikan AÎM2(R). Penyelesaian. (i) ú û ù ê ë é -= ú û ù ê ë é -ú û ù ê ë é = -2 1 1 2 2 1 1 2 0 0 λ λ λ λ A λI sehingga p(l) = det(lI – A) = (l – 2)2 _{– 1 = l}2 _{– 4l + 3 = (l– 1)(l– 3).} (ii) Pembuat nol p(l) adalah nilai-nilai eigen dari A, jadi

l1= 1 atau l2= 3.

(iii) Untuk setiap nilai eigen li, i = 1, 2, diperiksa persamaan nilai eigen untuk

menentukan vektor eigen.

(a) l1= 1. Diperiksa (1.I2 – A)v = 0. Ini berarti bahwa

ú û ù ê ë é = ú û ù ê ë é ú û ù ê ë é -0 0 1 1 1 1 b a , dengan v b a = ú û ù ê ë é . Diperoleh ú û ù ê ë é = ú û ù ê ë é ú û ù ê ë é 0 0 0 0 1 1 b a . Penyelesaian umumnya adalah

þ ý ü î í ì Î ú û ù ê ë é-R b b : 1 1 . Jadi suatu pasangan eigennya adalah

÷÷ ø ö çç è æ ú û ù ê ë é-1 1 , 1 . (b) l2= 3. Diperiksa (3I2 – A)v = 0. Ini berarti bahwa

ú û ù ê ë é = ú û ù ê ë é ú û ù ê ë é -0 0 1 1 1 1 d c , dengan v d c = ú û ù ê ë é .

Diperoleh ú û ù ê ë é = ú û ù ê ë é ú û ù ê ë é -0 0 0 0 1 1 d c . Penyelesaian umumnya adalah

þ ý ü î í ì Î ú û ù ê ë é R d d : 1 1 . Jadi suatu pasangan eigennya adalah

÷÷ ø ö çç è æ ú û ù ê ë é 1 1 , 3 .

CONTOH 7.2.2 Selesaikan masalah nilai eigen untuk BÎM2(R). ú û ù ê ë é -= 0 1 1 0 B Penyelesaian. ú û ù ê ë é -= -λ λ B λI 1 1 sehingga p(l) = l2 + 1.

Karena p(l) tidak mempunyai akar real, maka B tidak mempunyai pasangan eigen.

CONTOH 7.2.3 Selesaikan masalah nilai eigen untuk CÎM2(C).

ú û ù ê ë é -= 0 1 1 0 C Penyelesaian. (i) p(l) = l2 + 1 = (l + i)(l – i). (ii) Pembuat nol p(l) adalah nilai-nilai eigen dari A, jadi

l1= –i atau l2= i.

(iii) Untuk setiap nilai eigen li, diperiksa persamaan nilai eigen untuk menentukan vektor eigen.

(a) l1= –i. Diperiksa ((–i)I2 – C)v = 0, berarti

ú û ù ê ë é = ú û ù ê ë é ú û ù ê ë é -0 0 1 1 b a i i , dengan _ú û ù ê ë é = b a v ÎC2. Diperoleh ú û ù ê ë é = ú û ù ê ë é ú û ù ê ë é -0 0 0 0 1 b a i . Penyelesaian umumnya adalah

þ ý ü î í ì Î ú û ù ê ë é C b i b : 1 .

Jadi suatu pasangan eigennya adalah

÷÷ ø ö çç è æ ú û ù ê ë é -1 , i i .

© 2010 Didit B. Nugroho (b) l2= i. Diperiksa (i.I2 – A)v = 0, berarti ú û ù ê ë é = ú û ù ê ë é ú û ù ê ë é -0 0 1 1 d c i i , dengan _ú û ù ê ë é = d c v ÎC2_. Penyelesaian umumnya adalah

þ ý ü î í ì Î ú û ù ê ë é - d R i d : 1 .

Jadi suatu pasangan eigennya adalah

÷÷ ø ö çç è æ ú û ù ê ë é -1 , i i .

CONTOH 7.2.4 Selesaikan masalah nilai eigen untuk DÎM2(C).

ú û ù ê ë é -= i i D 2 4 3 Penyelesaian. (i) ú û ù ê ë é -= -i λ i λ D λI 2 4 3 , p(l) = (l– 3i)(l – i) + 8 = l2 _{– 4il + 5.} (ii) Pembuat nol p(l) adalah

i i i 3 2 2 20 16 4 ± - - _{= ±} sehingga nilai eigennya adalah l1= –i atau l2= 5i. (iii) Diperiksa persamaan nilai eigen untuk setiap nilai eigen.

(a) l1= –i. Diperiksa ((–i)I2 – D)v = 0, berarti

ú û ù ê ë é = ú û ù ê ë é ú û ù ê ë é -0 0 2 2 4 4 b a i i , dengan _ú û ù ê ë é = b a v ÎC2. Penyelesaian umumnya adalah

þ ý ü î í ì Î ú û ù ê ë é-C b i b : 1 .

Jadi suatu pasangan eigennya adalah

÷÷ ø ö çç è æ ú û ù ê ë é -1 , i i . (b) l2= 5i. Diperiksa (5i.I2 – D)v = 0, berarti ú û ù ê ë é = ú û ù ê ë é ú û ù ê ë é - 0 0 4 2 4 2 d c i i , dengan _ú û ù ê ë é = d c v ÎC2. Penyelesaian umumnya adalah

þ ý ü î í ì Î ú û ù ê ë é C d i d : 1 2 . Jadi suatu pasangan eigennya adalah

÷÷

ø

ö

çç

è

æ

ú

û

ù

ê

ë

é

1

2

,

5

i

i

.

Pada saat menyelesaikan persamaan karakteristik, dapat diperoleh akar real dan atau kompleks dan karena itu suatu matriks dapat mempunyai nilai eigen dan vektor eigen real atau kompleks. Juga, dalam menyelesaikan untuk vektor eigen akan diperoleh suatu himpunan tak berhingga dari vektor-vektor. Himpunan tak berhingga tersebut adalah suatu ruang bagian dan tepatnya dinamakan ruang eigen. Lebih khusus lagi, jika l adalah suatu nilai eigen dari A maka ruang eigen yang bersesuaian dengan l adalah ruang nol NS(lI – A).

DEFINISI 7.2.3 Diberikan operator linear T : V ® V pada ruang vektor V atas

field F, dan l sebagai nilai eigen dari A Î Mn(F). Ruang eigen dari A yang

berkorespondensi dengan nilai eigen l, didefinisikan oleh

El = {vÎV : T(v) = lv}

= {xÎFn _{: Ax = lx}}

= {xÎFn _{: (lI – A)x = 0}.}

CONTOH 7.2.5 Diberikan matriks _ú

û ù ê ë é -= 1 1 4 2 F Î M2(R). Polinomial

karakteristik dari A yaitu

det(lI – F) = (l– 2)(l + 1) – 4 = l2 – l – 6 Diperoleh nilai-nilai eigen dari F yaitu l1= 3 dan l2= – 2.

(i) Untuk l1= 3, diambil ú

û ù ê ë é = b a

v ÎR2_{, maka sistem linear (3I – F)v = 0:}

ú û ù ê ë é 0 4 1 0 4 1 Þ _ú û ù ê ë é 0 0 0 0 4 1 . Jadi vektor eigen yang bersesuaian dengan l1= 3 yaitu

ú û ù ê ë é-= ú û ù ê ë é-= 1 4 4 b b b v .

Lebih lanjut, ruang eigen yang bersesuaian dengan l1 = 3 adalah semua vektor yang direntang oleh _ú

û ù ê ë é-1 4 atau þ ý ü î í ì Î ú û ù ê ë é-= a a R E : 1 4

3 . Dengan kata lain,

þ ý ü î í ì ú û ù ê ë é-1 4

adalah basis untuk ruang eigen yang bersesuaian dengan l1. (ii) Untuk l2= –2, diambil ú

û ù ê ë é = d c

v ÎR2_{, maka sistem linear (–2I – F)v = 0:}

ú û ù ê ë é -0 1 1 0 4 4 Þ _ú û ù ê ë é -0 0 0 0 1 1 . Jadi vektor eigen yang bersesuaian dengan l2= –2 yaitu

ú û ù ê ë é = ú û ù ê ë é = 1 1 d d d v .

Ruang eigen yang bersesuaian dengan l2= –2 adalah

þ ý ü î í ì Î ú û ù ê ë é = - d d R E : 1 1 2 . Basis

untuk ruang eigen yang bersesuaian dengan l2 adalah

þ ý ü î í ì ú û ù ê ë é 1 1 .

© 2010 Didit B. Nugroho

DEFINISI 7.2.4 Diberikan A ÎMn(F) yang mempunyai nilai eigen l1, l2, …, ln.

(i) Spektrum (spectrum) dari A, dinotasikan s(A), adalah himpunan nilai-nilai eigen dari A, atau dengan kata lain

s(A) = {l1, l2, …, ln}.

(ii) Radius spektral (spectral radius), dinotasikan r(A), adalah nilai mutlak (atau modulus) terbesar dari nilai-nilai eigen, atau dengan kata lain

r(A) = maks{|l1|, |l2|, …, |ln|}.

Diandaikan A Î Mn(F) dengan l sebagai suatu nilai eigen. Kerangkapan aljabar (algebraic multiplicity) dari l, dinotasikan al, adalah banyaknya pengulangan nilai eigen l sebagai akar dari persamaan karakteristik. Kerangkapan geometris

(geometris multiplicity) dari l, dinotasikan gl, adalah banyaknya vektor eigen bebas linear yang berkorespondensi dengan nilai eigen l. Kerangkapan geometris didefinisikan

gl = dim(NS(lI – A)) = dim(El)

dengan sifat 1 £gl£al.

CONTOH 7.2.6 Diberikan matriks

ú ú ú û ù ê ê ê ë é -= 11 4 4 8 1 4 16 8 5 G ÎM3(R). 2 ) 3 )( 1 ( 11 4 4 8 1 4 16 8 5 ) ( = - + + -= λ λ λ λ λ λ p_A .

Jadi s(G) = {l1 = 1, l2 = – 3} dengan kerangkapan aljabar dari nilai-nilai eigennya adalah a1 = 1 dan a–2 = 2.

Vektor eigen v yang berkorespondensi untuk l1= 1 harus memenuhi

ú ú ú û ù ê ê ê ë é = ú ú ú û ù ê ê ê ë é -0 0 0 12 4 4 8 0 4 16 8 4 v , dengan ú ú ú û ù ê ê ê ë é = c b a v ÎR3_,

atau ekuivalen dengan

ú ú ú û ù ê ê ê ë é 0 0 0 0 0 1 1 0 0 2 0 1 .

Diperoleh vektor eigen yang bersesuaian dengan l1= 1 yaitu

ú ú ú û ù ê ê ê ë é -= ú ú ú û ù ê ê ê ë é -= 1 1 2 2 c c c c v .

Ruang eigen yang berkorespondensi dengan l1= 1 adalah

ï þ ï ý ü ï î ï í ì Î ú ú ú û ù ê ê ê ë é -= c c R E : 1 1 2 2 dengan basisnya adalah −2 −1

Selanjutnya, dengan jalan yang sama akan diperoleh vektor eigen yang bersesuaian dengan l2= –3 yang mempunyai bentuk

s r ú ú ú û ù ê ê ê ë é-+ ú ú ú û ù ê ê ê ë é -1 0 2 1 1 1

dengan r, s ÎR. Diperoleh ruang eigen yang berkorespondensi dengan suatu nilai eigen

l2 = –3 yaitu ï þ ï ý ü ï î ï í ì Î ú ú ú û ù ê ê ê ë é-+ ú ú ú û ù ê ê ê ë é -= - r s r s R E : , 1 0 2 1 1 1

3 . Basis untuk ruang eigen yang

berkorespondensi dengan l2= –3 adalah

ï þ ï ý ü ï î ï í ì ú ú ú û ù ê ê ê ë é-ú ú ú û ù ê ê ê ë é -1 0 2 , 1 1 1

. Jadi kerangkapan geometris dari

l2adalah g–3 = 2.

7.3 Sifat-sifat Polinomial Karakteristik

TEOREMA 7.3.1 JikaAÎMn(F) danpA(l) = det(lIn – A), maka

(a) pA(l) adalah suatu polinomial berderajatndalaml: pA(l) = a0 + a1l + … + anln;

(b) an = 1;

(c) an – 1 = –tr(A); (d) a0 = (–1)ndet(A).

Bukti. Dapat dituliskan

det(lIn – A) =

å

±

(

-

)

(

-

)

(

-

)

s 1,s(1) 2,s(2) ,s( ) ...λI A_{n n} A λI A λI

dengan s merupakan semua kemungkinan permutasi dari kolom A. Akibatnya p(l) adalah suatu polinomial berderajat n. Suku yang berkorespondensi dengan permutasi identitas diperoleh dengan mengalikan unsur-unsur diagonal, dalam kasus ini

(l – a11)(l – a22)…(l – ann) = ln – (a11 + a22 + … + ann)ln–1

+ suku-suku berderajat lebih rendah.

Semua suku-suku lain mempunyai paling banyak (n – 2) faktor-faktor diagonal l – aii,

sehingga polinomialnya berderajat £ n – 2 dalam l. Dari persamaan tersebut, koefisien untuk ln dan ln–1 berturut-turut adalah

an = 1, an–1 = – (a11 + a22 + … + ann) = –tr(A).

Selanjutnya dengan mengambil l = 0 maka p(0) = det(–A) = (–1)n_{.det(A) = a}

0, dan karena itu suku konstan sama dengan positif atau negatif dari determinan matriks.n

Secara khusus, untuk matriks 2´2, misalnya _ú

û ù ê ë é = d c b a A , polinomial

karakteristiknya mempunyai bentuk

pA(l) = l2 –(a + d)l + (ad – bc)

= l2 _{– tr(A).l + det(A).}

TEOREMA 7.3.2 Matriks-matriks yang serupa mempunyai polinomial karakteristik yang sama.

© 2010 Didit B. Nugroho

Bukti. det(lIn – PAP–1) = det(lPInP–1 – PAP–1)

= det P(lIn – A)P–1

= det(P).det(lIn – A).det(P–1)

= ) det( 1 ). det( ). det( P A λI P _n = det(lIn – A). n

DEFINISI 7.3.1 Polinomial p(l) dikatakan terpisah (split) jika terdapat skalar k,

l1, l2, …, lnÎF sehingga

p(l) = k(l – l1)…(l – ln).

Definisi di atas dapat diartikan bahwa jika polinomial karakteristik dari suatu matriks adalah terpisah, maka matriks mempunyai n nilai eigen. Perlu dicatat bahwa nilai eigen tersebut tidak perlu berbeda.

TEOREMA 7.3.3 Diberikan matriks AÎMn(F) dan diandaikan bahwa polinomial karakteristik pA(l) = a0 + a1l + … + anlnadalah terpisah, danl1, …, ln adalah

nilai-nilai eigen dariA, maka

(a) ₁ 1 ) ( tr -= -= =

å

n n i i a A λ ; dan (b) ₀ ( 1) det( ) 1 A a λ n n i i = =

-Õ

= .

Bukti. Karena pA(l) terpisah, maka A mempunyai n nilai eigen l1, …, ln dan

pA(l) = k(l – l1)…(l – ln) dengan k ÎF. Karena an = 1 (Teorema 7.3.1), maka k = 1.

Jika pA(l) diekspansikan, maka akan diperoleh pA(l) = ln +

å

= -n i n i λ λ 1 1 ) 1

( + suku berderajat lebih rendah. Secara khusus

å

= - = -n i i n λ a 1 1 ( 1),

dan berdasarkan Teorema 7.3.1(c) diperoleh bagian (a). Kemudian,

Õ

= -= n i i n A λ p 1 ) 1 ( ) 0 ( ,

sehingga berdasarkan Teorema 7.3.1(d) diperoleh bagian (b). n

AKIBAT 7.3.1 Jika l = 0 adalah suatu nilai eigen dari A Î Mn(F), maka A adalah singular.

Bukti. Berdasarkan Teorema 7.3.3(b), jika li = 0 untuk suatu i, maka ) det( ) 1 ( 0 1 A λ n n i i = =

-Õ

= Þ det(A) = 0, dan karena itu A tidak inversibel. n

CONTOH 7.3.1 Diberikan _ú û ù ê ë é -= 1 1 3 2

A . Persamaan karakteristik dari A yaitu l2 – 3l + 5 = 0 yang mempunyai akar-akar

2 11 3 2 , 1 i λ = ± . 2 11 3 2 11 3 ) ( 1 3 1 2 ) ( tr A = + = =- a₁ =λ₁+λ₂ = + i+ - i. 4 20 2 11 3 2 11 3 ) 1 ( 5 3 2 ) det( 2 _{0 1 2 ÷}÷= ø ö ç ç è æ -÷ ÷ ø ö ç ç è æ ₊ = -= = + = a λ λ i i A .

CONTOH 7.3.2 Diberikan matriks

ú ú ú û ù ê ê ê ë é -= 1 4 3 3 1 0 7 2 3 B .

Persamaan karakteristik untuk B:

1 4 3 3 1 0 7 2 3 -λ λ λ = 0

(

3-λ

)(

(

λ-1

)

2+12

)

+3

(

-6-7

(

λ-1

)

)

= 0

(

λ2 -5λ- 2

)

λ = 0

yang mempunyai penyelesaian l1 = 0,

2 33 5 3 , 2 = ±

λ . Oleh karena itu, A adalah matriks singular.

TEOREMA 7.3.4 (Teorema Cayley-Hamilton Versi Matriks) Diberikan matriksAÎMn(F) mempunyai polinomial karakteristikp(l), maka

p(A)= On. Ini berarti bahwa jika polinomial karakteristikAadalah

pA(l) = ln + an–1ln–1 + … + a1l1 + a0,

maka

An + an–1An–1 + … + a1A1 + a0In = On.

Bukti. Untuk suatu matriks persegi Xn, dipunyai det(X).I = X.adj(X). Diambil X = lI – A yang memberikan persamaan karakteristik dari A yaitu pA(l) = det(X) = det(lI – A).

Karena itu pA(l)I = (lI – A).adj(lI – A). Masukan dalam adj(lI – A) adalah polinomial

dalam l berderajat £n – 1. Karena itu adj(lI – A) = B0 + lB1 + … +ln – 1Bn – 1 dengan Bj

adalah matriks. Ditulis pA(l) = a0 + a1l + … + anln. Dengan membandingkan koefisien kedua sisi dari pA(l)I = (lI – A).adj(lI – A) diperoleh:

untuk l0 _{: a} 0I = –A.B0 l1 _{: a} 1I = –A.B1 + B0 l2 _{: a} 2I = –A.B2 + B1 … ln – 1 _{: a} n – 1I = –A.Bn – 1 + Bn – 2 ln _{: a} nI = Bn – 1.

© 2010 Didit B. Nugroho Jadi a0I = –A.B0 a1A = –A2.B1 + A.B0 a2A2 = –A3.B2 + A2B1 … an – 1An – 1 = –An.Bn – 1 + An – 1Bn – 2 anAn = AnBn – 1.

Dengan menjumlahkan persamaan-persamaan tersebut, diperoleh

a0I + a1A + a2A2 + … + anAn = On atau p(A)= On. n

TEOREMA 7.3.5 (Teorema Cayley-Hamilton Versi Operator)

Jika diberikan T Î L(V, V) dengan V adalah suatu ruang vektor berdimensi n, dan T mempunyai persamaan karakteristik p(l), maka p(T) = T0 dengan T0 = I adalah

transformasi identitas padaV.

CONTOH 7.3.3 Buktikan Teorema Cayley-Hamilton untuk matriks

ú û ù ê ë é = 1 2 2 1 C .

Penyelesaian. Persamaan karakteristik untuk C yaitu

pC(l) = (l – 1) 2 –4 = l2 – 2l – 3. Jadi, p(C) = C2 _{– 2C – 3I} 2 = _ú û ù ê ë é 1 2 2 1 ú û ù ê ë é 1 2 2 1 – 2 _ú û ù ê ë é 1 2 2 1 + _ú û ù ê ë é 1 0 0 1 = _ú û ù ê ë é 5 4 4 5 – _ú û ù ê ë é 2 4 4 2 + _ú û ù ê ë é 1 0 0 1 = _ú û ù ê ë é 0 0 0 0 .

Jika A Î Mn(F), maka Teorema Cayley Hamilton memperbolehkan untuk

menyatakan Ap (pÎZ+, p³n) dan A–1 (jika A adalah inversibel) sebagai suatu kombinasi linear dari matriks-matriks I, A, A2_{, …, A}n–1_.

Sebagai contoh, untuk _ú

û ù ê ë é = 1 2 2 1

A akan dinyatakan A4 _{dan A}–2 _{dalam suku-suku}

A dan I. Dipunyai p(A) = A2 _{– 2A – 3I} 2 = O2, karena itu A2 _{= 2A + 3I} 2. (7.3) Jadi A4 _{= A}2_.A2 _{= (2A + 3I} 2)( 2A + 3I2), yaitu A4 _{= 4A}2 _{+ 9I + 6A + 6A,} menggunakan persamaan (7.3), disubstitusikan A2_{, dan diperoleh}

A4 _{= 4(2A + 3I}

Berarti

A4 _{= 21I + 20A,} atau secara numerik

ú û ù ê ë é = 41 40 40 41 4 A .

A adalah tak singular karena

det(A) = p(0) = –3 ¹ 0. Jadi, (7.3) dapat dikalikan dengan A–1 untuk memperoleh

A–1_A2 _{= 2A}–1_{A + 3A}–1_I. Diselesaikan untuk A–1_{, diperoleh}

(

A I

)

A 2 3 1 1 ₌ -- _, sehingga

(

A I A

)

I A I A A A A 4 4 9 1 ) 2 ( 3 1 ). 2 ( 3 1 2 1 1 2 ₌ - - _{= - - = +} -- _. Menggunakan (7.3), diperoleh

(

A I I A

)

A 2 3 4 4 9 1 2 _{= + +} -- _, atau A I A 9 2 9 7 2 ₌ -- _,

atau secara numerik

ú û ù ê ë é -= -5 4 4 5 9 1 2 A .

7.4 Diagonalisasi dan Diagonalisasi Ortogonal

Hasil berikut ini menunjukkan bahwa transformasi keserupaan mempertahankan beberapa sifat penting dari suatu matriks.

TEOREMA 7.4.1 Diberikan AdanBadalah matriks yang serupa. (a) det(A) = det(B);

(b) tr(A) = tr(B);

(c) JikaAdanBadalah nonsingular, makaA–1 _{serupa denganB}–1_; (d) AdanBmempunyai nilai eigen yang sama;

(e) PXB = XA, denganXAdanXBadalah vektor eigen dariAdanB, berturut-turut. Bukti.

(a) Karena A dan B serupa berarti terdapat suatu matriks inversibel P sehingga P–1_{AP =}

B. Dengan mengambil determinan kedua sisi, diperoleh det(P–1_{AP) = det(B)} det(P–1_{).det(A).det(P) = det(B)} (det(P))–1_{.det(A).det(P) = det(B)} det(A) = det(B).

(b) Bentuk P-1AP = B dapat dituliskan menjadi AP = PB. Dengan mengambil trace

kedua sisi, diperoleh

tr(AP) = tr(PB) tr(A).tr(P) = tr(P).tr(B)

© 2010 Didit B. Nugroho

(c) Jika A dan B adalah nonsingular berarti A dan B mempunyai invers, karena itu

A–1_APB–1 _{= A}–1_PBB–1

PB–1 _{= A}–1_P

P–1_PB–1 _{= P}–1_A–1_P

B-1 _{= P}–1_A–1_P yang berarti A–1 _{serupa dengan B}–1_.

(d) Berdasarkan

det(lI – B) = det(lP-1P – P-1AP) = det(P-1(lI – A)P) = det(lI – A), berarti B mempunyai nilai eigen yang sama dengan A.

(e) Karena AP = PB, maka APXB = PBXB = lPXB. Ini menunjukkan bahwa PXB adalah

suatu vektor eigen dari A.n

Suatu hal yang menarik adalah keserupaan antara suatu matriks persegi dan suatu matriks diagonal.

DEFINISI 7.4.1 (Diagonalisasi) Diberikan AÎMn(F). Matriks A dikatakan dapat didiagonalisasi (diagonalizable) jika A serupa dengan suatu matriks diagonal D. Ini berarti bahwa A dapat didiagonalisasi jika terdapat suatu matriks tak singular P

sehingga P–1AP = D. Selanjutnya matriks P dikatakan mendiagonalisasi (diagonalizes) A.

DEFINISI 7.4.2 Diberikan T adalah operator linear pada suatu ruang vektor V

berdimensi berhingga. T dapat didiagonalisasi jika terdapat suatu basis a untuk V

sehingga [T]a adalah diagonal.

TEOREMA 7.4.2 Diberikan T adalah operator linear pada suatu ruang vektor V berdimensi berhingga dan diberikanbadalah suatu basis untukV.

Tdapat didiagonalisasi jika hanya jika [T]bdapat didiagonalisasi.

Bukti. Untuk T dapat didiagonalisasi, berarti terdapat suatu basis a untuk V sehingga [T]a = D,

dengan D adalah matriks diagonal. Diketahui bahwa

[T]a = [I]b,a [T]b [I]a,b.

Jika dituliskan [I]a,b = P, maka didapatkan D = P–1_[T]

b P.

Ini berarti bahwa [T]b dapat didiagonalisasi.

Untuk [T]b dapat didiagonalisasi, berarti terdapat suatu matriks inversibel P

sehingga

P–1_[T]

b P = D

dengan D adalah diagonal.

Diambil b = {v1, v2, …, vn} dan didefinisikan a = {w1, w2, …, wn} dengan wj =

å

= n i i ijv p 1

untuk pij adalah unsur-unsur matriks P. Di sini hanya perlu dibuktikan bahwa a adalah

bebas linear. Diperiksa persamaan V 0 =

å

= n j j jw a 1 Û

å å

=0_V = = n j n i i ij j p v a 1 1 Û _÷÷ =0_V ø ö ç ç è æ

å å

= = n j i n i ij j v a p 1 1 .

Karena vi bebas linear maka V 0 =

å

= n i ij j a p 1 ÛPA = 0V dengan ú ú ú û ù ê ê ê ë é = n a a A ! 1

. Karena P adalah inversibel, maka A = 0V dan akibatnya a adalah bebas

linear. Jadi a adalah basis untuk V. Dengan mengambil P = [I]a,b, diperoleh

[T]a = [I]b,a [T]b [I]a,b = P–1[T]b P = D

dan disimpulkan bahwa T dapat didiagonalisasi. n

Berikut ini dibicarakan bagaimana masalah pendiagonalan berhubungan dengan eksistensi dari vektor-vektor bebas linear.

TEOREMA 7.4.3 Diberikan operator linear T pada suatu ruang vektor V yang berdimensi berhingga.

Tdapat didiagonalisasi jika hanya jika terdapat suatu basisa = {v1, …, vn} dan skalar l1, l2, …, lnÎFsehingga

T(vi) = livi, i = 1, 2, …, n.

Bukti. Jika a = {v1, …, vn} dan l1, l2, …, lnÎF ada sehingga T(vi) = livi, maka jelas

[T]b = diag(l1, l2, …, ln). Ini berarti bahwa T dapat didiagonalisasi.

Untuk T yang dapat didiagonalisasi, berarti terdapat suatu basis untuk V, namakan a = {v1, …, vn}, dan suatu matriks diagonal D, dituliskan D = diag(l1, l2, …,

ln), sehingga [T]b = D. Jelas

T(v1) = l1v1, T(v2) = l2v2, …, T(vn) = lnvn. n

AKIBAT 7.4.1 Diberikan A Î Mn(F). Matriks A dapat didiagonalisasi jika hanya jika terdapat suatu basis {v1, …, vn} untukFndan l1, l2, …, lnÎFsehingga

Avi = livi, i = 1, 2, …, n.

Bukti. Diperhatikan transformasi linear TA : Fn®Fn yang dirumuskan oleh TA(v) = Av.

Jika b adalah basis baku untuk Fn_{, maka [T}

A]b = A. Berdasarkan Teorema 7.4.2, diketahui

bahwa A dapat didiagonalisasi jika hanya jika TA dapat didiagonalisasi dan berdasarkan

Teorema 7.4.3 bahwa TA dapat didiagonalisasi jika hanya jika terdapat suatu basis a =

{v1, …, vn} untuk Fn dan skalar-skalar l1, l2, …, lnÎF sehingga TA(vi) = Avi = livi. n

Akibat 7.4.1 mengatakan bahwa T dapat didiagonalisasi jika hanya jika T

mempunyai n vektor eigen bebas linear. Ini berarti bahwa jika A Î Mn(F), maka

pernyataan-pernyataan berikut ekuivalen : 1. A dapat didiagonalisasi.

2. A mempunyai n vektor eigen yang bebas linear.

Dengan mengaplikasikan Akibat 7.4.1 untuk Contoh 7.2.1 sampai Contoh 7.2.4, dapat dinyatakan bahwa matriks A dapat didiagonalisasi, matriks B tidak dapat didiagonalisasi, matriks C dan D dapat didiagonalisasi.

CONTOH 7.4.1 Diberikan T : P2[x](R) ®P2[x](R) yang dirumuskan oleh

T(a + bx + cx2) = (a + 2b + 2c) + (2a + b + 2c)x + (2a + 2b + c)x2. Apakah T dapat didiagonalisasi?

© 2010 Didit B. Nugroho

Penyelesaian. Dipilih basis b = {1, x, x2} untuk P2(R) dan ditentukan [T]b. T(1) = 1 + 2x + 2x2 T(x) = 2 + x + 2x2 T(x2) = 2 + 2x + x2 Diperoleh A T _β = ú ú ú û ù ê ê ê ë é = 1 2 2 2 1 2 2 2 1 ] [ .

Berikutnya diselesaikan masalah eigen untuk A.

pA(l) = det(lI – A) = (5 – l)(1 + l)2. Diperoleh l1 = 5 dan l2 = –1. (a) Untuk l1 = 5, (5I – A)v = 0Û ú ú ú û ù ê ê ê ë é -0 0 0 4 2 2 2 4 2 2 2 4

yang direduksi menjadi

ú ú ú û ù ê ê ê ë é -0 0 0 0 0 0 1 1 0 1 0 1 . Suatu penyelesaian sistem adalah

1 1 1 1 v = ú ú ú û ù ê ê ê ë é . (b) Untuk l2 = –1, (–I – A)v = 0Û ú ú ú û ù ê ê ê ë é -0 0 0 2 2 2 2 2 2 2 2 2

yang direduksi menjadi

ú ú ú û ù ê ê ê ë é 0 0 0 0 0 0 0 0 0 1 1 1 . Dua penyelesaian yang saling bebas adalah

2 0 1 1 v = ú ú ú û ù ê ê ê ë é - dan ₃ 1 0 1 v = ú ú ú û ù ê ê ê ë é -.

Disimpulkan bahwa matriks A dapat didiagonalisasi dan karena A = [T]b, maka operator

linear T dapat didiagonalisasi. Selain itu juga diketahui bahwa P–1AP = D dengan

ú ú ú û ù ê ê ê ë é -= 1 0 1 0 1 1 1 1 1 P dan D = diag(5, –1, –1).

Hasil di bawah ini menyatakan bahwa jika A mempunyai n nilai eigen berbeda, maka vektor eigen yang berkorespondensi adalah bebas linear.

TEOREMA 7.4.4 Diberikan T sebagai operator linear pada ruang vektor V berdimensi berhingga dan diandaikanTmempunyai pasangan eigen

(l1, v1), (l2, v2),…, (ln, vn). Jika liberbeda, maka {v1 , v2, …, vn} adalah bebas linear.

Bukti. Dimisalkan P(k) adalah pernyataan ”Jika (l1, v1), …, (ln, vn) adalah pasangan

eigen yang bersesuaian dan li berbeda, maka {v1, v2, …, vn} bebas linear”.

Akan dibuktikan pernyataan tersebut dengan menggunakan induksi.

P(1) adalah benar karena T(v1) = l1v1 dan v1¹ 0, jadi {v1} bebas linear.

Diandaikan bahwa pernyataan P(k) benar dan akan ditunjukkan pernyataan P(k + 1) juga benar. Diambil (k +1) pasangan eigen

(l1, v1), …, (lk+1, vk+1)

dengan l1, …, lk+1 semuanya berbeda. Akan ditunjukkan kebebaslinearan himpunan {v1, …, vk+1} dengan mempertimbangkan

a1v1 + a2v2 + … + akvk + ak+1vk+1 = 0V. (7.4)

Diaplikasikan T untuk persamaan (7.4):

T(a1v1 + a2v2 + … + akvk + ak+1vk+1) = T(0V) a1T(v1) + a2T(v2) + … + akT(vk) + ak+1T(vk+1) = 0V

a1l1v1 + a2l2v2 + … + aklkvk + ak+1lk+1vk+1 = 0V. (7.5)

Selanjutnya lk+1(7.4) – (7.5) yang menghasilkan

(lk+1 – l1)a1v1 + … + (lk+1 – lk)akvk = 0V.

Ini adalah kombinasi linear dari vektor-vektor bebas linear (berdasarkan hipotesis induksi) v1, v2, …, vk dan juga hanya satu cara agar vektor nol dapat dibentuk yaitu jika

semua koefisiennya adalah nol. Karena lk+1 – li¹ 0 untuk i = 1, 2, …, k, sebab nilai-nilai

eigen adalah berbeda, maka dapat disimpulkan bahwa a1 = a2 = … = ak = 0. Selanjutnya

dari persamaan (7.4) akan dihasilkan ak+1 = 0, dan dapat disimpulkan bahwa {v1, …, vk+1} adalah bebas linear, dan P(k + 1) adalah benar. Jadi P(k) benar untuk semua kÎZ+.n AKIBAT 7.4.2 DiberikanT : V® Vsebagai operator linear pada suatu ruang vektor Vberdimensin. JikaTmempunyainnilai eigen berbeda, makaTterdiagonalisasi.

Bukti. Berdasarkan Teorema 7.4.4, T mempunyai n vektor eigen yang bebas linear dan terdiagonalisasi berdasarkan Teorema 7.4.3. n

PROSES DIAGONALISASI. Diandaikan bahwa A adalah suatu matriks n×n dengan masukan-masukan real.

Langkah 1. Menentukan apakah n akar-akar polinomial karakteristik det(A – lI) adalah real.

Langkah 2. Jika tidak, maka A tidak terdiagonalisasi. Jika ya, maka dicari vektor eigen yang berkorespondensi untuk nilai-nilai eigen. Menentukan apakah dapat ditemukan n eigen vektor bebas linear.

Langkah 3. Jika tidak, maka A tidak terdiagonalisasi. Jika ya, maka dituliskan

[

v v vn

]

P= 1 2 ! dan D = diag(l1, l2, …, ln),

dengan l1, l2, …, lnÎR adalah nilai-nilai eigen dari A, dan v1, v2, …, vn

berturut-turut adalah vektor-vektor eigen yang berkorespondensi. Selanjutnya P–1_{AP = D.}

© 2010 Didit B. Nugroho

CONTOH 7.4.2 Diberikan matriks

ú ú ú û ù ê ê ê ë é -= 5 0 0 0 3 2 0 2 3 B .

Ditentukan matriks P yang mendiagonalisasi B sebagai berikut.

Langkah 1. Polinomial karakteristik untuk B yaitu

pB(l) = det(lI – B) = (l – 5)2(l – 1)

Diperoleh nilai eigen untuk B yaitu l1 = 5, dan l2 = 1 yang merupakan bilangan real.

Langkah 2. Untuk l1 = 5, dibentuk sistem linear (l1I – B)v = 0 yaitu

ú ú ú û ù ê ê ê ë é = ú ú ú û ù ê ê ê ë é ú ú ú û ù ê ê ê ë é 0 0 0 0 0 0 0 2 2 0 2 2 3 2 1 x x x

yang mempunyai penyelesaian x1 = –x2 dengan x2, x3ÎR. Jadi vektor eigen untuk B yang bersesuaian dengan l1 = 5 adalah

ú ú ú û ù ê ê ê ë é + ú ú ú û ù ê ê ê ë é-= ú ú ú û ù ê ê ê ë é + ú ú ú û ù ê ê ê ë é-= ú ú ú û ù ê ê ê ë é-= 1 0 0 0 1 1 0 0 0 3 2 3 2 2 3 2 2 x x x x x x x x v . Diperoleh ï þ ï ý ü ï î ï í ì ú ú ú û ù ê ê ê ë é = ú ú ú û ù ê ê ê ë é-= 1 0 0 , 0 1 1 2 1 v

v adalah basis untuk ruang eigen yang

bersesuaian dengan l1 = 5.

Untuk l2 = 1, dibentuk sistem linear (l2I – A)v = 0 yaitu

ú ú ú û ù ê ê ê ë é = ú ú ú û ù ê ê ê ë é ú ú ú û ù ê ê ê ë é -0 0 0 0 0 0 0 2 2 0 2 2 3 2 1 x x x

yang mempunyai penyelesaian x1 = x2 dan x3 = 0 dengan x2ÎR. Jadi vektor eigen B yang bersesuaian dengan l2 = 1 adalah

ú ú ú û ù ê ê ê ë é = ú ú ú û ù ê ê ê ë é = 0 1 1 0 2 2 2 x x x v . Diperoleh ï þ ï ý ü ï î ï í ì ú ú ú û ù ê ê ê ë é = 0 1 1 3

v adalah basis untuk ruang eigen yang bersesuaian dengan l2 = 1.

Mudah diperiksa bahwa v1, v2, v3 adalah bebas linear.

Langkah 3. Matriks P yang mendiagonalisasi B yaitu

ú ú ú û ù ê ê ê ë é-= 0 1 0 1 0 1 1 0 1 P , dengan P –1BP = diag(5, 5, 1).

CONTOH 7.4.3 Diberikan matriks _ú û ù ê ë é -= 1 2 2 3

C . Apakah matriks C dapat

didiagonalisasi?

Penyelesaian.

Polinomial karakteristik untuk C yaitu

pC(l) = det(lI – C) = (l + 1)2.

Diperoleh nilai eigen untuk C yaitu l = –1. Selanjutnya dibentuk sistem linear (–I – C)v =

0 yang mempunyai penyelesaian

ú û ù ê ë é = 1 1 2 x v , xÎR. Karena itu þ ý ü î í ì ú û ù ê ë é 1 1

merupakan basis untuk ruang eigen yang bersesuaian dengan l = –1. Dengan kata lain ruang eigen tersebut berdimensi 1 yang berarti C tidak mempunyai dua vektor yang bebas linear yang berakibat C tidak dapat didiagonalisasi.

CONTOH 7.4.4 Diberikan matriks _ú

û ù ê ë é = 3 0 0 3

F mempunyai nilai eigen l = 3. Matriks F dapat dituliskan kembali menjadi

I I F _ú û ù ê ë é = ú û ù ê ë é = 3 0 0 3 3 0 0 3 .

Karena I = I–1 maka matriks F dapat didiagonalisasi dengan mengambil matriks P = I

sehingga P–1_{FP = D.}

Berdasarkan ketiga contoh terakhir di atas, dapat diambil suatu kesimpulan yaitu bahwa matriks An dapat didiagonalisasi meskipun matriks tersebut tidak mempunyai n

nilai eigen yang berbeda. Atau dengan kata lain, untuk matriks A berukuran n´n, A

mempunyai n nilai eigen berbeda adalah suatu syarat cukup (tetapi tidak perlu) untuk dapat didiagonalisasi. Tetapi jika beberapa nilai eigen adalah sama, tidak banyak yang dapat dinyatakan secara umum.

TEOREMA 7.4.5 Jika l1, l2, …, ln adalah nilai-nilai eigen dari matriksA, maka

l1–1, l2–1, …, ln–1 adalah nilai-nilai eigen dari A–1 dengan asumsi A–1 ada, yaitu

diasumsikan bahwali¹ 0, "i.

Hasil di bawah ini menyatakan kapan suatu operator dapat didiagonalisasi.

TEOREMA 7.4.6 Diberikan T sebagai operator linear pada ruang vektor V berdimensi berhingga. Tdapat didiagonalisasi jika hanya jika

(i) p(l) terpisah; dan

(ii) g_li =a_li untuk semua nilai eigen dariT, yaitu l1, l2, …, lp.

Bukti. Berdasarkan Akibat 7.4.2, diketahui bahwa T terdiagonalisasi jika hanya jika T

mempunyai n vektor eigen bebas linear, dengan n = dim(V). Diandaikan

(

λ λ

) (

λ λ

)

(

λ λ

)

( )

λ λ

p( )= - ₁ al1 - ₂ al2... - _p alpg

© 2010 Didit B. Nugroho

Selanjutnya dihitung banyaknya vektor eigen bebas linear yang dimiliki T.

l1 memberikan g_l1 vektor eigen bebas linear,

l2 memberikan g_l2 vektor eigen bebas linear, …

lp memberikan g_lp vektor eigen bebas linear.

Jadi T mempunyai

p

N=g_l1+g_l2 +...+g_l vektor eigen bebas linear. Berdasarkan sifat 1 £gl£al, diperoleh

å

å

= = £ = p i p i i i N 1 1 l l a g .

Karena p(l) adalah polinomial berderajat n, maka

n λ p i i = +

å

= )) ( ( derajat 1 g a_l . Diperoleh )) ( ( derajat 1 λ n N p i i g a = -£

å

= l . Diperhatikan bahwa N = n jika hanya

(i) derajat(g(l)) = 0, yaitu p(l) terpisah; dan (ii)

i

i l

l a

g = . n

CONTOH 7.4.5 Diberikan matriks _ú

û ù ê ë é = 1 2 2 1 G ÎMn(R). pG(l) = (l – 3)(l + 1).

(i) pG(l) terpisah. Lebih jauh:

l1 = 3: a3 = 1 dan 1 £g3£a3 Þ g3 = 1 l2 = –1: a–1 = 1 dan 1 £g–1£a–1 Þ g–1 = 1 (ii) i i l l a g = untuk i = 1, 2.

Disimpulkan bahwa G dapat didiagonalisasi atas R.

CONTOH 7.4.6 Diberikan matriks _ú

û ù ê ë é -= 1 2 2 1 H ÎMn(R).

Karena pH(l) = (l – 1)2 + 4, jelas bahwa pH(l) ¹ 0 untuk setiap lÎR. Karena p(l) tidak

terpisah, maka H tidak dapat didiagonalisasi atas R.

CONTOH 7.4.7 Diberikan matriks _ú

û ù ê ë é -= 1 2 2 1 J ÎMn(C). pJ(l) = (l + 2i – 1)(l – 2i – 1).

(i) pJ(l) terpisah. Lebih jauh

l1 = 2i – 1 dengan a_l1 =g_l1 =1, dan l2 = –2i – 1 dengan a_l2 =g_l2 =1. (ii)

i i l

l a

g = untuk i = 1, 2.

CONTOH 7.4.8 Diberikan matriks ú ú ú û ù ê ê ê ë é = 5 2 2 2 5 2 2 2 5 K . pK(l) = –(l – 9)(l – 3)2.

(i) pK(l) terpisah dengan l1 = 9 dan l2 = 3.

a9 = 1, begitu juga g9 = 1.

a3 = 2, dan 1 £g3£g3 = 2. Harus ditentukan g3.

Diperiksa (3I – K)v = 0 yang mempunyai bentuk

ú ú ú û ù ê ê ê ë é 0 2 2 2 0 2 2 2 0 2 2 2 .

Karena rk(3I – K) = 1, maka nul(3I – K) = 3 – 1 = 2, dan disimpulkan bahwa

g3 = 2. (ii) i i l l a g = untuk i = 1, 2. Jadi K dapat didiagonalisasi.

CONTOH 7.4.9 Diberikan matriks

ú ú ú ú û ù ê ê ê ê ë é -= 5 8 0 16 2 3 4 4 1 0 1 2 1 0 2 5 L . pL(l) = –(l – 3)3(l + 5). pL(l) terpisah dengan l1 = 3 dan l2 = –5.

Diperoleh juga a–5 = 1 = g–5, a3 = 3, dan 1 £g3£a3 = 3.

Untuk menentukan g3, harus diperiksa (3I – L)v = 0 yang mempunyai bentuk

ú ú ú ú û ù ê ê ê ê ë é -0 8 8 0 16 0 2 0 4 4 0 1 0 2 2 0 1 0 2 2 ® ú ú ú ú û ù ê ê ê ê ë é 0 0 0 0 0 0 0 0 0 0 0 16 8 16 0 0 1 0 2 2 .

Jelas bahwa rank dari matriks koefisien adalah 2 dan nulitas dari matriks koefisien adalah 4 – 2 = 2. Jadi g3 = 2. Karena g3¹a3, disimpulkan bahwa L tidak dapat didiagonalisasi.

Diagonalisasi Ortogonal

Sekarang diperhatikan ruang Euclid Rn _{sebagai suatu ruang hasil kali dalam}

dengan hasil kali dalam Euclid. Diberikan sembarang matriks A berukuran n×n dengan masukan-masukan real, diharapkan untuk menemukan apakah terdapat suatu basis orthonormal dari Rn _{yang memuat vektor-vektor eigen dari A.}

Dalam proses diagonalisasi yang sudah dibicarakan sebelumnya, kolom-kolom dari matriks P adalah vektor-vektor eigen dari A, dan vektor-vektor tersebut membentuk suatu basis untuk Rn. Diketahui bahwa basis adalah ortonormal jika hanya jika matriks P

adalah ortogonal.

DEFINISI 7.4.3 Matriks A Î Mn(R) dapat didiagonalisasi secara ortogonal

(orthogonally diagonalizable) jika terdapat suatu matriks ortogonal P dengan masukan-masukan real sehingga D = P-1AP = PTAP adalah matriks diagonal. Selanjutnya matriks P

© 2010 Didit B. Nugroho

Pertama kali, akan ditentukan apakah matriksnya terdiagonalisasi secara ortogonal. Untuk itu perlu untuk dibahas bagaimana menemukan suatu matriks ortogonal

P menggunakan diagonalisasi.

Untuk mempelajari pertanyaan pertama tersebut, hasil berikut ini memberikan suatu batasan pada matriks-matriks yang terdiagonalisasi secara ortogonal.

TEOREMA 7.4.6 Diandaikan bahwaAadalah suatu matriks yang terdiagonalisasi secara ortogonal dengan masukan-masukan real, makaAadalah simetris.

Bukti. Diandaikan bahwa A terdiagonalisasi secara ortogonal, maka terdapat suatu matriks ortogonal P dan suatu matriks ortogonal D, dengan masukan-masukan untuk keduanya adalah real, sehingga PT_{AP = D. Karena P}T_{P = PP}T _{= I dan D}T _{= D, maka}

dipunyai

A = PDPT _{= PD}T_PT_.

Jadi

AT_{= (PDP}T₎T _{= (P}T₎T_(DT₎T_PT _{= PDP}T _{= A,}

yang berarti bahwa A adalah simetris. n

Pada kenyataannya, pertanyaan pertama sebelumnya terjawab oleh hasil berikut ini yang dinyatakan tanpa bukti.

TEOREMA 7.4.7 Diandaikan bahwa A Î Mn(R). Matriks A terdiagonalisasi secara ortogonal jika dan hanya jikaAadalah simetris.

Akhir dari bagian ini disediakan untuk menemukan suatu cara mendiagonalisasi secara ortogonal suatu matriks simetris dengan masukan-masukan real. Dimulai dengan menyatakan hasil di bawah ini tanpa bukti. Bukti yang diperlukan dihasilkan dari teori ruang vektor kompleks.

TEOREMA 7.4.8 Diandaikan bahwa A adalah suatu matriks simetris dengan masukan-masukan real, maka semua nilai eigen dariAadalah real.

Di sini idenya adalah mengikuti proses diagonalisasi yang telah dibahas sebelumnya, mengetahui kapan A terdiagonalisasi, dan diharapkan menemukan suatu basis untuk Rn yang memuat eigen vektor dari A. Selanjutnya diinginkan untuk mengortogonalisasi basis tersebut dengan proses Gram-Schmidt. Langkah terakhir ini dapat diingat secara sederhana dengan melihat hasil berikut ini.

TEOREMA 7.4.9 Diandaikan bahwa u1 dan u2 adalah vektor-vektor eigen dari

suatu matriks simetris A dengan masukan-masukan real, berkorespondensi dengan nilai-nilai eigen berbeda l1 dan l2 secara berturut-turut, maka u1•u2 = 0. Dengan kata lain,

vektor-vektor eigen dari suatu matriks real simetris yang berkorespondensi terhadap nilai-nilai eigen berbeda adalah ortogonal.

Bukti. Catat bahwa jika dituliskan u1 dan u2 sebagai kolom-kolom matriks, maka karena A adalah simetris, dipunyai

2 1 1 2 1 2 1 2 2 1 u u Au u A u (Au ) u u Au Au • = T = T T = T = • .

Berdasarkan itu bahwa

l1u1•u2 = Au1•u2 = u1•Au2 = u1•l2u2. Jadi (l1 – l2)(u1•u2) = 0. Karena l1¹l2, maka haruslah u1•u2 = 0. n

PROSES DIAGONALISASI ORTOGONAL. Diandaikan bahwa A adalah suatu matriks simetris n×n dengan masukan-masukan real.

Langkah 1. Menentukan n akar-akar real l1, l2, …, ln dari polinomial karakteristik det(lI – A), dan mencari n vektor eigen bebas linear u1, u2, …, un dari A

yang berkorespondensi dengan nilai-nilai eigen tersebut seperti dalam proses diagonalisasi.

Langkah 2. Diaplikasikan proses ortogonalisasi Gram-Schmidt terhadap vektor-vektor eigen u1, u2, …, un untuk memperoleh vektor-vektor eigen ortogonal v1, v2, …, vn, dan dicatat bahwa vektor-vektor eigen yang berkorespondensi

dengan nilai-nilai eigen berbeda adalah ortogonal.

Langkah 3. Dinormalisasi vektor-vektor eigen ortogonal v1, v2, …, vn untuk

memperoleh vektor-vektor eigen ortonormal w1, w2, …, wn dari A.

Vektor-vektor ini membentuk suatu basis ortonormal untuk Rn_{. Dituliskan}

[

w w wn

]

P= 1 2 ! dan D = diag(l1, l2, …, ln),

dengan l1, l2, …, lnÎR adalah nilai-nilai eigen dari A dan w1, w2, …, wn Î Rn _{secara berturut-turut adalah vektor-vektor eigen yang telah}

diortogonalisasi dan dinormalisasi. Selanjutnya PTAP = D.

Dicatat bahwa jika diaplikasikan proses ortogonalisasi Gram-Schmidt terhadap vektor eigen yang berkorespondensi untuk nilai eigen yang sama, maka vektor-vektor baru yang dihasilkan dari proses ini adalah juga vektor-vektor-vektor-vektor eigen yang berkorespondensi untuk nilai-nilai eigen tersebut.

CONTOH 7.4.10 Akan dicari P yang mendiagonalisasi M secara ortogonal.

ú ú ú û ù ê ê ê ë é = 2 2 1 2 5 2 1 2 2 M .

Langkah 1. Polinomial karakteristik M yaitu pM(l) = det(lI – N) = (l – 7)(l – 1)2.

Diperoleh nilai-nilai eigen dari M yaitu l1 = 7 dan akar-akar ganda l2 = l3 = 1. Suatu vektor eigen yang berkorespondensi untuk l1 = 7 adalah suatu penyelesaian dari sistem (7I – M)u = 0, yaitu

ú ú ú û ù ê ê ê ë é = 1 2 1 1 u .

Vektor-vektor eigen yang berkorespondensi untuk l2 = l3= 1 adalah suatu penyelesaian dari sistem (I – M)u = 0, yaitu

ú ú ú û ù ê ê ê ë é -= 1 0 1 2 u dan ú ú ú û ù ê ê ê ë é -= 0 1 2 3 u

yang bebas linear.

Langkah 2. Diaplikasikan proses ortogonalisasi Gram-Schmidt untuk u2 dan u3, diperoleh: ú ú ú û ù ê ê ê ë é -= 1 0 1 2 v dan ú ú ú û ù ê ê ê ë é -= 1 1 1 3 v

© 2010 Didit B. Nugroho

yang saling ortogonal. Dicatat bahwa tidap perlu dilakukan sesuatu untuk terhadap u1 pada langkah ini, lihat Teorema 7.4.9. Disimpulkan bahwa

ú ú ú û ù ê ê ê ë é = 1 2 1 1 v , ú ú ú û ù ê ê ê ë é -= 1 0 1 2 v , ú ú ú û ù ê ê ê ë é -= 1 1 1 3 v membentuk suatu basis ortogonal untuk R3.

Langkah 3. Dinormalisasi setiap vektor basis ortogonal untuk memperoleh

ú ú ú û ù ê ê ê ë é = 1 2 1 6 1 1 w , ú ú ú û ù ê ê ê ë é -= 1 0 1 2 1 2 w , ú ú ú û ù ê ê ê ë é -= 1 1 1 3 1 1 w .

Diambil matriks P yang mendiagonalisasi M secara ortogonal yaitu

[

]

ú ú ú ú û ù ê ê ê ê ë é -= = 3 1 2 1 6 1 3 1 6 2 3 1 2 1 6 1 3 2 1 w w 0 w P , maka ú ú ú ú û ù ê ê ê ê ë é -= = -3 1 3 1 3 1 2 1 2 1 6 1 6 2 6 1 1 _PT ₀ P dan PTMP = diag(7, 1, 1).

CONTOH 7.4.11 Diperhatikan matriks

ú ú ú û ù ê ê ê ë é -= 20 9 0 30 13 0 12 6 1 N .

Polinomial karakteristik N yaitu pN(l) = det(lI – N) = (l + 1)(l – 2) (l – 5). Diperoleh

nilai-nilai eigen dari N yaitu l1 = –1, l2 = 2, dan l3 = 5. Suatu vektor eigen yang berkorespondensi dengan l1 = –1 adalah suatu penyelesaian dari sistem (–I – N)u = 0:

ú ú ú û ù ê ê ê ë é = 0 0 1 1 u .

Suatu vektor eigen yang berkorespondensi dengan l2 = 2 adalah suatu penyelesaian dari sistem (2I – N)u = 0, yaitu ú ú ú û ù ê ê ê ë é = 1 2 0 2 u .

Suatu vektor eigen yang berkorespondensi dengan l3 = 5 adalah suatu penyelesaian dari sistem (5I – N)u = 0, yaitu ú ú ú û ù ê ê ê ë é -= 3 5 1 3 u .

Dicatat bahwa u1, u2, u3 berkorespondensi dengan nilai-nilai eigen berbeda dari N, maka vektor-vektor tersebut tidak ortogonal. Matriks N tidak simetris, dan juga Teorema 7.4.9 tidak dapat diaplikasikan dalam kasus ini.

CONTOH 7.4.12 Diperhatikan matriks

ú ú ú û ù ê ê ê ë é -= 7 2 0 2 6 2 0 2 5 Q .

Matriks P yang mendiagonalisasi Q secara ortogonal dicari sebagai berikut.

Langkah 1. pQ(l) = det(lI – Q) = (l – 3)(l – 6)(l – 9).

Diperoleh nilai-nilai eigen dari Q yaitu l1 = 3, l2 = 6, dan l3 = 9. Suatu vektor eigen yang berkorespondensi dengan l1 = 3 adalah suatu penyelesaian dari sistem (3I – Q)u = 0, yaitu

ú

ú

ú

û

ù

ê

ê

ê

ë

é

-=

1

2

2

1

u

.

Suatu vektor eigen yang berkorespondensi dengan l2 = 6 adalah suatu penyelesaian dari sistem (6I – Q)u = 0, yaitu

ú

ú

ú

û

ù

ê

ê

ê

ë

é

-=

2

1

2

2

u

.

Suatu vektor eigen yang berkorespondensi dengan l3 = 9 adalah suatu penyelesaian dari sistem (9I – Q)u = 0, yaitu

ú

ú

ú

û

ù

ê

ê

ê

ë

é-=

2

2

1

2

u

.

Langkah 2. Karena nilai-nilai eigennya berbeda maka u1, u2, u3 adalah ortogonal, dan tidak perlu diaplikasikan proses ortogonalisasi Gram-Schmidt.

Langkah 3. Dinormalisasi setiap vektor u1, u2, u3 untuk memperoleh

ú ú ú û ù ê ê ê ë é -= 1 2 2 3 1 1 w , ú ú ú û ù ê ê ê ë é -= 2 1 2 3 1 2 w , ú ú ú û ù ê ê ê ë é-= 2 2 1 3 1 1 w .

Diambil matriks P yang mendiagonalisasi Q secara ortogonal yaitu

[

]

ú ú ú û ù ê ê ê ë é -= = 2 2 1 2 1 2 1 2 2 3 1 3 2 1 w w w P , maka ú ú ú û ù ê ê ê ë é -= = -2 2 1 2 1 2 1 2 2 3 1 1 _PT P dan PT_{QP = diag(3, 6, 9).}

© 2010 Didit B. Nugroho

7.5 Pangkat Matriks dan Persamaan Diferensial

TEOREMA 7.5.1 Diberikan matriks A Î M2(F) yang mempunyai nilai eigen

berbeda l1 danl2 yang berturut-turut berkorespondensi dengan vektor eigen v1 danv2.

Jika P adalah matriks dengan kolom-kolomnya adalah v1 dan v2 secara berturut-turut,

makaPtidak singular dan

ú û ù ê ë é = -2 1 1 0 0 λ λ AP P .

Bukti. Diambil Av1 = l1v1 dan Av2 = l2v2. Akan ditunjukkan bahwa sistem persamaan homogen

xv1 + yv2 = 0

hanya mempunyai penyelesaian trivial, dan karena itu matriks P = [v1v2] tidak singular. Diandaikan

xv1 + yv2 = 0 (7.6)

maka diperoleh A(xv1 + yv2) = A0 = 0 atau x(Av1) + y(Av2) = 0. Oleh karena itu

xl1v1 + yl2v2 = 0. (7.7)

Selanjutnya persamaan (7.6) dikalikan dengan l1 dan dieliminasikan dengan persamaan (7.7), diperoleh

(l2– l1)yv2 = 0.

Akibatnya y = 0 karena l2 – l1 ¹ 0 dan v2 ¹ 0, sehingga dari persamaan (7.6) akan diperoleh x = 0.

Lebih lanjut, persamaan Av1 = l1v1 dan Av2 = l2v2 memberikan hasil

AP = A

[

v₁ v₂

]

=

[

Av₁ Av₂

]

=

[

λ₁v₁ λ₂v₂

]

=

[

]

_ú û ù ê ë é 2 1 2 1 ₀ 0 λ λ v v = _ú û ù ê ë é 2 1 0 0 λ λ P . Jadi, ú û ù ê ë é = -2 1 1 0 0 λ λ AP P .n

CONTOH 7.5.1 Diberikan matriks _ú

û ù ê ë é = 2 1 1 2 A . Dengan memperhatikan

pembahasan Contoh 7.2.1 dapat diambil _ú

û ù ê ë é-= 1 1 1 v dan _ú û ù ê ë é = 1 1 2 v sebagai vektor-vektor eigen yang berturut-turut berkorespondensi dengan nilai-nilai eigen l1 = 1 dan l2 = 3.

Karena itu diperoleh _ú

û ù ê ë é-= 1 1 1 1 P dengan _ú û ù ê ë é = -3 0 0 1 1_AP P .

CONTOH 7.5.2 Untuk suatu matriks B diketahui bahwa tr(B) = 6, det(B) = 8 dan vektor eigen B yaitu

ú ú û ù ê ê ë é -= 2 2 2 2 1 v dan ú ú û ù ê ê ë é = 2 2 2 2 2 v . Tentukan matriks B.