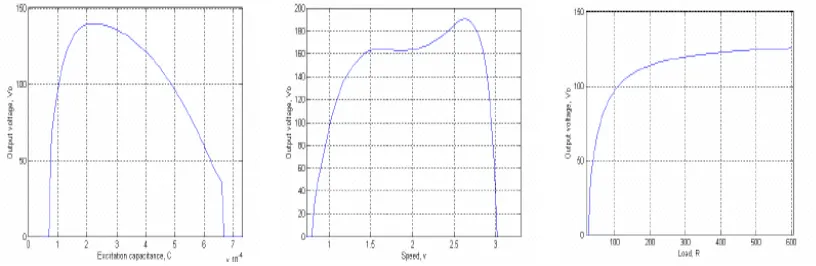
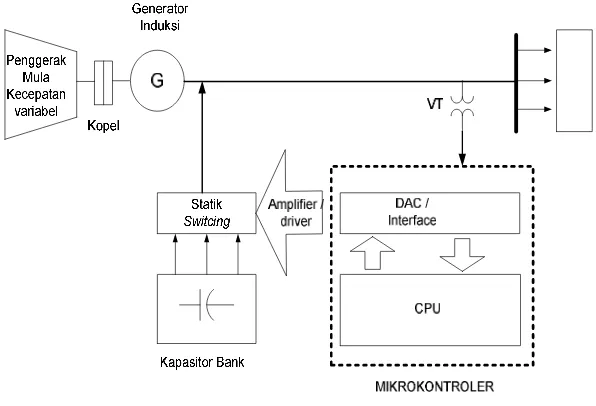
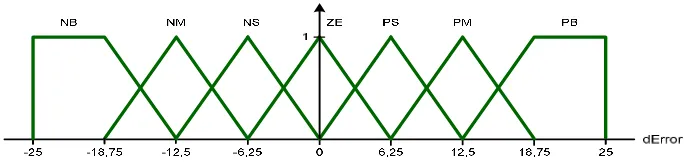
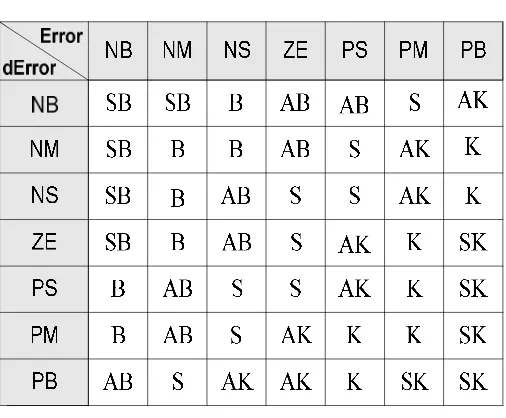
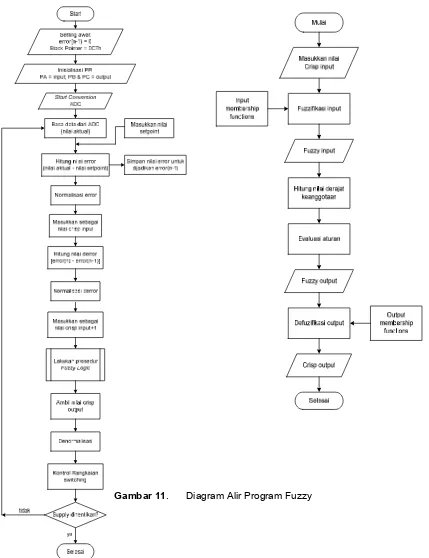
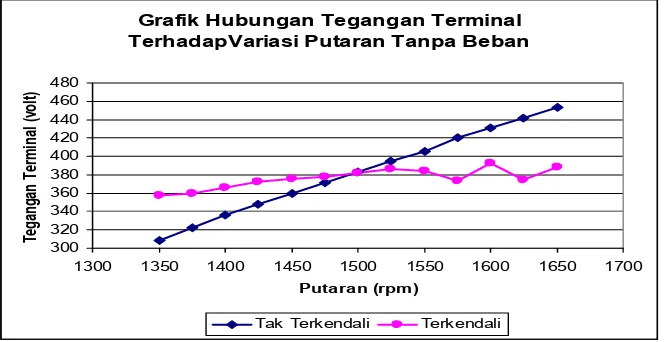
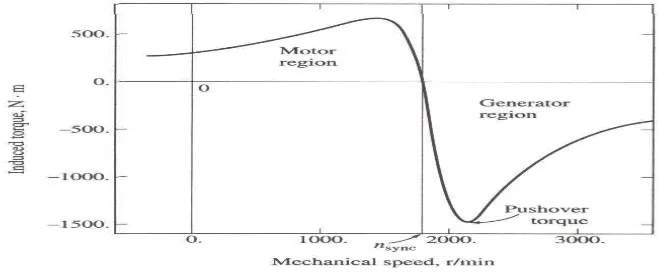
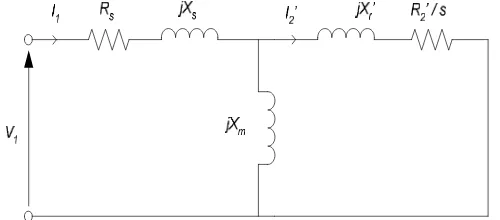
ARTIKEL REALISASI KONTROLER BERBASIS LOGIKA FUZZY PADA PENGENDALIAN EKSITASI GENERATOR INDUKSI PENGUATAN SENDIRI BAGI PEMBANGKIT LISTRIK NON KONVENSIONAL REALISASI KONTROLER BERBASIS LOGIKA FUZZY PADA PENGENDALIAN EKSITASI GENERATOR INDUKSI PENGUATAN SEND
Teks penuh
Gambar
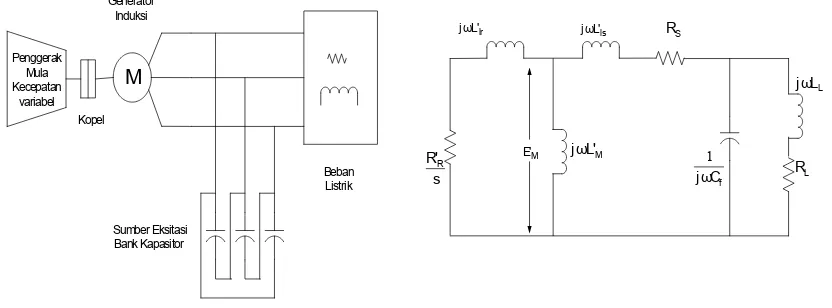
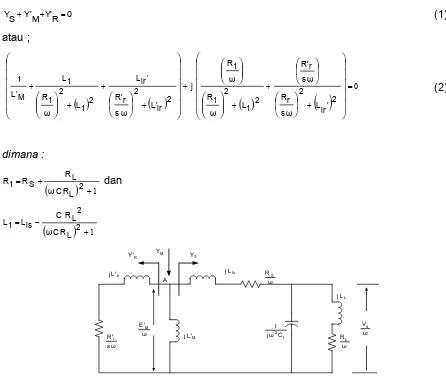
Dokumen terkait
Jika yang menghadiri bukan direktur utama/penanggung jawab perusahaan, harus membawa surat kuasa bermaterai Rp.6.000,- dan fotocopy KTP personil yang dikuasakan;e. Dokumen –
Kedua : Ketetapan pemenang ini dibuat dengan memperhatikan ketentuan yang berlaku dalam pengadaan Barang/Jasa. Ditetapkan di :
Kepada masyarakat dan Penyedia Barang yang akan mengajukan pengaduan dan sanggahan kami tunggu selambat-lambatnya 3 (tiga) hari kerja setelah pengumuman ini diterbitkan.
Paket pengadaan ini terbuka untuk penyedia yang teregistrasi pada Layanan Pengadaan Secara Elektronik ( LPSE ) dan memiliki Surat Izin Usaha Perdagangan (SIUP), memiliki
Form Nilai Akhir Semester Mengisi Raport Siswa Raport Siswa End Database Nilai Softskill Database Nilai Akhir Database Mata Pelajaran Database Transaksi Siswa Database
Hasil penelitian menunjukkan bahwa pengembangan media pembelajaran dengan menggunakan Permainan Edukatif Akuntansi untuk mata pelajaran akuntansi keuangan kelas XI
Dalam bab ini penulis akan menguraikan profil PT Asuransi Ramayana, Tbk Unit Syariah kemudian menguraikan dan menganalisis kekuatan, kelemahan, peluang, dan
This stu dy aimed to find and describe the relationship between students’ collocation knowledge and their reading comprehension. The population of this study was the