modul kelas xii ips 2012

h

tt

p

:/

/m

a

te

m

a

tr

ic

k

.b

lo

g

s

p

o

t.

c

o

m

NO KOMPETENSI INDIKATOR KET

1. Menggunakan logika matematik

a

dalam pemecahan masalah

Menentukan ingkaran atau kesetaraan dari uatu

1

Menentukan kesimpulan dari beberapa prem 2

2. Memahami konsep yang berkait

an

dengan aturan pangkat, akar da n

logaritma, fungsi aljabar sederh ana,

fungsi kuadrat dan grafiknya, persamaan dan pertidaksamaa n

kuadrat, komposisi dan invers f ungsi,

sistem persamaan linear, progr am

linear, matriks, barisan dan der et,

serta mampu menggunakannya dalam

pemecahan masalah.

Menentukan hasil operasi bentuk pangkat, a kar, dan

3

Menyelesaikan masalah yang berkaitan den gan grafik

2

Menentukan komposisi dua fungsi dan invers suatu

2

Menyelesaikan masalah yang berkaitan den gan

2

Menyelesaikan pertidaksamaan kuadrat. 1

Menentukan penyelesaian dari sistem persa maan

1

Menyelesaikan masalah sehari-hari yang berkaitan

1

Menentukan nilai optimum bentuk objektif d ari

daerah himpunan penyelesaian sistem

2

Menyelesaikan masalah sehari-hari yang berkaitan

1

Menyelesaikan masalah matriks yang berkai tan

dengan kesamaan, determinan, dan atau inv 3

Menentukan suku ke-n atau jumlah n suku pertama

2

Menyelesaikan masalah sehari-hari yang berkaitan

1

3. Memahami limit fungsi aljabar,

turunan fungsi, nilai ekstrim, da n

integral fungsi serta menerapka nnya

dalam pemecahan masalah.

Menghitung nilai limit fungsi aljabar. 2

Menentukan turunan fungsi aljabar dan aplik 2

Menentukan integral fungsi aljabar. 2

Menentukan luas daerah dengan mengguna kan

1

4. Mengolah, menyajikan, dan

menafsirkan data dan memaha mi

kaidah pencacahan, permutasi, kombinasi dan peluang kejadian serta

mampu menerapkannya dalam pemecahan masalah.

Menyelesaikan masalah sehari-hari yang berkaitan

dengan kaidah pencacahan, permutasi, atau 1

Menyelesaikan masalah yang berkaitan den gan

2

Menentukan unsur-unsur pada diagram lingkaran

1

Menghitung nilai ukuran pemusatan dari dat a dalam

1

h

tt

p

:/

/m

a

te

m

a

tr

ic

k

.b

lo

g

s

p

o

t.

c

o

m

A. Nilai Kebenaran Pernyataan

Majemuk

1. Konjungsi

p



q (dibaca “p dan q”) bernilai benar

hanya jika keduanya benar. 2. Disjungsi

p V q (dibaca “p atau q”) satu saja benar maka bernilai benar.

3. Implikasi

p → q (dibaca “jika p maka q”) bernilai salah hanya jika p benar tetapi q salah. 4. Biimplikasi

p ↔ q (dibaca “p jika dan hanya jika q”) bernilai benar jika p dan q memiliki nilai kebenaran yang sama.

B. Ingkaran / Negasi Pernyataan

1.

p v q

ingkarannya

~ p Λ ~ q

2.

p Λ q

ingkarannya

~ p v ~ q

3.

p



q

ingkarannya

p Λ ~ q

4.Semua p adalah A ingkarannya ada p

bukan A.

5.Beberapa q adalah A ingkarannya semua q bukan A.

C. Menentukan kesimpulan

1. Modus Ponen :

P1 : p



q

P2 : p

K : q

2. Modus Tolens :

P1 : p



q

P2 : q

K : p

3. Silogisme

P1 : p



q

P2 : q



r

K : p



r

4. Ekuivalensi ( kesamaan/ ≡ )

p



q ≡ p v q ≡ q



p

1. Diketahui pernyataan:

(1) ~p↔q (4) ~p → q

(2) ~p Λ q (5) ~p v q

(3) ~p → ~q

Jika pernyataan p bernilai salah dan pernyataan q bernilai benar, maka yang bernilai salah

adalah pernyataan

….

a. (1) d. (4)

b. (2) e. (5)

c. (3)

Penyelesaian:

P salah, maka ~p benar ; q benar, maka ~q salah;

(3). ~p → ~q = B → S = S. Jadi jawabannya C.

2. Diketahui pernyataan : ‘Jika semua siswa rajin maka semua siswa lulus ujian ”

Ingkaran dari pernyataan tersebut adalah ….

a

.

Ada siswa yang rajin dan beberapa siswa tidak lulus ujian

b .

Ada siswa yang tidak rajin dan beberapa siswa tidak lulus ujian

c .

Ada siswa yang tidak lulus ujian dan semua siswa rajin

d .

Jika ada siswa yang rajin maka beberapa siswa tidak lulus ujian

e .

Jika ada siswa yang lulus ujian maka beberapa siswa rajin belajar

Penyelesaian :

( i ) Ingkaran jika p maka q adalah p dan ~ q

Jadi jawabannya adalah :

Semua siswa rajin dan ada siswa yang tidak lulus ujian

Atau dapat ditulis dengan :

Ada siswa yang tidak lulus ujian dan semua siswa rajin

Jawaban : C

1) Nilai kebenaran yang tepat untuk

pernyataan (p  q)  p, pada tabel di samping adalah ....

p Q (p  q)  p B

B S S

B S B S

.... .... .... .... a. SBSB

b. SSSB c. SSBB d. SBBB e. BBBB

Ingkaran “jika maka” tidak lagi menggunakan “jika

h

tt

p

:/

/m

a

te

m

a

tr

ic

k

.b

lo

g

s

p

o

t.

c

o

m

2) Diketahui pernyataan p bernilai salah dan

pernyataan q bernilai benar. Pernyataan berikut yang bernilai salah adalah ….

a . b . c . d . e .

p V q

p V q

p  ( p V q )

( p V q ) p

( p  q )  p

3) Nilai kebenaran pernyataan majemuk

(~pq ) V ~q pada tabel berikut adalah … . ( UN 2011 )

p q (~pq ) V ~q

B B S S

B S B S

.... .... .... ....

4) Negasi dari pernyataan “Jika semua anak

lulus maka semua guru bergembira” adalah a. Jika semua anak tidak lulus ujian maka

semua guru tidak bergembira

b. Jika ada anak tidak lulus ujian maka semua guru tidak bergembira

c. Jika ada guru tidak bergembira maka semua anak tidak lulus ujian

d. Semua anak tidak lulus ujian dan ada guru tidak bergembira

e. Semua anak lulus ujian dan beberapa guru tidak bergembira

5) Negasi dari pernyataan : “ Jika permintaan

naik maka harga naik ” adalah ....

a . b . c . d . e .

Permintaan naik tetapi harga tidak naik Permintaan naik dan harga naik

Permintaan naik atau harga tidak naik Permintaan tidak naik tetapi harga naik Permintaan tidak naik dan harga tidak naik

6) Negasi dari pernyataan : ” Permintaan

terhadap suatu produk tinggi dan harga

barang naik ” adalah ....

a. Permintaan terhadap suatu produk

tinggi atau harga barang tidak naik

b. Permintaan terhadap suatu produk

tidak tinggi atau harga barang naik

c. Permintaan terhadap suatu produk

tinggi dan harga barang tidak naik

d. Permintaan terhadap suatu produk

tidak tinggi dan harga barang tidak naik

e. Permintaan terhadap suatu produk

tidak tinggi atau harga barang tidak naik

7) Ingkaran dari : ” beberapa siswa

memakai kacamata ” adalah ....

a. beberapa siswa tidak memakai

kacamata

b. semua siswa memakai kacamata

c. ada siswa tidak memakai

kacamata

d. tidak benar semua siswa memakai

kacamata

e. semua siswa memakai kacamata

8) Dari argumentasi berikut :

Jika ibu tidak pergi maka adik senang. Jika adik senang maka dia tersenyum. Kesimpulan yang sah adalah …

a. Ibu tidak pergi atau adik tersenyum

b. Ibu pergi dan adik tidak tidak tersenyum

c. Ibu pergi atau adik tidak tersenyum

d. Ibu tidak pergi dan adik tersenyum

e. Ibu pergi atau adik tersenyum

9) Diberikan premis – premis :

Premis ( 1 ) : p  q

Premis ( 2 ) : q  r

Premis ( 3 ) : r

Kesimpulan yang sah adalah ….

a

. b . c .

r q p

d. e.

p

q

10) Diketahui premis – premis : ( UN 2010 )

P1 : Jika guru matematika tidak datang maka semua siswa senang

P2 : Ada siswa yang tidak senang

Kesimpulan yang sah dari premis – premis di atas adalah…

a. Guru matematika tidak datang b. Semua siswa senang

h

tt

p

:/

/m

a

te

m

a

tr

ic

k

.b

lo

g

s

p

o

t.

c

o

m

c. Guru matematika senang d. Guru matematika datang e. Ada siswa yang tidak senang

11) Diketahui premis-premis: ( UN 2011 )

(1) Jika semua warga negara membayar pajak, maka banyak fasilitas umum dapat

dibangun.

(2) Tidak banyak fasilitas umum dapat dibangun.

Kesimpulan yang sah dari kedua premis di atas adalah … .

a. Semua warga negara tidak membayar pajak

b. Ada warga negara tidak membayar pajak c. Semua warga negara membayar pajak d. Semua warga negara membayar pajak dan

h

tt

p

:/

/m

a

te

m

a

tr

ic

k

.b

lo

g

s

p

o

t.

c

o

m

A. Bentuk Pangkat

1. _am_an _amn _5.

m m a b b a              

2. m n

n m

a

a

a



 _6.

n m n

a

m



a

3. m _m

a

a





1

_{7. a}0 _1,a0

4.

a

m m



a

1

)

(

B. Bentuk Akar

1. Operasi penjumlahan dan pengurangan :

a. a bc b(ac) b

b. a b c b (a c) b

2. Operasi Perkalian

b a b

a.  .

Contoh: 32  16.2 16 24 2

3. Operasi Pembagian

b a b a



Contoh : 1,5

2 3 4 9 4 9 25 ,

2    

4. Merasionalkan Penyebut Bentuk akar :

( i ). b

b a b b b a b a   .

( ii ).

c b c b a c b c b c b a c b a         2 ) ( .

C. Konsep Logaritma

1. Definisi logaritma : a_logb_c_ ac _b

2. Sifat – sifat logaritma :

( i ). a_log(b_.c_)a_logb_a_logc

( ii ) b c

c

b a a

a_{log( ) log  log}

(iii). a_logbn _n_.a_logb

(iv). b

m b a am log 1 log 

(vi). a_logb_.b_logc_.c_logd_.d_loge_a_loge

(vii). a b b _p p a log log log 

(viii). alog10 , karena _a0 _1

1. Jika a = 32 dan b = 27, maka nilai dari

3 1 5 1

b

a



adalah ....

a. 5 1 b. 6 1 c. 5 d. 6 e. 8 Penyelesaian :

( i ). ubah 32 dan 27 menjadi bilangan

berpangkat, 32 = 25 _{, dan 27 = 3}3

( ii ). ₅1 ₃1

b

a  =

32

27

(

2

)

(

3

)

3

2

3

5

1 3 5 1 5 3 1 5 1













( C )

2. Bentuk sederhana dari

3 2

5

adalah ....

a. 3

3 5

b. 3 c. 3

6 5

d. 3

9 5 e. 3 12 5 Penyelesaian : 3 6 5 3 . 2 3 5 3 3 . 3 2 5 3 2 5  

 ( jawaban : C )

3. Nilai dari log8. log9

25 1

log 2 3

5 _{ adalah ....}

a. 2 b. 4 c. 7 d. 8 e. 11 Penyelesaian : 9 log . 8 log 25 1

log 2 3

5 _{ =}

2 3 3 2 2

5

log

2

.

log

3

5

1

log



= 3 log . 2 . 2 log . 3 5

log 2 2 3

5  _

=( 2).5log5 3.2

 

= (-2 ) + 6

= 4 . jadi jawabannya B.

b

b

h

tt

p

:/

/m

a

te

m

a

tr

ic

k

.b

lo

g

s

p

o

t.

c

o

m

1. Bentuk sederhana

dari (6-2 _a2₎3 _{: ( 12}3 _a3 ₎-2 _{adalah ....}

b. 2-1 _{d. 2}6 _a12

c. 2 e. 2-6 _a-12

d. 2 a12

2. Diketahui m = 16

dan n = 27. Nilai  ₄3

m

. 3

2

n

= ...

a. –72 c. 9

6

e. 72

b. ₆₄9 d. ₈9

3. Bentuk sederhana

dari

1

1 9

5 5

32

2 

 

   

 

b a

b

a _{adalah ….}

a

. ( 2ab)4

d

. ( 2ab)

-1

b

. ( 2ab)2

e

. ( 2ab)

-4

c .

2ab

4. Bentuk sederhana

dari _{3 2 3}

2 4 2

6 3

 

y x

y x

adalah ….

a

. x2y

2

1 d

. x2y

24 1

b

. x2y

18

1 e

. ₂₄1 x6y

c

. x y

6 18

1

5. Bentuk sederhana

dari 50 1082 12 32 adalah ....

a. 7 2 2 3

b. 13 2 14 3

c. 9 2  4 3

d. 9 2  2 3

e. 13 2 2 3

6. Hasil dari



2 2 6



2 6



= ....

a. ₂



_{1 2}



b. ₂



_{2 2}



c. ₂



_{3 1}



d. ₃



_{3 1}



e. ₄



_{2 31}



7. Bentuk

3 2 5

2 3



ekuivalen dengan ….

a

. 13

6 6 2

15  d

. 13

3 10 2 4 

b

. 13

6 6 2

15  e

. 13

3 4 2 10 

c

. 13

6 4 2 10 

8. Hasil dari

96 7 54 5 150

2   adalah ….

a. -33 6

b. -23 6

c. -3 6

d. 3 6

e. 33 6

9. Bentuk

sederhana dari

3 2

3 2

 

adalah ….

a. 74 3

b. 72 3

c.  72 3

d. 7 4 3

e.  7 4 3

10. Diketahui 2 _{log 3}

= m, dan 2 _{log 5 = n. Nilai} 2 _{log 90 adalah ....}

a. 2m + 2n b. 1 + 2m + n

c. 1 + m2 _{+ n}

d. 2 + 2m + n

e. 2 + m2 _{+ n}

11. Diketahui 2_{log 3}

= x, dan 2_{log 5 = y maka} 4_{log 45 adalah ....}

a. (2x + y) b. (x + y)

c. (2 )

2 1

y x

d. ( )

2 1

y x

e. (2 )

2 1

h

tt

p

:/

/m

a

te

m

a

tr

ic

k

.b

lo

g

s

p

o

t.

c

o

m

12. Nilai dari

5_{log 9 3. log 2}5 1_{. log 25 2. log 6}5 5 5_{log 2} 2

    adalah …

a .

2 d. -1

b .

1 e. -2

c .

0

13. Nilai dari

27 log 8 log 9

log 2 3

3 _{  adalah ….}

a . b . c . d . e .

1 2 3 4 5

14. Jika

2 log ,

3 8

log 3

9 _{ m maka = ….}

a.

4

m

b. 3m

c.

2

m

d.

m

e. m

1

15. Nilai dari

8 log 27 log 4

log 3 2

2 _{  adalah ….}

a . b . c . d . e .

1 2 3 4 5

16. Nilai dari

6 log

3 9 log 3 8

log 

= ….( UN 2010 )

a. 1 b. 2 c. 3 d. 6

e. 36

17. Nilai dari

54 log 2

log . 25

log 5 3

9 _{ = …. ( UN 2011 )}

a. -3

b. -1

c. 0

d. 2

h

tt

p

:/

/m

a

te

m

a

tr

ic

k

.b

lo

g

s

p

o

t.

c

o

m

1. Bentuk umum fungsi kuadrat : f ( x )=ax2 ₊

bx + c, a ≠ 0

2. Grafik fungsi kuadrat berupa parabola

3. Grafik fungsi kuadrat ditinjau dari tanda

( nilai ) a dan D

( dengan D = b2 _{– 4.a.c )}

 Untuk a > 0/ a positif

( grafik selalu

terbuka ke atas ) ada 3 jenis :`

 Untuk a < 0 ( grafik terbuka ke

bawah )

4. Unsur – unsur grafik fungsi kuadrat :

Menentukan unsur – unsur grafik fungsi kuadrat

jika diketahui persamaan grafiknya ( y = a x2 _{+ b x}

+ c ) atau diketahui gambarnya:

 Untuk menentukan titik potong dengan

sumbu X :

Cari saja dua bilangan x1 dan x2 yang

memenuhi

x1 + x2 =

a b 

maka titik potong dg sumbu X-nya adalah (x1

, 0 ) dan

( x2 , 0 )

 Untuk menentukan persamaan sumbu

simetri :

Gunakan rumus x = a b

2

 atau

x =

2

2 1

x

x



 Untuk menentukan titik potong dengan

sumbu Y :

Lihat saja c nya pada persamaan tersebut. Sebab titik potong dengan sumbu Y adalah ( 0, c )

Contoh : y = 3 x2 _{+ 5x + 1 ; maka titik}

potong dengan sumbu Y- nya adalah ( 0,1 )

Jika y = -2 x2 _{+3x – 4; maka titik}

potong dengan sumbu Y-nya adalah ( 0, -4 )

 Titik puncak/ titik balik



x

_b

,

y

_b



a b x_b

2



 atau dapat di cari dengan xb =

2

2 1

x

x



a D y_b

4



 atau subtitusikan xb ke

persamaan, sehingga menjadi

c bx ax

y_b  _b2 _b 

Dan ingat D_b2_ 4ac _{( diskriminan )}

1. Koordinat titik ekstrem kurva

dengan persamaan

y = x2 _{– 4x +9 adalah….}

a. ( -2 , 21)

b. ( -2 , 9 )

X a>0

D>0 a>0

D=0 D<0a>0

Grafik terbuka ke

atas dan memotong sumbu X di dua titik berbeda

Grafik terbuka ke

atas dan menyinggu

ng sumbu X

Grafik terbuka ke

atas dan tidak memotong

ataupun menyinggu

ng sumbu X

X X

Jadi a>0 membuat grafik terbuka ke atas, dan D menentukan keadaan grafik memotong atau menyinggung atau tidak sama sekali terhadap

sumbu X

X Y

Titik puncak / titik balik ( pada grafik

di samping berupa titik balik

maksimum )

Titik potong dg Sumbu X,

di titik tersebut y =

0

Garis / Sumbu simetri( di tengah

antara dua titik potong dg sumbu

X ) Titik potong

dengan sumbu Y, di titik tersebut x =

h

tt

p

:/

/m

a

te

m

a

tr

ic

k

.b

lo

g

s

p

o

t.

c

o

m

c. ( 0 , 9)

d. ( 2 , 9 )

e. ( 2 , 5 )

Penyelesaian :

Jelas a = 1, b= -4, c = 9

Titik ekstrim = titik balik = titik puncak

2

2

4

1

.

2

)

4

(

2















a

b

x

_b

5 9 8 4 9 2 . 4 2 9

4 2

2_{        }

 _{b b}

b x x

y

( jadi untuk mencari yb dengan cara

menggantikan x dengan xb pada

persamaan yang diketahui ) Jadi titik ekstrimnya : ( 2, 5 ) ( E )

2. Koordinat titik potong grafik fungsi

kuadrat y = 3x2 _{+ 7x – 6 dengan sumbu X}

adalah ....

a. 

    

0 , 3 2

dan



 3,0



d.



 3,0



dan

   

 

 ,0 2 3

b. 

    

0 , 3 2

dan



3,0



e. 

    

2 3 ,

0 dan



0,3



c. 

    

0 , 2 3

dan



 3,0



Penyelesaian :

( i ). Titik potong dengan sumbu X, jelas y-nya / yang dibelakang harus 0, jadi pilihan E jelas salah. ( ii ). Kemudian cari dua bilangan di posisi x yang

jumlahnya = a b  =

3 7

 , maka jawabannya

( A ) sebab

3 7 3

9 2 ) 3 ( 3 2

     

1. Koordinat titik balik dari grafik

fungsi kuadrat yang persamaannya y = (x – 6) (x + 2) adalah ....( UN 2010 )

a. (–2, 0)

b. (–1, –7)

c. (1, –15)

d. (2, –16)

e. (3, –24)

2. Koordinat titik potong kurva y = x2

– 2x – 8 dengan sumbu X adalah ….

a. (-4 , 0) dan ( -2 , 0)

b. (-4 , 0) dan ( 2 , 0)

c. (-2 , 0) dan (4 , 0)

d. (2 , 0) dan ( 4 , 0)

e. (2 , 0) dan (8 , 0)

3. Koordinat titik puncak dari grafik y

= x2 _{– 6x + 5 adalah ....}

a. (6, 5) d. ( – 3,32)

b. (3, – 4) e. ( – 6,5)

c. (3, – 14)

4. Nilai minimum fungsi kuadrat f( x )

= 2x2 _{– 2x + 6 adalah ....}

a.

2 11

b.

2 9

c.

2 7

d.

2 5

e.

2 1

5. Koordinat titik potong grafik fungsi

kuadrat _y3_x2 _{ x} 2 _{dengan sumbu X dan}

sumbu Y adalah … .( UN 2010 )

a. (-1,0), 

    

0 , 3 2

, dan (0,2)

b. 

  

 

 ,0 3 2

, (1,0), dan (0, -2)

c. 

  

 

 ,0 3 2

, (1,0), dan 

  

 



3 2 , 0

d. 

  

 

 ,0 3 2

, (-1,0), dan (0, -1)

e. 

    

0 , 2 3

, (1,0), dan (0, 3)

6. Persamaan sumbu simetri grafik

fungsi kuadrat

y = 5x2 _{-20x + 1 adalah ....( UN 2011 )}

a. x = 4

b. x = 2

c. x = -2

d. x = -3

h

tt

p

:/

/m

a

te

m

a

tr

ic

k

.b

lo

g

s

p

o

t.

c

o

m

2

1

6

Ini artinya titik potong dg sumbu Y; yaitu ( 0,6 )

y = x2 _{– 3x + 2}

y = x2 _{+ 3x + 2}

y = 3x2 _{+ 9x + 6}

y = 3x2 _{– 9x + 6}

y = -3x2 _{+ 9x + 6}

X

Y

Menyusun Persamaan Grafik

Fungsi Kuadrat

1. Jika diketahui titik – titk potong dengan sumbu

X ( ( x1 , 0 ) dan ( x2 , 0 ) diketahui )

Persamaannya :

y



a

(

x



x

₁

).(

x



x

₂

)

Cara singkatnya : y = x2 – ( x1 + x2 ) x + x1 .x2 , kemudian disesuaikan ( lihat contoh )

2. Jika diketahui koordinat titik puncak / titik balik

(( xb , yb ) diketahui )

Persamaannya : ya(x x_b)2 y_b

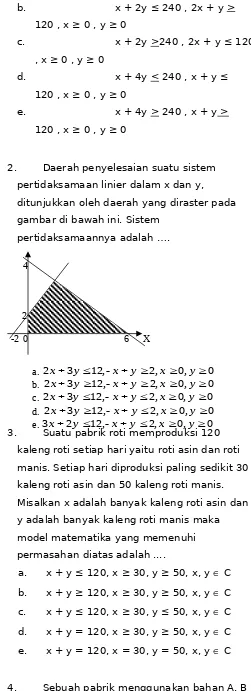
1. Persamaan grafik fungsi di bawah ini adalah ….

= -3x2 _{+ 9x + 6}

Penyelesaian :

Jelas x1 = 1 dan x2 = 2 dan memotong sumbu Y di

titik ( 0, 6 ) Cara Biasa :

Y = a ( x – 1 ) . ( x – 2 )

Y = a ( x2 _{-3x + 2 )}

Grafik memotong sumbu Y di titk ( 0, 6 ),

Artinya untuk x = 0, y = 6, maka : 6 = a ( 02 _–

3.0 + 2 )

6 = a.2 2a = 6

a = 3 Jadi Persamann fungsinya adalah :

Y = 3. ( x2 _{-3x + 2 )}

Y = 3 x2 _{-9x + 6 ( pilihan D )}

Cara singkat :

susun saja bentuk y = x2 _{– ( x1 + x2 ) x + x1 .x2}

y = x2 _{– 3 x + 2 ( berarti a=1,} b=-3, c=2 )

kemudian lihat bahwa grafik memotong sumbu y

di ( 0,6 ), maka c harus 6, padahal :

pada y = x2 _{– 3 x + 2, c = 2 sehingga agar 2}

jadi 6 kalikan saja dengan 3. maka

hasilnya :

y = 3. (x2 _{– 3 x + 2)}

y = 3x2 _{– 9 x + 6 ( jawaban D ).}

2. Persamaan grafik fungsi kuadrat mempunyai titik ekstrim (–1, 4) dan melalui titik (0, 3) adalah ....( UN 2010 )

a. y = –x2 _{+ 2x – 3}

b. y = –x2 _{+ 2x + 3}

c. y = – x 2 _{– 2 x + 3}

d. y = –x2 _{– 2x – 5}

e. y = –x2 _{– 2x + 5}

Penyelesaian :

Jelas xb = -1, yb = 4, dan grafik melalui titik ( 0,3 )

Cara Biasa



 (1)



2 4

a x y



1



24

a x y

Grafik melalui ( 0,3 ) berarti untuk x = 0, y = 3 , maka :

3 = a ( 0 +1 )2 _{+ 4}

3 = a .1 + 4 3 = a + 4

Maka a = -1, sehingga persamaannya : y = -1.

(x+1)2 ₊₄

Y = -1.(x2

+2x+1)+4

Y = -x2 _-2x-1+4

Y = -x2 _{-2x +3}

( C ) Cara singkat :

Jelas bahwa grafik melalui titik ( 0,3 ) ini tidak lain titik potong dengan sumbu Y, berarti c=3, sehingga pilihan yang mungkin adalah B dan C.

Jelas xb = -1, padahal xb =

2

2 1

x

x



,



x1 + x2 =2 xb = 2.(-1)=-2

dan kita punya bahwa x1 + x2 =

a b

 , maka

antara pilihan B dan C pilih saja yang nilai a b 

= -2.

Jadi jawabannya C.

Kesimpulan dari cara singkat adalah : pilih

saja pilihan yang memenuhi a b

h

tt

p

:/

/m

a

te

m

a

tr

ic

k

.b

lo

g

s

p

o

t.

c

o

m

-8

1. Persamaan grafik fungsi kuadrat dibawah ini adalah ....

2. Persamaan grafik fungsi di bawah ini adalah ….

(0,-3)

3. Persamaan grafik di bawah ini adalah ….

4. Persamaan grafik fungsi di bawah ini adalah …

–2 4

5. Persamaan grafik fungsi pada gambar di bawah ini adalah ....

( petunjuk : grafik menyinggung sumbu X,

berarti x1 = x2 =2 atau pakai titik puncak )

6. Persamaan grafik fungsi kuadarat yang memotong sumbu X di titik (1,0) dan (3,0) serta melalui titik ( -1,-16)adalah … .

a. _{y }2_x2 _ 8_x6

b. _yx2 _4_x 21

c. _{y x}2_4_x 5

d. _y2_x2 _8_x 6

e. _{y }2_x2 _4_x 10_{( UN 2011 )}

Akar-Akar Persamaan Kuadrat

1. Bentuk umum Persamaan kuadrat :

R c b a a c bx

ax2   0, 0, , , 

2. Menentukan akar akar persamaan kuadrat Cara Biasa : - Faktorisasi

0 ) ).(

( 1

0

2

  

  

n ax m ax a

c bx ax

- Melengkapkan kuadrat sempurna

- Rumus abc

a ac b

b x

2 4 2

2 , 1

   

Cara Singkat : ( jika memungkinkan ) Pakai saja rumus jumlah dan hasil kali akar – akar persamaan kuadrat



a b x x₁ ₂ 



a c x x₁ ₂ 

Dengan maksud : cari saja dua bilangan ( x₁

dan x₂) yang memenuhi rumus jumlah dan

hasil kali tersebut.

Catatan : biasanya cukup dicari/ dipilih saja

dua bilangan ( x₁ dan x₂) yang

memenuhi

a b x

x₁ ₂  .

3. Jumlah dan hasil kali akar – akar persamaan kuadrat

Jika x₁ dan x₂akar – akar persamaan

kuadrat _ax2 _bxc0, _{maka berlaku :}

a. y = –2x2 _{+ 4x + 3}

b. y = –2x2 _{+ 2x + 3}

c. y = –x2 _{– 2x + 3}

d. y = –x2 _{+ 2x – 3}

e. y = –x2 _{+ 2x + 3}

3

-1 3

x

y

o

(1,-2)

a. y = x2 ₊₃

b. y = x2 _-3

c. y = -x2 ₊₃

d. y = x2 _{- 2x -3}

e. y = -x2 _{+ 2x}

-3

9

5

Y = f(x)

2 X

Y a. y = -x2 + 4x + 5 b. y = -x2 _{- 4x + 5}

c. y = -2x2 _{+ x + 5}

d. y = -2x2 _{- x + 5}

e. 2

2 1

x y  + x +5

a. y = –x2 _{+ 2x}

– 8

b. y = –x2 _{+ 2x}

+ 8

c. y = –x2 _{– 2x}

+ 8

d. y = –x2 _{– 2x}

– 8

a. 2 2

2

1 2 _{ }

 x x

y

b. 2 2

2

1 2 _{ }

 x x

y

c. 2 2

2

1 2 _{ }

 x x

y

d. 2 2

2

1 2 _{ }



 x x

y

e. 2 2

2

1 2_{ }



 x x

y

dengan m + n = b; dan m.n

= a.c

2

2 Y

h

tt

p

:/

/m

a

te

m

a

tr

ic

k

.b

lo

g

s

p

o

t.

c

o

m

a b x x₁  ₂ 

a c x x₁ ₂ 

4. Persamaan yang sering digunakan terkait

jumlah dan hasil kali akar – akar persamaan kuadrat :

 2



_{1 2}



2 _{1 2}

2 2

1

x

x

x

2

.

x

x

x









a c a

b . 2

2       _ 

a

c

a

b

.

2

2 2







c b

a ca

b

x x

x x x x

x x x

x 

      

2 1

2 1

2 1

1 2

2

1 . .

1 1



2 1

2 1 2 2 1 2

1 2 2 2 1 2

1 2 2 1 1 1 2 2 1

.

.

.

2

)

(

.

.

.

.

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

















Catatan : akar persamaan kuadrat tidak selalu

dinyatakan dalam x₁ dan x₂, kadang

dinyatakan dalam α dan β, p dan q, dsb. 5. Menyusun Persamaan Kuadrat ( PK )

Kasus 1 :

Jika diketahui akar – akarnya ( x1 dan x2 )

Maka Cara penyelesaiannya :

Cara I : pakai pola

(

x



x

1

).(

x



x

2

)



0

Cara II : pakai pola

(

1 2

)

1

.

2

0

2









x

x

x

x

x

x

Kasus 2 :

Jika akar – akar persamaan kuadrat yang akan disusun berhubungan dengan akar – akar persamaan kuadrat yang lain

Maka Cara penyelesaiannya :

Dengan mengubah bentuk dari akar – akar

tersebut agar dapat disubtitusi ke persamaan

kuadrat yang lain

Secara lengkapnya perhatikan uraian berikut :

Jika Diketahui persamaan kuadrat ax2 _{+ bx + c}

=0, memiliki akar – akar α dan β, maka :

( i ). Untuk menyusun persamaan kuadrat baru

yang memiliki akar – akar

k



dan k

,Caranya :

Ganti saja x pada ax2 _{+ bx + c =0}

dengan k x

, sehingga diperoleh PK

baru :

0

)

.(

)

(

2



b



c



a

_kx

k

x _{dan seterusnya...}

( kali masuk jadi bagi )

( ii ). Untuk menyusun PK baru yang akar –

akarnya k



dan k



, Caranya :

Ganti saja x pada ax2 + bx + c =0

dengan

kx

, sehingga diperoleh PK baru :

a( kx )2 _{+b.kx + c = 0 , dan seterusnya ...}

( bagi masuk jadi kali )

( iii ). Untuk menyusun PK baru yang akar-

akarnya



kdan  k, Caranya :

Ganti saja x pada ax2 _{+ bx + c =0} dengan x k, sehingga diperoleh PK baru :

a(x – k)2 _{+ b.(x - k) + c = 0, dan}

seterusnya ... ( + masuk jadi - )

( iv ). Untuk menyusun PK baru yang akar-

akarnya





k

dan   k, Caranya :

Ganti saja x pada ax2 _{+ bx + c =0} dengan

x



k

, sehingga diperoleh PK baru :

a(x + k)2 _{+ b.(x + k) + c = 0, dan}

seterusnya ... ( - masuk jadi + )

Catatan : cara ini dipakai untuk kasus PK baru yang bentuk akar- akarnya simetris ( x1 dan x2 serupa ),dan tidak

berlaku untuk akar – akar yang bentuknya tidak simetris ( misalkan akan disusun PK

baru yang akar – akarnya k



dan   k )

1. Akar – akar persamaan kuadrat 5x2

– 6x - 8 =

0 adalah ....

a.



₅4 dan -2

b. ₅4 dan -2

c. ₅4 dan 2

h

tt

p

:/

/m

a

te

m

a

tr

ic

k

.b

lo

g

s

p

o

t.

c

o

m

e.



₅1 dan 2

Penyelesaian : Cara Singkat :

Jelas : Nilai

5

6

5

)

6

(











a

b

, maka pilih saja

pada pilihan tersebut yang jika dijumlahkan

nilainya

5 6

.

Sehingga jawabannya D, karena - ₅4 + 2 =

5 6 5

10 4

  

2. Persamaan kuadrat 4x2 _{+ 3x + 6 = 0}

mempunyai akar – akar  dan . Nilai 2 _{+ }2

= ....

a.

4 3 5

 d.

4 1 2

b.

16 7 2

 e.

4 3 3

c.

16 5 2



Penyelesaian :

Jelas 2 _{+ }2 _{= ( α + β )}2 _{– 2.αβ}

=

4 6 . 2 4 3 2

      _

= 3

16 9



=

16 7 2 16

39 16

48 9

    

( jawaban :

B )

3. Akar – akar persamaan kuadrat x2

– 3x + 1 = 0

adalah α dan β . Persamaan kuadrat baru yang

akar – akarnya 3α dan 3β adalah ....

a . b . c . d . e .

x2 _{+ 3x + 3 =0}

x2 _{- 3x + 3 =0}

x2 _{+ 3x - 3 =0}

x2 _{- 9x + 3 =0}

x2 _{- 9x + 9 =0}

Penyelesaian :

Ganti saja x pada persamaan x2 _{– 3x + 1 = 0}

dengan

3

x

, maka Persamaan kuadratnya adalah

:

1 0

3 . 3 3

2

       

x x

1 0

9 2

   x

x _{( x 9 )}

_x2 _{ 9x90 ( E )}

1. Akar – akar persamaan kuadrat 2x2

– 9x +

7 = 0 adalah ....

a. 1 dan 7

b.

2 1

dan 7

c. 1 dan

2 1 3

d. 1 dan

-2 1 3

e. -1 dan -7

2. Akar-akar persamaan kuadrat x2 _{–3x + 2}

= 0 adalah A dan B, dengan A > B. Nilai A + 2B adalah ....

a. –5 d. 4

b. –4 e. 5

c. –1

3. Akar-akar dari 2x2 _{– 3x – 9 = 0 adalah x}

1

dan x2.

Nilai dari x12 + x22 = ....

a.

4 1

11 d.

4 3 6



b.

4 3

6 e.

4 1 11



c.

4 1 2

4. Akar – akar persamaan kuadrat 3 x2 _{– 4 x}

+ 2 = 0 adalah α dan β. Nilai dari ( α + β )2 _-

2αβ = ....

a.

9 10

d.

3 1

b. 1 e. 0

c.

h

tt

p

:/

/m

a

te

m

a

tr

ic

k

.b

lo

g

s

p

o

t.

c

o

m

5. Diketahui akar- akar persamaan kuadrat

2x2 _{– 7x – 6 = 0 adalah x}

1 dan x2. Nilai

2 1

1 1

x x 

adalah ….( UN 2010 )

a. -3

b.

6 7



c.

14 3

d.

7 4

e.

7 6

6. Persamaan kuadrat 3x2 _{– x + 2 = 0}

mempunyai akar – akar  dan . Nilai (  +  )2

+ 2 = ....

a.

3 1

d.

9 13

b.

9 5

e. 2

c.

9 7

7. Persamaan kuadrat 2x2 _{+ 3x + 6 = 0}

mempunyai akar – akar  dan . Nilai 2 _{+ }2

= ....

a.

4 3 5



b.

4 3 3



c.

4 3 2



d.

4 1 3

e.

4 3 3

8. Akar-akar persamaan kuadrat

0 2 4

2 _{ x }

x adalah  dan . Nilai dari

 

2 2



=….

a. –4

b. –2

c. –1

d. 4

e. 5

9. Persamaan kuadrat x2 _{- 3x – 2 = 0}

mempunyai akar-akar x1 dan x2. Nilai dari x12

x2+ x1.x22 = ....

a.

5 7

d.

4 21

b.

4 11

e. 6.

c. 3

10. Akar – akar persamaan kuadrat x2 _{– 3x +}

1 = 0adalah x1dan x2 . Persamaan kuadrat

baru yang akar – akarnya 2x1 dan 2x2

adalah ....

a . b . c . d . e .

x2 _{+ 3x + 3 =0}

x2 _{- 3x + 3 =0}

x2 _{+ 3x - 3 =0}

x2 _{+ 6x + 4 =0}

x2 _{- 6x + 4 =0}

11. Akar – akar persamaan kuadrat 2x2 _{+ x +}

6 = 0 adalah  dan . Persamaan kuadrat baru

yang akar – akarnya

3 3





dan

adalah ....

a . b . c. d . e .

6x2 _{+ x + 2 =0}

6x2 _{+ x + 3 =0}

18x2 _{- 3x + 6 =0}

18x2 _{+ 2x - 6 =0}

18x2 _{+ 2x + 6 =0}

12. Akar – akar persamaan kuadrat x2 _{– 3x +}

1 = 0 adalah x1dan x2 . Persamaan kuadrat

baru yang akar – akarnya 3x1 dan 3x2

adalah ....

a . b . c . d . e .

x2 _{+ 3x + 3 =0}

x2 _{- 3x + 3 =0}

x2 _{+ 3x - 3 =0}

x2 _{- 9x + 3 =0}

h

tt

p

:/

/m

a

te

m

a

tr

ic

k

.b

lo

g

s

p

o

t.

c

o

m

13. Jika x1 dan x2 akar-akar persamaan 3x2 - x

+ 9 = 0, maka nilai

1 2 2 1

x

x

x

x



= ….( UN 2011 )

a.

27 53



b.

27 3



c.

27 1

d.

27 3

e.

27 54

14. Akar-akar persamaan kuadrat 2x2 _{- 13x – 7}

= 0 adalah x1 dan x2. Jika x2 > x1, maka nilai

2x1 + 3x2 = ….( UN 2011 )

a. -12,5

b. -7,5

c. 12,5

d. 20

h

tt

p

:/

/m

a

te

m

a

tr

ic

k

.b

lo

g

s

p

o

t.

c

o

m

1. Bentuk umum pertidaksamaan kuadrat :

0 0 0 0

2 2 2 2

  

  

  

  

c bx ax

c bx ax

c bx ax

c bx ax

dengan a ≠ 0

2. Menentukan pembuat nol ( x1 dan x2 )

Untuk menentukan x1 dan x2 , caranya : Cari /

pilih saja dua bilangan yang memenuhi

a b x x₁ ₂ 

3. Menentukan daerah penyelesaian Pakai saja metode : SSBT ( Sama →

Samping, Beda → Tengah ) , dengan maksud

jika tanda dari a dan tanda pertidaksamaan

itu

Sama maka daerah penyelesaiannya daerah Samping dari pembuat nol, dan jika tanda

antara a dan tanda pertidaksamaan Beda

maka daerah penyelesaiannya adalah daerah Tengah antara pembuat nol.

Apabila tanda pertidaksamaan mengandung sama dengan, maka penyelesaiannya juga mengandung tanda sama dengan, dan sebaliknya.

1. Himpunan penyelesaian dari sistem

pertidaksamaan 3 - 2x - x2 _{< 0 adalah ....}

a.



x 3x3,xR



b.



x 3x1,xR



c.



x 2x3,xR



.

d.



xx3ataux1,xR



.

e.



xx1atau.x3,xR



Penyelesaian :

Jelas a = -1, b = -2, dan c = 3, maka nilai

2

) 1 (

) 2 (











_ab _ _{, sehingga pembuat nolnya}

adalah -3 dan 1 ( sebab -3+1 = -2 ).

Maka sudah pasti jawaban yang mungkin hanya D.

2. Himpunan penyelesaian dari _x2 _{5x 60}

adalah ….

a.



x/ 6x1, xR



b.



x/ 6x1,xR



c.



x/x-1atau x6,xR



d.



x/x6atau x1,xR



e.



xx6atau x1,xR



Penyelesaian :

Jelas a = 1, b = 5, maka nilai



_ab





₁5





5

_,

sehingga pembuat nolnya adalah -6 dan 1,

kemudian pada soal tanda pertidaksamaan

tidak mengandung sama dengan , dan a positif sedangakan pertidaksamaannya kurang dari nol ( < 0 ) / negatif, berarti a dan tanda

pertidaksamaan Beda tanda

maka daerah penyelesaiannya daerah Tengah

antara -6 dan 1 . Jadi jawabannya A.

3. Himpunan penyelesaian dari _x2 _{5x 60}

adalah . .

a.



x/ 6x1,xR



b.



x/ 6x1,xR



c.



x/x -1atau x6,xR



d.



x/x-6atau x1,xR



e.



x/x6atau x1,xR



Penyelesaian :

Jelas soal serupa dengan soal no. 2, hanya

berbeda tanda pertidaksamaannya, yaitu ada tanda sama dengan dan bertanda positif ( ≥0 ),

berarti antara a dan tanda pertidaksamaan

Sama tanda, maka daerah penyelesaiannya

daerah Samping. Jadi jawabannya E.

1. Himpunan penyelesaian dari

pertidaksamaan kuadrat 2x2_+5x



₁₂

adalah....

a. {x | -4



x



2 3

h

tt

p

:/

/m

a

te

m

a

tr

ic

k

.b

lo

g

s

p

o

t.

c

o

m

b. {x|

-2 3



x



4}

c. {x| -3



x



1}

d. {x| x



-3 atau x



1}

e. {x| x



-4 atau x



2 3

}

2. Penyelesaian dari pertidaksamaan kuadrat

2x2_-11x



_{-12 adalah....}

a. -4



x



-2 3

b.

2 3



x



4

c. -4



x



2 3

d. x



2 3

atau x



4

e. x



2 atau x



3

3. Himpunan penyelesaian pertidaksamaan

) 3 2 ( 2 5 2

 

 x x

x adalah....

a.



x│

x





3

atau



2



x

b.



x│x2 atau



3



x

c.



x│

x



2

atau x3



d.



x│ 3x2



e.



x│ 2x3



( petunjuk : ubah dulu bentuknya agar jelas a dan b –nya )

4. Penyelesaian dari x ( 2x + 5 ) ≤ 12 adalah ....

a. x ≤ -4 atau x ≥ ₂3

b. x ≤ ₂3 atau x ≥ 4

c. -4 ≤ x ≤ - ₂3

d. - ₂3 ≤ x ≤ 4

e. -4 ≤ x ≤ ₂3

5. Himpunan penyelesaian dari x2 _{– 10x + 21 <}

0, xЄ R adalah ….

a.



x│x3 atau



R x x 7, 

b.



x│x7 atau



R x x3, 

c.



x│ 7x3,xR



d.



x│ 3x7,xR



e.



x│3x7,xR



( UN

2010 )

6. Himpunan penyelesaian dari -2x2 _{+ 11x -5}



0, xЄ R adalah …. ( UN 2011 )

a.



x│x5 atau

    

2 1

x

b.



x│

2 1



x atau x5



c.



x│

      

2 1

5 x

d.



x│

    

 5

2 1

x

e.



x│

   

 5

2 1

h

tt

p

:/

/m

a

te

m

a

tr

ic

k

.b

lo

g

s

p

o

t.

c

o

m

Menentukan fungsi komposisi

Misalkan f ( x ) dan g ( x ) dan h ( x ) adalah fungsi – fungsi yang terdefinisi dalam himpunan bilangan

real. Rf ∩ Dg ≠ Ф, dan Rg ∩ Df ≠ Ф serta Rg ∩ Dh ≠

Ф, maka berlaku :

1. {f ο g}(x) = f(x) ο

g(x) = f



g(x)



2. {g ο f}(x) = g(x) ο

f(x) = g



f(x)



3. { f ο g ο h}(x) =

f(x) ο g(x) ο h(x) =

f



g



h

(

x

)





1. Diketahui fungsi f : R  R dan g : R  R

dengan f(x)2x1 dan ( ) 3 2 7

   x x x

g

Rumus (gof)(x) = . . . .

a. 3x2 _{+ 3x – 6}

b. 6x2 _{+ 2x – 13}

c. 12x2 _{+ 6x – 5}

d. 12x2 _{+ 14x – 3}

e. 12x2 _{+ 12x – 3}

Penyelesaian :

Jelas f(x)2x1, dan ( ) 3 2 7

 

 x x

x

g

maka :



( )





2 1



) )(

(g f x g f x g x

3 14 12

6 2 3 12 12

7 1 2 ) 1 4 4 ( 3

7 ) 1 2 ( ) 1 2 ( 3

2 2 2

2

  

    

     

    

x x

x x

x

x x

x

x x

( jawaban D )

Catatan : g (2x+1 ) berarti mengganti x pada g(x) dengan 2x+1

2. Jika f(x) = x2 _{+2, maka f (x+1) = ....}

a. x2 _{+ 2x + 3}

b. x2 _{+ x + 3}

c. x2 _{+ 4x + 3}

d. x2 _{+ 3}

e. x2 _{+ 4}

Penyelesaian :

Jelas ( ) 2 2

 x x

f , maka :

2 ) 1 ( ) 1

(_{x  x} 2 _

f

3 2

2 1 2

2 2

  

   

x x

x x

( jawaban A )

Catatan : ( a + b )2 _{= a}2 _{+ 2ab + b}2

( a - b )2 _{= a}2 _{- 2ab + b}2

1. Diketahui f : R



R, g : R



R , f (x) = 3

- x2 _{dan g(x) = 2x - 1, rumus komposisi}

(fog)(x) =....

a. 7 – 4x - 8x2

b. 2 + 4x - 4x2_.

c. 8 – 7x - 4x2

d. 2 – 4x - 6x2

e. 2 + 4x - 6x2

2. Diketahui f : R



R, g : R



R , f (x) =

3x + 4 dan g(x) = 2 + x2_{, komposisi}

(gof)(x) =....

a. 9x2 _{+ 24x + 18}

b. 4x2 _{+ 4x +1}

c. 6x2 _{– 20x + 18}

d. 6x2 _{+ 4x -18}

e. 9x2 _{+ 24x -16.}

3. Diketahui fungsi f : R  R dan g : R  R

dengan f(x)x 2dan _g(_x)_x2 _ 2_x 3_.

Rumus (gof)(x) adalah . . . .

a. x2 _{– 6x + 5}

b. x2 _{– 6x – 3}

c. x2 _{– 2x + 6}

d. x2 _{– 2x + 2}

h

tt

p

:/

/m

a

te

m

a

tr

ic

k

.b

lo

g

s

p

o

t.

c

o

m

4. Diketahui fungsi f(x)_ = 2x + 1 dan g(x) =

x2 _{– 3x + 5, maka (gof)(x)= ....}

a. 4x2 _{– 2x + 3}

b. 4x2 _{– 6x + 3}

c. 4x2 _{– 2x + 9}

d. 2x2 _{-6x + 6}

e. 2x2 _{– 2x + 5}

5. Fungsi f: R



R dan g : R



R , jika fungsi

f(x)=x-2 dan g(x)= 2x2_{+3x+4 maka (gof)}

(x)=....

a. x2_-5x+12

b. x2_-5x+6

c. x2_-11x+6

d. 2x2_+3x+6

e. 2x2_-5x+6

6. Diketahui fungsi f : R → R dan g : R → R yang

dinyatakan dengan f(x) = x2 _{– 3x – 5 dan g(x)}

= x – 2. Komposisi dari kedua fungsi (f o g) (x) = ....

a. x2 _{– 3x + 5}

b. x2 _{– 7x + 5}

c. x2 _{+ x – 7}

d. x2 _{– 3x – 3}

e. x2 _{– 3x – 7}

7. Jika fungsi f : R → R dan g : R → R yang

dinyatakan dengan f(x) = 4x – 2dan g(x) = x2

+ 8x – 2, maka (g o f) (x) = ....

a. 8x2 _{+ 16x – 4}

b. 8x2 _{+ 16x + 4}

c. 16x2 _{+ 8x – 4}

d. 16x2 _{- 16x + 4}

e. 16x2 _{+ 16x + 4 ( UN 2010 )}

Menentukan fungsi invers

1. Definisi :

Jika f :A B yang dinyatakan dengan

pasangan terurut f 



(a,b)aA,bB



maka

invers f adalah f1_:B A _{yang dinyatakan}

dengan f1 



₍b_,a₎bB_,aA



2. Cara menentukan fungsi invers :

Bentuk I :

f(x) = ax + b, maka

a b x x f 1_{( )} 

Contoh : f(x) = -2x + 5, maka

2 5 2

5 )

(

1 _x x x

f  

  



Bentuk II :

f(x) = ax - b, maka

a b x x f1_{( )} 

Contoh : f(x) = 3x – 6, maka

2 3

6 )

( ₃1

1 _  _{ }

 _x x _x

f

Catatan : a berupa konstanta/ bilangan baik positif maupun negatif

Bentuk III :

f(x) = d cx

b ax

 

, dengan x ≠



d_c maka

a cx

b dx x

f

   

1_{( ) ,}

dengan x ≠ a_c

secara mudah kita katakan : “ tukar saja a

dan d sekaligus ubah tandanya “ catatan : a adalah koefisien dari x yang berada di atas, dan d adalah konstanta ( bukan koefisiaen x ) yang berada di bawah ( Ingat ! : a harus yang nempel pada x di bagian atas )

Contoh :

f(x) =

2 5 3

 

 x x

, dengan x ≠ 2 , maka

3 5 2 ) ( 1

 

  



x x x

f , dengan x ≠  3

Paket Soal 10 :

1. Diketahui f(x) = , 3

3 1 2

 

 x x

x

dan

f-1_{(x) adalah invers dari f (x), maka f}-1_(x)

= ....

a. , 2

2 1 3

 

 x x

x

b. , 4

4 5 3

 

 x x

x

.

c. , 5

5 3 2

 

 x x

x

d. , 3

3 1 2

 

 x x

x

+ jadi -

Kali a jadi bagi a

h

tt

p

:/

/m

a

te

m

a

tr

ic

k

.b

lo

g

s

p

o

t.

c

o

m

e. , 1

1 2 2     x x x

2. Diketahui f(x) =

4 5 , 5 4 3 2     x x x

dan f-1_{(x) adalah invers dari f (x), maka f}-1_(x)

= .... a. 4 3 , 3 4 5 2     x x x b. 4 3 , 3 4 2 5     x x x . c. 4 3 , 3 4 5 2     x x x d. 4 3 , 3 4 5 2    x x x e. 4 3 , 3 4 2 5    x x x

3. Diketahui fungsi f ditentukan oleh

3 5 , 5 3 2 ) (     x x x x

f dan _f1_{adalah fungsi}

invers dari f, maka _f1(_x)_=….

a. 5 1 , 1 5 3 2     x x x b. 2 5 , 5 2 1 3     x x x

c. , 3

3 2 5     x x x d. 3 1 , 1 3 2 5    x x x

e. , 3

3 5 2     x x x

4. Funsi invers dari f(x) =

1 x 3 x 2 4   , x



-3 1

, adalah ....

a. 4 x 3 2 x 4   

, x



3 4 b. 2 x 3 x 4  

, x



3 2  c. 2 x 3 4 x  

, x



3 2 d. 1 x 3 2 x 4  

, x



3 1 e. 2 x 3 4 x 4  

, x



-3 2

5. Diketahu f-1_{(x) invers dari f(x) =}

1 x 3 x 2 4  

, x



3 1



maka f-1_{(x) =....}

a. 4 x 2 3 x   

, x



2

b. 4 x 2 x 3  

, x



2

c. 3 x 4 2 x  

, x



4 3 d. 4 x 2 3 x  

, x



-2

e. 2 3 4   x x

, x



3 2



6. Diketahu f-1_{(x) invers dari f(x) =}

1 2 3   x x

, x



2 1



maka f-1_{(x) =....}

a. , 3

3 1 2    x x x

b. , 3

3 1 2      x x x . c. 2 1 , 1 2 3     x x x d. 2 1 , 1 2 3    x x x

e. , 0

2 3    x x x

7. Funsi invers dari f(x) =

5 2 2 3   x x ,

x



-2 5

, adalah ....

a. 3 2 2 5   x x

, x



2 3 b. 3 2 2 5   x x

, x



2 3  c. x x 2 3 2 5  

, x



2 3 d. 2 3 5 2   x x

, x



3 2 e. x x 3 2 5 2  

, x



3 2

( UN

h

tt

p

:/

/m

a

te

m

a

tr

ic

k

.b

lo

g

s

p

o

t.

c

o

m

8. Diketahu f-1_{(x) invers dari f(x) =}

2 3

2 x

 , maka f-1_{(x) =.... ( UN 2011 )}

a. (1 )

3 2

x 

b. (1 )

3 2

x 

c. (1 )

2 3

x 

d. (1 )

2 3

x  

e. ( 1)

3 2



h

tt

p

:/

/m

a

te

m

a

tr

ic

k

.b

lo

g

s

p

o

t.

c

o

m

1. Bentuk umum SPLDV :















2 2 2 1 1 1

c

y

b

x

a

c

y

b

x

a

2. Cara menentukan himpunan penyelesaian ( HP :



(x,y)



) :

a. Eliminasi dan subtitusi

b. Menggunakan invers matriks, dengan

konsep : B A X maka B AX 1 ,   

Catatan : jika















2 2 2 1 1 1

c

y

b

x

a

c

y

b

x

a

dinyatakan

dalam matriks maka menjadi :







































2 1 2 2 1 1

c

c

y

x

b

a

b

a

c. Menggunakan Determinan Matriks :







































2 1 2 2 1 1

c

c

y

x

b

a

b

a

, maka :

D

D

x



x _dan

D D

y y

 ; dengan

1 2 2 1 2 2 1 1 .

.b a b

a b a

b a

D  

1 2 2 1 2 2 1 1 .

.b c b

c b c

b c

Dx   

1 2 2 1 2 2 1

1 _{a .c a .c}

c a

c a

Dy   

d. Cara Tebak Saja/ di kira – kira bilangan

yang cocok.

1. Himpunan penyelesaian dari

sistem persamaan          1 3 2 7 3 y x y x

, adalah ....

a. { - 2,-1 } b. { - 2,1 } c. { -1,-2 } d. { -1,-2 } e. {2,1}

Penyelesaian :

Jelas jawabannya B { - 2, 1 }, sebab jika disubtitusikan/ digantikan ke dalam x dan y, maka memenuhi kedua persamaan tersebut. 3.(-2) – 1 = -6 – 1 = -7, dan

2.(-2) + 3.1 = -4 + 3 = -1

2. Diketahui sistem persamaan;

         0 8 2 5 0 7 3 2 y x y x

jika x dan y penyelesaian dari sistem

persamaan diatas maka nilai x2 _{- y}2 _adalah....

a. -2 d. 3.

b. -1 e. 5

c. 2 Penyelesaian :          0 8 2 5 0 7 3 2 y x y x

dapat diubah menjadi

       8 2 5 7 3 2 y x y x

Tebak saja : 4 + 3 = 7, berarti x = 2 dan y = -1, di cek untuk persamaan kedua : 5. 2 + 2.(-1) = 10 – 2 = 8 Cocok.

Jadi x = 2, dan y = -1, sehingga nilai x2 _{– y}2 _{= 2}2 _–

( -1 )2 _{=4-1 = 3 .}

Jadi jawabannya D.

Catatan : jika jawaban sulit ditebak, silahkan Anda menempuh cara lain.

1. Himpunan penyelesaian dari

h

tt

p

:/

/m

a

te

m

a

tr

ic

k

.b

lo

g

s

p

o

t.

c

o

m

b. { - 4, - 3 } c. { 4, - 3 } d. { 3, - 4 } e. { -3, 4 }

2. Himpunan penyelesaian sistem

persamaan linier















2

2

7

2

y

x

y

x

adalah ….

a.







1

,



4





b.







1

,

4





c.





1

,



4





d.





1

,

0





e.





1

,

4





3. Himpunan penyelesaian sistem

persamaan linier















2

6

2

3

y

x

y

x

, adalah ….

a.





0

,

2





b.





0

,

3





c.





2

,

0





d.





2

,



1





e.





2

,

1





4. Himpunan penyelesaian dari















39

2

7

4

3

2

y

x

y

x

adalah



(

x

₁

,

y

₁

)



. Nilai

....

2 1 2

1



y



x

a. b . c. d . e.

7 8 26 29 104

5. Diketahui sistim persamaan;

  

 

 

1 3 2

11 3 4

y x

y x

jika x dan y penyelesaian dari sistim persamaan diatas maka nilai 2(x + y) adalah....

a. -2 b. 6 c. -4 d. 8 e. 2

6. Himpunan penyelesaian dari