2Konsep dan Notasi New

Konsep dan Notasi Bahasa

Teori Bahasa

Teori Otomata dan bahasa formal, berkaitan dalam hal pembangkitan kalimat / generation yaitu,

menghasilkan semua kalimat dalam bahasa L berdasarkan aturan yang dimilikinya. Dan pengenalan kalimat / recognition yaitu, menentukan suatu string (kalimat) termasuk sebagai salah satu anggota himpunan L.

Teori bahasa membicarakan bahasa formal (formal language), terutama untuk kepentingan perancangan kompilator (compiler) dan pemroses naskah (text processor). Bahasa formal adalah kumpulan kalimat.

Semua kalimat dalam sebuah bahasa dibangkitkan oleh sebuah tata bahasa (grammar) yang sama. Sebuah bahasa formal bisa dibangkitkan oleh dua atau lebih tata bahasa berbeda. Dikatakan bahasa formal karena grammar diciptakan mendahului pembangkitan setiap kalimatnya. Bahasa manusia bersifat sebaliknya;

grammar diciptakan untuk meresmikan kata-kata yang hidup di masyarakat. Dalam pembicaraan selanjutnya ‘bahasa formal’ akan disebut ‘bahasa’ saja.

Automata

Arti menurut American Heritage Dictionary : 1. a robot

2. one that behaves in an automatic or mechanical fashion Arti dalam dunia matematika

Berkaitan dengan teori mesin abstrak, yaitu mesin sekuensial yang menerima input, dan mengeluarkan output, dalam bentuk diskrit.

Contoh :

Mesin Jaja / vending machine Kunci kombinasi

Bahasa adalah kumpulan kalimat. Kalimat adalah rangkaian kata. Kata adalah komponen terkecil kalimat yang tidak bisa dipisahkan lagi.

Contoh : Si Kucing kecil menendang bola besar

The little cat kicks a big ball

for i := start to finish do A[i] := B[i]*sin(i*pi/16.0)

Bhs Indonesia Bhs Inggris Bhs Pascal

Dalam bahasa pemrograman, kalimat dikenal sebagai ekspresi, dan kata sebagai token.

Kata terdiri atas beberapa karakter. Kelompok karakter yang membentuk sebuah token dinamakam lexeme untuk token tersebut. Setiap token yang dihasilkan, disimpan dalam tabel simbol.

Grammar dan bahasa

Pengertian dasar

1. Setiap anggota alfabet, dinamakan sebagai simbol terminal atau token

2. Kalimat adalah deretan hingga simbol-simbol terminal

3. Bahasa adalah himpunan kalimat-kalimat. Anggota bahasa bisa tak hingga kalimat

4. Himpunan simbol terminal dinyatakan sebagai V_N, sedangkan himpunan simbol non terminal dinyatakan sebagai V_T.

5. Simbol-simbol berikut adalah simbol terminal :_{• Huruf kecil awal alfabet, misal x, y, z.}

• Simbol operator, misal +, -, dan x • Simbol tanda baca, misal (,), dan ;

• String yang tercetak tebal, misal, if, then, dan else

6. Simbol-simbol berikut adalah simbol non terminal • Huruf besar awal alfabet, misal X, Y, Z.

• Huruf S sebagai simbol awal

Grammar dan bahasa

7. Huruf besar akhir alfabet melambangkan simbol terminal atau non terminal, misal X, Y, Z

8. Huruf kecil akhir alfabet melambangkan string yang tersusun atas simbol-simbol terminal, misalnya : x, y, z.

9. Huruf yunani melambangkan string yang tersusun atas simbol terminal atau simbol-simbol non terminal atau campuran keduanya, misalnya : , , dan 

10. Sebuah produksi dilambangkan sebagai   , artinya : dalam sebuah derivasi dapat

dilakukan penggantian simbol  dengan simbol .

11. Simbol  dalam produksi berbentuk    disebut ruas kiri produksi sedangkan simbol 

disebut ruas kanan produksi.

12. Pengertian terminal berasal dari kata terminate (berakhir), maksudnya derivasi berakhir jika sentensial yang dihasilkan adalah sebuah kalimat (yang tersusun atas simbol-simbol

terminal itu).

13. Pengertian non terminal berasal dari kata not terminate (belum/tidak berakhir), maksudnya derivasi belum/tidak berakhir jika sentensial yang dihasilkan mengandung simbol non

Grammar dan bahasa

14. String adalah deretan terbatas (finite) simbol-simbol. Sebagai contoh, jika a, b, dan c adalah tiga buah simbol maka abcb adalah sebuah string yang dibangun dari ketiga simbol tersebut.

15. Jika w adalah sebuah string maka panjang string dinyatakan sebagai w dan didefinisikan sebagai cacahan (banyaknya) simbol yang menyusun string tersebut. Sebagai contoh, jika w

= abcb maka w= 4.

16. String hampa adalah sebuah string dengan nol buah simbol. String hampa dinyatakan dengan simbol  (atau ^) sehingga = 0. String hampa dapat dipandang sebagai simbol

hampa karena keduanya tersusun dari nol buah simbol.

17. Simbol adalah sebuah entitas abstrak (seperti halnya pengertian titik dalam geometri). Sebuah huruf atau sebuah angka adalah contoh simbol.

18. Alfabet adalah hinpunan hingga (finite set) simbol-simbol

19. Derivasi adalah proses pembentukan sebuah kalimat atau sentensial. Sebuah derivasi dilambangkan sebagai :  .

20. Sentensial adalah string yang tersusun atas simbol-simbol terminal atau simbol-simbol non terminal atau campuran keduanya.

Grammar dan Klasifikasi Chomsky

Grammar G didefinisikan sebagai pasangan 4 tuple : V_N, V_T, S, dan Q, dan dituliskan sebagai G(V_N, V_T, S, Q), dimana :

V_T : himpunan simbol-simbol terminal (atau himpunan token -token, atau alfabet) V_N : himpunan simbol-simbol non terminal

S  V_N : simbol awal (atau simbol start)

Q : himpunan produksi

Aturan produksi dinyatakan sebagai   , artinya  menurunkan 

Berdasarkan komposisi bentuk ruas kiri dan ruas kanan produksinya ( ), Noam Chomsky

mengklasifikasikan 4 tipe grammar :

1. Grammar tipe ke-0 : Unrestricted Grammar (UG) Ciri : ,   (VTVN)*, > 0

2. Grammar tipe ke-1 : Context Sensitive Grammar (CSG) Ciri : ,   (VTVN)*, 0 <   

3. Grammar tipe ke-2 : Context Free Grammar (CFG) Ciri :   V_N,   (VTVN)*

4. Grammar tipe ke-3 : Regular Grammar (RG)

Ciri :   VN,   {VT, VTVN} atau   VN,   {VT, VNVT}

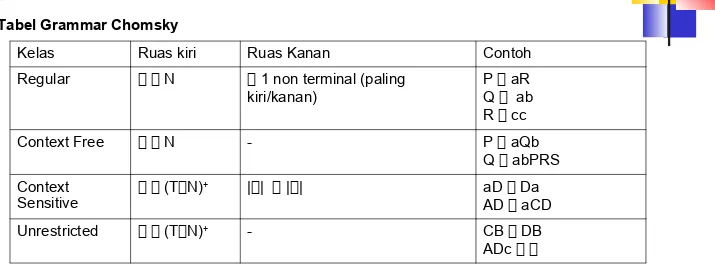
Tabel Grammar Chomsky

Kelas Ruas kiri Ruas Kanan Contoh

Regular   N  1 non terminal (paling

kiri/kanan)

P  aR

Q  ab

R  cc

Context Free   N - P  aQb

Q  abPRS

Context

Sensitive  

(TN)+ ||  || aD  Da

AD  aCD

Unrestricted   (TN)+ - CB  DB

ADc  

Tipe sebuah grammar (atau bahasa) ditentukan dengan aturan sebagai berikut :

Unrestricted

Cotext Sensitive

Kontext free

regular

Hirarki

Chomsky

Type Grammar Kelas Bahasa Mesin Pengenal Bahasa

Unrestricted Grammar (UG)/type-0 Unrestricted Mesin Turing (Turing Machine), TM

Context Sensitive Grammar

(CSG)/type-1 Context Sensitive Linear Bounded Automaton, LBA Context Free Gammar (CFG)/type-2 Context Free Automata Pushdown (Pushdown

Automata), PDA

Regular Grammar (RG)/type-3 Regular Automata Hingga (Finite Automata) Mesin Pengenal bahasa

Catatan :

Contoh Analisa Penentuan Type Grammar

1. Grammar G dengan Q = {S  aB, B  bB, B  b}. Ruas kiri semua produksinya terdiri dari

sebuah V maka G kemungkinan tipe CFG atau RG. Selanjutnya karena semua ruas kanannya terdiri dari sebuah V atau string VV maka G adalah RG.

2. Grammar G dengan Q = {S  Ba, B  Bb, B  b}. Ruas kiri semua produksinya terdiri dari

sebuah V maka G kemungkinan tipe CFG atau RG. Selanjutnya karena semua ruas kanannya terdiri dari sebuah V atau string VV maka G adalah RG.

3. Grammar G dengan Q = {S  Ba, B  bB, B  b}. Ruas kiri semua produksinya terdiri dari

sebuah V maka G kemungkinan tipe CFG atau RG. Selanjutnya karena ruas kanannya mengandung string VV (yaitu bB) dan juga string VV (Ba) maka G bukan RG, dengan kata lain G adalah CFG. Selanjutnya karena semua ruas kirinya lebih pendek atau sama dengan ruas kananya maka G adalah CSG.

6. Grammar G dengan Q = {aS  ab, SAc  bc}. Ruas kirinya mengandung string yang

Derivasi Kalimat dan Penentuan Bahasa

Tentukan bahasa dari masing-masing gramar berikut : A. G dengan Q = {1. S  aAa, 2. A  aAa, 3. A  b}.

Jawab :

Derivasi kalimat terpendek : Derivasi kalimat umum :

S  aAa (1) S  aAa (1)

Derivasi kalimat terpendek : Derivasi kalimat umum :

Derivasi Kalimat dan Penentuan Bahasa

C. G dengan Q = {1. S  aSBC, 2. S  abC, 3. bB  bb,

4. bC  bc, 5. CB  BC, 6. cC  cc}.

Jawab :

Derivasi kalimat terpendek 1: Derivasi kalimat terpendek 3 :

S  abC (2) S  aSBC (1)

 abc (4)  aaSBCBC (1)

Derivasi kalimat terpendek 2 :  aaabCBCBC (2)

S  aSBC (1)  aaabBCCBC (5)

 aabCBC (2)  aaabBCBCC (5)

 aabBCC (5)  aaabBBCCC (5)

 aabbCC (3)  aaabbBCCC (3)

 aabbcC (4)  aaabbbCCC (3)

 aabbcc (6)  aaabbbcCC (4)

 aaabbbccC (6)

 aaabbbccc (6)

Menentukan Grammar Sebuah Bahasa

1. Tentukan sebuah gramar regular untuk bahasa L = { a n  1}

Jawab :

Q(L) = {S  aSa}

2. Tentukan sebuah gramar bebas konteks untuk bahasa : L : himpunan bilangan bulat non negatif ganjil

Jawab :

Langkah kunci : digit terakhir bilangan harus ganjil.

Buat dua buah himpunan bilangan terpisah : genap (G) dan ganjil (J) Q(L) = {S  JGSJS, G  02468, J  13579}

3. Tentukan sebuah gramar bebas konteks untuk bahasa :

L = himpunan semua identifier yang sah menurut bahasa pemrograman Pascal dengan batasan : terdiri dari simbol huruf kecil dan angka, panjang identifier boleh lebih dari 8 karakter

Jawab :

Langkah kunci : karakter pertama identifier harus huruf.

Menentukan Grammar Sebuah Bahasa

4. Tentukan gramar bebas konteks untuk bahasa L(G) = {abn,m  1, n  m}

Jawab :

Langkah kunci : sulit untuk mendefinisikan L(G) secara langsung. Jalan keluarnya adalah dengan mengingat bahwa x  y berarti x > y atau x < y.

L = L L, L ={abn > m  1}, L = {ab1  n < m}.

Q(L) = {A  aAaC, C  aCbab}, Q(L) = {B  BbDb, D aDbab}

Q(L) = {S AB, A  aAaC, C  aCbab, B  BbDb, D aDbab}

5. Tentukan sebuah gramar bebas konteks untuk bahasa :

L = bilangan bulat non negatif genap. Jika bilangan tersebut terdiri dari dua digit atau lebih maka nol tidak boleh muncul sebagai digit pertama.

Jawab :

Token, Lexeme, dan Pattern

Token adalah symbol terminal pada teori bahasa. Token merupakan bagian hasil dari pemecahan sumber program yaitu penerjemahan lexeme pada saat melakukan scanner. Token

mereprentasikan identifier (nama variabel, fungsi, tipe atau nama yang didefinisikan pemakai), keyword, literal string, operator, label, simbol tanda (tanda kurung, koma, titik koma), constant, relation, identity, number, variable.

Lexeme adalah string yang merupakan masukan dari analisis Leksikal. Lexeme adalah kelompok karakter yang membentuk sebuah token.

Token tertentu harus memenuhi aturan yang disebut Pattern. Token merupakan sekumpulan karakter yang sesuai dengan pattern-nya.

Diagram Status / State Transition Diagram

Berguna untuk mendapatkan token, yaitu melakukan analisis leksikal. Misal suatu bahasa memiliki himpunan simbol terminal/token berikut : (t_PLUS, t_MIN, t_ID, t_INT).

Maka diagram state-nya :

*t_ID(identifier) bisa berupa nama atau keyword.

Notasi BNF

Aturan-aturan produksi dapat dinyatakan dalam bentuk BNF ( Backus Naur Form )

Beberapa simbol yang dipakai dalam notasi BNF

::= Identik dengan simbol pada aturan produksi

| Menyatakan “atau”

< > Mengapit simbol variabel / non terminal

{ } Pengulangan 0 sampai n kali [ ] 0 atau 1 kali muncul

( ) contoh x(yz) = xy | xz

Contoh, terdapat aturan produksi sebagai berikut :

E T | T+E | T-E, T a

Notasi BNF :

Diagram Sintaks

Diagram sintaks merupakan alat bantu dalam pembentukan parser / analisis sintaks. Notasi yang terdapat dalam diagram sintaks :

• Empat persegi panjang melambangkan simbol variabel / non terminal. • Bulatan melambangkan simbol terminal

Misal, terdapat aturan produksi :

T F*T | F/T | F