APLIKASI SISTEM PERSAMAAN DIFERENSIAL OR

APLIKASI SISTEM PERSAMAAN DIFERENSIAL ORDE SATU Untuk memenuhi tugas mata kuliah Persamaan Diferensial

Yang dibina oleh Bapak Dr. Baiduri, M.Si

Oleh

Kelompok VIII

PENDIDIKAN MATEMATIKA

FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN UNIVERSITAS MUHAMMADIYAH MALANG

Kata Pengantar...i

Daftar Isi...ii

BAB I Materi PD yang Sesuai ... BAB II Aplikasi PD ... BAB II Latihan Soal ... BAB II Kesimpulan ...

DAFTAR PUSTAKA

MATERI PERSAMAAN DIFERENSIAL 1.1 Pengertian Sistem Persamaan Diferensial dan Jenis-jenisnya

Sistem persamaan diferensial adalah suatu sistem yang memuat n buah persamaan diferensial, dengan n buah fungsi yang tidak diketahui, dimana n

merupakan bilangan bulat positif lebih besar sama dengan 2 (Finizio dan Ladas, 1982:132). Antara persamaan diferensial yang satu dengan yang lain saling keterkaitan dan konsisten.

Bentuk umum dari suatu sistem n persamaan orde pertama mempunyai bentuk sebagai berikut :

dy₁

dx =f1(x , y1, y2, … , yn)

dy₂

dx =f2(x , y1, y2, … , yn) ...

dy_n

dx =fn

(

x , y1, y2, … , yn

)

...

(1.1)

dengan y1, y2, …, yn adalah variabel bebas dan x adalh variabel

terikat, sehingga y₁=y₁(x), y₂=y₂(x), … y_n=y_n(x) , dimana dyn

dx

merupakan derivatif fungsi y_n terhadap x , dan f_n adalah fungsi yang tergantung pada variabel y₁, y₂, … , y_n dan x (Claudia,2004:702).

Bentuk lain sistem persamaan diferensial linier orde satu dapat ditulis sebagai berikut. (Ross, 1984: 510)

y1 '

=a11(x)y1+a12(x)y2+…+a1n(x)yn+g1(x) y2'=a21(x)y1+a22(x)y2+…+a2n(x)yn+g2(x)

...

yn '

=an1(x)y1+an2(x)y2+…+ann(x)yn+gn(x) ...(1.2)

untuk a_ijx , j=1,2,3,… , n adalah fungsi terhadap t . Juga

dY

Persamaan (1.2) disebut sistem persamaan diferensial linier homogen jika f_i(x)=0,∀i=1,2,… , n dan disebut linier tak homogen jika ada

fn(x)≠0 . Kemudian disebut sistem persamaan diferensial linier dengan koefisien konstanya jika a_ij(x)=a_ij(kostanta) , 1≤ i , j≤ n .

¿ ¿ SPD Linier Homogen

2.

¿ ¿ SPD Linier tak Homogen

3.

y11=5y1−y2+4

y₂1_=2y

1+3 y2 ¿}¿

4.

¿ ¿ SPD Linier Koef. Variabel

1.2 Hubungan PD Orde n dengan Sistem PD

Persamaan diferensial orde n linier, koefisien konstanta dapat ditransformasi menjadi sistem persamaan difensial orde 1 dengan variabel benas n buah.

Sehingga persamaan diferensialnya menjadi sistem persamaan difensial orde 1 dengan n variabel.

y1'=y2

Sehingga diperoleh SPDL :

y1

1.3 Solusi Sistem Persamaan Diferensial SPDL dapat ditulis dalam bentuk :

y1'=a11(x)y1+a12(x)y2+…+a1n(x)yn+g1(x)

y2 '

...

yn'=an1(x)y1+an2(x)y2+…+ann(x)yn+gn(x)

Fungsi-fungsi y1(x), y2(x), ... , yn(x) yang didefinisikan pada interval I  dikatakan solusi dari SPDL jika fungsi-fungsi tersebut dan turunannya ada pada I dan memenuhi SPDL.

Masalah mencari solusi dari SPDL pada selang I  R yang memenuhi syarat awal y1(x0) = a1, y2(x0) = a2 , ... , yn(x0) = an , maka disebut masalah nilai awal

xo  R, (a1, a2, …, an)  Rn, (xo,a1, a2, …, an)  I x Rn Contoh

Selidiki apakah fungsi-fungsi

Jadi, y₁ dan y₂ merupakan solusi dari SPD tersebut dan memenuhi syarat awal yang diberikan

1.4 Solusi SPDL Homogen Koefisien Konstanta

Diberikan SPDL homogen dengan koefisien konstanta sebagai berikut :

dx

dt=ax+by dy

dt=cx+dy ...(1)

Dalam menyelesaikan masalah yang berkaitan dengan SPDL homogen koefisien konstanta, terdapat beberapa cara penyelesaian. Salah satu cara penyelesaian tersebut adalh dengan metode eliminasi-substitusi

Diambil Operator diferensial dengan Dx=dx

dt dan Dy= dy

dt maka

SPDL di atas adapt ditulis menjadi :

Dx=ax+by atau (D−a)x−by=0… … … …(2) Dy=cx+dy atau (D−c)x−dy=0… … … …(3)

Jika kita mengeliminir x dari (1) dan (2), maka kita kalikan (1) dengan c dan (2) dengan (D – a) sehingga diperoleh

c (D - a)x – bcy = 0 c (D - a)x – (D - a)(D - d)y = 0

(D - a)(D - d) - bc]y = 0

(D2 _{– (a + d)D + ad – bc)y = 0 ...(4)}

Persamaan (4) merupakan persamaan diferensial linier (PDL) order-2 dalam

y. Jika kita mengeliminir y akan di peroleh PDL order-2 dalam x. Persamaan karekteristik dari (4) adalah :

r2−(a+d)r+ (ad−bc)=0… … … .(5)

Karena (5) merupakan persamaan kuadarat dalam r maka kemungkinan nilai-nilai r adalah sebagai berikut:

Solusi umum dari sistem (1) adalah y=c₁er1t₊c 2e

r2t

b. Real dan sama ( r₁=r₂=r )

Solusi umum dari sistem (1) adalah y=c₁er1t₊c 2x e

r2t

c. Kompleks ( r=a ±bi )

Solusi umum dari sistem (1) adalah c1cosbx+c1sinbx

y=eαx¿ )

(Kartono,1994:117-118) dalam (Yunitasari,2007:9) Setelah didapatkan solusi umum dari y, kita substitusikan nilai y tersebut ke dalam persamaan (2) untuk mendapatkan solusi umum dari x sehingga di dapatkan solusi umum dari (1).

Dengan memasukan syarat awal ke dalam solusi umum, maka konstanta-konstanta yang muncul ( C₁, C₂, C₃, … ,C_n ) dapat diketahui nilainya.

1.5 Solusi SPDL Tak Homogen Koef Konstanta

Mencari solusi SPDL tak homogen dapat dialakukan dengan mencari solusi persamaan homogennya terlebih dahulu. Kemudian mencari solusi khususnya dengan beberapa cara, diantaranya yaitu dengan menggunkan metode koefisien taktentu. Metode koefisien tertentu merupakan teknik untuk mencari solusi partikulir ( y_p ).

Jika diberikan persamaan linier tak homogen dengan koefisien konstanta y” + p y’ + p y’ + qy = b(x) dan akar persamaan karakteristik dari persamaan homogennya diketahui, maka untuk mencari yp dilakukan prosedur berikut:

1. Jika b(x) = an xn + … + a1 x + a0, maka

ii. Yp = x k _(Anxn _{+ … + A1x + A0), bila r = 0 merupakan akar} kelipatan k, k = 1,2.

2. Jika b(x) = (an xn + … + a1 x + a0) ebx, maka

i. yp = An xn _{+ … + A1x + A0 )e} bx _{, bila r = b bukan akar.}

ii. yp = x k _(Anxn _{+ … + A1 x + A0)e} bx _{, bila r = b merupakan akar} kelipatan k,

3. Jika b(x) = (an xn + … + a1x + a0) ebx sin

β

x + (bmxm + … + b1x + b0) e bxcos x, dan N = max (n,m), maka

i. yp = (ANx N _{+ … + A1x + A0)e} bx _sin

β

_{x + (BNx}N _{+ … +B1x + B0} )e bx _cos

β

_{x bila r = b +}

β

_{i bukan akar}

ii. yp = xk_(ANxN _{+ … + A1x + A0)e}bx _sin

β

_{x + x}k _(BNxN _{+ … + B1x} + B0)e bx_cos

β

_{x, bila r = b +}

β

_{i akar kelipatan k, k = 1,2.}

BAB II APLIKASI

Banyak masalah dalam ilmu pengetahuan dan teknik menyangkut pengkajian suatu sistem selama periode waktu tertentu. Kebanyakan masalah ini dimodelkan dengan menggunakan suatu sistem persamaan diferensial, dengan berbagai variabel bebas. Bidang kajian persamaan diferensial tidak hanya bukan sebagai salah satu bagian tercantik dari matematika, namun ia juga merupakan alat yang penting di dalam memodelkan benbagai fenomena dan masalah dalam bidang ilmu-ilmu fisika, kimia, biologi, ekonomi, transportasi dan teknik

Berikut ini merupakan pengaplikasian sistem persamaan diferensial dam berbagai bidang, yaitu :

1. Teknik

persamaannya terdiri dari beberapa persamaan diferensial yaitu dalam bentuk SPDL.

Derajat kebebasan (degree of freedom) adalah derajat independensi yang diperlukan untuk menyatakan posisi suatu sistem pada saat. Sehingga struktur yang mempunyai n- tingkat akan mempunyai n- derajat kebebasan atau struktur dengan dengan derajat kebebasan banyak.

Persamaan gerak struktur MDOF dapat disusun dengan pernyataan keseimbangan gaya-gaya efektif yang berhubungan dengan masing-masing derajat kebebasannya. Pada umumnya terdapat empat gaya pada setiap koordinat i : beban luar yang dikenakan fi(t) dan gaya-gaya yang diakibatkan oleh gerak, yakni inersia f_{I i} , peredaman f_Di dan elastik

f_Si sehingga berdasarkan pada prinsip d’Alembert untuk masing-masing derajat kebebasan kesetimbangan dinamika dapat dinyatakan sebagai berikut :

fI1+fD1+fS1=F1(t)

fI2+fD2+fS2=F2(t)

fI3+fD2+fS3=F3(t) (3.1)

⋮

f¿+fDN+fSN=FN(t)

Atau dapat dinyatakan dalam bentuk

FI+FD+FS=F(t) (3.2)

dengan

FI=m .´y F_D=c .´y

F_S=k . y (3.3)

+¿_⋯+k_1N y_N f_S1=k₁₁y₁+k₁₂y₂+k₁₃y₃¿

Sehingga secara umum +¿_⋯+k¿yN

f_Si=k_i1y₁+k_i2y₂+k_i3y₃¿

Dalam bentuk matriks gaya elastic dapat di tulis sebagai berikut

f_S1

Dengan k sebagai matriks kekakuan struktur dan y adalah vektor perpindahan yang menyatakan bentuk perpindahan struktur

Pada gaya redaman kita asumsikan bahwa peredaman dipengaruhi oleh kecepatan dan redaman tipe viskos. Susunan gaya redam diberikan sebagai berikut

f_I1 f_I2 ⋯ fIi

=

m₁₁ m₁₂ m₁₃ m₂₁ m₂₂ m₃₂

⋯ mi1

⋯ mi2

⋯ mi3

⋯ m_1N ⋯ m_2N ⋯ ⋯ m⋯3N

´

y1 ´

y₂ ⋯

´y_N

atau

F_I=m´y

dengan m adalah matriks massa dan ´y adalah vektor percepatan . Situasi tersebut dapat dilihat pada gambar berikut :

Strukrur bangunan gedung bertingkat n pada gambar di atas mempunyai n derajat kebebasan. Biasanya jumlah derajat kebebasan suatu struktur dihubungkan langsung dengan jumlah tingkatnya. Persamaan diferensial gerakan pada umumnya, disusun berdasarkan pada goyangan struktur mode pertama. Berdasarkan pada keseimbnagan dinamik pada free body diagram dan prinsip d’Alembert yang telah dijelaskan sebelumnya maka diperoleh

m₁´y₁+

₍

c₁+c₂

)

´y₁−c₂´y₂+

₍

k₁+k₂

)

y₁−k₁y₂=F₁(t)

m₁´y₂−c₂´y₁+

₍

c₁+c₃

₎

´y₂−c₃´y₃−k₂y₁+

₍

k₂+k₃

₎

y₂−k₃y₃=F₂(t) .

.

mn´yn+cn

(

´yn− ´yn−1)+cn+1´yn+kn

(

yn−yn−1

)

+kn+1yn=Fn(t)

2. Biologi a. Ekologi

Dalam bidang biologi khususnya ekologi, sistem persamaan diferensial digunakan untuk memodelkan interaksi dua populasi. Interaksi populasi yang paling terlihat adalah yang melibatkan pemangsaan, dimana seekor pemangsa memakan mangsa.

1) Model Predator-Prey

Pada model mangsa-pemangsa, kajian matematis dapat menjelaskan munculnya fenomena turun-naiknya jumlah mangsa dan pemangsa dalam suatu periode tertentu

Sekitar tahun 1920 terdapat penurunan dan kenaikan jumlah ikan-ikan di Laut Adriatic yang terjadi secara berkala. Saat terjadi penurunan jumlah ikan nelayan di daerah tersebut sangat dirugikan. Penjelasan akan fenomena tersebut diberikan pertama kali oleh Vito Volterra, di tahun 1926 melalui model predator-prey atau model mangsa-pemangsa. Ikan-ikan di Laut Adriatic merupakan mangsa, sedangkan Ikan-ikan hiu sebagai pemangsa. Model tersebut juga dikenal sebagai model Lotka-Volterra karena Lotka juga menemukan model yang sama di waktu yang relatif bersamaan.

Bayangkan suatu lingkungan yang tertutup dimana terdapat sejumlah rusa (mangsa) dan singa (pemangsa). Andaikan di lingkungan itu terdapat berlimpah rumput, namun bagi singa sumber makanannya hanya rusa. Misalkan x(t) dan y(t) berturut-turut menyatakan jumlah mangsa dan pemangsa di lingkungan tersebut saat t . Jika mangsa dan pemangsa tidak saling berinteraksi maka model pertumbuhannya masing-masing adalah

x'=ax

y'=−by

Sebaliknya jumlah pemangsa akan bertambah dengan laju qxy . Sehingga model mangsa-pemangsa menjadi

x'

=ax−pxy

y'=−by+qxy

Perhatikan bahwa model di atas mempunyai dua titik equilibrium (0,0) dan (a/p , b/q) .

Contoh

Pelajari perilaku kualitatif solusi SPD berikut:

x'

=x(1−0,5y)

y'=y(−0,75+0,25x)

Pada gambar di atas, dapat kita lihat bahwa model pada contoh

saat jumlah pemangsa mencapai nilai maksimum. Karena banyaknya pemangsa maka jumlah mangsa berkurang terus hingga mencapai nilai minimum. Selanjutnya dengan bertambahnya waktu jumlah pemangsa berkurang karena persaingan untuk mendapatkan makanan diantara mereka sendiri. Hal ini mengakibatkan jumlah pemangsa berkurang terus hingga mencapai jumlah minimal. Sementara itu jumlah mangsa bertambah karena sedikitnya jumlah pemangsa, hingga jumlah mangsa mencapai nilai maksimum.

2) Model Interaksi Dua Spesies

Pada model interaksi dua spesies, parameter-parameter sistem persamaan differensial dapat menentukan apakah akan terjadi kesetimbangan diantara dua spesies tersebut, ataukah salah satu dari spesies tersebut akan punah.

Bayangkan di suatu lingkungan yang tertutup terdapat kelinci dan rusa yang sama-sama makan rumput. Misalkan x(t) dan y(t) berturut-turut menyatakan jumlah kelinci dan rusa di lingkungan tersebut saat t . Jika kelinci tinggal di lingkungan itu tanpa ada rusa, maka kelinci akan bertumbuh secara logistik. Demikian pula dengan rusa, sehingga model pertumbuhan kelinci dan rusa masing-masing adalah

x'=a1x−b1x2

y'

=a2y−b2y2

Jika kelinci dan rusa sama-sama tinggal di lingkungan itu, maka makanan mereka terbatas karena kehadiran spesies yang lain. Sehingga model pertumbuhan kelinci dan rusa menjadi

x'=a1x−b1x2−c1xy

y'=a2y−b2y2−c2xy

Perhatikan bahwa model di atas mempunyai empat titik equilibrium (0,0), (0, a2/b2¿,(a1/b1,0) dan satu titik equilibrium (p , q) dengan

p , q keduanya tak nol. Contoh

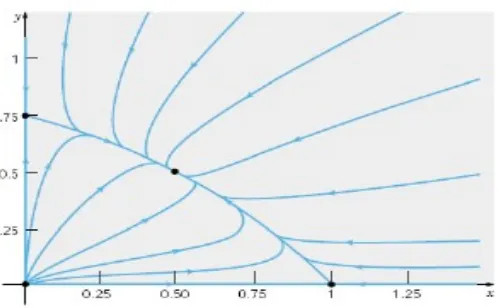
Pelajari perilaku kualitatif solusi SPD berikut

x'

=x(1−x−y)

Model di atas mempunyai empat titik equilibrium (0,0),(0, 0.75), (1,0), dan (0.5, 0.5). tampak dari phase portrait bahwa hanya terdapat satu titik equilibrium (0.5, 0.5) yang stabil. Ini berarti bahwa akan terjadi kesetimbangan antara kedua spesies tersebut.

b. Polusi Kolam

Diasumsikan berikut.

1. Simbol f (t) adalah laju aliran polusi ke dalam kolam 1 (lb / min). 2. Simbol f1, f2, f3 menyatakan tingkat aliran polusi dari kolam 1, 2, 3,

masing-masing (gal / min). Hal ini diasumsikan bahwa polusi dicampur dengan baik dalam setiap kolam.

3. Tiga kolam memiliki volume V1, V2, V3 (gal), yang tetap konstan. 4. Simbol x1 (t), x2 (t), x3 (t) menunjukkan jumlah (lbs) polusi

masing-masing di kolam 1, 2, 3,.

Polutan fluks adalah laju aliran konsentrasi polusi, misalnya, kolam 1 dikosongkan dengan fluks f1 kali x1 (t) / V1. Sebuah analisis kompartemen diringkas dalam diagram berikut.

Diagram ditambah kompartemen analisis diberikan oleh persamaan diferensial berikut.

x' 1(t)=

f₃ V3

x₃(t)−f1 V1

x'₂(t)=f1 V1

x₁(t)−f2 V2

x₂(t)

x '₃=f2

V2

x₂(t)−f3

V3

x₃(t)

c. Arus nutrisi dalam Aquarium

Pertimbangkan sebuah kapal dari air yang mengandung isotop radioaktif, yang akan digunakan sebagai pelacak untuk rantai makanan, yang terdiri dari varietas plankton air A dan B.

Plankton adalah organisme air yang melayang dengan arus, biasanya di lingkungan seperti Chesapeake Bay. Plankton dapat dibagi menjadi dua kelompok, fitoplankton dan zooplankton. fitoplankton yang tanaman seperti drifter: diatom dan alga lainnya. Zooplankton yang mirip binatang drifter: copepoda, larva, dan krustasea kecil.

Misal :

x (t) = konsentrasi isotop dalam air, y (t) = konsentrasi isotop di A z (t) = konsentrasi isotop di B. d. Pestisida di Tanah dan Pohon

Asumsikan bahwa jumlah pestisida disemprotkan pada tanah tidak diperhatikan. Pestisida yang disemprotkan pada pohon memiliki tingkat pengaliran tertentu untuk tanah, dan sebaliknya, pestisida di dalam tanah memiliki tingkat penyerapan tertentu ke dalam pohon. Pestisida digunakan secara berulang untuk mengontrol serangga, yang berarti tingkat penggunaan pestisida di pohon-pohon bervariasi dengan waktu. Quantize pestisida penyemprotan sebagai berikut.

x (t) = jumlah pestisida di pohon-pohon, y (t) = jumlah pestisida dalam tanah,

r (t) = jumlah pestisida disemprotkan pada pohon, t = waktu dalam tahun.

Sebuah model diperoleh dari analisis input-output, mirip dengan model tangki air garam:

x'_(t)=−2x(t

)−y(t)+r(t)

y'_{(t)=−2x(t)−3y(t)}

Dalam kebun buah-buahan murni, data awal x (0) = 0, y (0) = 0, karena pohon dan tanah awalnya tidak mengandung pestisida. Solusi dari model jelas tergantung pada r (t). Ketergantungan homogen diperlakukan dengan metode variasi parameter infra. rumus perkiraan adalah

x(t)≈

∫

0 t

(

1.10e1.6(t−u)

−0.12e−2.6(t−u)

₎

r(u)du

y(t)≈

∫

0 t

(

0.49e1.6(t−u)

−0.49e−2.6(t−u)

₎

r(u)du

Tingkat eksponensial 1,6 dan -2,6 masing-masing mewakili akumulasi pestisida ke dalam tanah dan pembusukan pestisida dari pepohonan. Tingkat aplikasi r (t) adalah langkah fungsi yang sama dengan konstanta positif pada interval kecil dari waktu dan nol di tempat lain, atau jumlah fungsi tersebut, mewakili aplikasi pestisida periodik.

a. Brine Tank Cascade

Pada tank air garam A, B, C masing-masing diisi dengan jumlah volume sebesar m, n, p seperti yang terlihat pada gambat berikut.

Air masuk pada tangki A dengan kecepatan r, kemudian A mengalir ke B dengan kecepatan r, selanjunya B mengalir ke C dengan kecepatan r. Terakhir dari tangki C mengalir keluar dengan kecepatan r. Hal tersebut menyebabkan volume tangki tetap konstan.

Misalkan r=a untuk menggambarkan ide di atas. Kita asumsikan terjadi pengaduakan secara seragam pada masing-masing tangki, yang berarti konsentrasi garam pada tiap tangki adalah sama.

Misal x₁(t), x₂(t), x₃(t) menunjukkan jumlah garam pada waktu t di setiap tangki. Tambahkan ke tangki A air yang tidak mengandung garam. Karena itu, garam di semua tank akhirnya hilang dari saluran air. Cascade dimodelkan oleh hukum keseimbangan kimia :

Tingkat Perubahan=Tingkat Masukan−Tingkat Keluaran

Penerapan hukum keseimbangan, dibenarkan dalam analisis kompartemen dibawah ini dengan hasil dalam sistem diferensial segitiga.

x '₁=−a

m x1

x '₂=a

mx1−

w n x4

x '3=

a nx1−

b. Daur Ulang Brine Tank Cascade

Misal tank air garam A, B, C diberi volume a, b, c, masing-masing, sebagai pada gambar berikut ini.

Misalkan cairan mengalir dari tangki A ke B pada tingkat r, mengalir dari tangki B ke C pada tingkat r, kemudian mengalir dari tangki C ke A pada tingkat r. Tangki volume tetap konstan karena daur ulang cairan konstan. Untuk tujuan ilustrasi, misalkan r = m.

Diasumsikan terjadi pengadukan seragam pada masing-masing tangki, yang berarti konsentrasi garam seragam pada setiap tangki.

Misal x1 (t), x2 (t), x3 (t) menunjukkan jumlah garam pada waktu t di setiap tangki. Tidak ada garam yang hilang dari sistem, karena daur ulang. Menggunakan analisis kompartemen, cascade daur ulang dimodelkan dengan sistem non-segitiga.

x '₁=−m

a x1+

m c x3

x '₂=m

a x1−

m b x2

x '3=

a bx2−

a cx3

4. Ekonomi

Peramalan Harga

Strategi pemasaran untuk sampo adalah untuk mengatur harga x (t) secara dinamis untuk menggambarkan permintaan pada produk. Persediaan yang diperlukan rendah akan mengurangi biaya keseluruhan produk.

Produksi P (t) dan penjualan S (t) diberikan dalam hal harga x (t) dan perubahan harga x '(t) dengan persamaan

P(t)=4−3

4x(t)−8x '

(t)(Produksi)

S(t)=15−4x(t)−2x'_{(t)(Penjualan} )

Persamaan diferensial untuk harga x(t) dan tingkat persediaan I (t) adalah

x'(t)=k

(

I(t)−I0

)

I'_(t)=P(t)−S (t)

Tingkat persediaan I0=50 merupakan tingkat yang diinginkan. persamaan dapat ditulis dalam hal x (t), I (t) sebagai berikut.

x'(t)=kI(t)−k I0

I'(t)

=13

4 x(t)−6kI(t)+6k I0−11

Jika k=1,x(0)=10dan I(0)=7, maka solusinya adalah

x(t)=44 13+

86 13e

I(t)=50+43e−13t/2

Perkiraaan harga x(t)≈3.39dollar pada tingkat persediaan I(t)≈50 didasarkan pada dua limit

lim t → ∞x(t)=

44

13,limt → ∞I(t)=50

5. Transportasi (pengangkutan barang)

Hutan Nasional di Amerika Serikat tidak memiliki akses login untuk jalan. Pada saat di lakukan penebangan maka menggunakan helikopter untuk memindahkan pohon yang ditebang ke area pemuatan terdekat untuk diangkut menggunakan truk ke pabrik. Pohon yang ditebang dibawa dengan disangkutkan pada tali/kabel yang tersambung pada helikopter. Sekali angkut dapat mengankut dua pohon menggunakan sebuah bandul yang terosilasi (ombang-ambing) selama penerbangan. Sudut osilasi yang terbentuk ialah θ₁,θ₂ yang terhubung oleh kabel dan diukur dari vektor gaya gravitasi sehingga memenuhi sistem persamaan diferensial sebagai berikut, diamana g adalah tetapan gravitas m1, m2 menunjukkan massa dari dua pohon dan L1, L2 adalah panjang kabel

m

(¿¿1+m2)

¿

L12 _θ

1 n +m2L 1L2 θ2 n +

m

(¿¿1+m2)

¿

L1g θ₁ = 0

m₂L 1L2 θ₂ n _{+ m}

2 L22 θ2 + m2 L2g θ2 = 0

Model ini diturunkan menjadi perpindahan yang lebih kecil θ₁,θ₂ yaitu

Panjang L1 dan L2 menyesuaikan pada setiap perjalanan yang ditempuh dan panjang pohon, sehingga pohon tidak bertabrakan satu sama lain saat diangkut helikopter. Terkadang dalam sekali mengangkut apabila pohon kecil maka dapat tiga atau lebih bandul yang digunakan, yang diperhatikan dalam pengangkutan adalah ketebalan pohon karena kabel yang digunakan menyesuaikan dengan tebal pohon.

Vektor- Model Matriks. Sudutnya θ₁,θ₂ memenuhi order kedua persamaan vektor-matriks

(

(m₁+m₂)L₁ m₂L₂

L1 L2

)

(

θ₁ θ2

)

''

=−

(

m1g+m2g 0 0 g

)

(

θ₁ θ2

)

.

Sistem ini ekuivalen dengan oder kedua sistem

−m₁g+m₂g L1m1

¿

m₂g L1m1

m₁g+m₂g L2m1

m −(¿¿1+m2)g

L2m1

(

θ1

θ₂

)

(

θ₁ θ₂

)

' ' =¿

LATIHAN SOAL

1. Sebuah bangunan bertingkat dua mempunyai massa dengan m1 = m2 = 5000kg, kekakuan kolom k1 = k2 =5000kg/s2 _{dan redaman c1 = c1 = 5000kg/ s}2_. Bangunan ini dipengaruhi gaya luar dengan F1= 10.000et _{dan F2= 5.000e}t_. tentukan besar simpangan pada setiap tingkat?

Penyelesaian:

SPDL dari contoh soal diatas yaitu

´

y1+2´y1− ´y2+2y1−y2=2et ...(3.5)

´

y2+ ´y1+ ´y2−y1+y2=et ...(3.6)

Diubah dalam polinomial operator D, dimana D= d

dt

(D2 _{+ 2D +2) y1 + (-D-1) y2 = 2e}t _(3.7)

(D-1) y1 + (D2 _{+ D + 1)y2 = e}t _(3.8) Eliminasi variabel tak bebas

(D2 _{+ 2D +2) y1 + (-D-1) y2 = 2e}t _{| (D-1) |} (D-1) y1 + (D2 _{+ D + 1)y2 = e | (D}t 2 _{+2D+2) |} (D4_+4D3_+6D2_+4D+1)=4et

Atau

d4_y 2

dt4 +4

d3_y 2

dt3 +6

d2_y 2

dt2 +4

dy2

dt +y2=4e

t _(3.9)

Kemudian menghitung y2 yaitu mencari solusi umum dari PD:

(

D2+4D3+6D2+4D+1

)

y2=4e

t

Persamaan karakteristiknya adalah r4+4r3+6r2+4r+1=0 Akar-akar persamaan karakteristiknya adalah r₁=r₂=r₃=r₄=−1

Solusi homogennya adalah y2h=c1e−t+c2x e−t+c3x2e−t+c4x3e−t

Untuk mencari solusi khususnya, kita gunakan metode koefisien tak tentu. Solusi khususnya diambil y2p=A et

Jadi solusi umum (3.9)

y2=y2h+y2p=c1e

Untuk menghitungvariabel tak bebas yang lain yaitu y₁ , masukkan y₂ ke dalam salah satu dari sistem ini:

¿−c₁e−t Jadi solusi umum sistem PD linier tak homogen ini adalah

y1=2c1e−t−2c2x e−t−2c3x2e−t−2c4x3e−t−et

2. Perhatikan gambar dibawah ini :

Masalah diatas dapat ditulis dalam sistem persamaan diferensial, sebagai

Solusi untuk sistem ini adalah

x₁(t)=e

Setelah 48 jam berlalu, jumlah polusi perkiraan dalam pound adalah

x₁(2880)=162.30, x₂(2880)=119.61,x₃(2880)=78.08 .

Pada aquarium di atas diasumsikan mengandung isotop radioktif untuk melacak rantai makanan pada plankton air. Plaktok air pada aquarium di atas termasuk pada kelompok fitoplanton yakni diatom dan alga. Konsentrasi isotop rdiaoaktif pada aquarium digambarkan oleh sistem sebagai berikut :

x'_{(t)=−3x(t)+6y(t)+5z} (t)

y'(t)=2x(t)−12y(t)

z'_(t

)=x(t)+6y(t)−5z(t)

x(0)=x₀, y(0)=0,z(0)=0

Tentukan solusi dari sistem dan juga konsentrasinya !

Jawab :

Solusi dari sistem persaaan diferensial yang menggambarkan kandungan radiokatif di atas adalah

x(t)=6c₁+(1+

√

6

)

c₂e(−10+√6)t₊

₍₁₋

_√

₆

₎

_c

3e(−10−√6)t

y(t)=c₁+c₂e(−10+√6)t

−c₃e(−10−√6)t

x(t)=12

5 c1−(2+

√

1.5)c2e(−10+√6)t+(−2+

√

1.5)c3e(−10−√6)t Konstanta c₁, c₂, c₃ terkait dengan isotop radioaktif awal.

Konsentrasi x(0)=x₀, y(0)=0,z(0)=0, dengan sistem 3 × 3 dari persamaan aljabar linier adalah

6c1+(1+

√

6)c2+(1−

√

6)c3=x0 c1+c2−c3=0

12

4. Perhatikan gambar dibawah ini

Air masuk pada tangki A dengan kecepatan 10 , kemudian A mengalir ke B dengan kecepatan10 , selanjunya B mengalir ke C dengan kecepatan 10. Terakhir dari tangki C mengalir keluar dengan kecepatan 10. Hal tersebut menyebabkan volume tangki tetap konstan. Kita asumsikan terjadi pengaduakan secara seragam pada masing-masing tangki, yang berarti konsentrasi garam pada tiap tangki adalah sama. Tentukan model matematika cascade dan solusinya !

Jawab :

Cascade dimodelkan oleh hukum keseimbangan kimia :

Tingkat Perubahan=Tingkat Masukan−Tingkat Keluaran

Penerapan hukum keseimbangan, dibenarkan dalam analisis kompartemen dibawah ini dengan hasil dalam sistem diferensial segitiga.

x '₁=−1 2 x1

x '₂=1 2x1−

1 4x2

x '3= 1 4 x2−

1 6 x3

Solusinya diberikan oleh persamaan :

40

60 20 r = 10

r = 10

A

B

−2e

5. Pada tank air garam A, B, C masing-masing diisi dengan jumlah volume seperti yang terlihat pada gambat berikut.

x₁(t)=c₁+

(

c₂−2c₃

)

e

−t 3 _cos(t

6)+

(

2c2+c3

)

e

−t 3 _sin(t

6)

x₂(t)=1

2c1+

(

−2c2−c3

)

e

−t 3 _cos( t

6)+

(

c2−2c3

)

e

−t 3 _sin( t

6)

x₃(t)=c₁+

₍

c₂+3c₃

₎

e

−t 3 _cos(t

6)+

(

−3c2+c3

)

e

−t 3 _sin(t

6)

BABA IV KESIMPULAN

Sistem persamaan differensial merupakan salah satu persamaan yang banyak dijumpai dalam kehidupan sehari-hari di berbagai bidang ilmu pengetahuan, misalnya dalam bidang sains dan teknik.

Pada bidang sains, persamaan diferensial dapat digunkana untuk menyelesaiakan permasalahan-permasalahan pada bidang seperti kimia maupun biologi. Pada biologi, sistem persamaan diferensial dapat digunkan untuk mengetahui interksi dalam popolasi, kemudian mengetahui ekosistem hewan maupun tumbuhan, tentang pestisida maupun polusi. Sedangkan pada kimia, dapat digunakan untuk mengetahui konsentari garam dan sebagainya.

Selain dua bidang di atas, sistem persaam diferensial juga berguna dalam bidang seperti ekonomi dan transportasi. Dalam bidang ekonomi, sistem persamaan diferensial dapat digunakan untuk meramalkan harga. Sedangkan pada bidang traspotasi, sistem persaaan diferensial dapat dimanfaatkan dalam proses pengangukatan barang, seperti pengankutan kayu oleh helikopter.

DAFTAR PUSTAKA

Baiduri. 2004. Persamaan Diferensial. Malang : UMM Press

Firia, Vivi A. 2011. Analisis Sistem Persamaan Diferensial Model Predator-Prey

dengan Perlambatan. Volume 2 Nomor 1 November 2011. ( )

Hendri, Yon dkk. Teknik Baru Menyelesaikan Sistem Persamaan Diferensial

Linear Orde Satu Nonhomogen. Fakultas Matematika dan Ilmu Pengetahuan

Oktaviani, Rizka dkk. 2014. Penyelesaian Numerik Sistem Persamaan Diferensial

Non Linear Dengan Metode Heun Pada Model Lotka-Volterra. Volume 03,

No. 1 (2014), hal 29 – 38. ( )

Redjeki, Sri. 2009. DIKTAT KULIAH MA2271 METODA MATEMATIKA Semester II 2009/2010. Prodi Matematika Fakultas MIPA Institut Teknologi Bandung. ( )

Yunitasari, Leni D. 2007. Aplikasi SPDL pada MDOF (Multi Degree Of Freedom). Skripsi. Universitas Muhammadiya Malang. (ta.umm.ac.id diakses pada 10 Juni 2016)