STUDI TENTANG METODE ASM PADA MASALAH TRANSPORTASI DENGAN VARIABEL FUZZY
SKRIPSI
YOGI NUGRAHA 130803027
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN 2017
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains
YOGI NUGRAHA 130803027
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN
PERSETUJUAN
Judul : Studi Tentang Metode ASM Pada Masalah Transportasi Dengan Variabel Fuzzy
Kategori : Skripsi
Nama : Yogi Nugraha
Nomor Induk Mahasiswa : 130803027
Program Studi : Sarjana (S1) Matematika
Departemen : Matematika
Fakultas : Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara
Disetujui di Medan, Juli 2017
Komisi Pembimbing:
Pembimbing 2, Pembimbing 1,
Drs. Ujian Sinulingga, M.Si Dr. Esther S. M. Nababan, M.Sc NIP. 19560303 198403 1 004 NIP. 19610318 198711 2 001
Disetujui Oleh,
Departemen Matematika FMIPA USU Ketua,
Dr. Suyanto, M. Kom
NIP. 19590813 198601 1 002
STUDI TENTANG METODE ASM PADA MASALAH TRANSPORTASI DENGAN VARIABEL FUZZY
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil karya sendiri. Kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, Juli 2017
Yogi Nugraha 130803027
PENGHARGAAN
Puji dan syukur penulis panjatkan kehadirat Allah SWT yang telah melimpahkan rahmat dan hidayah-Nya kepada penulis, sehingga penulis dapat menyelesaikan skripsi ini tepat pada waktunya. Skripsi dengan judul “Studi tentang Metode ASM pada Masalah Transportasi dengan Variabel Fuzzy”. Salawat dan salam semoga selalu tercurahkan kepada Nabi Muhammad SAW, yang telah memberikan contoh teladan sebagai pedoman hidup bagi seluruh umat manusia.
Dalam menyelesaikan skripsi ini, banyak pihak yang telah membantu penulis. Untuk itu, penulis menyampaikan ucapan terima kasih yang sebesar- besarnya dan penghargaan yang setinggi-tingginya kepada:
1. Ibu Dr. Esther Sorta M. Nababan, M.Sc dan Bapak Drs. Ujian Sinulingga, M.Si selaku dosen pembimbing yang senantiasa membantu dan mengarahkan saya dalam menyelesaikan skripsi ini.
2. Ibu Dra. Normalina Napitupulu, M.Sc dan Bapak Dr. Syahriol Sitorus, M.IT selaku dosen pembanding yang memberikan kritik dan saran yang membangun dalam menyelesaikan skripsi penulis.
3. Bapak Dr. Kerista Sebayang, M.S selaku Dekan FMIPA serta seluruh Staf pegawai di Fakultas Matematika Dan Ilmu Pengetahuan Alam USU.
4. Bapak Dr. Suyanto, M.Kom dan Bapak Drs. Rosman Siregar, M.Si selaku Ketua dan Sekretaris jurusan Matematika serta seluruh Bapak dan Ibu dosen yang telah mendidik penulis selama menjalani pendidikan di Fakultas Matematika Dan Ilmu Pengetahuan Alam USU.
5. Yang teristimewa kepada kedua orangtua tercinta, Ayahanda Sukarman, Ibunda Eli Sofyan serta saudara-saudari penulis Rizky Perdana, Rico Fazrin, Raci Prayoga dan Devi Karlina, Amd yang selalu memberikan dukungan berupa do’a, meteri, serta motivasi kepada penulis.
6. Yang tak terlupakan seluruh rekan-rekan kuliah Matematika stambuk 2013, adik-adik stambuk 2014, 2015, 2016 dan Organisasi, terkhusus kepada Helda Oktaviani, Mawar Riza dan Tondi Marulizar yang berjuang
Terima kasih penulis ucapkan kepada seluruh pihak yang telah membantu dalam proses pembuatan skripsi.
Medan, Juli 2017
Yogi Nugraha 130803027
STUDI TENTANG METODE ASM PADA MASALAH TRANSPORTASI DENGAN VARIABEL FUZZY
ABSTRAK
Masalah Transportasi merupakan masalah pendistribusian dari sumber-sumber yang menyediakan produk yang sama ke tempat-tempat tujuan secara optimal.
Pada praktiknya, masalah transportasi tersebut memiliki jumlah supply dan demand yang tidak selalu dapat diketahui dengan pasti dan dapat berubah-ubah dari waktu ke waktu. Sehingga dapat dikatakan bahwa masalah tersebut adalah masalah transportasi dengan keadaan fuzzy. Masalah transportasi fuzzy dapat diselesaikan dengan metode ASM, tetapi terlebih dahulu masalah transportasi fuzzy tersebut diubah ke dalam bentuk linier dengan menggunakan metode pendekatan “New Approach” agar lebih mudah pengerjaannya. Setelah itu, selesaikan masalah transportasi tersebut menggunakan metode ASM untuk mendapatkan hasil yang optimal. Metode ASM adalah salah satu metode optimalisasi masalah transportasi yang langsung menguji keoptimuman dari tabel transportasi. Metode ASM diawali dengan mengurangi biaya pada baris atau kolom dengan biaya terkecil. Jika pada waktu pengurangan biaya pada baris ada kolom yang belum nol maka mengurangi biaya pada kolom dengan biaya terkecil.
Jika pada waktu pengurangan biaya pada kolom ada baris yang belum nol maka mengurangi biaya pada baris dengan biaya terkecil. Setelah mengurangkan biaya pada baris atau kolom akan ada biaya nol pada baris dan kolom. Setelah itu dihitung jumlah nol pada tiap-tiap baris dan kolom (tidak termasuk nol yang dipilih). Pilih jumlah nol yang minimum lalu alokasikan persediaan dan permintaan pada sel yang biayanya nol. Pencarian ini tetap berlanjut sampai semua permintaan terpenuhi dan semua persediaan habis.
Kata Kunci : Masalah Transportasi, Variabel Fuzzy, Metode Pendekatan “New Approach”, Metode ASM.
ABSTRACT
Transportation problem is the problem of distribution of resources that provide the same product to places of interest optimally. In practice, the transportation problem having a number of supply and demand can not always be known with certainty and may change from time to time. So it can be said that the problem is the transportation problem with fuzzy. Fuzzy transportation problem can be solved by ASM method, but first fuzzy transportation problem is converted into a linear form using a "New Approach" for easier process. After that, finish the transportation problems using ASM to obtain optimal results. ASM method is a method of optimizing the transport problems that directly test the optimum value of the transportation tableau. ASM method begins by reducing the cost to the row or column with the smallest cost. If at the time the cost reduction on the line there is a column that is not zero, reducing costs in the column with the smallest cost. If at the time the cost reduction in the column there are rows that have not zero, reducing costs in line with the smallest cost. After subtracting the cost of the row or column will be zero cost to the rows and columns. After the calculated number of zeros in each row and column (excluding zero selected). Select the minimum number of zeroes and then allocate the supply and demand on the cell that costs zero. This search continues until all requests are fulfilled and all the supplies run out.
Keywords: Transportation Problem, Fuzzy Variable, "New Approach" method, ASM method.
DAFTAR ISI
Halaman
PERSETUJUAN i
PERNYATAAN ii
PENGHARGAAN iii
ABSTRAK v
ABSTRACT vi
DAFTAR ISI vii
DAFTAR TABEL ix
DAFTAR GAMBAR xi
BAB 1 PENDAHULUAN 1
1.1 Latar Belakang 1
1.2 Perumusan Masalah 3
1.3 Batasan masalah 3
1.4 Tujuan Penelitian 3
1.5 Manfaat Penelitian 3
1.6 Tinjauan Pustaka 4
1.7 Metodologi Penelitian 8
BAB 2 TINJAUAN PUSTAKA 10
2.1 Program Linier 10
2.2 Masalah Transportasi 11
2.2.1 Sejarah Permasalaha Transportasi 11
2.2.2 Definisi dan Ciri-Ciri Masalah Transportasi 12 2.2.3 Asumsi Dasar Masalah Transportasi 13
2.2.4 Model Transportasi 14
2.2.5 Keseimbangan Transportasi 16
2.3 Himpunan Fuzzy 17
2.3.1 Pengertian Himpunan Fuzzy 17
2.3.2 Fungsi Keanggotaan 19
2.3.2.1 Fungsi Keanggotaan Linier 20
2.3.2.2 Fungsi Keanggotaan Segitiga (Triangular) 21 2.3.2.3 Fungsi Keanggotaan Trapesium (Trapezoidal) 22 2.3.2.4 Fungsi Keanggotaan Bentuk Bahu 22 2.3.2.5 Fungsi Keanggotaan Bentuk S (Sigmoid) 23 2.3.2.6 Fungsi Keanggotaan Bentuk Lonceng (Bell
Curve)
24 2.4 Masalah Tranportasi dengan Variabel Fuzzy 27 2.5 Metode Pendekatan untuk Menyelesaikan Masalah Transportasi
Fuzzy
29 2.6 Metode Pendekatan “New Approach” untuk Menyelesaikan
Masalah Transportasi Fuzzy menjadi Transportasi Linier
33 2.7 Metode ASM untuk Menyelesaikan Masalah Transportasi
dengan Variabel Fuzzy
34
3.2 Metode Penyelesaian 37
BAB 4 HASIL DAN PEMBAHASAN 39
4.1 Masalah Transportasi 39
4.2 Masalah Transportasi dengan Variabel Fuzzy 40 4.3 Metode ASM untuk Menyelesaikan Masalah Transportasi Fuzzy 40 4.4 Contoh Kasus Masalah Transportasi dengan Variabel Fuzzy 41
4.4.1 Contoh Kasus dengan Keanggotaan Triangular yang Seimbang
41 4.4.2 Contoh Kasus dengan Keanggotaan Triangular yang
Tidak Seimbang
45 4.4.3 Contoh Kasus dengan Keanggotaan Trapezoidal yang
Seimbang
49 4.4.4 Contoh Kasus dengan Keanggotaan Trapezoidal yang
Tidak Seimbang
54
4.5 Pembahasan 59
BAB 5 KESIMPULAN DAN SARAN 61
5.1 Kesimpulan 61
5.2 Saran 61
DAFTAR PUSTAKA 63
DAFTAR TABEL
Nomor Tabel Judul Halaman
Tabel 2.1 Gambaran Umum Masalah Transportasi 15
Tabel 2.2 Masalah Transportasi Fuzzy 28
Tabel 4.1 Masalah Transportasi Fuzzy dengan Keangotaan Triangular yang Seimbang
41 Tabel 4.2 Hasil Penyelesaian Dengan Keanggotaan Triangular 42 Tabel 4.3 Hasil Penyelesaian Supply dengan Keanggotaan Triangular 43 Tabel 4.4 Hasil Penyelesaian Demand dengan Keanggotaan Triangular 43 Tabel 4.5 Hasil Penyelesaian Total Supply dan Demand dengan
Keanggotaan Triangular
43 Tabel 4.6 Masalah Transportasi Linier dengan Keanggotaan Triangular 43 Tabel 4.7 Hasil Pengolahan Data Menggunakan Metode ASM 44 Tabel 4.8 Hasil Akhir Masalah Transportasi Fuzzy dengan Keanggotaan
Triangular
44 Tabel 4.9 Masalah Transportasi Fuzzy dengan Keangotaan triangular
yang Tidak Seimbang
45 Tabel 4.10 Hasil Konversi ke Masalah Transportasi Seimbang 45 Tabel 4.11 Hasil Penyelesaian dengan Keanggotaan Triangular 46 Tabel 4.12 Hasil Penyelesaian Supply dengan keanggotaan Triangular 47 Tabel 4.13 Hasil Penyelesaian Demand dengan Keanggotaan Triangular 47 Tabel 4.14 Hasil Penyelesaian Total Supply dan Demand dengan
Keanggotaan Triangular
47 Tabel 4.15 Masalah Transportasi Linier dengan Keanggotaan Triangular 48 Tabel 4.16 Hasil Pengolahan Data Menggunakan Metode ASM 48 Tabel 4.17 Hasil Akhir Masalah Transportasi Fuzzy dengan Keanggotaan
Triangular
49 Tabel 4.18 Masalah Transportasi Fuzzy dengan Keanggotaan Trapezoidal 50 Tabel 4.19 Hasil Penyelesaian dengan Keanggotaan Trapezoidal 50 Tabel 4.20 Hasil Penyelesaian Supply dengan Keanggotaan Trapezoidal 51 Tabel 4.21 Hasil Penyelesaian Demand dengan Keanggotaan Trapezoidal 51 Tabel 4.22 Hasil Penyelesaian Total Supply dan Demand dengan
Keanggotaan Trapezoidal
52 Tabel 4.23 Masalah Transportasi Linier dengan Keanggotaan Trapezoidal 52 Tabel 4.24 Hasil Pengolahan Data Menggunakan Metode ASM 52 Tabel 4.25 Hasil Akhir Masalah Transportasi Fuzzy dengan Keanggotaan
Trapezoidal
53 Tabel 4.26 Masalah Transportasi Fuzzy dengan Keanggotaan Trapezoidal 54 Tabel 4.27 Hasil Konversi ke Masalah Transportasi Seimbang 54 Tabel 4.28 Hasil Penyelesaian dengan Keanggotaan Trapezoidal 55 Tabel 4.29 Hasil Penyelesaian Supply dengan Keanggotaan Trapezoidal 56 Tabel 4.30 Hasil Penyelesaian Demand dengan Keanggotaan Trapezoidal 56 Tabel 4.31 Hasil Penyelesaian Total Supply dan Demand dengan
Keanggotaan trapezoidal
57
Trapezoidal
DAFTAR GAMBAR
Nomor Gambar Judul Halaman
Gambar 2.1 Masalah Umum Model Transportasi 14
Gambar 2.2 Fungsi Keanggotaan Linear Naik 20
Gambar 2.3 Fungsi Keanggotaan Linear Turun 21
Gambar 2.4 Fungsi Keanggotaan Triangular 22
Gambar 2.5 Fungsi Keanggotaan Trapezoidal 22
Gambar 2.6 Fungsi Keanggotaan Bentuk Bahu 23
Gambar 2.7 Fungsi Keanggotaan Bentuk S (Pertumbuhan) 23 Gambar 2.8 Fungsi Keanggotaan Bentuk S (Penyusutan) 24 Gambar 2.9 Fungsi Keanggotaan Bentuk Lonceng (PI) 25 Gambar 2.10 Fungsi Keanggotaan Bentuk Lonceng (Beta) 26 Gambar 2.11 Fungsi Keanggotaan Bentuk Lonceng (Gauss) 27
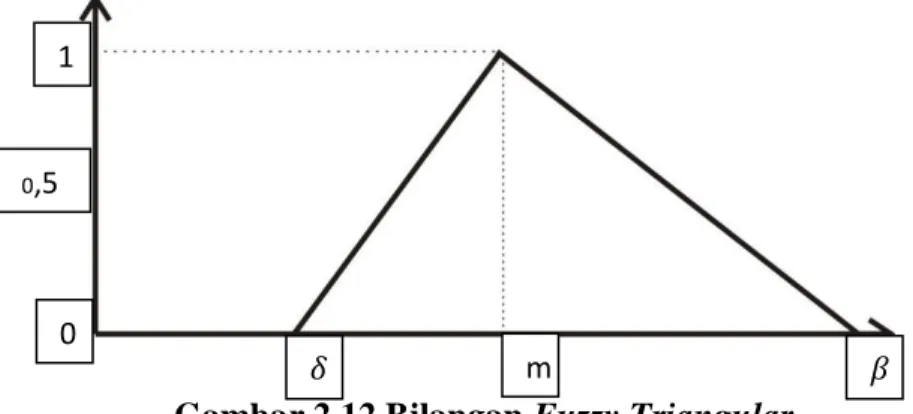
Gambar 2.12 Bilangan Fuzzy Triangular 33
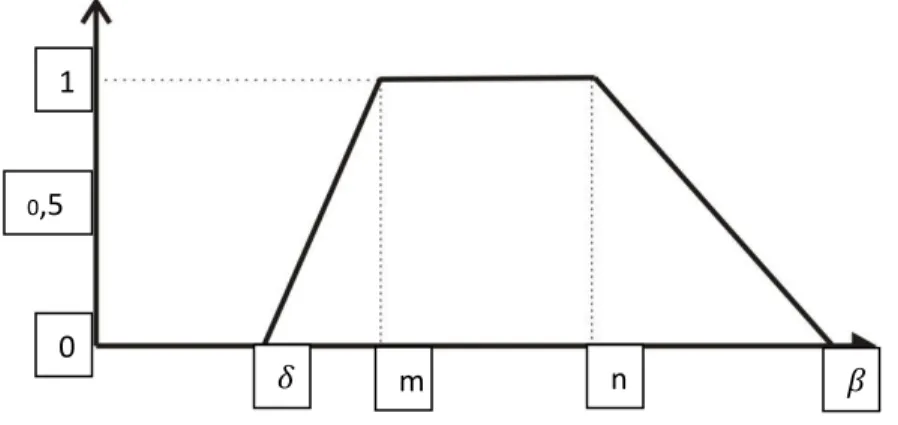
Gambar 2.13 Bilangan Fuzzy Trapezoidal 34
Gambar 3.1 Alur Penyelesaian Masalah Transportasi Fuzzy 38
PENDAHULUAN
1.1. Latar Belakang
Transportasi merupakan bentuk khusus dari program linear yang digunakan untuk memecahkan masalah yang berhubungan dengan transportasi (pengangkutan) untuk meminimalkan biaya, jarak tempuh dan sebagainya sehingga dapat memaksimalkan laba/keuntungan yang diperoleh. Permasalahan transportasi merupakan permasalahan yang sering terjadi dalam kehidupan sehari-hari.
Transportasi merupakan bentuk khusus dari program linier yang digunakan untuk memecahkan masalah yang berhubungan dengan transportasi (pengangkutan).
Pada umumnya, masalah transportasi berkaitan dengan mendistribusikan suatu komoditi dari kelompok pusat pemasok (yang disebut sumber) ke pusat penerima (yang disebut tujuan) dalam rute tertentu yang dapat meminimumkan biaya total. Masalah pokok dalam alokasi pendistribusian ini adalah bagaimana cara agar komoditi tersebut dapat melewati jalur-jalur tertentu, dari sumber yang menyediakannya ke tempat-tempat tujuan dengan biaya yang dapat ditekan seminimal mungkin. Metode transportasi dirancang untuk melakukan optimalisasi variabel yang digunakan dalam memecahkan masalah transportasi, termasuk didalamnya masalah pengiriman dari beberapa sumber ke beberapa tujuan dengan tetap berorientasi pada biaya minimum, dimana setiap sumber mempunyai kapasitas tertentu dan setiap tujuan mempunyai permintaan tertentu pula. Pada model transportasi, yang harus diperhatikan adalah bahwa total kuantitas pada seluruh baris harus sama dengan total kuantitas pada seluruh kolom, jika tidak, maka perlu ditambahkan kuantitas dummy.
Berdasarkan pada keadaan pasar yang ada, parameter dari transportasi yang berupa nilai permintan dan persediaan tidak selalu dapat diketahui dengan pasti dan tidak selalu stabil. Pada masalah transportasi nilai dari biaya pengiriman, jumlah penawaran (supply) maksimum pada sumber, dan jumlah permintaan
2
(demand) minimum pada tujuan terhadap suatu barang tidak selalu dapat diketahui dengan pasti dan dapat berubah-ubah dari waktu ke waktu.
Ketidakpastian dari nilai ini dapat terjadi karena kurangnya informasi tentang nilai tersebut. Pada biaya pengiriman yang tidak pasti dapat terjadi karena berubah- ubahnya harga bahan bakar, jalur transportasi yang padat, serta cuaca yang buruk bisa menyebabkan kenaikan biaya pengiriman barang. Pada jumlah supply ketidakpastian dapat terjadi karena tidak pastinya jumlah ketersediaan bahan mentah produksi, terjadinya kerusakan mesin produksi, dan terjadinya kegagalan saat produksi yang mengakibatkan penurunan pada jumlah supply. Sedangkan ketidakpastian dari nilai demand dapat terjadi karena adanya perubahan situasi pasar. Permintaan terhadap suatu barang ketika kondisi pasar baik cenderung lebih besar dibandingkan ketika kondisi pasar buruk. Sebuah cara yang sering kali digunakan untuk menyatakan ketidakpastian ini adalah bilangan fuzzy. Masalah transportasi dengan jumlah supply, jumlah demand, dan biaya angkutannya dinyatakan dengan bilangan fuzzy disebut sebagai masalah transportasi fuzzy.
Dalam menyelesaikan masalah transportasi fuzzy bisa menggunakan metode ASM (Abdul Quddos, Shakeel Javaid, dan M. M. Khalid). Metode ASM merupakan metode alternatif untuk menyelesaikan masalah transportasi fuzzy.
Metode ASM adalah salah satu metode optimalisasi masalah transportasi yang langsung menguji keoptimuman dari tablo transportasi. Metode ASM diawali dengan mengurangi biaya pada baris atau kolom dengan biaya terkecil. Jika pada waktu pengurangan biaya pada baris ada kolom yang belum nol maka mengurangi biaya pada kolom dengan biaya terkecil. Jika pada waktu pengurangan biaya pada kolom ada baris yang belum nol maka mengurangi biaya pada baris dengan biaya terkecil. Setelah mengurangkan biaya pada baris atau kolom akan ada biaya nol pada baris dan kolom. Setelah itu dihitung jumlah nol pada tiap-tiap baris dan kolom (tidak termasuk nol yang dipilih). Pilih jumlah nol yang minimum lalu alokasikan persediaan dan permintaan pada sel yang biayanya nol. Pencarian ini tetap berlanjut sampai semua permintaan terpenuhi dan semua persediaan habis.
Berdasarkan uraian diatas, maka penulis memberi tulisan ini dengan judul “Studi Tentang Metode ASM pada Masalah Transportasi dengan Variabel Fuzzy”.
1.2. Perumusan Masalah
Berdasarkan latar belakang, yang menjadi masalah adalah bagaimana metode ASM dalam menyelesaikan masalah transportasi fuzzy.
1.3. Batasan Masalah
Batasan masalah dalam penelitian ini adalah:
1. Berkaitan dengan masalah transportasi fuzzy.
2. Masalah yang diteliti merupakan masalah transportasi seimbang dan masalah transportasi tidak seimbang.
3. Masalah transportasi fuzzy terdiri atas dua fungsi keanggotaan, yaitu fungsi keanggotaan segitiga (triangular) dan fungsi keanggotaan trapesium (trapezoidal).
4. Penggunaan metode ASM dalam menyelesaikan masalah transportasi fuzzy.
1.4. Tujuan Penelitian
Tujuan dari penelitian ini adalah memberi gambaran mengenai efektifitas metode ASM dalam menyelesaikan masalah transportasi fuzzy dalam meminimalkan total biaya pendistribusian barang.
1.5. Manfaat Penelitian
Manfaat penelitian ini adalah:
1. Untuk menambah pengetahuan pembaca, khususnya mengenai penyelesaian masalah transportasi dengan variabel fuzzy menggunakan metode ASM.
2. Sebagai tambahan referensi bacaan bagi mahasiswa yang akan melakukan penelitian yang serupa.
4
1.6. Tinjauan Pustaka
Transportasi adalah variasi khusus dari program linear yang digunakan untuk mengatur distribusi dari sumber-sumber yang menyediakan barang yang sama, ke tempat-tempat yang membutuhkan barang secara optimal. (Pangestu et al, 1984).
Tranportasi digunakan untuk mencari solusi optimal dari masalah distribusi barang. Tahun 1939, L.V. Kantorovitch mempelajari berbagai masalah yang berhubungan dengan transportasi. Kemudian, tahun 1941 F.L. Hitchcock merumuskan model matematika dari masalah transportasi yang kini menjadi model baku yang sering disebut model Hitchcock. T.C. Koopmans tahun 1949 dan G.B. Dantzig tahun 1951 juga turut mengembangkan metode transportasi.
Charnes dan Cooper (1961) memperkenalkan program tujuan ganda sebagai pendekatan untuk menyelesaikan masalah yang tidak dapat diselesaikan dengan program linear yang disebabkan oleh tujuan yang bertentangan. Kemudian Ijiri (1965) dan Jaaskelainen (1969) melanjutkan dan melengkapinya sehingga dapat dipakai secara operasional.
Menurut Taha, dalam arti sederhana, model transportasi berusaha menentukan sebuah rencana transportasi sebuah barang dari sejumlah sumber ke sebuah tujuan. Data dalam model ini mencakup :
1. Tingkat penawaran di setiap sumber dan jumlah permintaan di setiap tujuan.
2. Biaya transportasi per unit barang dari setiap sumber ke setiap tujuan.
Tujuan dari model transportasi adalah menentukan jumlah yang harus dikirimkan dari setiap sumber ke setiap tujuan sedemikian rupa sehingga biaya transportasi total diminimumkan. Sebuah tujuan dapat menerima permintaannya dari satu sumber atau lebih. (Taha, 1996).
Bentuk umum model transportasi linier adalah sebagai berikut:
nj
ij ij m
i
x c Z
1 1
Dengan batasan,
n
j
i
ij
a
x
1
,
i1,2,...,m
m
i
j
ij
b
x
1
,
j 1,2,...,n 0
x
ij untuk semua i danj
Pemodelan masalah transportasi linier dapat dilihat sebagai berikut, Tabel 1.1 Gambaran Umum Masalah Transportasi
Destination (D i)
Supply ) (a i
Source ) (Si
D1 D2 ... Dn
S 1 11
c c 12 ... c1n
a 1
x 11 x 12 ... x1n
S 2 c 21 c 22 ….. c2n
a 2
x 21 x 22 ….. x2n
. . .
... ... ... ... .
. . .
. .
. . .
. . .
. . .
S m
1
c m cm2 ... cmn
a m 1
x m xm2 ... xmn
Demand )
(bj b 1 b 2 ... b n
Keterangan :
S : Source (sumber) sejumlah i, i i 1,2,3,...,m
Dj: Destination (tujuan) sejumlah j , j1,2,3,...,n a : Jumlah penawaran pada sumber i, i i 1,2,3,...,m
bj : Jumlah permintaan pada tujuan j, j 1,2,3,...,n
ij :
c Biaya transportasi dari sumber i ke tujuan j , i 1,2,3,...,m
:
x
Jumlah barang yang diangkut dari sumber i ke tujuan j, j 1,2,3,...,n6
Keseimbangan Masalah Transportasi
Suatu model transportasi dikatakan seimbang apabila total supply (sumber) sama dengan total demand (tujuan). Dengan kata lain :
nj j m
i
i b
a
Dalam persoalan sebenarnya, batasan ini tidak terlalu terpenuhi atau dengan kata lain, jumlah supply yang tersedia mungkin lebih besar atau lebih kecil daripada jumlah yang diminta. Jika hal ini terjadi, maka model persoalannya disebut sebagai model yang tidak seimbang (unbalanced). Dengan kata lain :
nj j m
i
i b
a atau
nj j m
i
i b
a
Jika jumlah demand melebihi jumlah supply, maka dibuat suatu sumber dummy yang akan men-supply kekurangan tersebut. Tetapi jika jumlah supply melebihi jumlah demand, maka dibuat suatu tujuan dummy untuk menyerap kelebihan tersebut.
Bilangan Fuzzy
Himpunan fuzzy didasarkan pada gagasan untuk memperluas jangkauan fungsi karakteristik sedemikian sehingga fungsi tersebut akan mencakup bilangan real pada interval [0,1]. Nilai keanggotaannnya menunjukkan bahwa suatu item dalam semesta pembicaraan tidak hanya berada pada 0 atau 1, namun juga nilai yang terletak diantaranya. Dengan kata lain, nilai kebenaran suatu item tidak hanya bernilai benar atau salah. Nilai 0 menunjukkan salah, nilai 1 menunjukkan benar dan masih ada nilai-nilai yang terletak antara benar dan salah.
Beberapa hal yang perlu diketahui dalam memahami sistem fuzzy :
Variabel Fuzzy. Merupakan variabel yang hendak dibahas dalam suatu sistem fuzzy, contoh : umur, temperature, permintaan dan sebagainya.
Himpunan Fuzzy. Merupakan suatu grup yang mewakili suatu kondisi atau keadaan tertentu dalam suatu variabel fuzzy, contoh :
Variabel umur dibagi menjadi 3 himpunan fuzzy : muda, parobaya, tua.
Variabel temperature ibagi menjadi 5 himpunan fuzzy : dingin, sejuk, normal, hangat dan panas.
Metode Pendekatan “New Approach”
New Approach merupakan suatu metode pendekatan baru yang digunakan untuk mengubah transportasi fuzzy ke bentuk transportasi linier. Dengan metode ini dapat mempermudah pengerjaan dalam menyelesaikan masalah transportasi fuzzy.
Metode ini dapat digunakan pada masalah transportasi dengan keanggotaan triangular dan trapezoidal.
Untuk bilangan fuzzy triangular, rumusnya sebagai berikut.
] 2
4[ ) 1
(A m MTri
Keterangan : ) ( A
MTri = Pendekatan nilai yang pasti untuk himpunan fuzzy triangular A, A dapat berupa himpunan permintaan fuzzy, himpunan persediaan fuzzy atau himpunan biaya fuzzy
, ,
m = Sembarang bilangan real dengan MTri(A)0 (H. Basirzadeh, 2011 : 1557)
Untuk bilangan fuzzy trapezoidal, rumusnya sebagai berikut.
] 4[
)1
(B mn MTra
Keterangan : ) (B
MTra = Pendekatan nilai yang pasti untuk himpunan fuzzy trapezoidal B , B dapat berupa himpunan permintaan fuzzy, himpunan persediaan fuzzy atau himpunan biaya fuzzy
, , , n
m = Sembarang bilangan real dengan MTra(B)0 (H. Basirzadeh, 2011 : 1557)
Metode ASM (Abdul Quddoos, Shakeel Javaid, M.M. Khalid)
Metode ASM adalah salah satu metode optimalisasi masalah transportasi yang langsung menguji keoptimuman dari tabel transportasi. Metode ASM memberikan solusi optimal secara langsung dengan iterasi yang lebih sedikit, untuk masalah
8
transportasi. Karena metode ini menghabiskan lebih sedikit waktu dan sangat mudah dimengerti dan diterapkan, maka akan jadi sangat membantu pengambil keputusan yang menangani masalah logistik dan supply chain. (A. Quddoos, Shakeel. J, M.M. Khalid, 2012).
Berikut langkah-langkah kerja Metode ASM menurut Quddous dkk pada tahun 2012 :
1. Buat tabel transportasi.
2. Mengurangi nilai/entri setiap baris pada tabel transportasi dengan nilai yang minimum pada setiap baris. Begitu juga pada kolom, kurangi nilai setiap kolom dengan nilai yang minimum pada setiap kolom.
3. Pilih entri yang bernilai nol pada baris dan kolom lalu hitung jumlah nol pada baris dan kolom (kecuali nol yang dipilih). Kemudian memilih nol yang selanjutnya dan hitung jumlah nol sesuai baris dan kolom dengan cara yang sama. Lakukan pada nol yang lainnya hingga seluruh nol didaftarkan.
4. Memilih nol dengan jumlah nol yang minimum dari hasil perhitungan langkah 3 dan memenuhi jumlah maksimum yang memungkinkan pada entri tersebut. Jika terjadi seri untuk beberapa nol dari langkah 3, pilih salah satu nol (biasanya dipilih dari baris yang terdekat) dari beberapa nol tersebut dan alokasikan dengan jumlah maksimum dari nilai persediaan/permintaan.
5. Hapus entri pada baris atau kolom jika persediaan/permintaan yang maksimum sudah dialokasikan ke entri tersebut.
6. Mengecek apakah hasil perhitungan terdapat minimal satu nilai nol yang terdapat pada tiap baris dan kolom. Jika tidak, maka ulangi kembali ke langkah 2, tetapi jika terpenuhi lanjutkan ke langkah berikutnya.
7. Mengulangi langkah 3 hingga seluruh persediaan dan permintaan telah habis dialokasikan ke entri-entri.
1.7. Metodologi Penelitian
Metodologi penelitian ini disusun sebagai berikut :
1. Menjelaskan tentang masalah transportasi.
2. Menjelaskan tentang dua macam masalah transportasi (masalah seimbang atau tidak seimbang).
3. Menjelaskan tentang variabel fuzzy.
4. Menjelaskan tentang masalah transportasi dengan variabel fuzzy.
5. Gunakan contoh kasus yang menggambarkan masalah transportasi fuzzy dengan fungsi keanggotaannya berbentuk triangular dan trapezoidal serta yang berkaitan dengan masalah tranportasi seimbang dan tidak seimbang.
6. Mengubah persamaan transportasi variabel fuzzy menjadi bentuk linier dengan metode pendekatan “New Approach”.
7. Menyelesaikannya dengan metode ASM untuk mendapatkan solusi yang optimal.
8. Membahas hasil penyelesaian.
9. Membuat kesimpulan.
BAB 2
TINJAUAN PUSTAKA
2.1 Program Linier
Linnear Programming adalah alat analisis atas masalah yang mempunyai variabel-variabel bersifat deterministic (terukur) dan masing masing mempunyai hubungan linear satu sama lain (Prawirosentono, 2005;12).
Menurut Suyadi Prawirosentono (2007 : 145), program linier adalah salah satu metode dalam ilmu manajemen untuk mengelola sumber daya yang terbatas untuk mencapai tujuan yang diinginkan. Program linier adalah cara menanggulangi masalah yang mempunyai variabel-variabel yang bergantung satu sama lain dan berhubungan secara linear.
Sedangkan menurut Jay Heizer dan Barry Rander (2005 : 588), program linear adalah suatu teknik matematik yang didesain untuk membantu para manajer operasi dalam merencanakan dan membuat keputusan yang diperlukan untuk mengalokasikan sumber daya.
Program linear merupakan model umum yang dapat digunakan dalam menyelesaikan masalah pengalokasian sumber-sumber yang terbatas secara maksimal dengan tujuan untuk memaksimalkan atau meminimalkan kuantitas (pada umumnya berupa laba atau biaya). Program linier banyak digunakan dalam bidang optimasi, ini karena berbagai masalah dalam riset operasi dapat dinyatakan sebagai masalah pemrograman linier.
Pemrograman linier telah terbukti merupakan salah satu alat riset operasi yang paling efektif. Keberhasilannya berakar dari keluwesannya menjabarkan berbagai situasi kehidupan nyata di bidang bidang berikut ini : militer, industri, pertanian, transportasi, ekonomi, kesehatan, dan bahkan ilmu social dan perilaku (Hamdy A Taha, 1996 : 15).
Salah satu masalah program linear adalah masalah sistem distribusi yang akan meminimalkan biaya pengiriman total dari beberapa sumber ke beberapa
tujuan yaitu dengan menggunakan metode transportasi yang akan di bahas pada penelitian ini.
2.2 Masalah Transportasi
2.2.1 Sejarah Permasalahan Transportasi
Persoalan transportasi merupakan persoalan linier programming.
Bahkan aplikasi dari teknik linier programming pertama kali adalah dalam merumuskan persoalan transportasi yang dasar pada mulanya dikembangkan oleh F.L Hitchcock pada tahun 1941 dalam studinya yang berjudul The Distribution of a product from several source to numerous locations. Ini merupakan ciri dari persoalan transportasi yaitu mengangkut sejenis produk seperti produk beras, minyak, daging, telur atau produk lainnya dari beberapa daerah asal (pusat produksi, depot atau gudang) ke beberapa derah tujuan (pasar, tempat proyek atau permukiman), pengaturan harus dilakukan sedemikian rupa agar sejumlah biaya transportasi minimum.
Pada tahun 1947, TC Koopmans secara terpisah menerbitkan suatu hasil studi mengenai Optimum utilization of the transportation system. Selajutnya, perumusan persoalan linear programming dan cara pemecahan yang sistematis dikembangkan oleh Prof. George Danzig yang sering disebut sebagai bapak linier programming. Prosedur pemecahan yang sistematis tersebut disebut metode simpleks.
Masalah transportasi menurut Ayu (1996) adalah masalah pemrograman linier khusus yang dapat dikatakan paling penting. Dasar masalah transportasi ini pertama kali dicetuskan oleh Hitchock dan kemudian dijelaskan dengan lebih mendetail oleh Koopmans. Pendekatan pertama diberikan oleh Kantrovich.
Formulasikan pemrograman linier dan metode sistematisnya pertama kali diberikan oleh Dantzig.
12
2.2.2 Definisi dan Ciri-Ciri Masalah Transportasi
Menurut Biegel (1999) transportasi adalah suatu pengaturan yang berhubungan dengan pelaksanaan pendistribusian yang lebih ekonomis dari produk-produk (barang barang) yang dihasilkan di beberapa pabrik dan keperluan untuk penempatannyadalam gudang yang lokasinya berbeda. Menurut Dimyati (1994) transportasi membahas masalah pendistribusian suatu komoditas atau produk dari sejumlah sumber (supply) kepada sejumlah tujuan (destination, demand), dengan tujuan meminimumkan ongkos pengangkutan yang terjadi.
Menurut Hari Purnomo, (2004) pemodelan transportasi adalah masalah pendistribusian sejumlah produk atau komoditas dari beberapa sumber distribusi (supply) kepada beberapa daerah tujuan (demand) dengan berpegang pada prinsip biaya disrtibusi minimal. Selain untuk mencari biaya distribusi minimal, pemodelan transportasi juga dapat digunakan untuk mencari perolehan/pendapatan maksimal daristrategi distribusi komoditi yang mempunyai keuntungan tertentu.
Menurut Siswanto (2007 : 265), secara khusus model transportasi berkaitan dengan masalah pendistribusian barang-barang dari pusat-pusat pengiriman atau sumber ke pusat-pusat penerimaan atau tujuan. Persoalan yang ingin dipecahkan oleh model transportasi adalah penentuan distribusi barang yang akan meminimumkan biaya total distribusi.
Menurut Jay Heizer dan Barry Render (2005 : 631), permodelan transportasi adalah mencari cara yang termurah untuk mengirimkan barang dari beberapa sumber ke beberapa tujuan. Untuk menggunakan model transportasi, kita harus mengetahui hal-hal berikut :
1. Titik asal dan kapasitas atau pasokan pada setiap periode.
2. Titik tujuan dan permintaan pada setiap periode.
3. Biaya pengiriman satu unit dari setiap titik asal ke titik tujuan.
Persoalan transportasi membahas masalah pendistribusian suatu komoditas atau produk dari sejumlah sumber supply kepada sejumlah tujuan (Destination demand) dengan tujuan meminimalkan ongkos penngiriman yang terjadi. Ciri-ciri khusus persoalan transportasi ini adalah:
1. Terdapat sejumlah sumber dan sejumlah tujuan tertentu.
2. Kuantitas komoditas atau barang didistribusikan dari setiap sumber dan yang diminta setiap tujuan, besarnya tertentu.
3. Komoditas yang dikirim atau diangkut dari suatu sumber ke suatu tujuan, besarnya sesuai dengan permintaan dan kapasitas sumber.
4. Ongkos pengangkutan komoditas dari suatu sumber ke suatu tujuan, besarnya tertentu.
(Bu’ulolo, Faigiziduhu. 2016)
2.2.3 Asumsi Dasar Masalah Transportasi
Model transportasi pada dasarnya merupakan sebuah program linier yang dapat dipecahkan oleh metode simpleks yang biasa. Tetapi strukturnya yang khusus memungkinkan pengembangan sebuah prosedur pemecahan, yang disebut teknik transportasi yang lebih efisien dalam hal perhitungan.
Asumsi dasar dari model ini adalah bahwa biaya transportasi di sebuah rute tertentu adalah proposional secara langsung dengan jumlah unit yang dikirimkan. Defenisi unit transportasi akan bervariasi bergantung pada jenis barang yang di kirimkan.
Model umum suatu persoalan transportasi dilandasi pada asumsi-asumsi berikut:
1. Bahwa suatu produk yang ingin diangkat tersedia dalam jumlah yang tetap dan diketahui.
2. Bahwa produk tersebut akan dikirim melalui jaringan transpotasi yang ada dengan memakai cara pengakutan tertentu dari pusat-pusat permintaan.
3. Bahwa jumlah permintaan di pusat permintaan pun diketahui dalam jumlah tertentu dan tetap.
4. Bahwa ongkos angkutan per-unit produk yang diangkut pun diketahui, sehingga tujuan kita untuk meminimumkan biaya total angkutan dapat tercapai.
Karena hanya ada satu jenis komoditas, pada dasarnya setiap daerah tujuan dapat menerima komoditas dari sembarang daerah sumber.
14
2.2.4 Model Transportasi
Model transportasi adalah kelompok khusus program linear yang menyelesaikan masalah pengiriman komoditas dari sumber (misalnya pabrik) ke tujuan (misalnya gudang). Tujuannya adalah untuk menentukan jadwal pengiriman dengan meminimalkan total biaya pengiriman dengan memenuhi batas pasokan dan kebutuhan. Aplikasi transportasi dapat dikembangkan didaerah operasi yang lain, misalnya inventory control, penjadwalan pekerja (employment scheduling), dan penilaian personal (personnel assignment).
Dilihat dari model matematika persolan program linier terdapat tipe/ ciri/
karakteristik khusus pada permasalahan transportasi, yaitu:
1). Semua fungsi kendala bertanda „=‟
2). Semua nilai aij bernilai 1 atau 0.
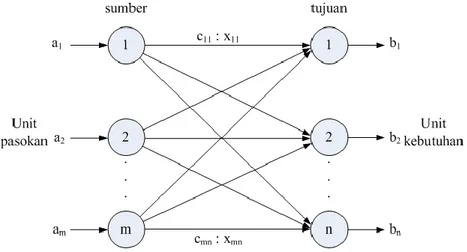
Gambar 2.1 Masalah Umum Model Transportasi
Masalah umum direpresentasikan oleh gambar 2.1. Ada m sumber dan n tujuan setiap sumber atau tujuan direpresentasikan dengan sebuah node. Panah menyatakan rute yang menghubungkan sumber dan tujuan. Panah (m,n) yang menggabungkan sumber m ke tujuan n membawa dua informasi : biaya transportasi per unit, cmn, dan jumlah yang dikirim, xmn. Jumlah pasokan pada sumber adalah am dan jumlah kebutuhan tujuan di n adalah bn. Tujuan model menentukan xmn yang tidak diketahui yang akan meminimalkan total biaya transportasi yang memnuhi batas pasokan dan kebutuhan.
Bentuk umum model transportasi linier adalah sebagai berikut:
nj
ij ij m
i
x c Z
1 1
Dengan batasan,
n
j
i
ij
a
x
1
,
i1,2,...,m
m i
j
ij b
x
1
, j 1,2,...,n
0
x
ij untuk semua i danj
Pemodelan masalah transportasi linier dapat dilihat sebagai berikut, Tabel 2.1 Gambaran Umum Masalah Transportasi
Destination (D i)
Supply ) (a i
Source ) (Si
D1 D2 ... Dn
S 1 11
c c 12 ... c1n
a 1
x 11 x 12 ... x1n
S 2 c 21 c 22 ….. c2n
a 2
x 21 x 22 ….. x2n
. . .
... ... ... ... .
. . .
. .
. . .
. . .
. . .
S m m1
c cm2 ... cmn
a m 1
x m xm2 ... xmn
Demand )
(bj b 1 b 2 ... b n
Keterangan :
S : Source (sumber) sejumlah i, i i 1,2,3,...,m
Dj: Destination (tujuan) sejumlah j , j1,2,3,...,n
16
a : Jumlah penawaran pada sumber i, i i 1,2,3,...,m
bj : Jumlah permintaan pada tujuan j, j 1,2,3,...,n
ij :
c Biaya transportasi dari sumber i ke tujuan j , i 1,2,3,...,m
dan
nj 1,2,3,...,
ij
:
x
Jumlah barang yang diangkut dari sumber i ke tujuan j, i 1,2,3,...,mdan
j1,2,3,...,n2.2.5 Keseimbangan Transportasi
Suatu model transportasi dikatakan seimbang apabila total supply (sumber) sama dengan total demand (tujuan). Dengan kata lain :
nj j m
i
i b
a
Dalam persoalan sebenarnya, batasan ini tidak terlalu terpenuhi atau dengan kata lain, jumlah supply yang tersedia mungkin lebih besar atau lebih kecil daripada jumlah yang diminta. Jika hal ini terjadi, maka model persoalannya disebut sebagai model yang tidak seimbang (unbalanced). Dengan kata lain :
nj j m
i
i b
a atau
nj j m
i
i b
a
Suatu model transportasi dikatakan seimbang apabila total supply (sumber) sama dengan total demand (tujuan). Dengan kata lain ,
iai
jbj . Dalam persoalan sebenarnya, batasan ini tidak terlalu terpenuhi, atau dengan kata lain, jumlah supply yang tersedia mungkin lebih besar atau lebih kecil daripada jumlah yang diminta. Jika hal ini terjadi, maka model persoalannya disebut sebagai model yang tidak seimbang (unbalanced). Batasan di atas dikemukankan hanya karena ia menjadi dasar dalam pengembangan teknik transportasi. Namun, setiap persoalan transportasi dapat dibuat seimbang dengan cara memasukkan variabel artifisial (semu). Jika jumlah demand melebihi jumlah supply, maka dibuat suatu sumberdummy yang akan men-supply kekurangan tersebut, yaitu sebanyak
i i j
jb
a
.Sebaliknya, jika jumlah supply melebihi jumlah demand, maka dibuat suatu tujuan dummy untuk menyerap kelebihan tersebut, yaitu sebanyak
iai jbj . Ongkos transportasi per unit (Cij) dari sumber dummy ke seluruh tujuan adalah nol. Hal ini dapat dipahami karena pada kenyataannya dari sumber dummy tidak terjadi pengiriman. Begitu pula dengan ongkos transportasi per unit (Cij) dari semua sumber ke tujuan dummy adalah nol.2.3 Himpunan Fuzzy
Fuzzy berarti “kabur” atau “samar-samar”. Himpunan fuzzy adalah himpunan yang keanggotaannya memiliki nilai kekaburan/kesamaran antara salah dan benar.
Konsep tentang himpunan fuzzy pertama kali diperkenalkan oleh Profesor Lotfi A.
Zadeh, seorang ilmuwan Amerika Serikat berkebangsaan Iran, dari Universitas California di Barkeley, melalui tulisannya “Fuzzy Sets” pada tahun 1965.
2.3.1 Pengertian Himpunan Fuzzy
Sebelum teori tentang himpunan fuzzy muncul, dikenal sebuah himpunan klasik yang seringkali disebut himpunan tegas (crisp set) yang keanggotaannya memiliki nilai salah atau benar secara tegas. Sebaliknya, anggota himpunan fuzzy memiliki nilai kekaburan antara salah dan benar. Himpunan tegas hanya mengenal dingin atau panas, sedangkan himpunan fuzzy dapat mengenal dingin, sejuk, hangat, dan panas. Perbedaan antara dua jenis himpunan tersebut adalah himpunan tegas hanya memiliki dua kemungkinan nilai keanggotaan, yaitu 0 atau 1. Artinya, untuk sebarang himpunan tegas 𝐴, jika sebuah unsur 𝑥 adalah bukan anggota himpunan 𝐴, maka nilai yang berhubungan dengan 𝑥 adalah 0. Dan jika unsur 𝑥 tersebut merupakan anggota himpunan 𝐴, nilai yang berhubungan dengan 𝑥 adalah 1.
18
Sedangkan dalam himpunan fuzzy, keanggotaan suatu unsur dinyatakan dengan derajat keanggotaan (membership values), yang nilainya terletak dalam interval [0,1] dan ditentukan dengan fungsi keanggotaan A:X [0,1]. Artinya, untuk sebarang himpunan fuzzy 𝐴, sebuah unsur x adalah bukan anggota himpunan 𝐴 jika A(x)0, unsur x adalah anggota penuh himpunan 𝐴 jika
1 ) (x
A , dan unsur xtersebut adalah anggota himpunan 𝐴 dengan derajat keanggotaan sebesar jika A(x), dengan 0 1.
Dengan demikian dapat dipeoleh suatu definisi untuk himpunan fuzzy, yakni:
Definisi :
Himpunan fuzzy dalam suatu himpunan sebarang 𝑋 adalah himpunan yang anggota-anggotanya dinyatakan dengan derajat keanggotaan, yang nilainya terletak dalam interval [0,1] dan ditentukan dengan fungsi keanggotaan
] 1 , 0 [ :X
A .
Domain himpunan fuzzy adalah keseluruhan nilai yang diijinkan dalam semesta pembicaraan dan boleh dioperasikan dalam suatu himpunan fuzzy. Seperti halnya semesta pembicaraan, domain merupakan himpunan bilangan real yang senantiasa naik (bertambah) secara monoton dari kirike kanan. Nilai domain dapat berupa bilangan positif maupun negatif.
Contoh domain himpunan fuzzy:
Muda = [0 45]
Parobaya = [35 55]
Tua = [45 +∞)
(Kusumadewi dan Purnomo, 2010).
Semesta pembicaraan adalah keseluruhan nilai yang diperbolehkan untuk dioperasikan dalam suatu variabel fuzzy. Semesta pembicaraan merupakan himpunan bilangan real yang senantiasa naik (bertambah) secara monoton dari kiri ke kanan. Nilai semesta pembicaraan dapat berupa bilangan positif maupun negatif. Adakalanya nilai semesta pembicaraan ini tidak dibatasi batas atasnya.
Contoh:
Semesta pembicaraan untuk variabel umur: [0 +∞) Semesta pembicaraan untuk variabel temperatur: [0 40]
(Kusumadewi dan Purnomo, 2010).
Himpunan fuzzy memiliki dua atribut, yaitu:
1. Linguistik, yaitu penamaan suatu grup yang mewakili suatu keadaan atau kondisi tertentu dengan menggunakan bahasa alami, seperti: Muda, Parobaya, Tua.
2. Numeris, yaitu suatu nilai (angka) yang menunjukkan ukuran dari suatu variabel seperti: 40, 25, 50, dan sebagainya
(Kusumadewi dan Purnomo, 2010)
2.3.2 Fungsi Keanggotaan
Setiap himpunan fuzzy dapat dinyatakan dengan suatu fungsi keanggotaan. Ada beberapa cara untuk menyatakan himpunan fuzzy dengan fungsi keanggotaannya.
Untuk semesta hingga diskrit biasanya dipakai cara daftar, yaitu daftar anggota dengan derajat keanggotaannya yang dibentuk sebagai himpunan pasangan berurutan
)}
, ( , ), , ( ), ,
{(x1 Ax1 x2 2x2 xn Axn
A
Contoh :
Misal 𝐴 adalah himpunan fuzzy “bilangan real yang dekat dengan 2”. Himpunan fuzzy 𝐴 dapat disajikan dengan menggunakan fungsi keanggotaan sebagai berikut:
lainnya x x
untuk untuk untuk x
x
Ax 2 3
2 1
0 3
1
Dengan fungsi keanggotaan ini, diperoleh: A(1)0, A(1.5)0.5, 7
. 0 ) 7 . 1
(
A , A(2)1, A(2.5)0.5, A(2.7)0.3, dan A(3)0. Maka, 𝐴 dapat ditulis sebagai himpunan pasangan berurutan:
1
{(
A , 0), (1.5, 0.5), (1.7, 0.7), (2, 1), (2.5, 0.5), (2.7, 0.3), (3, 0)}
20
Kebanyakan himpunan fuzzy berada dalam semesta himpunan semua bilangan riil Ʀ dengan fungsi keanggotaan yang dinyatakan dalam bentuk suatu formula matematis. Formula matematis fungsi keanggotaan dalam himpunan fuzzy tersebut diantaranya adalah fungsi keanggotaan Linier naik dan turun, fungsi keanggotaan Segitiga (Triangular), fungsi keanggotaan Trapesium (Trapezoidal), fungsi keanggotaan bentuk Bahu, fungsi keanggotaan bentuk S, fungsi keanggotaan bentuk Lonceng (Bell Curve).
2.3.2.1 Fungsi Keanggotaan Linier
Ada 2 keadaan himpunan fuzzy yang linier, yaitu : Linear naik dan Linear turun a. Representasi Linier Naik
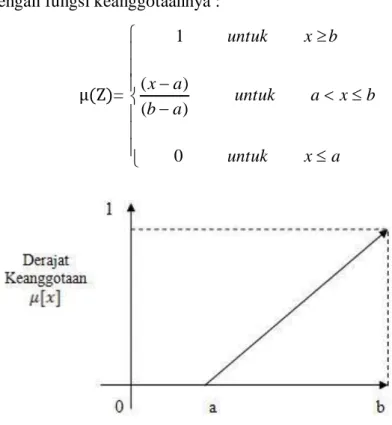
Definisi :
Kenaikan himpunan dimulai pada nilai domain yang memiliki derajat keanggotaan nol [0] bergerak ke kanan menuju ke nilai domain yang memiliki derajat keanggotaan lebih tinggi.
Dengan fungsi keanggotaannya :
µ(Z)=
a x untuk
b x a untuk a
b a x
b x untuk
0 ) (
) (
1
Gambar 2.2 Fungsi Keanggotaan Linier Naik
b. Representasi Linier Turun Definisi :
Garis lurus dimulai dari nilai domain dengan derajat keanggotaan tertinggi pada sisi kiri, kemudian bergerak menurun ke nilai domain yang memiliki derajat keanggotaan lebih rendah
Dengan fungsi keanggotaannya :
µ(Z)=
b x untuk
b x a untuk a
b x b
a c untuk
0 ) (
) (
1
Gambar 2.3 Fungsi Keanggotaan Linier Turun
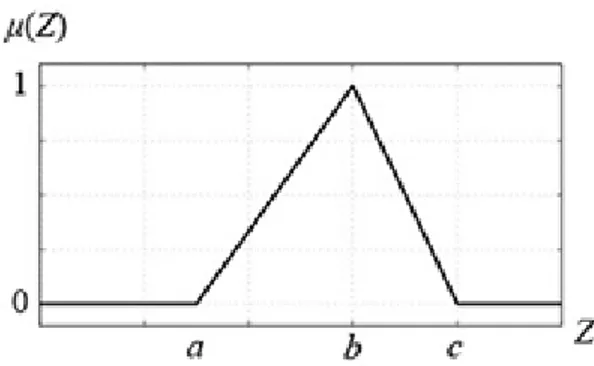
2.3.2.2 Fungsi Keanggotaan Segitiga (Triangular) Definisi :
Suatu fungsi keanggotaan himpunan fuzzy disebut fungsi keanggotaan segitiga jika mempunyai tiga buah parameter, yaitu 𝑎, 𝑏, 𝑐 ∈ ℝ , dengan aturan:
µ(Z)=
lainnya untuk
c Z b untuk b
c Z c
b Z a untuk a
b a Z
0
22
Gambar 2.4 Fungsi Keanggotaan Triangular
2.3.2.3 Fungsi Keanggotaan Trapesium (Trapezoidal) Definisi :
Suatu fungsi keanggotaan himpunan fuzzy disebut fungsi keanggotaan trapesium jika mempunyai empat buah parameter, yaitu 𝑎, 𝑏, 𝑐, 𝑑 ∈ ℝ , dengan aturan:
µ(Z)=
lainnya untuk
d Z c untuk
c d
Z d
c Z b untuk
b Z a untuk
a b
a Z
0 1
Gambar 2.5 Fungsi Keanggotaan Trapezoidal
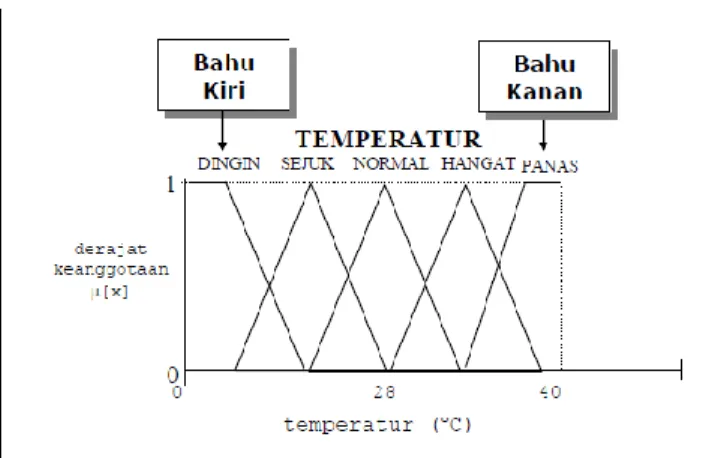
2.3.2.4 Fungsi Keanggotaan Bentuk Bahu Definisi :
Daerah yang terletak di tengah-tengah suatu variabel yang direpresentasikan dalam bentuk segitiga, pada sisi kanan dan kirinya akan naik dan turun (misalkan:
Dingin bergerak ke sejuk bergerak ke hangat dan bergerak ke panas). Tetapi terkadang salah satu sisi dari variabel tersebut tidak mengalami perubahan.
Sebagai contoh, apabila telah mencapai kondisi panas, kenaikan temperatur akan tetap berada pada kondisi panas. Himpunan fuzzy „bahu‟, bukan segitiga, digunakan untuk mengakhiri variabel suatu daerah fuzzy. Bahu kiri bergerak dari benar ke salah, demikian juga bahu kanan bergerak dari salah ke benar.
Gambar 2.6 Fungsi Keanggotaan Bentuk Bahu
2.3.2.5 Fungsi Keanggotaan Bentuk S (Sigmoid) Definisi :
Kurva Pertumbuhan dan Penyusutan merupakan kurva-S atau sigmoid yang berhubungan dengan kenaikan dan penurunan permukaan secara tak linear.
Kurva-S untuk Pertumbuhan akan bergerak dari sisi paling kiri (nilai keanggotaan = 0) ke sisi paling kanan (nilai keanggotaan = 1). Fungsi keanggotaannya akan tertumpu pada 50% nilai keanggotaannya yang sering disebut dengan titik infleksi
Gambar 2.7 Fungsi Keanggotaan Bentuk S (Pertumbuhan)
24
Kurva-S untuk Penyusutan akan bergerak dari sisi paling kanan (nilai keanggotaan = 1) ke sisi paling kiri (nilai keanggotaan = 0) seperti telihat pada gambar di bawah ini:
Gambar 2.8 Fungsi Keanggotaan Bentuk S (Penyusutan)
2.3.2.6 Fungsi Keanggotaan Bentuk Lonceng (Bell Curve) Definisi :
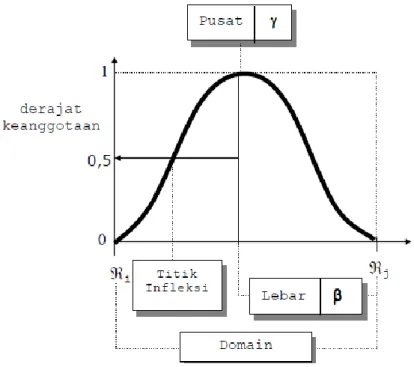
Untuk merepresentasikan bilangan fuzzy, biasanya digunakan kurva berbentuk lonceng. Kurva berbentuk lonceng ini terbagi atas 3 kelas, yaitu: himpunan fuzzy PI, beta, dan Gauss. Perbedaan ketiga kurva ini terletak pada gradiennya.
a. Kurva PI
Kurva PI berbentuk lonceng dengan derajat keanggotaan 1 terletak pada pusat dengan domain (γ), dan lebar kurva (β). Nilai kurva untuk suatu nilai domain x diberikan sebagai:
Dengan fungsi keanggotaannya :
x x
S
x x
S x
2, ,
; 1
2, ,
; )
, , (
Gambar 2.9 Fungsi Keanggotaan Bentuk Lonceng (PI)
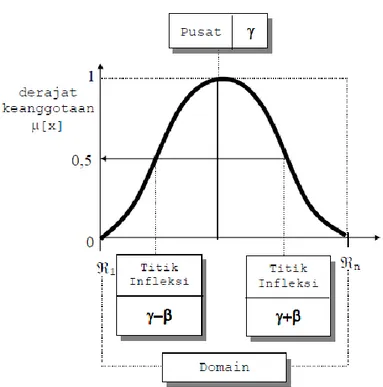
b. Kurva Beta
Seperti halnya kurva PI, kurva BETA juga berbentuk lonceng namun lebih rapat. Kurva ini juga didefinisikan dengan 2 parameter, yaitu nilai pada domain yang menunjukkan pusat kurva (γ), dan setengah lebar kurva (β) . Nilai kurva untuk suatu nilai domain x, diberikan sebagai:
Dengan fungsi keanggotaanya :
x
x B
1 ) 1 ,
; (
26
Gambar 2.10 Fungsi Keanggotaan Bentuk Lonceng (Beta)
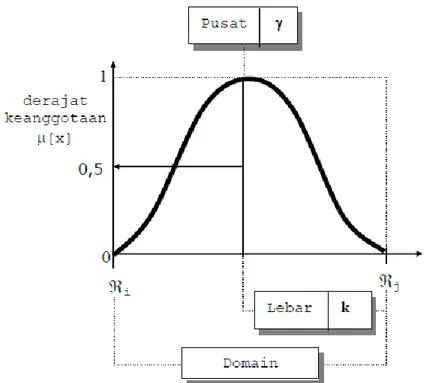
c. Kurva Gauss
Jika kurva PI dan kurva BETA menggunakan 2 parameter yaitu (γ) dan (β), kurva GAUSS juga menggunakan (γ) untuk menunjukkan nilai domain pada pusat kurva, dan (k) yang menunjukkan lebar kurva. Nilai kurva untuk suatu nilai domain x diberikan sebagai:
Dengan fungsi keanggotaanya :
)2
) (
,
;
(x k e k x
G
Gambar 2.11 Fungsi Keanggotaan Bentuk Lonceng (Gauss)
Ada beberapa jenis fungsi keanggotaan fuzzy, tetapi pada penelitian ini hanya digunakan 2 jenis keanggotaan fuzzy yaitu fungsi keanggotaan triangular dan trapezoidal.
2.4 Masalah Transportasi dengan Variabel Fuzzy
Untuk menyelesaikan masalah transportasi fuzzy, maka harus dimodelkan dulu ke dalam suatu tabel, adapun fungsi tujuan dari masalah transportasi fuzzy adalah meminimumkan
m
i n
j
ij ijX C Z
1 1
~
~
~
Dengan,
n j
i
ij a
x
1
~
~ i = 1,…,m
m i
j
ij b
x
1
~ ~ j = 1,…,n
~xij 0 i = 1,…,m , j= 1,…,n (Pandian, 2010 : 1826)
28
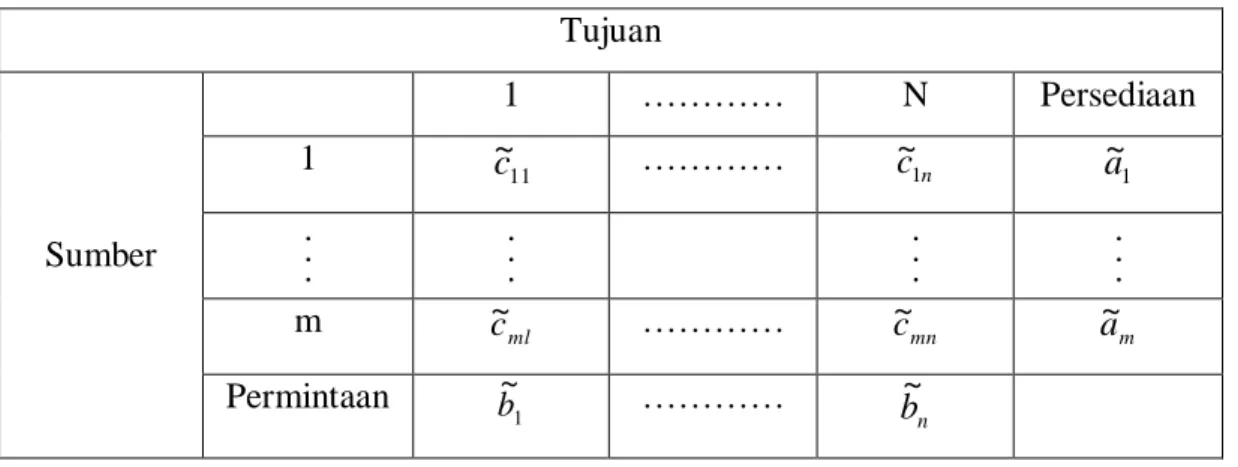
Tabel untuk masalah transportasi fuzzy, dapat diihat di bawah ini
Tabel 2.2 Masalah Transportasi Fuzzy Tujuan
Sumber
1 ………… N Persediaan
1 ~c 11 ………… c~ 1n ~a 1
. . .
. . .
. . .
. . .
m c~ ml ………… c~ mn a~ m
Permintaan
1
b~ …………
b~n
Keterangan :
m = jumlah dari titik persediaan n = jumlah dari titik permintaan
xij
~ = jumlah tidak pasti dari unit barang yang dikirimkan dari titik persediaan i ke titik permintaan j. i1,2,...,m
j 1,2,...,n
c~ij= biaya tidak pasti per unnit barang yang didistribusikan dari titik i persediaan ke titik permintaan j. i1,2,...,m
n j 1,2,...,
a~ = persediaan tidak pasti pada titik persediaan ke i i i1,2,...,m b~j
= permintaan tidak pasti pada permintaan ke j j1,2,...,n
Definisi 1:
Misalkan ~ ( , , ) c b a
A dan ~ ( , , ) f e d
B adalah dua bilangan fuzzy triangular.
Maka,
1. ~ ~ ( , , ) ( , , ) ( , , )
f c e b d a f e d c b a B
A
2. A~ ΘB~
= (a,b,c)Θ(d,e, f) = (ad,be,c f) (H. Basirzadeh, 2011 : 1559)
Definisi 2:
Misalkan ~ ( , , , ) d c b a
A dan ~ ( , , , ) h g f e
B adalah dua bilangan fuzzy trapezoidal. Maka,
1. ~ ~ ( , , , ) ( , , , ) ( , , , )
h d g c f b e a h g f e d c b a B
A
2. A~ ΘB~
= (a,b,c,d)Θ(e,f,g,h) = (ah,bg,c f,d e) (H. Basirzadeh, 2011 : 1559)
Definisi 3:
Suatu himpunan dari alokasi x~ij yang memenuhi baris dan kolom ekuivalen merupakan solusi feasible fuzzy. (Mohanaselvi, 2012 : 371)
Definisi 4:
Suatu solusi feasible fuzzy untuk masalah transportasi fuzzy dengan m sebagai sumber dan n sebagai tujuan dikatakan solusi feasible dasar fuzzy jika jumlah alokasinya(mn1). Jika jumlah alokasi pada solusi dasar fuzzy kurang dari
) 1
(mn , ini disebut sebagai solusi feasible dasar fuzzy yang merosot.
(Mohanaselvi, 2012 : 371)
Definisi 5:
Suatu solusi feasible fuzzy dikatakan solusi fuzzy yang optimal jika total biaya transportasi fuzzy minimum. (Mohanaselvi, 2012 : 371)
2.5 Metode untuk Menyelesaikan Masalah Transportasi Fuzzy
Menurut Rendy (2011), terdapat beberapa tahapan yang harus dilakukan untuk menyelesaikan permasalahan transportasi, yaitu:
1. Menentukan solusi fisibel basis awal.
2. Menentukan entering variable dari variabel-variabel nonbasis. Bila semua variabel sudah memenuhi kondisi optimum, STOP. Bila belum, lanjutkan ke langkah 3.
30
3. Tentukan leaving variabel di antara variabel-variabel basis yang ada, kemudian hitung solusi yang baru. Kembali ke langkah 2.
Ada beberapa metode yang digunakan untuk menentukan solusi layak awal yaitu :
A. Metode North-West Corner
Menurut Ramdhani (2011), dalam permasalahan model transportasi pada Program Linier, ada banyak cara yang dapat digunakan untuk menemukan solusi, salah satunya dengan metode Northwest Corner. Metode ini merupakan metode untuk menentukan solusi awal yang pengalokasiannya berawal dari pojok kiri atas (Barat Laut/North West) hingga ke pojok kanan bawah (Tenggara/South East).
Selanjutnya, pengalokasian dilakukan pada kotak X[i, j1] bila permintaan di kolom j telah terpenuhi dan pada kotak X[i1, j] bila permintaan di baris i telah terpenuhi.
Metode ini adalah yang paling sederhana di antara tiga metode yang telah disebutkan untuk mencari solusi awal. Langkah-langkahnya diringkas seperti berikut (Mulyono, 1999:117):
1) Mulai pada pojok barat laut tabel dan alokasikan sebanyak mungkin pada X tanpa menyimpang dari kendala penawaran atau permintaan (artinya 11
X ditetapkan sama dengan yang terkecil di antara nilai 11 S dan 1 D ). 1 2) Ini akan menghabiskan penawaran pada sumber 1 dan atau permintaan
pada tujuan 1. Akibatnya, tidak ada lagi barang yang dapat dialokasikan ke kolom atau baris yang telah dihabiskan dan kemudian baris atau kolom itu dihilangkan . kemudian alokasikan sebanyak mungkin ke kotak di dekatnya pada baris atau kolom yang tidak dihilangkan. Jika baik kolom maupun baris telah dihabiskan , pindahlah ke kotak berikutnya.
3) Lanjutkan dengan cara yang sama sampai semua penawaran telah dihabiskan dan keperluan permintaan telah dipenuhi.