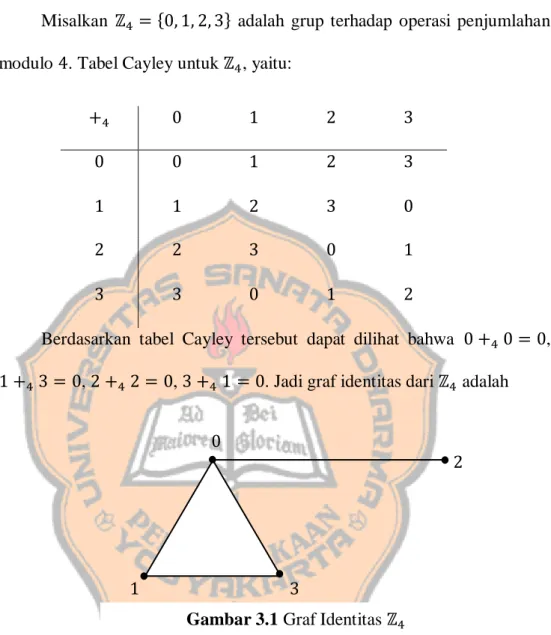
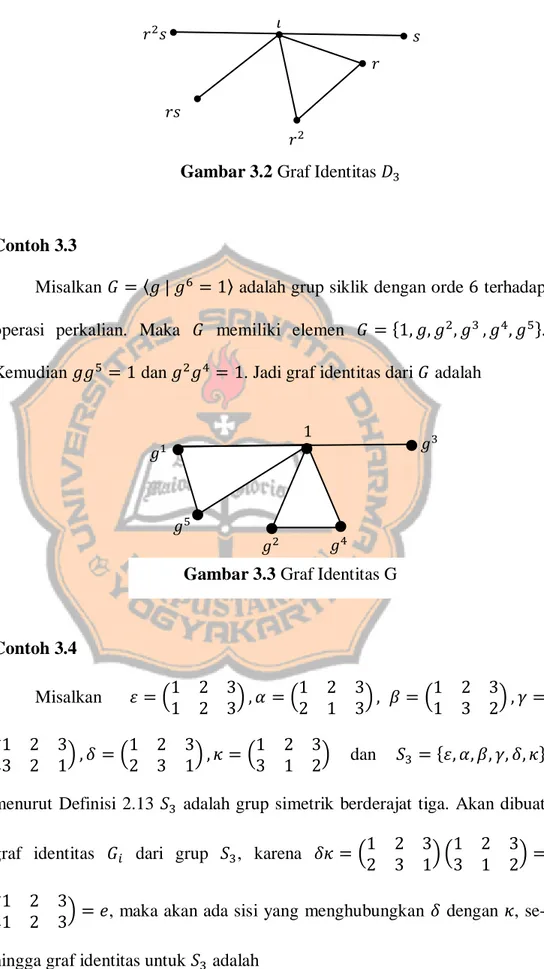
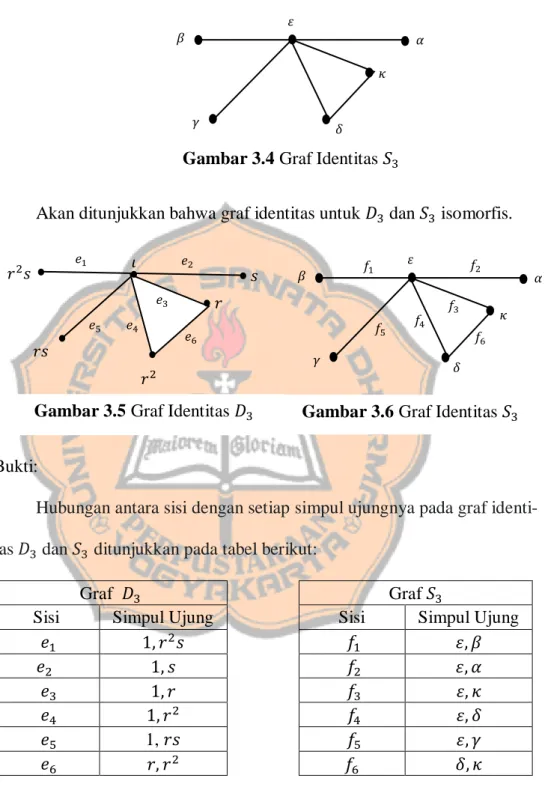
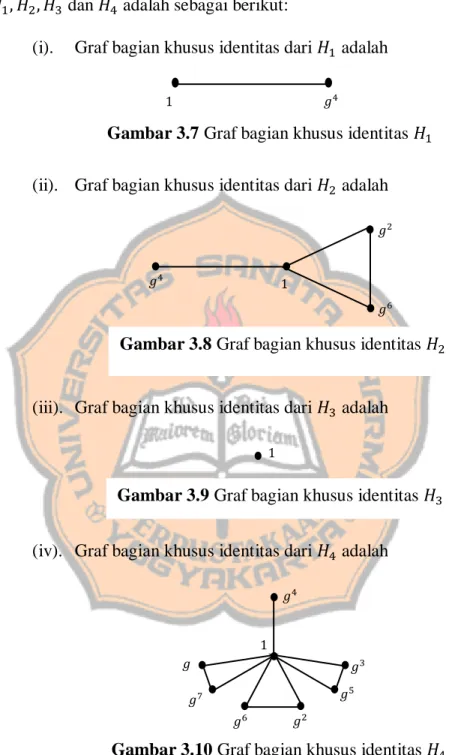
GRAF IDENTITAS DARI GRUP BERHINGGA
Skripsi
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Matematika
Program Studi Matematika
Oleh:
Priscila Septinina Henryanti 163114023
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA YOGYAKARTA
IDENTITY GRAPH OF FINITE GROUP
Paper
Presented as a Partial Fulfillment of the Requirements to Obtain the Degree of Sarjana Matematika
Mathematics Study Program
Written by:
Priscila Septinina Henryanti 163114023
MATHEMATICS STUDY PROGRAM DEPARTMENT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY
SANATA DHARMA UNIVERSITY YOGYAKARTA
vi MOTTO
NIKMATI PROSESNYA KARENA SETIAP ORANG MEMILIKI JALAN HIDUPNYA MASING-MASING.
vii
HALAMAN PERSEMBAHAN
Skripsi ini saya persembahkan sebagai ucapan syukur dan cinta kepada:
1. Tuhan Yesus Kristus dan Bunda Maria yang selalu memberkati penulis. 2. Mama dan Papa tersayang yang selalu memberikan dukungan secara moril
dan materi.
3. Dosen Fakultas Sains dan Teknologi yang telah memberikan ilmu kepada penulis.
ix ABSTRAK
Teori graf merupakan suatu bagian dari ilmu matematika yang bermanfaat dan dapat diaplikasikan ke berbagai disiplin ilmu. Selain itu, teori graf juga dapat diterapkan ke berbagai bidang dalam matematika, salah satunya adalah Teori Grup. Graf identitas 𝐺𝑖 dari suatu grup berhingga (𝐺,∗) adalah graf dengan simpul-simpulnya adalah elemen dari grup berhingga tersebut, setiap elemen bukan identitas bertetangga dengan elemen identitas, dan dua buah simpul 𝑎, 𝑏 yang berbeda bertetangga jika 𝑎 ∗ 𝑏 = 𝑒, dimana 𝑒 adalah elemen identitas dari grup 𝐺 itu. Dalam tulisan ini akan dibahas tentang sifat graf identitas dari beberapa grup berhingga, pewarnaan graf identitas dari grup berhingga, dan sifat grup yang baik dan buruk secara grafis.
x ABSTRACT
Graph theory is a part of mathematics which is useful and can be applied to various disciplines. Besides, graph theory can also be applied to various fields in mathematics, one of which is Group Theory. The identity graph 𝐺𝑖 of a finite group (𝐺,∗) is a graph whose vertices are elements of the finite group, each non-identity element is adjacent to the identity element, and two different vertices 𝑎, 𝑏 are adjacent if 𝑎 ∗ 𝑏 = 𝑒, where 𝑒 is the identity element of the group 𝐺. In this paper, we will discuss the properties of the identity graphs of finite groups, the colouring of identity graphs of finite groups, and the characteristics of good and bad groups graphically.
xiii
DAFTAR ISI
JUDUL... i
HALAMAN JUDUL DALAM BAHASA INGGRIS... ii
HALAMAN PERSETUJUAN PEMBIMBING... iii
HALAMAN PENGESAHAN... iv
PERNYATAAN KEASLIAN KARYA... v
MOTTO... vi
HALAMAN PERSEMBAHAN... vii
LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI... viii
ABSTRAK... ix
ABSTRACT... x
KATA PENGANTAR... xi
DAFTAR ISI... xiii
BAB I PENDAHULUAN... 1 A. Latar Belakang... 1 B. Perumusan Masalah... 3 C. BatasanMasalah... 3 D. Tujuan Penulisan... 3 E. Manfaat Penulisan... 3 F. Metode Penulisan... 3 G. Sistematika Penulisan... 4 BAB II……….. 5
A. RELASI DAN FUNGSI……….... 5
1. RELASI……… 5 2. FUNGSI……… 7 B. TEORI GRUP………...…... 14 1. GRUP………... 14 2. GRUP BAGIAN………..………. 29 3. GRUP SIKLIK………...………...……... 33
xiv
4. GRUP SIMETRIK………..………. 36
5. GRUP DIHEDRAL………..……..…...………….. 47
6. KOSET………..……….. 50
7. GRUP BAGIAN NORMAL………..………. 58
8. GRUP FAKTOR……….. 61
C. TEORI GRAF………...………... 64
1. GRAF………... 64
2. ISOMORFISMA GRAF………..………...…. 67
3. PEWARNAAN SIMPUL GRAF………..…………...…... 69
BAB III GRAF IDENTITAS DARI GRUP BERHINGGA………. 73
BAB IV PENUTUP………...…...…….... 121
A. KESIMPULAN………..…………..121
B. SARAN………..……..122
xv DAFTAR GAMBAR Gambar 2.1………. 45 Gambar 2.2………. 46 Gambar 2.3………. 65 Gambar 2.4………. 67 Gambar 2.5………. 67 Gambar 2.6………. 68 Gambar 2.7………. 71 Gambar 2.8………. 72 Gambar 3.1………. 74 Gambar 3.2………. 75 Gambar 3.3………. 75 Gambar 3.4………. 76 Gambar 3.5………. 76 Gambar 3.6………. 76 Gambar 3.7………. 78 Gambar 3.8………. 78 Gambar 3.9………. 78 Gambar 3.10………...……… 78 Gambar 3.11………...………… 79 Gambar 3.12………...………… 79 Gambar 3.13………...………… 79 Gambar 3.14………...……… 80 Gambar 3.15………...……… 81 Gambar 3.16………...……… 81 Gambar 3.17………...……… 81 Gambar 3.18………...……… 82 Gambar 3.19………...……… 82 Gambar 3.20………...……… 83 Gambar 3.21………...……… 86
xvi Gambar 3.22………...……… 88 Gambar 3.23………...……… 89 Gambar 3.24………...……… 89 Gambar 3.25………...……… 90 Gambar 3.26………...……… 92 Gambar 3.27………...……… 93 Gambar 3.28…...……… 94 Gambar 3.29………...……… 95 Gambar 3.30………...……… 96 Gambar 3.31………...……… 96 Gambar 3.32………...………... 98 Gambar 3.33………...………... 98 Gambar 3.34………...………..………... 100 Gambar 3.35………...101 Gambar 3.36………...101 Gambar 3.37………...101 Gambar 3.38………...104 Gambar 3.39………...104 Gambar 3.40………...105 Gambar 3.41………...106 Gambar 3.42………...107 Gambar 3.43………...108 Gambar 3.44………...110 Gambar 3.45………...110 Gambar 3.46………...112 Gambar 3.45………...112 Gambar 3.48………...115
1 BAB I PENDAHULUAN
A. Latar Belakang
Dalam dunia matematika terdapat berbagai macam cabang, dian-taranya adalah aljabar abstrak dan matematika diskret. Aljabar abstrak dan matematika diskret masing-masing mempelajari hal yang berbeda. Dalam aljabar abstrak dibahas mengenai grup, gelanggang, lapangan, dan sifat-sifatnya. Sedangkan dalam matematika diskret dibahas mengenai himpunan, relasi, graf, kombinatorik, dan lain-lain. Di antara topik-topik tersebut terdapat dua topik yang cukup menarik yaitu grup dan graf.
Ketika membicarakan aljabar abstrak atau struktur aljabar, hal pertama yang akan muncul adalah grup. Teori grup menjadi topik yang sangat penting dalam aljabar abstrak karenanya topik ini seringkali be-rada di bab pertama dalam buku aljabar abstrak. Grup dan sifat-sifatnya juga mendasari topik-topik yang dibahas selanjutnya dalam aljabar abs-trak, seperti gelanggang dan lapangan. Begitu pula dengan penerapan graf dalam grup, grup menjadi komponen yang penting karena akan dibentuk penggambaran dari suatu grup secara nyata.
Misalkan himpunan 𝐺 tidak kosong dan operasi ∗ didefinisikan pada 𝐺. Pasangan (𝐺,∗) disebut grup jika memenuhi:
1. Operasi ∗ bersifat asosiatif pada 𝐺.
2. Himpunan 𝐺 memuat elemen identitas terhadap ∗.
3. Setiap elemen dalam 𝐺 memiliki invers terhadap ∗. (Mil-ler,C.C., 2013: 20)
Graf merupakan pasangan himpunan berhingga (𝑉, 𝐸), ditulis dengan notasi 𝐺(𝑉, 𝐸), yang dalam hal ini 𝑉 adalah himpunan tidak
kosong dari simpul (vertices) dan 𝐸 adalah himpunan tidak kosong dari sisi (edges) yang menghubungkan sepasang simpul.
Sebelumnya telah dikenal istilah graf Cayley dari grup. Gagasan ini mula-mula dikemukakan oleh seorang matematikawan bernama Ar-thur Cayley. Graf Cayley dari grup merupakan gambaran grafis dari suatu grup yang diberikan oleh himpunan pembangkitnya. Tetapi, ter-nyata tidak hanya graf Cayley saja yang dapat memberikan gambaran mengenai sebuah grup. Graf identitas dari suatu grup juga dapat men-jadi solusi lain untuk menggambarkan suatu grup.
Graf identitas dari grup dapat terbentuk karena setiap grup pasti memiliki elemen identitas. Misalkan 𝐺 adalah grup berhingga dan 𝑒 adalah elemen identitas dari 𝐺. Graf identitas dari 𝐺 dengan elemen identitas 𝑒 dapat didefinisikan sebagai berikut:
1. Setiap elemen dari 𝐺 adalah simpul dari graf identitas
2. Untuk setiap 𝑎 di 𝐺, 𝑎 ≠ 𝑒, simpul 𝑎 bertetangga dengan simpul 𝑒 3. Untuk setiap 𝑎 dan 𝑏 di 𝐺, 𝑎 ≠ 𝑏, 𝑎, 𝑏 ≠ 𝑒, simpul 𝑎 bertetangga
dengan simpul 𝑏 jika dan hanya jika 𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎 = 𝑒.
Pewarnaan graf adalah upaya untuk memberikan warna pada se-tiap simpul atau sisi pada graf. Pada graf identitas dari grup berhingga kita juga dapat memberikan warna pada setiap simpulnya. Tetapi ter-dapat perbedaan dalam memberikan warna pada simpul di graf biasa dengan graf identitas dari grup berhingga. Perbedaan ini terletak pada syarat pemberian warna tersebut. Pada graf biasa setiap simpul yang bertetangga diberikan warna yang berbeda, sedangkan pada graf iden-titas dari grup berhingga pewarnaan diberikan untuk setiap elemen grup bagian 𝐻 dari grup 𝐺, di mana setiap elemen pada grup bagian 𝐻 akan diberikan warna yang sama.
Penerapan graf dalam teori grup akan melibatkan dua hal penting yaitu teori grup dan teori graf. Beberapa pokok bahasan teori grup yang berhubungan dengan topik ini antara lain grup bagian, grup modulo,
grup siklik, dan grup dihedral. Sedangkan beberapa pokok bahasan te-ori graf yang berhubungan dengan topik ini adalah graf sederhana dan pewarnaan graf.
B. Rumusan Masalah
Perumusan masalah yang akan dibahas pada tugas akhir ini ada-lah:
1. Bagaimana membentuk graf identitas dari grup berhingga? 2. Bagaimana mewarnai suatu graf identitas dari grup berhingga? 3. Bagaimana kriteria baik atau buruknya grup secara grafis?
C. Batasan Masalah
Batasan masalah pada tugas akhir ini antara lain:
1. Grup yang akan dibahas adalah grup dengan himpunan yang berhingga.
2. Membahas mengenai graf identitas dari grup berhingga.
D. Tujuan Penulisan
Tujuan dari penulisan tugas akhir ini adalah mempelajari tentang pembentukan sebuah graf identitas dari grup berhingga.
E. Metode Penulisan
Metode penulisan yang digunakan dalam tugas akhir ini adalah studi pustaka dari buku-buku dan jurnal yang berkaitan dengan graf dan teori grup yang telah dipublikasikan.
F. Manfaat Penulisan
Manfaat dari penulisan tugas akhir ini adalah:
1. Dapat memahami tentang pembentukan graf identitas dari grup berhingga.
G. Sistematika Penulisan BAB I PENDAHULUAN A. LATAR BELAKANG B. RUMUSAN MASALAH C. BATASAN MASALAH D. TUJUAN PENULISAN E. METODE PENULISAN F. MANFAAT PENULISAN G. SISTEMATIKA PENULISAN BAB II TEORI GRUP DAN TEORI GRAF
A. RELASI DAN FUNGSI 1. RELASI 2. FUNGSI B. TEORI GRUP 1. GRUP 2. GRUP BAGIAN 3. GRUP SIKLIK 4. GRUP SIMETRIK 5. GRUP DIHEDRAL 6. KOSET
7. GRUP BAGIAN NORMAL 8. GRUP FAKTOR
C. TEORI GRAF 1. GRAF
2. ISOMORFISMA GRAF
3. PEWARNAAN SIMPUL GRAF BAB III GRAF IDENTITAS DARI GRUP BAB IV PENUTUP
A. KESIMPULAN B. SARAN
5 BAB II
TEORI GRUP DAN TEORI GRAF
Dalam bab ini akan dijelaskan dasar-dasar teori grup dan teori graf yang digunakan dalam penulisan tugas akhir ini. Dasar-dasar teori grup yang akan diba-has meliputi: grup, grup bagian, grup siklik, grup simetrik, grup dihedral, koset, grup bagian normal, dan grup faktor. Sedangkan pada teori graf akan dibahas dasar-dasar teori yang meliputi: graf, isomorfisma graf, dan pewarnaan simpul graf. A. Relasi dan Fungsi
Definisi 2.1 (Susilo, 2012)
Darab Cartesius dua buah himpunan 𝐴 dan 𝐵, dengan notasi 𝐴 × 𝐵, adalah himpunan semua pasangan terurut (𝑥, 𝑦) dengan 𝑥 ∈ 𝐴 dan 𝑦 ∈ 𝐵, yaitu 𝐴 × 𝐵 = {(𝑥, 𝑦) | 𝑥 ∈ 𝐴 ⋀ 𝑦 ∈ 𝐵}.
1. Relasi
a. Relasi Biner (Susilo, 2012)
Relasi biner 𝑅 antara elemen-elemen dalam himpunan 𝑋 dengan e-lemen-elemen dalam himpunan 𝑌 didefinisikan sebagai himpunan bagian dari darab Cartesius 𝑋 × 𝑌, yaitu
Relasi 𝑅 antara elemen dalam himpunan 𝑋 dengan elemen-elemen dalam himpunan 𝑌 seringkali juga disebut relasi 𝑅 dari himpunan 𝑋 ke himpunan 𝑌. Jika elemen 𝑥 ∈ 𝑋 berelasi 𝑅 dengan elemen 𝑦 ∈ 𝑌, maka hal itu dinyatakan dengan lambang
(𝑥, 𝑦) ∈ 𝑅 atau kadang-kadang dengan lambang
𝑥𝑅𝑦.
Sebaliknya, jika elemen 𝑥 ∈ 𝑋 tidak berelasi 𝑅 dengan elemen 𝑦 ∈ 𝑌, maka hal itu dinyatakan dengan lambang
(𝑥, 𝑦) ∉ 𝑅 atau kadang-kadang dengan lambang
𝑥𝑅𝑦. b. Invers dari Relasi Biner (Susilo, 2012)
Bila 𝑅 adalah relasi biner antara elemen-elemen dalam himpunan 𝑋 dengan elemen-elemen dalam himpunan 𝑌 (relasi dari himpunan 𝑋 ke him-punan 𝑌), maka invers dari relasi 𝑅, dengan notasi 𝑅−1 adalah relasi antara elemen-elemen dalam himpunan 𝑌 dengan elemen-elemen dalam him-punan 𝑋 dengan (𝑦, 𝑥) ∈ 𝑅−1 bila dan hanya bila (𝑥, 𝑦) ∈ 𝑅. Jadi,
2. Fungsi
Definisi 2.2 (Susilo, 2012)
Fungsi (pemetaan) dari himpunan 𝑋 ke himpunan 𝑌 adalah relasi khusus yang memasangkan setiap elemen dalam himpunan 𝑋 dengan tunggal elemen dalam himpunan 𝑌, yang biasa ditulis dengan notasi 𝑓 ∶ 𝑋 → 𝑌.
Himpunan 𝑋 disebut domain dari fungsi 𝑓 dan dilambangkan dengan dom 𝑓, sedangkan himpunan 𝑌 disebut kodomain dari fungsi 𝑓 dan dilambangakan dengan kod 𝑓.
Definisi 2.3 (Susilo, 2012)
Jika 𝑥 ∈ 𝑋, maka elemen 𝑦 ∈ 𝑌 yang berelasi dengan elemen 𝑥 itu disebut dengan bayangan (atau peta) dari 𝑥 oleh fungsi 𝑓, dan dilambangkan dengan 𝑦 = 𝑓(𝑥).
Definisi 2.4 (Susilo, 2012)
Jika 𝑦 ∈ 𝑌, maka elemen 𝑥 ∈ 𝑋 sedemikian sehingga 𝑦 = 𝑓(𝑥) disebut
prabayangan (atau prapeta) dari 𝑦, dan dilambangkan dengan 𝑥 = 𝑓−1(𝑦).
Contoh 2.1
Misalkan 𝑋 = {1, 2, 3, 4} dan 𝑌 = {𝑎, 𝑏, 𝑐, 𝑑, 𝑒}, maka relasi 𝑅 = {(1, 𝑏), (2, 𝑐), (3, 𝑐), (4, 𝑑)}
adalah suatu fungsi dari himpunan 𝑋 ke himpunan 𝑌 sebab setiap elemen dalam 𝑋 berelasi dengan tepat satu elemen dalam 𝑌.
Definisi 2.5 (Susilo, 2012)
Dua buah fungsi 𝑓 ∶ 𝑋 → 𝑌 dan 𝑔 ∶ 𝑋 → 𝑌 dikatakan sama, yaitu 𝑓 = 𝑔, jika dan hanya jika 𝑓(𝑥) = 𝑔(𝑥) untuk setiap 𝑥 ∈ 𝑋.
Definisi 2.6 (Susilo, 2012)
Suatu fungsi 𝑓 ∶ 𝑋 → 𝑌 disebut fungsi injektif jika dan hanya jika untuk setiap 𝑥1, 𝑥2 ∈ 𝑋 berlaku apabila 𝑓(𝑥1) = 𝑓(𝑥2) maka 𝑥1= 𝑥2, yaitu bila dua elemen dalam domain mempunyai bayangan yang sama, maka kedua elemen tersebut adalah elemen yang sama.
Definisi 2.7 (Susilo, 2012)
Suatu fungsi 𝑓 ∶ 𝑋 → 𝑌 disebut fungsi surjektif jika dan hanya jika untuk setiap 𝑦 ∈ 𝑌 terdapat 𝑥 ∈ 𝑋 sedemikian sehingga 𝑦 = 𝑓(𝑥), yaitu setiap ele-men dalam kodomain memiliki prabayangan.
Definisi 2.8 (Susilo, 2012)
Suatu fungsi 𝑓 ∶ 𝑋 → 𝑌 disebut fungsi bijektif jika dan hanya jika fungsi 𝑓 tersebut adalah fungsi yang injektif dan sekaligus surjektif, maka pada suatu fungsi bijektif, setiap elemen dalam domain mempunyai tepat satu bayangan, dan setiap elemen dalam kodomain juga mempunyai tepat satu bayangan.
Contoh 2.2
Fungsi 𝑓 ∶ ℝ → ℝ, di mana ℝ adalah himpunan semua bilangan real, dengan 𝑓(𝑥) = 2𝑥 + 1 untuk setiap 𝑥 ∈ ℝ, adalah fungsi yang injektif dan sur-jektif dan oleh karenanya merupakan fungsi bisur-jektif.
a) Fungsi tersebut adalah fungsi injektif, sebab bila 𝑓(𝑥1) = 𝑓(𝑥2), maka 2𝑥1+ 1 = 2𝑥2+ 1, sehingga 2𝑥1 = 2𝑥2, maka 𝑥1 = 𝑥2. b) Fungsi tersebut adalah fungsi surjektif, sebab untuk setiap elemen
𝑦 ∈ ℝ terdapat 𝑥 =𝑦−1
2 ∈ ℝ, sedemikian sehingga 𝑓(𝑥) = 2𝑥 + 1 = 2 (𝑦−1
2 ) + 1 = 𝑦 − 1 + 1 = 𝑦.
c) Fungsi tersebut adalah fungsi bijektif karena merupakan fungsi yang injektif dan sekaligus surjektif.
Definisi 2.9 (Susilo, 2012)
Suatu fungsi 𝑓 ∶ 𝑋 → 𝑋 disebut fungsi identitas bila untuk setiap 𝑥 ∈ 𝑋 berlaku 𝑓(𝑥) = 𝑥.
Definisi 2.10 (Susilo, 2012)
Jika 𝑓 ∶ 𝑋 → 𝑌 adalah suatu fungsi, maka invers dari fungsi 𝑓, yaitu 𝑓−1, adalah suatu relasi dari himpunan 𝑌 ke himpunan 𝑋 dengan aturan:
(𝑦, 𝑥) ∈ 𝑓−1 jika dan hanya jika 𝑦 = 𝑓(𝑥) ≡ (𝑥, 𝑦) ∈ 𝑓
untuk setiap 𝑦 ∈ 𝑌 dan 𝑥 ∈ 𝑋. Jelas bahwa relasi 𝑓−1 itu belum tentu merupa-kan fungsi dari 𝑌 ke 𝑋.
Contoh 2.3
Perhatikan fungsi 𝑓 ∶ 𝑋 → 𝑌 pada Contoh 2.1 invers dari fungsi 𝑓 terse-but adalah relasi 𝑓−1 dari himpunan 𝑌 ke himpunan 𝑋, yaitu:
𝑓−1 = {(𝑏, 1), (𝑐, 2), (𝑐, 3), (𝑑, 4)}
yang bukan merupakan fungsi, sebab ada elemen dalam 𝑌, yaitu 𝑎 dan 𝑒, yang tidak berelasi dengan elemen manapun dalam 𝑋, serta ada elemen dalam 𝑌, yaitu 𝑐, yang berelasi dengan lebih dari satu elemen dalam 𝑋.
Teorema 2.1
Jika 𝑓 ∶ 𝑋 → 𝑌 adalah fungsi, maka 𝑓−1 merupakan fungsi jika dan hanya jika 𝑓 adalah suatu fungsi bijektif, dan 𝑓−1 juga merupakan fungsi bi-jektif.
Bukti:
(⇒) Jika 𝑓−1 ∶ 𝑌 → 𝑋 adalah fungsi, maka untuk setiap 𝑦 ∈ 𝑌 ada e-lemen 𝑥 ∈ 𝑋 sedemikian sehingga 𝑥 = 𝑓−1(𝑦), berarti untuk setiap 𝑦 ∈ 𝑌 ada elemen 𝑥 ∈ 𝑋 sedemikian sehingga 𝑦 = 𝑓(𝑥). Jadi 𝑓 adalah fungsi yang sur-jektif. Misal 𝑥1, 𝑥2 ∈ 𝑋, jika 𝑓(𝑥1) = 𝑓(𝑥2) = 𝑦 ∈ 𝑌, maka 𝑥1 = 𝑓−1(𝑦) dan 𝑥2 = 𝑓−1(𝑦). Karena 𝑓−1 adalah fungsi, maka 𝑓−1(𝑦) adalah elemen tunggal dalam 𝑋 sehingga 𝑥1 = 𝑥2. Jadi 𝑓 adalah fungsi yang injektif. Terbukti bahwa 𝑓 ∶ 𝑋 → 𝑌 adalah suatu fungsi bijektif.
(⇐) Selanjutnya, misalkan 𝑓 ∶ 𝑋 → 𝑌 adalah suatu fungsi yang bijektif. Karena 𝑓 surjektif, maka untuk setiap 𝑦 ∈ 𝑌 ada elemen 𝑥 ∈ 𝑋 sedemikian
hingga 𝑦 = 𝑓(𝑥), berarti untuk setiap 𝑦 ∈ 𝑌 ada elemen 𝑥 ∈ 𝑋 sedemikian se-hingga 𝑥 = 𝑓−1(𝑦), yaitu setiap elemen dalam 𝑌 berelasi dengan suatu e-lemen dalam 𝑋 dengan relasi 𝑓−1. Untuk 𝑦
1, 𝑦2 ∈ 𝑌, misalkan 𝑦1 = 𝑓(𝑥1) dan 𝑦2 = 𝑓(𝑥2), sehingga 𝑥1= 𝑓−1(𝑦
1) dan 𝑥2 = 𝑓−1(𝑦2). Jika 𝑦1 = 𝑦2, maka 𝑓(𝑥1) = 𝑓(𝑥2). Karena 𝑓 adalah fungsi yang injektif, maka akibatnya 𝑥1= 𝑥2, sehingga 𝑓−1(𝑦1) = 𝑓−1(𝑦2). Jadi elemen-elemen dalam 𝑌 berelasi dengan e-lemen tunggal dalam 𝑋 dengan relasi 𝑓−1 tersebut. Dengan demikian terbukti bahwa 𝑓−1 ∶ 𝑌 → 𝑋 adalah suatu fungsi. Karena 𝑓 ∶ 𝑋 → 𝑌 adalah fungsi, maka untuk setiap 𝑥 ∈ 𝑋 ada 𝑦 ∈ 𝑌 sedemikian sehingga 𝑦 = 𝑓(𝑥), yaitu 𝑥 = 𝑓−1(𝑦). Jadi 𝑓−1∶ 𝑌 → 𝑋 adalah fungsi surjektif. Untuk 𝑦
1, 𝑦2 ∈ 𝑌, misalkan 𝑓−1(𝑦
1) = 𝑥1 dan 𝑓−1(𝑦2) = 𝑥2. Maka 𝑦1 = 𝑓(𝑥1) dan 𝑦2 = 𝑓(𝑥2). Jika 𝑓−1(𝑦
1) = 𝑓−1(𝑦2), maka 𝑥1= 𝑥2. Karena 𝑓 adalah fungsi, maka haruskah 𝑓(𝑥1) = 𝑓(𝑥2), sehingga 𝑦1 = 𝑦2. Jadi 𝑓−1 ∶ 𝑌 → 𝑋 adalah fungsi injektif. Dengan demikian terbukti bahwa 𝑓−1 tersebut adalah fungsi yang bijektif.■
Definisi 2.11 (Susilo, 2012)
Jika diberikan dua buah fungsi 𝑓 ∶ 𝑋 → 𝑌 dan 𝑔 ∶ 𝑌 → 𝑍, maka
kompo-sisi kedua fungsi tersebut didefinisikan sebagai fungsi 𝑔 ∘ 𝑓 ∶ 𝑋 → 𝑍 dengan aturan (𝑔 ∘ 𝑓)(𝑥) = 𝑔(𝑓(𝑥)) untuk setiap 𝑥 ∈ 𝑋.
Perhatikan bahwa untuk fungsi 𝑓 dan 𝑔 tersebut di atas, 𝑓 ∘ 𝑔 tidak dide-finisikan, kecuali jika 𝑋 = 𝑌 = 𝑍, yaitu jika 𝑓 ∶ 𝑋 → 𝑋 dan 𝑔 ∶ 𝑋 → 𝑋, maka komposisi kedua fungsi tersebut adalah fungsi-fungsi 𝑔 ∘ 𝑓 ∶ 𝑋 → 𝑋 dan 𝑓 ∘ 𝑔 ∶ 𝑋 → 𝑋.
Karena 𝑓 ∶ 𝑋 → 𝑌 adalah fungsi, maka setiap 𝑥 ∈ 𝑋 mempunyai ba-yangan tunggal 𝑓(𝑥) ∈ 𝑌, dan karena 𝑔 ∶ 𝑌 → 𝑍 adalah fungsi, maka 𝑓(𝑥) ∈ 𝑌 mempunyai bayangan tunggal 𝑔(𝑓(𝑥)) ∈ 𝑍. Maka setiap 𝑥 ∈ 𝑋 mempunyai bayangan tunggal (𝑔 ∘ 𝑓)(𝑥) ∈ 𝑍. Jadi 𝑔 ∘ 𝑓 ∶ 𝑋 → 𝑍 adalah fungsi.
Teorema 2.2
(i) Komposisi dua buah fungsi yang injektif adalah fungsi yang injektif. (ii) Komposisi dua buah fungsi yang surjektif adalah fungsi yang
surjek-tif.
(iii)Komposisi dua buah fungsi yang bijektif adalah fungsi yang bijektif. Bukti:
(i) Misalkan 𝑓 ∶ 𝑋 → 𝑌 dan 𝑔 ∶ 𝑌 → 𝑍 adalah dua buah fungsi yang jektif. Akan dibuktikan bahwa 𝑔 ∘ 𝑓 ∶ 𝑋 → 𝑍 adalah fungsi yang in-jektif. Ambil sebarang elemen 𝑥1, 𝑥2 ∈ 𝑋 sedemikian sehingga 𝑔 ∘ 𝑓(𝑥1) = 𝑔 ∘ 𝑓(𝑥2). Berdasarkan definisi komposisi fungsi, maka 𝑔(𝑓(𝑥1)) = 𝑔(𝑓(𝑥2)). Karena 𝑔 adalah fungsi yang injektif, maka 𝑓(𝑥1) = 𝑓(𝑥2). Kemudian karena 𝑓 adalah fungsi yang injektif, maka 𝑥1 = 𝑥2. Terbukti bahwa 𝑔 ∘ 𝑓 adalah fungsi yang injektif. (ii) Misalkan 𝑓 ∶ 𝑋 → 𝑌 dan 𝑔 ∶ 𝑌 → 𝑍 adalah dua buah fungsi yang
jektif. Akan dibuktikan bahwa 𝑔 ∘ 𝑓 ∶ 𝑋 → 𝑍 adalah fungsi yang sur-jektif. Ambil sebarang elemen 𝑧 ∈ 𝑍. Karena 𝑔 adalah fungsi yang surjektif, maka ada elemen 𝑦 ∈ 𝑌 sedemikian sehingga 𝑔(𝑦) = 𝑧. Karena 𝑓 adalah fungsi yang surjektif, maka ada elemen 𝑥 ∈ 𝑋
sedemikian sehingga 𝑓(𝑥) = 𝑦, sehingga (𝑔 ∘ 𝑓)(𝑥) = 𝑔(𝑓(𝑥)) = 𝑔(𝑦) = 𝑧. Jadi ada elemen 𝑥 ∈ 𝑋 sedemikian sehingga (𝑔 ∘ 𝑓)(𝑥) = 𝑧. Terbukti bahwa 𝑔 ∘ 𝑓 ∶ 𝑋 → 𝑍 adalah fungsi yang surjektif. (iii)Misalkan 𝑓 ∶ 𝑋 → 𝑌 dan 𝑔 ∶ 𝑌 → 𝑍 adalah dua buah fungsi yang
bi-jektif. Karena 𝑓 dan 𝑔 adalah fungsi yang injektif, maka 𝑔 ∘ 𝑓 adalah fungsi yang injektif. Karena 𝑓 dan 𝑔 adalah fungsi yang surjektif, maka 𝑔 ∘ 𝑓 adalah fungsi yang surjektif. Jadi 𝑔 ∘ 𝑓 adalah fungsi yang injektif dan surjektif, yaitu 𝑔 ∘ 𝑓 ∶ 𝑋 → 𝑍 adalah fungsi yang bijektif.■
Teorema 2.3
Jika 𝑓 ∶ 𝑋 → 𝑌 adalah suatu fungsi, 𝑖𝑋 ∶ 𝑋 → 𝑋 dan 𝑖𝑌 ∶ 𝑌 → 𝑌 keduanya adalah fungsi identitas, maka 𝑓 ∘ 𝑖𝑋 = 𝑓 dan 𝑖𝑌∘ 𝑓 = 𝑓.
Bukti:
Untuk setiap 𝑥 ∈ 𝑋 berlaku (𝑓 ∘ 𝑖𝑋)(𝑥) = 𝑓(𝑖𝑋(𝑥)) = 𝑓(𝑥), sehingga 𝑓 ∘ 𝑖𝑋 = 𝑓, dan (𝑖𝑌∘ 𝑓)(𝑥) = 𝑖𝑌(𝑓(𝑥)) = 𝑓(𝑥), sehingga 𝑖𝑌∘ 𝑓 = 𝑓.■
Teorema 2.4
Jika 𝑓 ∶ 𝑋 → 𝑌 adalah fungsi yang bijektif, maka 𝑓−1∘ 𝑓 = 𝑖
𝑋 dan 𝑓 ∘ 𝑓−1 = 𝑖
𝑌, yaitu keduanya adalah fungsi identitas. Bukti:
Ambil sebarang elemen 𝑥 ∈ 𝑋. Maka 𝑦 = 𝑓(𝑥) ∈ 𝑌. Karena 𝑓 ∶ 𝑋 → 𝑌 adalah fungsi yang bijektif, maka menurut Teorema 2.1 𝑓−1 ∶ 𝑌 → 𝑋 adalah
juga fungsi yang bijektif, sehingga 𝑓−1(𝑦) = 𝑥. Jadi (𝑓−1∘ 𝑓)(𝑥) = 𝑓−1(𝑓(𝑥)) = 𝑓−1(𝑦) = 𝑥 = 𝑖
𝑋(𝑥). Terbukti bahwa 𝑓−1∘ 𝑓 = 𝑖𝑋.
Ambil sebarang elemen 𝑦 ∈ 𝑌. Karena 𝑓−1 ∶ 𝑌 → 𝑋 adalah fungsi yang bijektif, maka 𝑥 = 𝑓−1(𝑦) ∈ 𝑋 dan 𝑓(𝑥) = 𝑦. Jadi (𝑓 ∘ 𝑓−1)(𝑦) = 𝑓(𝑓−1(𝑦)) = 𝑓(𝑥) = 𝑦 = 𝑖
𝑌(𝑦). Terbukti bahwa 𝑓 ∘ 𝑓−1 = 𝑖𝑌.■
B. Teori Grup 1. Grup
Definisi 2.12 (Miller, 2013)
Misalkan 𝐺 adalah himpunan tak kosong. Operasi pada 𝐺 adalah fungsi 𝑓 ∶ 𝐺 × 𝐺 → 𝐺. Operasi tersebut disebut juga operasi biner.
Definisi operasi tersebut berarti:
i) Untuk setiap pasangan (𝑎, 𝑏) ∈ 𝐴 × 𝐴, 𝑓(𝑎, 𝑏) terdefinisi tunggal. ii) Untuk setiap pasangan (𝑎, 𝑏) ∈ 𝐴 × 𝐴, 𝑓(𝑎, 𝑏) adalah elemen di 𝐴.
Contoh 2.4
Misalkan + dan ∙ adalah operasi biner penjumlahan biasa dan perkalian biasa dalam ℤ, dan misalkan 𝐴 = {𝑛3 ∶ 𝑛 ∈ ℤ+}. Tentukan apakah 𝐴 tertutup terhadap (a) penjumlahan dan (b) perkalian.
Pada bagian (a), perhatikan bahwa 13 = 1 dan 23 = 8 di 𝐴, tetapi 1 + 8 = 9 dan 9 ∉ 𝐴. Jadi 𝐴 tidak tertutup terhadap penjumlahan.
Kemudian untuk bagian (b), misalkan 𝑟 ∈ 𝐴 dan 𝑠 ∈ 𝐴 sedemikian hingga 𝑟 = 𝑛3 dan 𝑠 = 𝑚3, untuk setiap 𝑛, 𝑚 ∈ ℤ+. Akibatnya, 𝑟𝑠 = 𝑛3𝑚3 =
(𝑛𝑚)3. Dengan karakteristik elemen di 𝐴 dan karena 𝑛𝑚 ∈ ℤ+, ini berarti bahwa 𝑟𝑠 ∈ 𝐴, sehingga 𝐴 tertutup terhadap perkalian.
Definisi 2.13 (Miller,2013)
Misalkan himpunan 𝐺 tak kosong dan operasi ∗ didefinisikan pada 𝐺. Pasangan terurut (𝐺,∗) disebut grup jika memenuhi sifat:
(i) Operasi ∗ bersifat asosiatif pada 𝐺; yaitu (𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑎 ∗ (𝑏 ∗ 𝑐) untuk setiap 𝑎, 𝑏, 𝑐 ∈ 𝐺.
(ii) Ada elemen identitas 𝑒 ∈ 𝐺 sedemikian hingga 𝑒 ∗ 𝑎 = 𝑎 ∗ 𝑒 = 𝑎 untuk setiap 𝑎 ∈ 𝐺.
(iii) Setiap elemen 𝑎 ∈ 𝐺 memiliki elemen invers 𝑎−1∈ 𝐺 sedemikian hingga 𝑎−1∗ 𝑎 = 𝑎 ∗ 𝑎−1= 𝑒.
Jika operasi ∗ memenuhi sifat komutatif yaitu jika 𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎 untuk setiap 𝑎, 𝑏 ∈ 𝐺, maka (𝐺,∗) adalah grup Abel.
Contoh 2.5
Diberikan himpunan 𝐺 = {−1,1}. Akan ditunjukan bahwa (𝐺,∙) adalah grup Abel terhadap operasi perkalian biasa.
Operasi ∙ bersifat tertutup terhadap himpunan 𝐺: −1 ∙ −1 = 1 ∈ 𝐺 −1 ∙ 1 = −1 ∈ 𝐺 1 ∙ −1 = −1 ∈ 𝐺
(i) Operasi ∙ bersifat asosiatif pada 𝐺 karena perkalian biasa bersifat asosiatif di ℤ.
(ii) 𝐺 memuat elemen identitas yaitu 𝑒 = 1 untuk operasi ∙.
Untuk −1 ∈ 𝐺, maka −1 ∙ 𝑒 = −1 ∙ 1 = −1 = 1 ∙ (−1) = 𝑒 ∙ (−1). Untuk 1 ∈ 𝐺, maka 1 ∙ 𝑒 = 1 ∙ 1 = 1 = 1 ∙ 1 = 𝑒 ∙ 1.
(iii) Setiap elemen di 𝐺 memiliki invers terhadap operasi ∙.
Misalkan −1 ∈ 𝐺, pilih −1 ∈ 𝐺, sehingga −1 ∙ (−1) = 1 = 𝑒, maka in-vers dari −1 adalah −1.
Misalkan 1 ∈ 𝐺, pilih 1 ∈ 𝐺, sehingga 1 ∙ (1) = 1 = 𝑒, maka invers dari 1 adalah 1.
(iv) Operasi ∙ bersifat komutatif pada 𝐺 karena perkalian biasa bersifat komu-tatif di ℤ.
Jadi (𝐺,∗) merupakan grup Abel.
Definisi 2.14 (Miller, 2013)
Misalkan 𝐺 adalah himpunan berhingga dan (𝐺,∗) merupakan grup ter-hadap operasi ∗. Tabel Cayley dari (𝐺,∗) adalah tabel yang label baris-baris dan kolom-kolomnya bersesuaian dengan elemen-elemen di 𝐺 dan entri dari baris dari elemen 𝑎 dan kolom dari elemen 𝑏 adalah hasil operasi 𝑎 ∗ 𝑏.
Diberikan himpunan 𝐺 = {−1,1} yang merupakan grup terhadap operasi perkalian biasa. Hasil dari operasi perkalian dengan menggunakan Tabel Cay-ley adalah sebagai berikut:
∙ −1 1
−1 1 −1
1 −1 1
Teorema 2.5 (Algoritma pembagian)
Jika 𝑎 dan 𝑏 adalah bilangan-bilangan bulat dan 𝑏 ≠ 0, maka terdapat secara tunggal bilangan bulat 𝑞 dan 𝑟 sedemikian hingga 𝑎 = 𝑞𝑏 + 𝑟 dan 0 ≤ 𝑟 < |𝑏|.
Bilangan bulat 𝑟 disebut sisa dari 𝑎 bila dibagi 𝑏 dan bilangan bulat 𝑞 disebut hasil bagi dari 𝑎 bila dibagi 𝑏.
Bukti:
Akan dibuktikan adanya bilangan bulat 𝑞 dan 𝑟, dengan memperhatikan kasus 𝑎 ≥ 0 dan 𝑎 < 0.
Bila 𝑎 ≥ 0, hasil tersebut akan dibuktikan dengan induksi pada 𝑎. Basis untuk induksi tersebut adalah dengan adanya kasus di mana 0 ≤ 𝑎 < |𝑏|. Se-hingga dapat diambil 𝑞 = 0 dan 𝑟 = 𝑎.
Kemudian misalkan 𝑘 ≥ |𝑏|, dan ada 𝑞 dan 𝑟 untuk semua bilangan bulat positif 𝑎 yang kurang dari 𝑘. Maka 0 ≤ 𝑘 − |𝑏| < 𝑘, dan dapat ditulis 𝑘 − |𝑏| = 𝑞1𝑏 + 𝑟 dengan 0 ≤ 𝑟 < |𝑏|.
Jadi 𝑘 = 𝑞𝑏 + 𝑟 dengan 𝑞 = 𝑞1+ 1, bila 𝑏 > 0, dan 𝑞 = 𝑞1 − 1, bila 𝑏 < 0. Dengan demikian langkah induksi selesai, dan hasil tersebut benar un-tuk 𝑎 ≥ 0.
Bila 𝑎 < 0, maka −𝑎 > 0, dan dapat ditulis−𝑎 = 𝑞2𝑏 + 𝑟2 dengan 0 ≤ 𝑟2 < |𝑏|.
Bila 𝑟2 = 0, maka 𝑎 = (−𝑞2)𝑏. Bila 𝑟2 ≠ 0, maka 𝑎 = 𝑞𝑏 + 𝑟 dengan 0 < 𝑟 = |𝑏| − 𝑟2 < |𝑏|, 𝑞 = −𝑞2− 1, bila 𝑏 > 0, dan 𝑞 = −𝑞2+ 1, bila 𝑏 < 0.
Untuk membuktikan ketunggalan 𝑞 dan 𝑟, misalkan bahwa 𝑎 = 𝑞1𝑏 + 𝑟1 = 𝑞2𝑏 + 𝑟2, dengan 0 ≤ 𝑟2 < 𝑟1 < |𝑏|. Maka (𝑞2− 𝑞1)𝑏 = 𝑟1− 𝑟2. Ruas kanan dari persamaan ini tidak negatif dan kurang dari |𝑏|, sedangkan ruas kirinya adalah kelipatan dari 𝑏. Jadi tiap ruas dari persamaan itu haruslah nol, dengan demikian maka 𝑞1 = 𝑞2 dan 𝑟1 = 𝑟2.■
Definisi 2.15 (Miller,2013)
Diberikan bilangan bulat 𝑛 dengan 𝑛 > 1. Untuk setiap bilangan bulat 𝑎, didefinisikan 𝑎(𝑚𝑜𝑑 𝑛) sebagai sisa tak negatif yang kurang dari 𝑛, jika 𝑎 dibagi 𝑛.
Contoh 2.7
9(𝑚𝑜𝑑 2) = 1 sebab 9 = (4)(2) + 1, dan −13(𝑚𝑜𝑑 6) = 5 sebab −13 = (−3)(6) + 5.
Teorema 2.6
Untuk setiap 𝑛 > 1, (ℤ𝑛, +𝑛) adalah grup Abel, dengan ℤ𝑛 = {0, 1, 2, ⋯ , 𝑛 − 1} dan +𝑛 didefinisikan sebagai operasi penjumlahan modulo 𝑛 yaitu 𝑎+𝑛𝑏 = (𝑎 + 𝑏)(𝑚𝑜𝑑 𝑛).
Bukti:
Untuk membuktikan bahwa ℤ𝑛 adalah grup, haruslah dibuktikan bahwa +𝑛 merupakan operasi pada himpunan ℤ𝑛. Untuk setiap 𝑎, 𝑏 ∈ ℤ𝑛, 𝑎 + 𝑏 terdefinisi tunggal dari penjumlahan biasa di ℤ, dengan demikian (𝑎 + 𝑏)(𝑚𝑜𝑑 𝑛) juga terdefinisi tunggal karena selalu terdapat sisa tak negatif yang kurang dari 𝑛 jika 𝑎 + 𝑏 dibagi 𝑛. Jadi 𝑎+𝑛𝑏 ∈ ℤ𝑛, dengan demikian +𝑛 meru-pakan operasi pada ℤ𝑛.
Bilangan 0 merupakan elemen identitas, 0 juga merupakan invers untuk 0, dan invers untuk elemen tak nol 𝑎 adalah 𝑛 − 𝑎, karena 𝑎+𝑛(𝑛 − 𝑎) = 𝑛(𝑚𝑜𝑑 𝑛) = 0.
Untuk setiap 𝑎, 𝑏, 𝑐 ∈ ℤ𝑛, akan diperlihatkan bahwa 𝑎 +𝑛 (𝑏 +𝑛 𝑐) = (𝑎 +𝑛 𝑏) +𝑛 𝑐. Menurut algoritma pembagian 𝑎 + 𝑏 = 𝑥𝑛 + 𝑦 dengan 0 ≤ 𝑦 ≤ 𝑛 untuk suatu 𝑥, 𝑦 ∈ ℤ. Maka 𝑎 +𝑛 𝑏 = 𝑦. Misalkan 𝑦 + 𝑐 = 𝑠𝑛 + 𝑡 dengan 0 ≤ 𝑡 ≤ 𝑛 untuk setiap 𝑠, 𝑡 ∈ ℤ sehingga 𝑦 +𝑛 𝑐 = 𝑡. Dengan demikian (𝑎 +𝑛 𝑏) +𝑛 𝑐 = 𝑡.
Demikian pula terdapat 𝑢, 𝑣 ∈ ℤ di mana 𝑏 + 𝑐 = 𝑢𝑛 + 𝑣 dengan 0 ≤ 𝑣 ≤ 𝑛, dan 𝑞, 𝑟 ∈ ℤ di mana 𝑎 + 𝑣 = 𝑞𝑛 + 𝑟 dengan 0 ≤ 𝑟 ≤ 𝑛, sehingga 𝑎 +𝑛( 𝑏 +𝑛 𝑐) = 𝑟.
Untuk memperlihatkan bahwa 𝑡 = 𝑟, perhatikan persamaan berikut dan fakta bahwa operasi penjumlahan biasa bersifat komutatif dan asosiatif pada ℤ: (𝑎 + 𝑏) + 𝑐 = (𝑥𝑛 + 𝑦) + 𝑐 = 𝑥𝑛 + (𝑦 + 𝑐) = 𝑥𝑛 + (𝑠𝑛 + 𝑡) = (𝑥 + 𝑠)𝑛 + 𝑡.
𝑎 + (𝑏 + 𝑐) = 𝑎 + (𝑢𝑛 + 𝑣) = 𝑢𝑛 + (𝑎 + 𝑣) = 𝑢𝑛 + (𝑞𝑛 + 𝑟) = (𝑢 + 𝑞)𝑛 + 𝑟.
Dengan demikian ((a+b)+c)(mod n)=t dan (a+(b+c))(mod n)=r. Tetapi di dalam ℤ, (𝑎 + 𝑏) + 𝑐 = 𝑎 + (𝑏 + 𝑐), dan (𝑎 + 𝑏 + 𝑐)(𝑚𝑜𝑑 𝑛) terdefinisi tunggal, sehingga didapat 𝑡 = 𝑟, yaitu 𝑎 +𝑛 (𝑏 +𝑛 𝑐) = (𝑎 +𝑛 𝑏) +𝑛 𝑐. Jadi operasi +𝑛 bersifat asosiatif pada ℤ𝑛.
Dengan demikian, (ℤ𝑛, +𝑛) adalah grup untuk setiap bilangan bulat 𝑛 > 1. Grup (ℤ𝑛, +𝑛) juga merupakan grup Abel karena 𝑎 + 𝑏 = 𝑏 + 𝑎 dalam ℤ.■
Contoh 2.8
Table Cayley grup Abel (ℤ5, +5) adalah sebagai berikut:
+5 0 1 2 3 4 0 0 1 2 3 4 1 1 2 3 4 0 2 2 3 4 0 1 3 3 4 0 1 2 4 4 0 1 2 3
Elemen identitas untuk operasi +5 pada ℤ5 adalah 0. Setiap elemen mem-iliki invers yang ditulis dengan notasi penjumlahan, yaitu −0 = 0, −1 = 4, −2 = 3, −3 = 2, dan −4 = 1.
Teorema 2.7 (Miller, 2013)
Misalkan (𝐺,∗) adalah grup terhadap operasi ∗.
(i) Terdapat tepat satu elemen di 𝐺 yang merupakan elemen identitas. (ii) Untuk setiap elemen 𝑎 ∈ 𝐺 terdapat tepat satu elemen di 𝐺 yang
merupakan invers dari 𝑎. Bukti:
Diasumsikan 𝐺 adalah grup terhadap operasi ∗.
(i) Karena 𝐺 adalah grup, maka ada elemen di 𝐺 yang merupakan e-lemen identitas, yaitu 𝑒. Misalkan 𝑢 merupakan ee-lemen lain dari 𝐺, yang juga merupakan elemen identitas. Akan ditunjukan bahwa 𝑒 = 𝑢. Karena 𝑒 adalah elemen identitas, maka 𝑒 ∗ 𝑢 = 𝑢. Demikian pula, karena 𝑢 adalah elemen identitas, maka 𝑒 ∗ 𝑢 = 𝑒, sehingga 𝑒 = 𝑒 ∗ 𝑢 = 𝑢. Jadi 𝑒 = 𝑢. Dengan demikian terdapat tepat satu e-lemen dari 𝐺 yang merupakan ee-lemen identitas.
(ii) Diberikan 𝑎 ∈ 𝐺. Karena 𝐺 adalah grup, maka ada 𝑏 ∈ 𝐺 dengan 𝑎 ∗ 𝑏 = 𝑒 = 𝑏 ∗ 𝑎. Misalkan terdapat elemen lain yaitu 𝑐 ∈ 𝐺, dengan 𝑎 ∗ 𝑐 = 𝑒 = 𝑐 ∗ 𝑎. Akan ditunjukan bahwa 𝑏 = 𝑐. Karena 𝑎 ∗ 𝑐 = 𝑒, maka 𝑏 ∗ (𝑎 ∗ 𝑐) = 𝑏 ∗ 𝑒 = 𝑏. Demikian pula, karena 𝑏 ∗ 𝑎 = 𝑒, maka (𝑏 ∗ 𝑎) ∗ 𝑐 = 𝑒 ∗ 𝑐 = 𝑐. Tetapi dengan sifat asosiatif 𝑏 ∗
(𝑎 ∗ 𝑐) = (𝑏 ∗ 𝑎) ∗ 𝑐, sehingga 𝑏 = 𝑐. Oleh karena itu ada tepat satu elemen di 𝐺 yang merupakan invers dari 𝑎.■
Teorema 2.8
Misal (𝐺, •) dan (𝐻, ⨁) adalah grup. Himpunan 𝐺 × 𝐻 = {(𝑥, 𝑦)|𝑥 ∈ 𝐺, 𝑦 ∈ 𝐻} merupakan grup terhadap operasi ∗ yang didefinisikan sebagai beri-kut: (𝑎, 𝑏) ∗ (𝑐, 𝑑) = (𝑎 • 𝑐, 𝑏 ⨁ 𝑑).
Bukti:
Akan dibuktikan bahwa 𝐺 × 𝐻 = {(𝑥, 𝑦)|𝑥 ∈ 𝐺, 𝑦 ∈ 𝐻} merupakan grup dengan operasi ∗ yang didefinisikan di atas.
(i) Diberikan 𝑎, 𝑐, 𝑒 ∈ 𝐺 dan 𝑏, 𝑑, 𝑓 ∈ 𝐻. Maka
((𝑎, 𝑏) ∗ (𝑐, 𝑑)) ∗ (𝑒, 𝑓) = (𝑎 • 𝑐, 𝑏 ⨁ 𝑑) ∗ (𝑒, 𝑓) = ((𝑎 • 𝑐) • 𝑒, (𝑏 ⨁ 𝑑) ⨁ 𝑓)
= (𝑎 • (𝑐 • 𝑒), 𝑏 ⨁ (𝑑 ⨁ 𝑓)) = (𝑎, 𝑏) ∗ (𝑐 • 𝑒, 𝑑 ⨁ 𝑓) = (𝑎, 𝑏) ∗ ((𝑐, 𝑑) ∗ (𝑒, 𝑓)) Jadi operasi ∗ bersifat asosiatif di 𝐺 × 𝐻
(ii) Diberikan (𝑎, 𝑏) ∈ 𝐺 × 𝐻. Misalkan 𝑒𝐺 merupakan elemen identitas di 𝐺 dan 𝑒𝐻 merupakan elemen identitas di 𝐻, maka (𝑒𝐺, 𝑒𝐻) ∈ 𝐺 × 𝐻 dan (𝑎, 𝑏) ∗ (𝑒𝐺, 𝑒𝐻) = (𝑎 • 𝑒𝐺, 𝑏 ⨁ 𝑒𝐻) = (𝑎, 𝑏) dan
(𝑒𝐺, 𝑒𝐻) ∗ (𝑎, 𝑏) = (𝑒𝐺 • 𝑎, 𝑒𝐻 ⨁ 𝑏 = (𝑎, 𝑏)
(iii) Diberikan (𝑎, 𝑏) ∈ 𝐺 × 𝐻. Maka ada 𝑎−1 ∈ 𝐺 sedemikian hingga 𝑎 • 𝑎−1 = 𝑒
𝑏 ⨁ 𝑏−1= 𝑒 𝐻 = 𝑏−1 ⨁ 𝑏. Maka (𝑎−1, 𝑏−1) ∈ 𝐺 × 𝐻 dan (𝑎, 𝑏) ∗ (𝑎−1, 𝑏−1) = (𝑎 • 𝑎−1, 𝑏 ⨁ 𝑏−1) = (𝑒 𝐺, 𝑒𝐻) dan (𝑎−1, 𝑏−1) ∗ (𝑎, 𝑏) = (𝑎−1• 𝑎, 𝑏−1 ⨁ 𝑏) = (𝑒 𝐺, 𝑒𝐻). Jadi (𝑎−1, 𝑏−1) ∈ 𝐺 × 𝐻 adalah invers dari (𝑎, 𝑏) ∈ 𝐺 × 𝐻.
Terbukti (𝐺 × 𝐻,∗) merupakan grup.■
Definisi 2.16 (Miller, 2013)
Grup (𝐺 × 𝐻, ∗) dengan operasi ∗ seperti yang didefinisikan pada Te-orema 2.8 disebut grup darab langsung dari grup 𝐺 dan grup 𝐻.
Contoh 2.9
Misalkan grup 𝐺 dan 𝐻 adalah (ℤ2, +2). Maka dapat dibentuk grup (ℤ2× ℤ2, +𝑛). Di mana himpunan Z2×Z2={(0,0),(0,1),(1,0),(1,1)}. Tabel Cayley untuk operasi di ℤ2× ℤ2 adalah sebagai berikut:
∗ (0,0) (0,1) (1,0) (1,1)
(0,0) (0,0) (0,1) (1,0) (1,1)
(0,1) (0,1) (0,0) (1,1) (1,0)
(1,0) (1,0) (1,1) (0,0) (0,1)
(1,1) (1,1) (1,0) (0,1) (0,0)
Elemen identitas untuk grup ( ℤ2× ℤ2, +𝑛) adalah (0,0) dan setiap elemen memiliki tepat satu invers yaitu (0,0)−1 = (0,0), (0,1)−1 = (0,1), (1,0)−1 = (1,0), dan (1,1)−1 = (1,1).
Untuk selanjutnya notasi (𝐺,∗) akan ditulis dengan 𝐺 saja dan operasinya ditulis dengan notasi perkalian serta elemen identitas dari 𝐺 ditulis dengan 𝑒 saja.
Teorema 2.9
Misalkan 𝐺 adalah grup
(i) Untuk setiap 𝑎 ∈ 𝐺, (𝑎−1)−1 = 𝑎.
(ii) Untuk setiap 𝑎, 𝑏 ∈ 𝐺, (𝑎𝑏)−1 = 𝑏−1𝑎−1. Bukti:
Misalkan 𝐺 adalah grup.
(i) Asumsikan 𝑎 ∈ 𝐺. Karena 𝐺 adalah grup maka terdapat elemen identitas 𝑒 ∈ 𝐺, dan 𝑎−1 ∈ 𝐺. Karena 𝑎𝑎−1 = 𝑒 = 𝑎−1𝑎, maka 𝑎 memenuhi definisi sebagai invers dari elemen 𝑎−1. Jadi (𝑎−1)−1 = 𝑎.
(ii) Asumsikan 𝑎, 𝑏 ∈ 𝐺, maka 𝑎−1, 𝑏−1 ∈ 𝐺.
(𝑎𝑏)(𝑏−1𝑎−1) = 𝑎(𝑏𝑏−1)𝑎−1 = 𝑎𝑒𝑎−1= 𝑎𝑎−1 = 𝑒 (𝑏−1𝑎−1)(𝑎𝑏) = 𝑏−1(𝑎−1𝑎)𝑏 = 𝑏−1𝑒𝑏 = 𝑏−1𝑏 = 𝑒. Jadi 𝑏−1𝑎−1 adalah invers dari 𝑎𝑏. Dengan demikian (𝑎𝑏)−1 = 𝑏−1𝑎−1.■
Definisi 2.17 (Miller,2013)
𝑎𝑛 = { 𝑎𝑎𝑎 ⋯ 𝑎 ⏟ jika 𝑛 > 0 sebanyak 𝑛 𝑒 𝑎−1𝑎−1⋯ 𝑎−1 ⏟ jika 𝑛 = 0 sebanyak − 𝑛 jika 𝑛 < 0
Dari Definisi 2.17 bila 𝐺 adalah grup dengan operasi penjumlahan, maka 𝑎𝑛 ditulis dengan notasi 𝑛𝑎 dan
𝑛𝑎 = { 𝑎 + 𝑎 + ⋯ + 𝑎 ⏟ jika 𝑛 > 0 sebanyak 𝑛 𝑒 −𝑎 + (−𝑎) + ⋯ + (−𝑎) ⏟ jika 𝑛 = 0 sebanyak − 𝑛 jika 𝑛 < 0 Contoh 2.10
Di dalam grup ℤ × ℚ, di mana ℤ menggunakan operasi penjumlahan bi-asa dan ℚ menggunakan operasi perkalian bibi-asa,
(2,1 3) 3 = (2 + 2 + 2,1 3∙ 1 3∙ 1 3) = (6, 1 27) (2,1 3) −3 = (−2 − 2 − 2, 3 ∙ 3 ∙ 3) = (−6, 9) (2,1 3) 0 = (0,1). Teorema 2.10
Misalkan 𝐺 adalah grup, 𝑎 ∈ 𝐺, dan 𝑚, 𝑛 ∈ ℤ. (i) 𝑎𝑛𝑎𝑚 = 𝑎𝑛+𝑚
(ii) (𝑎𝑛)𝑚 = 𝑎𝑛𝑚
(iii) 𝑎−𝑛 = (𝑎−1)𝑛 = (𝑎𝑛)−1 Bukti:
Misalkan 𝐺 adalah grup, 𝑎 ∈ 𝐺, dan 𝑚, 𝑛 ∈ ℤ.
Karena 𝑚, 𝑛 ∈ ℤ maka 𝑚 atau 𝑛 mungkin positif, negatif, atau 0. Jadi teorema ini akan dibagi ke dalam beberapa kasus.
(i) 𝑎𝑛𝑎𝑚 = 𝑎𝑛+𝑚 Untuk 𝑛 > 0 dan 𝑚 > 0 𝑎𝑛𝑎𝑚= (𝑎𝑎 ⋯ 𝑎)⏟ 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 𝑛 (𝑎𝑎 ⋯ 𝑎) ⏟ 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 𝑚 = 𝑎𝑎 ⋯ 𝑎⏟ 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 𝑛+𝑚 = 𝑎𝑛+𝑚 Untuk 𝑛 > 0 dan 𝑚 = 0 𝑎𝑛𝑎𝑚 = 𝑎𝑛𝑎0 = 𝑎𝑛𝑒 = 𝑎𝑛 = 𝑎𝑛+0 = 𝑎𝑛+𝑚 Untuk 𝑛 > 0 dan 𝑚 < 0 jika −𝑚 > 𝑛 ≡ −𝑚 − 𝑛 > 0 ≡ −(𝑚 + 𝑛) > 0, maka 𝑎𝑛𝑎𝑚 = 𝑎⏟ −1𝑎−1⋯ 𝑎−1 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 −(𝑛+𝑚) = 𝑎𝑛+𝑚 jika −𝑚 < 𝑛 ≡ 𝑛 − (−𝑚) > 0 ≡ 𝑛 + 𝑚 > 0, maka 𝑎𝑛𝑎𝑚 = 𝑎𝑎 ⋯ 𝑎⏟ 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 𝑛+𝑚 = 𝑎𝑛+𝑚 jika −𝑚 = 𝑛 ≡ 𝑚 + 𝑛 = 0, maka 𝑎𝑛𝑎𝑚 = 𝑒 = 𝑎0 = 𝑎𝑛+𝑚 Untuk 𝑛 = 0 dan 𝑚 > 0 𝑎𝑛𝑎𝑚 = 𝑎0𝑎𝑚 = 𝑒𝑎𝑚 = 𝑎𝑚 = 𝑎0+𝑚 = 𝑎𝑛+𝑚 Untuk 𝑛 = 0 dan 𝑚 = 0 𝑎𝑛𝑎𝑚= 𝑎0𝑎0 = 𝑒𝑒 = 𝑒 = 𝑎0 = 𝑎0+0= 𝑎𝑛+𝑚 Untuk 𝑛 = 0 dan 𝑚 < 0 𝑎𝑛𝑎𝑚 = 𝑎0𝑎𝑚 = 𝑒𝑎𝑚 = 𝑎𝑚 = 𝑎0+𝑚 = 𝑎𝑛+𝑚
Untuk 𝑛 < 0 dan 𝑚 > 0 jika −𝑛 > 𝑚 ≡ −𝑛 − 𝑚 > 0 ≡ −(𝑛 + 𝑚) > 0, maka 𝑎𝑛𝑎𝑚 = 𝑎⏟ −1𝑎−1⋯ 𝑎−1 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 −(𝑛+𝑚) = 𝑎𝑛+𝑚 jika −𝑛 < 𝑚 ≡ 𝑚 − (−𝑛) > 0 ≡ 𝑚 + 𝑛 > 0, maka 𝑎𝑛𝑎𝑚 = 𝑎𝑎 ⋯ 𝑎⏟ 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 𝑛+𝑚 = 𝑎𝑛+𝑚 jika −𝑛 = 𝑚 ≡ 𝑛 + 𝑚 = 0, maka 𝑎𝑛𝑎𝑚 = 𝑒 = 𝑎0 = 𝑎𝑛+𝑚 Untuk 𝑛 < 0 dan 𝑚 = 0 𝑎𝑛𝑎𝑚 = 𝑎𝑛𝑎0 = 𝑎𝑛𝑒 = 𝑎𝑛 = 𝑎𝑛+0 = 𝑎𝑛+𝑚 Untuk 𝑛 < 0 dan 𝑚 < 0 𝑎𝑛𝑎𝑚 = (𝑎⏟ −1𝑎−1⋯ 𝑎−1) 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 −𝑛 (𝑎−1𝑎−1⋯ 𝑎−1) ⏟ 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 −𝑚 = 𝑎−1𝑎−1⋯ 𝑎−1 ⏟ 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 −(𝑛+𝑚) = 𝑎𝑛+𝑚 (ii) (𝑎𝑛)𝑚 = 𝑎𝑛𝑚 Untuk 𝑛 > 0 dan 𝑚 > 0 (𝑎𝑛)𝑚= ( 𝑎𝑎 ⋯ 𝑎⏟ 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 𝑛 ) ( 𝑎𝑎 ⋯ 𝑎⏟ 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 𝑛 ) ⋯ ( 𝑎𝑎 ⋯ 𝑎⏟ 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 𝑛 ) ⏟ 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 𝑚 = 𝑎𝑎 ⋯ 𝑎⏟ 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 𝑛𝑚 = 𝑎𝑛𝑚 Untuk 𝑛 > 0 dan 𝑚 = 0 (𝑎𝑛)𝑚 = (𝑎𝑛)0 = 𝑒 = 𝑎0 = 𝑎𝑛0= 𝑎𝑛𝑚 Untuk 𝑛 > 0 dan 𝑚 < 0
(𝑎𝑛)𝑚= ( 𝑎𝑎 ⋯ 𝑎⏟ 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 𝑛 ) −1 ( 𝑎𝑎 ⋯ 𝑎⏟ 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 𝑛 ) −1 ⋯ ( 𝑎𝑎 ⋯ 𝑎⏟ 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 𝑛 ) −1 ⏟ 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 −𝑚 = 𝑎⏟ −1𝑎−1⋯ 𝑎−1 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 −𝑛𝑚 = 𝑎𝑛𝑚 Untuk 𝑛 = 0 dan 𝑚 > 0 (𝑎𝑛)𝑚 = (𝑎0)𝑚 = 𝑒𝑚 = 𝑒 = 𝑎0 = 𝑎0𝑚 = 𝑎𝑛𝑚 Untuk 𝑛 = 0 dan 𝑚 = 0 (𝑎𝑛)𝑚 = (𝑎0)0 = 𝑒0 = 𝑒 = 𝑎0 = 𝑎𝑛𝑚 Untuk 𝑛 = 0 dan 𝑚 < 0 (𝑎𝑛)𝑚 = (𝑎0)𝑚 = 𝑒𝑚 = 𝑒 = 𝑎0 = 𝑎0𝑚 = 𝑎𝑛𝑚 Untuk 𝑛 < 0 dan 𝑚 > 0 (𝑎𝑛)𝑚 = (𝑎⏟ −1𝑎−1⋯ 𝑎−1 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 −𝑛 ) (𝑎⏟ −1𝑎−1⋯ 𝑎−1 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 −𝑛 ) ⋯ (𝑎⏟ −1𝑎−1⋯ 𝑎−1 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 −𝑛 ) ⏟ 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 𝑚 = 𝑎⏟ −1𝑎−1⋯ 𝑎−1 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 −𝑛𝑚 = 𝑎𝑛𝑚 Untuk 𝑛 < 0 dan 𝑚 = 0 (𝑎𝑛)𝑚 = (𝑎𝑛)0 = 𝑒 = 𝑎0 = 𝑎𝑛0= 𝑎𝑛𝑚 Untuk 𝑛 < 0 dan 𝑚 < 0 (𝑎𝑛)𝑚 = (𝑎⏟ −1𝑎−1⋯ 𝑎−1 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 −𝑛 ) −1 (𝑎⏟ −1𝑎−1⋯ 𝑎−1 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 −𝑛 ) −1 ⋯ (𝑎⏟ −1𝑎−1⋯ 𝑎−1 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 −𝑛 ) −1 ⏟ 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 −𝑚
= 𝑎𝑎 ⋯ 𝑎⏟ 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 𝑛𝑚 = 𝑎𝑛𝑚 (iii) 𝑎−𝑛 = (𝑎−1)𝑛 = (𝑎𝑛)−1 Untuk 𝑛 > 0 berarti −𝑛 < 0 𝑎−𝑛 = 𝑎⏟ −1𝑎−1⋯ 𝑎−1 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 −(−𝑛)=𝑛 = (𝑎−1)𝑛 (𝑎𝑛)−1 = (𝑎𝑎 ⋯ 𝑎)⏟ 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 𝑛 −1 = 𝑎⏟ −1𝑎−1⋯ 𝑎−1 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 𝑛 = (𝑎−1)𝑛 Untuk 𝑛 = 0 𝑎−𝑛 = 𝑎0 = 𝑒 = (𝑎−1)0 = (𝑎−1)𝑛 (𝑎𝑛)−1 = (𝑎0)−1= 𝑎0 = 𝑒 = (𝑎−1)0 = (𝑎−1)𝑛 Untuk 𝑛 < 0 berarti −𝑛 > 0 𝑎−𝑛 = 𝑎𝑎 ⋯ 𝑎⏟ 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 −𝑛 = (𝑎⏟ −1)−1(𝑎−1)−1⋯ (𝑎−1)−1 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 −𝑛 = (𝑎−1)𝑛 (𝑎𝑛)−1= (𝑎⏟ −1𝑎−1⋯ 𝑎−1) 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 −𝑛 −1 = (𝑎−1)−1(𝑎−1)−1⋯ (𝑎−1)−1 ⏟ 𝑠𝑒𝑏𝑎𝑛𝑦𝑎𝑘 −𝑛 = (𝑎−1)𝑛.■ Definisi 2.18 (Miller, 2013)
Misalkan 𝐺 adalah grup dan 𝑎 ∈ 𝐺. Jika terdapat bilangan bulat positif 𝑛 dengan 𝑎𝑛 = 𝑒, maka bilangan positif terkecil 𝑛 yang memenuhi 𝑎𝑛 = 𝑒 dise-but orde dari 𝑎, dinotasikan dengan 𝑜𝑟𝑑(𝑎). Jika tidak ada bilangan positif 𝑛 yang memenuhi 𝑎𝑛 = 𝑒, maka dikatakan bahwa 𝑎 memiliki orde tak hingga.
Diberikan grup (ℤ7, +7) dan 3 ∈ ℤ7. Akan dicari bilangan bulat terkecil 𝑛 sedemikian hingga 3𝑛 = 0, yaitu (3 + 3 + 3 + ⋯ + 3)(𝑚𝑜𝑑 7) = 0 (3 sebanyak 𝑛 suku). 31 = (3)(𝑚𝑜𝑑 7) = 3 32 = (3 + 3)(𝑚𝑜𝑑 7) = 6 33 = (3 + 3 + 3)(𝑚𝑜𝑑 7) = 2 34 = (3 + 3 + 3 + 3)(𝑚𝑜𝑑 7) = 5 35 = (3 + 3 + 3 + 3 + 3)(𝑚𝑜𝑑 7) = 1 36 = (3 + 3 + 3 + 3 + 3 + 3)(𝑚𝑜𝑑 7) = 4 37 = (3 + 3 + 3 + 3 + 3 + 3 + 3)(𝑚𝑜𝑑 7) = 0
Dengan demikian bilangan bulat positif terkecil yang membuat 3𝑛 habis dibagi 7 adalah 𝑛 = 7. Jadi 𝑜𝑟𝑑(3) = 7.
2. Grup Bagian
Akan didefinisikan bahwa himpunan bagian dari suatu grup yang juga merupakan grup disebut grup bagian (subgrup).
Definisi 2.19 (Miller, 2013)
Misalkan 𝐺 adalah grup. Himpunan bagian tak kosong 𝐻 ⊆ 𝐺 disebut
grup bagian dari 𝐺 jika dan hanya jika 𝐻 juga merupakan grup dengan operasi yang sama yang didefinisikan di 𝐺.
Diberikan grup 𝐺 dan 𝐻 ⊆ 𝐺. Himpunan 𝐻 adalah grup bagian dari 𝐺 jika dan hanya jika
(i) 𝐻 tidak kosong.
(ii) 𝐻 tertutup terhadap operasi di 𝐺. (iii) 𝐻 tertutup terhadap invers. Bukti:
(⇒) Asumsikan 𝐻 adalah grup bagian dari 𝐺. Dari definisi grup bagian, berarti 𝐻 adalah himpunan tak kosong. Karena 𝐻 merupakan grup bagian, dari 𝐺 berarti 𝐻 merupakan grup terhadap operasi di 𝐺. Maka 𝐻 tertutup terhadap operasi di 𝐺 dan setiap elemen di 𝐻 pasti memiliki invers di 𝐻 agar 𝐻 menjadi grup, jadi 𝐻 tertutup terhadap invers.
(⇐) Misalkan 𝐻 adalah himpunan bagian dari 𝐺 dan 𝐻 memenuhi tiga sifat di atas. Akan ditunjukkan bahwa 𝐻 merupakan grup bagian dari 𝐺, yaitu 𝐻 adalah grup terhadap operasi di 𝐺. Berdasarkan (i) 𝐻 memiliki elemen dengan demikian 𝐻 adalah himpunan bagian tak kosong dari 𝐺. Dengan operasi dari 𝐺, 𝑎𝑏 haruslah terdefinisi tunggal untuk setiap 𝑎, 𝑏 ∈ 𝐻. Poin (ii) menja-min bahwa hasilnya di 𝐻, jadi operasi di 𝐺 juga merupakan operasi di 𝐻.
Karena operasi di 𝐺 bersifat asosiatif dan 𝐻 ⊆ 𝐺 maka operasi tersebut pasti bersifat asosiatif di 𝐻. Dari (iii) setiap elemen dari 𝐻 memiliki invers di 𝐻. Harus dibuktikan bahwa 𝐻 memiliki elemen identitas terhadap operasi di 𝐺. Karena 𝐻 tidak kosong, maka ada 𝑥 ∈ 𝐻. Dari (iii) terdapat 𝑥−1 ∈ 𝐻. Dari (ii) 𝑥𝑥−1 ∈ 𝐻, atau 𝑒 ∈ 𝐻. Jadi 𝐻 adalah grup dengan operasi di 𝐺, atau 𝐻 adalah grup bagian dari 𝐺.■
Berdasarkan Teorema 2.11, dapat dikatakan bahwa setiap grup 𝐺 me-miliki dua grup bagian yang jelas, yaitu grup 𝐺 itu sendiri dan grup bagian
trivial yang terdiri dari elemen identitas saja. Sedangkan grup bagian dikatakan
sebagai grup bagian sejati jika 𝐻 ≠ 𝐺 atau 𝐻 ≠ {𝑒} . (Artin, 2010)
Contoh 2.12
Misalkan grup (ℤ16, +16). Apakah himpunan 𝐻 = {0, 4, 8, 12} merupa-kan himpunan bagian dari (ℤ16, +16)?
Jelas 𝐻 ≠ ∅ karena 𝐻 memiliki elemen yaitu 0, 4, 8, dan 12. Tabel Cay-ley untuk himpunan 𝐻 dengan operasi +16
+16 0 4 8 12
0 0 4 8 12
4 4 8 12 0
8 8 12 0 4
12 12 0 4 8
Terlihat bahwa 𝐻 tertutup terhadap +16. Setiap elemen memiliki invers dalam 𝐻 yaitu 0−1 = 0, 4−1= 12, 8−1 = 8 dan 12−1 = 4. Jadi 𝐻 tertutup ter-hadap invers. Dengan Teorema 2.11, 𝐻 merupakan grup bagian dari (ℤ16, +16).
3. Grup Siklik
Untuk setiap 𝑎 ∈ 𝐺 didefinisikan himpunan yang dibangkitkan oleh 𝑎 dan dinotasikan dengan 〈𝑎〉 sebagai 〈𝑎〉 = {𝑎𝑛 ∶ 𝑛 ∈ ℤ}.
Bila operasi di 𝐺 adalah penjumlahan, maka 〈𝑎〉 = {𝑛𝑎 | 𝑛 ∈ ℤ}
Contoh 2.13
Diberikan grup (ℤ6, +6). Elemen dari 〈2〉 adalah 〈2〉 = {0, 2, 4}, elemen dari 〈3〉 = {0, 3}.
Teorema 2.12 (Miller, 2013)
Jika 𝐺 adalah grup dan 𝑎 ∈ 𝐺, maka himpunan 〈𝑎〉 = {𝑎𝑛 ∶ 𝑛 ∈ ℤ} meru-pakan himpunan bagian dari 𝐺, dan 〈𝑎〉 disebut grup bagian siklik yang
dibang-kitkan oleh 𝑎. Bukti:
Himpunan 〈𝑎〉 adalah himpunan bagian dari 𝐺, karena 𝐺 tertutup ter-hadap perkalian, maka harus dibuktikan bahwa 〈𝑎〉 adalah grup bagian dari 𝐺.
(i) Karena 0 adalah bilangan bulat, 𝑎0 adalah elemen dari himpunan 〈𝑎〉 sehingga 〈𝑎〉 ≠ ∅.
(ii) Misalkan 𝑥, 𝑦 ∈ 〈𝑎〉. Terdapat bilangan bulat 𝑚, 𝑛 dengan 𝑥 = 𝑎𝑚, 𝑦 = 𝑎𝑛. Kemudian 𝑥𝑦 = 𝑎𝑚𝑎𝑛 = 𝑎𝑚+𝑛, dan karena 𝑚 + 𝑛 juga bilangan bulat maka 𝑥𝑦 ∈ 〈𝑎〉. Jadi 〈𝑎〉 tertutup terhadap operasi di 𝐺.
(iii) Misalkan 𝑥 ∈ 〈𝑎〉. Maka terdapat bilangan bulat 𝑚 dengan 𝑥 = 𝑎𝑚. Dengan demikian 𝑥−1 = (𝑎𝑚)−1 = 𝑎−𝑚, dan karena – 𝑚 adalah bilangan bulat maka 𝑥−1 ∈ 〈𝑎〉. Jadi 〈𝑎〉 tertutup terhadap invers
Berdasarkan Teorema 2.11, 〈𝑎〉 adalah grup bagian dari 𝐺.■
Definisi 2.21 (Miller, 2013)
Grup 𝐺 disebut grup siklik jika dan hanya jika terdapat 𝑎 ∈ 𝐺 sedemikian sehingga 𝐺 = 〈𝑎〉.
Contoh 2.14
Grup (ℤ, +) adalah grup siklik. Akan dibuktikan bahwa ℤ = 〈1〉. Dari definisi 〈𝑎〉, jelas bahwa 〈𝑎〉 ⊆ 𝐺 untuk setiap 𝑎 ∈ 𝐺, sehingga 〈1〉 ⊆ ℤ. Kemudian akan dibuktikan bahwa ℤ ⊆ 〈1〉. Menurut Definisi 2.17, misal 𝑛 ∈ ℤ, untuk 𝑛 > 0, 𝑛 = 1 + 1 + ⋯ + 1 = 𝑛(1), sehingga 𝑛 ∈ 〈1〉. Untuk 𝑛 = 0, 0 = 0(1), sehingga 0 ∈ 〈1〉. Untuk 𝑛 < 0, misalkan 𝑛 = −𝑚 untuk suatu 𝑚 > 0, 𝑛 = −𝑚 = −1 + (−1) + ⋯ + (−1) = 𝑚(1) = (−𝑛)(1), sehingga 𝑛 ∈ 〈1〉. Maka untuk setiap 𝑛 ∈ ℤ terbukti bahwa ℤ ⊆ 〈1〉. Dengan demikian ℤ = 〈1〉.
Teorema 2.13
Jika 𝐺 adalah grup siklik, maka 𝐺 adalah grup Abel. Bukti:
Ambil sebarang 𝑥, 𝑦 ∈ 𝐺. Karena 𝐺 adalah grup siklik, maka ada 𝑎 ∈ 𝐺 sedemikian sehingga untuk setiap 𝑥, 𝑦 ∈ 𝐺 ada 𝑛, 𝑚 ∈ ℤ yang berlaku 𝑥 = 𝑎𝑛 dan 𝑦 = 𝑎𝑚, maka
𝑥𝑦 = 𝑎𝑛𝑎𝑚 = 𝑎𝑛+𝑚 = 𝑎𝑚+𝑛 = 𝑎𝑚𝑎𝑛 = 𝑦𝑥.
Karena untuk setiap 𝑥, 𝑦 ∈ 𝐺 berlaku 𝑥𝑦 = 𝑦𝑥, maka terbukti 𝐺 adalah grup Abel.■
Definisi 2.22 (Gallian, 2010)
Jumlah elemen dalam suatu grup 𝐺 berhingga disebut orde dari grup, dan dinotasikan dengan |𝐺|.
Teorema 2.14
Misalkan 𝑎 adalah elemen dari grup 𝐺 dan 𝑎𝑛 = 𝑒 untuk suatu bilangan bulat positif 𝑛. Jika 𝑚 adalah bilangan bulat positif terkecil sedemikian se-hingga 𝑎𝑚 = 𝑒, maka 〈𝑎〉 memiliki orde 𝑚 dan 〈𝑎〉 = {𝑎0 = 𝑒 = 𝑎𝑚, 𝑎1, 𝑎2, ⋯ , 𝑎𝑚−1}.
Bukti:
Diketahui 𝑚 adalah bilangan bulat positif terkecil sedemikian sehingga 𝑎𝑚 = 𝑒. Akan dibuktikan bahwa elemen
𝑎0 = 𝑒 = 𝑎𝑚, 𝑎1, 𝑎2, ⋯ , 𝑎𝑚−1 semuanya berbeda. Andaikan
untuk 𝑖 ≠ 𝑗 berlaku 𝑎𝑖 = 𝑎𝑗 dengan 𝑖, 𝑗 ∈ ℤ, 0 ≤ 𝑖 < 𝑚, 0 ≤ 𝑗 < 𝑚. Tanpa menghilangkan keumumannya asumsikan bahwa 𝑖 ≥ 𝑗. Maka
𝑎𝑖−𝑗 = 𝑎𝑖𝑎−𝑗 = 𝑎𝑖(𝑎𝑗)−1= 𝑎𝑖(𝑎𝑖)−1 = 𝑒 dimana 0 ≤ 𝑖 − 𝑗 < 𝑚. Karena 𝑚 adalah bilangan bulat positif terkecil sedemikian sehingga 𝑎𝑚 = 𝑒 dan karena 𝑖 − 𝑗 < 𝑚, pastilah benar bahwa 𝑖 − 𝑗 = 0, dan karenanya 𝑖 = 𝑗. Kontradiksi dengan 𝑖 ≠ 𝑗. Jadi 〈𝑎〉 memuat 𝑚 elemen yang berbeda 𝑎0 = 𝑒 = 𝑎𝑚, 𝑎1, 𝑎2, ⋯ , 𝑎𝑚−1. Jadi {𝑎0 = 𝑒 = 𝑎𝑚, 𝑎1, 𝑎2, ⋯ , 𝑎𝑚−1} ⊆ 〈𝑎〉.
Selanjutnya akan dibuktikan bahwa pangkat dari 𝑎 sama dengan salah satu dari elemen 𝑎0, 𝑎1, 𝑎2, ⋯ , 𝑎𝑚−1. Misalkan untuk sebarang 𝑎𝑘, dengan Al-goritma Pembagian terdapat bilangan bulat 𝑞 dan 𝑟 sedemikian sehingga
𝑘 = 𝑚𝑞 + 𝑟 dengan 0 ≤ 𝑟 < 𝑚. Jadi
𝑎𝑘 = 𝑎𝑚𝑞+𝑟 = 𝑎𝑚𝑞𝑎𝑟= (𝑎𝑚)𝑞𝑎𝑟 = 𝑒𝑞𝑎𝑟 = 𝑎𝑟
di mana 𝑟 adalah elemen dari himpunan {0, 1, 2, ⋯ , 𝑚 − 1}. Dengan demikian 〈𝑎〉 ⊆ {𝑎0 = 𝑒 = 𝑎𝑚, 𝑎1, 𝑎2, ⋯ , 𝑎𝑚−1}.
Terbukti bahwa 〈𝑎〉 = {𝑎0 = 𝑒 = 𝑎𝑚, 𝑎1, 𝑎2, ⋯ , 𝑎𝑚−1} dan karena 〈𝑎〉 me-miliki elemen sebanyak 𝑚 maka menurut Definisi 2.22 〈𝑎〉 meme-miliki orde 𝑚.■
Berdasarkan Teorema 2.14 di atas, jika 𝐺 adalah grup siklik dengan pem-bangkit 𝑎 ∈ 𝐺 dan 𝐺 berorde 𝑛, maka 𝐺 dapat dituliskan sebagai𝐺 = 〈𝑎〉 = {𝑎1, 𝑎2, ⋯ , 𝑎𝑛−1, 𝑎𝑛 = 𝑒}.
4. Grup Simetrik
Definisi 2.23 (Miller, 2013)
Misalkan 𝐴 merupakan himpunan tak kosong. Permutasi dari 𝐴 adalah fungsi bijektif dari 𝐴 ke 𝐴.
Perhatikan himpunan bilangan bulat ℤ. Fungsi 𝑓 ∶ ℤ → ℤ yang didefi-nisikan dengan 𝑓(𝑛) = 𝑛 + 1 merupakan permutasi dari ℤ. Untuk menunjuk-kannya akan ditunjukkan bahwa 𝑓 merupakan fungsi bijektif. Misalkan 𝑎, 𝑏 ∈ ℤ dengan 𝑓(𝑎) = 𝑓(𝑏). Menurut definisi dari 𝑓, 𝑎 + 1 = 𝑏 + 1. Dengan me-ngurangkan satu pada kedua sisi maka 𝑎 = 𝑏, sehingga 𝑓 injektif. Kemudian misalkan untuk sebarang 𝑧 ∈ ℤ akan ditunjukkan bahwa ada 𝑥 ∈ ℤ dengan 𝑓(𝑥) = 𝑧. Karena 𝑧 ∈ ℤ maka 𝑧 − 1 ∈ ℤ juga, 𝑓(𝑧 − 1) = (𝑧 − 1) + 1 = 𝑧, maka 𝑥 = 𝑧 − 1, sehingga 𝑓(𝑥) = 𝑧. Dengan demikian 𝑓 adalah fungsi yang bijektif. Jadi 𝑓 adalah permutasi dari ℤ.
Teorema 2.15
Untuk setiap himpunan tak kosong 𝐴 himpunan 𝑆𝐴 = {𝑓 ∶ 𝐴 → 𝐴 | 𝑓 𝑎𝑑𝑎𝑙𝑎ℎ 𝑝𝑒𝑟𝑚𝑢𝑡𝑎𝑠𝑖 𝑑𝑎𝑟𝑖 𝐴} merupakan grup terhadap operasi kompo-sisi fungsi. Grup 𝑆𝐴 disebut sebagai grup simetrik pada 𝐴.
Bukti:
Misalkan 𝐴 adalah himpunan tak kosong, dan 𝑆𝐴 adalah himpunan dari semua permutasi dari 𝐴. Misalkan 𝑓, 𝑔 ∈ 𝑆𝐴, karena 𝑓 dan 𝑔 adalah dua fungsi yang bijektif maka 𝑓 ∘ 𝑔 bijektif, sehingga 𝑓 ∘ 𝑔 ∈ 𝑆𝐴. Jadi operasi komposisi fungsi bersifat tertutup terhadap himpunan 𝑆𝐴.
Akan ditunjukkan 𝑆𝐴 merupakan grup terhadap operasi komposisi fungsi dengan menggunakan definisi Grup.
((𝑓 ∘ 𝑔) ∘ ℎ)(𝑥) = (𝑓 ∘ 𝑔)(ℎ(𝑥)) = 𝑓 (𝑔(ℎ(𝑥))) = 𝑓((𝑔 ∘ ℎ))(𝑥) = (𝑓 ∘ (𝑔 ∘ ℎ))(𝑥).
Dengan demikian ((𝑓 ∘ 𝑔) ∘ ℎ)(𝑥) = (𝑓 ∘ (𝑔 ∘ ℎ))(𝑥). Jadi operasi komposisi fungsi bersifat asosiatif di 𝑆𝐴.
(ii) Fungsi 𝜀 ∶ 𝐴 → 𝐴 dengan 𝜀(𝑥) = 𝑥 untuk setiap 𝑥 ∈ 𝐴 adalah fungsi bi-jektif, jadi 𝜀 ∈ 𝑆𝐴. Untuk setiap 𝑓 ∈ 𝑆𝐴 dan 𝑥 ∈ 𝐴 dengan Teorema 2.3 berlaku
(𝑓 ∘ 𝜀)(𝑥) = 𝑓(𝜀(𝑥)) = 𝑓(𝑥) dan (𝜀 ∘ 𝑓)(𝑥) = 𝜀(𝑓(𝑥)) = 𝑓(𝑥). Jadi 𝑓 ∘ 𝜀 = 𝑓 = 𝜀 ∘ 𝑓. Dengan demikian 𝜀 ∈ 𝑆𝐴 merupakan elemen identitas terhadap operasi komposisi fungsi.
(iii) Untuk setiap 𝑓 ∈ 𝑆𝐴, akan ditunjukkan invers dari 𝑓. Dengan Teorema 2.1, karena 𝑓 adalah fungsi yang bijektif maka 𝑓−1 bijektif, sedemikian sehingga dengan Teorema 2.4,
𝑓−1∘ 𝑓 = 𝜀(𝑥) dan 𝑓 ∘ 𝑓−1 = 𝜀(𝑥)
Karena 𝑓−1∘ 𝑓 = 𝜀 = 𝑓 ∘ 𝑓−1, maka 𝑓−1 merupakan invers dari 𝑓. Oleh karena itu setiap elemen dari 𝑆𝐴 memiliki invers di 𝑆𝐴.
Dengan demikian 𝑆𝐴 merupakan grup terhadap operasi komposisi fungsi.■
Definisi 2.24 (Miller, 2013)
Untuk setiap 𝑘 ∈ ℕ, grup simetrik 𝑆𝑘 merupakan grup yang terdiri dari semua permutasi dari himpunan {1, 2, ⋯ , 𝑘} terhadap operasi komposisi.
Contoh 2.16
Grup simetrik 𝑆3 adalah himpunan dari permutasi dari {1, 2, 3} yang bi-asa disimbolkan dengan:
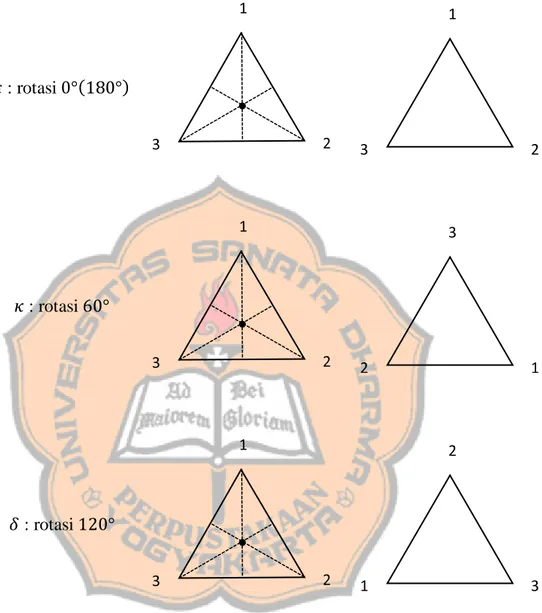
𝜀 = (1 2 3 1 2 3) 𝛼 = ( 1 2 3 2 1 3) 𝛽 = ( 1 2 3 1 3 2) 𝛾 = (1 2 3 3 2 1) 𝛿 = ( 1 2 3 2 3 1) 𝜅 = ( 1 2 3 3 1 2)
Operasi komposisi di 𝑆3 ditunjukkan dengan Tabel Cayley berikut:
∘ 𝜀 𝛼 𝛽 𝛾 𝛿 𝜅 𝜀 𝜀 𝛼 𝛽 𝛾 𝛿 𝜅 𝛼 𝛼 𝜀 𝛿 𝜅 𝛽 𝛾 𝛽 𝛽 𝜅 𝜀 𝛿 𝛾 𝛼 𝛾 𝛾 𝛿 𝜅 𝜀 𝛼 𝛽 𝛿 𝛿 𝛾 𝛼 𝛽 𝜅 𝜀 𝜅 𝜅 𝛽 𝛾 𝛼 𝜀 𝛿 Definisi 2.25 (Miller, 2013)
Misalkan 𝑘 ∈ ℕ, 𝑘 > 1 dan 𝛼 ∈ 𝑆𝑘. Elemen 𝛼 adalah siklus jika 𝛼 me-miliki bentuk 𝛼 = (𝑎1𝑎2⋯ 𝑎𝑛) untuk suatu 1 < 𝑛 ≤ 𝑘 dimana:
a) 𝑎𝑖 adalah elemen yang berbeda dari {1, 2, ⋯ , 𝑘}
b) 𝛼(𝑎𝑖) = 𝑎𝑖+1 untuk 𝑖 < 𝑛, 𝛼(𝑎𝑛) = 𝑎1, dan c) Elemen dari {1, 2, ⋯ , 𝑘} yang tidak ditunjukkan dalam siklus
Suatu siklus merupakan transposisi jika siklus tersebut memiliki bentuk 𝛼 = (𝑎1𝑎2). Siklus 𝛼 = (𝑎1𝑎2⋯ 𝑎𝑛) dan 𝛽 = (𝑏1𝑏2⋯ 𝑏𝑟) saling asing di 𝑆𝑘 jika {𝑎1, 𝑎2, ⋯ , 𝑎𝑛} ∩ {𝑏1, 𝑏2, ⋯ , 𝑏𝑟} = ∅.
Untuk setiap transposisi 𝛼 maka 𝛼−1 = 𝛼.
Teorema 2.16
Setiap permutasi dari himpunan berhingga dapat dinyatakan sebagai komposisi dari siklus-siklus yang saling asing.
Bukti:
Misalkan 𝛼 adalah permutasi dari himpunan 𝐴 = {1, 2, ⋯ , 𝑛}. Untuk menunjukan bahwa 𝛼 dapat ditulis sebagai siklus yang saling asing, pertama-tama pilih elemen dari 𝐴, misalkan 𝑎1, dan misalkan
𝑎2 = 𝛼(𝑎1), 𝑎3 = 𝛼(𝛼(𝑎1)) = 𝛼2(𝑎 1), dan seterusnya, sampai diperoleh 𝑎1 = 𝛼𝑚(𝑎
1) untuk suatu 𝑚. Bilangan 𝑚 ada karena barisan 𝑎1, 𝛼(𝑎1), 𝛼2(𝑎
1), ⋯ berhingga, jadi akan ada pengulangan, ka-takanlah 𝛼𝑖(𝑎1) = 𝛼𝑗(𝑎
1) untuk suatu 𝑖 dan 𝑗 dengan 𝑖 < 𝑗. Maka 𝑎1 = 𝛼𝑚(𝑎
1), dimana 𝑚 = 𝑗 − 𝑖. Hubungan antara 𝑎1, 𝑎2, ⋯ , 𝑎𝑚 sebagai 𝛼 = ( 𝑎1, 𝑎2, ⋯ , 𝑎𝑚) ⋅ ⋅ ⋅.
Tiga titik di bagian akhir menunjukkan bahwa mungkin himpunan 𝐴 da-lam proses ini tidak semuanya dipakai. Kemudian pilih elemen 𝑏1di 𝐴 yang tidak muncul di siklus pertama dan dibuat siklus baru seperti sebelumnya, yaitu misalkan 𝑏2 = 𝛼(𝑏1), 𝑏3 = 𝛼2(𝑏
1), dan seterusnya, sampai diperoleh 𝑏1 = 𝛼𝑘(𝑏
siklus yang dibangun sebelumnya. Jika demikian, maka 𝛼𝑖(𝑎1) = 𝛼𝑗(𝑏1) un-tuk suatu 𝑖 dan 𝑗. Tetapi kemudian 𝛼𝑖−𝑗(𝑎
1) = 𝑏1, dan karenanya 𝑏1 = 𝑎𝑡 un-tuk suatu 𝑡. Hal ini kontradiksi dengan cara 𝑏1 dipilih. Kemudian proses ini dilanjutkan untuk semua elemen dari 𝐴, sehingga permutasinya akan muncul sebagai
𝛼 = ( 𝑎1, 𝑎2, ⋯ , 𝑎𝑚)( 𝑏1, 𝑏2, ⋯ , 𝑏𝑘) ⋯ ( 𝑐1, 𝑐2, ⋯ , 𝑐𝑠).
Dengan cara ini, terlihat bahwa setiap permutasi dapat ditulis sebagai komposisi dari siklus yang saling asing.■
Contoh 2.17
Dalam grup 𝑆6 didefinisikan 𝛼 = (1 2 3 4 5 6
2 1 4 3 5 6) dan 𝛽 = (
1 2 3 4 5 6
1 3 4 2 6 5).
Permutasi 𝛼 dan 𝛽 dapat dituliskan dalam bentuk siklus sebagai 𝛼 = (1 2)(3 4) dan 𝛽 = (2 3 4)(5 6).
Definisi 2.26
Misalkan 𝑘 ∈ ℕ, 𝑘 > 1. Permutasi di 𝑆𝑘 adalah genap jika permutasi
tersebut dapat dinyatakan sebagai komposisi dari transposisi berjumlah genap. Sedangkan permutasi di 𝑆𝑘 adalah ganjil jika permutasi tersebut dapat dinya-takan sebagai komposisi dari transposisi berjumlah ganjil.
Contoh 2.18
Pada grup simetrik 𝑆3 dalam Contoh 2.16, setiap elemen yang bukan identitas dapat dituliskan dalam bentuk siklus sebagai 𝛼 = (1 2), 𝛽 = (2 3),
𝛾 = (1 3), 𝛿 = (1 2 3), dan 𝜅 = (1 3 2). Jadi 𝑆3 = {𝜀, (1 2), (2 3), (1 3), (1 2 3), (1 3 2)}. Pada elemen (1 2), (2 3), (1 3) ketiga elemen tersebut sudah dalam bentuk transposisi dan berjumlah ganjil. Se-dangkan, (1 2 3) = (1 3)(1 2) dan (1 3 2) = (1 2)(1 3) keduanya dapat dibentuk menjadi transposisi dan berjumlah genap.
Teorema 2.17
Untuk 𝑘 ∈ ℕ, 𝑘 > 1, himpunan semua permutasi genap di 𝑆𝑘 adalah grup bagian dari 𝑆𝑘 yang disebut grup selang-seling dalam {1, 2, ⋯ , 𝑘} dan dinotasi-kan dengan 𝐴𝑘.
Bukti:
Misalkan 𝑘 ∈ ℕ, 𝑘 > 1 dan didefinisikan 𝐴𝑘 = {𝛼 ∈ 𝑆𝑘 | 𝛼 𝑎𝑑𝑎𝑙𝑎ℎ 𝑝𝑒𝑟𝑚𝑢𝑡𝑎𝑠𝑖 𝑔𝑒𝑛𝑎𝑝}. Karena permutasi identitas 𝜀 selalu meru-pakan permutasi genap karena 𝜀 = (1 2)(1 2) maka 𝜀 ∈ 𝐴𝑘 dan 𝐴𝑘 ≠ ∅. An-daikan 𝛼, 𝛽 ∈ 𝐴𝑘. Jadi 𝛼 dan 𝛽 keduanya adalah permutasi genap. Misalkan 𝛼 adalah komposisi dari 2𝑛 transposisi dan 𝛽 adalah komposisi dari 2𝑚 transpo-sisi. Dengan demikian 𝛼𝛽 adalah komposisi dari 2𝑛 + 2𝑚 transposisi, dan 2𝑛 + 2𝑚 adalah genap. Jadi 𝛼𝛽 ∈ 𝐴𝑘 dan 𝐴𝑘 tertutup terhadap komposisi. Se-lanjutnya untuk 𝛼 ∈ 𝐴𝑘, jika 𝛼 = 𝑡1𝑡2⋯ 𝑡2𝑛 ditulis sebagai komposisi dari transposisi maka menurut Teorema 2.9.
𝛼−1 = (𝑡1𝑡2⋯ 𝑡2𝑛)−1= (𝑡2𝑛)−1(𝑡2𝑛−1)−1⋯ (𝑡1)−1 = 𝑡2𝑛𝑡2𝑛−1⋯ 𝑡1 Maka 𝛼−1 dapat ditulis sebagai 2𝑛 transposisi. Jadi 𝛼−1∈ 𝐴
𝑘 dan 𝐴𝑘 tertutup terhadap invers. Dengan demikian 𝐴𝑘 adalah grup bagian dari 𝑆𝑘.■