PENDEKATAN REGRESI UNTUK ANALISIS VARIANSI

PENDEKATAN REGRESI UNTUK ANALISIS VARIANSI

SKRIPSI

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Oleh : DWI NOVIATI NIM : 993114020

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SANATA DHARMA YOGYAKARTA

Cita-cita adalah semangat hidup

karena hidup tanpa cita-cita

bagaikan menghitung bintang di langit

Dan seandainya pohon-pohon di bumi menjadi

pena, dan laut

menjadi tinta, ditambahkan kepadanya tujuh laut

lagi sesudah keringnya,

niscaya tidak akan babis-habisnya dituliskan

kalimat Allah.

Sesungguhnya Allah Maha Perkasa Lagi Maha

Bijaksana.

( Surat luqman, ayat 27 )

Kupersembahkan karya ini untuk :

Tuhan Y.M.E

Ayah ( Alm ) dan Ibu sebagai

tanda cinta dan wujud baktiku

PERNYATAAN KEASLIAN KARYA

Saya menyatakan dengan sesugguhnya bahwa skripsi yang saya tulis ini tidak memuat karya orang lain, kecuali yang telah disebut dalam kutipan dan daftar pustaka, sebagaimana layaknya karya ilmiah.

Yogyakarta, ………...

Penulis

ABSTRAK

ABSTRACT

The hypothesis testing of two mean values is done by using the z-tests and t-tests. But if there are three or more mean values then the testing is done by using Analysis of Variance (ANOVA). ANOVA is a method to descript the total variance of the data into some components coming from many sources of variance. The common model of one way classification ANOVA is

ij i ij

KATA PENGANTAR

Puji dan syukur penulis panjatkan kepada Tuhan Yang Maha Esa atas rahmat, kasih, dan karuniaNya, sehingga penyusunan skripsi yang berjudul “Pendekatan Regresi Untuk Analisis Variansi” dapat diselesaikan..

Dalam menulis skripsi ini banyak kesulitan dan hambatan yang penulis hadapi. Namun berkat bantuan dan dukungan dari berbagai pihak, akhirnya dapat terselesaikan. Untuk itu penulis ingin menyampaikan terimakasih yang sebesar-besarnnya kepada :

1. Bapak Ir. Ig. Aris Dwiatmoko, M.Sc sebagai dosen pembimbing skripsi yang telah meluangkan waktunya dengan kesabarannya membantu dan membimbing penulis sehingga penyusunan skripsi ini dapat diselesaikan. 2. Romo Dr. Frans. Susilo, SJ. selaku dosen pembimbing akademik.

3. Bapak Y.G. Hartono, S.Si, M.Sc. selaku Ketua Program Studi Matematika FMIPA USD Yogyakarta.

4. Ibu Lusia Krismiyati Budiasih, S.Si, M.Si dan ibu Enny Murwaningtyas, S.Si, M.Si selaku dosen penguji. Terimakasih atas kritik, saran, dan masukkan serta bimbingan selama menyelesaikan revisi.

5. Ibu Dra Maria Agustiani, M.Si. (Alm) yang telah memberi dorongan dan semangat selama perkulihan.

6. Ibu dan bapak dosen FMIPA yang telah memberikan ilmu yang sangat berguna bagi penulis.

8. Ayah (Alm) dan ibu tercinta, terimakasih atas kasih sayang, doa, dukungan moral dan material yang diberikan selama ini.

9. Terimakasih untuk adik-adikku lina, Erna, Bayu, ika, dini dan jepri yang memberiku semangat yang tiada henti-hentinya selama ini.

10.Sahabat-sahabat terbaikku : Ria, vivin, Chres, Vera, terimakasih atas doa, dukungan, dan tidak bosan-bosannya memberiku semangat.

11.Teman-teman seperjuanganku angkatan “99 : Apri, Nana, Desi, Yoslin, Eny, Yuda, Wondo, Antok, Hebby, Nia, Thomas, Delisa, Sigit, Mike, Andri, Alie, Catur, Ice, Wiwid, Johan, Naga, Nadi, Tanto, Yuli, Karlo, terimakasih atas kebersamaannya selama ini.

12.Semua angkatan “98, “00 dan “01. Buat Ajeng, very, makasih atas doa dan dukungannya selama ini.

13.Teman-teman kostku : Iin, Ita, Silvi, Tiyas, Valen, elly, Diah, Nety, terimakasih atas persahabatan yang indah selama ini.

14.Semua pihak yang tidak dapat disebutkan satu persatu yang telah membantu dalam penyusunan skripsi ini.

Penulis menyadari bahwa skripsi ini masih banyak kekurangannya. Meskipun demikian, penulis berharap skripsi ini dapat bermanfaat dan menjadi referensi bagi pembaca.

Yogyakarta, ………

DAFTAR ISI

Halaman

HALAMAN JUDUL ... i

HALAMAN PERSETUJUAN PEMBIMBING ……… ii

HALAMAN PENGESAHAN ……… iii

HALAMAN PERSEMBAHAN ……… iv

PERNYATAAN KEASLIAN KARYA ……… v

ABSTRAK ……… vi

ABSTRACT ……… vii

KATA PENGANTAR ……… viii

DAFTAR ISI ……….. x

DAFTAR TABEL ………... xiii

DAFTAR LAMPIRAN………... xiv

BAB I PENDAHULUAN ……….. 1

A. Latar Belakang Masalah ……… 1

B. Perumusan Masalah ………... 2

C. Pembatasan Masalah ……… 3

D. Tujuan Penulisan ……… 3

E. Manfaat Penulisan ……… 3

F. Metode Penulisan ……… 3

BAB II LANDASAN TEORI ………... 5

A. Analisis Variansi ……… 5

1. Distribusi F ……… 6

2. Analisis Variansi Klasifikasi Satu Arah ……… 10

3. Analisis Variansi Kasifikasi Dua Arah Tanpa Interaksi … 18 4. Analisis Variansi Klasifikasi Dua Arah Dengan Interaksi 28

5. Contoh Analisis Variansi ……… 41

B. Analisis Regresi ……….. 44

1. Regresi linier Sederhana ……… 44

2. Metode Kuadrat Terkecil ……….. 46

3. Regresi Berganda ……… 51

4. Pengujian Hipotesis ……… 55

C. Matriks Tak Singular……… 56

BAB III PENDEKATAN REGRESI UNTUK ANALISIS VARIANSI… 59 A. Pendekatan Regresi untuk Klasifikasi Satu Arah ……… 60

B. Pendekatan Regresi untuk Klasifikasi Dua Arah tanpa Interaksi ………. 65

C. Pendekatan Regresi untuk Klasifikasi Dua Arah dengan Interaksi ……… 70

BAB IV APLIKASI PENDEKATAN REGRESI UNTUK ANALISIS VARIANSI … ……….. 75

A. Tingkat Sisa Kerusakan Otak Selama Proses Penyembuhan 75

BAB V KESIMPULAN ……… 87

DAFTAR PUSTAKA ……… 88

DAFTAR TABEL

Halaman

DAFTAR LAMPIRAN

Halaman

Lampiran 1 ……… 89

Lampiran 2 ……… 93

BAB I

PENDAHULUAN

A. Latar Belakang Masalah

Variansi merupakan suatu ukuran penyebaran atau pemencaran nilai. Variansi dapat menggambarkan tingkat atau taraf keberagaman antar nilai. Variansi bersama dengan rata-rata banyak digunakan untuk menentukan kesimpulan mengenai populasi, melalui pendugaan dan pengujian hipotesis parameter. Variansi dari sekumpulan data menggambarkan derajat perbedaan atau variasi nilai yang ada dalam kelompok yang diperoleh dengan menghitung rata-rata dari kumpulan data tersebut.

Pengujian kesamaan rata-rata dari dua populasi dengan menggunakan sampel bebas, adalah dengan menggunakan uji z dan uji t. Uji z digunakan untuk menguji hipotesis mengenai rata-rata dari populasi normal, dengan sampel lebih dari 30 serta variansi populasi diketahui. Uji t digunakan untuk menguji hipotesis mengenai rata-rata dari dua populasi dengan sampel kurang dari 30 dan variansi populasi tidak diketahui. Pengujian hipotesis dengan uji z dan uji t hanya terbatas pada dua populasi saja. Jika lebih dari dua populasi maka menjadi tidak efisien karena:

1. Harus melalui pengujian tiap-tiap pasang sebanyak dua kombinasi k

populasi )(₂C_k .

Sekarang bagaimana menguji atau membandingkan dua atau lebih rata-rata populasi secara bersamaan atau simultan. Untuk melakukan pengujian secara simultan tersebut digunakan metode lain yang disebut analisis variansi (ANOVA). Uji Statistik dalam analisis variansi menggunakan distribusi F.

Namun analisis variansi dapat juga diselesaikan melalui pendekatan regresi. Analisis variansi dan analisis regresi digunakan untuk menyatakan hubungan antara variabel bebas dengan variabel tak bebas. Dalam analisis regresi variabel tak bebas dan variabel bebas bersifat kuantitatif. Sedangkan dalam analisis variansi, variabel tak bebas bersifat kuantitatif, tetapi variabel bebasnya bersifat kualitatif. Variabel kualitaif adalah variabel yang tidak memungkinkan dilakukannya pengukuran numerik. Pengamatannya berupa memasukkan suatu kriteria kedalam satu dari beberapa kategori yang saling terpisah. Pengamatan – pengamatan tersebut tidak dapat diurutkan secara berarti ataupun diukur, hanya diklasifikasikan. Agar dapat dilakukan perhitungan maka variabel yang sifatnya kualitatif diubah lebih dahulu kebentuk yang bersifat kuantitatif. Analisis variansi dengan variabel bebas bersifat kualitatif, dapat diselesaikan melalui pendekatan regresi yang variabel bebasnya bersifat kuantitatif, dengan menambahkan variabel boneka (Dummy variable).

B. Perumusan Masalah

Pokok permasalahan yang akan dibahas dalam skripsi ini adalah :

C. Pembatasan Masalah

Pada skripsi ini akan dibahas bentuk-bentuk analisis variansi dengan efek tetap saja. Asumsi-asumsi yang mendasari analisis regresi tidak diuji karena pada penulisan skripsi ini hanya menggunakan metodenya saja. Sedangkan mengenai matriks tak singular, teorema yang mendukung tidak dibuktikan.

D. Tujuan Penulisan

Tujuan penulis menyusun skripsi ini adalah untuk:

1. Menyusun model regresi melalui data yang berasal dari analisis variansi.

2. Melakukan pengujian hipotesis rata-rata dengan menggunakan pendekatan regresi.

E. Manfaat Penulisan

Manfaat penulisan ini adalah untuk memperdalam analisis variansi dan analisis regresi, serta mengetahui bahwa ANOVA dapat diselesaikan dengan menggunakan analisis regresi.

F. Metode Penulisan

G. Sistematika Penulisan

Sistematika penulisan dalam pembahasan mengenai pendekatan regresi untuk analisis variansi adalah sebagai berikut:

Bab I pendahuluan memberi gambaran umum mengenai isi skripsi meliputi latar belakang masalah, perumusan masalah, pembatasan masalah, tujuan penulisan, manfaat penulisan dan sistematika penulisan.

Bab II membahas tentang landasan teori meliputi distribusi F , bentuk-bentuk analisis variansi, analisis regresi dan matriks tak singular.

Bab III membahas tentang pendekatan regresi untuk analisis variansi dengan masing-masing bentuk klasifikasinya serta pengujian hipotesis.

Bab IV berisi tentang aplikasi pendekatan regresi untuk analisis variansi dengan menggunakan data.

BAB II

LANDASAN TEORI

A. Analisis Variansi

Analisis variansi (ANOVA) adalah suatu metode untuk menguraikan keragaman total data menjadi komponen-komponen yang mengukur berbagai sumber keragaman. Dasar pengujian yang digunakan didasarkan pada distribusi F. Distribusi F digunakan untuk menguji :

1. Apakah dua sempel berasal dari populasi dengan variansi yang sama. 2. Membandingkan dua atau lebih rata-rata populasi secara simultan. Dalam ANOVA memerlukan syarat-syarat berikut:

1. Populasi-populasi yang diteliti memiliki distribusi normal.

2. Populasi-populasi tersebut memiliki standar deviasi yang sama atau variansi yang sama.

3. Sampel yang diambil dari populasi tersebut bersifat bebas dan sampel yang diambil secara acak.

Dalam ANOVA akan dibandingkan keragaman yang ada di antara kelompok dan keragaman yang ada di dalam kelompok itu sendiri. Apabila keragaman di antara kelompok lebih besar dari pada keragaman di dalam kelompok, maka populasi-populasi tersebut mempunyai rata-rata yang berbeda.

1. Distribusi F

Distribusi F didefinisikan sebagai distribusi dari perbandingan dua variabel random Chi-square yang saling bebas, masing-masing dibagi dengan derajat bebasnya. Statistik F dapat ditulis sebagai

2 1

r V

r U

F = .

U dan V menyatakan variabel random bebas, masing-masing berdistribusi Chi-square, dengan derajat bebas r₁ dan r₂.

Teorema 2.1

Misalkan dua variabel random Chi-square yang saling independent u dan v yang mempunyai derajat bebas r₁ dan r₂.

2 1

r V

r U

F =

Variabel random F dikatakan memiliki distribusi F dengan derajat bebas r₁ dan

2

r bila fungsi densitasnya :

( )

( ) (

(

)

)

( )

selainnya ,

w , r

w r w r

r

r r r r w

g _{r r}

) r ( r

0

0 1

2 2

2

2

2 1

2 2

2 1

2 2 1 2 1

1

2 1 1 1

=

∞ < <

⎥ ⎦ ⎤ ⎢

⎣ ⎡

+ Γ

Γ ⎥⎦ ⎤ ⎢⎣ ⎡ + Γ =

⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + −

Bukti:

(

) (

)

selainnya v u v u v u r r v u h r r r r , 0 0 , 0 , 2 ) ( exp 2 2 2 1 ) , ( 2 ) 2 ( 2 ) 2 ( 2 ) ( 2 1 2 1 2 1 = ∞ < < ∞ < < ⎥⎦ ⎤ ⎢⎣ ⎡₋ + Γ Γ = ₊ − −

Didefinisikan variabel random baru

2 1 r V r U

W = . Akan ditunjukkan fungsi densitas

) (

1 w

g dari W. Persamaan

2 1 r v r u

w= . Andaikan v=z.

Didefinisikan sebuah transformasi satu-satu yang memetakan himpunan

{

< <∞ < <∞

}

=

{

< <∞ < <∞

}

= u v u v pada B w z w z

A ( , ):0 ,0 ( , ):0 , 0

karena 2 1 r v r u

w= dan z=v . Gantikan v dengan z akan menjadi

2 1 r z r u

w= maka zw

r r u

2 1

= sehingga dw

r z r du 2 1 =

sehingga didapat nilai mutlak dari transformasi jacobian adalah J =(r₁ r₂)z.

Fungsi densitas gabungang(w,z) dari variabel random W dan Z =V adalah

(

) (

)

⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ Γ Γ = − − + 2 1 2 1 2 ) 2 ( 2 ) 2 ( 2 1 2 ) ( 2 1 1 2 exp 2 2 2 1 ) , ( 2 1 2 1 _r z r r w r z z r zw r r r z w g r r r r

dengan (w,z)∈B dan 0 untuk yang lainnya. Fungsi densitas marjinal g₁(w) dari

w adalah

∫

∞

∞ −

= g(w,z)dz )

w ( g₁

( ) (

_{r r}

)

( ) r_rzw z exp z r_rw r_rz dz

( ) (

)

( ) ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ Γ Γ = − − − − ∞ +

∫

2 1 2 2 2 2 2 2 2 2 2 1 0 2 2 1 2 1 1 1 2 1 2 2 2 1 r z r ) z ( ) w ( ) z ( r r r r ) r ( ) r ( ) r ( ) r ( / r r dz r w r z exp ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − 1 2 ₂ 1

( ) (

)

( ) (w) (z) (z) (z)

r z r r r r r ) r ( ) r ( ) r ( ) r ( / r r 2 2 2 2 2 2 2 1 2 2 2 1 0 2 2 1 2 1 1 1 2 1 2 2 2

1 − − −

− ∞ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ Γ Γ =

∫

dz r w r z exp _⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − 1 2 ₂ 1

( ) (

)

( ) dz

r w r z exp ) z ( ) w ( r r r r ) r r ( ) r ( r / r r ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ Γ Γ = − + − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∞ +

∫

1 2 2 2 2 1 2 1 2 2 2 2 2 2 1 0 2 2 1 2 1 1 1 2 1

(

)

( ) (

)

r dz

w r z exp z r r ) w ( r

r (r r )

) r r ( r r ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − Γ Γ =∞

∫

− + + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 1 2 2 2 2 2 1 0 2 2 2 2 1 2 2 2 2 1 2 1 2 1 1 1

Jika variabel integrasinya diubah dengan _⎟⎟

⎠ ⎞ ⎜⎜ ⎝ ⎛ + = 1 2 ₂ 1 r w r z

y , dapat diperlihatkan

bahwa _⎟⎟

⎠ ⎞ ⎜⎜ ⎝ ⎛ + = 1 2 ₂ 1 r w r z

y maka

1 1 1 ₁ 2 − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + = r w r y z

sehingga dy

r w r dz 1 2 1 1 2 − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + =

masukkan kedalam persamaan berikut

(

)

( ) (

)

( )

r dy

w r z z r r w r r w g r r r r r r ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − Γ Γ =

∫

∞ ₊ + − − 1 2 exp 2 2 2 ) ( ) ( 2 1 0 2 ) 2 ( 2 ) ( 2 1 2 ) 2 ( 2 2 1 1 2 1 2 1 1 1

(

)

(

) (

)

r dy

w r z z r r w r r w g r r r r r r ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − Γ Γ =

∫

∞ ⎟⎠ ⎞ ⎜ ⎝ ⎛ + − + − 1 2 exp ) ( 2 2 2 ) ( ) ( 2 1 0 2 2 2 ) ( 2 1 2 ) 2 ( 2 2 1 1 2 1 2 1 1 1 =

(

)

(

) (

)

2 ) ( 2 1 2 ) 2 ( 2 2 1 2 1 1 1 2 2 2 ) ( r r r r r r w r r + − Γ Γ

∫

∞ ⎟⎠ ⎞ ⎜ ⎝ ⎛ + − − ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + 0 2 2 1 2 1 2 1 1 2 r r r w r y

( )

dy

r w r y exp ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − −1 2 1 ₁ 2

(

)

( ) (

)

⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − − ∞ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − + − ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + Γ Γ =

∫

2 2 1 2 1 0 2 2 2 2 2 2 1 2 2 2 2 1 2 1 2 1 2 1 2 1 1 1 1 2 2 2 2 r r r r r r ) r r ( ) r ( r r w r y r r ) w ( r r

( )

dy

r w r y exp ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − −1 2 1 ₁ 2

(

) ( )

( ) (

)

⎥⎥⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + Γ Γ = − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − + − ₁ 2 1 2 2 1 2 1 2 2 2 2 1 2 2 2 2 1 1 2 1 2 2 2 2 2 1 2 1 2 1 1 1 r w r r w r r r w r r r r r r ) r r ( ) r ( r

( )

y dy exp y r r −

∫

∞ _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − 0 2 2 2 1

(

) ( )

( ) (

)

1 2 1 1 2 1 2 2 1 1 2 2 2 1 2 2 2 2

1 _{2 2 1 1 2 1}

2 2 2 2 1 2 1 2 1 1

1 _⎟⎟ −

(

)

(

) (

)

( )

selainnya w

r w r w r

r

r r r r

r r r r

, 0

0 , 1

2 2

2

2

2 1

2 ) 2 (

2 1

2 2 1 2 1

2 1 1 1

=

∞ < <

⎥ ⎦ ⎤ ⎢

⎣ ⎡

+ Γ

Γ ⎥⎦

⎤ ⎢⎣

⎡ + Γ =

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + −

2. Analisis Variansi Klasifikasi Satu Arah

Misalkan terdapat k populasi. Dari masing-masing populasi diambil sampel berukuran n. Populasi tersebut menyebar normal dengan rata-rata

k

μ μ

μ₁, ₂,..., dan variansi sama σ2. Akan dilakukan pengujian hipotesis :

k

H₀ :μ₁ =μ₂ =...=μ .

1

H : ∃μi ≠μj,i≠ j.

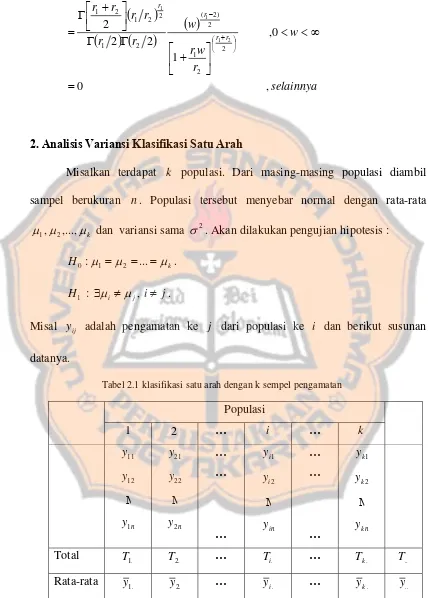
Misal yij adalah pengamatan ke j dari populasi ke i dan berikut susunan datanya.

Tabel 2.1 klasifikasi satu arah dengan k sempel pengamatan

Populasi

1 2 … i … k

11

y

12

y

Μ

n

y₁

21

y

22

y

Μ

n

y₂

… …

…

1 i

y

2 i

y

Μ

in

y

… …

…

1 k

y

2 k

y

Μ

kn

y

Total T_1. T_2. … T_i. … T_k. T_..

Dimana . i

T = Total semua pengamatan sampel dari populasi ke i. ..

T = Total semua nk pengamatan. .

i

y = Rata-rata semua pengamatan sampel dari populasi ke i. ..

y = Rata-rata semua nk pengamatan. Setiap pengamatan dapat dituliskan dalam bentuk

ij i ij

y =μ +ε (2.1)

Bila ε_ij adalah simpangan pengamatan ke j dalam sampel ke i dari rata-rata populasi ke i. Bentuk lain dari persamaan ini diperoleh dengan substitusi

i i μ α

μ = + , sedangkan μ adalah rata-rata semua μi artinya

k

k

i i

∑

=

= 1 μ μ

maka persamaan (2.1) menjadi

ij i ij

y =μ +α +ε (2.2)

dengan ketentuan

(

)

0

1 1

= − =

∑

∑

= =

k

i i k

i

i μ μ

α

dengan α_i sebagai pengaruh populasi ke i.

Jadi menduga μ,α_idan ε_ij dengan membuat jumlah kuadrat sisa atau galat sekecil mungkin. Jumlah kuadrat galat ditulis dengan

(

JKG

)

.

(

)

∑∑

= =

= k

i n

j ij

JKG

1 1 2 ε

(

)

∑∑

= =

− −

= k

i n

j

i ij

y

1 1

2 α

μ (2.3)

Penduga bagi μ adalah μˆ maka

(

)

(

)

0

1 1

2

= ∂

⎭ ⎬ ⎫ ⎩

⎨ ⎧

− − ∂

= ∂

∂

∑∑

= =

μ α μ

μ

k

i n

j

i ij

y JKG

(

)

0

2

1 1

= − −

−

∑∑

= =

k

i n

j

i ij ˆ

y μ α

0

1 1 1 1 1 1

= −

−

∑∑

∑∑ ∑∑

= = = = = =

k

i n

j

k

i n

j

k

i n

j i ij ˆ

y μ α

∑∑

∑∑

= = = =

= − −

k

i n

j

k

i n

j ij ˆ

y

1 1 1 1

0 0

μ

∑∑ ∑∑

= = = =

=

k

i n

j

k

i n

j ij

y ˆ

1 1 1 1

μ

kn y ˆ

k

i n

j ij

∑∑

= =

= 1 1

μ

..

y ˆ =

μ (2.3a)

Penduga bagi αi adalah αˆ maka i

(

)

(

)

0 1 1

2

= ∂

⎭ ⎬ ⎫ ⎩

⎨ ⎧

− − ∂

= ∂

∂

∑∑

= =

i k

i n

j

i ij

i

y JKG

α

α μ

(

)

0 2

1 1

= − −

−

∑∑

= =

k

i n

j

i ij ˆ ˆ

y μ α

0

1 1 1 1 1 1

= −

−

∑∑

∑∑ ∑∑

= = = = = =

k

i n

j

k

i n

j

k

i n

j i

ij ˆ ˆ

y μ α

∑∑

∑∑

∑∑

= = = = = =

− =

k

i n

j

k

i n

j

k

i n

j ij

i y ˆ

ˆ

1 1 1 1 1 1

μ α

karena μˆ = y.. maka

∑∑

∑∑

∑∑

= = = = = =

− =

k

i n

j

k

i n

j

k

i n

j .. ij

i y y

ˆ

1 1 1 1 1 1

α

∑

= −

= n

j

.. .

i

i y kny

ˆ kn

1 α

kn y kn y ˆ

n

j

.. .

i

i

∑

= −

= 1

α

kn y kn ny

ˆ i. ..

i

− =

α

.. . i

i y

k y

ˆ = −

α

.. . i i y y

ˆ = −

α (2.3b)

Apabila ε_ij adalah galat, penduganya adalah e_ij, akan diperoleh dengan memasukkan parameter μˆ,αˆi pada persamaan (2.2) sehingga didapat

(

i. ..

)

.. ij

ij y y y y

e = − − −

. i ij ij y y

e = − (2.3c)

Parameter yang didapat disubstitusikan dalam persamaan (2.2) menjadi

(

y y

)

(

y y

)

y

Dengan sedikit merubah susunannya menjadi

(

yij −y..

)

=

(

yi. −y..

)

+

(

yij −yi.

)

Kemudian kedua ruas dikuadratkan dan dijumlahkan diperoleh bentuk berikut

(

)

[

(

)

(

)

]

(

)

(

)

(

) (

)

[

]

(

)

(

)

(

)

(

)

∑∑

∑∑

∑∑

∑∑

∑∑

∑∑

= =

= =

= =

= =

= = = =

− +

− −

+ − =

− + − −

+ −

=

− + − =

−

k

i n

j

i ij

k

i n

j

i ij i

k

i n

j i k

i n

j

i ij i ij i

i k

i n

j

k

i n

j

i ij i

ij

y y

y y y y y

y

y y y y y y y

y

y y y y y

y

1 1

2 .

1 1

. ..

. 1 1

2 .. . 1 1

2 . .

.. . 2

.. .

1 1 1 1

2 . ..

. 2

..

2 2

Penjumlahan yang ditengah sama dengan nol, karena

(

)

i.

n

j ij n

j

. i

ij y y ny

y − =

∑

−

∑

=

=1 1

⎟⎟ ⎟ ⎟ ⎟

⎠ ⎞

⎜⎜ ⎜ ⎜ ⎜

⎝ ⎛

−

=

∑

∑

=

= n

y n y

n

j ij n

j ij

1

1

0 =

Penjumlahan yang pertama tidak mempunyai j sebagai subkrip, maka dapat dituliskan sebagai

(

)

(

)

∑∑

∑

= = =

− =

−

k

i n

j

k

i

.. . i ..

.

i y n y y

y

1 1 1

2 2

sehingga menjadi

(

)

(

)

∑∑

(

)

∑∑

∑

= =

= = =

− +

− =

− k

i n

j

. i ij k

i n

j

k

i

.. . i ..

ij y n y y y y

y

1 1

2

1 1 1

2 2

Ruas kiri disebut jumlah kuadrat total, ditulis dengan

(

JKT

)

. Ruas kanan suku pertama disebut jumlah kuadrat antar kelompok, ditulis

(

JKK

)

. Suku kedua disebut jumlah kuadrat dalam kelompok, ditulis

(

JKG

)

.

Sehingga jumlah kuadrat total dapat dituliskan sebagai berikut

JKG JKK

JKT = +

Untuk memudahkan perhitungan dilakukan penyederhanaan rumus berikut

(

)

(

)

∑

∑

∑

∑

∑∑

∑∑

∑∑

= = = = = =

= =

= =

+ −

=

+ −

=

− =

k

i

k

i

k

i n

j n

j ij n

j ij k

i n

j

ij ij k

i n

j ij

y y

y y

y y y y

y y JKT

1 1 1 1

2 .. 1

.. 1

2 1 1

2 .. .. 2

1 1

2 ..

2 2

dengan

∑∑

= =

= k

i n

j ij .. y

y

1 1

dan

kn y y.. = ..

∑∑

= =

+ −

= k

i

.. ..

.. n

j

ij kny y kny

y

1

2

1 2

2

∑∑

= =

+ −

= k

i

.. ..

n

j

ij kny kny

y

1

2 2

1 2

2

∑∑

= =

−

= k

i

.. n

j

ij kny

y

1

2

1 2

∑∑

= =

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −

= k

i

.. n

j ij

kn y kn y

1

2

1 2

∑∑

= =

− = k

i

.. n

j ij

kn y y

1

2

1 2

(

)

∑

=

− = k

i

.. . i y

y n JKK

1

2

(

)

∑

=

+ −

= k

i

.. .. . i .

i y y y

y n

1

2 2

2

∑

∑

∑

= =

=

+ −

= k

i k

i i k

i

i n y y n y

y n

1 2 .. 1

.. . 1

2 . 2

dengan _..

k

i . i ky

y =

∑

=1

dan

n y y

n

j ij

. i

∑

=

= 1

∑

∑

=

= _{− +}

⎟⎟ ⎟ ⎟ ⎟

⎠ ⎞

⎜⎜ ⎜ ⎜ ⎜

⎝ ⎛

= k

i

.. ..

.. n

j ij

y kn y k y n n

y

n

1

2 2

1

2

2 2

1

.. k

i . i

y kn n

y

n ⎟ −

⎠ ⎞ ⎜ ⎝ ⎛

=

∑

=

2 1

2

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − =

∑

=

kn y kn n

y

.. k

i . i

kn y n

y

.. k

i . i 2 1

2 −

=

∑

= _(2.4b)

JKK JKT

JKG = − (2.4c)

Tabel 2.2 analisis variansi satu arah

Sumber Jumlah Kuadrat Derajat Bebas Kuadrat Tengah

hitung

F

Kelompok _{JKK k} −₁ 2

(

₁

)

1 =JKK k−

s f =s₁2 s₂2

Galat _{JKG k}

(

_n−₁

)

2

(

₁

)

2 =JKG k n−

s

Total _{JKT nk}−₁

Langkah-langkah pengujian Hipotesis 1. Rumusan hipotesis

k

H₀:μ₁=μ₂ =...=μ .

1

H : ∃μi ≠μj,i≠ j.

2. Tentukan α . 3. Wilayah kritis.

0

H ditolak bila f_hitung < f_α

[

k −1,k

(

n−1

)

]

. 4. Perhitungan.

5. Tabel analisis variansi. 6. Kesimpulan.

Telah diketahui bahwa setiap pengamatan ditulis sebagai berikut ij

i ij

y =μ +ε

dan diketahui pula bahwa i i μ α

μ = + atau μ_i −μ =α_i

kedua hipotesis H₀:μ₁ =μ₂ =...=μ_k dan H₀ :α₁ =α₂ =...=α_k =0 adalah sama. Jadi pada dasarnya menguji kesamaan rata-rata antara kelompok adalah sama dengan menguji pengaruh perlakuan.

3. Analisis Variansi Klasifikasi Dua Arah Tanpa Interaksi

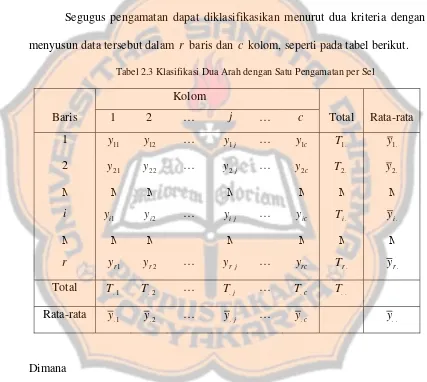
Segugus pengamatan dapat diklasifikasikan menurut dua kriteria dengan menyusun data tersebut dalam r baris dan c kolom, seperti pada tabel berikut.

Tabel 2.3 Klasifikasi Dua Arah dengan Satu Pengamatan per Sel

Kolom

Baris 1 2 … j … c Total Rata-rata

1 y₁₁ y₁₂ … y_1j … y_1c T_1. y_1.

2 y₂₁ y₂₂ … y_2j … y_2c T_2. y_2.

Μ Μ Μ Μ Μ Μ Μ

i

1 i

y y_i2 … y_ij … y_ic T_i. y_i.

Μ Μ Μ Μ Μ Μ Μ

r y_r1 y_r2 … y_rj … y_rc Tr_. yr. Total T_.1 T_.2 … T_.j … T_.c T_..

Rata-rata 1 .

y y_.2 … y_.j … y_.c y_..

Dimana . i

T = Total semua pengamatan dalam baris ke i.

j

T_. = Total semua pengamatan dalam kolom ke j. .

.

T = Total semua rcpengamatan .

i

Rata-rata populasi pada baris ke i adalah

c

c

j ij

i

∑

=

= 1

.

μ μ

Rata-rata populasi bagi kolom ke j adalah

r

r

i ij

j

∑

=

= 1 .

μ μ

Rata-rata rc populasi adalah

rc

r c ij

∑∑

=

μ μ

Setiap pengamatan dapat dituliskan dalam bentuk ij

ij ij

y =μ +ε (2.5)

Dimana ε_ij adalah simpangan nilai pengamatan y_ij dari rata-rata populasi μ_ij. Bila α_i adalah pengaruh baris ke i dan β_j adalah pengaruh kolom ke j maka diperoleh

j i ij μ α β

μ = + +

Sehingga persamaan diatas menjadi ij j i ij

y =μ+α +β +ε (2.6)

Kemudian disyaratkan

∑

∑

= =

= =

r

i

c

j j i

1 1

0

0 β

Nilai ,μ,α_i, β_j dapat diperoleh dengan metode kuadrat terkecil. Nilai tersebut didapatkan dengan meminimumkan jumlah kuadrat galat, dan ditulis

(

JKG

)

.

∑∑

= =

= r

i c

j ij

JKG

1 1 2

ε

(

)

∑∑

= =

− − −

= r

i c

j

j i ij

y

1 1

2 β α

μ (2.7)

Penduga nilai μ adalah μˆ maka

(

)

(

)

0 1 1

2

= ∂

⎭ ⎬ ⎫ ⎩

⎨ ⎧

− − − ∂

= ∂

∂

∑∑

= =

μ

β α μ

μ

r

i c

j

j i ij

y JKG

(

)

0

2

1 1

= − − −

−

∑∑

= =

r

i c

j

j i ij ˆ

y μ α β

0

1 1 1 1 1 1 1 1

= −

− −

∑∑

∑∑ ∑∑

∑∑

= = = = = = = =

r

i c

j

r

i c

j

r

i c

j

r

i c

j j i

ij ˆ

y μ α β

0 0 0

1 1 1 1

= − − −

∑∑

∑∑

= = = =

r

i c

j

r

i c

j ij ˆ

y μ

0

1 1

= −

∑∑

= =

μˆ rc y

r

i c

j ij

rc y ˆ

r

i c

j ij

∑∑

= =

= 1 1

μ

..

y ˆ =

μ (2.7a)

Penduga nilai α_i adalah αˆ maka _i

(

)

(

)

0

1 1

2

= ∂

⎭ ⎬ ⎫ ⎩

⎨ ⎧

− − − ∂

= ∂

∂

∑∑

= =

i r

i c

j

j i ij

i

y JKG

α

β α μ

(

)

0 2

1 1

= − − −

−

∑∑

= =

r

i c

j

j i ij ˆ ˆ

y μ α β

0

1 1 1 1 1 1 1 1

= −

− −

∑∑

∑∑ ∑∑

∑∑

= = = = = = = =

r

i c

j

r

i c

j

r

i c

j

r

i c

j j i

ij ˆ ˆ

y μ α β

0 0

1 1 1 1 1 1

= − −

−

∑∑

∑∑ ∑∑

= = = = = =

r

i c

j

r

i c

j

r

i c

j i

ij ˆ ˆ

y μ α

0

1 1 1 1 1 1

= −

−

∑∑

∑∑ ∑∑

= = = = = =

r

i c

j

r

i c

j

r

i c

j i

ij ˆ ˆ

y μ α

∑∑

∑∑

∑∑

= = = =

= =

−

= r

i c

j

r

i c

j ij r

i c

j

i y ˆ

ˆ

1 1 1 1

1 1

μ α

karena μˆ = y_.. maka

∑∑

∑∑

∑∑

= = = =

= =

−

= r

i c

j

r

i c

j .. ij

r

i c

j

i y y

ˆ

1 1 1 1

1 1 α

∑

=

− = c

i

.. .

i i y rcy

ˆ rc

1 α

rc y rc y ˆ

.. c

i . i i

− =

∑

=1 α

rc y rc y c

ˆ i. ..

i

− =

α

.. . i

i y

r y

ˆ = −

α

.. . i i y y

ˆ = −

Penduga nilai β adalah βˆ maka _j

(

)

(

)

0 1 1

2

= ∂

⎭ ⎬ ⎫ ⎩

⎨ ⎧

− − − ∂

= ∂

∂

∑∑

= =

j r

i c

j

j i ij

j

y JKG

β

β α μ

β

(

)

0

2

1 1

= − − −

−

∑∑

= =

r

i c

j

j i ij ˆ ˆ ˆ

y μ α β

0

1 1 1 1 1 1 1 1

= −

− −

∑∑

∑∑ ∑∑

∑∑

= = = = = = = =

r

i c

j

r

i c

j

r

i c

j

r

i c

j j i

ij ˆ ˆ ˆ

y μ α β

0 0

1 1 1 1 1 1

= −

− −

∑∑

∑∑

∑∑

= = = = = =

r

i c

j

r

i c

j

r

i c

j j

ij ˆ ˆ

y μ β

∑∑

∑∑

∑∑

= = = =

= =

−

= r

i c

j

r

i c

j ij r

i c

j

j y ˆ

ˆ

1 1 1 1

1 1

μ

β

karena αˆ_i = y_i.−y_.. maka

∑∑

∑∑

∑∑

= = = =

= =

−

= r

i c

j

r

i c

j .. ij

r

i c

j

j y y

ˆ

1 1 1 1

1 1 β

.. r

i j .

j y rcy

ˆ

rc =

∑

−

=1 β

rc y rc y ˆ

.. r

i j .

j

− =

∑

=1 β

rc y rc y r

ˆ .j ..

j

− =

β

.. j .

j y

c y

ˆ _{= −}

β

.. j . j y y

ˆ _{= −}

Apabila ε_ij adalah galat, diduga dengan e_ij, akan diperoleh melalui substitusi penduga μ,α_i,β_j kedalam persamaan (2.6) sehingga didapat

(

i. ..

)

(

.j ..

)

..

ij

ij y y y y y y

e = − − − − −

.. j . . i ij

ij y y y y

e = − − + (2.7d)

Parameter yang telah didapat disubstitusikan dalam persamaan (2.6) menjadi

(

i. ..

)

(

.j ..

) (

ij i. .j ..

)

..

ij y y y y y y y y y

y = + − + − + − − +

Dengan sedikit merubah susunannya akan menjadi

(

yij −y..

)

=

(

yi.−y..

)

+

(

y.j −y..

) (

+ yij −yi.−y.j +y..

)

Kemudian kedua ruas dikuadratkan dan dijumlakan diperoleh persamaan berikut

(

)

(

(

)

(

) (

)

)

∑∑

∑∑

= = = =

+ − − + − + − =

−

r

i c

j

r

i c

j

.. j . . i ij ..

j . ..

. i ..

ij y y y y y y y y y

y

1 1 1 1

2 2

2 2

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)(

. . ..

)

1 1

.. .

.. . . 1 1

.. .

.. . 1 1

.. .

1 1

2 .. . .

1 1 1 1

2 .. . 2

.. .

2 2 2

y y y y y y

y y y y y y

y y y y

y y y y y

y y

y

j i ij r

i c

j j

j i ij r

i c

j i

j r

i c

j i

r

i c

j

j i ij r

i c

j

r

i c

j j i

+ − − −

+

+ − − −

+

− −

+

+ − − +

− +

− =

∑∑

∑∑

∑∑

∑∑

∑∑

∑∑

= =

= =

= =

= =

= = = =

(

)

∑

(

)

∑

(

)

∑∑

(

)

∑∑

= = = =

= =

+ − − +

− +

− =

− r

i

c

j

r

i c

j

.. j . . i ij ..

j . ..

. i r

i c

j

..

ij y c y y r y y y y y y

y

1 1 1 1

2 2

2

1 1

2

Ruas kiri disebut jumlah kuadat total

(

JKT

)

, sedang ruas kanan suku pertama disebut jumlah kuadrat karena baris

(

JKB

)

, suku kedua disebut jumlah kuadrat karena kolom

(

JKK

)

, suku ketiga disebut jumlah kuadrat galat

(

JKG

)

.

Sehingga jumlah kuadrat total dapat dituliskan sebagai berikut

JKG JKK

JKB

JKT = + +

Untuk memudahkan perhitungan maka dilakukan penyederhanaan rumus sebagai berikut

(

)

∑∑

= =

−

= r

i c

j

.. ij y

y JKT

1 1

2

(

)

∑∑

= =

+ −

= r

i c

j

.. .. ij ij y y y

y

1 1

2 2

2

∑∑

∑∑

∑∑

= = = = = =

+ −

= r

i c

j

r

i c

j

r

i c

j .. ij

..

ij y y y

y

1 1 1 1 1 1

2 2

2

dengan

∑∑

= =

= r

i c

j ij

y ..

y

1 1

dan

rc y

y ..

.. =

∑∑

= =

+ −

= r

i

.. ..

.. c

j

ij y rcy rcy

y

1

2

1 2

2

∑∑

= =

+ −

= r

i

.. ..

c

j

ij rcy rcy

y

1

2 2

1 2

2

∑∑

= =

−

= r

i

.. c

j

ij rcy

y

1

2

1 2

2

1 1 2

∑∑

= =

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −

= r

i

.. c

j ij

rc y rc y

∑∑

= =

− = r

i

.. c

j ij

rc y y

1

2

1 2

(

)

∑

=

− = r

i

.. . i y

y c JKB

1

2

(

)

∑

=

+ −

= r

i

.. .. . i .

i y y y

y c

1

2 2

2

∑

∑

∑

= =

=

+ −

= r

i

r

i .. .

i .. r

i .

i cy y c y

y c

1 1

2

1 2

2

dengan _..

r

i . i ry

y =

∑

=1

dan

c y y

c

j ij

. i

∑

=

= 1

2 2

1 1

2 .. ,, .. r

i c

j ij

y rc y r y c c

y

c − +

⎟⎟ ⎟ ⎟ ⎟

⎠ ⎞

⎜⎜ ⎜ ⎜ ⎜

⎝ ⎛

=

∑

∑

= =

2 2

2

1

2 _{.. ..}

r

i . i

y rc y rc c

y

c ⎟ − +

⎠ ⎞ ⎜ ⎝ ⎛

=

∑

=

2 1

2

.. r

i . i

y rc c

y

− =

∑

=

2 1

2

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − =

∑

=

rc y rc c

y

.. r

i . i

rc y c

y

.. r

i . i 2 1

2 −

(

)

∑

= −

= c

j

.. j . y

y r JKK

1

2

(

)

∑

=

+ −

= c

j

.. .. j . j

. y y y

y r

1

2 2

2

∑

∑

∑

= =

=

+ −

= c

j

c

i .. j

. .. c

j j

. ry y r y

y r

1 1

2

1 2

2

dengan _..

c

j j . cy

y =

∑

=1

dan

r y y

r

i ij

j .

∑

=

= 1

2 2

1 1

2 _{.. ,, ..}

r

j r

i ij

y rc y c y r r

y

r − +

⎟ ⎟ ⎟ ⎟

⎠ ⎞

⎜ ⎜ ⎜ ⎜

⎝ ⎛

=

∑

∑

= =

2 2

2

2

2 .. .. r

i j .

y rc y rc r

y

r _⎟⎟ − +

⎠ ⎞ ⎜⎜ ⎝ ⎛

=

∑

=

2 1

2

.. c

i j .

y rc c

y

− =

∑

=

2 1

2

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − =

∑

=

rc y rc r

y

.. c

i j .

rc y r

y

.. c

j j . 2 1

2

−

=

∑

= (2.8c)

JKK JKB JKT

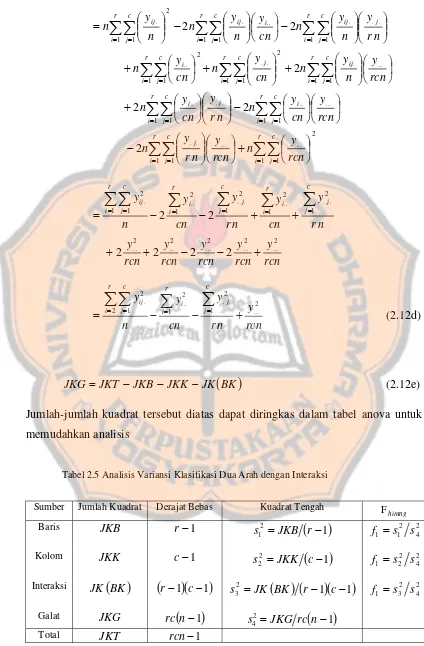
Jumlah-jumlah kuadrat tersebut dapat diringkas dalam tabel anova untuk memudahkan analisis.

Tabel 2.3 Analisis Variansi Dua Arah tanpa Interaksi

Sumber Jumlah Kuadrat Derajat Bebas Kuadrat Tengah

hitung

F

Baris _{JKB r}−₁ 2

(

₁

)

1 =JKB r−

s 32

2 1 1 s s

f =

Kolom _{JKK c}−₁ 2

(

₁

)

2 = JKK c−

s f₂ =s₂2 s₃2

Galat JKG

(

r−1

)(

c−1

)

s₃2 = JKG

(

r−1

)(

c−1

)

Total JKT rc−1

Langkah-langkah pengujian hipotesis 1. Rumusan hipotesis.

a. H₀′ :α₁ =α₂ =...=α_r =0.

1

H′: 0∃αi ≠ .

b. H₀′′:β₁ =β₂ =...=β_c =0. H₁′′: 0∃β_j ≠ .

2. Tentukan α . 3. Wilayah kritis

a. H0 ditolak bila f1 > fα

[

r−1,rc

(

n−1

)

]

. b. H₀ ditolak bila f₂ > f_α

[

c−1,rc

(

n−1

)

]

. 4. Perhitungan.

4. Analisis Variansi Klasifikasi Dua Arah Dengan Interaksi

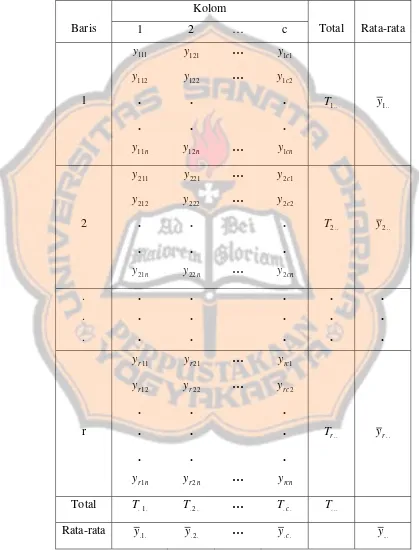
Tabel 2.4 Klasifikasi Dua Arah dengan Beberapa Pengamatan per Sel

Kolom

Baris 1 2 … c Total Rata-rata

111

y y₁₂₁ … y_1c1

112

y y122 … y1c2

1 . . . T_1.. y_1..

. . . n

y11 y12n … y1cn 211

y y₂₂₁ … y_2c1

212

y y222 … y2c2

2 . . . T_2.. y_2..

. . . n

y₂₁ y_22n … y_2cn

. . . . . .

. . . . . .

. . . . . .

11 r

y y_r21 … y_rc1

12 r

y y_r22 … y_rc2

. . .

r . . . T_r.. y_r..

. . . n

r

y₁ y_r2n … y_rcn

Total T_.1. T.2. … T.c. T...

Dimana :

. ij

T = Total pengamatan dalam sel ke ij. ..

i

T = Total pengamatan dalam baris ke i. .

.j

T = Total pengamatan dalam kolom ke j. ...

T = Total semua rcnpengamatan. .

ij

y = Rata-rata pengamatan dalam sel ke ij. ..

i

y = Rata-rata pengamatan dalam baris ke i. .

j .

y = Rata-rata pengamatan dalam kolom ke j. ...

y = Rata-rata semua rcnpengamatan.

Rata-rata umum pengamatan adalah

rcn y

y

r

i c

j n

k ijk

...

∑∑∑

= = =

= 1 1 1

Rata-rata baris ke i adalah

cn y

y

c

j n

k ijk

.. i

∑∑

= =

= 1 1

Rata-rata kolom ke j adalah

n r

y y

r

i n

k ijk

. j .

∑∑

= =

= 1 1

Rata-rata sel ke ijadalah

n y y

n

k ijk

. ij

∑

=

= 1

Setiap pengamatan dalam sel yijk dapat dituliskan dalam bentuk ijk

ij ijk

Dimana ε_ijk merupakan simpangan nilai y_ijk yang teramati pada sel ke ij dari rata-rata populasi μ_ij. Misalkan

( )

αβ _ij melambangkan pengaruh interaksi baris ke

i dan kolom ke j, maka α_i adalah pengaruh baris ke i, dan β_j adalah pengaruh kolom ke j serta μ adalah rata-rata umum.

Sehingga persamaannya menjadi

( )

ij j

i

ij μ α β αβ

μ = + + +

maka persamaan (2.9) menjadi

( )

ij ijk j

i ijk

y =μ+α +β + αβ +ε (2.10)

dan kemudian dikenakan syarat

0 1

=

∑

=

r

i i

α 0

1

=

∑

=

c

j j

β

( )

0

1

=

∑

=

r

i

ij

αβ

( )

0

1

=

∑

=

c

j

ij

αβ

Nilai dari μ,α,β,(αβ ) diperoleh melalui pendugaan dengan menggunakan metode kuadrat terkecil, sehingga jumlah kuadrat semua simpangan itu minimum. Jumlah kuadrat semua simpangan disebut jumlah kuadrat galat

(

JKG

)

.

∑∑∑

= = =

= r

i c

j n

k ijk

JKG

1 1 1 2 ε

( )

(

)

∑∑∑

= = =

− − − −

= r

i c

j n

k

ij j

i ijk

y

1 1 1

2 αβ β

α

μ (2.11)

Penduga untuk nilai μ adalah μˆ maka

(

)

(

( )

)

0 1 1 1

2

= ∂

⎭ ⎬ ⎫ ⎩

⎨ ⎧

− − − − ∂

= ∂

∂

∑∑∑

= = =

μ

αβ β

α μ

μ

r

i c

j n

k

ij j

i ijk

( )

(

)

0

2

1 1 1

= − − − − −

∑∑∑

= = = r i c j n k ij j i ijk ˆ

y μ α β αβ

( )

0

1 1 1 1 1 1

1 1 1 1 1 1

1 1 1

= − − − −

∑∑∑

∑∑∑

∑∑∑

∑∑∑

∑∑∑

= = = = = = = = = = = = = = = r i c j n k ij r i c j n k j r i c j n k i r i c j n k r i c j n k ijk ˆ

y μ α β αβ

0 0 0 0

1 1 1 1 1 1

= − − − −

∑∑∑

∑∑∑

= = = = = = r i c j n k r i c j n k ijk ˆ y μ 0

1 1 1

= −

∑∑∑

= = = μˆ rcn y r i c j n k ijk rcn y ˆ r i c j n k ijk

∑∑∑

= = =

= 1 1 1

μ

...

y ˆ =

μ (2.11a)

Penduga untuk nilai α_i adalah αˆ maka _i

(

)

(

( )

)

0

1 1 1

2 = ∂ ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ − − − − ∂ = ∂ ∂

∑∑∑

= = = i r i c j n k ij j i ijk i y JKG α αβ β α μ α

( )

(

)

0

2

1 1 1

= − − − − −

∑∑∑

= = = r i c j n k ij j i ijk ˆ ˆ

y μ α β αβ

( )

0

1 1 1 1 1 1

1 1 1 1 1 1

1 1 1

= − − − −

∑∑∑

∑∑∑

∑∑∑

∑∑∑

∑∑∑

= = = = = = = = = = = = = = = r i c j n k ij r i c j n k j r i c j n k i r i c j n k r i c j n k

ijk ˆ ˆ

y μ α β αβ

( )

0

1 1 1 1 1

1 1 1 1 1 1

1 1 1

= ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − − −

∑∑∑

∑∑∑

∑∑∑

∑∑ ∑

∑∑∑

= = = = = = = = = = = = = = c j n