Pada skripsi ini akan dibahas bilangan keterhubungan pelangi kuat untuk graf terhubung tak trivial dan graf lainnya seperti pohon, graf siklus, graf roda dan graf bipartit. Pendistribusian soal ujian nasional dan kertas suara PILKADA merupakan beberapa penerapan dari bilangan keterhubungan pelangi kuat pada graf. Pada pendistribusian soal ujian nasional dan kertas suara PILKADA, bilangan keterhubungan pelangi kuat digunakan untuk menentukan jumlah kelompok pengawalan pendistribusian.
In this thesis strong rainbow connection number of a nontrivial connected graph and other graphs such as tree, cycle graph, wheel graph and bipartite graph will be discussed. The distribution of the national examination papers and PILKADA ballot papers are some applications of strong rainbow connection numbers of a graph. In the distribution of the national examination papers and PILKADA ballot papers strong rainbow connection numbers are used to determine the number of distributing escort groups.
i
BILANGAN KETERHUBUNGAN PELANGI KUAT
PADA GRAF
SKRIPSI
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains
Program Studi Matematika
Disusun oleh: Natalya Dewi Hutami
NIM: 133114002
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA
FAKULTAS SAINS DAN TEKNOLOGI UNIVERSITAS SANATA DHARMA
ii
STRONG RAINBOW CONNECTION NUMBER IN GRAPH
A THESIS
Presented as Partial Fulfillment of the
Requirements to Obtain the Degree of Sarjana Sains Mathematics Study Program
Written by: Natalya Dewi Hutami Student ID: 133114002
MATHEMATICS STUDY PROGRAM DEPARTMENT OF MATEMATICS FACULTY OF SCIENCE AND TECHNOLOGY
SANATA DHARMA UNIVERSITY YOGYAKARTA
vii ABSTRAK
Pada skripsi ini akan dibahas bilangan keterhubungan pelangi kuat untuk graf terhubung tak trivial dan graf lainnya seperti pohon, graf siklus, graf roda dan graf bipartit. Pendistribusian soal ujian nasional dan kertas suara PILKADA merupakan beberapa penerapan dari bilangan keterhubungan pelangi kuat pada graf. Pada pendistribusian soal ujian nasional dan kertas suara PILKADA, bilangan keterhubungan pelangi kuat digunakan untuk menentukan jumlah kelompok pengawalan pendistribusian.
viii ABSTRACT
In this thesis strong rainbow connection number of a nontrivial connected graph and other graphs such as tree, cycle graph, wheel graph and bipartite graph will be discussed. The distribution of the national examination papers and PILKADA ballot papers are some applications of strong rainbow connection numbers of a graph. In the distribution of the national examination papers and PILKADA ballot papers strong rainbow connection numbers are used to determine the number of distributing escort groups.
ix DAFTAR ISI
HALAMAN JUDUL DALAM BAHASA INDONESIA……….i
HALAMAN JUDUL DALAM BAHASA INGGRIS……….ii
LEMBAR PERSETUJUAN PEMBIMBING……….iii
LEMBAR PENGESAHAN………...iv
PERNYATAAN KEASLIAN KARYA………..v
LEMBAR PERSETUJUAN PUBLIKASI KARYA ILMIAH………...vi
ABSTRAK………vii
BAB II GRAF DAN PEWARNAAN SISI………10
B. Fungsi………...14
C. Teori Graf………...18
D. Jarak dan Keterhubungan………...26
E. Macam-macam Graf……….32
F. Pewarnaan Sisi Pada Graf………..…..38 BAB III BILANGAN KETERHUBUNGAN PELANGI KUAT PADA GRAF..45 A. Bilangan Keterhubungan Pelangi Pada Graf………46
B. Bilangan Terhubung Pelangi Kuat Pada Graf………..52
C. Aplikasi………83
BAB IV PENUTUP
A. Kesimpulan………..98
B. Saran………...100
1 BAB I PENDAHULUAN
Pada bab ini akan dibahas tentang latar belakang, rumusan dan batasan masalah, tujuan dan manfaat penulisan, serta akan disertakan sistematika penulisan skripsi.
A. Latar Belakang
Teori graf merupakan salah satu cabang matematika yang penting untuk dipelajari karena dapat memberikan banyak manfaat dalam menyelesaikan per-masalahan dalam kehidupan. Konsep teori graf diperkenalkan oleh seorang matematikawan Swiss yang bernama Leonhard Euler pada tahun 1736 ketika mencoba menyelesaikan masalah Jembatan Königsberg. Kota Königsberg di Prussia (sekarang menjadi Kaliningrad di Rusia) dibangun pada pertemuan dua buah cabang sungai Pregel. Kota Königsberg terdiri dari sebuah pulau dandaratan sepanjang tepi sungai yang dihubungkan oleh tujuh jembatan yang ditunjukkan pada Gambar 1.1.
Gambar 1.1. Ilustrasi Jembatan Kota Königsberg
melewati setiap jembatan satu kali. Dalam menyelesaikan masalah tersebut, Euler merepresentasikan peta Kota Königsberg ke dalam graf pada Gambar 1.2, di
mana titik menggambarkan daratan dan dan
menggambarkan tujuh jembatan.
Gambar 1.2. Graf Kota Königsberg
Euler memberikan jawaban bahwa tidak mungkin seseorang dapat berjalan – jalan mengelilingi kotadiawalidan diakhiri di tempat yang sama dengan melewati setiap jembatan tepat satu kali.
Gdikatakan terhubung jika dan hanya jika setiap dua titik u, v terhubung(Epp, 2010).
Sebuah pewarnaan sisi pada graf Gadalah sebuah pemberian warna pada sisi – sisi dalam graf G, di mana satu warna untuk setiap sisi. Jika sisi- sisi yang bertetangga diwarnai dengan warna yang berbeda maka pewarnaan sisi dikatakan pewarnaan sisi sejati. Pewarnaan sisi - k adalah suatu pewarnaan sisi sejati yang menggunakan kwarna. Suatu graf G disebut graf yang sisi – sisinya dapat diwarnai –k jika terdapat pewarnaan sisi –k pada G. Indeks kromatik G dinotasikan dengan adalah bilangan bulat positif terkecil k sedemikian sehingga G merupakan graf yang sisinya dapat diwarnai–k (Chartrand dan Zhang, 2009).
dibutuhkan sedemikian sehingga tidak terjadi pengulangan kata sandi angka pada setiap agen pemerintahan.
Lintasan dari u ke v adalah jalan dari u ke vdi mana tidak terjadi pe-ngulangan titik maupun sisi (Epp, 2010). Misalkan graf G adalah graf terhubung tak trivial dank adalah sebuah bilangan bulat positif, didefinisikan pewarnaan sisi , sehingga setiap dua sisi yang bertetangga boleh memiliki warna yang sama. Suatu lintasan u – v di G disebut lintasan pelangi jika tidak ada dua sisi pada lintasan tersebut yang memiliki warna yang sama. Graf dengan pewarnaanc disebut graf terhubung pelangi jika terdapat lintasan pelangi - , untuk setiap pasang titik . Dalam hal ini pewarnaan c disebut pewarnaan pelangi. Jika terdapat k warna di G maka pewarnaan c disebut pewarnaan-k pelangi. Selanjutnya bilangan bulat positif terkecilk sedemikian sehingga terdapat pewarnaan pelangi-k pada G disebut bilangan keterhubungan pelangi. Bilangan keterhubungan pelangi dari G dinotasikan dengan (Chatrand dan Zhang, 2009).
Selanjutnya bilangan keterhubungan pelangi kuat pada suatu graf terhubung Gadalah bilangan bulat positif terkecilk sedemikian sehingga terdapat pewarnaan
pelangi kuat- pada G. Bilangan keterhubungan pelangi kuat dinotasikan dengan (Chartrand dan Zhang, 2009). Dapat ditunjukkan bahwa ) untuk setiap graf terhubung. Yang dimaksud dengan ukuran adalah jumlah sisi pada graf G. Eksetrisitas pada adalah jarak dari titik ke suatu titik terjauh diG. Diameter dari Gadalah maksimum dari eksentrisitas titik-titik di G(Buckley dan Lewinter, 2003). Jika terdapat graf terhubung tak trivial Gdengan ukuran dan memiliki diameter yang dinotasikan dengan yaitu jarak maksimum antara dua titik di G maka
Gambar 1.3.ContohJalur Pendistribusian Soal UN Ke Sekolah- Sekolah Di Kabupaten Jember
Peta jalur distribusi dapat digambar secara ulang menjadi graf dengan bentuk berbeda seperti pada Gambar 1.4.
Gambar 1.4. Graf Jalur Pendistribusian Soal UN
Misalkan titik adalah SMA yang akan
Berdasarkan penjelasan di atas dalam tugas ahkir ini akan dibahas lebih lanjut mengenai bilangan keterhubungan pelangi kuat pada graf .
B. Rumusan Masalah
Perumusan masalah yang akan dibicarakan pada tugas akhir ini adalah: 1. Apa yang dimaksud dengan bilangan keterhubungan pelangi kuat pada
graf?
2. Bagaimana cara menentukan bilangan keterhubungan pelangi kuatpada graf?
3. Bagaimana penerapan bilangan keterhubunganpelangi kuat pada graf dalam kehidupan?
C. Batasan Masalah
Pada tugas akhir ini dibatasi pada masalah-masalah sebagai berikut:
1. Graf yang digunakan yaitu grafpohon, graf siklus, graf roda, graf bipartit. 2. Pewarnaan yang digunakan adalah pewarnaan sisi pada graf.
3. Penulis tidak membahas mengenai algoritma perhitungan.
D. Tujuan Penulisan
Tujuan dari penulisan tugas ahkir ini adalah sebagai berikut:
1. Mengetahui apa yang dimaksud bilangan keterhubungan pelangi pada graf.
3. Mengetahui penerapan bilangan keterhubungan pelangi kuat pada dalam kehidupan.
E. Manfaat penulisan
Manfaat yang diharapkan dari penulisan tugas ahkir ini adalah memberikan motivasi kepada pembaca untuk mempelajari salah satu konsep baru dari teori graf yaitu bilangan keterhubungan pelangi kuat dan dapat mengetahui penerapan bilangan keterhubungan pelangi kuat dalam kehidupan.
F. Metode Penulisan
Metode yang digunakan dalam penulisan tugas akhir ini adalah metode studi pustaka yaitu dengan membaca dan mempelajari buku-buku atau jurnal-jurnal yang berkaitan dengan bilangan keterhubungan pelangi kuat pada graf.
BAB II GRAF DAN PEWARNAAN SISI A. Himpunan
B. Fungsi C. Teori Graf
D. Jarak dan Keterhubungan E. Macam-macam Graf F. Pewarnaan sisi pada graf
BAB III BILANGAN KETERHUBUNGAN PELANGI PADA GRAF A. Bilangan keterhubungan Pelangi Pada Graf
B. Bilangan keterhubungan Pelangi Kuat Pada Graf C. Aplikasi
10 BAB II
GRAF DAN PEWARNAAN SISI
Pada bab ini akan dijelaskan dasar-dasar teori graf yang digunakan dalam penulisantugas akhir ini. Dasar-dasar teori meliputi: himpunan,fungsi, teori graf, jarak dan keterhubungan, macam-macam graf dan pewarnaan sisi pada graf. A. Himpunan
Dalam kehidupan sehari-hari sering dijumpai penggunaan konsep himpunan, misalnya himpunan hewan berkaki empat, himpunan warna pelangi, himpunan fakultas di Universitas Sanata Dharma, Himpunan Mahasiswa Matematika (HMM), dan lain-lain. Konsep himpunan tidak hanya diterapkan secara intuitif dalam kehidupan, namun konsep himpunantelah dikembangkan menjadi konsep dasar dalam matematika. Pada subbab ini akan dijelaskan mengenai himpunan.
Definisi 2.1
Himpunan adalah suatukumpulan atau koleksi objek-objek yang mempunyai
kesamaan sifat tertentu dan dilambangkan dengan huruf besar.
Contoh 2.2
adalah himpunan semua bilangan asli. adalah himpunan semua bilangan bulat.
Definisi 2.3
Suatu himpunanA dalam semesta X dikatakan himpunan bagian dari himpunan B jika dan hanya jika setiap anggota dari himpunanA juga merupakan anggota dari himpunanB. Secara matematis ditulis dengan
Definisi 2.4
Suatu himpunan Adikatakanberhinggajika banyaknya elemen yang termuat di Adapat dihitung.
Definisi 2.5
Kardinalitas dari himpunan berhinggaX adalah jumlah elemen yang termuat
di dalamX. Kardinalitas dari himpunan berhingga X dinotasikan dengan |X|.
Definisi 2.6
Gabungan dua buah himpunan A dan B adalah himpunan semua elemen dari
Definisi 2.7
Irisan dua himpunan dan adalah himpunan semua elemen dari semesta
yang merupakan anggota dan anggota , dinotasikan dengan . Secara matematis ditulis dengan
Bila maka dan disebut dua buah himpunan saling asing atau saling lepas.
Definisi 2.8
Selisih dua buah himpunan dan adalah himpunan semua elemen dalam
semesta yang merupakan anggota himpunan dan bukan anggota himpunan dan dinotasikan dengan . Secara matematis ditulis dengan
Definisi 2.9
Hasil kali kartesius buah himpunan adalah himpunan A
Definisi 2.10
Hasil kali kartesius dua buah himpunan dan adalah himpunan semua
pasangan terurut dengan dan dan dinotasikan dengan . Secara matematis ditulis dengan
Berikut merupakan contoh dari himpunan berhingga, himpunan bagian, kardinalitas dua buah himpunan, gabungan dua buah himpunan, irisan dua buah himpunan, selisih dua buah himpunan, hasil kali kartesius dua buah himpunan.
Contoh 2.11
Misalkan dan . Maka diperoleh bahwa: 1. dan merupakan himpunan berhingga.
2.
a. untuk setiap , yaitu setiap himpunan bagian tidak kosong.
b. untuk setiap i dan j dengan , yaitu setiap dua himpunan bagian yang tidak sama adalah saling lepas (atau secara ekivalen, jika dua himpunan bagian beririsan, maka kedua himpunan bagian itu adalah sama).
c. yaitu gabungan semua himpunan bagian adalah himpunan .
Contoh 2.13
Misalkan . Maka keluarga himpunan- himpunan bagian dari yaitu merupakan suatu partisi dari .
B. Fungsi
Pada subbab ini akan dibahas konsep relasi dan fungsi secara formal dam matematis meliputi definisi dan contoh tentang relasi, fungsi dan jenis fungsi. Definisi 2.14
Relasi dari himpunan A ke himpunan B adalah himpunan bagian dari .
Berikut merupakan contoh dari relasi dua himpunan dan cara penyajian relasi menggunakan diagram panah.
Contoh 2.15
Diberikan dua buah himpunan dan maka
. Jadi merupakan
relasi dari himpunan Cdan himpunanD seperti pada Gambar 2.1
Gambar 2.1. Relasi Dari Himpunan C Ke HimpunanD
Selanjutnya adalahrelasi khusus antara elemen-elemen dalam himpunan X dan elemen-elemen dalam himpunan Y.
Definisi 2.16
Fungsi (pemetaan) adalah relasi khusus f antara elemen-elemen dalam suatu
himpunan X dengan elemen-elemen dalam himpunan Y. Kekhususannya terletak dalam dua hal, yaitu
a. Setiap elemen dalam himpunan Xberelasi dengan suatu elemen dalam himpunanY.
Fungsi dari himpunan X ke himpunan Y dinotasikan dengan . Jika , maka elemen yang berelasi dengan elemen itu oleh fungsi f disebut bayangan dari dan dilambangkan dengan .
Contoh 2.17
Misalkan dan . Maka relasi
merupakan suatu fungsidari himpunan F ke himpunan G, sedangkanrelasi bukan merupakan fungsitetapi merupakan relasi dari himpunan Fke himpunan G, sebab berelasi dengan lebih dari satuelemen di G yaitu a dan b,seperti yang terlihat pada Gambar 2.2.(b).
Gambar 2.2. (a) Fungsi Dari Himpunan FKe Himpunan G, (b) Relasi Himpunan FKe Himpunan G
Berikut ini dijelaskan pengertian fungsi injektif, surjektif dan bijektif beserta contohnya.
Definisi 2.18
sedemikian sehingga . Lalu suatu fungsi disebut fungsi bijektif (korespondensi satu-satu) jika fungsi tersebut adalah fungsi injektif
dan sekaligus surjektif.
Contoh 2.19
Misalkan , dan adalah suatu fungsi maka
merupakan fungsi injektif tetapi tidak surjektif sebab untuk tidak terdapat sedemikian sehingga seperti terlihat pada Gambar 2.3. Selanjutnya misalkan , dan
adalah suatu fungsi maka merupakan
fungsi surjektif tetapi tidak injektif sebab tetapi seperti terlihat pada Gambar 2.3. Sedangkan misalkan adalah suatu fungsi maka merupakan fungsi injektif dan surjektif sehingga dapat disebut fungsi bijektif seperti terlihat pada Gambar 2.3.
Definisi 2.20
Atap dari suatu bilangan real x adalah bilangan bulat terkecil yang lebih besar
atau sama dengan x dan dinotasikan dengan .
Contoh 2.22
Misalkanx = 8.3 dan x = 9 maka berdasarkan Definisi 2.21 berturut-turut diperoleh dan .
C. Teori Graf
Pada subbab ini akan dibahas mengenai teori graf meliputi definisi dan contoh graf, keterhubungan dan jenis graf
Definisi 2.23
Graf G adalah pasangan himpunan dengan adalah himpunan
tak kosong dari obyek – obyek yang disebuttitik dan adalah himpunan (mungkin kosong) pasangan tak berurutan dari titik–titik yang berbeda dari yang disebut sisi,di mana setiap sisi dipasangkan dengan himpunan yang elemennya disebut titik ujung dari sisi tersebut.
Contoh 2.24
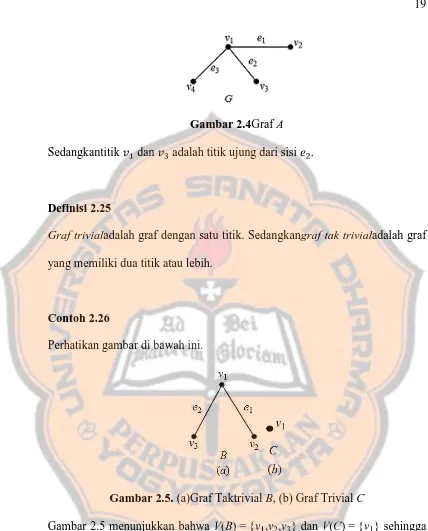
Gambar 2.4 menyatakan graf A dengan
Gambar 2.4Graf A Sedangkantitik dan adalah titik ujung dari sisi
Definisi 2.25
Graf trivialadalah graf dengan satu titik. Sedangkangraf tak trivialadalah graf
yang memiliki dua titik atau lebih.
Contoh 2.26
Perhatikan gambar di bawah ini.
Gambar 2.5. (a)Graf Taktrivial B, (b) Graf Trivial C
Gambar 2.5 menunjukkan bahwa dan sehingga
Definisi 2.27
Dua buah titik dikatakan bertetangga jika dan hanya jika terhubung oleh suatu sisi. Sisi tersebut dikatakan bersisiandengan setiap titik ujungnya.
Contoh 2.28
Perhatikan pada Gambar 2.5(b). Pada gambar tersebut titik dan dihubungkan oleh sisi sehingga titik dan dikatakan bertetangga, tetapi titik tidak bertetangga dengan titik sebab tidak dihubungkan oleh suatu sisi, sehingga sisi dikatakan bersisian dengan titik .
Definisi 2.29
Dua buah sisi yang bersisian pada titik ujung yang sama disebut bertetangga.
Contoh 2.30
Perhatikan Gambar 2.5(a). Gambar tersebut menunjukkan sisi dan sisi bersisihan pada titik ujung , sehingga dan dikatakan bertetangga.
Definisi 2.31
Contoh 2.32
Perhatikan gambar di bawah ini.
Gambar 2.6. Graf D
Sisi memiliki satu titik ujung yaitu titik , sehingga merupakan gelung dariD.
Definisi 2.33
Misalkan Gadalah suatu graf. Sisi – sisi di G yang mempunyai himpunan ttik ujung yang sama disebut sisi pararel dari G.
Contoh 2.34
Pada Gambar 2.6, sisi dan menghubungkan dua titik yang sama yaitu dan sehingga dan merupakan sisi pararel. Sedangkan dan tidak menghubungkan dua titik yang sama, maka dan bukan merupakan sisi pararel.
Definisi 2.35
maksimal dari G adalah derajat terbesar dari titik-titik pada G dan dinotasikan
dengan .
Contoh 2.36
Perhatikan Gambar2.6.Gambar tersebut menunjukkan bahwa
1. Terdapat tiga sisi yang bersisihan dengan titik yaitu sisi , dan sehinggadeg .
2. Terdapat dua sisi yang bersisihan dengan titik yaitu sisi dan sehinggadeg .
3. Terdapat satu sisi dan satu gelung yang bersisihan dengan titik yaitu sisi dan sehinggadeg .
Jadi .
Definisi 2.37
Suatu graf sederhana adalah graf yang tidak mempunyai gelung atau sisi
pararel.
Contoh 2.38
Definisi 2.39
Misalkan G adalah graf. Orde dari adalah jumlah titik - titik dalam graf G, dinotasikan dengan .
Contoh 2.40
Graf A pada Gambar 2.4 menunjukkan bahwa ,
sehingga .
Definisi 2.41
Misalkan G adalah graf, ukuran dari G adalah jumlah sisi dalam graf G. Ukuran graf G dinotasikan dengan .
Contoh 2.42
Graf A pada Gambar 2.4 menunjukkan bahwa ,
sehingga .
Definisi 2.43
Misalkan G adalah graf. Sebuah jalan W dari titik u ke titik v adalah barisan selang seling berhingga yang terdiri dari titik dan sisi yang bertetangga pada G dari titik – titik di G. Sehingga jalan disajikan dalam bentuk
di mana menyatakan titik-titik dan menyatakan sisi-sisi, , , dan untuk setiap , - dan adalah titik ujung dari . Jalan dari titik u ke titik v singkatnya disebut jalan u-v.
Jalan pada suatu graf bisa dinyatakan hanya dengan barisan titik asalkan tidak memuat sisi pararel. Jika tidak memuat sisi pararel maka setiap jalan di tidak menimbulkan dwimakna dan dapat dijelaskan dengan barisan titik saja. Pada skripsi ini jalan dinyatakan dengan barisan titik apabila graf tidak memuat sisi pararel.
Contoh 2.44
Perhatikan Gambar 2.6. Untuk titik dan , merupakan jalan . Oleh karena merupakan sisi pararel maka jalan dinyatakan menggunakan barisan titik dan sisi. Untuk titik dan , merupakan jalan dan bisa nyatakan menggunakan barisan titik saja karena bukan merupakan sisi pararel.
Definisi 2.45
Contoh 2.46
Perhatikan Gambar 2.5(a). Pada gambar tersebut, merupakan lintasan .
Definisi 2.47
Jalan tertutup adalah jalan yang diawali dan diakhiri di titik yang sama.
Contoh 2.48
Perhatikan Gambar 2.6. Untuk titik di graf D, jalan merupakan jalan tertutup pada graf D.
Definisi 2.49
Sirkuit pada G adalah jalan tertutup yang terdiri dari minimal satu sisi dan
tidak terjadi pengulangan sisi.
Contoh 2.50
Perhatikan gambar di bawah ini.
Gambar 2.7. Graf E
Definisi 2.51
Siklus adalah lintasan yang diawali dan diakhiri di titik yang sama.
Contoh 2.52
Perhatikan Gambar 2.7. Pada gambar tersebut jalan
bukan merupakan siklus karena terdapat pengulangan titik yaitu dan . Sedangkan jalan merupakan siklus pada graf E.
Definisi 2.53
Panjang dari suatu jalan adalah jumlah dari sisi – sisi di dalam sebuah jalan
Contoh 2.54
Perhatikan pada Gambar 2.7. Pada graf E, jalan merupakan jalan dari titik ke , di mana , , adalah sisi-sisi pada jalan, maka panjang jalan dari titik ke adalah jumlah sisi-sisi pada jalan tersebut yaitu tiga.
Definisi 2.55
Contoh 2.56
Perhatikan Gambar 2.7. Untuk dua titik dan , lintasan merupakan lintasan dengan panjang dua, selanjutnya lintasan merupakan lintasan dari titik dengan panjang dua, lalu lintasan
merupakan lintasan dari titik ke dengan panjang dua, sedangkan lintasan merupakan lintasan dari titik dengan panjang satu. Oleh karena itu lintasan merupakan lintasan geodesik antara titik dan , sebab lintasan tersebut memiliki panjang yang minimal dibanding lintasan lainnya.
D. Jarak dan Keterhubungan Definisi 2.57
Misalkan adalah graf. Dua titik dan di dikatakan terhubung jika dan hanya jika terdapat sebuah jalan dari ke .
Contoh 2.58
Perhatikan gambar di bawah ini.
Gambar 2.8. Graf F
Untuk dua titik dan terdapat jalan dari ke , sehingga titik dan dapat dikatakan terhubung.
Suatu graf dikatakan graf terhubung jika dan hanya jika untuk setiap dua titik dan pada terhubung.
Contoh 2.60
Perhatikan Gambar 2.8. Untuk setiap dua titik u dan v pada F terdapat jalan dari titik u kev maka Fmerupakan graf terhubung seperti yang terlihat pada Tabel 2.1.
Tabel 2.1. Jalan dari titik u ke v untuk setiap , di F
Titik u
Jalan titik u ke v Titik v
Selanjutnya perhatikan gambar di bawah ini.
Gambar 2.9. Graf G
Untuk dua titik dan pada graf G, tidak terdapat jalan dari titik ke , sehingga graf G tidak terhubung.
Misalkan diberikan dua buah titik pada graf G Jarak antara titik dan didefinisikan sebagai banyaknya sisi dari suatu geodesik - diG dan dinotasikan dengan d(u,v).
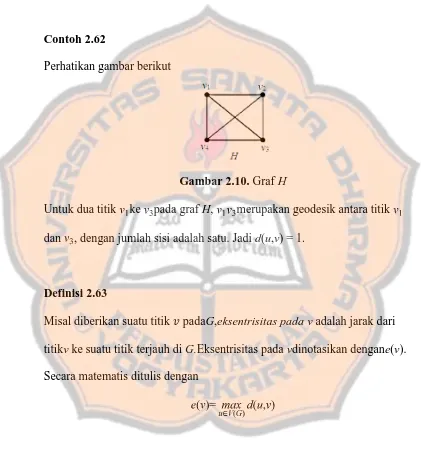
Contoh 2.62
Perhatikan gambar berikut
Gambar 2.10. Graf H
Untuk dua titik ke pada graf H, merupakan geodesik antara titik dan , dengan jumlah sisi adalah satu. Jadi d(u,v) = 1.
Definisi 2.63
Contoh 2.64
Perhatikan gambar berikut , akan dicari e( ).
Gambar 2.11. Graf I Untuk suatu titik pada grafI diperoleh bahwa:
Definisi 2.65
Misalkan G adalah graf. Diameter dari Gadalah maksimum dari eksentrisitas titik-titik diG dan dinyatakan dengan diam(G).
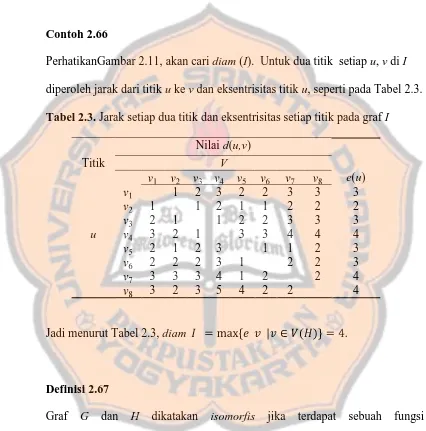
Contoh 2.66
PerhatikanGambar 2.11, akan cari diam (I). Untuk dua titik setiap u, v di I diperoleh jarak dari titik u ke v dan eksentrisitas titik u, seperti pada Tabel 2.3. Tabel 2.3. Jarak setiap dua titik dan eksentrisitas setiap titik pada graf I
Titik
Jadi menurut Tabel 2.3, diam .
Definisi 2.67
Graf G dan H dikatakan isomorfis jika terdapat sebuah fungsi bijektif sedemikian sehingga setiap pasang titik u dan vbertetangga di G jika dan hanya jika dan bertetangga di H. Fungsi fyang mememenuhi syarat di atas disebut isomorfisma dari GkeH, dan
Contoh 2.68
Gambar 2.12menyatakan graf Jdan K. Fungsi didefinisikan
dengan , , , . Dapat ditunjukkanbahwa
f adalah fungsi bijektifdari ke dan untuk setiap dua titik u dan v di E, u dan v bertetangga jika dan hanya jika f (u)dan f (v) bertetangga pada
Gambar 2.12.
(a) (b) Gambar 2.12.(a)Fungsi bijektif dari ke , (b) Graf
E. Macam-Macam Graf
Pada bagian ini akan dibahas definisi dan contoh dari macam-macam graf dan gabungan graf.
Definisi 2.69
Graf lengkap dengan n titik adalah suatu graf sederhana dengan n titik dan
Contoh 2.70
Gambar 2.13 merupakan salah satu contoh dari graf lengkap.
Gambar 2.13. Graf
Definisi 2.71
Misalkan adalah graf sederhana. Graf disebut pohon jika dan hanya jika tidak memuat sirkuit dan terhubung.
Contoh 2.72
Gambar 2.14. Graf PohonL
Gambar 2.14merupakan sebuah pohon, sedangkan Gambar 2.15 bukan merupakan sebuah pohon sebab memuat sirkut .
Definisi 2.73
Graf bipartit lengkap dengan titik adalah sebuah graf sederhana di mana
titik-titiknya dapat dipartisi menjadiU danW, dengan
dan yang memenuhi sifat-sifat berikut: untuk semua i, dan untuk semuaj,
1. Terdapat sisi dari setiap titik ke setiap titik . 2. Tidak terdapat sisi dari suatu ke suatu titik . 3. Tidak terdapat sisi dari suatu ke suatu titik Graf bipartit lengkap dengan titik dinotasikan dengan .
Contoh 2.74
Perhatikan gambar di bawah ini.
Definisi 2.75
Untuk , graf siklusdengan n titik adalah suatu siklus dengan titik. Graf siklus dengan titik dinotasikan dengan .
Contoh 2.76
Gambar 2.17merupakan salah satu contoh dari graf siklus.
Gambar 2.17. Graf
Definisi 2.77
Jika dan adalah graf yang saling asing, gabungan adalah graf
dengan dan .
Contoh 2.78
Misalkan diberikan dua buah graf K2 dan K3 seperti gambar di bawah ini.
(a) (b)
HimpunanV(K2) = {v1, v2} dan V(K3) = {v3, v4, v5} maka diperoleh himpunan
V(K2 K3) = { v1, v2, v3, v4, v5} dan E(K2 K3) = { v1, v2, v3, v4, v5} sehingga
dapat dibentuk gaf K2 K3, seperti pada gambar berikut.
Gambar 2.19. Graf K2 K3
Definisi 2.79
Jika G danHadalah dua graf yang saling asing, penggabungan
terbentuk dengan menambahkan sisi pada setiap titik sedemikian sehingga setiap titik terhubung dengan setiap titik . Jika dan berturut-turut memiliki m(G) dan n(H) titik, maka untuk membentuk graf haruslah menambahkan sisi pada graf .
Contoh 2.80
Perhatikan Gambar 2.18, akan dibentuk grafK2 K3.Graf K2 dan K3
berturut-turut memiliki m(K2) = 2 dan m(K3) = 3 sehingga m(K2).m(K3) = 6. Untuk
membentuk graf K2 K3 menambahkan sisi pada setiap titik di K2 sedemikian
sehingga setiap titik di K2 terhubung dengan setiap titik K3, dengan
sedemikiansehingga v1beturut-turut terhubung dengan v3,v4 dan v5seperti pada
Gambar 2.20.
Gambar 2.20. Ilustrasi penambahan sisi pada v1
Selanjutnya tambahkan berturut-turut sisi e5, e6 dan e7 pada v2 sedemikian
sehingga v1 berturut-turut terhubung dengan v3, v4 dan v5 seperti pada gambar
berikut seperti pada Gambar 2.21.
Gambar 2.21. Ilustrasi penambahan sisi pada v2
Jadi terbentuklah penggabungan K2 K3 seperti pada gambar berikut.
Definisi 2.81
Untuk graf roda adalah graf hasil penggabungan dari dengan . Graf roda dinotasikan dengan .
Contoh 2.82
Perhatikan gambar-gambar di bawah ini.
Gambar 2.23. (a) Graf , (b) Graf , (c) Graf
Gambar 2.23(a) merupakan penggabunganK1 C4 yang disebut
.Selanjutnya Gambar 2.23(b) merupakan penggabungan K1 C5 yang
disebut . Sedangkan Gambar 2.23(c) merupakan penggabungan K1 C6
yang disebut .
F. Pewarnaan Sisi Pada Graf
Pada subbab ini akan dibahas mengenai pewarnaan sisi pada graf, yang diberikan dalam definisi dan contoh-contoh.
Definisi 2.83
tersebut yang bertetangga. Sedangkan bilangan kebebasan sisi adalah jumlah maksimal sisi dari G dalam himpunan bebas.Bilangan kebebasan sisi dinotasikan dengan .
Contoh 2.84
Diberikan sebuah graf N. Akan dicari bilangan kebebasan sisi dari N.
Gambar 2.24. Graf N
Berdasarkan gambar diatas diperoleh bahwaH= , I= , J= ,K= merupakan himpunan kebebasan sisi. Jadi
= 3.
Definisi 2.85
Sebuah pewarnaan sisi pada graf Gadalah pemberian warna pada sisi – sisi dalam graf , di mana satu warna untuk setiap sisi .
Contoh 2.86
Gambar 2.25. Graf Dengan Pewarnaan Sisi-5
Definisi 2.87
Jika sisi- sisi yang bertetangga diwarnai dengan warna yang berbeda maka pewarnaan sisi dikatakan pewarnaan sisi sejati.
Contoh 2.88
Gambar 2.25 menunjukkan bahwa setiap dua sisi yang bertetangga memiliki warna yang berbeda, sehingga graf O menggunakan pewarnaan sisi sejati.
Definisi 2.89
Pewarnaan sisi - k adalah suatu pewarnaan sisi sejati yang menggunakan k
warna.
Contoh 2.90
Definisi 2.91
Misalkan diberikan pewarnaan sisi – k pada graf tak kosong G, dengan
menggunakan 1,2,….,k warna dan misalkan adalah himpunan
Contoh 2.94
Perhatikan gambar di bawah ini.
Gambar 2.26. Graf O Dengan Pewarnaan Sisi -
Karena terdapat pewarnaan sisi denganpadaO maka O adalah graf yang sisi- sisinya dapat diwarnai .
Definisi 2.95
Misalkan G adalah graf dengan pewarnaan sisi sejati. Indeks kromatik dari G adalah jumlah minimum warna yang diperlukan sedemikian sehingga sisi – sisi yang bertetangga di G diwarnai dengan pewarnaan sisi sejati. Indeks kromatik pada graf G dinotasikan dengan .
Contoh 2.96
Perhatikan Gambar 2.26. Gambar tersebut menunjukkan bahwa graf O dapat diwarnai menggunakan minimal tiga warna, sehingga indeks kromatiknya atau .
Teorema 2.97
Bukti:
Misalkan G adalah graf dan . Himpunan adalah kelas warna sisi pada pewarnaan sisi – k dari graf G. Berarti ada sisi di G yang tidak termuat di Karena maka merupakan partisi dariE(G). Sehingga untuk setiap i . Oleh karena itu
Jadi yang ekivalen dengan , sehingga
.
Karena grafG diwarnai dengan pewarnaan sisi-k berarti sisi – sisi yang bertetangga di G diberi kwarna berbeda. Suatu sisi dikatakan bertetangga jika bersisian dengan suatu titik yang sama. Pewarnaan sisi pada sebuah grafG harus memberikan warna yang berbeda pada sisi-sisi yang bertetangga sehingga untuk setiap titik v di G jumlah warna yang digunakan untuk mewarnai sisi yang bersisian dengan titik v harus sesuai dengan derajat titik v pada G atau deg . JadiContoh 2.98
Diberikan graf P dan pewarnaan sisi-4, dengan himpunan warna {1,2,3,4} di mana1=warna merah, 2=warna biru, 3=warna hijau, 4=warna jingga. Akan dicari .
Gambar 2.27.GrafP
Gambar 2.27 menunjukkan graf P dengan orde dan ukuran . Himpunan kebebasan sisi yang dapat dibentuk antara lain:A={ , , }, B={ , , }, C={ , , }. Sehingga berdasarkan Definisi 2.83didapatkan
45 BAB III
BILANGAN KETERHUBUNGAN PELANGI KUAT PADA GRAF
Konsep bilangan keterhubungan pelangi merupakan salah satu variasi dari pewarnaan sisi. Bilangan keterhubungan pelangi diperkenalkan oleh Chartrand, Johns, McKeon and Zhang pada tahun 2006. Konsep baru ini dilatarbelakangi oleh ditemukannya kelemahan dalam pegiriman informasi pada agen pemerintahan. Departemen Keamanan Dalam Negeri Amerika Serikat dibentuk tahun 2003 sebagai respon atas ditemukannya kelemahan dalam pengiriman informasi setelah terjadinya serangan teroris pada 11 September 2001. Keamanan informasi harus terjaga karena berhubungan langsung dengan keamanan nasional dan juga terdapat prosedur yang memungkinkan para agen pemerintah untuk mengakses informasi, sehingga setiap jalur pengiriman informasi membutuhkan kata sandi angka yang banyak.
A. Bilangan Keterhubungan Pelangi Pada Graf
Pada subbab ini akan dibahas mengenai lintasan pelangi, graf terhubung pelangi, pewarnaan pelangi dan bilangan terhubung pelangi meliputi definisi, contoh dan teorema.
Definisi 3.1
Misalkan graf G adalah graf terhubung tak trivial dan adalah sebuah bilangan bulat positif. Didefinisikan pewarnaan sisi , sehingga dua sisi yang bertetangga dapat memiliki warna yang sama. Suatu lintasan dari titik u ke v di G disebut lintasan pelangi jika tidak ada dua sisi pada lintasan tersebut yang memiliki warna yang sama.
Contoh 3.2
Perhatikan graf dengan pewarnaan sisi – 3, dengan himpunan warna {1, 2, 3} di mana 1=warna merah, 2=warna biru, 3=warna hijau. Akan ditunjukkan bahwa terdapat lintasan pelangi di P.
Tabel 3.1. Lintasan pelangi untuk setiap dua titik pada graf
Titik
Jalan - v
Tabel 3.2. Lanjutan Tabel 3.1
Titik
Jalan - v
Definisi 3.3
pewarnaan sisi disebut terhubung pelangi jikauntuk setiap pasang titik terdapat lintasan pelangi.
Contoh 3.4
Graf Petersen pada Gambar3.1dapat dikatakan terhubung pelangi sebab menurut Tabel3.1 dan Tabel 3.2 setiap dua titik dan di terdapat lintasan pelangi . Sedangkan graf Q dengan pewarnaan sisi 3 yang himpunan warnanya {1, 2, 3} seperti pada Gambar 3.2 bukan terhubung pelangi, sebab tidak terdapat lintasan pelangi - .Warna merah menyatakan warna 1, warna biru menyatakan warna 2 dan warna hijau menyatakan warna 3.
Gambar3.2. Graf Q Dengan Pewarnaan Sisi
Definisi 3.5
Contoh 3.6
Pewarnaan sisi graf pada Gambar3.1 merupakan pewarnaan pelangi karena menyebabkan terhubung pelangi. Sedangkan pewarnaan sisi graf Q dengan pada Gambar3.2 bukan pewarnaan pelangi karena tidak
menyebabkan Qterhubung pelangi.
Definisi 3.7
Misalkan adalah graf terhubung tak trivial.Bilangan bulat positif terkecil sedemikian sehingga terdapat pewarnaan pelangi pada disebut bilangan keterhubungan pelangi pada G. Bilangan keterhubungan pelangi pada
dinotasikan dengan .
Teorema 3.8
Misalkan adalah graf terhubung tak trivial maka . Bukti:
Misalkan G adalah graf dengan pewarnaan sisi c dan . Sehingga berdasarkan Definisi 2.61 danDefinisi 2.63maka
Ini berarti terdapat dua titik di , misal dan yang dihubungkan geodesik dengan panjang . Oleh karena geoesik adalah geodesik terpanjang sehingga minimal warna yang diperlukan untuk mewarnai graf sedemikian sehingga setiap dua titik dan di terdapat lintasan pelangi
adalah warna .Oleh karena itu
Contoh 3.9Berdasarkan Gambar3.1 terdapat pewarnaan pelangi pada graf Petersen
berarti Oleh karena maka akan dicari .
Tabel 3.3. Jarak setiap dua titikdi graf pewarnaan pelangi di , sebab jika diberikan suatu pewarnaan sisi pada dan didefinisikan sebagai pemberian dua warna pada sisi-sisi di terdapat dua sisi yang berwarna sama yaitu dan seperti pada Gambar3.3.
Gambar3.3. Graf Petersen Dengan Pewarnaan Sisi
B. Bilangan Keterhubungan Pelangi Kuat Pada Graf
Pada subbab ini akan dibahas mengenai pelangi geodesik, pewarnaan pelangi kuat, terhubung pelangi kuat,bilangan keterhubungan pelangi dan bilangan keterhubungan pelangi kuat pada graf terhubung tak trivial, graf pohon, graf siklus, graf roda dan graf bipartit meliputi definisi, contoh dan teorema.
Definisi 3.10
Misalkan adalah pewarnaan sisi pada graf terhubung tak trivialG. Untuk dua titik u dan v di G, suatu pelangi geodesik adalah lintasan pelangi - dengan panjang .
Contoh 3.11
Gambar3.4 menunjukkan graf Petersen dengan pewarnaan sisi . Untuk suatu titik dan , lintasan adalah lintasan pelangi dengan panjang . Sehingga lintasan pelangi adalah pelangi geodesik - . Sedangkan lintasan bukan pelangi geodesik - sebab tidak memiliki panjang minimum.
Definisi 3.12
Suatu graf terhubung tak trivial G dikatakan terhubung pelangi kuat jikaG memuat pelangi geodesiku-v untuk setiap titik u dan v diG.
Contoh 3.13
Graf Petersen P dengan pewarnaan sisi pada Gambar3.4 terhubung pelangi kuat sebab graf P memuat lintasan pelangi geodesik u-v untuk setiap titik u danv di .
Tabel 3.5. Pelangi geodesik untuk setiap dua titik pada graf P
Titik
Pelangi geodesik
Tabel 3.6. Lanjutan Tabel 3.5
Titik
Sedangkan graf P dengan pewarnaan sisi pada Gambar3.1 terhubung pelangi tapi tidak terhubung pelangi kuat sebab tidak terdapat pelangi geodesik .
Definisi 3.14
Misalkan G adalah graf. Pewarnaan sisi pada G dikatakan pewarnaan sisi pelangi kuat jika pewarnaan itu menyebabkan graf terhubung pelangi kuat. Pewarnaan sisi pelangi kuat singkatnya disebut pewarnaan pelangi kuat. Sedangkan pewarnaan pelangi kuat yang menggunakan warna disebut pewarnaan pelangi kuat – .
Contoh 3.15
Pewarnaan sisi graf Petersen pada Gambar3.4 merupakan pewarnaan pelangi kuat sebab menyebabkan graf Pterhubung pelangi kuat. Sedangkan pewarnaan sisi graf Petersen pada Gambar3.1 bukan merupakan pewarnaan pelangi kuat sebab tidak menyebabkan graf P terhubung pelangi kuat.
Misalkan G adalah graf terhubung tak trivial.Bilangan bulat positif terkecil sedemikian sehingga terdapat pewarnaan pelangi kuat pada Gdisebut bilangan keterhubungan pelangi kuat pada G. Bilangan keterhubungan
pelangi kuat pada dinotasikan dengan .
Teorema3.17
Misalkan G adalah graf terhubung tak trivial, maka Bukti:
Misalkan G adalah suatu graf terhubung tak trivial dengan . Karena sehingga terdapat pewarnaan pelangi pada G Oleh karena terdapat pewarnaan pelangi di G, ini berarti terhubung pelangi. Sehingga terdapat lintasan pelangiu-v, untuk setiap pasang titik u,v .
Kasus 1: Misalkan untuk setiap pasang titik , terdapat lintasan pelangi yang merupakan pelangi geodesik , berarti terhubung pelangi kuat sehingga pewarnaan sisi merupakan pewarnaan pelangi kuat . Jadi
Kasus 2: Misalkan untuk suatu titik dan , setiap lintasan pelangi bukan merupakan pelangi geodesik, ini berarti tidak terhubung pelangi kuat. Oleh karena itu pewarnaan sisi bukan pewarnaan pelangi kuat. Sehingga
Jadi berdasarkan kasus 1 dan 2
Teorema3.18
Misalkan adalah graf terhubung tak trivial, dengan ukuran m(G) maka .
Bukti:
Sudah cukup jelas bahwa pasti tidak pernah melampaui ukuran graf .
Contoh 3.19Misalkan adalah graf Petersen dengan . Menurut Contoh 3.9 maka menurut Teorema 3.17 dan Teorema3.18 diperoleh bahwa . Namun pewarnaan pelangi pada Gambar3.1 bukan merupakan pewarnaan pelangi kuat karena tidak menyebabkan terhubung pelangi maka . Karena pewarnaan sisi merupakan pewarnaan pelangi kuat sehingga Oleh karena dan
maka
Dari Teorema 3.8, Teorema 3.17 dan Teorema3.18 maka didapatkan sebuah pertidaksamaan
Contoh 3.20
Akan dicari dan untuk graf . Perhatikan gambar berikut
T
Gambar 3.5. Graf Penyelesaian:
Akan dicari
Tabel 3.7. Jarak tiap dua titik dan eksentrisitas tiap titik pada T
2, 3} di mana 1=warna merah, 2=warna biru, 3=warna hijau. Misalkan
, .
Gambar 3.6. Graf T Dengan Pewarnaan Sisi
Menurut Gambar 3.6 , tidak terdapat lintasan pelangi , berarti tidak terhubung pelangi, sehingga tidak terdapat pewarnaan pelangi di , muncul kontradiksi. Jadi maka dengan kata lain terdapat pewarnaan pelangi-4 dengan himpunan warna {1, 2, 3, 4}, seperti pada Gambar 3.7di mana 1=warna merah, 2=warna biru, 3=warna hijau dan 4=warna ungu.
Akan dicari
Karena maka menurut pertidaksamaan (2)
Diasumsikan .Bilangan berarti terdapat pewarnaan pelangi seperti pada Gambar 3.7. Untuk setiap dua titik dan di akan dicari lintasan pelangi dengan panjang .
Tabel 3.8.Pelangi geodesik tiap dua titik diT
Titik
Pelangi geodesik
Tabel 3.9. Lanjutan Tabel 3.8
Titik
Karena untuk setiap dua titik dan terdapat lintasan pelangi kuat, maka T terhubung pelangi kuat, sehingga pewarnaan pelangi juga merupakan pewarnaan pelangi kuat . Jadi .
Teorema 3.21
Misalkan dan adalah graf terhubung tak trivial. Maka
jika dan hanya jika Bukti :
Untuk , akan dibuktikan jika dan hanya jika
dengan kata lain jumlah maksimum sisi-sisi dari suatu geodesik di adalah 2. Selanjunya karena maka terdapat pewarnaan pelangi di . Karena diam dan terdapat pewarnaan pelangi di , maka lintasan pelangi adalah pelangi geodesik
maka pewarnaan pelangi adalah pewarnaan pelangi kuat . Jadi .
Misalkan adalah graf terhubung tak trivial dengan . Menurut Teorema 3.17diperoleh bahwa . Karena bukan merupakan
Gambar3.8. (a) Graf , (b) Graf Dengan Pewarnaan Sisi
adalah 1 warna, misalkan warna warna merah. Jadi . Maka menurut Teorema3.21
Teorema 3.23
Misalkan adalah graf terhubung tak trivial dengan ukuran . Maka
jika dan hanya jika adalah sebuah pohon. Bukti
Misalkan akan dibuktikan adalah sebuah pohon. Diasumsikan adalah bukan sebuah pohon. Maka memuat suatu sirkuit
di mana . Maka pewarnaan sisi yang memberikan warna 1 untuk sisi dan dan warna berbeda dari
himpinan warna untuk sisi lainnya pada
Gambar3.9. Graf Dengan Pewarnaan
Jadi . Kontradiksi dengan . Sehingga
haruslah sebuah pohon.
Misalkan adalah sebuah pohon dengan ukuran . Akan dibuktikan .
Diasumsikan bahwa . Oleh karena
sehingga terdapat pewarnaan pelangi
dari . Maka terdapat sisi dan yang diwarnai dengan warna yang sama. Misalkan diambil salah satu titik atau dan salah satu titik atau yaitu titik dan sehingga terdapat lintasan yang memuat sisi dan diilustrasikan Gambar3.10.
Gambar3.10. Graf pohon
lain yang tidak memuat sisi dan yang merupakan lintasan pelangii , hal tersebut menunjukkan bahwa terdapat sirkuit di , kontradiksi dengan adalah pohon dengan ukuran . Jadi
Contoh 3.24Gambar3.11 menyatakan suatu graf
Gambar3.11. Graf pohon
Karena graf merupakan pohon dengan , jadi menurut
Teorema3.42 diperoleh bahwa .
Teorema 3.25
Misalkan adalah graf siklus dengan banyak titik di mana . Maka .
Bukti:
Kasus 1:
Untuk genap. Misalkan , untuk setiap bilangan bulat sehingga . Maka menurut pertidaksamaan (1),
. Pewarnaan sisi dari didefinisikan sebagai berikut,
Diilustrasikan dalam Gambar3.12 dengan 1=warna merah, 2=warna biru, k=hijau, (k-1)=ungu.
Gambar3.12. Graf Dengan Pewarnaan Sisi
Untuk setiap dua titik dan terdapat pelangi geodesik seperti yang terlihat dalam Gambar3.11 maka terhubung pelangi kuat, maka pewarnaan sisi adalah suatu pewarnaan pelangi kuat– . Karena merupakan pewarnaan pelangi kuat – maka dan menurut pertidaksamaan
Kasus 2:
Untuk ganjil. Misalkan , untuk bilangan bulat . Didefinisikan pewarnaan sisi dari sebagai berikut,
Dengan kata lain , ,…,
, sehingga untuk setiap dua titik dan terdapat pelangi geodesik , maka pewarnaan pelangi adalah suatu pewarnaan pelangi kuat . Karena pewarnaan pelangi adalah pewarnaan pelangi kuat sehingga , maka menurut pertidaksamaan
(2) . Karena diam sehingga , jadi
atau Akan dibuktikan bahwa .
Asumsikan sehingga terdapat suatu pewarnaan pelangi , misalkan dan tanpa mengurangi perumuman misalkan . Dipandang titik-titik dan . Misalkan lintasan
Gambar 3.13. Graf Dengan Pewarnaan Sisi
Ini berarti tidak terdapat lintasan pelangi . Jadi bukan pewarnaan pelangi . Kontradiksi dengan pewarnaan pelangi . Jadi
. Oleh karena berdasarkan persamaan (2)
di-peroleh bahwa , sehingga .
Jadi
Contoh 3.26
Diketahui graf siklus , akan dicari nilai dan . Penyelesaian:
Menurut Teorema3.46 diperoleh bahwa .
Gambar3.14. Graf Dengan Pewarnaan Sisi
Teorema 3.27
Bilangan keterhubungan pelangi dari graf roda untuk adalah
Bukti:
Berdasarkan definisi , itu berarti terdapat dengan dan satu titik yang terhubung dengan setiap titik di . Akan dibagi menjadi 3 kasus:
Kasus1:
Untuk , karena , menurut pembuktian Teorema3.22 diperoleh
bahwa .
Kasus 2:
dan
Seperti yang terlihat dalam Gambar3.15
(a) (b) (c)
Gambar 3.15.(a) Graf Dengan Pewarnaan Sisi , (b) Graf Dengan Pewarnaan Sisi , (c) Graf Dengan Pewarnaan Sisi
Oleh karena pewarnaan sisi merupakan pewarnaan pelangi , maka diperoleh bahwa .
Kasus 3:
Untuk ,karena bukan graf lengkap sehingga diperoleh wa . Diasumsikan . Ini berarti terdapat pewarnaan pelangi di dengan himpunan warna {1, 2} di mana 1=warna merah dan 2=warna biru. Karena terdapat pewarnaan pelangi di berarti untuk setiap dua titik dan terdapat lintasan pelangi
Misalkan adalah pewarnaan pelangi dari . Diasumsikan
Gambar3.16. Graf
Karena satu- satunya lintasan yang memiliki panjang 2 adalah
sehingga jika maka supaya terdapat lintasan pelangi . Dengan cara yang sama didapatkan jika maka . Karena maka Selanjutnya jika
maka . Sehingga karena dan
maka tidak terdapat lintasan pelangi . Ini kontradiksi dengan terdapat pewarnaan pelangi pada Jadi .
Didefinisikan pewarnaan sisi dengan pada sebagai berikut
Gambar3.17. Graf Dengan Pewarnaan Sisi
Karena setiap dua titik dan terdapat lintasan pelangi sehingga pewarnaan sisi adalah pewarnaan pelangi sehingga diperoleh
Oleh karena , jadi untuk .
Contoh 3.28Gambar3.18. Graf Dengan Pewarnaan Pelangi
Teorema3.29
Bilangan keterhubungan pelangi pada graf roda untuk adalah
Bukti:
Misalkan terdiri dari graf dan satu titik yang terhubung dengan setiap titik di . Akan dibagi menjadi 3 kasus
Kasus 1: Untuk , graf dan menurut Teorema 3.27diperoleh bahwa maka berdasarkan Teorema 3.21diperoleh bahwa
.
Kasus 2: Untuk ,menurut Teorema 3.27 diperoleh bahwa maka berdasarkan Teorema 3.21. diperoleh bahwa
Kasus 3: Untuk , akan dibuktikan . Misalkan maka
terdapat suatu bilangan bulat sehingga . Selanjutnya akan ditunjukkan
Pertama-tama akan ditunjukkan . Diasumsikan
maka terdapat pewarnaan pelangi kuat pada . Karena maka dapat dibentuk himpunan sedemikian sehingga dan semua sisi dengan memiliki warna yang sama. Maka terdapat dua titik sehingga jumlah sisi pada geodesik di lebih dari sam dengan 3 atau dan jumlah sisi pada geodesik
di sama dengan 2 atau . Karena
merupakan satu-satunya geodesik di , akibatnya tidak terdapat pelangi geodesik di . Ini berarti tidak terdapat pewarnaan pelangi
kuat ,kontradiksi dengan . Jadi .
Selanjutnya, akan ditunjukkan Didefinisikan suatu pewarnaan
sisi pada sebagai berikut
Karena setiap dua titik terdapat pelangi geodesik di sehingga pewarnaan sisi adalah pewarnaan pelangi kuat . Maka diperoleh
bahwa . Jadi untuk .
Contoh 3.30
Diberikan graf sebuah graf , akan dicari nilai dari . Menurut Teorema3.29 terdapat pewarnaan pelangi kuat pada , dengan kata lain
3 dengan himpunan warna {1, 2, 3} di mana 1= warna merah, 2= warna biru, 3= warna hijau, seperti pada gambar dibawah ini.
Gambar3.19. Graf Dengan Pewarnaan Sisi
Teorema 3.31
Bilangan keterhubungan pelangi kuat dari graf bipartit untuk suatu bilangan bulat dan dengan adalah
Bukti:
Untuk himpunan titik-titik pada dapat dipartisi menjadi dua
himpunan, misalkan dan , karena di
terdapat pewarnaan pelangi kuat di adalah seperti yang ditunjukkan pada Gambar3.20. Jadi benar bahwa .
Gambar3.20. Graf Dengan Pewaranaan Pelangi Kuat Selanjutnya diasumsikan untuk , , maka
Sehingga maka .
Akan ditunjukkan bahwa . Asumsikan . Maka
terdapat pewarnaan yaitu pewarnaan pelangi kuat . Himpunan titik-titik dapat dipartisi menjadi dua himpunan, misalkan dan
, dengan dan , sehingga
kardinalitas dan berturut- turut dan . Untuk setiap titik didefinisikan suatu kode yang disebut kode warna dari , di mana untuk seperti pada Gambar3.21.
Karena terdapat pewarnaan pelangi kuat sehingga untuk setiap , maka banyaknya warna berbeda pada kode warna dari titik- titik di paling banyak . Tetapi karena karena maka terdapat dua titik berbeda yaitu dan di sehingga kode
kode . Lintasan dan berturut- turut merupakan satu- satunya
geodesik dan geodesik dan karena untuk terurut di . Selanjutnya
s kali
dan adalah himpunan hasil kali seluruh elemen dalam setiap pasangan terurut di .Jadi .
Misalkan titik- titik di dilabeli dengan anggota dari sedemikian sehingga dilabeli dengan anggota dari . Untuk setiap dengan didefinisikan label dari dengan
untuk setiap yang diilustrasikan dengan Gambar3.22.
Gambar3.22. Graf
sehingga untuk . Didefinisikan pewarnaan
dengan untuk dan
. Sehingga kode warna dari adalah kode
, maka titik-titik berbeda di memiliki kode warna berbeda. Selanjutnya akan ditunjukkan bahwa adalah pewarnaan pelangi kuat
geodesik dan karena kode warna berbeda untuk setiap titik- titik berbeda di maka geodesik adalah pelangi geodesik . Diambil sebarang dua titik dan di . Karena titik-titik tersebut memiliki kode warna berbeda sehingga adalah pelangi geodesik
di untuk suatu dengan . Selanjutnya diambil sebarang dua titik dan di sedemikian sehingga . Lintasan merupakan satu-satunya geodesik dan karena terdapat suatu
dengan sehingga , maka geodesik
adalah pelangi geodesik . Oleh karena itu terbukti bahwa adalah pewarnaan pelangi kuat dari . Jadi .
Contoh 3.32Diberikan graf bipartit , akan dicari nilai dari Menurut Teorema
3.31 bahwa , dengan kata lain terdapat
Gambar3.23. Graf Dengan Pewarnaan Sisi
Toerema 3.33
Bilangan keterhubungan pelangi dari graf untuk suatu bilangan bulat dan dengan adalah
Bukti:
Diketahui bahwa sehingga maka .
Misalkan himpunan titik- titik di dipartisi menjadi himpunan dan
, di mana dan ,
Kasus 1: Jika maka . Menurut Teorema 3.31 diperoleh bahwa dan karena diam maka menurut pertidaksamaan (2) diperoleh bahwa . Jadi
.
Kasus 2: Jika maka . Menurut Teorema 3.31 diperoleh
bahwa dan karena diam maka menurut
pertidaksamaan (2) diperoleh bahwa . Jadi
atau . Akan dibuktikan .
Asumsikan maka terdapat pewarnaan pelangi di . Sehingga terdapat kode untuk setiap di
dengan untuk . Karena
Asumsikan ini berarti terdapat pewarnaan pelangi di . Sehingga terdapat kode
untuk setiap di dengan untuk
sisi pada lintasan genap, maka lintasan pelangi
yang terdapat di adalah lintasan pelangi yang memiliki panjang 2. Namun setiap sisi pada lintasan pelangi tersebut berwarna sama sehingga tidak terdapat lintasan pelangi di . Sehingga tidak terdapat pewarnaan pelangi pada . Ini kontradiksi dengan . Jadi
Selanjutnya akan dibuktikan Untuk membuktikan , akan ditunjukan terdapat pewarnaan pelangi di .
Misalkan , dan .
Himpunan adalah hasil kali kartesius dari himpunan sebanyak . Dengan kata lain
Untuk setiap titik di didefinisikan,
kode ,
untuk dan dengan .Dengan kata
lain , , …., , dan seterusnya.
Sedangkan untuk setiap titik di didefinisikan,
kode
Selanjutnya diambil sebarang dua titik akan dibuktikan terdapat pewarnaan pelangi pada dengan membagi menjadi 3 kasus:
Kasus 1: Untuk . Karena kode kode maka terdapat dengan yang ). Maka lintasan adalah lintasan pelangi . Jadi terdapat pewarnaan pelangi di . Kasus 2: Untuk dan . Misalkan dengan
. Karena maka dan dengan
. Sehingga lintasan merupakan lintasan pelangi yang sisi-sisinya berwarna dan Jadi terdapat pewarnaan pelangi di
Kasus3: Untuk . Ambil sebarang sedemikian sehingga c dan maka lintasan adalah lintasan pelangi yang sisi-sisinya berwarna , 1, 2 dan 3.
, dengan kata lain terdapat pewarnaan pelangi di seperti yang ditunjukkan Gambar3.24.
Gambar3.24
C. Aplikasi
Pada subbab ini akan dijelaskan aplikasi bilangan keterhubungan pelangi kuat pada graf dalam kehidupan sehari-hari.
Contoh 3.35
M.Sc, Ph.D. Diknas akan mendistribusikan soal-soal ujian nasional ke seluruh sekolah di kabupaten Jember (pelaksanaan UN SMA 2014). Soal ini bersifat rahasia sehingga membutuhkan tim pengawas pendistribusian soal UN yang terdiri dari unsur Universitas Negeri Jember (UNEJ), Lembaga Penjaminan Mutu Pendidikan (LPMP), Polisi resort (Polres), Pendidikan Nasional (Diknas), dan pihak sekolah. Misal jalur untuk menjangkau sekolah-sekolah direpresentasikan pada graf Rdi manaj merupakan pusat penyimpanan soal dan titik awal pendistribusian soal, sedangkan titik a, b, c, d, e, f, g, h, i, k, l, m, n, o, p mewakili sekolah-sekolah di kabupaten Jember . Permasalahan yang
muncul adalah:Bagaimana caramenentukan jumlah kelompok pengawalan pendistribusian soal UN?
Gambar3.25. Graf R
Solusi:
Diberikan graf S seperti pada gambar di atasdan didefinisikanfungsi
dengan , , , , ,
, , , , ,
, , dan . Dapat ditunjukkan bahwa f adalah fungsi bijektif dari ke seperti pada berikut.
Gambar 3.27. Fungsi Bijektif Dari V(R) Ke V(S)
Tabel 3.10. Dua titik u dan v yang bertetangga di R dan dua titik f(u)dan f(v)
Titik merepresentasikan titik j pada graf R, sedangkan
menggunakan konsep bilangan terhubung pelangi dan bilangan terhubung pelangi kuat, sebab apabila menggunakan konsep tersebut akan didapatkan minimumjumlah kelompok pengawalan pendistribusian soal UN. Oleh karena graf S tidak termasuk kedalam graf khusus yang dijelaskan pada bab sebelumnya, sehingga untuk menentukan dan menggunakan pertidaksamaan berikut.
.
Bilangan dan menyatakan minimal jumlah kelompok pengawalan dan warna tiap sisi pada pewarnaan pelangi kuat menunjukkan kelompoknya. Pertama-tama akan dicari . Untuk menentukan maka terlebih dahulu dicari jarak tiap dua titik dan eksentrisitas dari setiap titi di S,seperti yang dijelaskan pada tabel berikut.
Tabel 3.12. Lanjutan dari Tabel 3.11 dan eksentrisitas tiap titik di
Menurut Definisi 2.65 diperoleh bahwadiam , sehingga menurut pertidaksamaan (2) diperoleh bahwa . Akan dibuktikan , asumsikan , berarti terdapat pewarnaan pelangi di S, dengan himpunan warna {1, 2, 3, 4, 5} di mana 1=warna merah, 2=warna biru, 3=warna hijau, 4=warna jingga, 5=warna ungu, seperti yang ditunjukkan pada Gambar3.28.
Akan ditunjukkan bahwa terdapat pewarnaan pelangi-5 pada graf. Perhatikan tabel-tabeldi bawah ini.
Tabel 3.13. Lintasan pelangi setiap dua titik di
Titik
Lintasan pelangi
Tabel 3.14. Lanjutan dari Tabel 3.13
titik
Tabel 3.15. Lanjutan dari Tabel 3.14
Titik
Lintasan pelangi
Tabel 3.16. Lanjutan dari Tabel 3.15
Titik
Tabel- tabel di atas menunjukkan bahwa untuk setiap dua titik dan di S terdapat lintasan pelangi di S. Jadi terdapat pewarnaan pelangi di dengan kata lain .
Oleh karena maka menurut pertidaksamaan (2) diperoleh
bahwa . Akan dibuktikan . Asumsikan bahwa .
Tabel 3.13-Tabel 3.16 juga menunjukkan bahwa lintasan pelangi untuk setiap dua titik dan di S juga merupakan pelangi geodesik dengan panjang , sehingga pewarnaan pelangi-5 juga merupakan pewarnaan pelangi kuat-5.
Jadi . Oleh karena graf R S
Gambar3.29. Jalur Pendistribusian Soal UNKeSekolah-Sekolah
Contoh 3.36
Gambar 3.30. Graf X
Penyelesaian:
Gambar 3.31. Graf
Diberikan graf seperti pada gambar di atasdan didefinisikanfungsi
dengan , , , , ,
, , , , dan .
Gambar 3.32.Fungsi Bijektif Dari Himpunan V(X) Ke V( )
Kemudian dapat ditunjukkan untuk setiap dua titik u dan v di X, u dan v bertetangga jika dan hanya jika f(u)dan f(v) bertetangga di , yang dijelaskan pada tabel di bawah ini. Jadi graf .
Tabel 3.10. Dua titik u dan v yang bertetangga di X dan dua titik f(u)dan f(v) yang bertetangga di
Titik vdi merepresentasikan titik P diX, sedangkan titik merepresentasikan kecamatan di Kota Bekasi dan sisi-sisi di graf Y merepresentasikan jalur pendistribusian dari satu kecamatan ke kecamatan lain.Permasalahan pendistribusian kertas suara PILKADA dapat diselesaikan menggunakan konsep bilangan terhubung pelangi dan bilangan terhubung pelangi kuat, sebab apabila menggunakan konsep tersebut akan didapatkan minimum jumlah kelompok pengawalan pendistribusian kertas suara.Pada permasalahan ini bilangan rc(X) dan src(X) menyatakan minimum jumlah kelompok pengawalan pendistribusian kertas suara.
Selanjutnya akan dicari rc(X) dan src(X), karenaX Y sehingga rc(X)=rc( ) dan src(X)=src( ). Menurut Teorema 3.27 diperoleh bahwa rc( )=3, sehingga terdapat pewarnaan pelangi pada , dengan himpunan warna {1, 2, 3},di mana 1= warna merah, 2=warna biru, 3=warna hijau, seperti pada Gambar 3.33.
Sedangkan menurut Teorema 3.29 diperoleh bahwa , sehingga terdapat pewarnaan pelangi kuat pada dengan himpunan warna {1, 2, 3, 4} di mana 1=warna merah, 2=warna biru, 3=warna hijau dan 4=warna unguseperti pada Gambar 3.34.
Gambar 3.34. Graf Dengan Pewarnaan Pelangi Kuat
warna 2=kelompok 2, warna 3=kelompok 3 dan warna 4=kelompok 4, seperti pada gambar berikut.
98 BAB IV PENUTUP
Pada bab ini dituliskan kesimpulan dari pembahasan bab-bab sebelumnya, serta saran bagi penelitian selanjutnya.
A. Kesimpulan
Misalkan G adalah graf terhubung tak trivial.Bilangan keterhubungan pelangi kuat pada grafGmerupakan bilangan bulat positif terkecil sedemikian sehingga terdapat pewarnaan pelangi kuat padaG.
Untuk graf terhubung tak trivial dalam skripsi ini telah dibuktikan beberapateorema:
Untuk menunjukkan hubungan antara diameter graf, bilangan keterhubungan pelangi, bilangan keterhubungan pelangi kuat dan ukuran graf, yaitu
. Untuk menentukan apabila diketahui , yaitu
jika dan hanya jika .