MAKALAH PENGARUH KONSTANTA KOSMOLOGI TERHADAP DINAMIKA ALAM SEMESTA

DINAMIKA ALAM SEMESTA

OLEH: HASANUDDIN, S.Si

ABDUL MUID, S.Si

JURUSAN FISIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS TANJUNG PURA

PONTIANAK 2010

l. Judul

Ndakolatt

2. Bidang Itmu

i&nyettrjui,

Ketua Jurusan Fisike

: Penganrh Konstanta Kosmologi terhadap

Dinamika

'Alam _Semesta

:

Fisika Pontianalq 20 Mei 2010 Penulis, NrP. 19r412162m8p1003 Usman,

DEA

ffi.

IshekJumrreng, M.Si

re.

r9740!D14m3121(M

Pengamatan kosmologi menunjukkan dinamika alam semesta mengembang dan dipercepat. Salah satu model dinamis yang mengasumsikan alam semesta homogen dan isotropis adalah model kosmologi standar Friedmann. Makalah ini menggunakan model kosmologi Friedmann untuk menentukan pengaruh konstanta kosmologi dalam persamaan medan Einstein terhadap dinamika alam semesta. Makalah ini juga menyajikan perhitungan sejumlah besaran dalam analisis tensor untuk metrik Robertson-Walker seperti simbol Christoffel, tensor Ricci, skalar Ricci, dan tensor Einstein. Dari persamaan Friedmann, diperoleh beberapa solusi model alam semesta terbuka dan tertutup berosilasi. Konstanta kosmologi mempengaruhi pengembangan dan ekspansi alam semesta.

Kata kunci : konstanta kosmologi, dinamika alam semesta

Cosmological Constant Effect on Dynamic of Universe

Abstract

Cosmological observation shows the universe are expanded and accelerated. One of the dynamical model that assumed homogeneous and isotropic universe is Friedmann standard cosmological model. This research applies the Friedmann model to find cosmological constant effect (in Einstein field equation) on dinamic of the universe. This research also gives calculations of some quantities in tensor analysis for Robertson-Walker metric such as Christoffel symbol, Ricci tensor, Ricci scalar, and Einstein tensor. Several solution of open and close oscillating universe model can be obtained from Friedmann equation. Cosmological constant influence’s expanding and oscillating of universe.

makalah ini berjudul ”Pengaruh Konstanta Kosmologi terhadap Dinamika

Alam Semesta”.

Dalam kesempatan ini penulis menyampaikan terima kasih kepada :

1. Bapak Prof. Dr. Thamrin Usman, DEA, selaku Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Tanjungpura.

2. Bapak Muh. Ishak Jumarang, M.Si, Selaku Ketua Jurusan Fisika Fakultas MIPA

3. Rekan dosen Fisika dan pihak lain yang telah banyak membantu penyelesaian makalah ini.

Penulis menyadari bahwa makalah ini tidak menutup kemungkinan terdapat kekurangan. Untuk itu, penulis senantiasa mengharapkan kritik dan saran yang bersifat konstruktif dari semua pihak demi perbaikan makalah ini.

Akhir kata, semoga makalah ini dapat memberikan manfaat bagi kita semua. Amin.

Pontianak, Mei 2010

Penulis

DAFTAR ISI ... v BAB I PENDAHULUAN... 1 1.1. Latar Belakang... 1 1.2. Perumusan Masalah... 3 1.3. Tujuan Penulisan... 3 1.4. Manfaat Penulisan... 3 BAB II PEMBAHASAN ... 4

2.1. Teori Relativitas Umum... 4

2.2. Metrik Robertson-Walker... 7

2.3. Kosmologi Standar...13

2.4. Dinamika Alam Semesta dalam Model Kosmologi Standar...15

2.5. Pengaruh Konstanta Kosmologi terhadap Dinamika Alam Semesta... 17

BAB III PENUTUP... 26

3.1. Kesimpulan... 26

3.2. Saran... 26

DAFTAR PUSTAKA... 27 ₂₇

BAB I PENDAHULUAN

1.1. Latar belakang

Seluruh kejadian atau peristiwa dalam fisika selalu dispesifikasi oleh koordinat ruang waktu, sehingga besaran-besaran dalam fisika biasanya dinyatakan dalam fungsi f=f(x,t). Variabel x merupakan variabel ruang sedangkan

t merupakan variabel waktu. Oleh karena itu, pemahaman tentang konsep

ruang-waktu merupakan sesuatu yang penting dalam fisika.

Teori relativitas yang dikembangkan oleh Albert Einstein merupakan salah satu teori yang paling berhasil menerangkan fenomena alam terutama mengenai konsep ruang waktu. Konsep ruang relatif dan waktu mutlak atau absolut dalam teori klasik Newton digantikan oleh konsep ruang waktu relatif dalam teori relativitas umum. Dalam perkembangannya, teori relativitas terbagi menjadi dua teori yaitu teori relativitas khusus yang secara geometri dirumuskan dalam ruang-waktu datar dan teori relativitas umum yang dirumuskan dalam ruang-ruang-waktu lengkung.

Teori relativitas umum pada hakikatnya adalah generalisasi dari teori gravitasi Newton. Berdasarkan teori relativitas umum, gravitasi dikaitkan dengan ruang-waktu lengkung. Perumusan ini secara matematis dinyatakan oleh persamaan medan gravitasi Einstein. Kebenaran teori relativitas umum telah dibuktikan melalui serangkaian pengamatan. Keberhasilan pertama teori relativitas umum adalah penjelasan mengenai anomali presisi perihelion orbit planet merkurius yang mengelilingi matahari. Kemudian pada tahun 1919, Sir Arthur Eddington mengumumkan bahwa pengamatan bintang dekat matahari saat gerhana matahari membenarkan prediksi relativitas umum bahwa benda massif dapat membelokkan cahaya. Dengan verifikasi ini teori relativitas umum dapat diterima secara ilmiah.

Salah satu objek kajian teori relativitas umum adalah kosmologi. Kosmologi merupakan cabang ilmu pengetahuan yang mempelajari alam semesta dalam skala besar (kosmos). Dalam kosmologi, galaksi-galaksi yang sangat besar dan jumlahnya banyak dianggap sebagai titik-titik sehingga dapat diasumsikan sebagai

fluida sempurna. Dengan mengisikan tensor metrik dan tensor energi momentum alam semesta ke dalam persamaan gravitasi Einstein dihasilkan sejumlah solusi berupa model-model alam semesta (Anugraha, 2003).

Semua solusi kosmologis dari teori relativitas umum memprediksikan bahwa alam semesta tidak statis. Hal ini bertentangan dengan pemahaman yang dianut oleh para ilmuwan pada masa itu. Kenyataan ini menyebabkan Einstein menambahkan suku yang dikenal sebagai konstanta kosmologi pada model alam semesta yang diusulkannya. Dengan adanya konstanta kosmologi ini, dapat diperoleh solusi alam semesta yang statis. Akan tetapi, pada tahun sekitar tahun 1920-an, Edwin Hubble menyimpulkan dari hasil pengamatannya terhadap spektrum galaksi, bahwa alam semesta saat ini sedang mengembang (berekspansi). Hasil ini tentu saja bertentangan dangan model kosmologi statis, sehingga Einstein menyatakan bahwa penambahan konstanta kosmologi yang dilakukannya merupakan kesalahan terbesar dalam karir ilmiahnya. Sehingga konstanta kosmologi dihilangkan dari persamaan medan gravitasi Einstein.

Salah satu model kosmologi dinamis yang dibangun berdasarkan teori relativitas umum adalah model kosmologi Friedmann, yang dibangun berdasarkan asumsi bahwa materi dan energi di alam semesta ini terdistribusi secara homogen dan isotropis. Karena keberhasilannya menjelaskan fenomena ekspansi (mengembangnya) alam semesta, model kosmologi Friedmann dijadikan sebagai salah satu pilar model kosmologi standar yang diakui oleh para ilmuwan saat ini.

Baru-baru ini, hasil pengamatan terbaru terhadap supernova jauh menunjukkan bahwa pengembangan alam semesta adalah dipercepat. Hal ini tentu saja bertolak belakang dari pemahaman para ilmuwan selama ini yang memahami bahwa proses pengembangan alam semesta akan mengalami perlambatan akibat adanya tarikan gravitasi. Kenyataan ini seolah-olah menunjukkan bahwa pada skala kosmik interaksi gravitasi dapat saling tolak-menolak. Oleh karena itu diperlukan penjelasan yang lebih baik tentang konsep gravitasi. Salah satu alternatif yang dapat digunakan adalah dengan memasukkan kembali konstanta kosmologi dalam persamaan medan gravitasi Einstein karena secara matematis, bentuk yang paling umum dari persamaan medan Einstein adalah bentuk dengan

mengikutsertakan konstanta kosmologi. Dengan penambahan suku konstanta kosmologi ini dapat dimungkinkan solusi pengembangan alam semesta yang dipercepat. Oleh karena itu, pada makalah ini akan dikaji pengaruh konstanta kosmologi terhadap dinamika alam semesta.

1.2. Perumusan masalah

Berdasarkan latar belakang di atas maka masalah yang akan dipecahkan dalam adalah :

1. Bagaimanakah dinamika alam semesta dalam model kosmologi Friedmann ? 2. Apakah pengaruh konstanta kosmologi terhadap dinamika alam semesta?

1.3. Tujuan penulisan

Berdasarkan masalah yang dirumuskan di atas, maka tujuan penulisan yang hendak dicapai adalah :

1. Menjelaskan dinamika alam semesta dalam model kosmologi Friedmann. 2. Menjelaskan pengaruh konstanta kosmologi terhadap dinamika alam semesta.

1.4. Manfaat penulisan

Melalui kajian ini diharapkan dapat bermanfaat sebagai fondasi dasar untuk kajian lebih lanjut dalam bidang fisika teori dan kosmologi.

BAB II PEMBAHASAN

2.1. Teori Relativitas Umum

Teori relativitas umum merupakan teori geometri dari gravitasi yang dipublikasikan oleh Albert Einstein pada tahun 1915/1916. Teori ini menggabungkan relativitas khusus, hukum Newton tentang gravitasi universal, dan konsep bahwa percepatan gravitasional dapat dideskripsikan dengan kelengkungan ruang dan waktu. Relativitas umum menyatakan kelengkungan ruang waktu dihasilkan oleh momentum dan massa-energi materi yang terdapat dalam ruang waktu.

Relativitas umum saat ini merupakan teori gravitasi yang paling sukses dan diterima secara universal yang didukung oleh sejumlah pengamatan. Keberhasilan pertama yang diraih teori relativitas umum adalah penjelasan mengenai anomali presisi perihelion orbit merkurius. Kemudian pada tahun 1919, Sir Arthur Eddington mengumumkan bahwa pengamatan bintang dekat matahari pada saat gerhana matahari membenarkan prediksi relativitas umum bahwa objek massif membelokkan cahaya. Kemudian banyak pengamatan dan eksperimen lainnya yang mendukung banyak prediksi relativitas umum. Misalnya, dilatasi waktu gravitasi, pergeseran merah gravitasi, penundaan sinyal, dan radiasi gravitasi.

Petunjuk untuk perumusan teori relativitas umum berasal dari prinsip ekuivalensi yang menyatakan bahwa tidak ada eksperimen yang dapat dilakukan untuk membedakan sebuah medan gravitasi dan percepatan seragam yang ekuivalen dalam ruang yang relatif kecil. Sebagai contoh, mari kita lihat kasus berikut. Misalnya kita berada dalam roket yang relatif diam terhadap bumi. Lalu kita jatuhkan sebuah bola dari keadaan diam dan bola itu bergerak menuju lantai dengan percepatan g=9,8 m/s2. Sekarang roket dipercepat dengan percepatan tetap 9,8 m/s2 dan roket itu berada dalam medan gavitasi yang mendekati nol. Sekali lagi kita jatuhkan bola tersebut dan bola bergerak menuju lantai dengan percepatan tetap 9,8 m/s2 juga. Ternyata dua eksperimen tersebut memberikan

hasil yang sama.

Konsekuensi dari pandangan ini adalah pengamat-pengamat inersial dapat dipercepat satu sama lain. Pendefinisian seperti ini tidak sesuai dengan hukum gerak Newton I dan tak dapat dihitung menggunakan relativitas khusus dalam geometri Euclidean. Geometri Euclidean sudah sangat dikenal dalam kehidupan sehari-hari dan memiliki ciri-ciri sebagai berikut :

1. jarak terdekat antara dua titik dalam ruang berupa garis lurus

2. dua garis sejajar berpotongan di tak hingga (tidak pernah berpotongan) 3. jumlah sudut dalam segitiga adalah 1800.

Oleh karena itu, teori relativitas umum dirumuskan dalam bahasa geometri

non-Euclidean. Salah satu contoh yang terkenal dari geometri non-Euclidean adalah

permukaan sebuah bola. Pada permukaan bola, jarak terdekat antara dua titik berupa lengkung, jumlah sudut dalam segitiga lebih dari 1800 dan garis-garis sejajar dapat berpotongan (Krane,1983).

Relativitas umum didasarkan pada beberapa prinsip dasar yang menuntun perkembangannya. Prinsip-prinsip itu adalah:

1. Prinsip umum relativitas : Hukum-hukum fisika harus sama untuk semua pengamat baik yang dipercepat atau tidak.

2. Prinsip kovarian umum : Hukum-hukum fisika harus memiliki bentuk yang

Gambar 2.1. (a) Dalam keadaan diam terhadap bumi, sebuah bola yang dilepaskan dipercepat menuju lantai roket (b) Dalam roket yang dipercepat melalui ruang bebas gravitasi, bola yang sama dilepaskan dan menuju lantai

sama dalam seluruh sistem koordinat.

3. Prinsip bahwa gerak inersial adalah gerak geodesik.

4. Prinsip invariant Lorentz lokal : Hukum-hukum relativitas khusus terpenuhi secara lokal untuk seluruh pengamat inersial.

5. Ruang waktu adalah lengkung : Hal ini mengizinkan efek gravitasi seperti gerak jatuh bebas dideskripsikan sebagai suatu bentuk gerak inersial.

6. Kelengkungan ruang waktu disebabkan oleh distribusi materi dan energi dalam ruang waktu : hal ini dideskripsikan dalam relativitas umum oleh persamaan medan Einstein.

Persamaan medan Einstein mendeskripsikan bagaimana distribusi materi-energi membentuk kelengkungan ruang waktu. Secara konseptual, persamaan Einstein dinyatakan sebagai

      =       Energi -Materi Kerapatan 8 waktu -ruang an kelengkung Kurva G π

di sini G adalah konstanta gravitasi Newton. Berdasarkan prinsip kovarian umum, maka secara matematis, persamaan medan gravitasi Einstein harus dinyatakan dalam bentuk tensor, karena transformasi tensor memiliki bentuk yang sama dengan transformasi koordinat umum. Dalam bentuk tensor, persamaan Einstein dinyatakan sebagai

µυ µυ πGT G =8

(2.1) dengan G_µν adalah tensor Einstein, T_µν menggambarkan distribusi materi dan

energi dan G adalah konstanta gravitasi universal. Tensor Gµνdan Tµν keduanya merupakan tensor simetris rank 2 dan dalam ruang-waktu berdimensi empat dapat dituliskan sebagai matriks 4x4.

Persamaan medan Einstein akan tereduksi menjadi hukum gravitasi Newton dalam kasus medan gravitasi lemah dan kecepatan yang jauh lebih kecil relatif terhadap kecepatan cahaya, yaitu untuk kasus 2 c2

r GM

<< . Kenyataan ini menunjukkan bahwa teori relativitas umum belum terlalu diperlukan untuk sistem tata surya karena teori gravitasi Newton masih memadai. Untuk sistem-sistem

yang memiliki 2 c2 r

GM

>> , seperti lubang hitam (black hole) dan alam semesta, maka teori relativitas umum berperan penting.

Ketika Einstein menerapkan teori relativitas umum pada skala kosmologi, Einstein memperkenalkan suatu bentuk alternatif dari persamaan medan untuk menyesuaikan dengan solusi alam semesta statis . Bentuk itu adalah

µυ µυ

µυ πGT g

G =8 +Λ

(2.2) dengan Λ adalah konstanta kosmologi dan g_µν adalah metrik ruang waktu.

Penambahan suku konstanta kosmologi Λ secara matematis tidak salah, tetapi bentuk tersebut tidak akan kembali ke teori gravitasi Newton pada kasus medan gravitasi lemah, sehingga diasumsikan bahwa nilai Λ adalah sangat kecil yang hanya signifikan pada skala kosmologi dan dapat diabaikan pada kasus medan gravitasi lemah.

Solusi dari persamaan medan Einstein adalah metrik ruang waktu. Metrik ini menjelaskan struktur ruang waktu yang dibentuk oleh tekanan-energi dan pemetaan koordinat untuk memperoleh solusi seperti itu (Anonim, 2007).

2.2. Metrik Robertson-Walker

Persamaan Einstein yang dinyatakan oleh persamaan (2.1) merupakan persamaan differensial non-linear yang sangat sulit untuk diselesaikan. Biasanya untuk menyelesaikannya kita harus mengambil asumsi-asumsi tertentu. Dalam kosmologi asumsi yang biasanya digunakan adalah bahwa alam semesta bersifat homogen dan isotropis. Asumsi ini biasanya dikenal sebagai asas kosmologi.

Kosmologi merupakan suatu ilmu yang menyelidiki struktur dinamik dan evolusi alam semesta secara keseluruhan; alam semesta dianggap sebagai suatu satu kesatuan, kelakuan materi terdekat dipengaruhi juga oleh wilayah yang paling jauh sehingga dari kajian struktur suatu galaksi, seseorang dapat mengambil informasi atas seluruh alam semesta (Sabbata and Gasperini, 1985). Asas kosmologi merupakan prinsip yang sangat penting dalam membangun model kosmologi. Asas ini didukung oleh berbagai observasi yang menunjukkan bahwa

distribusi materi-energi di alam semesta adalah homogen dan isotropis (serba sama dalam segala arah pengamatan).

Distribusi materi dan radiasi dalam alam semesta yang teramati adalah homogen dan isotropis. Ini berlaku pada daerah yang sangat luas sekitar pada skala 103 Mpc (1 pc kira-kira sama dengan 3x106 m). Pada skala ini tidak hanya kerapatan rata-rata saja yang homogen tetapi kehomogenan pada sifat lainnya seperti tipe-tipe galaksi, kerapatan cluster galaksi, komposisi kimia dan komposisi stelarnya. Jadi, dapat disimpulkan pada skala yang luas, alam semesta adalah homogen. Pada skala ini juga alam semesta terlihat isotropis di setiap titik. Ini berarti tidak mungkin mengadakan pengamatan lokal yang dapat membedakan suatu arah pada langit dari lainnya (Schutz, 1985).

Metrik untuk ruang yang homogen dan isotropis adalah metrik Robertson-Walker (RW) simetris yang ditulis dalam bentuk

      + + − − = 2 2 2 2 2 2 2 2 2 2 sin 1 ) ( r dθ r θdϕ kr dr t a dt ds (2.3) Dengan (t,r,θ,φ) adalah koordinat-koordinat ruang-waktu empat dimensi.

Biasanya digunakan konvensi indeks _x0 =_{t, x}1=_r,x2 =θ _{dan x}3 =ϕ_{. Dalam}

notasi yang lebih ringkas, metrik Robertson-Walker dapat dituliskan sebagai

ν µ µνdx dx g ds2 = (2.4) dengan indeksµ,ν =0,1,2,3

Komponen-komponen g_µν= 0 untuk indeks µ ≠ν. Komponen-komponen g_µν

yang tidak nol diberikan oleh persamaan berikut

θ 2 2 2 33 2 2 22 2 2 11 00 sin ) ( ) ( 1 ) ( 1 r t a g r t a g kr t a g g − = − = − − = = (2.5) Tafsiran geometris dari metrik Robertson-Walker diatas adalah sebagai berikut :

a(t) adalah faktor skala kosmik yang tergantung terhadap waktu, dan k adalah

Apabila k = +1 maka ruang tersebut berbentuk bola, jika k = 0 maka ruang tersebut berbentuk flat (datar), sedangkan jika k = -1 maka ruang tersebut berbentuk hiperbolik. Faktor skala a(t) memiliki dimensi panjang dan radius r adalah dari 0 ke 1 untuk k=1. Perhatikan bahwa untuk k=+1, keliling suatu bola 1 dimensi (1D) dari jari-jari koordinat r dalam bidang φ=konstan adalah 2πa(t)r, dan luas bola 2 dimensi (2D) dengan jari-jari koordinat r adalah 4πa(t)2r2.

Bagaimanapun jari-jari fisik bola 1D dan 2D itu adalah

∫

rdr −kr t a 0 2 / 1 2 2 ) 1 /( ) ( dan bukan a(t)r.

Koordinat waktu dalam persamaan (2.3) adalah waktu proper yang terukur oleh pengamat yang diam terhadap kerangka acuan bersama (r, θ, φ)=konstan. Istilah acuan bersama dipilih sebagai berikut : pengamat yang diam dalam kerangka acuan bersama akan tetap diam, (r, θ, φ) tetap tidak berubah dan pengamat yang awalnya bergerak terhadap kerangka ini akan diam di dalamnya.

Bagian spasial dari metrik akan dituliskan sebagai

υ µ µυdx dx h dl2 = (2.6) dimana µ,υ =0,1,2,3. hµ,υ = - gµ,υ (Kolb and Turner, 1990).

Untuk mengilustrasikan konstruksi metrik, tinjau kasus sederhana 2 dimensi spasial. Contoh dari ruang 2 dimensi yang homogen dan isotropis adalah :

(i) Bidang datar “x-y” (R2)

(ii) Bola 2 dimensi kurvatur positif (S2) (iii) Bidang hiperbola kurvatur negatif (H2).

Pertama, tinjau bola 2 dimensi (2-D). Untuk visualisasi bola diperkenalkan suatu dimensi spasial fiksi dan tandai kurva 2D ini dalam ruang Euclid 3D dengan koordinat kartesian x1, x2, x3. Persamaan radius a bola 2D adalah

2 2 3 2 2 2 1 x x a x + + = _(2.7)

Elemen panjang dalam ruang Euclid 3D adalah

2 3 2 2 2 1 2 dx dx dx dl = + + _(2.8)

dari dl menggunakan persamaan (2.8) 2 2 2 2 1 2 2 2 2 1 1 2 2 2 1 2 _{( )} x x a dx x dx x dx dx dl − − + + + = (2.9)

sekarang diperkenalkan koordinat r’ dan θ dalam suku x1 dan x2 oleh

θ θ sin ' cos ' 2 1 r x r x = = (2.10) Secara fisik, r’ dan θ berhubungan dengan koordinat polar dalam bidang x3

(x32=a2-r’2). Dalam koordinat baru ini, persamaan (2.9) menjadi

2 2 2 2 2 2 2 ' ' ' θ d r r a dr a dl + − = (2.11) Akhirnya, dengan definisi koordinat tak berdimensi r ≡ r’/a (0 ≤ r ≤ 1), maka metrik spasial menjadi

      + − = 2 2 2 2 2 2 1 r r dθ dr a dl (2.12) Perhatikan kesamaan metrik ini dengan metrik R-W dengan k=1. Sekarang sudah jelas bahwa a(t) adalah jari-jari ruang.

Bola 2D ditunjukkan dalam Gambar 2.2. Kutub adalah pada r=0 dan equator adalah pada r=1. Titik lokus dari r konstan menyapu sepanjang garis lintang bola, sementara titik lokus dari θ konstan menyapu sepanjang garis bujur bola.

Sistem koordinat lainnya yang biasa digunakan untuk bola 2D adalah koordinat yang ditentukan oleh sudut polar dan azimuth (θ,φ) dari sistem koordinat bola dan berhubungan dengan xi melalui

θ ϕ θ ϕ θ cos sin sin cos sin 3 2 1 a x a x a x = = = (2.13) Dalam koordinat ini persamaan (2.9) menjadi

[

2 2 2

]

2 2 sin θ ϕ θ d d a dl = + _(2.14)

Bentuk ini menunjukkan fakta bahwa ruang adalah bola 2D dengan radius a. Volume dari bola 2D secara mudah dihitung

2 0 2 2 0 2 4 sin a a d d h x d V ϕ θ θ π π π

∫

∫

∫

= = = (2.15) Sebagaimana seperti yang diharapkan (h adalah determinan metrik spasial).

Bola 2D adalah homogen dan isotropis. Setiap titik dalam ruang adalah ekuivalen terhadap semua titik lainnya dan tidak ada arah yang lebih disukai. Dengan kata lain, ruang mengikuti prinsip kosmologi yaitu tidak ada pengamat yang berada pada posisi yang lebih disukai dalam alam semesta. Ruang ini tak terbatas; tidak ada tepi pada bola 2D. Walaupun ruang tak terbatas tetapi volumenya terbatas.

Ekspansi atau kontraksi alam semesta 2D ini ekuivalen dengan peningkatan atau pengurangan jari-jari bola 2D, a. Karena alam semesta adalah homogen dan isotropis, faktor skala (radius a) hanya dapat merupakan fungsi dari waktu. Ketika bola 2D mengembang atau mengerut, koordinat-koordinat (dalam kasus ini r dan θ) tidak berubah. Jarak antara 2 titik yang bergerak bersama dalam ruang diskalai dengan a (oleh karena itu dinamakan dengan faktor skala).

Rumus ekuivalen untuk ruang dengan kurvatur negatif konstan dapat diperoleh dengan mengganti a→ia dalam persamaan (2.12). Metrik yang berhubungan dengan bentuk persamaan (2.12) untuk kasus kurvatur negatif adalah

      + + = 2 2 2 2 2 2 1 r r dθ dr a dl (2.16)

dan metrik yang berhubungan dengan bentuk persamaan (2.14) adalah

[

2 2 2

]

2 2 sinh θ ϕ θ d d a dl = + _(2.17)

Bidang hiperbolik tidak terbatas dengan volume yang tak terhingga karena 0≤θ≤∞.

Model datar dapat diperoleh dari contoh di atas dengan memberikan nilai radius a menjadi tak berhingga. Model datar tidak terbatas dengan volume yang tak berhingga pula. Untuk model datar, faktor skala tidak mewakili jari-jari fisik sebagaimana dalam kasus model tertutup atau jari-jari imajiner sebagaimana dalam kasus model terbuka, tetapi mewakili bagaimana jarak fisik antara titik-titik yang bergerak bersama diskalai ketika ruang mengembang atau mengerut.

Generalisasi model 2D yang didiskusikan di atas ke model 3D spasial adalah trivial. Dalam koordinat kartesian bola 3D didefinisikan sebagai a2= x12 + x22 + x32

+ x42. Metrik spasialnya adalah

2

dl = dx12 + dx22 + dx32 + dx42. Koordinat x4 dapat

dieliminasi sehingga metrik spasialnya menjadi

(

)

2 3 2 2 2 1 2 2 3 3 2 2 1 1 2 3 2 2 2 1 2 x x x a dx x dx x dx x dx dx dx dl − − − + + + + + = (2.18) Dalam koordinat x1=r’sin θ cos φ, x2= r’sin θ sin φ, x3=r’cos θ, metrik yang

diberikan oleh persamaan (2.3) dengan k=+1 dan r=r’/a. Dalam sistem koordinat yang menggunakan 3 koordinat anguler (χ, θ,φ) dari sistem koordinat bola 4D,

x1=a sin χ sin θ cos φ, x2= a sin χ sin θ sin φ, x3= a sin χ cos θ, x4= a cos χ, metrik

yang dihasilkan adalah

(

)

[

2 2 2 2 2

]

2 2 sin sin χ θ θ ϕ χ d d d a dl = + + _(2.19)

Volume bola 3D adalah V=∫d3x√h=2π2a3.

Sebagaimana dalam contoh 2D, model terbuka 3D diperoleh dengan menggantikan a→ia, yang menghasilkan metrik dalam bentuk persamaan (2.3) dengan k=-1 yaitu persamaan (2.16) atau dalam bentuk persamaan (2.19) dengan sin χ→ sinh χ, yaitu persamaan (2.18).

Akhirnya, metrik dapat pula dinyatakan dalam waktu konformal η (yang didefinisikan sebagai dη =dt/a(t)) yaitu :

      − − − − = 2 2 2 2 2 2 2 2 2 2 sin 1 ) (η η r dθ r θdϕ kr dr d a ds (2.20) Untuk memudahkan dalam memahami geometri ruangnya, berikut adalah gambaran ruang tertutup (k=+1), terbuka (k=-1), dan datar (k=0) di dalam ruang lengkung dua dimensi.

2.3. Kosmologi Standar

Dinamika alam semesta yang mengembang dideskripsikan oleh dinamika faktor skala a(t). Untuk mencari kebergantungan a(t) terhadap waktu secara ekplisit, seseorang harus menyelesaikan evolusi faktor skala dengan menggunakan persamaan Einstein (persamaan 2.2).

µυ µυ πGT G =8

(2.21) Untuk menghitung G_µν dapat dilakukan dengan menggunakan definisi tensor Einstein yang diberikan oleh persamaan berikut

R g R G_{µν µν µν} 2 1 − = (2.22) Dengan R_µν dan R adalah masing-masing adalah tensor Ricci dan skalar Ricci yang didefinisikan sebagai

β υα α µβ β αβ α µυ α υ µα α α µυ µυ =Γ , −Γ , +Γ Γ −Γ Γ R (2.23) µυ µυ_R g R= (2.24) Di sini gµν adalah tensor metrik yang merupakan invers dari g_µν, sehingga

komponen-komponennya adalah

(

)

(

_{2 2 2}

)

1 33 1 2 2 22 1 2 2 11 00 sin ) ( ) ( 1 ) ( 1 − − − − = − =       − − = = θ r t a g r t a g kr t a g g (2.25) Sedangkan µ αβ

Γ _{merupakan simbol Christoffel yang dapat dihitung dengan}

menggunakan persamaan berikut (Spiegel,1998)

      ∂ ∂ − ∂ ∂ + ∂ ∂ = Γµ µµ _{β αµ α βµ µ αβ} αβ g x g x g x g 2 1 (2.26)

Dalam persamaan (2.26) bentuk

α β µυ, Γ _{berarti ∂} β

( )

Γµυα ∂ x _.

Dengan asumsi yang minimal mengenai ruas kanan persamaan Einstein dimungkinkan untuk mengetahui sifat medan dasar yang menghasilkan tensor tekanan Tµνwalaupun tidak secara detil. Agar konsisten dengan metrik simetri, tensor tekanan-energi total T_µν harus berupa matriks diagonal dan sifat isotropis mengharuskan komponen spasial yang sama. Realisasi yang sederhana dari tensor tekanan-energi adalah fluida sempurna yang dicirikan oleh kerapatan energi ρ(t) dan tekanan p(t): ) , , , ( p p p diag T_υµ = ρ − − − _(2.27)

Komponen µ=0 dari kekekalan tekanan-energi (Tµυ,υ=0) menghasilkan hukum

I termodinamika dalam bentuk )

( )

( _a3 _{pd a}3

d ρ =− _(2.28)

atau ekuivalen dengan bentuk

(

)

[

a p

]

a dp

d 3 ρ+ = 3 _(2.29)

Arti fisis persamaan (2.29) adalah jelas bahwa perubahan energi dalam elemen volume gerak bersama, d(ρa3), sama dengan negatif tekanan dikali perubahan volume, -pd(a3). Untuk persamaan keadaan sederhana p=wρ, dimana w tak

tergantung terhadap waktu, kerapatan energi ρ ~ a-3(1+w). Contoh yang menarik adalah konstanta ) ( ) 0 ( ) ( 3 4 3 1 ∝ ⇒ − = ∝ ⇒ = ∝ ⇒ = − − ρ ρ ρ ρ ρ p VAKUM ENERGI a p MATERI a p RADIASI (2.30) Awal alam semesta didominasi oleh radiasi. Kemudian alam yang “tua”

didominasi oleh materi (atau dominasi kurvatur jika k ≠ 0). Jika alam semesta mengalami inflasi, terdapat periode awal ketika tekanan didominasi oleh energi vakum. Sekali kita tahu evolusi ρ dan p dalam suku dari faktor skala a(t), maka kita dapat menyelesaikan a(t) (Kolb and Turner, 1990).

2.4. Dinamika Alam Semesta dalam Model Kosmologi Standar

Persamaan dinamika yang mendreskipsikan evolusi faktor skala a(t) diperoleh dari persamaan medan gravitasi Einstein. Komponen tak nol dari metrik Robertson-Walker adalah a a R • • − = 3 00 (2.31) µν µν g a k a a a a R           + + − = • • • 2 2 2 2 2 (2.32)

Dan skala rinci adalah

        + + − = • • • 2 2 2 6 a k a a a a R (2.33)

Komponen 0-0 persamaan Einstein menghasilkan persamaan Friedmann ρ π 3 8 2 2 2 G a k a a = + • (2.34)

sementara komponen µ-µ menghasilkan

Gp a k a a a a _π 8 2 _{2 2} 2 − = + + • • • (2.35)

Dari persamaan (2.7) dan (2.8) menghasilkan persamaan

(

p

)

G a a 3 3 4 + − = • • ρ π (2.36) Nilai •

a >0 artinya kecepatan bernilai positif dan alam semesta mengembang.

Karena masa lalu ρ+3p selalu bernilai positif, maka nilai

• •

a <0. Ini berarti

percepatan ekspansi alam semesta bernilai negatif atau ekspansi alam semesta mengalami perlambatan. Hal ini juga berarti bahwa pada masa lalu a memiliki nilai 0. Menurut big bang peristiwa ini dinamakan waktu nol atau asal mula waktu. Pada a=0 terdapat singularitas yang tidak diketahui.

Perlambatan ekspansi alam semesta ini bertentangan dengan pengamatan baru-baru ini. Alam semesta yang teramati adalah mengembang dipercepat. Energi yang dihasilkan dari ledakan big bang menghasilkan momentum sesaat sementara interaksi gaya tarik gravitasi mengakibatkan perlambatan alam semesta. Jangkauan interaksi gaya tarik gravitasi dari 0 sampai tak hingga. Nilai

• •

a bisa

lebih dari 0 jika memenuhi syarat bahwa tekanan negatif (p<-1/3ρ).

Rata-rata ekspansi alam semesta ditentukan oleh parameter Hubble H a a

•

= _.

Parameter Hubble tidak konstan, tetapi secara umum bervariasi sebagai t-1. Waktu Hubble (atau jari-jari Hubble) H-1 menentukan skala waktu untuk ekspansi. Konstanta Hubble, H0, merupakan nilai ekspansi rata-rata saat ini. Persamaan

Friedmann dapat dibentuk menjadi 1 1 8 3 2 2 2 = − =Ω− G H a H k π ρ (2.37) Dengan Ω adalah rasio kerapatan terhadap kerapatan kritis ρc:

c ρ ρ = Ω (2.38) G H c _π ρ 8 3 2 = (2.39) Karena H2a2 ≥0, terdapat hubungan antara tanda k terhadap Ω-1. Persamaan

(2.39) menunjukkan pentingnya kerapatan kritis. Jika kerapatan alam semesta lebih besar dari kerapatan kritis (Ω>1), ruas paling kiri bernilai positif sehingga

k=+1 dan tipe alam semesta sama adalah tertutup. Jika kerapatan alam semesta

sama dengan kerapatan kritis (Ω=1) maka nilai k=0 dan tipe alam semesta sama adalah datar. Jika kerapatan alam semesta lebih kecil dari kerapatan kritis (Ω<1) maka nilai k=-1 dan tipe alam semesta sama adalah terbuka. Jadi, kerapatan kritis sangat menentukan konstanta kurva atau tipe alam semesta.

Dari hukum termodinamika I yang dinyatakan dalam bentuk

( )

3

( )

3 a pd a d ρ =− _(2.40) didapat ( w) a− + ≈ 31 ρ _(2.41) ( w) t a ≈ 231+ _(2.42)

sehingga memberikan hasil a~t1/2 untuk w=1/3 (dominasi radiasi), a~t2/3 untuk

w=0 (dominasi materi), a~exp(H0t) untuk w=-1 (dominasi energi vakum).

2.5. Pengaruh Konstanta Kosmologi terhadap Dinamika Alam Semesta

Pembahasan di atas tanpa melibatkan konstanta kosmologi Λ. Persamaan Friedmann yang terbentuk dengan melibatkan konstanta kosmologi adalah

3 3 8 2 2 2 Λ + = + • ρ πG a k a a (2.43)

Komponen µ-µ tensor Einstein menghasilkan

(

)

3 3 3 4 Λ + + − = • • p G a a ρ π (2.44) Di sini nilai • •

a dapat bernilai positif jika nilai Λ>4πG(ρ+3p). Adanya nilai Λ yang

cukup besar dapat mempercepat ekspansi alam semesta.

Telah diketahui bahwa nilai kerapatan alam semesta tergantung dari a. Jika a semakin besar maka kerapatan alam semesta semakin berkurang. Semakin kecil kerapatan massa alam semesta maka semakin besar pengaruh konstanta kosmologi.

Dari persamaan (2.44) dapat dibentuk persamaan ( ) k a a Ge a Ht w − Λ + = − + • 3 3 8 31 2 2 2 π (2.45) Dari hasil observasi, perbandingan antara kerapatan ρ dan tekanan p adalah 10-6 sehingga kita dapat mengambil p=0. Integralkan persamaan (2.35), akan diperoleh

C a k a a _− Λ =      + • 3 3 1 2 (2.46) dengan C adalah konstanta integrasi.

Kemudian dengan menggunakan persamaan (2.44), akan diperoleh nilai dari konstanta tersebut ρ π 3 3 8 _a C = (2.47) yang berarti bahwa penyebaran materi berbanding terbalik dengan pertambahan volume alam semesta yang diasumsikan berbentuk bola. Persamaan (4.17) bisa kita tuliskan sebagai

k a a C a = + Λ − • 2 2 3 1 (2.48) Persamaan di atas dikenal sebagai persamaan Friedmann untuk faktor skala alam semesta a(t) tanpa tekanan. Persamaan Friedmann tersebut memiliki nilai-nilai parameter yang bersesuaian dengan

C>0, -∞<Λ<+∞, k=-1,0,+1. 2.5.1 Solusi untuk Λ=0

Persamaan (2.48) akan berbentuk

k a C a = − •2 (2.49) solusinya bergantung pada nilai k yang bersesuaian.

2.5.1.a. untuk k =-1 1 2 + = • a C a (2.50) Solusinya adalah

(

cosh 1

)

2 1 ) (t = C ξ− a (2.51)

Gambar 2.4. Grafik faktor skala a(t) terhadap waktu (t) untuk kasus k=-1. a(t)

(

ξ −ξ

)

= sinh 2 1 C t (2.52) Grafik dari persamaan tersebut adalah Gambar 4.1.

Alam semesta mengembang tanpa batas, pada awal pengembangannya cukup cepat, atau dengan kata lain da/dt>0.

2.5.1.b. Untuk k =0 a C a = •2 (2.53) Solusinya adalah 3 / 2 3 / 1 4 9 ) (t C t a       = (2.54) Grafik dari persamaan di atas adalah Gambar 2.5.

Gambar 2.5. Grafik faktor skala a(t) terhadap waktu (t) untuk kasus k=0.

Dari grafik tersebut dapat kita simpulkan bahwa alam semesta mengembang tanpa batas, atau dengan kata lain da/dt>0.

2.5.1.c. Untuk k=1 1 2 − = • a C a (2.55) Solusi persamaan tersebut adalah

(

1 cosξ

)

2 1 ) (t = C − a (2.56)

(

ξ sinξ

)

2 1 − = C t (2.57) Bentuk dari grafik persamaan tersebut adalah Gambar 2.6.

Dari grafik tersebut dapat disimpulkan bahwa alam semesta tertutup dan berosilasi. Pada awalnya alam semesta mengembang sampai waktu tertentu, pengembangannya berlangsung cukup cepat, namun setelah melewati satu titik dimana da/dt=0, alam semesta mulai membalik. Proses ini berlangsung terus menerus tanpa batas.

Dari ketiga grafik diatas, geometri alam semesta kita bergantung pada nilai konstanta kurvatur k, untuk nilai k= 0, -1 alam semesta terbuka, sedangkan untuk nilai k=1 alam semesta tertutup dan berosilasi. Bahasan pada subbab ini akan

Gambar 2.6. Grafik faktor skala a(t) terhadap waktu (t) untuk kasus k=1.

khusus memfokuskan pada model kosmologi untuk konstanta kosmologi sama dengan nol. Jika digambarkan dalam satu grafik akan terlihat jelas perbedaan antara ketiga model tersebut (gambar 2.7).

Alam semesta yang mempunyai indeks kelengkungan sama dengan -1 mempunyai kelengkungan ruang yang negatif, dan dinamakan sebuah alam semesta terbuka (open universe). Alam semesta ini akan terus mengembang.

Alam semesta yang mengandung indeks kelengkungan sama dengan nol dinamakan sebuah alam semesta datar (flat universe). Alam semesta ini pun akan terus mengembang dengan kecepatan menuju nol.

Alam semesta yang mempunyai indeks kelengkungan sama dengan +1 mempunyai kelengkungan ruang yang positif, dan dinamakan sebuah alam semesta tertutup (closed universe). Alam semesta seperti ini mula-mula mengembang sampai mencapai jari-jari kelengkungan yang maksimum pada suatu waktu t1, dan setelah itu akan mengempis kembali ke sebuah fasa yang sangat

rapat pada waktu t2=2t1. Waktu t2 ini dikenal sebagai waktu kematian alam

semesta.

2.5.2 Solusi untuk k=0

Persamaan (2.48) akan berbentuk

2 2 3 1 a a C a = + Λ • (2.58)

Gambar 2.7. Grafik faktor skala a(t) terhadap waktu (t) untuk kasus k=-1,0,1. a(t)

Gambar 4.5. Grafik faktor skala a terhadap nilai konstanta kosmologi dan waktu untuk kasus k=0 dan Λ>0.

a(t)

Solusi dari persamaan ini akan bergantung pada nilai dari konstanta kosmologinya.

2.5.2.a. Solusi untuk Λ>0

( )

[

_1/2

]

1/3 3 / 1 1 3 cosh 2 3 ) (  Λ −      Λ = C t t a (2.59) Bentuk grafik dari persamaan tersebut adalah

Dari grafik di atas dapat disimpulkan alam semesta mengembang tanpa batas, sedangkan konstanta kosmologi apabila nilainya semakin besar akan menyebabkan alam semesta mengembang juga dipercepat.

2.5.2.b. Solusi untuk Λ<0

( )

[

(

( )

)

]

3 / 1 2 / 1 3 / 1 3 cos 1 2 3 ) (t C t a _ − −Λ      Λ − = (2.60) Bentuk grafik dari persamaan tersebut adalah Gambar 4.6.

Model osilasi, pengembangan alam semesta pada akhirnya akan membalik pada suatu waktu dan mulai mengerut. Pengerutan ini akan menyebabkan segala sesuatu runtuh ke dalam suatu titik tunggal yang kemudian akan meledak lagi, memulai babak pengembangan baru. Proses ini berulang dalam waktu tidak terbatas.

Gambar 4.6. Grafik faktor skala a terhadap nilai konstanta kosmologi dan waktu untuk kasus k=0 dan Λ<0

2.5.3. Solusi untuk k=-1 dan Λ>0

1 3 1 ₂ 2 + Λ + = • a a C a (2.61) Solusi yang bersesuaian adalah

( )

                    Λ                 _Λ + +       Λ = − t C C t a 2 1 2 1 3 1 2 3 1 sinh 4 9 1 1 2 3 (2.62)

Bentuk grafik dari persamaan tersebut adalah

Gambar 4.7. Grafik faktor skala a(t) terhadap waktu (t) untuk kasus k=-1 dan Λ>0 a(t)

Dari grafik di atas dapat disimpulkan alam semesta mengembang tanpa batas, sedangkan konstanta kosmologi apabila nilainya semakin besar akan menyebabkan alam semesta selain mengembang juga dipercepat.

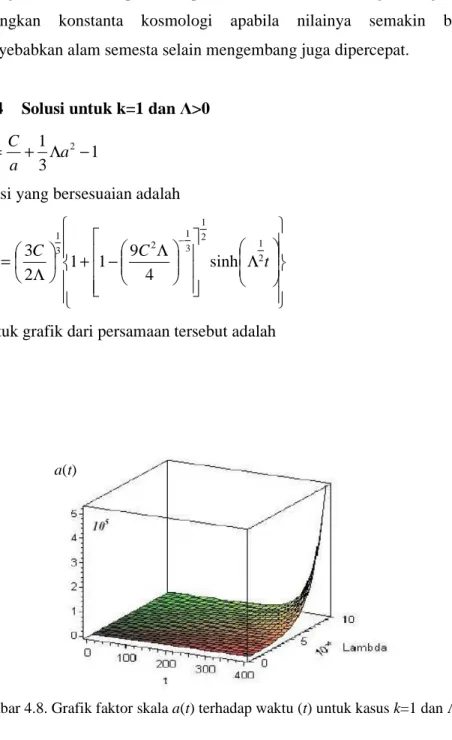
2.5.4 Solusi untuk k=1 dan Λ>0

1 3 1 2 2 − Λ + = • a a C a (2.63) Solusi yang bersesuaian adalah

( )

                    Λ                 _Λ − +       Λ = − t C C t a 2 1 2 1 3 1 2 3 1 sinh 4 9 1 1 2 3 (2.64)

Bentuk grafik dari persamaan tersebut adalah

Dari grafik di atas dapat disimpulkan alam semesta mengembang tanpa batas, sedangkan konstanta kosmologi apabila nilainya semakin besar akan menyebabkan alam semesta selain mengembang juga dipercepat.

Gambar 4.8. Grafik faktor skala a(t) terhadap waktu (t) untuk kasus k=1 dan Λ>0 a(t)

Dalam kasus ini, akan diperoleh grafik yang unik untuk nilai konstanta kosmologi tertentu (Gambar 4.9).

Model lemaitre, pada awalnya alam semesta mengembang dengan cepat, tetapi memiliki percepatan negatif, sehingga pada waktu tertentu alam semesta mengembang dengan laju mendekati nol. Selanjutnya karena konstanta kosmologi berperan dominan, maka alam semesta terus mengembang tanpa batas.

.

Gambar 4.9. Grafik faktor skala a(t) terhadap waktu (t) untuk kasus k=1 dan Λ>0 a(t)

BAB III PENUTUP

2.1. Kesimpulan

Dari hasil pembahasan di atas dapat disimpulkan bahwa :

1. Hasil penyelesaian persamaan medan Einstein tanpa konstanta kosmologi menunjukkan dua pola alam semesta. Pertama, alam semesta yang mengembang tanpa batas, dimana da/dt>0 dan d2a/dt2>0. Kedua, alam semesta yang berosilasi. Pada awalnya alam semesta mengembang kemudian akan membalik pada suatu waktu dan mulai mengerut. Pengerutan ini akan menyebabkan segala sesuatu runtuh ke dalam satu titik tunggal yang kemudian akan meledak lagi, memulai babak pengembangan baru. Proses ini berulang dalam waktu tidak terbatas.

2. Konstanta kosmologi yang ditambahkan pada persamaan medan Einstein menyebabkan geometri ruang waktu berubah. Apabila konstanta kosmologi bernilai positif, maka alam semesta akan mengembang tanpa batas. Semakin besar nilai konstanta kosmologinya, maka alam semesta akan mengembang semakin cepat. Apabila konstanta kosmologi bernilai negatif, maka alam semesta akan berosilasi. Semakin besar nilai konstanta kosmologinya, maka alam semesta akan runtuh dan berosilasi semakin cepat.

2.2. Saran

Bentuk mana yang tepat untuk alam semesta kita saat ini, tentu belum dapat digambarkan dari solusi Friedmann. Dengan memasukkan data astronomi dengan tingkat ketelitian yang tinggi (dark matter dan dark energy), dan juga mempertimbangkan keadaan awal alam semesta (inflasi dan nukleosintesis), maka akan menjadi peran penting dalam menjawab teka-teki ini, sehingga akan bisa diperoleh pemodelan alam semesta secara baik.

DAFTAR PUSTAKA

Anonim, 2007, General Relativity, http://en.wikipedia.org/ wiki /mathematics_ of_general_relativity, (5 juni 2007)

Anugraha, Rinto, N.Q.Z., 2003, Kajian Metrik De Sitter serta Dinamika Gerak

Foton dan Partikel, Jurnal Fisika Indonesia, 7:48-60

Krane, Kenneth, 1983, Modern Physics, John Wiley & Sons, New York

Kolb, Edward and Turner, Michael., 1990, The Early Universe, Westview Press, Chicago

Lawrie, Ian D., 1990, A Unified Grand Tour of Theoretical Physics, Institute of Physics Publishing Bristol and Philadelphia, London.

Sabbata, Venzo and Gasperini, Maurizio., 1985, Introduction To Gravitation, World Scientific Publishing Co Pte Ltd., Torino

Schutz, Bernard F., 1985, A First Course in General Relativity, Cambridge University Press, Cambridge.

Spiegell, Murray R., 1998, Analisis Vektor dan Pengantar Analisis Tensor, Wospakrik, Hans J. (alih bahasa), Erlangga, Jakarta.