BAB 3 ANALISIS VEKTOR

download on www.enggar.tk

BAB 3

ANALISIS VEKTOR

3.1. Pendahuluan

Vektor merupakan suatu besaran yang mempunyai arah. Vektor dinyatakan dengan besar vektor dan arahnya. Penggambaran vektor bergantung pada sistem koordinat yang dipilih.

Pada bab sebelumnya telah dibahas pengenalan vektor dan aljabar vektor. Bab ini akan membahas tentang sistem koordinat, vektor satuan pada sistem koordinat yang bersangkutan, diantaranya sistem koordinat polar, silinder, dan bola. Dalam bab ini juga dibahas mengenai operasi vektor, operator vektor, beberapa operasi tentang operator, dan differensial vektor.

Pada akhir bab ini dibahas integral garis, teorema Green pada bidang, teorema Divergensi, dan teorema Stokes.

Setelah mengikuti kuliah ini mahasiswa diharapkan dapat melakukan operasi vektor, operasi operator differensial, mengenal dan menggunakan sistem koordinat kurviliner, melakukan integrasi lipat dua, dan tiga.

3.2. Sistem Koordinat

A. Sistem Koordinat Kartesian

Dalam sistem koordinat Kartesian, suatu vektor dilukiskan dalam tiga arah, yaitu arah sumbu-X, arah sumbu-Y, dan arah sumbu-Z.dimana masing-masing sumbu koordinat saling tegak lurus, dan mengikuti aturan putaran sekrup. Putaran dari sumbu-X ke sumbu-Y seperti sekrup diputar menghasilkan gerak sekrup yang menyatakan arah dari sumbu-Z.

download on www.enggar.tk

Setiap sumbu koordinat mempunyai vektor satuan yang besarnya satu dan searah dengan arah sumbu koordinatnya,

xˆ

: vektor satuan pada sumbu-X,

yˆ

: vektor satuan pada sumbu-Y, dan

zˆ

: vektor satuan pada sumbu-Z.

Penggambaran suatu vektor dinyatakan oleh ketiga vektor satuan tersebut yang disertai besar atau panjang komponen vektor pada arah tersebut.

Misal :

A(3,4,5) : digambarkan oleh

3

x

ˆ



4

y

ˆ



5

z

ˆ

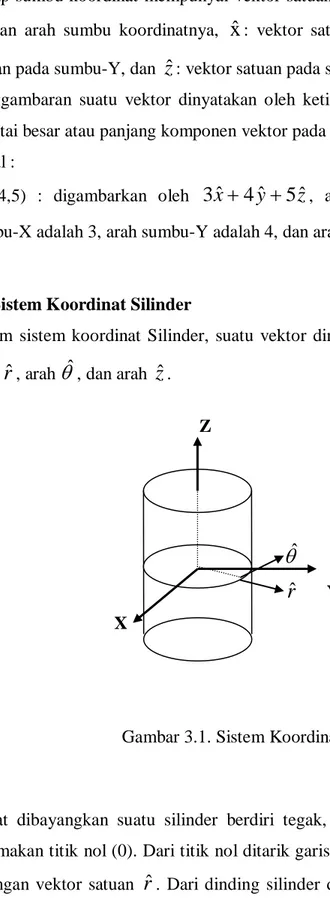
, artinya komponen vektor arah sumbu-X adalah 3, arah sumbu-Y adalah 4, dan arah sumbu-Z adalah 5.

B. Sistem Koordinat Silinder

Dalam sistem koordinat Silinder, suatu vektor dinyatakan dalam tiga arah, yaitu arah

rˆ

, arah



ˆ

, dan arah

zˆ

.

Z



ˆ

rˆ

Y

X

Gambar 3.1. Sistem Koordinat Silinder

Dapat dibayangkan suatu silinder berdiri tegak, titik di tengah-tengah silinder dinamakan titik nol (0). Dari titik nol ditarik garis keluar silinder dinamakan arah r dengan vektor satuan

rˆ

. Dari dinding silinder ditarik garis singgung mendatar

download on www.enggar.tk

yang tegak lurus dengan arah r dinamakan vektor  dengan vektor satuan



ˆ

, berputar berlawanan arah jarum jam pada bidang XY. Dari titik nol ditarik garis lurus tegak membentuk sumbu-Z dengan vektor satuan

zˆ

.

Hubungan sistem koordinat Silinder dengan sistem koordinat Kartesian dapat dilihat pada uraian berikut.

Y

x = r cos  y r y = r sin 

r = r x X

Gambar 3.2. Sistem Koordinat Polar

Vektor r diuraikan pada arah

xˆ

, dan

yˆ

melalui persamaan :

θ

Sin

r

ˆ

θ

Cos

r

ˆ

y

x

r





Vektor satuan arah r adalah :

θ

Sin

ˆ

θ

Cos

ˆ

ˆ

x

y

r





Vektor satuan arah  adalah vektor satuan arah r tetapi  ditambah 90 :



θ

90



ˆ

Sin



θ

90



Cos

ˆ

ˆ

_

_x

_

_

_y

_



θ

Cos

ˆ

θ

Sin

ˆ

y

x







Vektor satuan arah z :

zˆ

Dapat ditunjukkan bahwa

rˆ

,



ˆ

,

zˆ

saling tegak lurus

download on www.enggar.tk

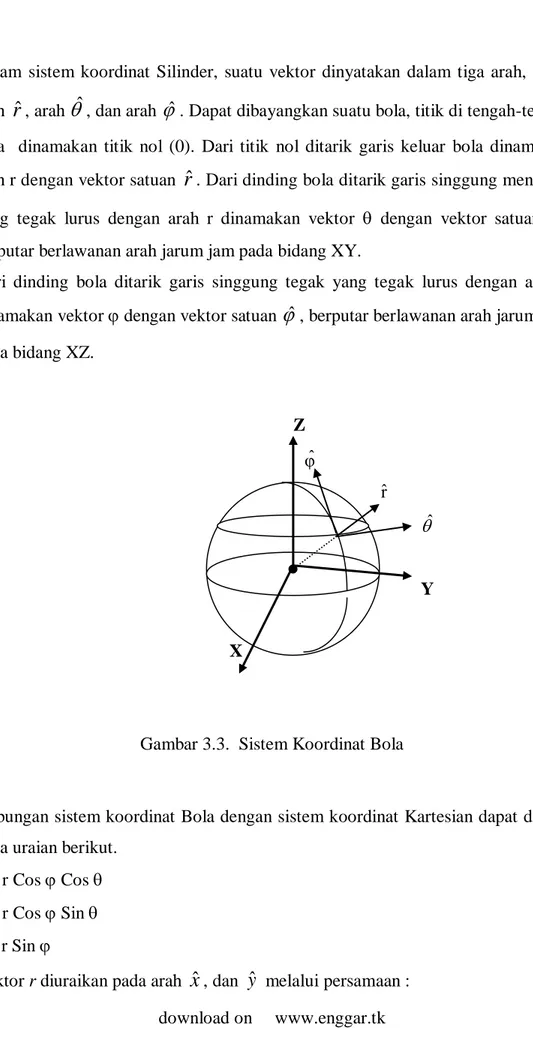
Dalam sistem koordinat Silinder, suatu vektor dinyatakan dalam tiga arah, yaitu arah

rˆ

, arah



ˆ

, dan arah



ˆ

. Dapat dibayangkan suatu bola, titik di tengah-tengah bola dinamakan titik nol (0). Dari titik nol ditarik garis keluar bola dinamakan arah r dengan vektor satuan

rˆ

. Dari dinding bola ditarik garis singgung mendatar yang tegak lurus dengan arah r dinamakan vektor  dengan vektor satuan



ˆ

, berputar berlawanan arah jarum jam pada bidang XY.

Dari dinding bola ditarik garis singgung tegak yang tegak lurus dengan arah r dinamakan vektor  dengan vektor satuan



ˆ

, berputar berlawanan arah jarum jam pada bidang XZ. Z φˆ rˆ ˆ Y X

Gambar 3.3. Sistem Koordinat Bola

Hubungan sistem koordinat Bola dengan sistem koordinat Kartesian dapat dilihat pada uraian berikut.

x = r Cos  Cos  y = r Cos  Sin  z = r Sin 

download on www.enggar.tk







Cos

θ

ˆ

r

Cos

Sin

θ

ˆ

r

Sin

Cos

r

ˆ

y

z

x

r







r berimpit dengan sumbu-X jika  = 0 , dan  = 0 r berimpit dengan sumbu-Y jika  = 0 , dan  = 90 r berimpit dengan sumbu-Z jika  = 90

Vektor satuan arah r adalah :







Cos

θ

ˆ

Cos

Sin

θ

ˆ

Sin

Cos

ˆ

ˆ

x

y

z

r







Vektor satuan arah  adalah vektor satuan

rˆ

tetapi  ditambah 90 dan  = 0 :

 

0 Cos



θ 90



ˆ Cos

  

0 Sin θ 90



ˆ Sin

 

0

Cos ˆ ˆ_{ x  y  z} 

θ

Cos

ˆ

θ

Sin

ˆ

y

x







Vektor satuan arah  adalah vektor satuan arah r tetapi  ditambah 90 :



90



Cos

θ

ˆ

Cos



90



Sin

θ

ˆ

Sin



90



Cos

ˆ

ˆ





















x

y

z







Cos

θ

ˆ

Sin

Sin

θ

ˆ

Cos

Sin

ˆ

y

z

x









Dapat ditunjukkan bahwa

rˆ

,



ˆ

,

φˆ

saling tegak lurus.

3.3. Operasi Vektor

Seperti halnya bilangan, sebuah vektor dapat dijumlahkan , dikurangkan , atau dikalikan dengan vektor lain menurut aturan yang berlaku bagi vektor.

A. Penjumlahan dan Pengurangan Vektor

Operasi penjumlahan atau pengurangan pada vektor dilakukan dengan menjumlahkan atau mengurangkan komponen-komponen vektor yang arahnya sama. Misal : z y x

y

ˆ

A

zˆ

A

A

xˆ







A

z y x

y

ˆ

B

zˆ

B

B

xˆ







B

download on www.enggar.tk



A

x

B

x



y

ˆ



A

y

B

y



zˆ



A

z

B

z



xˆ















B

A



A

_x

B

_x



y

ˆ



A

_y

B

_y



zˆ



A

_z

B

_z



xˆ















B

A

B. Perkalian

Operasi perkalian pada vektor dapat menghasilkan skalar atau vektor

B.1. Operasi Dot

Operasi dot dari dua buah vektor menghasilkan skalar dimana perkalian dilakukan berdasarkan komponen vektor yang arahnya sama. Untuk komponen vektor yang arahnya saling tegak lurus menghasilkan nol.

θ

Cos

B

A

B

A





,  adalah sudut yang dibentuk oleh A dan B.

Untuk vektor satuan :

1

ˆ

ˆ

ˆ

ˆ

ˆ

ˆ



x



y



y



z



z



x

0

ˆ

ˆ

ˆ

ˆ

ˆ

ˆ



y



y



z



z



x



x

Misal : z y x

y

ˆ

A

zˆ

A

A

xˆ







A

z y x

y

ˆ

B

zˆ

B

B

xˆ







B



xˆ



xˆ



A

_x

B

_x





y

ˆ



y

ˆ



A

_y

B

_y





zˆ



zˆ



A

_z

B

_z





B

A

Tinjau suatu benda yang mendapatkan gaya F dan berpindah sejauh d.

F 

download on www.enggar.tk d

Gambar 3.4. Kerja yang dilakukan gaya F

Benda melakukan kerja sebesar :

θ

Cos

W



F



d



F

d

B.2. Operasi Cross

Operasi cross pada dua buah vektor A dan B dirumuskan :

θ

Sin

B

A

B

A

C







,  adalah sudut yang dibentuk oleh A dan B.

Arah vektor C saling tegak lurus dengan A dan B. Untuk vektor satuan :

0

ˆ

ˆ

ˆ

ˆ

ˆ

ˆ



x



y



y



z



z



x

y

x

z

x

z

y

z

y

x

ˆ



ˆ



ˆ

,

ˆ



ˆ



ˆ

,

ˆ



ˆ



ˆ

Misal :

A



xˆ

A

_x



y

ˆ

A

_y



zˆ

A

_z z y x

y

ˆ

B

zˆ

B

B

xˆ







B

z y x z y x

B

B

B

A

A

A

zˆ

yˆ

xˆ





B

A

 

z y x z y x

A

A

A

B

B

B

zˆ

yˆ

xˆ

1





download on www.enggar.tk =



B



A

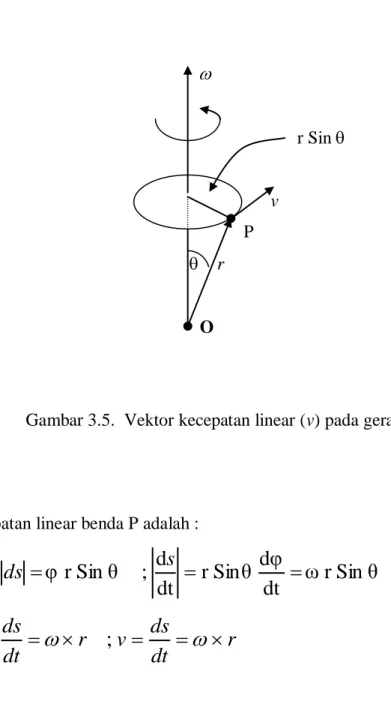
Operasi Cross tidak bersifat komutatif. Sebagai contoh kita tinjau benda titik P bergerak berputar dengan tali sepanjang r dan kecepatan sudut . Benda titik P dilukiskan seperti gambar berikut :

 r Sin  v P  r O

Gambar 3.5. Vektor kecepatan linear (v) pada gerak melingkar

Kecepatan linear benda P adalah :

θ

Sin

r

ω

dt

φ

d

θ

Sin

r

dt

d

;

θ

Sin

r

φ







s

ds

r

dt

ds

v

r

dt

ds

_

_

_

_

_

_

_

;

download on www.enggar.tk

Operasi Dot dan Cross dapat dioperasikan secara berurutan yang akan menghasilkan bentuk skalar atau vektor bergantung ururtan operasinya.



B

C



A





:

B



C

dioperasikan terlebih dahulu, kemudian hasilnya dioperasikan Dot dengan A, menghasilkan skalar.



B

C



A





:

B



C

dioperasikan terlebih dahulu, kemudian hasilnya dioperasikan Cross dengan A, menghasilkan vektor.

Operasi Triple Product Menghasilkan Skalar



B

C



A





=





z y x z y x z y x

C

C

C

B

B

B

zˆ

yˆ

xˆ

A

zˆ

A

yˆ

A

xˆ









B

C



A





= z y x z y x z y x

C

C

C

B

B

B

A

A

A

Gunakan sifat determinan bahwa Setiap pertukaran baris / kolom yang berdekatan hasilnya dikalikan dengan (-1), sehingga



B

C



A





= z y x z y x z y x

C

C

C

B

B

B

A

A

A

= (-!) z y x z y x z y x

C

C

C

A

A

A

B

B

B



B

C



A





= z y x z y x z y x

A

A

A

C

C

C

B

B

B

=

B





C



A



download on www.enggar.tk = z y x z y x z y x

B

B

B

A

A

A

C

C

C

=

C





A



B



Akhirnya didapatkan hasil persamaan :



B

C



A





=

B





C



A



=

C





A



B



Operasi Triple Product Menghasilkan Vektor



B

C



A





=





z y x z y x z y x

C

C

C

B

B

B

zˆ

yˆ

xˆ

A

z

A

y

A

x













=































y x y x x z x z z y z y z y x

_C

_C

B

B

z

C

C

B

B

y

C

C

B

B

x

A

z

A

y

A

x















B

C



A





= y x y x x z x z z y z y z y x

C

C

B

B

C

C

B

B

C

C

B

B

A

A

A

zˆ

yˆ

xˆ

=





















x z x z z y x y x y

C

C

B

B

A

C

C

B

B

A

x























y x y x x z y z y z

_C

_C

B

B

A

C

C

B

B

A

y





















z y z y y x z x z x

_C

_C

B

B

A

C

C

B

B

A

z



download on www.enggar.tk =

x





B

_x



A

_y

C

_y



A

_z

C

_z





C

_x



A

_y

B

_y



A

_z

B

_z

















B

_y

A

_z

C

_z



A

_x

C

_x



C

_y

A

_z

B

_z



A

_x

B

_x





y













B

z

A

x

C

x

A

y

C

y

C

z

A

x

B

x

A

y

B

y



z









Jika pada komponen arah

xˆ

ditambahkan suku

A

_x

B

_x

C

_x, pada komponen arah

yˆ

ditambahkan suku

A

_y

B

_y

C

_y , dan pada komponen arah

zˆ

ditambahkan suku

z z z

B

C

A

, maka akan didapatkan :











B

_x

A

_y

C

_y



A

_z

C

_z



A

_x

B

_x



C

_x

A

_y

B

_y



A

_z

B

_z



A

_x

B

_x





xˆ











B

_y

A

_z

C

_z



A

_x

C

_x



A

_y

B

_y



C

_y

A

_z

B

_z



A

_x

B

_x



A

_y

B

_y





y

ˆ











B

z

A

x

C

x

A

y

C

y

A

z

B

z

C

z

A

x

B

x

A

y

B

y

A

z

B

z



zˆ











Jika disusun kembali akan menghasilkan :



xˆ

B

_x



y

ˆ

B

_y



zˆ

B

_z



A

_x

C

_x



A

_y

C

_y



A

_z

C

_z







xˆ

C

x



y

ˆ

C

y



zˆ

C

z



A

x

B

x



A

y

B

y



A

z

B

z



Hasil ini dapat dituliskan menjadi persamaan :



B

C



B



A

C



C



A

B



A













Tinjau benda titik P bermassa m bergerak berputar dengan tali sepanjang r dan kecepatan sudut .

Benda titik P dapat dilukiskan seperti gambar berikut :



L v P  r

download on www.enggar.tk

Gambar 3.6. Benda titik P berputar dengan kecepatan v

Dari uraian sebelumnya didapatkan : Kecepatan benda P adalah :

r

v







Percepatan benda adalah :



r



v

a









dt

d

dt

d

0

dt

d

;

dt

d

dt

d











r

ω

r

ω

a





r



v

















Kasus khusus : r , atau  = 90





 

















r

r

a

r

2

ω





; dinamakan percepatan sentripetal Momentum sudut angular benda P adalah :

 

v

r

L





m



r



r







m



Kasus khusus : r , atau  = 90



 





r

r

r

r



L



m













2

mr



 

ωr r mvr m   L 3.4. Differensial Vektor

Vektor disusun oleh komponen-komponen vektor pada setiap arah sumbu koordinat. Komponen-komponen vektor dapat berupa fungsi dari variabel lain

download on www.enggar.tk

(misalnya t, waktu) secara eksplisit. Disisi lain vektor dapat berupa suatu hasil perkalian dot atau cross dengan vektor lain.

A. Vektor Berupa Fungsi Eksplisit dari Suatu Variabel

Vektor tersusun oleh komponen yang berupa fungsi eksplisit dari variabel pengamatan t. Vektor berubah setiap saat (fungsi dari t).

z y x

y

ˆ

A

zˆ

A

A

xˆ







A

, dimana

 

t

;

A

A

 

t

;

A

A

 

t

A

A

_x



_{x y}



_{y z}



_z

 

 

x

 

y

 

A

z

dt

d

zˆ

A

dt

d

y

ˆ

A

dt

d

xˆ

dt

d

_

_

_

A

dt

dA

zˆ

dt

dA

yˆ

dt

dA

xˆ

x



y



z



Tinjau kedudukan suatu partikel pada saat t (fungsi dari t) yang dilukiskan oleh persamaan :

Z

ˆ

Y

ˆ

X

ˆ

y

z

x

r







, dimana XX

 

t ;YY

 

t ;ZZ

 

t

Kecepatan partikel pada saat t adalah :

dt

dZ

ˆ

dt

dY

ˆ

dt

dX

ˆ

dt

d

z

y

x

r

v









z y x

y

z

x

ˆ

v



ˆ

v



ˆ

v



Percepatan partikel pada saat t adalah :

dt

dv

zˆ

dt

dv

yˆ

dt

dv

xˆ

dt

d

_x y _z









v

a

2 2 2 2 2 2

dt

Z

d

zˆ

dt

Y

d

yˆ

dt

X

d

xˆ







download on www.enggar.tk z y x

y

ˆ

a

zˆ

a

a

xˆ







Pada gerak melingkar, sistem koordinat Polar dapat dipandang mempunyai vektor satuan yang berubah terhadap waktu.

θ

Sin

yˆ

θ

Cos

xˆ

ˆ





r

θ

Cos

y

ˆ

θ

Sin

xˆ

ˆ

_

_

_



 

t

θ

θ



Jika dilakukan differensial pada

rˆ

dan



ˆ

, akan didapat :

)

θ

(Sin

dt

d

y

ˆ

)

θ

(Cos

dt

d

xˆ

ˆ

dt

d





r

dt

θ

d

)

θ

(Sin

θ

d

d

y

ˆ

dt

θ

d

)

θ

(Cos

θ

d

d

xˆ





dt

θ

d

θ

Cos

y

ˆ

dt

θ

d

θ

Sin

xˆ







dt

θ

d

ˆ





)

θ

Cos

(

dt

d

y

ˆ

)

θ

Sin

(

dt

d

xˆ

ˆ

dt

d







θ

dt

θ

d

)

θ

Cos

(

θ

d

d

y

ˆ

dt

θ

d

)

θ

Sin

(

θ

d

d

xˆ







dt

θ

d

θ

Sin

y

ˆ

dt

θ

d

θ

Cos

xˆ







dt

θ

d

ˆr





Jika kedudukan suatu partikel pada sistem koordinat tersebut dilukiskan oleh :

 

t

;

A

A

 

t

A

A

;

A

θˆ

A

rˆ

_r



_{θ r}



_{r θ}



_θ



A

maka kecepatan partikel tersebut adalah :

θ θ r r

A

dt

ˆ

d

A

dt

d

ˆ

A

dt

ˆ

d

A

dt

d

ˆ

_

































A

r

r

θ

θ

dt

d

v

download on www.enggar.tk

dt

θ

d

A

ˆ

dt

θ

dA

ˆ

dt

θ

d

A

ˆ

dt

dA

ˆ

r

_θ

_r

_θ

_r

_θ

r





















_















_



dt

θ

d

A

dt

dA

ˆ

dt

θ

d

A

dt

dA

ˆ

r _θ

_θ

θ _r

r

B. Differensial pada Operasi Perkalian

Suatu vektor yang dioperasikan perkalian dot atau cross dapat didifferensial dengan cara differensial berantai.

B A K  

B

A

B

A

K

_

_

_

_

dt

d

dt

d

dt

d

B

A

L





B

A

B

A

L









dt

d

dt

d

dt

d



B

C



A

M









B

C



A



B

C



A

M

_

_

_

_

_

_

dt

d

dt

d

dt

d



B

C



A

C

B

C

B

A



















_

_

_





dt

d

dt

d

dt

d



B

C



A

C

B

A

C

B

A



















_















 





dt

d

dt

d

dt

d



B

C



A

N









B

C



A



B

C



A

N













dt

d

dt

d

dt

d

download on www.enggar.tk



B

C



A

C

B

C

B

A



















_

_

_





dt

d

dt

d

dt

d



B

C



A

C

B

A

C

B

A



















_















 





dt

d

dt

d

dt

d

Pada gerak melingkar, suatu partikel berputar pada lingkaran dengan jari-jari konstan dan kecepatan konstan dilukiskan oleh persamaan :







r

r

r

2 konstan







v

v

v

2 konstan

Differensial kedua persamaan menghasilkan :

r

r

r

r

r

r











dt

d

dt

d

)

(

dt

d

dt

d

2

0



r





r

atau

r



v



0

v

v

v

v

v

v











dt

d

dt

d

)

(

dt

d

dt

d

2

0



v



v

atau

v



a



0

Hasil di atas didifferensial lagi

v

r

v

r

v

r











dt

d

dt

d

)

(

dt

d

v

v

a

r









0

; atau 2

v







a

r

Hubungan dengan sudut  antara rdan aadalah :

2

-v

θ

Cos



a

r

download on www.enggar.tk

Untuk

a



berupa percepatan sentripetalyang mengarah ke pusat lingkaran ( =

180), didapat besarnya a adalah :

r

v

a

2



3.5. Turunan Berarah

A. Medan Skalar dan Medan Vektor

Pandang suatu plat besi berukuran besardimana di satu sisi dipanaskan sehingga terjadi aliran panas. Pada suatu titik dapat diamati temperatur sesaat, perubahan temperature, laju perubahan temperature, kecepatan aliran panas yang bergantung arah pengamatan, dan lain-lain. Dikatakan bahwa plat besi tersebut merupakan medan temperatur, dan disebut medan skalar karena temperatur merupakan besaran fisika yang berbentuk skalar. Bentuk lain dari medan skalar antara lain medan energi potensial gravitasidi dekat permukaan bumi.

Medan vektor merupakan suatu keadaan yang dapat diamati kuantitas fisikanya yang berbentuk vektor, misalnya medan listrik, medan magnet, medan kecepatan, dan lain-lain. Pengamat dapat mengamati perubahan fisika (vektor) pada suatu titik, misalnya percepatan, kuat medan magnet, arus listrik yang mengalir pada seutas kawat, dan lain-lain.

B. Operator Gradient ()

Pandang suatu medan skalar (x,y,z), akan diamati perubahan  terhadap jarak s dari titik A(x0, y0, z0) ke suatu titik B(x, y, z) pada arah uˆ . uˆ merupakan vektor

arah satuan , 2 2 2

_b

_c

a

1

c)

zˆ

b

yˆ

a

xˆ

(

uˆ











.

download on www.enggar.tk B(x, y, z)

s

A(x0, y0, z0)

Gambar 3.7. Garis hubung titik A ke titik B

Dapat dilukiskan suatu persamaan garis hubung antara titik A(x0, y0, z0) ke titik

B(x, y, z) yang berjarak s pada arah uˆ adalah :

c)

zˆ

b

yˆ

a

xˆ

(

s

uˆ

)

z

zˆ

y

yˆ

x

xˆ

(

z)

zˆ

y

yˆ

x

xˆ

(







₀



₀



₀









dengan anggapan

1

c

b

a

1

2 2 2

_

_



Akan didapatkan tiga persamaan : x-x0 = as ; x = x0 + as

y-y0 = bs ; y = y0 + bs

z-z0 = cs ; z = z0 + cs

Dari ketiga persamaan tersebut dapat dipandang bahwa  merupakan fungsi dari s saja sehingga perubahan  terhadap s dituliskan :

ds

dz

z

φ

ds

dy

y

φ

ds

dx

x

φ

ds

φ

d



















c

z

φ

b

y

φ

a

x

φ



















c)

zˆ

b

yˆ

a

xˆ

(

)

z

φ

zˆ

y

φ

yˆ

x

φ

xˆ

(

























download on www.enggar.tk

uˆ

φ

)

z

zˆ

y

yˆ

x

xˆ

(





















uˆ

φ







Pernyataan

ds

φ

d

merupakan turunan berarah, dan operator gradient atau del () didefinisikan sebagai :

z

zˆ

y

yˆ

x

xˆ





















;  = gradient 

Operator gradient atau del () bekerja hanya pada medan skalar.

Jika diberikan medan  (x,y,z) = x2y + xz, suatu titik P pada medan tersebut mempunyai koordinat P(1,2,-1), dan dicari perubahan medan  di titik P pada arah

zˆ

yˆ

2

xˆ

2







u

. Vektor arah satuan

(2

xˆ

2

y

ˆ

zˆ

)

3

1

ˆ







u

x

zˆ

x

y

ˆ

z)

(2xy

xˆ

φ







2





;



φ



xˆ

(2xy



z)



y

ˆ

x

2



zˆ

x

3

5

)

zˆ

y

ˆ

2

xˆ

(2

3

1

)

zˆ

y

ˆ

xˆ

(3

uˆ

φ

ds

φ

d





















Contoh lain berupa medan temperatur Tx2 y2 xyz273

, di titik (-1,2,3) dicari ke arah mana kenaikan temperatur tercepat dan berapa perubahannya.

xy

zˆ

xz)

2y

(

y

ˆ

yz)

(2x

xˆ

z

T

zˆ

y

T

y

ˆ

x

T

xˆ

T

































zˆ

2

y

ˆ

7

xˆ

4

T)

(



_(1,2,3)







 

T

uˆ

Cos

θ

uˆ

T)

(

ds

dT

1,2,3) ( 1,2,3) (













Agar bernilai maksimum dipilih nilai  = 0, sehingga arahkenaikan temperatur tercepat adalah

4

xˆ



7

yˆ



2

zˆ

dan perubahan temperaturnya adalah



ds

dT

_

_

_

)

zˆ

2

yˆ

7

xˆ

(4

69

69

1

)

zˆ

2

yˆ

7

xˆ

(4







download on www.enggar.tk

C. Operasi Divergen

Operator  dapat dioperasikan seperti layaknya vektor.

)

V

zˆ

V

y

ˆ

V

xˆ

(

)

z

zˆ

y

y

ˆ

x

xˆ

(



_x



_y



_z























V

z

V

y

V

x

V

_x y _z



















= divergen V D. Operasi Curl z y x

V

V

V

z

y

x

zˆ

yˆ

xˆ



















V









































































y

V

x

V

zˆ

x

V

z

V

yˆ

z

V

y

V

xˆ

z y x z y x E. Operasi Laplacian



























)

z

zˆ

y

y

ˆ

x

xˆ

(

φ

)

z

φ

zˆ

y

φ

yˆ

x

φ

xˆ

(

























φ

2 2 2 2 2 2

z

φ

y

φ

x

φ

















= divergen gradient  φ 2  

0

φ

2

_

download on www.enggar.tk 2 2 2 2

t

φ

v

1

φ









; dinamakan persamaan Gelombang

t

φ

v

1

φ

2 2









; dinamakan persamaan diffusi atau persamaan konduksi panas

3.6. Integral Garis

Dalam persoalan Fisika sering dijumpai suatu besaran yang bergantung lintasan, misalnya besaran kerja yang didefinisikan :

r

F d

dW





Kerja dW yang dilakukan oleh gaya F bergantung pada pemilihan lintasan dr yang pada umumnya berupa kurva, lingkaran, atau garis lurus penghubung titik A dan titik B. Z dr B A F Y X

Gambar 3.8. Lintasan dari titik A ke titik B

Jika dihitung kerja W sepanjang lintasan AB, didapat :







B

d

A

r

F

W

download on www.enggar.tk

Bentuk W seperti ini dinamakan integral garis. Sebagai contoh, tinjau suatu gaya yang berbentuk

F



xˆ

xy



yˆ

y

2yang melakukan kerja sepanjang lintasan dari titik O(0,0) ke titik A(2,1) seperti gambar berikut :

Y B A(2,1) (1) (3) (4) (2) O C X

Gambar 3.9. Lintasan OA berupa lintasan (1), (2), (3), dan (4)

dy

y

xydx

d

;

dy

y

ˆ

dx

xˆ

d

r





F



r





2 1. Lintasan dari O ke B, kemudian dari B ke A



















B O A B A O 1

d

d

d

W

F

r

F

r

F

r

Lintasan OB : x = 0, dx = 0 ; y = 0-1 , sehingga

3

1

3

1

dy

y

d

3 1₀ 1 0 2 B O

















_



F

r

y

Lintasan BA : y = 1, dy = 0 ; x = 0-2 , sehingga

2

x

2

1

xdx

d

2 2₀ 2 0 A B











_



F

r

3

5

3

1

2

d

W

A O 1





F



r







download on www.enggar.tk 2. Lintasan dari O ke C, kemudian dari C ke A



















C O A C A O 2

d

d

d

W

F

r

F

r

F

r

Lintasan OC : y = 0, dy = 0 ; x = 0-2 , sehingga

0

d

B O







F

r

Lintasan CA : x = 2, dx = 0 ; y = 0-1 , sehingga

3

1

y

3

1

dy

y

-d

3 1₀ 1 0 2 A C















_



F

r

3

1

d

W

A O 2





F



r





3. Lintasan dari O ke A berupa garis lurus y = ½ x ; dy = ½ dx ; x = 0-2













































_

_

_

dx

2

1

x

2

1

dx

x

2

1

x

d

W

2 2 0 2 0 A O 3

F

r







2 0 2 2

dx

x

8

1

x

2

1





2 0 2

dx

x

8

3

2 0 3

x

8

1

_



= 1

4. Lintasan dari O ke A berupa parabola y = ¼ x2 ; dy = ½ xdx ; x = 0-2

download on www.enggar.tk













































_

_

_

xdx

2

1

x

4

1

dx

x

4

1

x

d

W

2 2 0 2 2 0 2 A O 4

F

r







2 0 5 3

_x

_dx

32

1

x

4

1

2 0 6 4

x

192

1

x

16

1







= 3 2

Lintasan OA bisa berupa lintasan yang bergantung waktu, t. Misal : x = 2t3 ; y = t2 , maka dx = 6t2dt ; dy = 2tdt , sehingga

     

t

t

t

dt

t



tdt



r

F

d

2

6

2

W

3 2 2 2 2 t 0 A O 4













dt

t

t

r

F

7 5 t 0 A O 4

d

12

2

W













t 0 6 8

_t

6

2

t

8

12

_

_



Jika benda saat t = 0 berada di titik O, dan t = 2 berada di titik A, maka W =

3 1088

Ada besaran yang mempunyai sifat khusus didalam operasi integral garis, yaitu hasil integral garis pada suatu lintasan sembarang bernilai tetap dan tidak bergantung pemilihan lintasan, akan tetapi hanya bergantung pada titik awal dan titik akhir. Tinjau medan W yang mempunyai sifat :

z

W

zˆ

y

W

yˆ

x

W

xˆ

W























F

; atau

z

W

F

;

y

W

F

;

x

W

F

_{x y z}



















download on www.enggar.tk





















B A z y x AB

d

(

xˆ

F

yˆ

F

zˆ

F

)

(

xˆ

dx

yˆ

dy

zˆ

dz)

W

B A

r

F



























B A

dz)

zˆ

dy

yˆ

dx

xˆ

(

)

z

W

zˆ

y

W

yˆ

x

W

xˆ

(







_













B A

dz

z

W

dy

y

W

dx

x

W



B A dW = W(B) – W(A)

Dapat dilihat bahwa kerja yang dilakukan oleh gaya F hanya bergantung pada kondisi awal W(A) dan kondisi akhir W(B), tidak bergantung pada lintasan yang dipilih. Gaya F tersebut dinamakan gaya Konservatif, dan W dinamakan medan konservatif. Sedangkan persamaan

dz

z

W

dy

y

W

dx

x

W

dW



















dinamakan differensial eksak dari W.

Tinjau medan gravitasi bumi g, suatu benda bermassa m berada pada ketinggian z dari permukaan bumimempunyai energi potensial V = mgz. Jika benda tersebut jatuh ke bumi maka gaya gravitasi F = mg melakukan kerja sebesar :

mgz

mgr

d

W

0 0 z













_

F

r

_z

Dapat dilihat bahwa : W = -V, atau

F = W = -V , dan mempunyai sifat : F = (W) = -(V) = 0

download on www.enggar.tk

Dari persamaan terakhir dapat dilihat bahwa medan gravitasi merupakan medan konservatif, dan gaya gravitasi merupakan gaya konservatif.

Sebagai contoh, tinjau suatu gaya yang dirumuskan :

zˆ

1)

(3xz

y

ˆ

x

xˆ

)

z

(2xy



3



2



2





F

Untuk melihat apakah Fbersifat konservatif, harus dilakukan operasi Curl F :

1

-13xz

x

z

-2xy

z

y

x

zˆ

yˆ

xˆ

2 2 3



















F

2x)

(2x

zˆ

)

3z

3z

(

y

ˆ

(0)

xˆ





2



2







= 0 F bersifat konservatif.

Besarnya usaha yang dilakukan gaya F dari titik O(0,0,0) ke titik A(x,y,z) adalah :

























( , , ) y,0) (x, (x,0,0) (0,0,0) y,0) (x, (x,0,0) A O

d

d

d

d

W

z y x

r

F

r

F

r

F

r

F

dimana lintasan OA sembarang.

1. Dari titik (0,0,0) ke titik (x,0,0) : y = 0 , dy = 0 , z = 0 , dz = 0

0

d

(x,0,0) (0,0,0)







F

r

2. Dari titik (x,0,0) ke titik (x,y,0) : dx = 0 , z = 0 , dz = 0

y

x

dy

x

d

2 y 0 2 y,0) (x, (x,0,0)







_



F

r

download on www.enggar.tk 3. Dari titik (x,y,0) ke titik (x,y,z) : dx = 0 , dy = 0

z)

(xz

dz

1

3xz

d

3 z 0 2 z) y, (x, y,0) (x,















_



F

r

Dari ketiga hasil integrasi, didapat W = x2y-xz3-z

V = -x2y+xz3 +z

Contoh lain, tinjau suatu muatan q diletakkan pada titik O(0,0,0). Pada jarak r dari muatan q timbul medan listrik (gaya per satuan muatan) sebesar :

r r E F 3 2 r q ˆ r q q   

Energi potensial V per satuan muatan didefinisikan sebagai usaha yang dilakukan oleh gaya F per satuan muatan (E) untuk membawa muatan q dari titik ~ ke titik r

adalah :





 









r r

r

r

r

q

r

E

d

d

V

3 r  









_

r

q

r

dr

q

2 r

r

q

)

V(









Didefinisikan V(~) = 0, maka

r

q

V



3.7. Teorema green pada Bidang

download on www.enggar.tk







b a

F(a)

F(b)

F(x)dx

dx

d

Tinjau dua buah fungsi P(x,y) dan Q(x,y), dan lintasan berupa Y d l c a b X Gambar 3.10. Lintasan l

Integral garis pada loop tertutup dari Q(x,y)dy dapat dituliskan :















l d c c d

y)dy

a,

Q(x

y)dy

b,

Q(x

y)dy

Q(x,











d c

dy

y)

Q(a,

y)

Q(b,

Integral garis pada loop tertutup dari P(x,y)dx dapat dituliskan :















l a b b a

c)dx

y

P(x,

d)dx

y

P(x,

y)dx

P(x,

download on www.enggar.tk













b a

dx

c)

Q(x,

d)

P(x,

Di sisi lain :









_

l A

dxdy

x

y)

Q(x,

y)dy

Q(x,











_

l A

dydx

y

y)

P(x,

y)dx

P(x,

Jika kedua persamaan di atas dijumlahkan akan didapat :































l A

)

,

(

)

,

(

y)dy

Q(x,

y)dx

P(x,

dx

dy

y

y

x

P

x

y

x

Q

Jika digunakan gaya konservatif

F



x

ˆ

F

_x



y

ˆ

F

_y dengan sifat

x

F

y

F

_x y











, maka













l l y x

dx

F

dy

P(x,

y)dx

Q(x,

y)dy

F

W

Fx = P(x,y) , dan Fy = Q(x,y)

0

dy

dx

)

y

F

x

F

(

y A x

_













_

Tinjau suatu gaya

F



xˆ

xy



yˆ

y

2,

d

r



xˆ

dx



y

ˆ

dy

;

F



d

r



xydx



y

2

dy

lintasan :

download on www.enggar.tk A(2,1)

y=¼ x2 , dy = ½ xdx

X

Gambar 3.11. Lintasan y = ¼ x2

Besarnya kerja yang dilakukan oleh gaya F pada lintasan tertutup c adalah :



xy

xˆ

y

y

ˆ





xˆ

dx

yˆ

dy



d

W

c 2

_

_









_

_

c

r

F







c 2

dy

y

xydx







l

y)dy

Q(x,

y)dx

P(x,

dengan

P(x,y) = xy, dan Q(x,y) = -y2 ,

sehingga

 

 

dy

dx

y

xy

x

y

A

]

[

dy

y

xydx

W

2 c 2



















_

_







A

dy

dx

x

 

 





1 0 y y 2 0 x

dy

xdx

download on www.enggar.tk

dy

x

2

1

1 0 y 2 0 2















_





1

y

2ydy

2 1₀ 1 0















_

Untuk menghitung luas suatu daerah atau bidang dapat dituliskan :





S

dy

dx

A

Tinjau suatu persamaan :





C

ydx

xdy

Dengan menganggap : P = -y , dan

1

y

P

_

_





Q = x, dan

1

y

Q

_





Maka :











_





_





_



_



A C

)

,

(

)

,

(

ydx

xdy

dx

dy

y

y

x

P

x

y

x

Q





A

2

dx

dy

Sehingga luas daerah atau bidang dapat dirumuskan :











A C

ydx

xdy

2

1

dy

dx

A

Untuk ellips dengan persamaan :

x = A Cos  , dan dx = -A Sin  d y = B Sin  , dan dy = B Cos  d luas ellips adalah :

download on www.enggar.tk











A C

ydx

xdy

2

1

dy

dx

A



AB)





Cos

θ

Sin

θ



dθ

2

1

2π 0 2 2







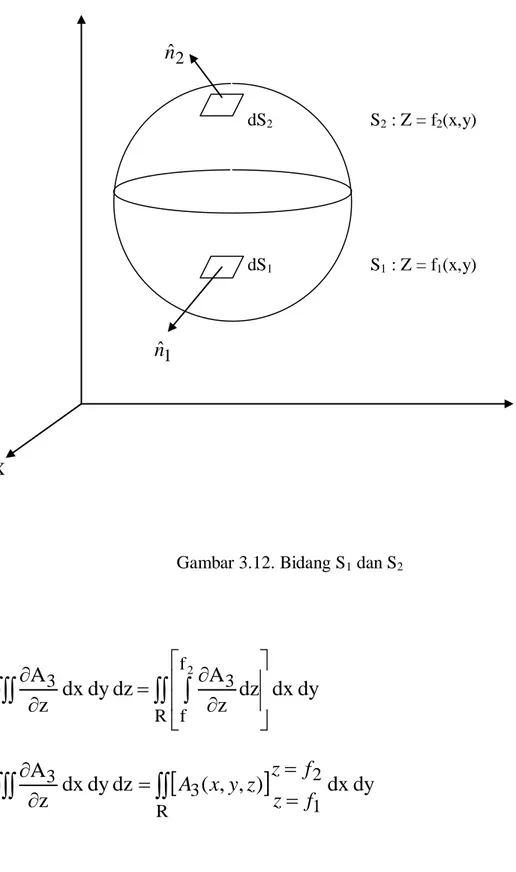
= AB 3.8. Teorema Stokes Definisikan 3 2 1

y

ˆ

A

z

ˆ

A

A

x

ˆ

A









S = suatu permukaan dengan vektor normal

nˆ

Dilakukan operasi vektor :





zˆ

y

A

yˆ

z

A

A

xˆ

₁ 1 1























zˆ

nˆ

y

A

yˆ

z

A

nˆ

A

xˆ

₁ 1 1

_

































)

nˆ

zˆ

(

y

A

)

nˆ

yˆ

(

z

A

_{1 1}

















vektor kedudukan dilukiskan sebagai :

zˆ

z

yˆ

y

xˆ

x

r









zˆ

y

z

yˆ

y

r















; ambil z = z(y)

)

zˆ

nˆ

(

y

z

yˆ

nˆ

y

rˆ

nˆ



















= 0 ….. diambil saling tegak lurus,

download on www.enggar.tk

)

zˆ

nˆ

(

y

z

-yˆ

nˆ















(

zˆ

nˆ

)

dS

y

z

z

A

z

A

dS

nˆ

A

xˆ

S 1 1 1





_





































S



Pada permukaan S, didefinisikan

A1(x,y,z) = A1(x,y,f(x,y)) = F(x,y) , sehingga

y

F

y

z

z

A

z

A

_{1 1}





















1. permukaan S diambil dengan vektor normal

nˆ

sejajar sumbu Z, didapat :





_

_

_

_



























C 1 C S S S 1

dx

dy

F

dx

A

dx

y

F

dS

)

nˆ

zˆ

(

y

F

dS

nˆ

A

xˆ



2. permukaan S diambil dengan vektor normal

nˆ

sejajar sumbu X, didapat





_

_

_

_



























C 2 C S S S 2

dy

dz

F

dy

A

dy

z

F

dS

)

nˆ

xˆ

(

z

F

dS

nˆ

A

yˆ



3. permukaan S diambil dengan vektor normal

nˆ

sejajar sumbu Y, didapat





_

_

_

_



























C 3 C S S S 3

dx

dz

F

dz

A

dz

x

F

dS

)

nˆ

yˆ

(

x

F

dS

nˆ

A

zˆ



Jika nomer 1, 2, dan 3 dijumlahkan untuk permukaan S utuh didapatkan :



























C C 3 C 2 C 1 S

r

d

A

dz

A

dy

A

dx

A

dS

nˆ

A









atau















C S

r

d

A

dS

nˆ

A









Perumusan ini memudahkan kita melakukan integrasi lipat dua ke integral lipat satu ( integral garis tertutup ).