BAB V PENUTUP. Berdasarkan pembahasan pada bab-bab sebelumnnya baik secara matematis maupun dalam studi kasus, diperoleh kesimpulan sebagai berikut:

55

5.1 Kesimpulan

Berdasarkan pembahasan pada bab-bab sebelumnnya baik secara matematis maupun dalam studi kasus, diperoleh kesimpulan sebagai berikut: 1. Dari hasil studi kasus pada 74 sungai di Indonesia yang daerah pengalirannya

lebih dari 1000 km2 tahun 2010 di bab IV diperoleh:

a. Kernel dengan infinite order akan memberikan hasil yang optimal jika kelipatan titik estimasi x dipilih sekecil mungkin atau titik-titik yang diestimasi hampir di seluruh bilangan real pada interval data yang digunakan. Hal tersebut dapat dilihat ketika kelipatan nilai estimasi x yang digunakan 0,1, 0,2 dan 0,3 maka nilai MSE terkecil sebagian besar dihasilkan pada estimasi yang menggunakan kernel dengan order tak hingga yaitu kernel sinus. Namun ketika kelipatan nilai estimasi x yang digunakan 0.5, 0,6 dan 0.7 maka nilai MSE terkecil sebagian besar dihasilkan pada estimasi yang menggunakan kernel dengan order berhingga yaitu kernel normal.

b. Perubahan nilai bandwidth pada setiap kelipatan nilai estimasi x mempengaruhi nilai MSE yang dihasilkan. Nilai bandwidth yang kecil yaitu 0.13 memberikan nilai MSE yang cukup besar dibandingkan 0.3445996 dan 0.5. Begitu juga berlaku pada nilai bandwidth yang besar yaitu 1. Hal ini disebabkan oleh sifat dari parameter bandwidth yaitu semakin kecil nilai bandwidth maka grafik yang dihasilkan akan semakin kasar dan menjauhi fungsi yang sebenarnya. Begitu juga ketika bandwidth yang dipilih besar maka grafik yang dihasilkan akan semakin halus. Sifat inilah yang mempengaruhi nilai MSE yang dihasilkan.

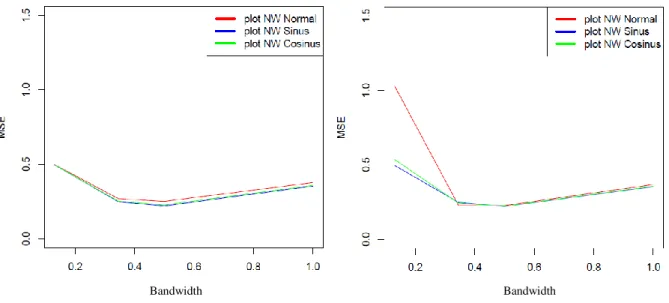
Tinggi rendahnya grafik memperlihatkan besar dan kecilnya nilai MSE. Dari grafik MSE di atas memperlihatkan bahwa nilai MSE yang dihasilkan pada bandwidth lebih dari 0,3445996 tidak begitu jauh berbeda antara kernel order berhingga maupun yang tak hingga. Namun pada bandwidth kurang dari 0,3445996 memperlihatkan bahwa terjadi perbedaan nilai MSE yang cukup signifikan dari ketiga kernel terlebih pada kelipatan titik x = 0,5 dan x = 0,7. Pada kelipatan titik x = 0,5 kernel normal menghasilkan nilai MSE yang paling besar. Sedangkan pada kelipatan titik x = 0,7 kernel cosinus menghasilkan nilai MSE yang paling besar dibandingkan kernel normal untuk bandwidth kurang dari 0,3445996. Grafik dari masing-masing kelipatan titik dapat dengan lengkap dilihat pada lampiran 4.

Berdasarkan studi kasus dengan pengambilan nilai kelipatan pada titik x antara 0,1 – 0,7, kernel sinus akan lebih unggul ketika titik-titik yang diestimasi hampir berada di seluruh bilangan real di selang data pengamatan. Sedangkan kernel normal akan lebih unggul ketika titik-titik yang diestimasi hanya pada beberapa bilangan real di selang data pengamatan. Namun secara keseluruhan nilai MSE yang terkecil paling banyak dihasilkan oleh kernel dengan order tak hingga yaitu kernel sinus.

Nilai MSE yang kecil dalam hal ini menunjukkan bahwa hasil estimasi yang dihasilkan oleh estimator dekat dengan nilai fungsi aslinya. Sehingga estimator Nadaraya Watson dengan kernel berorder tak hingga khususnya sinus dapat memberikan hasil estimasi yang tidak jauh berbeda dengan keadaan yang sebenarnya. Dalam hal ini untuk mengestimasi volume sungai di Indonesia pengamat tidak harus melakukan observasi terlebih dahulu. Sehingga pemerintah dapat lebih hemat dalam hal biaya, tenaga dan juga waktu dalam mengestimasi volume sungai di Indonesia.

Berikut grafik MSE dari masing-masing kelipatan nilai x:

Bandwidth Bandwidth

a. Grafik MSE dengan kelipatan titik x = 0.1 b. Grafik MSE dengan kelipatan titik x = 0.3

Bandwidth Bandwidth

c. Grafik MSE dengan kelipatan titik x = 0.5 d. Grafik MSE dengan kelipatan titik x = 0.7

2. pada kelipatan x sebesar 0,3, nilai MSE yang terkecil masih didominasi oleh kernel infinite order yaitu sinus dengan bandwidth 0,13, 0,5 dan 1. Sedangkan pada bandwidth 0,3445996 nilai MSE yang terkecil dihasilkan oleh kernel normal.

3. pada kelipatan x sebesar 0,4, nilai MSE yang terkecil dihasilkan oleh kernel infinite order yaitu sinus dengan bandwidth 0,13 dan 1. Sedangkan pada bandwidth 0,3445996 dan 0,5 nilai MSE yang terkecil dihasilkan oleh kernel normal.

4. pada kelipatan x sebesar 0,5, nilai MSE yang terkecil dihasilkan oleh kernel infinite order yaitu sinus dengan bandwidth 0,13. Sedangkan pada bandwidth 0,3445996, 0,5 dan 1 nilai MSE yang terkecil dihasilkan oleh kernel normal. 5. pada kelipatan x sebesar 0,6 dan 0,7 di setiap nilai bandwidth yang dipilih

terlihat bahwa nilai MSE yang terkecil dihasilkan oleh estimator dengan menggunakan kernel normal.

Ketika kelipatan x dipilih yang kecil, dalam kasus ini kelipatan x kurang dari 0,4, maka estimator dengan menggunakan kernel infinite order yaitu sinus akan menghasilkan nilai MSE yang kecil yang berarti bahwa kernel sinus akan memiliki performance lebih baik, berapapun bandwidth yang dipilih, dibandingkan kernel yang lainnya. Sedangkan nilai MSE terkecil akan dihasilkan oleh estimator dengan menggunakan kernel normal ketika kelipatan x yang dipilih cukup besar dalam kasus ini untuk kelipatan x lebih dari 0,4.

Dari tabel di atas, nilai MSE yang terkecil dihasilkan oleh estimator yang menggunakan kernel sinus dengan ketentuan sebagai berikut 12 MSE kecil dihasilkan oleh estimator dengan menggunakan kernel normal, 15 dihasilkan oleh estimator dengan kernel sinus dan 1 dihasilkan oleh estimator dengan kernel cosinus. Sehingga dari hasil tabel di atas terlihat bahwa MSE terkecil paling banyak dihasilkan oleh estimator yang menggunakan kernel sinus. Berikut akan ditampilkan grafik dari MSE dari masing-masing kelipatan titik x.

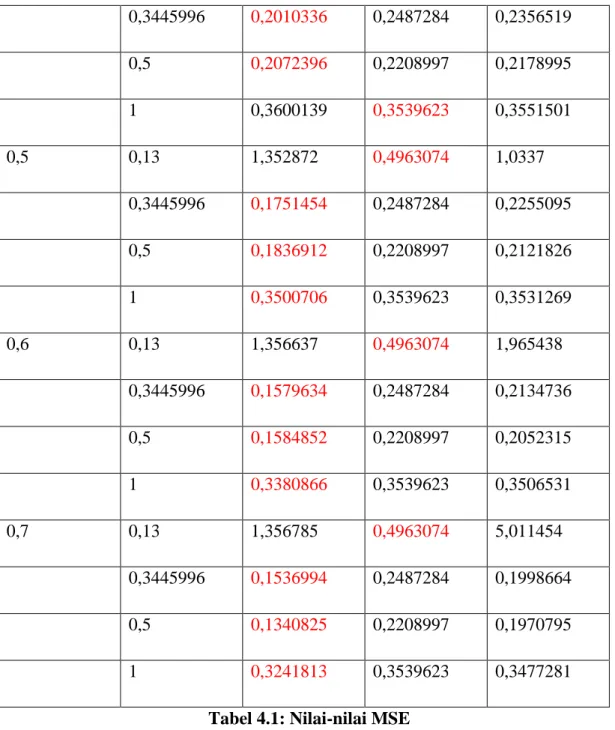
0,3445996 0,2010336 0,2487284 0,2356519 0,5 0,2072396 0,2208997 0,2178995 1 0,3600139 0,3539623 0,3551501 0,5 0,13 1,352872 0,4963074 1,0337 0,3445996 0,1751454 0,2487284 0,2255095 0,5 0,1836912 0,2208997 0,2121826 1 0,3500706 0,3539623 0,3531269 0,6 0,13 1,356637 0,4963074 1,965438 0,3445996 0,1579634 0,2487284 0,2134736 0,5 0,1584852 0,2208997 0,2052315 1 0,3380866 0,3539623 0,3506531 0,7 0,13 1,356785 0,4963074 5,011454 0,3445996 0,1536994 0,2487284 0,1998664 0,5 0,1340825 0,2208997 0,1970795 1 0,3241813 0,3539623 0,3477281

Tabel 4.1: Nilai-nilai MSE

Nilai-nilai MSE yang dihasilkan seperti yang terlihat pada tabel di atas berbeda antara yang satu dengan yang lain, yaitu:

1. pada kelipatan x sebesar 0,1 dan 0,2 setiap nilai bandwidth yang dipilih terlihat bahwa nilai MSE yang terkecil dihasilkan oleh estimator dengan menggunakan kernel berorder infinite khususnya kernel sinus.

besar akan menghasilkan grafik yang semakin mulus. Dari keempat gambar di atas terlihat bahwa pada masing-masing kelipatan titik x grafik yang dihasilkan saling berhimpit, sehingga belum dapat diambil kesimpulan kernel manakah yang memberikan performance terbaik. Maka kebaikan estimasi akan dilihat melalui nilai MSE ketiga kernel dari masing-masing kelipatan nilai x dan bandwidth. Berikut nilai-nilai MSE yang dihasilkan setelah melakukan pegolahan data dengan menggunakan program R:

Kelipatan

Titik Estimasi Bandwidth

Nilai MSE

Normal Sinus Cosinus

0,1 0,13 0,4982647 0,4963074 0,4957802 0,3445996 0,269451 0,2487284 0,2530287 0,5 0,2515239 0,2208997 0,2274729 1 0,3768402 0,3539623 0,3585203 0,2 0,13 0,6237044 0,4963074 0,5001564 0,3445996 0,2533656 0,2487284 0,2495126 0,5 0,2422269 0,2208997 0,2255545 1 0,3734509 0,3539623 0,3578464 0,3 0,13 1,030359 0,4963074 0,536074 0,3445996 0,2291352 0,2487284 0,2436954 0,5 0,227195 0,2208997 0,2223609 1 0,3678283 0,3539623 0,3567232 0,4 0,13 1,303002 0,4963074 0,6681886

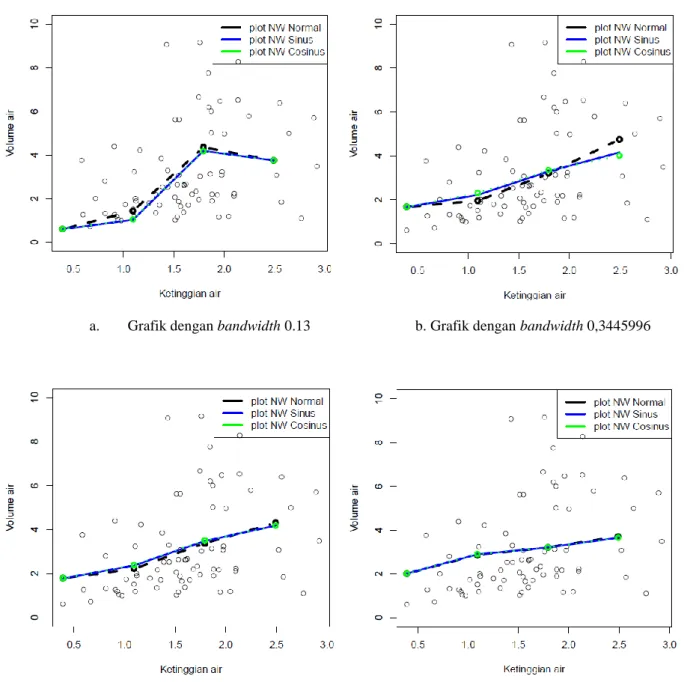
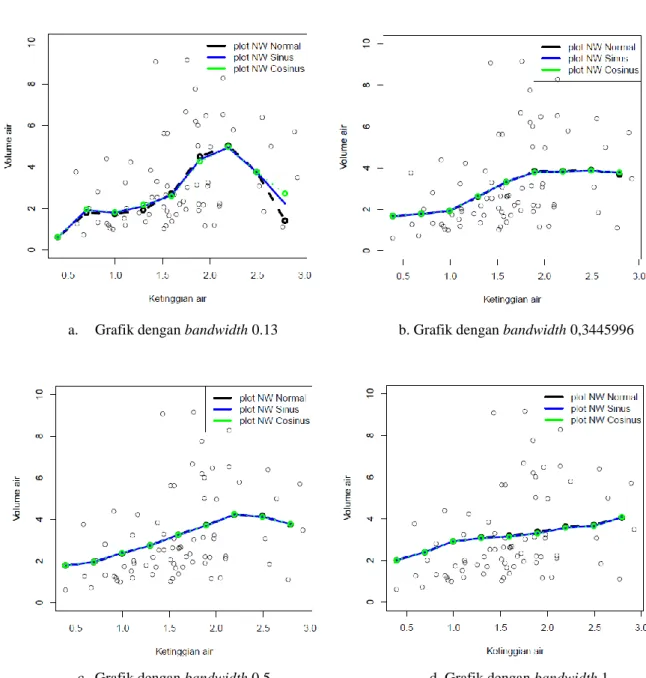
a. Grafik dengan bandwidth 0.13 b. Grafik dengan bandwidth 0,3445996

d. Grafik dengan bandwidth 0.5 d. Grafik dengan bandwidth 1

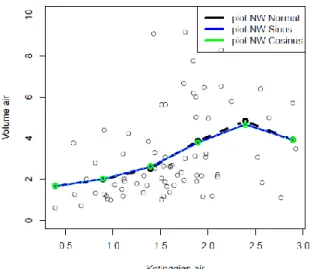
Gambar 4.4 Grafik estimasi dengan kelipatan nilai x sebesar 0,7

Grafik dari setiap kelipatan titik x dengan bandwidth yang berbeda-beda menunjukkan bahwa semakin kecil bandwidth yang dipilih maka grafik yang dihasilkan akan semakin kasar. Sedangkan sebaliknya pemilihan bandwidth yang

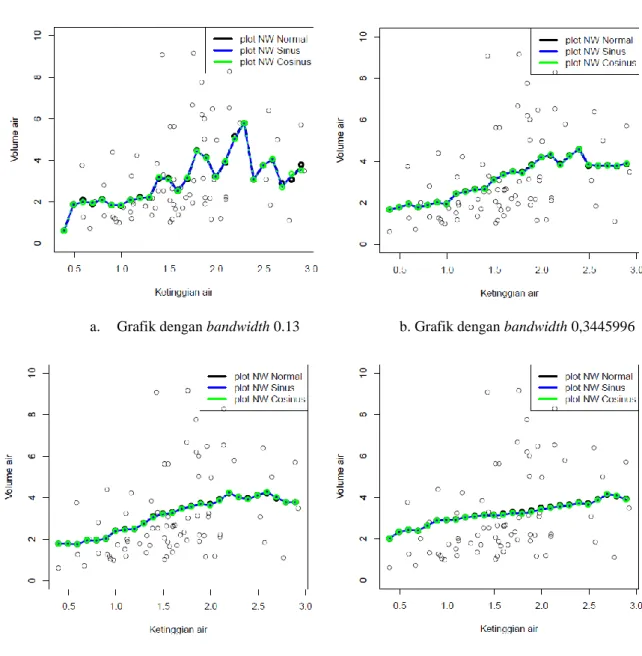
a. Grafik dengan bandwidth 0.13 b. Grafik dengan bandwidth 0,3445996

c. Grafik dengan bandwidth 0.5 d. Grafik dengan bandwidth 1

a. Grafik dengan bandwidth 0.13 b. Grafik dengan bandwidth 0,3445996

c. Grafik dengan bandwidth 0.5 d. Grafik dengan bandwidth 1

Berikut grafik hasil proses estimasi menggunakan data aliran sungai dengan nilai kelipatan titik-titik x 0,1; 0,3; 0,5 dan 0,7, grafik hasil estimasi dapat dilihat lebih lngkap pada lampiran 3:

a. Grafik dengan bandwidth 0.13 b. Grafik dengan bandwidth 0,3445996

c. Grafik dengan bandwidth 0.5 d. Grafik dengan bandwidth 1

4.2 Pengolahan Data dengan Program R

Proses yang dilakukan dalam melakukan pengolahan data dengan R untuk melakukan estimasi adalah sebagai berikut:

1. Masukkan data berpasangan (xi,yi)

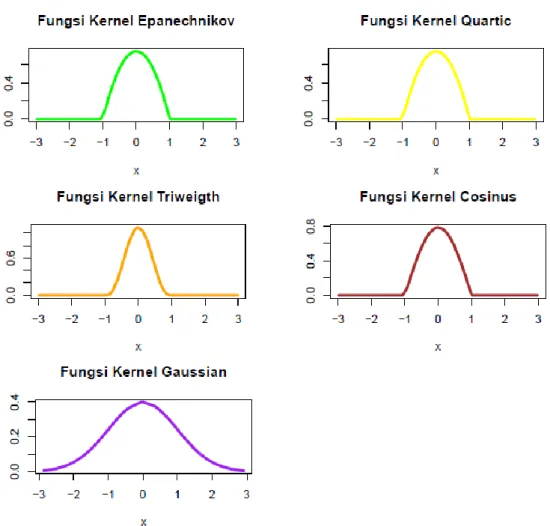
2. Masukkan kernel yang digunakan sebagai pembanding. Kernel yang digunakan adalah sebagai berikut:

Kernel yang normal:

 

1 exp 1 2 , 2 2 K x x x     _ _       

Kernel yang sinus: K x

 

sin

 

x x

 

Kernel yang cosinus:

 

 

 





2 2 cos cos 2 x _x K x x   

3. Masukkan nilai kelipatan untuk titik x yang akan diestimasi 4. Masukkan nilai bandwidth.

5. Plot pasangan data (xi,yi)

6. Plot hasil estimasi dengan kernel order berhingga (normal) 7. Plot estimasi dengan kernel order tak hingga (sinus dan cosinus) 8. Mendapatkan nilai MSE dari ketiga kernel

9. Membandingkan antara ketiga nilai MSE dari ketiga kernel

Dalam proses estimasi melalui studi kasus, nilai bandwidth yang digunakan adalah 0,13, 0,3445996, 0,5, 1. Bandwidth dipilih dari yang kecil sampai yang besar yang dapat digunakan sebagai pembanding nilai-nilai MSE dari ketiga kernel yang digunakan dan juga yang dapat memperlihatkan pengaruh peranan bandwidth terhadap hasil estimasi. Bandwidth 0,3445996 merupakan bandwidth optimum dari proses smoothing menggunakan ksmooth. Pada studi kasus ini, kelipatan titik estimasi yang dipilih adalah 0,1, 0,2, 0,3, 0,4, 0,5, 0,6 dan 0,7. Kelipatan titik-titik tersebut dipilih agar dapat digunakan sebagai pembanding dalam melihat nilai MSE yang dihasilkan. Sehingga dari perbandingan tersebut dapat ditentukan kernel manakah yang mempunyai performance yang lebih baik.

44

Pada bab ini akan dibahas studi kasus dari hasil pengamatan rata-rata volume air sungai di Indonesia yang pengalirannya lebih dari 1000 km2. Melalui regresi nonparametrik dengan menggunakan estimator Nadaraya Watson data tersebut akan dibandingkan nilai MSE antara kernel yang berorder tak hingga dan berhingga. Fungsi kernel yang digunakan untuk yang berorder tak hingga adalah

 

sin

 

x K x x   dan

 



 

₂

 



2 cos cos 2 x _x K x x  

 , sedangkan untuk fungsi kernel

berorder hingga yang digunakan adalah kernel Normal. Data yang dapat dilihat pada lampiran 1 tersebut akan diolah dengan menggunakan program R

4.1 Informasi Data

Data yang digunakan pada studi kasus ini diambil dari Statistik Indonesia, Statistical Yearbook of Indonesia 2013 yang dapat dilihat pada situs resmi Badan Pusat Statistik (BPS). Data yang digunakan dalam penelitian ini berjumlah 74 sungai di Indonesia yang daerah pengalirannya lebih dari 1000 km2 tahun 2010.

Dalam proses estimasi dengan pendekatan nonparametrik salah satu syarat yang harus dipenuhi adalah data harus kontinu. Dalam studi kasus ini, penulis menggunakan data sungai di Indonesia yang daerah pengalirannya lebih dari 1000 km2 tahun 2010 dimana variabel independen yaitu tinggi aliran air (juta m) dan volume air (juta dam3) sebagai variabel dependen

Data aliran sungai dalam penelitian ini digunakan untuk membandingkan performance antara estimator dengan fungsi kernel yang berorder berhingga dan tak hingga.

 

 

 

1 ˆ 0 ˆ q P a x nh o h f x           . (3.4)

3. Membuktikan estimator r xˆ

 

berdistribusi normal secara asimtotik Berdasarkan persamaan 3.2

   

 

 

 

 

1 2 ˆ ˆ ˆ ˆ ˆ a x a x r x r x f x f x    .

   

 



_ˆ



ˆ1

_{ }

 

 

_{ }

ˆ2

 

ˆ ˆ q a x q nha x nh r x r x o h nh o h f x f x      _  _   .

Maka berdasarkan lemma 3.2.3 dan persamaan 3.3 dan 3.4:

   

 





 

_{ }

   

2 2 0, ˆ q d N K s ds x f x nh r x r x o h f x          



 

 

 

2 2 0, d K s ds x N f x         _{ }      



. ∎

 

 

q

f x o h

 .

b. Nilai variansi dari a xˆ₁

 

 



1





   



1 1 ˆ var var n i i i x X a x K r X r x nh  h       _{  }  _   





   





2



   



2 2 2 1 x u x u E K r u r x E K r u r x nh h h  _{    }  _{    }     _{  }  _ _{  }  _         _   _  

   





2

 

 

2 2 2 1 x u q E K r u r x f x o h nh h       _{ }   _{   }  _{ } _{ }      

   





₂

 

 

 

2 2 2 1 x u _q K r u r x f u du f x o h nh h    _{    }   _{  }  _{  }   





  



  



₂





 

 

2 2 1 1 . q K s r x sh r x f x sh ds f x o h nh h    _{ }   _     _{  } 





Akan dibuktikan bahwa ˆ1

 

 

 

0

P q

a x  f x o h  . Berdasarkan teorema 2.2.2, didapatkan:

 

 

 

  



  







 

 

2 2 1 2 2 1 ˆ 1 . q q P a x f x o h K s r x sh r x f x sh ds nh f x o h h       _{ } _{     }   _   _{ }  _{ }



Ketika n maka var



a xˆ₁

 



0. Berdasarkan definisi 2.2.6 maka

 

 

 

1

ˆ q P 0

a x  f x o h  sehingga nh a x



ˆ₁

 

 f x o h

 

 

q



P0. Telah dibuktikan bahwa f xˆ

 

P f x

 

, sehingga

 

2 ₂



 



1 K s x sh f x sh ds nh   _    _    _{ }    



. Ketika n  diperoleh

 

2 1 1 0 n i i E b x n            



. Sehingga

 

2

 

2

   

1 1 0, n d i i b x N K s ds x f x n     _{  }  





atau

 

2

 

2

   

2 ˆ d 0, nh a x  N K s ds x f x  



. (3.3) 2. Membuktikan a xˆ₁

 

 f x o h

 

 

q P0. a. Nilai ekspektasi dari a xˆ₁

 

adalah

 



   



1 1 1 ˆ n i i i x X E a x E K r X r x nh  h         _{  }  _   _



_{  }

   





1 x u E K r u r x h h       _{  }  _    

   





 

1 x u K r u r x f u du h h       _{ }   



  



  







K s r x sh r x f x sh ds   



   .

Menggunakan definisi 2.2.7, didapatkan:

 

   

 

 

 

 

 

 

1 ˆ ' ! ' ! q q q p p p r sh E a x K s r x sh o h q f sh f x f x sh o h ds p               _{ }              



 

k

 

 

q o h f x o h  

Andaikan

 

i i i x X K h b x h          , maka ₂

 

 

1 1 ˆ n _i i nh a x b x n  



. Didapatkan:

 



_i



0 E b x 

 





var var i i i x X K h b x h          _{ }           2 2 i i x X K h E h         _{ }         



 

  

2 2 x sh f x sh K s ds  

_

  .

Berdasar definisi 2.2.7 dan asumsi 3.2.1 didapatkan

 





₂

 

2

   

var b xi 



K s ds x f x .

Akan dibuktikan bahwa b x_i

 

memenuhi definisi 2.2.9.

 

2 2 1 1 1 1 n n i i i i i x X E b x E K h n nh            _{  }      _{ }          





2 2 1 1 n i i i x X E K h nh        _      _{ }  _{ }     



_ _ 2 1 1 x u E K h h nh       _      _{ }  _{ }      _ _

Maka berdasarkan Lemma 2.2.1:

 

 

 

 

   

ˆ ˆ ˆ p g x g x r x r x f x f x    .

Sehingga terbukti r xˆ

 

merupakan estimator yang konsisten secara asimtotik pada kurva regresi r x

 

ketika h0 dan nh .

Teorema 3.2.1 Jika x berada dalam interval terbuka dimana f x mempunyai

 

turunan kontinu terbatas p dan r x mempunyai turunan kontinu terbatas q maka

 

berdasarkan asumsi 3.2.1 – 3.2.6,

   

 



_ˆ



2

_{ }

 

2

 

0, d q x nh r x r x o h N K z dz f x        _{  } 



. Bukti:

 

i i i Y r X 

     

i i i Y r X r x r x 







  



    









1 1 1 1 1 1 1 1 . n n n h i i h i h i i i i i n h i i i K x X Y K x X r x K x X r X r x n n n K x X n             









Sehingga,

   

 

 

 

 

1 2 ˆ ˆ ˆ ˆ ˆ a x a x r x r x f x f x    . (3.2) dengan ₁

 



    





1 1 ˆ n _{h i i} i a x K x X r X r x n  



  dan ₂

 





1 1 ˆ n _{h i i} i a x K x X n   



 .

Langkah berikutnya akan dianalisis distribusi asimtotis dari komponen aˆ₂

 

x dan kekonvergenan dari komponen

 

 

1 ˆ ˆ a x f x .

Berdasarkan lemma 3.2.1 dan lemma 3.2.2, telah didapatkan:

 



ˆ



 

 

p E f x  f x o h dan

 

 

ˆ 1 2

   

1 1 var f x K s f x ds o O nh nh n         _{ } _{ }    



. Sehingga,

 



 

 







2

   

2 1 1 1 ˆ p K s f x ds o O nh nh n P f x f x o h          _{ } _{ }        



,

ketika n  berakibat var



f xˆ

 



0. Berdasarkan definisi 2.2.6 maka

 

 

ˆ p

f x f x .

∎

b. Berdasarkan asumsi 3.2.1 – 3.2.4 serta lemma 3.2.1 dan 3.2.2 akan dibuktikan bahwa g xˆ

 

konvergen dalam probabilitas ke g x

 

.

Pembuktian kekonsistenan dari g xˆ

 

hampir serupa dengan dengan f xˆ

 

yaitu dengan menggunakan definisi dari kekonvergenan dalam peluang dan juga ketaksamaan Chebychev. Akan dibuktikan lim



ˆ

   



0

nP g x g x   ,

untuk semua  0.

Berdasarkan teorema 2.2.2, lemma 1 dan lemma 2 maka:

 



 









2

 



ˆ var ˆ ˆ g x P g x E g x      =

 



 







 

 



2 2



 

_{ }

2 2 1 1 ˆ ( k , r x x f x K z dz o O nh nh n P g x g x o h       _{   }  _{ } _{ }        



ketika n  berakibat var



g xˆ

 



0. Berdasarkan 2.2.6 maka

 

 

ˆ p

g x g x .

b. Berdasarkan definisi 2.2.4 dan lemma 3.2.1 dan lemma 3.2.2 maka:

 







2

 

2

 



 

 

 

2 2 1 1 ˆ r x x f x k . MSE g x K s ds o O o h nh nh n     _{    }    _{ } _{  } _    



Ketika n  maka nilai MSE g x



ˆ

 



secara asimtotik adalah

 





1 ˆ MSE g x O n       . ∎

Sifat-sifat dari f xˆ

 

dan g xˆ

 

telah dipahami secara terpisah, analisis berikutnya akan mengkaji kekonsistenan dari estimator r xˆ

 

. Sebelum mencari kekonsistenan dari etimator tersebut, akan dibuktikan terlebih dahulu kekonsistenan dari estimator f xˆ

 

dan g xˆ

 

.

Lemma 3.2.3 Berdasarkan asumsi 3.2.1 – 3.2.4 serta lemma 3.2.1 dan 3.2.2 maka:

a. f xˆ

 

pf x

 

b. g xˆ

 

pg x

 

. Bukti:

a. Akan dibuktikan bahwa f xˆ

 

konvergen dalam probabilitas ke f x

 

dengan menggunakan asumsi 3.2.1 – 3.2.4 serta lemma 3.2.1 dan 3.2.2. Berdasarkan definisi dari konvergen dalam probabilitas, akan dibuktikan:

 

 



ˆ



lim 0

nP f x  f x   , untuk semua  0.

Dengan menggunakan teorema 2.2.2, maka:

 

 

 





 

2

 

ˆ var ˆ ˆ f x P f x E f x      .

pada semua bilangan real ℝ, dengan menggunakan ekspansi deret Taylor pada perkalian

  

rf u disekitar x, berdasarkan asumsi 3.2.1 dan definisi 2.2.5 maka:







2



h E K x u y  f x r x

   

2

 

1 K s ds o nh nh       _{ }



.

Sehingga covariansi dari f xˆ

 

dan g xˆ

 

adalah:

   



ˆ



1







2



1

















ˆ cov f x g x, E K_h x u y E K_h x u E K_h x u y n n     _   _

   

2

_{ }

1 1 f x r x K s ds o O nh nh n         _{ } _{ }    



. ∎

Akibat 3.2.1 Berdasarkan asumsi 3.2.1 serta lemma 3.2.1 dan lemma 3.2.2 maka nilai MSE dari masing-masing f xˆ

 

dan g xˆ

 

:

a. MSE f x

 

ˆ

 

O 1 n        b. MSE g x



ˆ

 



O 1 n       . Bukti:

a. Berdasarkan definisi 2.2.4 dan lemma 3.2.1 dan lemma 3.2.2 maka:

 

 

   

 

2 2 1 1 1 ˆ p MSE f x K s f x ds o O o h nh nh n     _{   }   _{ } _{  } _    



.

Ketika n  maka nilai MSE f x



ˆ

 



secara asimtotik adalah

 

 

_ˆ 1 MSE f x O n       . ∎

   













1 1 1 1 ˆ _ˆ cov , cov , n n h i h j j i j f x g x K x X K x X Y n  n     _   _ 



















2 1 cov _{h i} , _{h j j} i j K x X K x X Y n 



 













1 cov K_h x u K, _h x u y n   



 























1 . h h h h E K x u K x u y E K x u E K x u y n   _      _







2



















1 h h h E K x u y E K x u E K x u y n    _     _







2



















1 1 h h h E K x u y E K x u E K x u y n n     _   _. Perhatikan untuk E K



_h



x u



2 y



:







2



1 ₂



  

, h h E K x u y K x u y f u y du dy n         _  _ 

 







 

 

2 1 h K x u y f y u f u du dy n        _  _ 

 





  

 

2 1 h K x u f u y f y u dy du n        _  _ 









  





2 1 h K x u f u E y X u du n      _   _ 







    

2 1 h K x u f u r u du n      _  _ 





  

 



2 1 K s f x sh r x sh ds nh      _   _ 



 .

Andaikan

 

rf mempunyai turunan kontinu terbatas k pada selang tertutup



 ,



dan

 

rf mempunyai turunan k+1 pada interval terbuka



 ,



yang memuat nilai x dengan k = min{p,q} dan andaikan

 

rf merupakan fungsi mulus

1 E K2_h



x u y



2 E K_h



x u y



2 n  _{   }   _{ }  _ _  _{ }. Perhatikan untuk E K_ 2_h



x u y



2_:









 

2 2 2 2 , h h E K x u y K x u y f u y du dy          

 

K2_h



x u y f y u f u du dy



2

 

 

    

_{ }

 2



  

2

 

h K x u f u y f y u dy du     







K2_h



x u f u E y X

  



2 u du



  

_

  2



  





 



2



h i K x u f u E r u  X u du   



   K2_h



x u f u

    



r2 u 2

 

u



du   

_

  . Sehingga:

 







    



 





 

 



2 2 2 2 1 ˆ var g x K _h x u f u r u u du g x o hk n       _     _ 





  

 













 

 



2 2 2 2 1 1 . k K s f x sh r x sh x sh ds g x o h nh  n   



     

Berdasarkan asumsi 3.2.1, definisi 2.2.5 dan definisi 2.2.7 maka:

 



_ˆ





2

 

2

 



 

2

 

1 1 var g x r x x f x K s ds o O nh nh n     _{   }   _{ } _{ }    



. ∎ c. cov



f xˆ

   

,g xˆ



r x f x

   

K2

 

s ds o 1 O 1 nh nh n         _{ } _{ }    



.





   

 

 

 

   





2 2 2 2 2 1 1 1 1 ' '' 2 . ! 1 ! h p p p p p p h s E K x u K s f x ds K s sh f x f x h h s h s f x f x ds p p                _       _      _{ }  _{ }





Sehingga:

 



















2



1 2 ˆ var f x n E K_ _h x u _ E K_{ h} x u _

   

 

 

 

   







 

 



2 2 1 2 2 1 1 ₂ 1 1 ' '' 2 ! 1 ! p p p p p p p h s n K s f x ds K s sh f x f x h h s h s f x f x ds f x o h p p               _{ }  _           _  _   _    _   





   

 

 

 

   







 

 



2 2 2 2 1 1 ₂ 1 1 1 ' '' 2 1 . ! 1 ! p p p p p p p h s K s f x ds K s sh f x f x nh nh h s h s f x f x ds f x o h p p  n            _{ }          _{ }   _{ }





Berdasarkan asumsi 3.2.1, definisi 2.2.5 maka variansi dari penyebut estimator Nadaraya Watson adalah sebagai berikut:

 

 

ˆ var f x 1 K2

   

s f x ds o 1 O 1 nh nh n         _{ } _{ }    



. ∎ b.



 







1 1 ˆ var var n h i i i g x K x X Y n     _  _ 



 ₂





1 1 var n h i i i K x X Y n     _  _ 



 1var K_h



x X Y



n    _  _

b.

 



 

 



 

 

2 2 2 1 1 ˆ var g x r x x f x K z dz o O nh nh n     _{   }     _{ } _{ }  



_{   } c. cov f xˆ

   

,g xˆ r x f x

   

K2

 

z dz o 1 O 1 nh nh n        _{      }  



_{   }. Bukti: a. Menurut persamaan (2.7):

 









1 1 ˆ var var n h i i f x K x X n     _  _ 



 ₂









1 1 var n h i i K x X n  



 1var



K_h



x X





n   n1



E K_ _h2



x u



_



E K_ _h



x u



_



2



. Perhatikan untuk 2





h E K_ x u _:







  

2 2 h h E K x u K x u f u du        



 

2 2 1 x u K f u du h h       _{ }  



  



2 1 K s f x sh ds h   

_

 .

Berdasarkan definisi 2.2.7, maka:





   

 

 

 









2 2 2 2 1 1 1 1 ' '' 2 ! 1 ! p p p h p p p h s h s E K x u K s f x sh f x f x f x h p h s f x ds p             _{ }        _{ }         _{  }



 

_

 

_{  }

1  1

_

_{  }

. 1 ! k k vh g x rf x K v dv k         



Sehingga bias dari pembilang estimator Nadaraya Watson adalah sebagai berikut:

 





 

 

 

_

_{  }

1  1

_

_{  }

_{ }

ˆ 1 ! k k vh E g x g x g x rf x K v dv g x k           



 



  

 



  

1 1 1 ! k k vh rf x K v dv k        



. Ketika suku sisa

 



  

 





1 1 1 ! k k vh rf x k    

 deret Taylor di atas merupakan order

kecil dari hk maka dengan menggunakan asumsi pembatasan dari sifat bandwidth h, n  maka h0, suku sisa deret Taylor di atas konvergen ke nol, yaitu:

 



  

 



  

 



  

 



  

1 1 1 1 0 0 1 ! lim lim 0 1 ! k k k k k h h vh rf x K v dv k v h rf x K v dv h k                  





.

Sehingga bias dari pembilang estimator Nadaraya Watson adalah

 



ˆ



 

 

k

E g x g x o h .

∎

Asumsi 3.2.4 Titik x merupakan titik kontinu dari 2

   

,

x f x C

  untuk C > 0 dan fungsi r serta fungsi f masing-masing terdiferensial di sekitar x.

Lemma 3.2.2 Jika x berada dalam interval terbuka dimana f x

 

mempunyai turunan kontinu terbatas p dan r x

 

mempunyai turunan kontinu terbatas q, berdasarkan asumsi 3.2.1 –3.2.4 maka:

a. var f xˆ

 

f x

 

K2

 

z dz o 1 O 1 nh nh n        _{      }  



_{   }

dengan menggunakan ekspansi deret Taylor pada perkalian

  

rf u disekitar x maka ekspektasi dari g xˆ

 

adalah sebagai berikut:

 



ˆ



    

_h



E g x r u f u K x u du   







 

  

r x vh f x vh K v dv   



 

  

   

_

 

_{  }

1  1

_

_{  }

' 1 ! k k vh rf x vh rf x rf x K v dv k                   



    

     

 

   

 

   



 

  

 



  

1 1 ' , ! 1 ! k k k k rf x K v dv vh rf x K v dv vh vh rf x K v dv rf x K v dv k k                  









dengan  terletak diantara x dan x hv .

Ketika K terintegralkan ke satu, semua momennya adalah nol dan ketika

     

g x r x f x maka:

 





    

     

 

   

 

   



 

  

 



  

1 1 ˆ ' ! 1 ! k k k k E g x rf x K v dv vh rf x K v dv vh vh rf x K v dv rf x K v dv k k                  









  

 

   

 

 

   

 

 

 

 



  

 



  

1 1 ' ! 1 ! k k k _k k rf x K v dv h rf x vK v dv h vh rf x v K v dv rf x K v dv k k                  









  

 

_

_{  }

1  1

_

_{  }

0 0 0 1 ! k k vh rf x rf x K v dv k             



Sehingga:

 





1 1 ˆ n _{h i i} i E g x E K x X Y n       _  _   _



_





1 1 n h i i i E K x X Y n     



_{ }  _ E K_{ h}



xX Y



_ E K_{ h}



x u y



_ K_h



x u y f u y du dy

  

,     

_{ }

 K_h



x u y f y u f u du dy



 

 

    

 

 K_h



x u f u

  

y f y u dy du

 

    







K_h



x u f u E y X

  



u du



  



  K_h



x u f u r u du

    

  



 r u f u K

    

_h x u du



  

_

 .

Bias untuk pembilang estimator Nadaraya-Watson adalah:

 



ˆ



 

    

_h



 

E g x g x r u f u K x u du g x    



  .

Andaikan

 

rf mempunyai turunan kontinu terbatas k pada selang tertutup



 ,



dan

 

rf mempunyai turunan k+1 pada interval terbuka



 ,



yang memuat nilai x dengan k = min{p,q} dimana p merupakan turunan kontinu terbatas dari fungsi f x

 

dan q merupakan turunan kontinu terbatas dari fungsi

 

Berdasarkan persamaan (2.4), bias dari penyebut estimator Nadaraya-Watson dengan kernel order tak hingga adalah:

 

 

 

ˆ ˆ bias_f x _E f x_ _ f x

 



 





 

 

1 1 1 ! p p f x sh f x K s ds f x p          





 





 

1 1 1 ! p p f x sh K s ds p        



.

Ketika suku sisa



 





1 1 1 ! p p f x sh p    _

 deret Taylor di atas merupakan order kecil

dari hp maka berdasarkan asumsi pembatasan dari sifat bandwidth h, n  maka

0

h , suku sisa deret Taylor di atas konvergen ke nol, yaitu:



 





 









 

1 1 1 1 0 0 1 ! lim lim 0 1 ! p p p p p h h f x sh K s ds p f x s h K s ds h p                  





. Sehingga bias_f xˆ

 

 _ o h

 

p . ∎

b. Bias pembilang estimator Nadaraya-Watson dengan kernel order tak hingga Menurut persamaan (2.9) estimator fungsi r adalah:

 

ˆ

 

_{ }

ˆ ˆ g x r x f x 









1 1 1 1 n h i i i n h k k K x X Y n K x X n     





.

Bukti:

a. Bias penyebut estimator Nadaraya-Watson dengan kernel order tak hingga. Menurut persamaan (2.8) : E f



ˆ_h

 

x



K s f x

  

sh ds









_

 .

Menurut definisi 2.2.7, kita dapatkan:





 

 

  

  

  



 





2 3 1 1 ' '' ''' 1! 2! 3! , ! 1 ! p p p p f x sh f x sh f x sh f x sh f x f x sh f x sh p p             

dengan  terletak diantara x dan x sh . Persamaan (2.8) menjadi:

 

 

ˆ

  



E f x K s f x sh ds   





   

  

  

  

  



 





2 3 1 1 ' '' ''' 1! 2! 3! ! 1 ! p p p p f x sh f x sh f x sh K s f x f x sh f x sh ds p p                    _



 

 

 

 

 

 

 

_{ }

 

 

_{ }



 





 

2 2 3 3 1 1 '' ' 2 ''' 6 ! . 1 ! p _p p p p h f x f x K s ds hf x K s s ds K s s ds h f x h f x K s s ds K s s ds p f x sh K s ds p                        













Fungsi K adalah fungsi yang berorder tak hingga yaitu K terintegralkan ke satu, semua momennya adalah nol sehingga:

 

 

ˆ

 

_{0 0 0} 1



_

 

_

1

 

1 ! p p f x sh E f x f x K s ds p             



 

1



_

 

_

1

 

1 ! p p f x sh f x K s ds p         



.

3.2 Sifat Asimtotik Estimator Nadaraya Watson dengan Kernel Berorder Tak Hingga

Kita akan menguji perilaku dari estimator Nadaraya-Watson kelas kernel baru yaitu kernel dengan order tak hingga untuk n pengamatan pasangan data

yang berdistribusi identik dan independen dengan densitas f. Untuk memahami estimator tersebut secara menyeluruh, kita akan memulai dengan suatu lemma yang mengukur perilaku asimtotik dari pembilang dan penyebut estimator tersebut yaitu f xˆ

 

dan g xˆ

 

dimana f xˆ

 

merupakan estimator densitas kernel dari f x

 

dan g xˆ

 

merupakan estimator dari g x

 

. Dalam prosesnya kita memerlukan beberapa asumsi. Kita akan memberikan batasan untuk perilaku bandwidth h ketika n dan pada distribusi bersyarat dari error.

Asumsi 3.2.1 Ketika n, bandwidth h0dan nh.

Asumsi 3.2.2 εi adalah random error dengan asumsi independen,



_{i i}



0

E  X x  dan E



2_i X_i x



2.

Asumsi 3.2.3 berdistribusi identik dan independen dengan densitas f.

Lemma 3.2.1 Jika x berada dalam interval terbuka dimana f x

 

mempunyai turunan kontinu terbatas p dan r x

 

mempunyai turunan kontinu terbatas q, maka berdasarkan asumsi 3.2.1 dan 3.2 2:

a. E f x_ ˆ

 

 _ f x

 

o h

 

p

b. ˆ

 

 

 

k

E g x_  _ g x o h

Permasalahan di atas dapat diselesaikan dengan membuat transisi dari 0 ke 1 pada daerah asal Fourier yang kurang kasar. Devroy dan Gyorfi, Hall dan Marron, pada kasus estimasi densitas spektral, Politis dan Romano, mempelajari kernel dari Tranformasi Fourier yang diberikan oleh:

 





1 1 2 2 1 1 2 1 0 1 jika s s s jika s jika s     _       .

Kernel yang bersesuaian adalah:

 



 

2

 



2 cos cos 2 x _x K x x    .





1 1 2 ix ix e e x i    

 

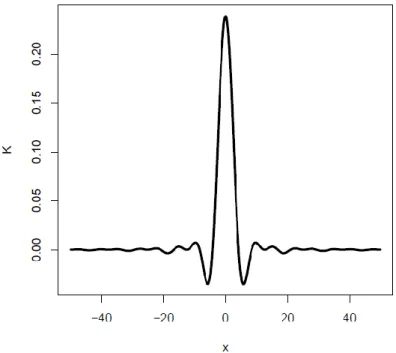
sin x x   .

Berikut gambar dari fungsi flat-top kernel di atas:

Pada gambar di atas terlihat bahwa bagian belakang atau ekor dari kernel tersebut sangat bergelombang. Ada dua permasalahan akibat dari hal ini. Pertama, ekor dari kernel tersebut yang turun secara pelan-pelan dan gerakan-gerakan negatif yang sangat besar meningkatkan K2

 

x dx







, yang juga akan meningkatkan variansi dari estimasinya. Kedua, gelombang besar yang jauh dari 0 menghasilkan bias sampel yang berhingga karena gelombang tersebut memberikan pengamatan yang cukup jauh dari x yang sangat berpengaruh dalam melakukan estimasi di titik x. Permasalahan-permasalahan tersebut membuat estimator fungsi kepadatan yang menggunakan kernel tersebut menjadi tidak stabil dalam bersaing kecuali untuk sampel yang berukuan sangat besar.

 

 

1 jika s c s g s jika s c       ,

dengan fungsi g dipilih sehingga membuat 

 

s , 2

 

s

 dan s

 

s dapat diintegralkan. Flat-top Kernel diberikan sebagai berikut:

 

1

 

2 isx K x  s e ds     

_

. (3.1)

Kernel yang memenuhi definisi di atas menjamin bahwa x K x dxi

 

0 







,

untuk semua bilangan bulat i. Menurut Politis dan Romano (1995) keuntungan menggunakan kernel ini adalah kita tidak perlu memilih fungsi kernel yang baru ketika ada data yang baru, kernel yang sama dengan bandwidth yang berbeda akan menyesuaikan kemulusan dari fungsi kepadatan yang tidak diketahui.

Berikut diberikan contoh yang memenuhi definisi di atas. Diberikan fungsi

 

s  sebagai berikut:

 

1 1 0 1 jika s s jika s  _{ }    . Menurut definisi 2.5.2:

 

1

 

2 isx K x  s e ds     



1 1 1 1 1 0. 1. 0. 2

isx isx isx

e ds e ds e ds            _   _ 







 1 1 1 1. 2 isx e ds       _ _ 



 1 1 1 1 2 isx e ix     





1 1 2 ix ix e e ix     

22

3.1 Kernel dengan Order Tak Hingga

Menurut Berg (2008) fungsi Kernel dikatakan mempunyai order v jika memenuhi: 1. v

 

R x K x dx



2. x K x dxi

 

0, i 1, 2,...,v 1     



.

Seperti yang telah dijelaskan pada bab sebelumnya yaitu jika banyak turunan dari fungsi tersebut tidak diketahui maka untuk mengestimasi jumlah turunan dari fungsi tersebut sangat sulit, sehingga kita kesulitan untuk memilih kernel dengan order berapakah yang digunakan.

Untuk mengurangi permasalahan tersebut, kita fokus pada fungsi kernel yang secara efektif mempunyai order kernel tak hingga. Kelas kernel tersebut secara otomatis mengurangi bias ke o(hp) tidak peduli berapa kali fungsi tersebut dapat diturunkan.

Definisi 3.1.1 (Berg, 2008). K(x) dikatakan berorder tak hingga jika memenuhi:

 

0, 1, 2,... i x K x dx i    



Definisi 3.1.2 (McMurry dan Politis, 2003). Sebuah flat-top Kernel K dengan order tak hingga secara umum dibentuk melalui Transformasi Fourier λ, yaitu untuk nilai tetap c > 0

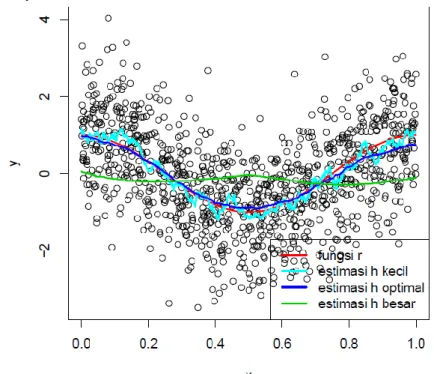
legend("bottomright",c("fungsi r","estimasi h kecil","estimasi h optimal","estimasi h besar"),lty=c(1,1,1,1),lwd=c(2,2,2,2),col=c(2,5,4,3)) 2. Hasil output

Menurut Hardle (1991) nilai-nilai statistik pembilang dari estimator Nadaraya-Watson dengan fungsi kernelnya mempunyai order dua adalah sebagai berikut:

 





2

   

 

2 2 ˆ '' , 0 2 h Bias g x  g x  K o h h

 





     

1 ₂ 2



 

1



2 ˆ var g x  nh  f x s x K o nh  , untuk nh 

 





 

1

 

₂ 2 4



   



2



 



1

 

₄ 2 2 ˆ '' , 4 0, h MSE g x nh f x s K g x K o nh o h h nh           dengan 2

 

2 s x E Y_ X x_.

Berdasarkan nilai statistik dari pembilang estimator Nadaraya-Watson di atas dan nilai statistik dari estimasi densitas kernel maka dapat diperoleh nilai MSE dari estimator Nadaraya-Watson yaitu:

 





 

_{ }

 

 

   

_{ }

 



 



 

2 2 4 1 1 2 ₂ 2 2 4 ' ' ˆ '' 2 4 , 0, . x h r x f x MSE r x nh K r x K o nh f x f x o h h nh         _  _       

Berikut diberikan contoh proses smoothing dengan estimator Nadaraya-Watson dari data yang dibangkitkan menggunakan program R:

1. Proses smoothing dalam R a=runif(1000) e=rnorm(1000) x=sort(a) r=cos(2*pi*x) y=r+e plot(x,y) lines(x,r,col=2,lwd=2) lines(ksmooth(x,y,bandwidth=0.03),col=5,lwd=2) lines(ksmooth(x,y,bandwidth=0.30),col=4,lwd=2) lines(ksmooth(x,y,bandwidth=1),col=3,lwd=2)

2.5 Estimator Nadaraya Watson

Estimasi kernel untuk fungsi regresi r(x) dikonstruksi sebagai berikut:

 





r x E Y X x 



y f y x dy

 

 

 

, y f x y dy f x 



.

Estimator fungsi regresi untuk fungsi densitas f yang tidak diketahui adalah:

 

 

 

1,2 ˆ _, ˆ ˆ h h h y f x y r x dy f x 











1 1 1 1 n h i i i n h k k K x X Y n K x X n     





 

 

ˆ ˆ g x f x  . (2.9)

Estimator fungsi regresi r xˆ

 

di atas merupakan rata-rata lokal yang diusulkan oleh Nadaraya-Watson sehingga disebut juga sebagai estimator Watson. Berdasarkan persamaan (2.1) maka Estimator Nadaraya-Watson mempunyai fungsi bobot sebagai berikut:

 













 

1 ˆ 1 h i h i i n h h k k K x X K x X W x f x K x X n      



,

dengan fˆ_h

 

x merupakan estimator densitas kernel.

Menurut Takezawa (2003) fungsi bobot dalam estimator Nadaraya-Watson mempunyai karakteristik sebagai berikut:

 

1 1 n i i W x  



.