PENAKSIRAN M A S T A T I S T I K A D A S A R 1 7 M A R E T 2014 U T R I W E N I M U K H A I Y A R

P E N A K S I R A N T I T I K P E N A K S I R A N S E L A N G S E L A N G K E P E R C A Y A A N U N T U K R A T A A N S E L A N G K E P E R C A Y A A N U N T U K V A R I A N S I M A 2 0 8 1 S T A T I S T I K A D A S A R 1 7 M A R E T 2 0 1 4 U T R I W E N I M U K H A I Y A R

PENAKSIRAN

METODE PENAKSIRAN

2 Penaksiran Titik 1 Penaksiran Selang 2

Nilai tunggal dari suatu parameter melalui pendekatan metode tertentu.

Nilai sesungguhnya dari suatu parameter berada di selang tertentu.

Contoh 1. Seorang mahasiswa mengulang kuliah Statdas, ketika di

awal perkuliahan, memiliki target nilai lulus matkul Statdas adalah A.

Contoh 2. Seiring berjalannya waktu, mahasiswa tersebut mengubah target nilai lulus matkul

Statdas adalah minimal AB Nilai : A = 4 IP :  AB = [3.5, 4]

ILUSTRASI

Parameter sampel menaksir parameter populasi

3 Parameter Populasi σ2 µ Parameter Sampel menaksir Populasi Sampel ? ? titik?? selang??

PENAKSIRAN TITIK

Statistik yang digunakan untuk mendapatkan

taksiran titik disebut penaksir atau fungsi

keputusan.



 X 2 2





s

4 X



Apakah dan

s

2

merupakan penaksir yang baik

PENAKSIR TAKBIAS DAN PALING

EFISIEN

Definisi

•

_{Statistik dikatakan penaksir takbias parameter}



_bila,



ˆ





_ˆ



E

[



ˆ

]



5



Dari semua penaksir takbias



yang mungkin

dibuat, penaksir yang memberikan variansi

terkecil disebut

penaksir



yang paling efisien

2 ˆ 2 ˆ 2 1  







PENAKSIR TAK BIAS UNTUK



DAN



2

Misalkan peubah acak X ~ N(,2₎

•

_{penaksir tak bias untuk}



_.

•

_{penaksir takbias untuk}



2

_.

6



  n i i X n X 1 1







    n i i X X n s 1 2 2 1 1

Bukti

: dengan menunjukkan bahwa,





]

[

X

E

2 2

]

[

s





E

PENAKSIRAN SELANG

 dan dicari sehingga memenuhi :

7 1

ˆ





ˆ

₂



ˆ ₁ 



 ˆ ₂



1



P taraf/koefisien keberartian 2

ˆ



_

ˆ

₂ 1

ˆ



2 1

ˆ

ˆ

_

_







1

ˆ





Taksiran selang suatu parameter populasi



:



dan : nilai dari peubah acak dan

2

1 ˆ

ˆ

_

_



 



Selang kepercayaan : perhitungan selang

berdasarkan sampel acak.

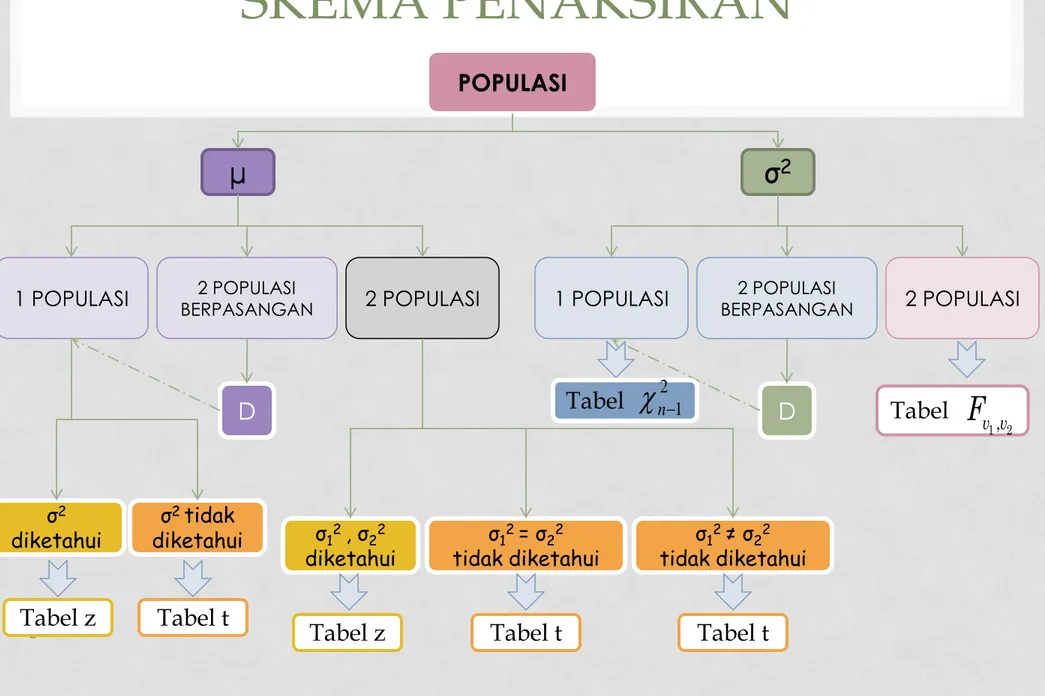
SKEMA PENAKSIRAN

8

POPULASI

µ σ2

1 POPULASI _BERPASANGAN 2 POPULASI 2 POPULASI

σ2 diketahui σ 2 _tidak diketahui D σ₁2 _{, σ} 22 diketahui σ1 2 _{= σ} 22 tidak diketahui σ1 2 _{≠ σ} 22 tidak diketahui

1 POPULASI _BERPASANGAN 2 POPULASI 2 POPULASI

D

Tabel z Tabel t _{Tabel z Tabel t Tabel t}

Tabel _n2_{1 Tabel}

1 2, v v

KURVA NORMAL BAKU (Z~N(0,1))

MENGHITUNG TABEL

z

9  = 0 1 -  /2 /2 z_1-/2 -z_1-/2 (1-/2)  = 5% maka z_1-/2 = z_0,975 =1,96  P(Z ≤ z_0,975) = 1 – 0,025 = 0,975 dan -z_1-/2 = -z_0,95= -1,96. P(-z_1-/2 ≤ Z ≤ z_1-/2)

KURVA

T-

STUDENT (T~

T

_V

)

MENGHITUNG TABEL

t

10 /2 /2  = 5% dan n =10 maka t_/2;n-1 = t_0,025;9 = 2,262  P(T ≤ t_0,025) = 0,025 dan -t_/2;n-1 = -t_0,025;9= -2,262  = 0 1 -  /2 /2 t_/2 -t_/2 P(-t_/2 ≤ T ≤ t_/2)

SELANG KEPERCAYAAN (1-



) UNTUK



•

Kasus 1 populasi,



2

diketahui

                1 2 1 2 1 Z z z P

n

z

X

n

z

X

_





_



2 1 2 1











11 TLP : _{~ (0,1)} / n Z N X  _                       1 2 1 2 1 _n z X n z X P

SELANG KEPERCAYAAN (1-



) UNTUK



•

Kasus 1 populasi,



2

tidak diketahui

              1 2 2 t T t P 2 2

s

s

X

t

X

t

n

n









 



12 2 2 1 s s P X t X t n n                

SK (1-) untuk  jika 2 tidak diketahui :

1 ~ / n X t s n   

CONTOH 1

•

_{Survey tentang waktu maksimum pemakaian}

komputer (jam) dalam seminggu di 50 buah

Warnet di Kota Bandung diketahui

berdistribusi normal dengan simpangan baku

10 jam

, dan rata-rata pemakaian maksimum

adalah 55 jam. Dengan menggunakan taraf

keberartian 2% carilah selang kepercayaannya !

CONTOH 2

• Survey tentang waktu maksimum pemakaian

komputer (jam) dalam seminggu di 50 buah Warnet di Kota Bandung diketahui berdistribusi normal. Rata-rata pemakaian maksimum adalah 55 jam dengan simpangan baku 10 jam. Dengan

menggunakan taraf keberartian 2% carilah selang kepercayaannya !

Dapatkah Anda membedakan contoh 1 dengan contoh 2?

ANALISIS CONTOH

Contoh 1

Contoh 2

Diketahui : n = 50 , , σ = 10 n = 50 , , S = 10

Ditanya : SK 98% untuk  ( = 0,02) SK 98% untuk  ( = 0,02) Jenis kasus : kasus menaksir  dengan 2

diketahui, kasus menaksir

 _dengan 2 tidak diketahui, Jawab : z_1-/2 = z_0,99 = 2,33 t_/2;n-1 = t_0,01;49 = 2,326 15 55 X  X 55 n z X n z X _   _  2 1 2 1      n S t X n S t X 2 2       

SOLUSI CONTOH 1 DAN 2

SELANG KEPERCAYAAN UNTUK



10 10 55 2,33 55 2,33 50  50     51,705   58,295 16

1. Jika



2

diketahui.

2. Jika



2

tidak diketahui.

10 10

55 2,326 55 2,326

50  50

   

SELANG KEPERCAYAAN (1-



) UNTUK



₁

_-



₂

KASUS 2 POPULASI

1. SK (1-) untuk (₁ -  ₂) jika ₁2 _{dan } 22 diketahui 17 2 2 2 2 1 2 1 2 1 2 1 / 2 1 2 1 2 1 / 2 1 2 1 2 (X X ) Z (X X ) Z n n n n     _{ }              ₂ X₁ ~ N(µ₁ , σ₁2) _X 2 ~ N(µ2 , σ22) ₁

SELANG KEPERCAYAAN (1-



) UNTUK



₁

_-



₂

KASUS 2 POPULASI 18

2. SK (1-) untuk (_1- ₂) jika ₁2 , ₂2 tidak diketahui dan ₁2 ≠ ₂2

2 2 2 2 1 2 1 2 1 2 ; / 2 1 2 1 2 ; / 2 1 2 1 2 (X  X )t_{ } s  s     (X  X )t_{ } s  s n n n n 2 2 2 1 2 1 2 2 2 2 2 1 1 2 2 1 2 dimana ( / ) ( / ) 1 1 s s n n s n s n n n            

3. SK (1-) untuk (_1- ₂) jika ₁2 , ₂2 tidak diketahui dan ₁2 = ₂2

SELANG KEPERCAYAAN (1-



) UNTUK



₁

_-



₂ KASUS 2 POPULASI 19 1 2 ; / 2 1 2 1 2 ; / 2 1 2 1 2 1 1 1 1 (X X ) t s_p (X X ) t s_p n n n n   _{ }        _{ }  2 2 2 1 1 2 2 1 2 ( 1) ( 1) dimana 2       p n S n S S n n 1 1 2 2 1 1 2 2 2 2 2 2 1 1 1 2 2 2 1 1 1 1 2 1 2 1 2 atau 2 2  _{ }   _{ }   _{ }   _{ }   _{ }   _{ }            



n



n



n



n p X X X X X X n X X n S n n JK JK n n dan v = n₁ + n₂ - 2

PENGAMATAN BERPASANGAN

Ciri-ciri:

• _{Setiap satuan percobaan mempunyai sepasang}

pengamatan

• Data berasal dari satu populasi yang sama

Contoh

• _{Produksi minyak sumur A pada tahun 1980 dan}

2000

• Penentuan perbedaan kandungan besi (dalam ppm) beberapa sampel zat, hasil analisis X-ray dan Kimia

SELANG KEPERCAYAAN (1-



) UNTUK



_D

SK untuk selisih pengamatan berpasangan

dengan rataan dan simpangan baku

S

_d

:

21 1; 1; 2 2 d d n D n

s

s

d

t

d

t

n

n





  





 

d

d

merupakan

rata-rata

dari selisih 2 kelompok data.

dimana “ “ dengan

n

: banyaknya pasangan.

KURVA KHI KUADRAT (X~ )

MENGHITUNG TABEL 22 0 2 2   2 2 1    2 v



2



/2 /2 1 -     _{  }           1 2 2 2 2 2 1 X P 023 , 19 2 9 ; 025 , 0 2 1 , 2     _ n  = 5% dan n =10 maka, 7 , 2 2 9 ; 975 , 0 2 1 , 2 1      _ n

SELANG KEPERCAYAAN (1-



) UNTUK

σ

2

•

Kasus 1 populasi

23 2 2 2 2 2 /2 1 /2 ( 1) ( 1) 1 n s n s P       _             2 2 2 1 2 ( 1) ~ _n n s X         _{  }           1 2 2 2 2 2 1 X P 2 2 2 2 2 ( 1); ( 1);1 2 2 ( 1) ( 1) n n n s n s          _{ }  SK (1 - ) 100% untuk 2 _:

KURVA FISHER (F~ )

MENGHITUNG TABEL F 24 0 2  f 2 1 f /2 /2 1 -                _{1 2} ; ₁, ₂ 1 2 , ; 2 1 v v F f v v f P 2 1,v v

F

36 , 4 8 , 9 ; 025 , 0 1 , 1 ; 2 1 2     f f n n 

 = 5% , n₁ = 10 dan n₂ = 9 maka, dan

24 , 0 1 , 4 1 1 1 9 , 8 ; 975 , 0 1 , 1 ; 2 1 , 1 ; 2 1 1 2 2 1          _{f f} f n n n n   1 , 1 ; 2 1 , 1 ; 2 1 1 2 2 1 1       n n n n f f  

SELANG KEPERCAYAAN (1-



) UNTUK



₁2

/



₂2

•

Kasus 2 populasi

25 1 2 2 2 2 1 2 2 _{, ,} 1 2 2 ~ v v s F f s     SK (1 - ) 100% untuk ₁2 _/ 22 :               _{1 2} ; ₁, ₂ 1 2 , ; 2 1 v v F f v v f P 2 1 1 2 2 2 2 1 1 1 2 2 2 ; , 2 2 2 2 ; , 2 1 1 v v v v s s P f s f_ s   _     _{ }  _{ }       2 1 1 2 2 2 2 1 1 1 2 2 2 _{; ,} 2 2 2 2 ; , 2 1 v v v v s s f s f_ s     

REFERENSI

• Devore, J.L. and Peck, R., Statistics – The Exploration and

Analysis of Data, USA: Duxbury Press, 1997.

• _{Pasaribu, U.S., 2007, Catatan Kuliah Biostatistika.}

• Wild, C.J. and Seber, G.A.F., Chance Encounters – A first

Course in Data Analysis and Inference, USA: John Wiley&Sons,Inc., 2000.

• _{Walpole, Ronald E. Dan Myers, Raymond H., Ilmu Peluang}

dan Statistika untuk Insinyur dan Ilmuwan, Edisi 4, Bandung: Penerbit ITB, 1995.

• Walpole, Ronald E. et.al., Probability & Statistics for Enginerrs

& Scientists, Eight edition, New Jersey : Pearson Prentice Hall, 2007.