PENGGUNAAN TURUNAN. Agustina Pradjaningsih, M.Si. Jurusan Matematika FMIPA UNEJ

PENGGUNAAN TURUNAN

Agustina Pradjaningsih, M.Si.

Jurusan Matematika FMIPA UNEJ agustina.fmipa@unej.ac.id

Pada materi sebelumnya telah dijelaskan bahwa Teorema Nilai Rata-Rata (TNR diferensial) memegang peranan penting dalam kalkulus.

Pembuktian TNR membutuhkan Teorema ROLLE (kalkulus diferensial) yang selanjutnya akan dipakai pada Penggunaan Turunan, Kalkulus Integral dan Analisis Numerik.

Penggunaan Turunan yang akan dibahas adalah

1. Penggambaran grafik fungsi 2. Pencarian nilai optimum

Pada materi tersebut dibutuhkan

beberapa teorema dan beberapa

konsep yang akan saling menunjang

satu sama lain.

Pada materi turunan dijelaskan bahwa kemiringan garis singgung merupakan tafsiran geometris dari TURUNAN fungsi, sehingga turunan dapat digunakan sebagai alat bantu menggambar grafik fungsi.

Bantuan tersebut dalam hal penentuan titik-titik garis singgung atau penentuan interval dimana grafik terletak di atas garis singgung atau dibawahnya dst.

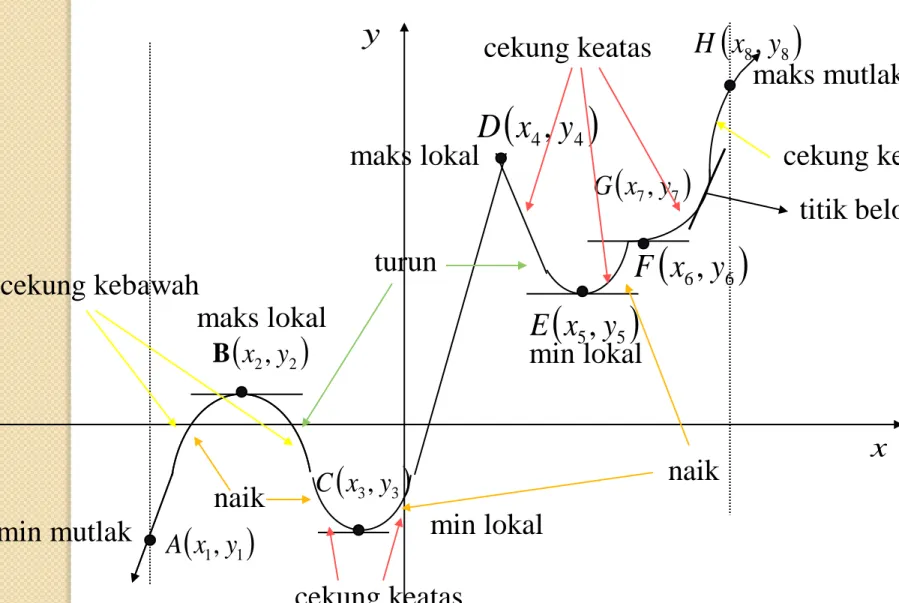
ILUSTRASI GRAFIK

^x₁^{, y}₁

A

^x₂^{, y}₂

B

^x₃^{, y}₃

C

^x₄^{, y}₄

D

x₅, y₅

E

^x₆^{, y}₆

F

^x₇^{, y}₇

G

y

x naik

cekung kebawah

cekung keatas

maks mutlak

min lokal maks lokal

min mutlak

maks lokal

min lokal

naik turun

cekung keatas

cekung kebawah titik belok

^x₈^{, y}₈

H

ekstrim relatif/ekstrim lokal

(i) F punya nilai maksimum relatif di c jika ada selang terbuka I memuat c dimana f terdefinisi, sehingga f(c)≥f(x),

xI a c b x

a c b x

(ii) F punya nilai minimum relatif di c jika ada selang terbuka I memuat c dimana f terdefinisi, sehingga f(c)≤f(x),

xI

Jika fungsi f mempunyai nilai maksimum relatif atau nilai minimum relatif di c, maka f dikatakan mempunyai ekstrim relatif di c.

Jika f(x) ada untuk semua nilai x dalam selang terbuka (a,b) dan jika f mempunyai ekstrim relatif di c dimana a<c<b maka f’(c) ada dan f’(c) = 0.

TEOREMA 1

(ii) f punya minimum relatif di c. Jika f’(c) ada maka

menurut definisi (ii)  >0 sehingga jika 0

c) ( -

) ( c

0  x     f x f 

c

c) (

- ) lim (

c) (

'  

 x

f x

f f

c x

B U K T

I

(i) f punya maksimum relatif di c. Jika f’(c) ada maka

menurut definisi (i)  >0 sehingga jika 0

c) ( -

) (

0  x  c    f x f  c

c) (

- ) lim (

c) (

'  

 x

f x

f f

c x

kasus (i)

 

 

 

  0 '(c) 0 c

) c lim (

c 0 ) c 0 (

c

0 )

c ( ' c 0

) c lim (

c 0 ) c c (

0





 



 

 













 



 

 











x f

f x

f

x

f x

x f x f

f x

f

x

f x

x f

c x

c x





-Jika x mendekati c dari kanan x – c > 0 & jika

berdasar teorema tambahan limit jika limitnya ada maka

-Jika x mendekati c dari kiri x – c < 0 & jika

berdasar teorema tambahan limit jika limitnya ada maka

0 )

c ( ' 0

) c ( ' 0

) c (

'  f  f 

Karena f’(c) ada dan f serta maka

-Jika x mendekati c dari kanan x – c > 0 & jika

berdasar teorema tambahan limit jika limitnya ada maka

-Jika x mendekati c dari kiri x – c < 0 & jika

berdasar teorema tambahan limit jika limitnya ada maka

 

 

 

  0 '(c) 0 c

) c lim (

c 0 ) c 0 (

c

0 )

c ( ' c 0

) c lim (

c 0 ) c c (

0





 



 

 













 



 

 











x f

f x

f

x

f x

x f x f

f x

f

x

f x

x f

c x

c x





0 )

c ( ' 0

) c ( ' 0

) c (

'  f  f 

Karena f’(c) ada dan f serta maka

kasus (ii)

Bila fungsi f didefinisikan di suatu bilangan c maka syarat perlu (bukan syarat cukup) agar f mempunyai ekstrim relatif di c adalah f’(c)=0 atau f’(c) tidak ada.

Bila c bilangan dalam daerah asal f

dan bila f ’(c)=0 atau f ’(c) tidak ada

maka c dikatakan bilangan kritis

dari f.

Andaikan f didefinisikan pada suatu selang yang memuat c, misalkan I.

Jika f(c) adalah titik ekstrim maka c haruslah suatu titik kritis , yakni c berupa salah satu :

1. Titik ujung dari selang

2. Titik stasioner dari f [f ’(c)=0]

3. Titik singular dari f [f ’(c) tidak ada]

TEOREMA 2

(1) f(c) nilai maksimum relatif f pada I Andaikan c bukan titik ujung dan bukan titik singular maka c titik stasioner. Karena f(c) maksimum dari definisi (i), f(c)≥f(x), xI

 f(x)-f(c)≤0.

(2) f(c) nilai minimum relatif f pada I

Andaikan c bukan titik ujung dan bukan titik singular maka c titik stasioner. Karena f(c) minimum dari definisi (ii), f(c)f(x), xI

 f(x)-f(c)0.

B U K T

I

 

 

 

 

0 )

c ( ' maka 0

) c ( ' serta 0

) c ( ' dan ada

) c ( ' Karena

0 )

c ( ' ) 0

c lim (

)

c ( '

shg ada,

) c ( ' singular

k bukan titi c

karena

) 0 c (

sehingga ,

0 maka

, c jika

0 )

c ( ' ) 0

c lim (

) c ( '

shg ada,

) c ( ' singular

k bukan titi c

karena

) 0 c (

sehingga ,

0

maka ,

c jika

-











 

 



 















 

 



 

















f f

f f

c f x

f x

f f

f c

x

f x

f

c x

x

c f x

f x

f f

f c

x

f x

f

c x

x

c x

c x

kasus (1)

. 0 )

c ( ' maka 0

) c ( ' serta 0

) c ( ' dan ada

) c ( ' karena

0 )

c ( ' ) 0

c ( )

lim ( )

c ( '

shg ada,

) c ( ' maka singular

k bukan titi c

karena

) 0 c ( )

(

sehingga 0

maka c

jika

0 )

c ( ' ) 0

c ( )

lim ( )

c ( '

shg ada,

) c ( ' maka singular

k bukan titi c

karena

) 0 c ( )

(

sehingga 0

maka c

jika











 

 

 















 

 

 



















f f

f f

c f x

f x

f f

f c

x f x

f

c x x

c f x

f x

f f

f c

x f x

f

c x x

c x

c x

kasus (2)

1. f(c) dikatakan nilai maksimum mutlak fungsi f jika c di daerah asal f dan f(c)≥f(x) untuk semua nilai x dalam daerah asal f.

2. f(c) dikatakan nilai minimum mutlak fungsi f jika c di daerah asal f dan f(c) ≤ f(x) untuk semua nilai x dalam daerah asal f.

ekstrim mutlak/ekstrim global

Ekstrim mutlak suatu fungsi f adalah nilai maksimum mutlak atau nilai minimum mutlak fungsi didaerah asal f.

Daerah asal disini bisa berupa

suatu selang ataupun himpunan

dst.

Misalkan f fungsi yg didefinisikan pd [-4,3]

Cari titik-titik kritisnya dan nilai ekstrim nya!

8 2 6

1 3

) 1

(x  x³  x²  x  f

Jawab

•titik-titik ujungnya adalah -4 dan 3

•titik stasionernya x =-3 dan x=2 [jika f ’(x)=0

•titik singularnya tidak ada.

titik-titik kritisnya adalah -4, -3, 2 dan 3

contoh 1

Nilai f(x) pada titik-titik kritisnya adalah x = -4  f(-4) = 18,67;

x = -3  f(-3) = 21,5;

x = 2  f(2) = 0,67;

x = 3  f(3) = 3,5 Jadi pada selang [-4,3]

f punyai nilai maksimum mutlak 21,5

f punya nilai minimum mutlak 0,67

8 2 6

1 3

) 1

(x  x³  x²  x f

Bila fungsi f kontinu pada selang tertutup [a,b] maka fungsi f mempunyai nilai maksimum dan nilai minimum mutlak (nilai ekstrim) pada [a,b] (syarat cukup bukan syarat perlu)

TEOREMA 3

Bukti dapat dilihat pada buku teks kalkulus lanjut, pada kuliah ini teorema ini hanya akan dipakai tanpa dibuktikan.

Cari titik kritis fungsi pd I

nilai maksimum & nilai minimum fungsi kontinu pada selang tertutup I

Terbesar Terkecil

Maksimum Minimum

ujung stasioner

singular Hitung fungsi f pd titik kritis

Jawab

f fungsi polinomial → f kontinu pada [-½,2] sehingga teorema-teorema nilai ekstrim dapat digunakan

contoh 2

Cari nilai maksimum dan minimum dari fungsi berikut pada [-½,2]

 

^{x 2x3 3x2}

f   

I.Dicari titik kritis

- Titik ujung adalah -½ dan 2

- Titik stasioner f’(x)=6x² +6x=-6x(x-1)=0 diperoleh x=0 dan x=1

- Titik singular tidak ada Jadi titik kritis -½,0,1,2

II. f(-½)=1, f(0)=0, f(1)=1, f(2)=-4

- Nilai maksimum 1 pada x=1 dan x= -½ - Nilai minimum –4 pada x =2

y

x

Andaikan f terdefinisi pada suatu selang I, (i) f naik pada I jika untuk setiap pasangan bilangan x₁ dan x₂ dalam I

x₁ x₂  f(x₁)f(x₂)

(ii) f turun pada I jika untuk setiap pasangan bilangan x₁ dan x₂ dalam I

x₁ x₂  f(x₁)f(x₂)

(iii) f monoton pada I jika f naik atau f turun pada suatu selang I.

kemonotonan

Misalkan f kontinu pada selang [a,b], dan terdiferensiasi pada (a,b):

(i)

Jika f’(x)0 untuk setiap x pada (a,b) maka f naik pada [a,b]

(ii)

Jika f’(x)0 untuk setiap x pada (a,b) maka f turun pada [a,b]

TEOREMA 4

Misalkan

x₁

,x

₂[a,b]

dgn

x₁x₂

. Karena f kontinu pada [x

₁

,x

₂

] dan terdiferensial pada (x

₁

,x

₂

), dari teorema TNR



bilangan c pada [x

₁

,x

₂

] sehingga

Dari x

₁x₂

→ x

₂

–x

₁0 & f’(c)0,

sehingga f(x

₂

)–f(x

₁

)0

 f(x₁

)f(x

₂

)

→ f naik pada [a,b]■

1 2

1

2

) ( )

(c) (

'

x x

x f

x f f



 

B U K T I

i

Misalkan x

₁

, x

₂[a,b] dgn x₁ x₂

.

Karena f kontinu pada [x

₁

,x

₂

] dan terdiferensial pada (x

₁

,x

₂

), dari teorema TNR



bilangan c pada [x

₁

,x

₂

] sehingga

Dari x

₁x₂

→ x

₂

–x

₁0 dan f’(c)<0,

sehingga f(x

₂

)–f(x

₁

)< 0

 f(x₁

)>f(x

₂

)

→ f turun pd [a,b]■

1 2

1

2) ( )

(c) (

' x x

x f x

f f



 

B U

K T

I

ii

Diberikan fungsi f(x) = 2x³+9x²-24x.

Dengan menggunakan teorema kemonotonan, cari dimana fungsi yang diberikan naik dan dimana turun.

24 18

6 )

( '

24 9

2 )

(

2

2 3













x x

x f

x x

x x

f

contoh 3

Jawab

) (1, dan

) 4 , (

pada naik

Jadi

0 4)

1)(

- ( 0

4 3

0 24

18 6

0 )

( ' jika

naik

i) (

2 2



























 f

x x

x x

x x

x f

f

) 1 , 4 ( pada turun

Jadi

0 4)

1)(

- ( 0

4 3

0 24

18 6

0 )

( ' jika

turun (ii)

2 2























 f

x x

x x

x x

x f

f

f(x) =2x³ + 9x² - 24x

-20 -10 0 10 20 30 40 50 60 70 80 90 100 110 120

-5 -4 -3 -2 -1 0 1 2 3 4

x y

Andaikan f terdefinisi pada (a,b) yang memuat c sehingga xc(a,b), titik (x,f(x)) pada grafik terletak 1. Diatas garis singgung pada grafik dititik (c,f(c))

maka grafik fungsi f cekung keatas dititik (c,f(c)).

2. Dibawah garis singgung pada grafik dititik (c,f(c)) maka grafik fungsi f cekung kebawah dititik (c,f(c)).

(c,f(c))

(c,f(c))

cekung kebawah cekung

keatas

kecekungan fungsi

Misalkan f fungsi terdiferensial pada selang terbuka yang memuat c, maka :

(i) f”(c)>0, f cekung keatas di (c,f(c)).

(ii) f”(c)<0, f cekung kebawah di (c,f(c)).

cekung keatas 0 x

y

cekung kebawah x 0

y

TEOREMA 5

c ,

c 0

) c ( ' )

( '

limit eorema

berdasar t

c 0

) c ( ' )

( lim '

0 )

c (

"

karena

c

) c ( ' )

( lim '

) c (

"





 



 

 





 





x x

f x

f

x

f x

f f

x

f x

f f

c x

c

B

x

U K T I

i

(c , f(c))

Q(x , f(x))

f(x)

T

c x

) c )(

c ( ' )

c

(

 

 f f x

y

Tinjau garis singgung pada grafik f dititik (c,f(c)). Persamaan garisnya :

Misalkan :

x bilangan pada selang terbuka sehingga x  c.

Q titik pada grafik f dengan titik (x , f(x)).

T titik perpotongan garis singgung dan garis sejajar sumbu y melalui Q.

) c )(

c ( ' )]

c ( )

( [

)]

c )(

c ( ' )

c ( [ ) (

















x f

f x

f TQ

x f

f x

f TQ

 0 TQ

Untuk membuktikan f cekung keatas dititik (c,f(c)) akan ditunjukkan xc diselang terbuka tersebut.

Menurut TNR terdapat bilangan d antara x dan c sehingga

Jadi

karena d antara x dan c, dan d pada selang terbuka yang sama sehingga dengan mengambil x = d.

Diperoleh

) c )(

d ( ' )

c ( )

c (

) c ( )

) ( d (

'    



  f x f f x

x

f x

f f

c 0 d

) c ( ' )

d (

' 



 f f

)]

c ( ' )

d ( ' )[

c (

) c )(

c ( ' )

c )(

d ( '

f f

x TQ

x f

x f

TQ















)).

c ( ,

c ( di keatas cekung

Jadi

0

positip bilangan

sama

yang tanda

punya

(c)]

' -

(d) '

[ dan c)

- (

sehingga

0 )

c ( ' )

d ( ' c

d c

0 c

- jika

0 )

c ( ' )

d ( ' c

d c

0 c

- jika

)]

c ( ' )

d ( ' )[

c (

Diketahui

f f

TQ

TQ f

f x

f f

x x

f f

x x

f f

x TQ











































c ,

c 0

) c ( ' )

( '

limit eorema

berdasar t

c 0

) c ( ' )

( lim '

0 )

c (

"

karena

c

) c ( ' )

( lim '

) c (

"





 



 

 





 





x x

f x

f

x

f x

f f

x

f x

f f

c x

c

B

x

U K T I

ii

) c )(

c ( ' )

c

(

 

 f f x

y

Tinjau garis singgung pada grafik f dititik (c,f(c)). Persamaan garisnya :

Misalkan :

x bilangan pada selang terbuka sehingga x  c.

Q titik pada grafik f dengan titik (x , f(x)).

T titik perpotongan garis singgung dan garis sejajar sumbu y melalui Q.

 0 TQ

Untuk membuktikan f cekung kebawah dititik (c,f(c)) akan ditunjukkan xc diselang terbuka tersebut.

) c )(

c ( ' )]

c ( )

( [

)]

c )(

c ( ' )

c ( [ )

(

















x f

f x

f TQ

x f

f x

f TQ

Menurut TNR terdapat bilangan d antara x dan c sehingga

Jadi

karena d antara x dan c, dan d pada selang terbuka yang sama sehingga dengan mengambil x = d.

Diperoleh

) c )(

d ( ' )

c ( )

c (

) c ( )

) ( d (

'    



  f x f f x

x

f x

f f

c 0 d

) c ( ' )

d (

' 



 f f

)]

c ( ' )

d ( ' )[

c (

) c )(

c ( ' )

c )(

d ( '

f f

x TQ

x f

x f

TQ















)).

c ( ,

c ( di kebawah cekung

Jadi

0

negatif bilangan

beda

yang tanda

punya

(c)]

' -

(d) '

[ dan c)

- (

sehingga

0 )

c ( ' )

d ( ' c

d c

0 c

- jika

0 )

c ( ' )

d ( ' c

d c

0 c

- jika

)]

c ( ' )

d ( ' )[

c (

Diketahui

f f

TQ

TQ f

f x

f f

x x

f f

x x

f f

x TQ











































Titik (c,f(c)) titik belok (balik) dari fungsi f jika mempunyai garis singgung di titik (c,f(c)) dan terdapat selang buka yang memuat c sehingga untuk x diselang tersebut berlaku :

(i) f”(x) < 0 jika x < c dan f”(x) > 0 jika x > c.

(ii) f”(x) > 0 jika x < c dan f”(x) < 0 jika x > c.

c c

titik belok

Bila fungsi f terdiferensial pada interval terbuka yang memuat c dan (c,f(c)) suatu titik belok (balik) dari grafik fungsi f maka f’’(c) ada dan f’’(c) = 0.

TEOREMA 6

Misalkan g(x)=f ’(x)  g’(x)=f”(x).

Karena (c,f(c)) titik belok grafik f menurut kecekungan fungsi maka f”(x) berganti tanda di c akibatnya g’(x) berganti tanda di c.

Berdasar teorema uji turunan pertama maka g mempunyai ekstrim relatif di c dan c bilangan kritis dari g.

Karena:

g’(c) = f”(c) dan f”(c) ada  g’(c) ada Sehingga berdasarkan teorema

g’(c) = 0 sehingga f”(c) = 0.■

B U

K T

I

Diberikan fungsi f(x)=1/3x³–x²–3x+4.

Tentukan titik belok, grafik cekung keatas dan cekung kebawah, sketsa grafik dan segmen garis singgung pembelokan grafik f ?

contoh 4

Jawab

f(x) = 1/3x³ – x² – 3x + 4

f’(x) = x²–2x–3 = (x–3)(x + 1) f”(x) = 2x – 2 = 2(x – 1)

f’(x) =(x – 3)(x + 1) = 0

titik kritis x = 3 dan x = -1 titik stasioner f(-1) = 17/3 (maksimum relatif)

f(3) = -5 (minimum relatif) f ”(x) = 2(x – 1) = 0

2(x – 1) > 0  (x – 1) > 0  x > 1

maka f ”(x) > 0 jika x > 1 cekung keatas 2(x – 1) < 0  (x – 1) < 0  x < 1

maka f”(x) < 0 jika x < 1 cekung kebawah titik belok x = 1 f(1) = 1/3

) (x

f f ' x( ) f ' x'( )

x ^Keterangan

x < -1 + - naik, cekung kebawah

x = -1 0 -4 Maksimum relatif

-1< x < 1 - - turun, cekung kebawah

x = 1 -4 0 Titik belok

1< x < 3 - + turun, cekung keatas

x = 3 -5 0 4 Minimum relatif

x > 3 + + naik, cekung keatas

173



13

Diberikan fungsi f(x)=(1–2x)³. Tentukan titik belok, titik dimana grafik cekung keatas dan cekung kebawah, sketsa grafik grafik f ?

contoh 5

Jawab

f(x) = (1 – 2x)³

f’(x) = -6(1 – 2x)² f”(x) = 24(1 – 2x)

f’(x)= -6(1 – 2x)² = 0

titik kritis x = ½ (titik stasioner) f(½) = 0

f ”(x) = 24(1 – 2x) = 0

(1 – 2x) > 0  x < ½

maka f ”(x) > 0 jika x < ½ cekung keatas (1 – 2x) < 0  x > ½

maka f”(x) < 0 jika x > ½ cekung kebawah titik belok x = ½  f (½) = 0.

x ^Keterangan

x < ½ - + turun, cekung keatas

x = ½ 0 0 0 Titik belok

x > ½ - - turun, cekung kebawah

) (x

f f ' x( ) f ' x'( )