MAKALAH PERAMALAN DATA TIME SERIES MENGGUNAKAN METODE BOX-JENKINS. OLEH : SHANTIKA MARTHA, S.Si NIP

MAKALAH

PERAMALAN DATA TIME SERIES

MENGGUNAKAN METODE BOX-JENKINS

OLEH :

SHANTIKA MARTHA, S.Si NIP. 198403082008122003

UNIVERSITAS TANJUNGPURA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM JURUSAN MATEMATIKA

PONTIANAK 2010

l.

2. J. Judul Makalah Bidang Ilmu Penyusun

a-

Nama

b.

GoV NIP

c.

Fakultas/ Jurusan LEMBARAN PENGESAIIAN

Peramalan Data Time Series Menggunakan Metode Box-Jenkins

Statistika

Shantilm Marttrq S.Si

Ill

a I 198403082008122003 FMIPA/ Matematika Mengetahui, Kefira Matematika 1017199802rcA1 Pontianak, Maret 2010 Penyusun, ShantikaMarttra S.Si NIP. 198403082008122003

,grfu

r019881 I 1001

i

KATA PENGANTAR

Alhamdulillahirabbil’alamin, puji syukur kehadirat Allah SWT karena berkat rahmat dan hidayah-Nya makalah yang berjudul “Peramalan Data Time Series Menggunakan Metode Box-Jenkins” dapat terselesaikan. Makalah ini membahas tentang tahapan analisis dengan menggunakan metode Box-Jenkins disertai dengan cara menganalisis data dengan bantuan program Minitab 14.

Akhirnya penulis mengucapkan terimakasih kepada semua pihak yang telah membantu dalam penyelesaian makalah ini. Penulis juga mengharapkan kritik dan saran dari pembaca demi kesempurnaan makalah. Semoga makalah ini dapat bermanfaat bagi kita semua.

Pontianak, Maret 2010

ii

DAFTAR ISI

KATA PENGANTAR ……….... i

DAFTAR ISI ……….. ii

BAB I PENDAHULUAN ... 1

BAB II ANALISIS TIME SERIES ... 3

BAB III KLASIFIKASI MODEL BOX-JENKINS ... 7

BAB IV METODOLOGI BOX-JENKINS ... 12

BAB V ANALISIS DATA MENGGUNAKAN MINITAB 14 ... 16

BAB VI PENUTUP ... 25

1

BAB I PENDAHULUAN

Peramalan adalah perkiraan atau prediksi tentang sesuatu yang akan terjadi pada waktu yang akan datang yang didasarkan pada data yang ada pada waktu sekarang dan waktu lampau (historical data). Peramalan bertujuan untuk memberikan informasi dasar yang diperlukan dalam menyusun suatu perencanaan. Perencanaan merupakan suatu usaha untuk menentukan suatu tindakan di masa yang akan datang dalam mencapai tujuan yang diinginkan. Perencanaan yang baik harus didasarkan atas suatu ramalan yang baik. Sedangkan untuk mendapatkan hasil ramalan yang baik maka diperlukan suatu metode peramalan yang baik pula. Metode peramalan yang baik yaitu jika hasil ramalan tidak berbeda jauh dengan kenyataannya, atau dengan kata lain metode tersebut menghasilkan penyimpangan antara hasil peramalan dengan nilai kenyataan yang sekecil mungkin.

Metode peramalan adalah cara memperkirakan secara kuantitatif apa yang akan terjadi pada masa depan berdasarkan data yang relevan pada masa lalu. Pada dasarnya terdapat dua jenis metode peramalan kuantitatif, yaitu:

a. Metode peramalan dengan menggunakan analisis pola hubungan antara variabel yang diperkirakan dengan variabel lain yang mempengaruhinya, yang disebut dengan metode korelasi atau sebab akibat (causal method). Metode ini terdiri dari metode regresi dan korelasi, metode ekonometri, dan metode input-output.

b. Metode peramalan dengan menggunakan analisis pola hubungan antara variabel yang diperkirakan dengan variabel waktu (analisis time series/ deret waktu). Metode ini terdiri dari metode smoothing, metode Box-Jenkins, dan proyeksi trend dengan regresi.

Dalam makalah ini penulis lebih menitik beratkan pada analisis time series, khususnya membahas tentang teknik peramalan dengan menggunakan metode Box-Jenkins. Metode Box-Jenkins merupakan salah satu metode yang biasa digunakan untuk melakukan peramalan jangka pendek. Untuk mendapatkan nilai

2 prediksi yang akan datang, metode Box Jenkins menggunakan nilai sebelumnya dari suatu variabel dan atau nilai kesalahannya di masa lalu. Metode ini telah banyak digunakan dalam peramalan, diantaranya untuk meramalkan Indeks Harga Saham Gabungan, deviden BUMN, jumlah pemakaian energi listrik, banyaknya hari hujan, jumlah sambungan telepon dan produksi pulsa, dan sebagainya.

Metode Box-Jenkins merupakan suatu metode yang dianggap paling lengkap serta sistematis dalam hal pemilihan model peramalan. Ada beberapa model peramalan yang biasa digunakan oleh para ahli ekonometrika, yaitu model Autoregressive (AR), model Moving Average (MA), model Autoregressive Moving Average (ARMA), dan model Autoregressive Integrated Moving Average (ARIMA), dimana keempat model tersebut menggunakan asumsi bahwa data yang digunakan untuk peramalan harus bersifat stasioner dan error/ residual yang dihasilkan merupakan proses white noise.

Oleh sebab itu, tujuan dari penulisan makalah ini adalah menjelaskan bagaimana cara menentukan model peramalan bagi data time series yang tepat dan memenuhi asumsi yang dipersyaratkan. Selain itu, makalah ini juga membahas tentang contoh bagaimana cara menganalisis data time series menggunakan bantuan program aplikasi Minitab 14.

3

BAB II

ANALISIS TIME SERIES

Data time series merupakan data statistik yang sering digunakan dalam metode peramalan. Data time series adalah data yang dikumpulkan dari waktu ke waktu untuk menggambarkan perkembangan suatu kegiatan (Supranto, 2000). Sedangkan menurut Awat (1995) data time series adalah data tentang nilai-nilai suatu variabel yang tersusun secara berderet dari waktu ke waktu, baik dari bulan ke bulan, maupun dari tahun ke tahun, yang dapat disimbolkan dari waktu t ke waktu t +1 sampai dengan t + n.

Ada beberapa istilah penting yang sering digunakan dalam analisis time series, yaitu:

1. Autokovarians

Autokovarians menunjukkan bagaimana elemen-elemen dari suatu time series saling bergantung satu dengan yang lainnya. Jika elemen-elemen dari suatu time series dinotasikan dengan x1, x2, …, xt, ... maka mean dan varians dari pengamatan terhadap waktu t adalah:

t = E (xt)

t2 = E [(xt - t)2]

Kovarians antara dua elemen xt dan xt+k dari suatu time series didefinisikan sebagai:

cov (xt , xt+k) = E [(xt – E[xt] ) (xt+k – E[xt+k] )] (2.1) = E [xt xt+k – xt+k E(xt)– xt E(xt+k) + E(xt)E(xt+k)]

Jika diasumsikan xt mempunyai varians yang identik dan E(xt) = E(xt+k) = 0 maka:

cov (xt , xt+k) = E [xt xt+k] = k untuk k = 1, 2, 3, ... (2.2) Untuk k = 0 maka 0 = E [xt xt] = var (xt) (2.3)

4 2. Autokorelasi

Autokorelasi adalah suatu ukuran yang mengukur besarnya hubungan linier antara suatu variabel dengan variabel itu sendiri dalam waktu yang berbeda. Autokorelasi menggambarkan susunan/ struktur data dan polanya.

Fungsi autokorelasi (ACF) dari {xt} pada lag k biasa ditulis k didefinisikan sebagai fungsi yang nilainya pada lag k adalah:

0 0 0 ) ( var ) ( var ) , ( cov       k k k t t k t t k x x x x      _(2.4)

Dalam praktek, harus dihitung nilai estimasi dari fungsi autokorelasi yang disebut dengan fungsi autokorelasi sampel. Fungsi tersebut didefinisikan dengan:





        _n t t k n t k t t k x x x x x x 1 2 1 ) ( ) )( (  (2.5)

Nilai dari fungsi autokorelasi sampel ini dapat digunakan untuk menentukan orde dari model Moving Average. Selain itu dengan melihat plot fungsi autokorelasi (ACF), maka dapat dilihat apakah data time series yang diamati adalah stasioner. Plot ini disebut dengan Correlogram.

Simpangan baku dari penduga ρk adalah



  q i i n 1 2 2 1 1 _ untuk k > q. 3. Autokorelasi Parsial

Autokorelasi parsial digunakan untuk mengukur tingkat keeratan antara xt dan xt-k apabila pengaruh dari time lag 1,2,3, …, k-1 dianggap terpisah. Koefisien autokorelasi parsial berorde m didefinisikan sebagai koefisien Autoregressive terakhir dari model AR berorde m (Makridakis, Wheelwright, dan McGee, 1999). Sebagai contoh:

xt = 1 xt-1 + t

xt = 1 xt-1 + 2 xt-2 + t

5 Koefisien terakhir x dari persamaan AR yaitu 1, 2 , …, dan m di atas merupakan koefisien autokorelasi parsial.

Penghitungan autokorelasi parsial bertujuan untuk membantu menentukan orde dari proses Autoregressive. Adapun nilai dari fungsi autokorelasi parsial sampel dirumuskan sebagai berikut:

) 1 ( ) ( 2 1 2 1 2 22 1 11          

dan untuk lag selanjutnya





          ₁ 1 , 1 1 1 , 1 1 k j j j k k j j k j k k kk       untuk k = 2,3,4, … (2.6) dengan kj k1,j kkk1,kj untuk j = 1,2, …,k-1

Nilai dari masing-masing kk juga akan membentuk suatu plot fungsi autokorelasi parsial sampel (PACF). Simpangan baku dari penduga kk adalah

n

1

untuk k > p.

4. Operator Lag

Jika x1, x2, …, xt adalah suatu time series maka operator lag (L) didefinisikan sebagai :

Ln xt = xt-n. (2.7)

Sebagai contoh: Lxt = xt-1

L2 xt = xt-2 , dan seterusnya.

Operator lag digunakan untuk mengalihkan perhatian ke keadaan pada waktu sebelumnya, atau dengan kata lain untuk menggeser data sebanyak n periode ke belakang. Misalnya kita ingin mengalihkan perhatian ke bulan yang sama pada tahun sebelumnya, maka dapat ditulis L12 xt = xt-12.

6 5. Kestasioneran Data

Suatu data time series dikatakan stasioner jika tidak terdapat perubahan mean dari waktu ke waktu dan tidak memperlihatkan adanya perubahan varians. Secara umum, suatu proses stokastik xt dikatakan stasioner (Judge et al, 1982) jika: (i). E (xt) =  untuk semua t

(ii). Var (xt) <  untuk semua t

(iii). Cov (xt , xt+k) = E [(xt - ) (xt+k - )] = k untuk semua t dan k

Adapun upaya yang dapat dilakukan untuk menstasionerkan data yang tidak stasioner adalah dengan cara melakukan pembedaan (differencing). Sebagai contoh:

Pembedaan orde pertama : x't = xt – xt-1

= xt – Lxt = (1 - L) xt Pembedaan orde kedua : x''t = x't – x't-1

= (xt – xt-1) – (xt-1 – xt-2) = xt – 2 xt-1 + xt-2 = xt – 2 Lxt + L2xt = (1 – 2L – L2) xt = (1 - L)2 xt

Dengan cara yang sama dapat ditunjukkan bahwa pembedaan orde ke-d adalah:

xdt = (1- L)d xt (2.8)

Pembedaan orde ke-d menunjukkan banyaknya pembedaan yang dilakukan untuk mendapatkan data time series yang stasioner. Hasil dari setiap pembedaan yang dilakukan disebut sebagai proses yang terintegrasi (integrated processes).

6. White Noise

Proses white noise merupakan proses stasioner. Proses white noise didefinisikan sebagai deret variabel acak yang independen dan berdistribusi identik. Suatu deret error dikatakan sebagai proses white noise jika memiliki nilai mean nol dan varians 2, ditulis {t}~ WN (0, 2).

7

BAB III

KLASIFIKASI MODEL BOX-JENKINS

Saat ini ada banyak metode serta model peramalan yang telah dikembangkan oleh para ahli, salah satunya ialah metoda Box-Jenkins. Metode ini diperkenalkan pertama kali pada tahun 1976 oleh George Box dan Gwilym Jenkins dan merupakan suatu metode yang dianggap paling lengkap serta sistematis dalam hal pemilihan model peramalan.

Ada empat model peramalan yang terdapat pada metode Box-Jenkins yaitu: 1. Model Autoregressive (AR)

Dalam model Autoregressive, nilai observasi dari xt secara langsung berhubungan dengan sejumlah p observasi pada waktu sebelumnya. Bentuk umum model Autoregressive dengan orde p, biasa ditulis AR (p) atau model ARIMA (p,0,0) dinyatakan sebagai berikut:

xt = ' + 1 xt-1 + 2 xt-2 + ... + p xt-p + t (3.1) dimana : ' = suatu konstanta

p = koefisien komponen AR dengan orde p xt = nilai observasi pada saat t

xt-p = nilai observasi pada p periode sebelumnya

t = nilai error pada saat t, t  WN (0, 2)

Jika L adalah suatu operator lag maka persamaan (3.1) dapat pula diubah dalam bentuk: xt - 1 xt-1 - 2 xt-2 - ... - p xt-p = ' + t xt - 1 Lxt - 2 L2xt - ... - p Lpxt = ' + t (1 - 1 L - 2 L2 - ... - p Lp ) xt = ' + t (L) xt = ' + t (3.2) dengan  (L)= 1 - 1 L - 2 L2 - ... - p Lp

8 Agar proses AR (p) pada persamaan di atas dapat dikatakan stasioner maka akar-akar dari persamaan karakteristik deret  (L) = 0 harus berada diluar unit circle (│gi│-1 >1), untuk i = 1, 2, …, p (Frain, 1992). Sebagai contoh: Persamaan karakteristik dari model AR (2) dengan 1 = 0,8 dan 2 = -0,15 adalah:

1 - 0,8L + 0,15L = 0 (1 - 0,5L) (1 - 0,3L) = 0 1 - 0,5L = 0 atau 1 - 0,3L = 0

L = 2 atau L = 10/3

Model AR (2) stasioner karena memiliki akar-akar karakteristik yang nilainya lebih dari 1 yaitu sebesar 2 dan 10/3.

Untuk mengestimasi parameter-parameter AR (1, 2, ..., p) dan varians error (e2) dapat digunakan metode kuadrat terkecil (least squares method). Diketahui besarnya nilai dari masing-masing observasi adalah:

xp+1 = 1 xp + ... + p x1 + p+1 xp+2 = 1 xp+1 + ... + p x2 + p+2 xn = 1 xn-1 + ... + p xn-p + n

Persamaan-persamaan di atas dapat ditulis ke dalam bentuk matriks menjadi:

                                                                  n 2 p 1 p p 2 1 p n 2 n 1 n 2 p 1 p 1 1 p p n 2 p 1 p ε ε ε x x x x x x x x x x x x           Atau: x_p X_p_p e (3.3)

Metode kuadrat error terkecil (Least Squares Error) adalah metode pendugaan terhadap parameter regresi dengan cara meminimumkan jumlah kuadrat error (S).

S = e'e = (xp - Xp p)' (xp - Xp p)

= x'px'p - p x'pXp - p X'pxp + p2 X'pXp

= x'px'p - 2p X'pxp + p2 X'p Xp

9 p ' p p p ' p p ' p p p ' p p p ' p p ' p p x X X X x X X X 0 X X x X S             2 2 2 2 p ' p p ' p p (X X ) X x ˆ  1 (3.4)

Substitusi persamaan (3.3) ke persamaan (3.4) sehingga diperoleh:

e X X X e X X X e X X X X X X X e X X X X ' p p ' p p p ' p p ' p p ' p p ' p p p ' p p ' p p p ' p p ' p p 1 1 1 1 1 ) ( ˆ ) ( ) ( ) ( ) ( ) ( ˆ                    1 2 1 1 1 1 ˆ ) ( ) ( ) )( ( ]} ) [( ]' ) {[( )] ˆ ( )' ˆ [( ˆ : adalah ˆ bagi matriks Covariansi -Variansi           p ' p p ' p p ' p p ' p ' p p ' p ' p p ' p p p p p p p X X X X X X X X e e' e X X X e X X X e E E E                       dimana p n p n e _      ( ˆ )'( ˆ ) 2 S xp Xpp xp Xpp  (3.5)

2. Model Moving Average (MA)

Jika nilai observasi dari xt dipengaruhi oleh sejumlah q error/ kesalahan pada masa lalu maka xt merupakan proses Moving Average. Bentuk umum model Moving Average dengan orde q, biasa ditulis MA (q) atau model ARIMA (0,0,q) dinyatakan sebagai berikut:

xt = ' + t - 1 t-1 - 2 t-2 - ... - q t-q (3.6) Dimana: ' = suatu konstanta

q = koefisien komponen MA dengan orde q xt = nilai observasi pada saat t

t = nilai error pada saat t, t  WN (0, 2)

10 Jika t-n = Lt dimana L adalah suatu operator lag maka persamaan di atas dapat ditulis:

xt = ' + (1 - 1 L - 2 L2 - ... - q Lq)t

xt = ' +  (L) t (3.7)

dimana  (L) = 1 - 1 L - 2 L2 - ... - q Lq

Jika akar-akar dari persamaan karakteristik deret  (L)= 0 berada di luar unit circle (│gi│-1 >1), untuk i = 1, 2, …, q maka proses MA (q) dikatakan invertible yang artinya xt dapat dituliskan sebagai proses AR berorde tak terbatas atau AR (∞).

Untuk mengestimasi parameter-parameter MA (1, 2, ..., p) dan varians error (e2) dapat digunakan metode kuadrat terkecil (least squares method). Jika t = xt + 1 t-1 + 2 t-2 + ... + q t-q maka jumlah kuadrat errornya adalah:

S = 2 1 1 1 1 2 ) ... ( q t q n t t t n t t x        





     (3.8)

Karena nilai error tidak dapat diobservasi maka dapat disubstitusi dengan observasi x1, x2, ..., xn. Hal ini dapat ditunjukkan dengan menyusun ulang persamaan MA (1) sebagai berikut:



                  1 1 2 2 1 1 1 2 1 1 1 1 1 ) ( j j t j t t t t t t t t t t x x x x x x x           

Sehingga persamaan (3.8) dapat juga ditulis sebagai berikut:

S = 2 1 1 2 2 1 1 1 2 ) ... ... (x x x xt q t x q t n t t t n t t             





     (3.9)

11 Nilai ˆ diperoleh dengan cara meminimumkan jumlah kuadrat error (S). _q Sedangkan varians error (e2) dihitung dengan rumus:

ˆ2 q n S e  _  (3.10)

3. Model Autoregressive Moving Average (ARMA)

Bentuk ini merupakan campuran dari proses AR (p) dan MA (q) biasa ditulis ARMA (p,q). Model ini dapat dinyatakan dalam bentuk:

xt = ' + 1 xt-1 + 2 xt-2 + ... + p xt-p + t - 1 t-1 - 2 t-2 - ... - q t-q xt - 1 xt-1 - 2 xt-2 - ... - p xt-p = ' + t - 1 t-1 - 2 t-2 - ... - q t-q xt - 1 Lxt - 2 L2xt - ... - p Lpxt = ' + t - 1 Lt - 2 L2 t - ... - q Lqt (1 - 1 L - 2 L2 - ... - p Lp ) xt = ' + (1 - 1 L - 2 L2 - ... - q Lq)t

(L) xt = ' +  (L) t (3.11) Dimana: ' = suatu konstanta

p = koefisien komponen AR dengan orde p

q = koefisien komponen MA dengan orde q xt = nilai observasi pada saat t

t = nilai error pada saat t, t  WN (0, 2)

4. Model Autoregressive Integrated Moving Average (ARIMA)

Model ARIMA (p,d,q) merupakan hasil modifikasi model ARMA (p,q) dengan memasukkan operator pembedaan sebesar (1–L)d agar data yang digunakan memenuhi kondisi stasioner. Bentuk umum dari ARIMA (p,d,q) dinyatakan sebagai berikut:

(L) (1-L)d xt = ' +  (L) t (3.12) dengan  (L) = 1 - 1 L - 2 L2 - ... - p Lp

12

BAB IV

METODOLOGI BOX-JENKINS

Ada empat tahap yang harus dilewati untuk mendapatkan suatu model peramalan yang tepat dengan menggunakan metode Box-Jenkins yaitu:

1. Tahap Identifikasi

Tahap ini digunakan untuk menduga apakah data mengikuti model AR (Autoregressive), MA (Moving Average), atau ARMA (Autoregressive Moving Average). Dalam melakukan peramalan, suatu data time series harus memenuhi syarat stasioner. Jika data asli belum stasioner, maka langkah pertama dari tahap ini adalah menstasionerkan data tersebut dengan melakukan proses pembedaan (differencing).

Untuk mengetahui apakah suatu data time series telah stasioner dapat dilihat dari plot time series. Jika n buah nilai dari suatu data time series memiliki mean dan varians yang konstan dan tidak berfluktuasi terhadap waktu pengamatan maka deret data tersebut dapat dikatakan stasioner. Selain menggunakan plot time series, kestasioneran data juga dapat dilihat dari plot autokorelasi. Jika autokorelasi berangsur-angsur berkurang secara perlahan atau tidak habis sama sekali maka diindikasikan bahwa data tidak stasioner sehingga perlu dilakukan pembedaan (biasanya tidak lebih dari sekali atau dua kali) sampai diperoleh data yang stasioner (Judge et al, 1982). Dari plot autokorelasi juga dapat dilihat ada tidaknya pola musiman dalam data (Iriawan & Astuti, 2006).

Apabila kestasioneran telah diperoleh, langkah selanjutnya adalah menentukan nilai-nilai p, d, dan q berdasarkan plot fungsi autokorelasi (ACF) dan fungsi autokorelasi parsial (PACF). Pada masing-masing plot ACF dan PACF terdapat dua garis putus-putus dengan nilai ±1.96 x 1/√n. Garis tersebut merupakan batas atas dan batas bawah pada selang kepercayaan 95% untuk suatu deret acak. Orde dari proses Autoregressive (AR) dan Moving Average (MA) dapat ditentukan dengan melihat banyaknya nilai dari koefisien korelasi dan koefisien autokorelasi parsial yang tidak berada dalam batas tersebut.

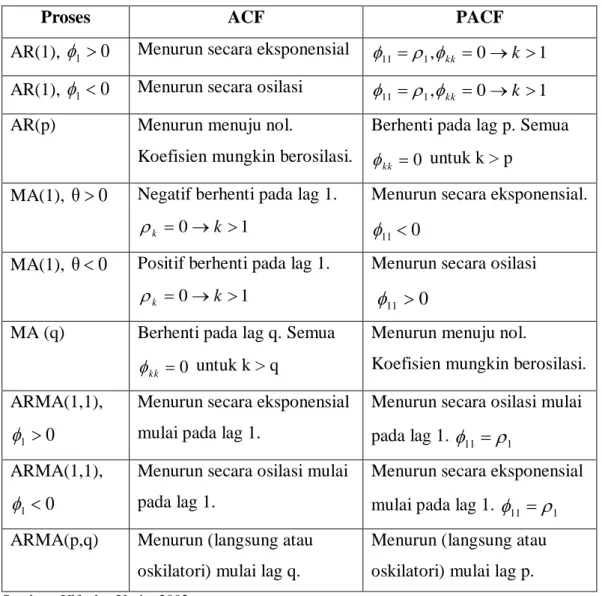
13 Tabel berikut dapat digunakan sebagai pedoman dalam menentukan nilai p dan q yang menunjukkan orde dari proses AR dan MA. Sedangkan nilai d ditentukan berdasarkan banyaknya pembedaan yang dilakukan untuk mendapatkan data time series yang stasioner.

Tabel Karakteristik ACF dan PACF

Proses ACF PACF

AR(1), ₁ 0 Menurun secara eksponensial _{, 0 1} 1

11  kk  k 



AR(1), ₁ 0 Menurun secara osilasi _{, 0 1}

1

11  kk  k 



AR(p) Menurun menuju nol.

Koefisien mungkin berosilasi.

Berhenti pada lag p. Semua 0

 kk

 untuk k > p MA(1), θ0 Negatif berhenti pada lag 1.

1 0 

 k

k



Menurun secara eksponensial. 0

11



MA(1), θ0 Positif berhenti pada lag 1. 1

0 

 k

k



Menurun secara osilasi 0

11 



MA (q) Berhenti pada lag q. Semua 0

 kk

 untuk k > q

Menurun menuju nol.

Koefisien mungkin berosilasi. ARMA(1,1),

0 1 



Menurun secara eksponensial mulai pada lag 1.

Menurun secara osilasi mulai pada lag 1. 1 11    ARMA(1,1), 0 1  

Menurun secara osilasi mulai pada lag 1.

Menurun secara eksponensial mulai pada lag 1. ₁₁ ₁ ARMA(p,q) Menurun (langsung atau

oskilatori) mulai lag q.

Menurun (langsung atau oskilatori) mulai lag p. Sumber : Ulfa dan Yasin, 2003

2. Tahap Estimasi

Setelah menentukan model yang akan digunakan dalam peramalan, maka tahap berikutnya adalah mengestimasi parameter-parameternya. Parameter merupakan karakteristik dari suatu populasi. Persamaan model AR, MA, ARMA ataupun ARIMA pada dasarnya merupakan suatu bentuk regresi. Oleh karena itu

14 parameter dari model tersebut dapat diestimasi menggunakan metode kuadrat terkecil sehingga diperoleh residual yang minimum. Dengan demikian, untuk memperoleh estimasi terbaik dari model AR, MA, ARMA ataupun ARIMA adalah dengan cara meminimumkan jumlah kuadrat error.

3. Tahap Pemeriksaan Diagnostik

Pemeriksaan diagnostik merupakan tahap untuk menguji kesesuaian dan kecukupan model peramalan. Setelah diperoleh nilai estimasi dari parameter model AR/ MA/ ARMA/ ARIMA, tahap selanjutnya adalah menguji signifikansi dari masing-masing parameter secara parsial dan menguji model secara keseluruhan. Suatu model dikatakan baik jika parameternya signifikan dan error/ residual yang dihasilkan bersifat random (tidak memiliki pola tertentu) dan merupakan proses white noise yang berarti residual bersifat independen (tidak saling berkorelasi) dan berdistribusi normal.

Seperti dalam analisis regresi, uji parameter bisa dilakukan dengan menggunakan statistik uji t atau P-value. Secara umum, parameter yang akan diuji signifikansinya dalam analisis time series hanyalah parameter AR ( ) dan parameter MA ( ), sedangkan signifikansi konstanta tidak perlu diuji (Iriawan & Astuti, 2006).

Sebagai contoh, akan diuji apakah parameter-parameter AR (i ) cukup signifikan dalam model. Hipotesis yang digunakan adalah:

H0 : i = 0

H1 : i ≠ 0, i = 1, 2, ..., p

Pengujian dilakukan dengan statistik uji t, yaitu:

) ˆ ( ˆ i i hit Se t  

 , dimana Se(



ˆ_i)adalah standard error dari



ˆ_i

dengan daerah penolakan H0 adalah │thitung│> tα/2; n-k dengan n = jumlah data dan k = jumlah parameter yang digunakan. Selain itu, pengujian juga dapat dilakukan dengan melihat P-value yaitu tolak H0 (dan terima H1) jika nilai P < α.

15 Sedangkan untuk menentukan apakah error/ residual merupakan proses white noise atau bukan dapat dilakukan pengujian terhadap nilai koefisien autokorelasi dan autokorelasi parsial dari error/ residual dengan menggunakan salah satu dari dua statistik berikut:

1. Uji Box-Pierce :



  K i i n Q 1 2  2. Uji Ljung-Box :



    K i i i n n n Q 1 2 ) 2 ( 

Dimana kedua statistik ini mengikuti distribusi Chi-Kuadrat dengan derajat bebas (db) = K – k dimana K menunjukkan jumlah lag dan k menunjukkan jumlah parameter model.

Hipotesis yang digunakan untuk dalam statistik uji Q adalah: H0 : ρi = 0 , dimana i = 1, 2, …, K

H1 : minimal ada satu lag yang ρi ≠ 0

Dengan daerah penolakan H0 adalah: Q > X 2(α, db)

Dengan membuat plot ACF dan PACF residual kita juga dapat menyimpulkan bahwa error/ residual yang dihasilkan merupakan proses white noise yaitu jika semua nilai ACF dan PACF tidak signifikan (tidak ada satu lag pun yang keluar batas).

4. Tahap Peramalan

Jika hasil pengujian menyimpulkan bahwa model tentatif layak dan telah memenuhi asumsi yang dipersyaratkan, maka model tersebut dapat digunakan untuk memprediksi nilai-nilai time-series untuk waktu yang akan datang.

Untuk melihat tingkat ketepatan model dalam peramalan maka dapat digunakan perhitungan nilai MAPE (Means Absolute Percentage Error) berikut:

MAPE = 100% ˆ 1  



 n x x x n t t t t

dengan xt = nilai aktual, xˆt = nilai peramalan, dan n = jumlah peramalan. Semakin kecil nilai MAPE maka semakin baik model peramalan tersebut.

16

BAB V

ANALISIS DATA MENGGUNAKAN MINITAB 14

Dalam bab ini membahas bagaimana cara menganalisis data dengan menggunakan bantuan program aplikasi Minitab 14 . Sebagai contoh, kita akan menentukan model ARIMA berdasarkan data bulanan dari jumlah pelanggan telepon kabel di Pontianak periode Desember 2002 – Januari 2007.

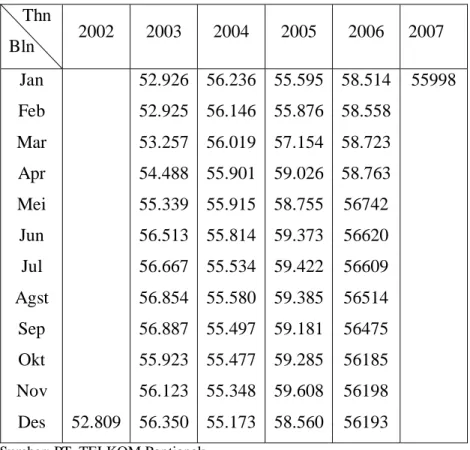
Tabel Jumlah Pelanggan Telepon Kabel di Pontianak Thn Bln 2002 2003 2004 2005 2006 2007 Jan Feb Mar Apr Mei Jun Jul Agst Sep Okt Nov Des 52.809 52.926 52.925 53.257 54.488 55.339 56.513 56.667 56.854 56.887 55.923 56.123 56.350 56.236 56.146 56.019 55.901 55.915 55.814 55.534 55.580 55.497 55.477 55.348 55.173 55.595 55.876 57.154 59.026 58.755 59.373 59.422 59.385 59.181 59.285 59.608 58.560 58.514 58.558 58.723 58.763 56742 56620 56609 56514 56475 56185 56198 56193 55998

Sumber: PT. TELKOM Pontianak

Langkah-langkah yang dilakukan untuk menganalisis data yang ada dalam tabel menggunakan program komputer Minitab 14 yaitu sebagai berikut:

1. Masukkan data ke dalam satu kolom (misalkan kolom C1) dan beri nama (Pelanggan).

2. Memeriksa pola data dan kestasionerannya berdasarkan plot time series, fungsi autokorelasi (ACF), dan fungsi autokorelasi parsial (PACF). Caranya:

17 Pilih Stat > Time Series > Time Series Plot.

Dalam kotak dialog, pilih Simple, klik OK.

Masukkan variabel “pelanggan” ke dalam kotak di bawah Series. Selanjutnya, klik OK, dan diperoleh output sebagai berikut:

Pilih Stat > Time Series > Autocorrelation.

Masukkan variabel “pelanggan” ke dalam kotak di bawah Series. Pilih Default number of lags.

18 Pilih Stat > Time Series > Partial Autocorrelation.

Masukkan variabel “pelanggan” ke dalam kotak di bawah Series. Pilih Default number of lags.

Selanjutnya, klik OK, dan diperoleh output sebagai berikut:

Interpretasi output :

Berdasarkan plot time series, tampak bahwa data jumlah pelanggan telepon tidak stasioner. Hal ini juga diperjelas dari plot fungsi autokorelasi (ACF) yang menurun secara perlahan-lahan serta nilai autokorelasi parsial pada lag pertama yang dominan. Dari plot autokorelasi (ACF) juga dapat disimpulkan bahwa data tidak dipengaruhi oleh faktor musiman karena tidak ada pola yang teratur dari waktu ke waktu.

3. Karena deret data belum stasioner maka perlu dilakukan pembedaan (differencing). Caranya:

Pilih Stat > Time Series > Differences.

Masukkan variabel “pelanggan” ke dalam kotak di bawah Series. Ketik “c2” ke dalam kotak Store differences in.

Ketik “1” ke dalam kotak Lag.

19 Ulangi langkah ke-2 sehingga diperoleh:

20 Hasil analisis plot time series, fungsi autokorelasi (ACF), dan fungsi autokorelasi parsial (PACF) menunjukkan data sudah stasioner pada pembedaan orde pertama. Dari proses pembedaan pertama terlihat bahwa tidak ada satu lag pun dari nilai autokorelasi maupun nilai autokorelasi parsial yang berada di luar garis putus-putus. Ini berarti bahwa pada data yang diperoleh berdasarkan proses pembedaan pertama tersebut tidak terdapat adanya proses Autoregressive (AR) maupun proses Moving Average (MA). Untuk menduga parameter model baik AR maupun MA dilakukan proses pembedaan kedua

4. Ulangi langkah ke-2 dan ke-3 sehingga diperoleh:

Interpretasi output :

Berdasarkan plot ACF dan PACF setelah dilakukan pembedaan kedua, terlihat bahwa nilai autokorelasi dan autokorelasi parsial pada lag 1 berada diluar garis putus-putus yang berada pada nilai = ± 1,96 x 1/√48 = ± 0,2829.

21 Ini berarti bahwa pada data tersebut terdapat adanya proses Autoregressive berorde 1 dan proses Moving Average berorde 1. Jadi ada 3 kombinasi model ARIMA yang mungkin bagi data jumlah pelanggan telepon kabel di Pontianak, yaitu ARIMA (1,2,0), ARIMA (0,2,1), dan ARIMA (1,2,1).

5. Langkah selanjutnya adalah pendugaan parameter yaitu mencari nilai koefisien parameter dari masing-masing model. Kemudian masing-masing parameter tersebut diuji signifikansinya dengan menggunakan statistik uji t dan nilai probabilitas.

Pilih Stat > Time Series > ARIMA

Dibawah Nonseasonal, isikan bilangan sesuai dengan model yang akan diuji. Pilih Graphs.

Dalam kotak dialog ARIMA-Graphs, di bawah Residual Plots beri tanda cek () pada ACF of residuals dan PACF of residuals. Fungsinya adalah mendeteksi proses white noise pada residual.

22 6. Untuk peramalan, pilih Forecast

Dalam kotak dialog ARIMA-Forecast, isikan bilangan 10 di sebelah Lead, artinya kita akan meramalkan 10 periode ke depan. Di sebelah origin, isikan 50, artinya kita akan meramalkan data mulai dari 51 hingga 60.

Kemudian klik OK.

Dalam kotak dialog ARIMA, pilih Storage

Dalam kotak dialog ARIMA-Storage, beri tanda cek () pada Residual. Klik OK dalam kotak dialog ARIMA-Storage.

Selanjutnya, klik OK, dan diperoleh output sebagai berikut:

Secara ringkas hasil pengujian masing-masing parameter bagi ketiga model ARIMA disajikan dalam tabel berikut:

23 Tabel Nilai Uji T dan Probabilitas bagi Masing-Masing Parameter serta

Jumlah Kuadrat Residual bagi masing-masing Model

Model Parameter Uji t P Jumlah Kuadrat Residual ARIMA (1,2,0) AR 1 C -3,22 -0,07 0,002 0,944 19.186.521 ARIMA (0,2,1) MA 1 C 14,17 -1,86 0,000 0,070 15.283.337 ARIMA (1,21) AR 1 MA 1 C 1,35 11,25 -1,45 0,182 0,000 0,154 14.594.730

Sumber: Hasil Perhitungan

Berdasarkan hasil pengujian terhadap masing-masing parameter secara parsial, maka dapat disimpulkan bahwa terdapat dua model ARIMA yang memiliki koefisien parameter yang signifikan karena memiliki nilai P < 0,05 yaitu model ARIMA (1,2,0) dan ARIMA (0,2,1). Sedangkan pada model ARIMA (1,2,1) terdapat salah satu parameter yang memiliki nilai P > 0,05 sehingga koefisien parameternya tidak signifikan. Karena hanya ada satu model yang akan digunakan dalam peramalan maka model yang dipilih adalah ARIMA (0,2,1) karena model tersebut memiliki jumlah kuadrat residual yang lebih kecil dibandingkan dengan model ARIMA (1,2,0).

Berikut adalah output model ARIMA (0,2,1) secara keseluruhan. ARIMA Model: pelanggan

Estimates at each iteration Iteration SSE Parameters 0 21696845 0,100 -6,400 1 19596697 0,250 -5,614 2 18078074 0,400 -5,224 3 17016252 0,550 -5,988 4 16404680 0,683 -8,842 5 16225801 0,744 -11,000 6 16149330 0,780 -11,739 7 16103890 0,805 -12,091 8 16068625 0,825 -12,262 9 16034455 0,844 -12,339 10 15994070 0,863 -12,348 11 15936226 0,884 -12,284 12 15834978 0,910 -12,112 13 15615171 0,945 -11,772 14 15419275 0,968 -11,620

24 15 15360361 0,980 -11,122

16 15355812 0,977 -10,085 17 15349845 0,979 -10,327

Unable to reduce sum of squares any further Final Estimates of Parameters

Type Coef SE Coef T P MA 1 0,9788 0,0691 14,17 0,000 Constant -10,327 5,560 -1,86 0,070 Differencing: 2 regular differences

Number of observations: Original series 50, after differencing 48 Residuals: SS = 15283337 (backforecasts excluded)

MS = 332246 DF = 46

Modified Box-Pierce (Ljung-Box) Chi-Square statistic Lag 12 24 36 48

Chi-Square 9,6 32,6 40,3 * DF 10 22 34 * P-Value 0,479 0,068 0,210 *

Tahap selanjutnya yaitu menguji model ARIMA (0,2,1) secara keseluruhan dengan menggunakan uji statistik Q dan Chi-Kuadrat (X2). Uji ini dilakukan untuk melihat independensi residual antar lag. Hasil di atas menunjukkan bahwa sampai pada lag 12 tidak ada korelasi antara residual pada lag t dengan residual pada lag 12, begitu pula untuk lag 24 dan 36. Hal ini disebabkan karena pada lag 12, 24, dan 36 memiliki nilai statistik Q (Ljung-Box-Pierce) < X2(5%; db) dan P > 0,05. Karena tidak terdapat korelasi antar residual, maka dapat disimpulkan bahwa residual telah memenuhi asumsi white noise sehingga model cocok digunakan untuk peramalan. Hal ini juga dapat diperkuat dengan tidak ada satu lag pun yang keluar batas pada plot ACF residual dan PACF residual.

Adapun persamaan model ARIMA (0,2,1) adalah: xt = -10,327 + 2xt-1 – xt-2 + t – 0,9788 t-1

dimana: xt = jumlah pelanggan telepon pada bulan ke-t.

xt-1 = jumlah pelanggan telepon pada satu bulan sebelumnya. xt-2 = jumlah pelanggan telepon pada dua bulan sebelumnya. t = nilai error pada bulan ke-t.

25

BAB VI PENUTUP

1. Kesimpulan

Pada makalah ini dijelaskan tentang langkah-langkah yang harus dilakukan untuk mendapatkan suatu model peramalan yang tepat dengan menggunakan metode Box-Jenkins yaitu mulai dari tahap identifikasi, estimasi parameter, pemeriksaan/uji diagnostik hingga peramalan. Metode Box-Jenkins tidak menghasilkan model yang deterministik sehingga kualitas model sangat tergantung pada kualitas data time series (hasil observasi/ pengamatan) yang digunakan.

Ada empat model peramalan yang terdapat pada metode Box-Jenkins yaitu model Autoregressive (AR), model Moving Average (MA), model Autoregressive Moving Average (ARMA), dan model Autoregressive Integrated Moving Average (ARIMA). Asumsi yang digunakan oleh keempat model tersebut adalah data yang digunakan untuk peramalan harus bersifat stasioner dan error/ residual yang dihasilkan merupakan proses white noise.

2. Saran

Perlu dilakukan persiapan yang cermat terhadap data pengamatan yang akan digunakan dalam peramalan karena kesalahan dalam mengidentifikasi karakteristik/ pola data yang diinput akan menyebabkan kekeliruan saat menentukan model peramalan. Data historis yang digunakan harus bersifat representatif dan dalam jumlah yang cukup agar diperoleh model yang layak untuk peramalan.

Model peramalan ini hanya efektif digunakan untuk peramalan jangka pendek dan kurang efektif untuk peramalan jangka panjang. Jika ingin meramalkan untuk waktu yang berbeda, sebaiknya model yang telah ada diperbaharui sesuai dengan data baru yang diperoleh.

26

DAFTAR PUSTAKA

Abraham, L. and Ledolter, J. 1983. Statistical Methods for Forecasting. John Wiley and Sons Inc. Canada.

Awat, N.J. 1995. Metode Statistik dan Ekonometri. Liberty. Yogyakarta.

Bowerman, B.L. and O’Connell, R.T. 1993. Forecasting and Time Series: An Applied Aproach. Duxbury Press. California.

Frain, J. 1992. Lecture Notes on Univariate Time Series Analysis and Box Jenkins Forecasting. http://www.tcd.ie/economics/staff/frainj/main/2005_ 06_MSc/Session20/UNIVAR4.pdf

Iriawan, N dan Astuti, S.P. 2006. Mengolah Data Statistik dengan Mudah Menggunakan Minitab 14. Andi. Yogyakarta.

Judge, G.G.; Hill, R.C.; Griffiths, W.E.; Lutkepohl, H. and Chao Lee, T. 1982. Introduction to the Theory and Practice of Econometrics. John Wiley and Sons Inc. New York.

Makridakis, S.; Wheelwright, S.C. dan McGee, V.E. 1999. Metode dan Aplikasi Peramalan. Jilid satu Edisi kedua. Alih Bahasa: Hari Suminto. Binarupa Aksara. Jakarta.

Supranto, J. 2000. Statistik: Teori dan Aplikasi. Jilid 1 Edisi keenam. Erlangga. Jakarta.

Ulfa, A dan Yasin, A. 2003. Model Alternatif Forecasting Deviden BUMN. Kajian Ekonomi dan Keuangan: 7(2): 37-58.

Wonnacott, T.H. and Wonnacott, R.J. 1981. Regression: A Second Course In Statistics. John Wiley and Sons Inc. New York.