BAB II MOTOR INDUKSI TIGA FASA. dengan putaran medan pada stator terdapat selisih putaran yang disebut slip.

BAB II

MOTOR INDUKSI TIGA FASA

2.1. Umum

Motor induksi merupakan motor arus bolak-balik (AC) yang paling luas digunakan dan dapat dijumpai dalam setiap aplikasi industri maupun rumah tangga. Pada motor ini putaran rotornya tidak sama dengan putaran medan stator, dengan kata lain putaran rotor dengan putaran medan pada stator terdapat selisih putaran yang disebut slip.

Motor ini memiliki konstruksi yang kuat, sederhana, handal, serta berbiaya murah. Di samping itu motor ini juga memiliki effisiensi yang tinggi saat berbeban penuh, tidak membutuhkan perawatan yang banyak dan dapat dihubungkan langsung ke sumber daya tiga fasa. Akan tetapi jika dibandingkan dengan motor DC, motor induksi masih memiliki kelemahan dalam hal pengaturan kecepatan.

Motor induksi tiga fasa sangat banyak dipakai sebagai penggerak di perindustrian karana memiliki keuntungan, tetapi ada juga kelemahannya.

Keuntungan motor induksi tiga fasa :

1. Motor induksi tiga fasa konstruksinya sangat sederhana dan kuat. 2. Mudah dioperasikan dan dapat diandalkan.

3. Motor induksi tiga fasa memiliki efisiensi yang tinggi pada kondisi kerja normal. 4. Perawatannya mudah.

Kerugiannya :

1. Kecepatan tidak bias bervariasi tanpa merubah efisiensi. 2. Kecepatan tergantung beban.

3. Pada torsi start memiliki kekurangan. 2.2. Konstruksi Motor Induksi Tiga Fasa

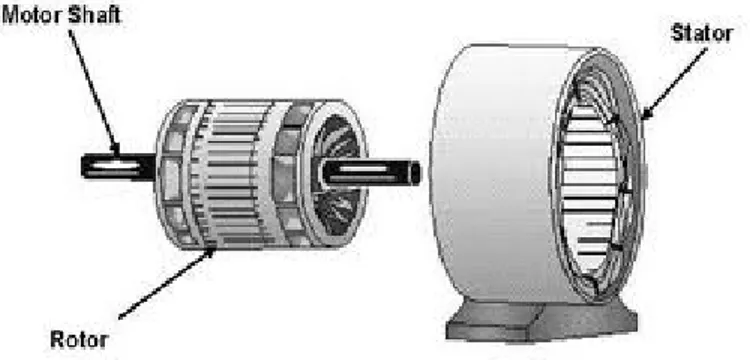
Secara umum motor induksi terdiri dari rotor dan stator. Rotor merupakan bagian yang bergerak, sedangkan stator bagian yang diam. Diantara stator dengan rotor ada celah udara (gap) yang jaraknya sangat kecil. Konstruksi motor induksi dapat diperlihatkan pada Gambar 2.1.

Gambar 2.1 Konstruksi motor induksi

Komponen stator adalah bagian terluar dari motor yang merupakan bagian

yang diam dan mengalirkan arus phasa. Stator terdiri atas susunan laminasi inti yang

memiliki alur (slot) yang menjadi tempat dudukan kumparan yang dililitkan dan

berbentuk silindris. Alur pada susunan laminasi diisolasi dengan kertas isolasi seperti

yang ditunjukkan pada gambar 2.2.(a). Tiap elemen laminasi ini dibentuk dari

lembaran besi seperti yang ditunjukkan pada gambar 2.2.(b). Tiap lembaran besi

tersebut memiliki beberapa alur dan beberapa tulang pengikat untuk menyatukan inti.

Tiap kumparan tersebar dalam alur yang disebut belitan phasa, belitan tersebut

terpisah listrik sebesar 120

0

. Kawat kumparan yang digunakan terbuat dari tembaga

yang dilapis dengan isolasi tipis (email). Kemudian susunan inti dan belitan stator

diletakkan dalam cangkang silindris seperti yang ditunjukkan pada gambar 2.2.(c).

Berikut ini contoh lempengan laminasi inti lempengan inti yang telah disatukan,

belitan stator yang telah diletakkan pada cangkang luar untuk motor induksi tiga

phasa.

(a) (b)

(c)

Gambar 2.2 Komponen stator motor induksi tiga phasa

Dimana : (a). Lempengan inti.

(b). Susunan inti dengan kertas isolasi pada beberapa alurnya.

2.3 Jenis Motor Induksi Tiga Phasa

Ada dua jenis motor induksi tiga fasa berdasarkan rotor yaitu :

1. Motor induksi tiga phasa sangkar tupai (squirrel-cage motor)

2. Motor induksi tiga phasa rotor belitan (wound-rotor motor)

Kedua motor ini bekerja pada prinsip yang sama dan mempunyai konstruksi stator yang sama tetapi berbeda dalam konstruksi rotor.

2.3.1 Motor induksi tiga phasa sangkar tupai (squirrel-cage motor)

Penampang motor sangkar tupai mempunyai konstruksi yang sederhana. Inti

stator pada motor sangkar tupai tiga phasa terbuat dari lapisan-lapisan pelat baja

beralur yang didukung dalam rangka stator yang terbuat dari besi tuang atau pelat baja

yang dipabrikasi, berikut bagian-bagian rotor sangkar dapat dilihat pada gambar 2.3.

Gambar 2.3 Bagian-bagian rotor sangkar

Batang rotor dan cincin ujung motor sangkar tupai yang lebih kecil adalah coran tembaga atau aluminium dalam satu lempeng pada inti rotor. Dalam motor yang lebih besar, batang rotor tidak dicor melainkan dibenamkan ke dalam alur rotor dan kemudian dilas dengan

kuat ke cicin ujung. Batang rotor motor sangkar tupai tidak selalu di tempatkan paralel terhadap poros motor tetapi kerapkali dimiringkan. Hal ini akan menghasilkan torsi yang lebih seragam dan juga mengurangi derau dengung magnetik sewaktu motor sedang berputar.

Pada ujung cincin penutup dilekatkan sirip yang berfungsi sebagai pendingin (kipas). Rotor jenis rotor sangkar standar tidak terisolasi, karena batangan membawa arus yang besar pada tegangan rendah.

2.3.2 Motor induksi tiga phasa rotor belitan (wound-rotor motor)

Motor rotor belitan (motor cicin slip) berbeda dengan motor sangkar tupai

dalam hal konstruksi rotornya. Seperti namanya, rotor dililit dengan lilitan terosilasi

serupa dengan lilitan stator. Lilitan phasa dihubungkan secara Bintang (Y) dan

masing-masing phasa ujung terbuka yang dikeluarkan oleh cincin slip (slip ring) yang

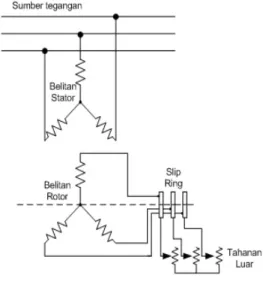
terpasang pada poros rotor. Secara sistematik dapat dilihat pada Gambar 2.4. Dari

gambar ini dapat dilihat bahwa cicin slip dan sikat semata-mata merupakan

penghubung tahanan kendali variable luar dalam rangkaian rotor.

Pada motor ini, cincin slip yang terhubung ke sebuah tahanan variable

eksternal yang berfungsi membatasi arus pengasutan dan yang bertanggung jawab

terhadap pemanasan rotor. Selama pengasutan, penambahan tahanan eksternal pada

rangkaian rotor belitan menhasilkan torsi penghasutan yang lebih besar dengan arus

pengasutan yang lebih kecil disbanding dengan rotor sangkar. Konstruksi motor tiga

phasa rotor belitan ditunjukkan pada gambar di bawah ini.

(a) (b)

Gambar 2.5

(a). Rotor belitan dengan tiga slip ring

(b). Konstruksi motor induksi tiga phasa dengan rotor belitan

2.4 Medan Putar

Apabila belitan stator dihubungkan dengan catu daya tiga fasa maka akan dihasilkan medan magnet yang berputar. Medan magnet ini dibentuk oleh kutub – kutubnya yang berada pada posisi yang tidak tetap pada stator tetapi berubah – ubah mengelilingi stator. Adapun magnitud dari medan putar ini selalu tetap yaitu sebesar 1.5 Φm dimana Φm adalah fluks yang disebabkan suatu fasa.

Untuk melihat bagaimana medan putar dibangkitkan, maka dapat diambil contoh pada motor induksi tiga fasa dengan jumlah kutub dua. Dimana ke-tiga fasanya R,S,T disuplai dengan sumber tegangan tiga fasa, dan arus pada fasa ini ditunjukkan sebagai IR, IS, dan IT, maka fluks yang dihasilkan oleh arus – arus ini adalah :

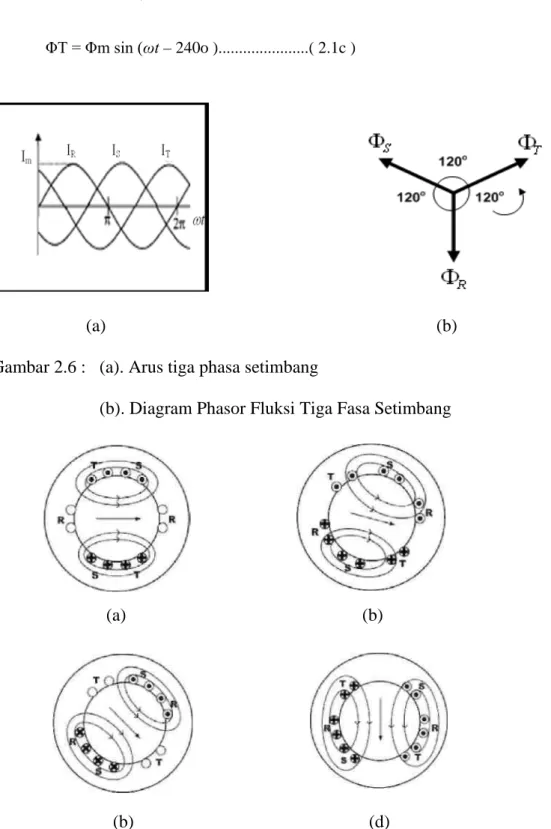
ΦR = Φm sin ωt ...( 2.1a ) ΦS = Φm sin (ωt – 120o )...( 2.1b ) ΦT = Φm sin (ωt – 240o )...( 2.1c )

(a)

(b)

Gambar 2.6 : (a). Arus tiga phasa setimbang

(b). Diagram Phasor Fluksi Tiga Fasa Setimbang

(a)

(b)

(b)

(d)

Gambar 2.7

a.

Pada keadaan 1 ( gambar 3.2 ), ωt = 0 ; arus dalam fasa R bernilai nol sedangkan

besarnya arus pada fasa S dan fasa T memiliki nilai yang sama dan arahnya

berlawanan. Dalam keadaan seperti ini arus sedang mengalir ke luar dari

konduktor sebelah atas dan memasuki konduktor sebelah bawah. Sementara

resultan fluks yang dihasilkan memiliki besar ya

ng konstan yaitu sebesar 1,5 Φm

dan dibuktikan sebagai berikut :

Φ

R

= 0 ; Φ

S

= Φm sin ( -120

O

) =

√3₂

Φm ;

ΦT = Φm sin ( -240

O

) =

√3

2

Φm

Oleh karena itu resultan fluks, Φr adalah jumlah phasor dari ΦT dan – ΦS

Sehinngga resultan fluks, Φr = 2 x

√3₂

Φm cos 30

O

_{= 1,5 Φm}

b. Pada keadaan 2, arus bernilai maksimum negatif pada fasa S, sedangkan pada R

dan fasa T bernilai 0,5 maksimum pada fasa R dan fasa T, dan pada saat ini ωt =

30o, oleh karena itu fluks yang diberikan oleh masing – masing fasa :

Φ

R

= Φm sin ( -120

o

) = 0,5 Φm

Φ

S

= Φm sin ( -90

o

) = -

Φm

Φ

T

= Φm sin (-210

o

) = 0,5 Φm

Maka jumlah phasor Φ

R

dan -

Φ

T

adalah = Φ

r

’ = 2 x 0,5 Φm cos 60 = 0,5 Φm.

Dari gambar diagram phasor tersebut dapat dilihat bahwa resultan fluks berpindah sejauh 30o dari posisi pertama.

c.

Pada keadaan ini ωt = 60

o

, arus pada fasa R dan fasa T memiliki besar yang sama

dan arahnya berlawanan ( 0,866 Φm ), oleh karena itu fluks yang diberikan oleh

masing – masing fasa :

Φ

R

= Φm sin ( 60

o

) =

√3₂

Φm

Φ

S

= Φm sin ( -60

o

) = -

√3₂

Φm

Φ

T

= Φm sin ( -180

o

) = 0

Maka magnitud dari flu

ks resultan : Φr = 2 x

√3

2

Φm cos 30

o

_{= 1,5 Φm}

Dari gambar diagram phasor tersebut dapat dilihat bahwa resultan fluks berpindah

sejauh 60

o

dari posisi pertama.

d.

Pada keadaan ini ωt = 90o, arus pada fasa R maksimum ( positif), dan arus pada fasa S dan fasa T = 0,5 Φm , oleh karena itu fluks yang diberikan oleh masing – masing fasa.

ΦR = Φm sin ( 90o_{) = Φm} ΦS = Φm sin ( -30o

) = - 0,5 Φm

Φ

T

= Φm sin (-150

o

) = -

0,5 Φm

Maka jumlah phasor -

Φ

T

dan –

Φ

S

adalah = Φr’ = 2 x 0,5 Φm cos 60 = 0,5 Φm.

Sehingga resultan fluks Φr = 0,5 Φm + Φm = 1,5 Φm.

Dari gambar diagram phasor tersebut dapat dilihat bahwa resultan fluks berpindah

sejauh 90

o

dari posisi pertama.

2.5 Slip

Slip dapat dinyatakan dalam putaran setiap menit, tetapi lebih umum

dinyatakan sebagai persen dari kecepatan sinkron.

Slip (s) =

𝑛𝑛

𝑠𝑠

−𝑛𝑛

𝑟𝑟

𝑛𝑛

𝑠𝑠

x 100 %...(2.1)

Dimana : n

r

= kecepatan rotor

Persamaan (2.2) diatas memberikan informasi sebagai berikut :

1. Saat s = 1 dimana n

r

= 0, ini berarti masih dalam keadaan diam atau akan

berputar.

2. s = 0 menyatakan bahwa n

s

= n

r

, ini berarti rotor berputar sampai kecepatan

sinkron. Hal ini dapat terjadi jika harus ada arus dc yang diinjeksikan ke

belitan rotor atau rotor digerakkan secara mekanik.

3. 0 < s < 1, ini berarti kecepatan rotor diantara keadaan diam dengan kecepatan

sinkron. Kecepatan rotor dalam keadaan inilah dikatakan tidak sinkron.

2.6 Prinsip Kerja Motor Induksi Tiga Phasa

Prinsip kerja motor induksi yaitu ;

1. Apabila sumber tegangan fasa dipasang pada kumparan stator, timbullah

medan putar dengan kecepatan

n

s

=

120 𝑓𝑓

𝑝𝑝

2. Medan putar stator tersebut akan memotong batang konduktor pada rotor.

3. Akibatnya pada kumparan timbul tegangan yang diinduksikan (ggl) sebesar

4. Karena kumparan rotor merupakan rangkaian tertutup, ggl akan menghasilkan

arus (I).

5. Adanya arus di dalam medan magnet menimbulkan gaya (F) pada rotor.

6. Bila kopel mula yang dihasilkan oleh gaya pada rotor cukup besar untuk

memikul kopel beban, rotor akan berputar searah dengan medan putar stator.

7. Perputaran rotor akan semakin meningkat hingga mendekati kecepatan

sinkron.

8. Perbedaan kecepatan antara n

r

dan n

s

disebut slip (s) dinyatakan dengan

Slip (s) =

𝑛𝑛

𝑠𝑠

−𝑛𝑛

𝑟𝑟

𝑛𝑛

_𝑠𝑠

x 100 %

Bila n

r

= n

s

tegangan tidak akan terinduksi dan arus tidak mengalir pada kumparan

jangkar rotor, dengan demikian tidak dihasilkan kopel motor, kopel motor akan

dihasilkan apabila n

r

lebih kecildari n

s.

2.6.1 Frekwensi Rotor

Ketika rotor masih dalam keadaan diam, dimana frekuensi arus pada rotor

sama seperti frekuensi masukan (sumber). Tetapi ketika rotor akan berputar, maka

frekuensi rotor akan bergantung kepada kecepatan relatif atau bergantung terhadap

besarnya slip. Untuk besar slip tertentu, maka frekuensi rotor sebesar f

’

yaitu,

n

s

- n

r

=

120𝑓𝑓 ’ 𝑃𝑃

diketahui bahwa n

s

=

120 𝑓𝑓 𝑝𝑝

dengan membagikan dengan salah satu, maka didapatkan

𝑓𝑓 ’ 𝑓𝑓

=

ns−nr

Maka f

’

= sf (Hz) ...(2.2)

Arus rotor bergantung terhadap frekuensi rotor f

’

= sf dan ketika arus ini mengalir

pada masing-masing phasa di belitan rotor, akan memberikan reaksi medan magnet.

Biasanya medan magnet pada rotor akan menghasilkan medan magnet yang berputar

yang besarnya bergantung atau relatif terhadap puataran rotor sebesar sn

s

.

Pada keadaan tertentu, arus rotor dan arus stator mengahsilkan distribusi

medan magnet yang sinusoidal dimana medan ini memiliki magnetudo yang konstan

dan kecepatan medan putar n

s

yang konstan.

2.6.2 Rangkaian Ekivalen

Untuk menentukan rangkaian ekivalen dari motor induksi tiga phasa,

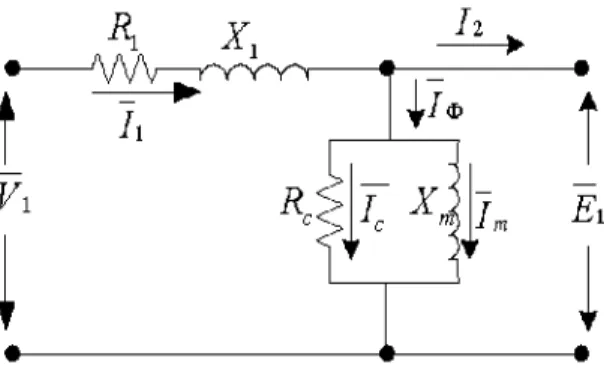
pertama-tama perhatikan keadaan stator.

Gambar 2.8 Rangkaian ekivalen stator

Besarnya tegangan terminal stator berbeda dengan ggl lawan sebesar jatuh tegangan

pada impedansi bocor stator, sehingga dinyatakan dengan persamaan

𝑉𝑉

� = 𝐸𝐸

1

��� + 𝐼𝐼

1

� ( 𝑅𝑅

1 1

+ j

𝑋𝑋

1

) Volt………..…………(2.3)

Dimana :

𝑉𝑉

����= Tegangan terminal stator (Volt)

₁

𝐸𝐸

1

����= ggl lawan yang dihasilkan oleh fluksi celah udara resultan (Volt)

𝐼𝐼𝐼𝐼� = arus stator (Ampere)

R

1

= resistansi efektif stator (Ohm)

X

1

= reaktansi bocor stator (Ohm)

Kedua perhatikan rangkaian ekivalen pada rotor sebagai berikut :

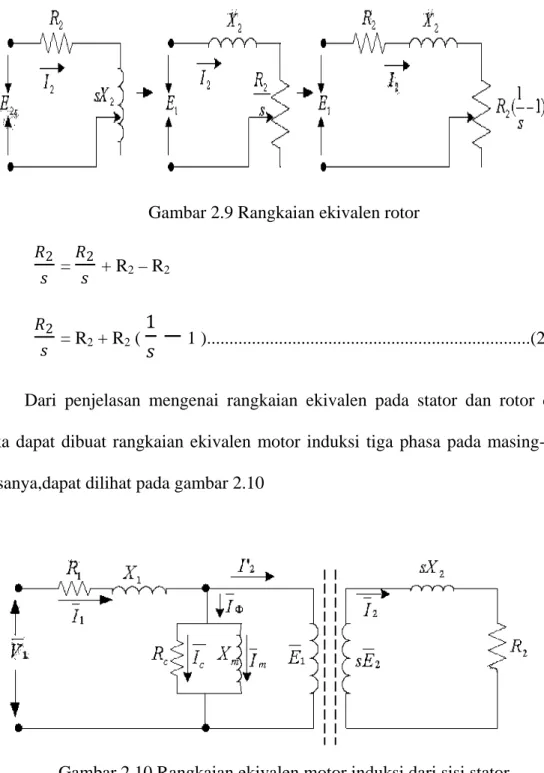
Gambar 2.9 Rangkaian ekivalen rotor

𝑅𝑅2 𝑠𝑠

=

𝑅𝑅2 𝑠𝑠

+ R

2

– R

2 𝑅𝑅2 𝑠𝑠

= R

2

+ R

2

(

1

𝑠𝑠

−

1 )...(2.4)

Dari penjelasan mengenai rangkaian ekivalen pada stator dan rotor di atas,

maka dapat dibuat rangkaian ekivalen motor induksi tiga phasa pada masing-masing

phasanya,dapat dilihat pada gambar 2.10

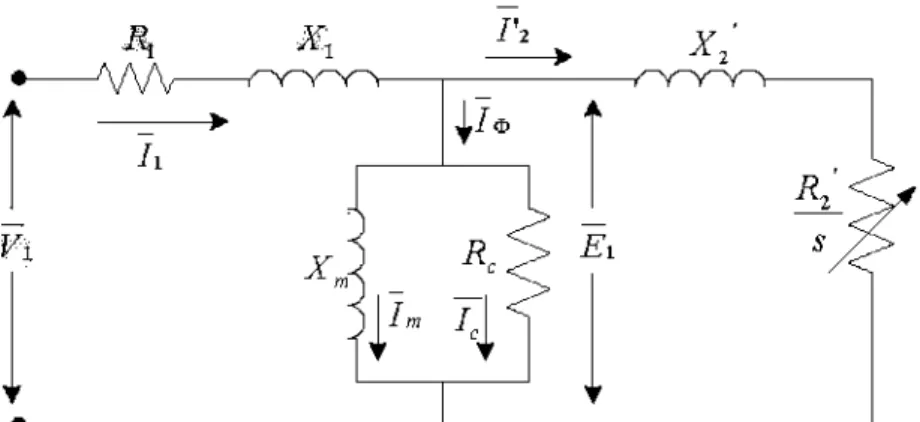
Untuk mempermudah perhitungan maka rangkaian ekivalen pada gambar 2.10 diatas

dapat dilihat dari sisi stator,rangkaian ekivalen motor induksi tiga phasa akan dapat

digambarkan sebagai berikut :

Gambar 2.11 Rangkaian ekivalen pendekatan motor induksi

Atau seperti gambar berikut :

Gambar 2.12 Rangkaian ekivalen motor induksi tiga phasa

Dimana :

X’

2

=

𝑎𝑎

2

X

2

R’

2

=

𝑎𝑎

2

R

2

Suatu persamaan torsi pada motor induksi dapat dihasilkan dengan bantuan teori rangkaian thevenin. Dalam bentuk umumnya, teorema thevenin mengijinkan penggantian sembarang jaringan yang terdiri atas undur-unsur rangkaian linier dan sumber tegangan fasor tetap. Rangkaian rotor direferensikan terhadap stator. Misalkan 𝑉𝑉₁ tegangan input motor, dengan melihat dari sisi terminal a-b,dapat dicari tegangan theveninnya.Perhatikan gambar berikut ini :

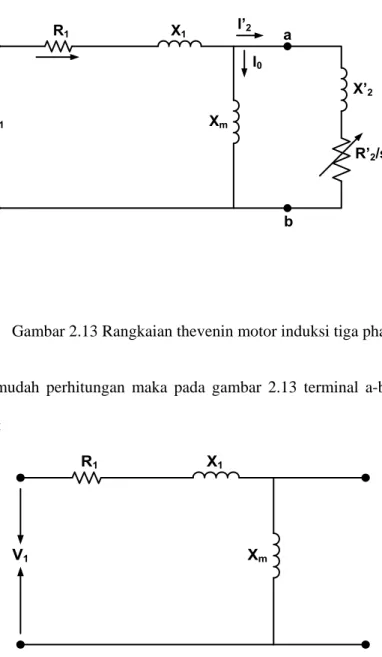
Gambar 2.13 Rangkaian thevenin motor induksi tiga phasa

Untuk mempermudah perhitungan maka pada gambar 2.13 terminal a-b dibuka. Perhatikan gambar berikut :

Gamabar 2.14 Rangkaian thevenin setelah terminal a-b dibuka

R1 I0 I’2 X1 Xm X’2 R’2/s V1 b a R1 X1 Xm V1

Dari Gambar 2.14 dapat dihitung tegangan thevenin (VTh)

𝑉𝑉

𝑇𝑇ℎ

=

𝑉𝑉

1

�

_{𝑅𝑅1+𝑗𝑗 (𝑋𝑋}𝑗𝑗 𝑋𝑋₁𝑚𝑚_{+ 𝑋𝑋𝑚𝑚 )}

�

(Volt)………..……….(2.5)

𝑍𝑍

𝑇𝑇ℎ

=

𝑅𝑅

𝑒𝑒

+

𝑗𝑗𝑋𝑋

𝑒𝑒

=

_𝑅𝑅𝑗𝑗𝑋𝑋₁𝑚𝑚_{+ 𝑗𝑗 (𝑋𝑋} (𝑅𝑅1 ₁+ 𝑗𝑗𝑋𝑋_{+𝑋𝑋𝑚𝑚}1 ₎) (Ohm)………..………(2.6)

Rangkaian ekivalen pada Gambar 2.14 berubah menjadi seperti Gambar 2.15 berikut

Gambar 2.15 Rangkaian ekivalen motor induksi tiga phasa

Dengan demikian 𝐼𝐼₂ dapat dihitung dengan persamaan :

𝐼𝐼2 = 𝑉𝑉𝑇𝑇ℎ

𝑅𝑅𝑒𝑒+𝑅𝑅′2_𝑠𝑠 + 𝑗𝑗 (𝑋𝑋𝑒𝑒+ 𝑋𝑋′2)

(Ampere)…………..……...(2.7)

Torsi (𝜏𝜏_𝑑𝑑) dapat juga dihitung dengan persamaan :

𝜏𝜏

𝑑𝑑

=

_𝜔𝜔𝑃𝑃𝑔𝑔_𝑠𝑠

=

_𝜔𝜔1_𝑠𝑠

𝑥𝑥 3𝐼𝐼′

2 2𝑅𝑅′2_𝑠𝑠 (Nm)………..………..(2.8)

Subsitusikan persamaan (2.7) diatas ke persamaan (2.8), maka didapat :

𝜏𝜏

𝑑𝑑

=

_𝜔𝜔3 𝑠𝑠

𝑉𝑉𝑇𝑇ℎ2 (𝑅𝑅′2 _𝑠𝑠 )

[(𝑅𝑅𝑒𝑒 +𝑅𝑅′2_𝑠𝑠 )2+ (𝑋𝑋𝑒𝑒+ 𝑋𝑋′2 )2 ]

Pada keadaan motor bekerja normal, rotor berputar pada arah putaran medan magnetic yang dihasilkan oleh arus stator, kecepatannya diantara nol sampai kecepatan serempak, dan slipnya diantara nol dengan satu.

2.7.1 Torsi Awal (Torsi start)

Pada saat pengasutan, ketika motor dalam keadaan diam, besar slipnta adalah satu, dan daya mekanis bernilai nol, torsi pengasutan didapat dengan mensubsitusikan besar s = 1 kepersamaan (2.9), maka didapat,

𝜏𝜏

𝑠𝑠𝑠𝑠𝑎𝑎𝑟𝑟𝑠𝑠 = 3 𝜔𝜔𝑠𝑠

𝑉𝑉_{𝑇𝑇ℎ 2𝑅𝑅2}

[(𝑅𝑅𝑒𝑒+ 𝑅𝑅′2 )2 (𝑋𝑋𝑒𝑒 + 𝑋𝑋′2 )2 ] (Nm)………..…….…(2.10)

Torsi awal (torsi start) 𝜏𝜏_{𝑠𝑠𝑠𝑠𝑎𝑎𝑟𝑟𝑠𝑠} besarnya dapat diatur (diubah) besarnya dengan menggunakan tahanan variable dari luar yang dihubungkan secara seri ke kumparan rotor melalui sikat ( pada motor induksi tiga fasa rotor belitan). Untuk mendapatkan torsi awal yang maksimum, maka tahanan rotor harus dinaikkan sampai �𝑅𝑅_𝑒𝑒2+ (𝑋𝑋_𝑒𝑒+ 𝑋𝑋′₂ ) , sehubungan dengan persamaan (2.9) yaitu 𝑆𝑆_{𝜏𝜏 𝑚𝑚𝑎𝑎𝑥𝑥} = 𝑅𝑅2

�(𝑅𝑅𝑒𝑒2+ (𝑋𝑋𝑒𝑒+ 𝑋𝑋′2 )2

dimana 𝑠𝑠𝜏𝜏 𝑚𝑚𝑎𝑎𝑥𝑥 = 1,0, nilai tahanan rotor

yang diperlukan akan didapat dengan menambahkan tahanan luar kekumparan rotor sebesar �𝑅𝑅𝑒𝑒 2 + (𝑋𝑋𝑒𝑒+ 𝑋𝑋′2 )2 - 𝑅𝑅2, sehingga didapatkan torsi yang maksimum.

2.7.2 Torsi Maksimum

Dari persamaan (2.4),torsi maksimum terjadi ketika daya celah udara bernilai maksimum. Karna daya celah udara sebanding dengan daya yang terpakai pada tahanan 𝑅𝑅′₂/𝑠𝑠 maka torsi induksi maksimum terjadi ketika daya yang dikonsumsi tahanan tersebut maksimum. Dengan berprinsip pada penyesuaian impedansi dalam teori rangkaian, daya

tersebut akan merupakan yang terbesar bila impedansi 𝑅𝑅′2

𝑠𝑠 sama dengan besar impedansi diantaranya dan tegangan 𝑉𝑉_𝑇𝑇ℎ, atau pada harga 𝑠𝑠_{𝜏𝜏 𝑚𝑚𝑎𝑎𝑥𝑥} slip yang mempunyai hubungan.

𝑅𝑅′2

𝑠𝑠𝜏𝜏 𝑚𝑚𝑎𝑎𝑥𝑥 = �(𝑅𝑅𝑒𝑒 2 _{+ (𝑋𝑋}

𝑒𝑒+ 𝑋𝑋′2 )2) ………..…..(2.11)

Dari sini didapat besar slip pada saat torsi maksimum 𝑠𝑠_{𝜏𝜏𝑚𝑚𝑎𝑎𝑥𝑥} adalah :

𝑠𝑠

𝜏𝜏𝑚𝑚𝑎𝑎𝑥𝑥

=

_�𝑅𝑅 𝑅𝑅′2

𝑒𝑒 2 +(𝑋𝑋𝑒𝑒 + 𝑋𝑋′2 )2) ………....……..(2.12)

Besar torsi maksimum didapat dengan mensubsitusikan slip pada torsi maksimum pada persamaan (2.12), persamaan besar torsi maksimumnya didapat :

𝜏𝜏

𝑚𝑚𝑎𝑎𝑥𝑥

=

3𝑉𝑉𝑇𝑇ℎ

2

2𝜔𝜔𝑠𝑠 [𝑅𝑅𝑒𝑒 + �𝑅𝑅𝑒𝑒2 + (𝑋𝑋𝑒𝑒 + 𝑋𝑋′2 )2 ]

(Nm)………(2.13)

Persamaan (2.12) menunjukkan bahwa slip yang terjadi saat torsi maksimum sangat bergantung pada besarnya harga 𝑅𝑅′₂, tetapi pada persamaan (2.13) yang mana persamaan ini mengindikasikan bahwa torsi maksimum 𝜏𝜏_{𝑚𝑚𝑎𝑎𝑥𝑥} tidak ada hubungan dengan 𝑅𝑅′₂. Maksudn dari hal ini bahwa jika 𝑅𝑅′₂ ditambah besarnya dengan menggunakan tahanan luar yang terhubung seri dengan kumparan rotor pada motor induksi jenis rotor belitan, besar torsi maksimum yang dihasilkan tidak berpengaruh. Sekarang yang berpengaruh terhadap torsi maksimum adalah tegangan masukan pada kumparan stator 𝑉𝑉₁, 𝑅𝑅_𝑒𝑒 yang sebanding denan tahanan kepada kumparan stator (𝑅𝑅₁), induktansi pada kumparan rotor (𝑋𝑋′₂) dan 𝑋𝑋_𝑒𝑒 yang sama sebanding dengan induktansi kumparan stator (𝑋𝑋₁). Dalam tinjauan yang sebenarnya, persamaan (2.13) menunjukkan bahwa :

1. 𝜏𝜏_{𝑚𝑚𝑎𝑎𝑥𝑥} sebanding dengan besarnya tegangan masuk (input) pada stator. 2. 𝜏𝜏_{𝑚𝑚𝑎𝑎𝑥𝑥} dipengaruhi oleh besarnya tahanan stator (𝑅𝑅₁).

3. 𝜏𝜏_{𝑚𝑚𝑎𝑎𝑥𝑥} dipengaruhi oleh dua induktansi,yaitu induktansi pada kumparan stator (𝑋𝑋₁) dan induktansi pada kumparan rotor (𝑋𝑋′₂).

2.7.3 Torsi beban Penuh

Telah diketahui bahwa persamaan untuk mendapat nilai torsi yaitu:

𝜏𝜏

𝑑𝑑

=

_𝜔𝜔3_𝑠𝑠 𝑉𝑉𝑇𝑇ℎ 2 ₍𝑅𝑅′2

𝑠𝑠 )

[(𝑅𝑅𝑒𝑒+ 𝑅𝑅′2_𝑠𝑠 )2 +(𝑋𝑋𝑒𝑒 + 𝑋𝑋′2 )2 ]

(Nm)………...…(2.14)

Pada saat motor berbeban penuh (full-load), motor berputar dengan kecepatan 𝑛𝑛_{𝑓𝑓𝑓𝑓} (kecepatan dengan beban penuh). Maka akan dihasilkan slip pada beban penuh (𝑠𝑠_{𝑓𝑓𝑓𝑓}) sebesar ;

𝑠𝑠

𝑠𝑠𝑠𝑠

=

𝑠𝑠𝑠𝑠− 𝑠𝑠_𝑠𝑠 𝑠𝑠𝑠𝑠𝑠𝑠 𝑠𝑠

Dengan menggunakan persamaan (2.14) dimana s digantikan dengan 𝑠𝑠_{𝑠𝑠𝑠𝑠}, maka didapat torsi pada saat beban penuh 𝑠𝑠_{𝑠𝑠𝑠𝑠} sebesar :

𝑠𝑠

_{𝑠𝑠𝑠𝑠}

=

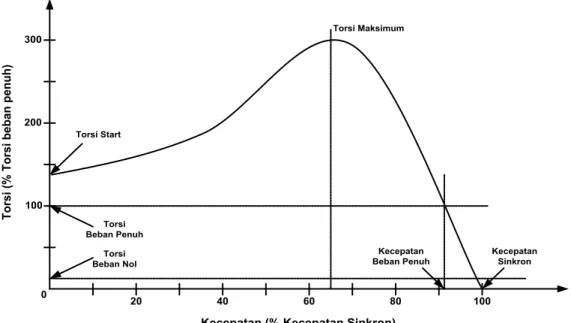
_𝑠𝑠3 𝑠𝑠 𝑠𝑠𝑠𝑠ℎ2 (𝑠𝑠 ′ 2 𝑠𝑠𝑠𝑠𝑠𝑠) [(𝑠𝑠𝑠𝑠+ 𝑠𝑠 ′ 2 𝑠𝑠𝑠𝑠𝑠𝑠)2+ (𝑠𝑠𝑠𝑠 + 𝑠𝑠′2 )2] (Nm)……….…….(2.15)

Gambar 2.16 Kurva torsi beban penuh terhadap kecepatan sinkron motor induksi

Kurva torsi kecepatan tipikal motor induksi ditujukkan pada Gambar 2.16 karakteristik penting yang terdapat dalam kurva tersebut adalah kurva torsi kecepatan. Dari gambar tersebut dapat dijabarkan :

 Jangkauan motor meliputi slip yang berada di 0<s<1. Kecepatan putaran antara diam daya mekanis keluaran (s=1) sampai kecepatan sinkron (s=0), dan putaran memiliki arah yang sama dengan putaran medan magnetic. Mesin menjadi motor ditandai dengan daya mekanis keluaran yang bernilai positif.

 Kurva torsi-kecepatan hampir mendekati linier antara keadaan beban nol dengan keadaan beban penuh. Pada daerah ini tahanana rotor jauh lebih besardibanding reaksi rotor, sehingga arus rotor, medan magnetik rotor dan torsi meningkat linier seiring dengan naiknya slip.

 Ada titik maksimum torsi yang terjadi ketika kenaikan putaran tidak lagi menaikkan besar torsi. Titik ini disebut sabagai titik torsi maksimum yang mampu dihasilkan motor. 20 0 300 200 100 100 80 60 40 Torsi Maksimum Torsi Start Torsi Beban Penuh Torsi Beban Nol Kecepatan

Beban Penuh KecepatanSinkron

Kecepatan (% Kecepatan Sinkron)

Torsi pengasutan motor lebih besar disbanding torsi beban penuh motor.

2.7.4

Torsi pada motor induksi motor belitan

Pada motor ini, terdiri atas belitan fasa bnyak, belitan ini dimasukkan ke dalam

alur-alur inti besi rotor. Belitan ini sama seperti belitan stator biasanya/selalu

merupakan belitan tiga fasa yang dihubungkan secara hubungan bintang (Y) dan

masing-masing phasa ujung terbuka dikeluarkan oleh cicin slip (slip ring) yang

terpasang pada rotor. Pada motor ini,cincin slip yang terhubung ketahanan variable

eksternal yang berfungsi membatasi arus penghasutan dan yang bertanggung jawab

terhadap pemanasan rotor. Selama penghasutan,penambahan tahanan eksternal pada

rangkaian rotor belitan menghasilkan torsi penghasutan yang lebih besar dengan arus

penghasutan yang lebih kecil dibandingkan dengan rotor sangkar.

Hubungan antara torsi dan slip untuk motor induksi dengan adanya penambahan tahanan luar pada belitan rotor ditunjukkan oleh gambar berikut. Untuk kurva torsi beban seperti yang ada pada gambar,dengan kecepatan 𝑠𝑠1 pada tahanan rotor sebesar 𝑠𝑠2, kecepatan yang dihasilkan 𝑠𝑠2 pada tahanan rotor 𝑠𝑠′2. dimana 𝑠𝑠′2>𝑠𝑠2 dan seterusnya.

Torsi awal (torsi start) besarnya dapat diatur (diubah) besarnya dengan menggunakan varibel dari luar ( Rluar ) yang dihubungkan seri ke kumparan rotor melalui sikat ( pada motor induksi tiga fasa rotor belitan ).

𝑠𝑠

_{𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠} = 3

𝑠𝑠

_𝑠𝑠

𝑠𝑠

_{𝑠𝑠ℎ 2(𝑠𝑠} 2+𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠) [(

𝑠𝑠

_𝑠𝑠+

𝑠𝑠

′2)2 (

𝑠𝑠

𝑠𝑠 +

𝑠𝑠

′2 )2 ] (Nm)………..(2.16)

Dari gambar diatas, kita dapat menyimpulkan untuk motor induksi rotor belitan bahwa:

1. Kecepatan motor dapat diatur dengan variasi tahanan rotor tetapi torsi maksimum tidak dapat dipengaruhi.

2. Torsi awal motor induksi dapat dipengaruhi dengan merubah-ubah besar tahanan rotor.

3. Arus awal dapat diperkecil dengan mengubah-ubah tahan rotor.

4. Factor daya motor pada saat start dapat diperbaiki dengan tahanan rotor.

2.8 Aliran Daya Pada Motor Induksi

Pada motor induksi, tidak ada sumber listrik yang langsung terhubung ke rotor,

sehingga daya yang melewati celah udara sama dengan daya yang dimasukkan ke

rotor. Daya total yang dimasukkan pada kumparan stator (P

in

) dirumuskan dengan

P

in

= 3V

1

I

1

cos

𝑠𝑠

Dimana :

V

1

= Tegangan sumber (Volt)

I

1

= Arus masukan (Ampere)

Torsi (Nm) r2'’’ ns n1 n2 n3 n4 r2'’ r2' r2 Tbeban Kurva Torsi beban Torsi maksimun

𝑠𝑠

= Perbedaan sudut phasa antara arus masukan dengan tegangan sumber

Sebelum daya ditransfer melalui celah udara, motor induksi mengalami

rugi-rugi berupa rugi-rugi-rugi-rugi tembaga stator (P

SCL

) dan rugi-rugi inti stator (P

C

). Daya yang di

transfer melalui celah udara (P

AG

) sama dengan penjumlahan rugi-rugi tembaga rotor

(P

RCL

) dan daya yang dikonversi (P

conv

). Daya yang melalui celah udara ini sering juga

disebut sebagai daya input rotor.

P

AG

= P

RCL

+ P

conv

(Watt)...(2.17)

= 3(I’

2

)

2

𝑠𝑠

′2

𝑠𝑠

= 3(I’

2

)

2

R’

2

+ 3(I’

2

)

2

R’

2 (1−

𝑠𝑠

)

𝑠𝑠

...(2.18)

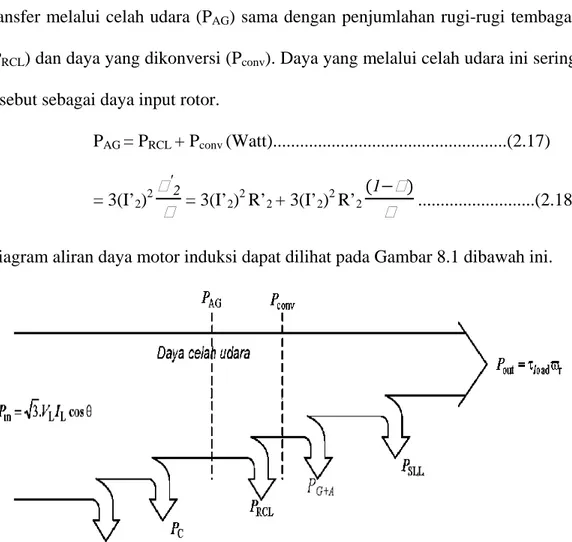
Diagram aliran daya motor induksi dapat dilihat pada Gambar 8.1 dibawah ini.

Gambar 2.17 Aliran daya motor induksi

Dimana :

- PSCL = rugi - rugi tembaga pada belitan stator (Watt)

- Pc = rugi - rugi inti pada stator (Watt)

- PRCL = rugi — rugi tembaga pada belitan rotor (Watt)

- PG+A = rugi - rugi gesek + angin (Watt)

- PSLL = stray losses (Watt)

- P

CONV

= daya mekanis keluaran (output) (Watt)

Hubungan antara rugi-rugi tembaga rotor dan daya mekanis dengan daya masukan

rotor dinyatakan dengan persamaan sebagai berikut :

P

RCL

= 3 (I’

2

)

2

R’

2

= sP

AG

(watt)...(2.19)

P

conv

= 3 (I’

2

)

2

(1−

𝑠𝑠

)

𝑠𝑠

R’

2

= (1 – s) sP

AG

(watt)...(2.20)

Dari gambar 8.1 dapat dilihat bahwa motor induksi juga mengalami rugi-rugi

gesek + angin (P

G+A

), sehingga daya mekanis keluaran sama dengan daya yang

dikonversi (P

CONV

) dikurangi rugi-rugi gesek + angin.

P

out

= P

conv

– P

G+A

Secara umum, perbandingan komponen daya pada motor induksi dapat dijabarkan

dalam bentuk slip yaitu

P

AG

: P

RCL

: P

conv

= 1 : s : 1 – s

2.9 Efisiensi

Efisiensi motor induksi adalah perbandingan antara daya masukan dan daya

keluaran. Sering dinyatakan dengan perbandingan antara masukan dengan keluaran

ditambah rugi-rugi, yang dirumuskan dalam persamaan (2.21)

Ƞ =

𝑠𝑠

_𝑠𝑠

𝑠𝑠𝑠𝑠𝑠𝑠 𝑠𝑠𝑠𝑠

=

𝑠𝑠

_{𝑠𝑠𝑠𝑠𝑠𝑠}−

𝑠𝑠

_{𝑠𝑠𝑠𝑠}

𝑠𝑠𝑠𝑠𝑠𝑠

=

𝑠𝑠

_{𝑠𝑠𝑠𝑠𝑠𝑠}

𝑠𝑠

𝑠𝑠𝑠𝑠𝑠𝑠+

𝑠𝑠

𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠

x 100

%...(2.21)

Pada motor induksi pengukuran efisiensi motor induksi ini sering dilakukan

dengan beberapa cara seperti :

− Mengukur langsung daya elektris masukan dan daya mekanis keluaran

− Mengukur langsung seluruh rugi-rugi dan daya masukan

− Mengukur setiap komponen rugi-rugi dan daya masukan

2.10 Desain Motor Induksi Tiga Phasa

Motor asinkron yang sering kita temukan sehari-hari misalnya adalah : kipas angin, mesin pendingin, kereta api listrik gantung, dan lain sebagainya. Untuk itu perlu diketahui kelas-kelas dari motor untuk mengetahui unjuk kerja dari motor tersebut. Adapun kelas-kelas tersebut adalah sebagai berikut :

1. Kelas A : Torsi start normal, arus start normal dan slip kecil

Tipe ini umumnya memiliki tahanan rotor sangkar yang rendah. Slip pada beban penuh kecil atau rendah namun efesiansinya tinggi. Torsi maksimum biasanya sekitar 21% dari torsi beban penuh dan slipnya kurang dari 20% motor kelas ini berkisar hingga 20 Hp.

2. Kelas B : Torsi start normal, arus start kecil dan slip rendah

Torsi start kelas ini hamper sama dengan kelas A tetapi arus startnya berkisar 75%𝑠𝑠_{𝑠𝑠𝑠𝑠}. Slip dan efesiensi pada beban penuh juga baik. Kelas ini umumnya berkisar antara 7,5 Hp sampai dengan 200 Hp. Penggunaan motor ini antara lain : kipas angin, boiler, pompa dan lainya.

3. Kelas C : Torsi Start tinggi dan arus Start kecil

Kelas ini memiliki resistansi rotor sangkar yang ganda yang lebih besar dibandingkan dengan kelas B. oleh sebab itu dihasilkan torsi start yang lebih tinggi pada arus start yang rendah, namun bekerja pada efisiensi dan slip yang rendah dibandingkan kelas A dan B.

4. Kelas D : torsi start tinggi,slip tinggi

Kelas ini biasanya memiliki resistansi rotor sangkar tunggal yang tinggi sehingga dihasilkan torsi start yang tinggi pada arus start yang rendah

Sebagai bahan tambahan pada keempat kelas tersebut diatas, NEMA juga memperkenalkan desain kelas E dan F, yang sering disebut motor induksi soft-start, namun disain kelas ini sekarang sudah ditinggalkan.

2.11 Parameter Motor Induksi Tiga Fasa

Parameter rangkaian ekivalen dapat dicari dengan melakukan pengukuran pada

percobaan tahanan DC, percobaan beban nol, dan percobaan rotor tertahan

(block-rotor). Dengan penelitian pada setiap rangkaian ekivalen, percobaan beban nol dapat

dibuat dengan memaksimalkan tahanan rotor

𝑠𝑠

2

′

𝑠𝑠

.

Hal ini bisa terjadi dalam keadaan

normal jika slip dalam nilai yang minimum. Slip yang mendekati nol terjadi ketika

tidak ada beban mekanis, dan mesin dikatakan dalam keadaan berbeban ringan.

Pengukuran rotor blok dilakukan dengan menahan rotor tetap dalam keadaan diam.

Pada kondisi ini slip bernilai satu yang merupakan nilai slip tertinggi, jadi nilai

𝑠𝑠

2 ′

𝑠𝑠

bernilai minimum. Untuk menentukan bentuk rangkaian ekivalen, pola fluksi dianggap

sinusoidal, demikian juga rugi-rugi yang diukur proporsional terhadap fluksi utama

dan kejenuhan diabaikan.

2.11.1 Parameter percobaan DC

Untuk memperoleh harga R

1

dilakukan dengan pengukuran DC yaitu dengan

menghubungkan sumber tegangan dc (V

dc

) pada dua terminal input dan arus DC nya

(I

dc

) lalu diukur. Disini tidak mengalir arus rotor karena tidak ada tegangan yang

terinduksi.

2.11.1.1

Kumparan hubungan bintang (Y)

Gambar rangkaian ketika kumparan motor induksi tiga fasa terhubung bintang

dan diberi suplai dc dapat dilihat pada Gambar 2.18 dibawah ini.

Gambar 3.1 Rangkaian phasa stator saat pengukuran DC

Harga R1dc dapat dihitung, untuk kumparan dengan hubungan Y, adalah sebagai

berikut :

R1dc =

1

2

𝑠𝑠𝑠𝑠𝑠𝑠

𝑠𝑠𝑠𝑠𝑠𝑠

(Ohm) ...(2.22)

2.11.1.2 Kumparan Hubungan Delta (∆)

Gambar rangkaian ketika kumparan motor induksi tiga pasa terhubung delta dan

diberi suplai dc, dapat dilihat pada gambar 2.19 dibawah ini :

Gambar 2.19.a Rangkaian kumparan motor induksi tiga phasa terhubung delta

Diketahui bahwa tahanan pada kumparan pada masing-masing Phasa adalah sama

maka

𝑠𝑠

_𝑠𝑠

=

𝑠𝑠

_𝑠𝑠

=

𝑠𝑠

_𝑠𝑠

= R. jadi gambar diatas dapat disderhanakan menjadi gambar

berikut :

Gambar 2.19.b Rangkaian kumparan motor induksi yang di sederhanakan Dimana RP = RB + RC Jadi RA =

𝑠𝑠

𝑠𝑠𝑠𝑠

𝑠𝑠

_𝑠𝑠 Dimana IA = Idc x

𝑠𝑠

𝑠𝑠

𝑠𝑠

_𝑠𝑠+

𝑠𝑠

_𝑠𝑠 RA RP IDC IA

IA = 2 3 Idc Maka RAdc = ₂

𝑠𝑠

𝑠𝑠𝑠𝑠 3

𝑠𝑠

𝑠𝑠𝑠𝑠 = 3 2

×

𝑠𝑠

_{𝑠𝑠𝑠𝑠}

𝑠𝑠

_{𝑠𝑠𝑠𝑠}

Harga 𝑠𝑠1 ini dinaikkan dengan factor pengali 1,1 – 1,5 untuk operasi harus bolak-balik,karena

pada operasi arus bolak-balik resistansi konduktor meningkat karena distribusi arus yang tidak merata dan medan magnet yang melintasi alur.

𝑠𝑠1𝑠𝑠𝑠𝑠 = k x 𝑠𝑠1𝑠𝑠𝑠𝑠 (Ohm)………...……(2.23)

Dimana k = factor pengali, besarnya 1,1 – 1,5

Karna besaran tahanan konduktor stator dipengaruhi oleh suhu, dan biasanya bila rugi-rugi motor ditentukan dengan pengukuran langsung pada motor, maka untuk mengetahui nilai tahanan yang paling mendekati, biasanya dilakukan dengan beberapa kali pengukuran dan mengambil besar rata-rata dari semua pengukuran yang dilakukan.

2.11.2 Parameter Percobaan beban Nol

Motor induksi dalam keadaan beban nol dibuat dalam keadaan berputar tanpa memikul beban pada ranting tegangan dan frekuensinya. Besar tegangan yang digunakan ke belitan stator perphasanya adalah 𝑠𝑠1 (tegangan Nominal), arus masukan sebesar 𝑠𝑠0 dan

dayanya 𝑠𝑠0. Nilai inoi semua didapat dengan melihat alat ukur pada saat percobaan beban nol.

Dalam percobaan beban nol, kecepatan motor induksi mendekati kecepatan sikronya. Dimana besar s→0, sehingga

𝑠𝑠

2

𝑠𝑠

→~ sehingga besar impendasi total bernilai tak berhingga yang

menyebabkan arus 𝑠𝑠′2 bernilai nol sehingga rangkaian ekivalen motor induksi pada

kecepatan motor pada pengukuran ini 𝑠𝑠_𝑠𝑠0 yang diperoleh tidak sama dengan 𝑠𝑠𝑠𝑠 maka slip

tidak sama dengan nol sehingga ada arus 𝑠𝑠2 yang sangat kecil mengalir pada rangkaian rotor,

arus 𝑠𝑠′₂ tidak diabaikan tetapi digunakan untuk menghitung rugi gesek + angin dan rugi-rugi inti pada percobaan beban nol. Pada pengukuran ini didapat rata-rata antara lainarus input (𝑠𝑠1 = 𝑠𝑠0 ), tegangan input (𝑠𝑠1= 𝑠𝑠0), daya input perphasa (𝑠𝑠0) dan kecepatan poros motor

(𝑠𝑠_𝑠𝑠0). Frekuensi yang digunakan untuk eksitansi adalah frekuensi sumber f.

Gambar 2.20 Rangkaian ekivalen pada saat beban nol

Dengan tidak adanya beban mekanis yang terhubung ke rotor dan tegangan normal diberikan ke terminal, dari gambar 2.20 didapat besar sudut phasa antara arus antara 𝑠𝑠0 dan 𝑠𝑠0 adalah :

ϴo = Cos-1

�

𝑠𝑠

0

𝑠𝑠

0

𝑠𝑠

0

�

………...…(2.24)

Dimana : P0 = Pnl = Daya saat beban nol perphasa V0 = V1 = Tegangan masukan saat beban nol I0 = Inl = Arus beban nol

Dengan P0 daya input perphasa. Sehingga beasr E1 dapat dinyatakan dengan E1 = V1<00 – (Iφ<00) (R1+jX1) (Volt) ………..………..(2.25)

𝑠𝑠𝑠𝑠𝑠𝑠 Adalah kecepatan rotor pada saat beban nol. Daya yang disisipkan oleh 𝑠𝑠_𝑠𝑠 dinyatakan dengan :

Pc = P0 – I20R1 (Watt) ………(2.26) 𝑠𝑠1 Didapat pada saat percobaan dengan tegangan DC.

Harga 𝑠𝑠_𝑠𝑠 dapat ditentukan dengan :

R1 =

𝑠𝑠

1

2

𝑠𝑠

0

(Ohm) ………...……(2.27)

Dalam keadaan yang sebenarnya 𝑠𝑠1lebih kecil jika dibandingkan dengan 𝑠𝑠𝑠𝑠 dan juga 𝑠𝑠𝑠𝑠

jauh lebih besar dari 𝑠𝑠_𝑠𝑠, sehingga impedansi yang didapat dari percobaan beban nol dianggap 𝑠𝑠𝑠𝑠1 dan 𝑠𝑠𝑠𝑠𝑠𝑠 yang diserikan.

|Znl| =

𝑠𝑠

1

𝑠𝑠

_{𝑠𝑠𝑠𝑠√3} ≈ j(X1 + Xm) (Ohm)………...……..…(2.28)

Sehingga didapat

Xm = 𝑠𝑠1

𝑠𝑠_{𝑠𝑠𝑠𝑠√3}

−

𝑠𝑠

1 (Ohm) ……….……..…..(2.29)

2.11.3 Parameter percobaan blok rotor

Pada pengukuran ini rotor dipaksa tidak berputar (𝑠𝑠_𝑠𝑠 = 0, sehingga s = 1) dan kumparan stator dihubungkan dengan tegangan seimbang. Karna slip s = 1, maka pada gambar 2.20 harga 𝑠𝑠_𝑠𝑠2 = 𝑠𝑠2, karena │𝑠𝑠′2 + 𝑠𝑠𝑠𝑠′2│<<│𝑠𝑠𝑠𝑠 ║𝑠𝑠𝑠𝑠𝑠𝑠│maka arus yang melewati │𝑠𝑠𝑠𝑠

motor induksi dalam keadaan rotor tertahan atau hubung singkat seperti ditujukan pada gambar 2.21.

Gamabar 2.21 Rangkaian ekivalen pada saat rotor tertahan (s = 1)

Impedansi perphasa pada saat rotor tertahan (𝑠𝑠_{𝑠𝑠𝑠𝑠}) dapat dirumuskan sebagai berikut : 𝑠𝑠𝑠𝑠𝑠𝑠 = 𝑠𝑠₁ + 𝑠𝑠₂ + j(𝑠𝑠₁ + 𝑠𝑠₂ ) = 𝑠𝑠_{𝑠𝑠𝑠𝑠} + j𝑠𝑠_{𝑠𝑠𝑠𝑠} (Ohm)………..….………(2.30)

Pengukuran ini dilakukan pada arus mendekati arus rating motor. Data hasil pengukuran ini meliputi : arus input (𝑠𝑠1 = 𝑠𝑠𝑠𝑠𝑠𝑠 ), tegangan input (𝑠𝑠1 = 𝑠𝑠𝑠𝑠𝑠𝑠 ) dan aya input

perphasa (𝑠𝑠_{𝑠𝑠𝑠𝑠} = 𝑠𝑠_{𝑠𝑠𝑠𝑠}), karena adanya distribusi arus yang tidak merata pada batang rotor akibat efek kulit, harga 𝑠𝑠′₂ menjadi tergantung frekuensi, maka umumnya dalam praktek, pengukuran rotor tertahan dilakukan dengan mengurangi frekuensi eksitasi menjadi 𝑠𝑠_{𝑠𝑠𝑠𝑠} untuk mendapatkan harga 𝑠𝑠′2 yang sesuai dengan frekuensi rotor pada saat slip rating. Dari

data-data tersebut, harga 𝑠𝑠_{𝑠𝑠𝑠𝑠} dan 𝑠𝑠_{𝑠𝑠𝑠𝑠} dapat dihitung :

𝑠𝑠𝑠𝑠𝑠𝑠 = 𝑠𝑠𝑠𝑠𝑠𝑠 𝑠𝑠12 (Ohm)………...…(2.31) 𝑠𝑠𝑠𝑠𝑠𝑠 = 𝑠𝑠1 + 𝑠𝑠2 (Ohm)………...(2.32) 𝑠𝑠_{𝑠𝑠𝑠𝑠} = 𝑠𝑠_𝑠𝑠𝑠𝑠𝑠𝑠 𝑠𝑠𝑠𝑠 (Ohm)……….…..(2.33) 𝑠𝑠𝑠𝑠𝑠𝑠 = �𝑠𝑠𝑠𝑠𝑠𝑠2 − 𝑠𝑠𝑠𝑠𝑠𝑠2 (Ohm)………...…(2.34)

Untuk menentukan harga 𝑠𝑠1 dan 𝑠𝑠2 digunakan metode empiris berdasarkan IEEE

standar 112. Hubungan 𝑠𝑠1 terhadap Xbr dapat dilihat pada table berikut :

Tabel 2.1 Distribusi Empiris dari Xbr Desain Kelas motor 𝑋𝑋1 𝑋𝑋′2 A B C D Rotor belitan 0,5 Xbr 0,4 Xbr 0,3 Xbr 0,5 Xbr 0,5 Xbr 0,5 Xbr 0,6 Xbr 0,7 Xbr 0,5 Xbr 0,5 Xbr

Di sini besar 𝑠𝑠_{𝑠𝑠𝑠𝑠} harus disesuikan dahulu dengan frekuensi rating f. 𝑠𝑠′_{𝑠𝑠𝑠𝑠} = _𝑠𝑠𝑠𝑠

𝑠𝑠𝑠𝑠 𝑠𝑠𝑠𝑠𝑠𝑠 (Ohm)………..…….(2.35) 𝑠𝑠′𝑠𝑠𝑠𝑠 = 𝑠𝑠₁- 𝑠𝑠′₂ (Ohm)………..…….(2.36)