BAB 2
LANDASAN TEORI
2.1 AHP (Analytical Hierarchy Process)
Metode AHP dikembangkan oleh Thomas Lorie Saaty dari Wharston Business School (1993). Prinsip kerjanya adalah dengan menguraikan masalah multi kriteria yang kompleks menjadi suatu hirarki yang melakukan pengukuran untuk menemukan skala rasio perbandingan berpasangan, baik untuk data diskrit maupun kontinu.
Metode ini dapat digunakan untuk menentukan ranking atau tingkatan
(hierarchy) dari berbagai alternative yang tersedia sehingga dapat mengarahkan pengambil keputusan untuk memilih alternative terbaik berdasarkan preferensi dan pertimbangannya.
Thomas Lorie Saaty (1993), mendefenisikan :
Hirarki adalah suatu representasi dari sebuah permasalahan yang kompleks dalam suatu struktur multi level dimana level pertama adalah tujuan, yang diikuti level faktor, kriteria, sub kriteria, dan seterusnya ke bawah hingga level terakhir dari alternatif.
Keunggulan yang dimiliki oleh metode AHP dalam memecahkan masalah pengambilan keputusan yang kompleks dengan tingkatan kriteria yang lebih banyak dan beragam,adalah :
a. AHP akan mengurutkan setiap alternatif yang tersedia dalam sebuah struktur hirarki yang lengkap, selanjutnya mengarah kepada konsekuesi dari kriteria yang akan dipilih (alternatif terbaik)
b. Memperhitungkan validitas sampai dengan batas toleransi inkonsistensi berbagai kriteria dan alternatif yang dipilih oleh pengambil keputusan. c. Memperhitungkan output dari setiap alternatif keputusan yang akan
diambil, sehingga dapat member gambaran yang jelas tentang alternatif terbaik yang akan diarahkan pada sebuah keputusan.
Terdapat 4 landasan aksiomatik yang terkandung dalam metode dasar AHP, yaitu:
1. Reciprocal Comparison artinya pengambilan keputusan harus dapat memuat matriks perbandingan berpasangan dan menyatakan preferensinya yang harus memenuhi syarat resiprokal yaitu apabila A lebih disukai daripada B dengan skala x, maka B lebih disukai daripada A dengan skala 1/x.
2. Homogenity artinya Setiap elemenyang dibandingkanharus merupakan dalam rumpun yang sama untuk dapat menghasilkan preferensi yang sesuai. Kalau aksioma ini tidak dipenuhi maka elemen- elemen yang dibandingkan tersebut tidak homogen dan harus dibentuk cluster (kelompok elemen) yang baru. 3. Independence artinya preferensi dinyatakan dengan mengasumsikan bahwa
kriteria tidak dipengaruhi oleh alternatif-alternatif yang ada melainkan oleh objektif keseluruhan. Ini menunjukkan bahwa pola ketergantungan dalam AHP adalah searah, maksudnya perbandingan antara elemen-elemen dalam satu tingkat dipengaruhi atau tergantung oleh elemen-elemen pada tingkat diatasnya.
2.2 Prinsip Dasar AHP (Analytical Hierarchy Process)
Dalam penggunaan AHP untuk menyelesaikan multi-criteria decision making, ada beberapa prinsip yang harus dipahami,yakni :
1. Decomposition
Adalah membagi problema yang utuh menjadi unsur-unsur dalam bentuk hirarki proses pengambilan keputusan, dimana setiap unsur tersebut saling berhubungan. Untuk mendapatkan hasil yang akurat, pemecahan dilakukan terhadap unsur-unsur sampai tidak mungkin dilakukan pemecahan lebih lanjut, sehingga didapatkan beberapa tingkatan dari persoalan yang hendak dipecahkan.Struktur hirarki keputusan tersebut dapat dikategorikan sebagai
complete dan incomplete.
Suatu hirarki (tingkatan) keputusan disebut complete jika semua elemen pada suatu tingkat memiliki hubungan / terhubung terhadap semua elemen yang ada pada tingkat berikutnya, sementara hirarki keputusan
incomplete, terdapat satu atau lebih elemen yang tidak memiliki hubungan dengan elemen di tingkat berikutnya.
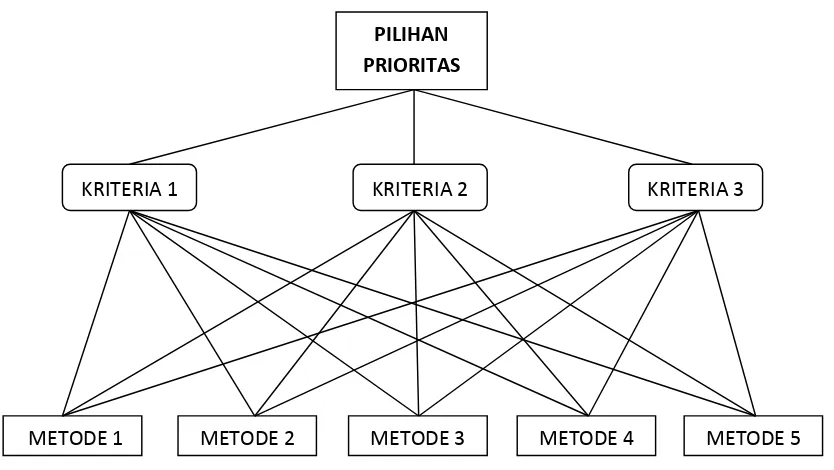
Atau dapat diilustrasikan dalam gambar berikut :
Gambar 2.1.Complete hierarchy
METODE 1 METODE 2 METODE 3 METODE 4 METODE 5
PILIHAN
PRIORITAS
2. Comparative judgment
Comparative Judgment dilakukan dengan membuat penilaian tentang kepentingan relatif dua elemen pada suatu tingkat tertentu dalam kaitannya dengan tingkatan diatasnya. Penilaian ini merupakan inti dari AHP karena akan berpengaruh terhadap urutaan prioritas dari elemen-elemenya. Hasil dari penilaian ini lebih mudah disajikan dalam bentuk matriks perbandingan berpasangan yang memuat tingkat preferensi beberapa alternatif untuk tiap kriteria.
Menurut Saaty, untuk berbagai persoalan, skala 1 sampai 9 adalah skala terbaik untuk mengekspresikan pendapat. Skala 1 yang menunjukkan tingkat yang paling rendah (equal importance) sampai dengan skala 9 yang menunjukkan tingkatan yang paling tinggi (erxtreme importance).
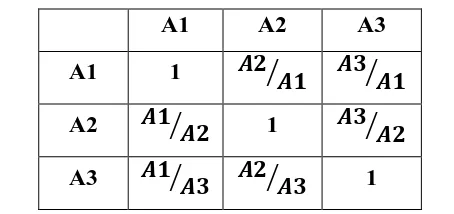
Pengisian nilai tabel perbandingan berpasangan dilakukan berdasarkan kebijakan pembuat keputusan dengan melihat tingkat kepentingan antar satu elemen dengan elemen yang lainnya. Proses perbandingan berpasangan, dimulai dari perbandingan kriteria misalnya A1, A2 dan A3. Maka susunan elemen-elemen yang dibandingkan tersebut akan tampak seperti pada tabel di bawah ini:
Tabel 2.1 Contoh Matriks Perbandingan Berpasangan
A1 A2 A3
A1 1 � ⁄� � ⁄�
A2 � ⁄� 1 � ⁄�
A3 � ⁄� � ⁄� 1
Untuk menentukan nilai kepentingan relatif antar elemen digunakan skala bilangan dari 1 sampai 9 yang dapat dilihat pada Tabel 2.2.
1. Apabila suatu elemen dibandingkan dengan dirinya sendiri maka diberi nilai 1.
3. Pengujian konsistensi dilakukan terhadap perbandingan antar elemen yang didapatkan pada tiap tingkat hirarki.
4. Konsistensi perbandingan ditinjau dari matriks perbandingan dan keseluruhan hirarki untuk memastikan bahwa urutan prioritas yang dihasilkan didapatkan dari suatu rangkaian perbandingan yang masih berada dalam batas-batas preferensi yang logis.
5. Setelah melakukan perhitungan bobot elemen, langkah selanjutnya adalah melakukan pengujian konsistensi matriks.
Untuk melakukan perhitungan ini diperlukan bantuan tabel Random Index (RI) yang nilainya untuk setiap ordo matriks dapat dilihat pada tabel berikut ini:
Tabel 2.2Random Index Urutan
Matriks 1 2 3 4 5 6 7 8
9 10
(RI) 0.00 0.01 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49
3. Synthesis of Priority (Penentuan Prioritas)
Untuk setiap kriteria dan alternatif, perlu dilakukan perbandingan berpasangan (Pairwise Comparisons).Nilai-nilai perbandingan relatif dari seluruh alternatif kriteria bisa disesuaikan dengan judgement yang telah ditentukan untuk menghasilkan bobot dan prioritas.Bobot atau prioritas dihitung dengan manipulasi matriks atau melalui penyelesaian persamaan matematika.
4. Logical Consistency (Konsistensi Logis)
2.3 Penggunaan Metode AHP
Terdapat beberapa langkah yang perlu diperhatikan dalam menggunakan metode AHP, antara lain (Suryadi & Ramdhani 1998):
1. Mendefinisikan masalah dan menentukan solusi yang diinginkan.
Tahap ini ialah untuk menentukan masalah yang akan dipecahkan secara jelas,
detail dan mudah dipahami. Dari masalah yang ada, selanjutnya dicoba untuk
menentukan solusi untuk masalah tersebut yang mungkin saja solusi dari
masalah tersebut berjumlah lebih dari satu.Solusi tersebut nantinya kita
kembangkan lebih lanjut dalam tahap berikutnya.
2. Membuat struktur hirarki yang diawali dengan tujuan umum dilanjutkan dengan subtujuan-subtujuan, kriteria dan kemungkinan alternatif-alternatif pada tingkatan kriteria yang paling bawah. Setelah menyusun tujuan utama sebagai level teratas akan disusun level hirarki yang berada di bawahnya yaitu
kriteria-kriteria yang cocok untuk mempertimbangkan atau menilai alternatif
yang kita berikan dan menentukan alternatif tersebut. Tiap kriteria mempunyai
intensitas yang berbeda-beda. Hirarki dilanjutkan dengan subkriteria (jika
mungkin diperlukan).
3. Membuat matriks perbandingan berpasangan yang menggambarkankontribusi relatif atau pengaruh setiap elemen terhadap masing-masing tujuan atau kriteria yang setingkat diatasnya. Perbandingan dilakukan berdasarkan penilaian dari pembuat keputusan dengan menilai tingkat kepentingan suatu elemen dibandingkan elemen lainnya.
4. Menghitung nilai lamda max dan menguji konsistensinya, jika tidak konsisten maka pengambilan data diulangi.
5. Mengulangi langkah 3, 4 dan 5 untuk seluruh tingkat hirarki.
6. Menghitung vektor eigen dari setiap matriks perbandingan berpasangan. Nilai vektor eigen merupakan bobot setiap elemen. Langkah ini untuk mengurutkan penilaian dalam penentuan prioritas elemen-elemen pada tingkat hirarki terendah sampai pencapaian tujuan.
Yang diukur dalam AHP adalah rasio konsistensi dengan melihat index konsistensi.Konsistensi yang diharapkan adalah yang mendekati sempurna agar menghasilkan keputusan yang mendekati valid. Walaupun sulit untuk mencapai yang sempurna, rasio konsistensi diharapkan kurang dari atau sama dengan 10 %.Jika nilai lebih dari 10% (persen) atau 0,1 maka penilaian data harus diperbaiki.
2.4 Penyusunan Prioritas
Penentuan susunan prioritas elemen dilakukan dengan menyusun perbandingan berpasangan yaitu membandingkan dalam bentuk berpasangan seluruh elemen untuk setiap sub hirarki yang kemudian perbandingan tersebut ditransformasikan ke dalam bentuk matriks.
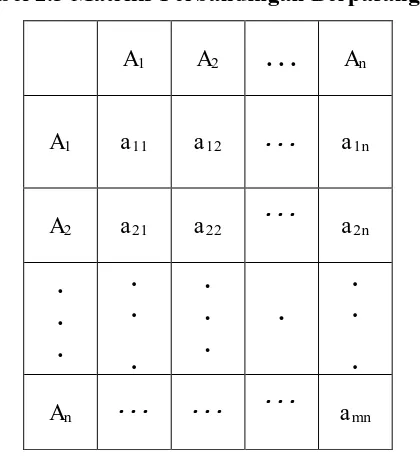
Contoh, terdapat n objek yang dinotasikan dengan (A1, A2,...,An) yang akan dinilai berdasarkan pada nilai tingkat kepentingannya antara lain A1 dan Aj
dipresentasikan dalam matriks perbandingan berpasangan seperti berikut :
Tabel 2.3 Matriks Perbandingan Berpasangan
lainnya.Thomas Lorie Saaty (1987), Untuk menilai perbandingan tingkat kepentingan satu elemen terhadap elemen lainnya digunakan skala 1 sampai 9 yang dimana bobot 1 sampai 9 tersebut diperoleh seperti terlihat pada tabel berikut :
Tabel 2.4 Skala Penilaian Perbandingan Berpasangan
2,4,6,8 Nilai-nilai antara dua nilai pertimbangan yang berdekatan.
Kebalikan Jika aktivitas i mendapat satu angka dibandingkan dengan aktivitas j, maka j memiliki nilai kebalikannya dibandingkan dengan i.
Model AHP didasarkan pada matriks perbandingan berpasangan, dimana elemen-elemen pada matriks tersebut merupakan “penilaian” dari pengambil keputusan. Seorang pengambil keputusanakan memberikan penilaian, mempersepsikan, ataupun memperkirakan kemungkinan dari sesuatu hal/peristiwa yang dihadapi. Matriks tersebut terdapat pada setiap tingkatan hirarkidari suatu struktur model AHP yang membagi habis suatu persoalan.
Baris 1 Kolom 2: jika A dibandingkan dengan B, maka B lebih penting/disukai/dimungkinkan daripada A yaitu sebesar 7, artinya : B “lebih mutlak penting” daripada A, dan seterusnya. Angka 7 bukan berarti bahwa Btujuhkali lebih besar dari A, tetapi B “lebih mutlak penting” dibandingkan A.
2.5Nilai Eigen dan Vektor Eigen
Sebelum kita membahas tentang nilai eigen dan vector eigen, terlebih dahulu kita bahas mengenai matriks, operasi matriks dan komponen-komponennya.
1. Matriks
Matriks adalah suatu kumpulan angka – angka (elemen-elemen) yang disusun menurut baris dan kolom sehinggu berbentuk persegi panjang, yang dimana panjang dan lebarnya ditunjukkan oleh banyaknya kolom-kolom dan baris-baris.
Sekumpulan himpunan objek (bilangan riil atau kompleks,variabel–variabel) yang disusun secara persegi panjang (yang terdiri dari baris dankolom) yang biasanya dibatasi dengan kurung siku atau biasa. Jika sebuah matriks memiliki m baris dan n
kolom maka matriks tersebut berukuran (ordo) × dan matriks dikatakan bujur sangkar (square matrix) jika = . Dan skalar –skalarnya berada dibaris ke-i dan n
kolom ke-j yang disebut matriks entri.
=
[
� � … � �
� � … � �
� � … � �
� � … � … �
� � … � … � ]
2. Perkalian Matriks
Perkalian matriks dilakukandengan cara : elemen-elemen tiap baris dikalikan dengan tiap kolom, lalu dijumlahkan pada baris yang sama
= ∑
�
=
∙
Contoh :
[ ] ∙ [ ] = [ ∙ + ∙∙ + ∙ ∙ + ∙∙ + ∙ ] = [ ]
3. Vektor dari n dimensi
Suatu vektor dengan n dimensi merupakan suatu susunan elemen – elemenyang teratur berupa angka–angka sebanyak n buah, yang disusun baik menurut baris, dari kirike kanan (disebut vektor baris atau row vector dengan ordo × ) maupun menurutkolom, dari atas ke bawah (disebut vektor kolom atau coloumn vector dengan ordo × ). Himpunan semua vektor dengan n komponen dengan entri riil dinotasikan dengan ℛ
Untuk vektor ⃗ dirumuskan sebagai berikut:
� ∈ �
⃗ ∈�
⃗ = [ � � �
] ∈�
4. Eigen value dan Eigen vector
Definisi : Jika A adalah matriks n x n maka vektor tak nol x di dalam ℛ dinamakan dinamakan eigen vector dari A jika Ax kelipatan skalar x, yakni :
Skalar � dinamakan eigen value dari A dan x dikatakan eigenvector yang bersesuaian dengan �. Untuk mencari eigen value dari matriks A yang berukuran maka dapat ditulis pada persamaan berikut :
= �
atau secara ekivalen
�� − =
Agar � menjadi eigen value, maka harus ada pemecahan tak nol dari persamaan ini. Akan tetapi, persamaan diatas akan mempunyai pemecahan tak nol jika dan hanya jika :
�� − =
Ini dinamakan persamaan karakteristik A, skalar yang memenuhi persamaan ini adalah eigen value dari A.
Bila diketahui bahwa nilai perbandingan elemen Ai terhadap elemen Aj adalah
� , maka secara teoritis matriks tersebut berciri positif berkebalikan, yakni � =
�
⁄ . Bobot yang dicari dinyatakan dalam vektor = , , , … . Nilai menyatakan bobot kriteria An terhadap keseluruhan set kriteria pada sub sistem tersebut.
Jika � mewakili derajat kepentingan i terhadap faktor j dan � manyatakan kepentingan dari faktor j terhadap faktor k, maka agar keputusan menjadi konsisten, kepentingan i terhadap faktor k harus sama dengan � � atau jika� � =
� untuk semua i,j,k maka matriks tersebut konsisten.
Untuk suatu matriks konsisten dengan faktor w, maka elemen � dapat ditulis menjadi :� = �
� ; ∀ , = , , , … , (1)
Jadi matriks konsisten adalah:
� . � =�� .�� =�� = � (2)
� =�� = � �
⁄ =� ; (3)
Dari persamaan tersebut di atas dapat dilihat bahwa :
� = �� = ∀, = , , , … , (4)
Dengan demikian untuk matriks perbandingan berpasangan yang konsisten menjadi:
∑ = � . .� = ; ∀, = , , , … , (5)
∑ = � . = ; ∀, = , , , … , (6)
Persamaan di atas ekivalen dengan bentuk persamaan matriks di bawah ini:
. = . (7)
Dalam teori matriks, formulasi ini diekspresikan bahwa w adalah eigenvector
dari matriks A dengan eigen value n. Perlu diketahui bahwa n merupakan dimensi matriks itu sendiri. Dalam bentuk persamaan matriks dapat ditulis sebagai berikut:
= [
Pada prakteknya, tidak dapat dijamin bahwa :
� =�� (9)
Salah satu faktor penyebabnya yaitu karena unsur manusia (decision maker) tidak selalu dapat konsisten mutlak (absolte consistent) dalam mengekpresikan preferensinya terhadap elemen-elemen yang dibandingkan. Dengan kata lain,
judgment yang diberikan tidak untuk setiap elemen persoalan pada suatu level hierarchy dapat saja inconsistent.
Jika :
dengan eigen value dari matriks A dan jika � = ; ∀, = , , , … , , maka ditulis
∑ � = (11)
Misalkan kalau suatu matriks perbandingan berpasangan bersifat ataupun memenuhi kaidah konsistensi seperti pada persamaan (2), maka perkalian elemen matriks sama dengan 1.
= [ ] � � = � b (12)
Eigen value dari matriks A,
− � =
− �� = (13)
| − ��| =
Kalau diuraikan lebih jauh untuk persamaan (13), hasilnya menjadi :
| − � − �| = (14)
Dari persamaan (14) kalau diuraikan untuk mencari harga eigen value maximum (λ-max) yaitu :
− � − =
− � + � − =
� − � =
� � − = � = ; � =
Dengan demikian matriks pada persamaan (12) merupakan matriks yang konsisten, dimana nilai λ – max sama dengan harga dimensi matriksnya.
2) Jika ada perubahan kecil dari elemen matriks maka aijeigen value-nya akan berubah
menjadi semakin kecil pula.
Dengan menggabungkan kedua sifat matriks (aljabar linier). Jika: a. Elemen diagonal matriks A
� = ∀, = , , , … ,
b. Dan untuk matriks A yang konsisten, maka variasi kecil dari � ; ∀ , =
, , , … , akan membuat harga eigen value yang lain mendekati nol.
2.6 Uji Konsistensi Indeks dan Rasio
Dalam teori matriks dapat diketahui kesalahan kecil pada koefisien akan menyebabkan penyimpangan kecil pada eigen value. Dengan mengkombinasikan apa yang telah diuraikan sebelumnya, jika diagonal utama dari matriks A bernilai satu dan jika A konsisten maka penyimpangan kecil dari � akan tetap menunjukkan eigen value terbesar � maks, nilainya akan mendekati n dan eigen value sisanya akan mendekati nol.
Penyimpangan dari konsistensi dinyatakan dengan indeks konsistensi dengan persamaan:
� =��� �−
− (15)
Dimana: � = Rasio penyimpangan (deviasi) konsistensi (consistency index)
� � � = nilai eigenmaksimum
n = ukuran matriks
diperlihatkan seperti tabel 2.3. Nilai ini bergantung pada ordo matriks n. Dengan demikian, Rasio Konsistensi dapat dirumuskan :
� =���� (16)
Nilai-nilai pada Random Index (RI) dapat dilihat pada tabel 2.3.Bila matriks bernilai CR lebih kecil dari 0,100, ketidakkonsistenan pendapat bisa diterima jika tidak maka penilaian perlu di ulang.
2.7Sampel dan Komponen-komponennya
Dalam teknik sampling, ada 3 elemen penting yang menjadi bagian dari teknik sampling itu sendiri, yakni :
1. Populasi
Adalah sekelompok orang, kejadian, atau benda, yang menjadi objek penelitian.Misalnya,jika yang diteliti adalah dampak penggunaan salah satu alat olahraga, maka populasinya adalah keseluruhan konsumen pengguna alat olahraga tersebut.Jika yang ingin diteliti adalah motivasi siswa untuk mengikuti pelajaran tertentu di sekolah “X” maka populasinya adalah seluruh siswa di sekolah “X”.Atau dapat juga dikatakan, keseluruhan elemen atau unsur yang menjadi objek penelitian, yang memiliki sifat-sifat tertentu yang menjadi perhatian dalam penelitian yang akan dilakukan.
2. Sampel
Adalah sebagian dari populasi yang dapat mewakili populasi itu sendiri, atau dapat juga dikatakan merupakan penduga atas populasi yang sedang diamati.Artinya sampel tidak akandapat didefenisikan tanpa adanya populasi. 3. Elemen/unsur
Dalam sebuah penelitian, untuk mendapatkan hasil yang maksimal dan akurat sesuai harapan peneliti, maka seharusnya dilakukan penelitian terhadap seluruh elemen dalam populasi yang diteliti tersebut, atau yang dinamakan “sensus”.Namun, sensus tidak selalu menjadi hal yang mudah untuk dilakukan mengingat hal-hal berikut :
1. Populasi yang sedemikian besar sehingga dalam prakteknya tidak dimungkinkan untuk meneliti setiap elemen dalam populasi tersebut
2. Keterbatasan waktu penelitian, biaya, dan sumber daya manusia dalam melakukan penelitian untuk setiap unsur dalam poopulasi.
3. Kesalahan (human error) dalam melakukan sensus karena besarnya populasi dan banyaknya elemen yang harus diteliti, yang mungkin disebabkan karena kelelahan fidik maupun mental, justru dapat menyebabkan bias terhadap hasil penelitian yang dilakukan.
4. Untuk suatu populasi yang homogen, penelitian terhadap seluruh elemen dalam populasi akanmenjadi tidak masuk akal, karena untuk suatu populasi yang homogen, akan tetap menghasilkan hasil penelitian yang sama ketika dilakukan penelitian pada sebagian elemen populasi maupun terhadap seluruh elemen populasi.
Oleh karena hal-hal di atas, seringkali sensus menjadi sesuatu hal yang dihindari dan tidak perlu untuk dilakukan untuk dalam sebuah penelitian. Namun, agar hasil penelitian yang dilakukan terhadap sampel masih tetap bisa dipercaya dalam artian mewakili karakteristik populasi, makaada cara-dara penarikan sampel yang harus dilakukan secara seksama. Cara pemilihan sampel ini disebut dengan teknik sampling.
Syarat sampel yang baik
Sampel yang valid ditentukan oleh dua pertimbangan. 1. Akurasi atau ketepatan
yaitu tingkat kekeliruan (bias)dalam sampel. Dengan kata lain makin sedikit tingkat kekeliruan yang ada dalam sampel, makin akurat sampel tersebut. Tolok ukur adanya “bias” atau kekeliruan adalah populasi.
2. Presisi
Kriteria kedua sampel yang baik adalah memiliki tingkat presisi estimasi. Presisi mengacu pada persoalan sedekat mana estimasi kita dengan karakteristik populasi.
Contoh : Dari 300 buruh sebuah pabrik, diambil sampel 50 buruh. Setelah diukur ternyata setiap orang menghasilkan 50 unit produk “X” perhari, namun berdasarkan laporan harian, pegawai bisa menghasilkan sampai rata-rata 60 unit produk “X” perhari. Artinya antara laporan harian yang dihitung berdasarkan populasi (sensus) dengan hasil penelitian yang dihasilkan dari sampel (survey), terdapat perbedaan 10 unit.Makin kecil tingkat perbedaan di antara rata-rata populasi dengan rata-rata sampel, maka makin tinggi tingkat presisi sampel tersebut.
Bias yang terjadi dalam setiap hasil penelitian dengan sampel dikenal dengan nama “sampling error”. Presisi diukur oleh simpangan baku (standard error). Makin kecil perbedaan di antara simpangan baku yang diperoleh dari sampel (dilambangkan dengan s) dengan simpangan baku dari populasi (dilambangkan dengan ) makin tinggi pula tingkat presisinya.
Di bawah ini digambarkan hubungan antara jumlah sampel dengan tingkat kesalahan seperti yang diuarakan oleh Kerlinger
Kecil besarnya sampel besar
Gambar.2 Hubungan antara jumlah sampel dengan tingkat kesalahan Ukuran sampel
Dalam penelitian kuantitatif, ukuran sampel atau jumlah sampel yang diambil menjadi persoalan yang penting karena hasil penelitian akan berdasar pada data dan angka, sementara pada penelitian yang menggunakan analisis kualitatif, ukuran sampel bukan menjadi nomor satu, karena yang dipentingkan adalah kekayaan informasi. Walau jumlahnya sedikit tetapi jika kaya akan informasi, maka sampelnya akan lebih bermanfaat.
Dalam hal penentuan besarnya sampel, selain tingkat kesalahan, ada lagi beberapa faktor lain yang perlu memperoleh pertimbangan yaitu:
1. derajat keseragaman, semakin tidak seragam sifat atau karakter setiap elemen populasi (heterogen), makin banyak sampel yang harus diambil. 2. rencana analisis, Jika rencana analisis yang dibuat mendetail atau rinci
maka jumlah sampelnya juga harus banyak.
3. biaya, waktu, dan tenaga yang tersedia . (Singarimbun dan Effendy, 1989).
Yang sering menjadi pertanyaan adalah : seberapa besar sampel yang harus diambil jika diketahui suatu populasi yang menjadi penelitian. Misalnya, jumlah siswa yang dijadikan populasi penelitian ada 500 siswa.Pertanyaannya adalah, berapa banyak siswa yang harus dijadikan sebagai sampel agar hasilnya mewakili populasi? 30?, 50?, 100?,atau 250?, jawabnya tidak mudah. Ada yang mengatakan, jika ukuran populasinya di atas 1000, sampel sekitar 10 % sudah cukup, tetapi jika ukuran populasinya sekitar 100, sampelnya paling sedikit 30%, dan kalau ukuran populasinya 30, maka sampelnya harus 100%.
kecil
k
e
sal
ah
Ada pula yang menuliskan, untuk penelitian deskriptif, sampelnya 10% dari populasi, penelitian korelasional, paling sedikit 30 elemen populasi, penelitian perbandingan kausal, 30 elemen per kelompok, dan untuk penelitian eksperimen 15 elemen per kelompok (Gay dan Diehl, 1992).
Roscoe (1975) dalam Uma Sekaran (1992) memberikan pedoman penentuan jumlah sampel sebagai berikut :
1. Sebaiknya ukuran sampel di antara 30 s/d 500 elemen
2. Jika sampel dipecah lagi ke dalam subsampel (laki/perempuan, SD/SLTP/SMU, dsb), jumlah minimum subsampel harus 30
3. Pada penelitian multivariat (termasuk analisis regresi multivariat) ukuran sampel harus beberapa kali lebih besar (10 kali) dari jumlah variabel yang akan dianalisa.
4. Untuk penelitian eksperimen yang sederhana, dengan pengendalian yang ketat, ukuran sampel bisa antara 10 s/d 20 elemen.
Krejcie dan Morgan (1970) dalam Uma Sekaran (1992) membuat daftar yang bisa dipakai untuk menentukan jumlah sampel sebagai berikut (Lihat Tabel)
2.8Teknik sampling
Secara umum, ada dua jenis teknik sampling yaitu, sampel acak atau random sampling / probability sampling, dan sampel tidak acak atau nonrandom samping/nonprobability sampling.
Yang dimaksud dengan random sampling/probability samplingadalah cara pengambilan sampel yang dimana setiap elemen dalam populasi memiliki kesempatan yang sama untuk menjadi sampel. Artinya jika elemen populasinya ada 100 dan yang akan dijadikan sampel adalah 25, maka setiap elemen tersebut mempunyai kemungkinan 25/100 untuk bisa dipilih menjadi sampel.
Yang dimaksud dengan nonrandom sampling atau nonprobability sampling, setiap elemen populasi tidak mempunyai kemungkinan yang sama untuk dijadikan sampel. Lima elemen populasi dipilih sebagai sampel karena letaknya dekat dengan rumah peneliti, sedangkan yang lainnya, karena jauh, tidak dipilih; artinya kemungkinannya 0 (nol).
Dua jenis teknik pengambilan sampel di atas mempunyai tujuan yang berbeda.Jika peneliti ingin hasil penelitiannya bisa dijadikan ukuran untuk mengestimasikan populasi, atau istilahnya adalah melakukan generalisasi maka seharusnya sampel representatif dan diambil secara acak.Namun jika peneliti tidak mempunyai kemauan melakukan generalisasi hasil penelitian maka sampel bisa diambil secara tidak acak.Sampel tidak acak biasanya juga diambil jika peneliti tidak mempunyai data pasti tentang ukuran populasi dan informasi lengkap tentang setiap elemen populasi.
2.9 Probability/Random Sampling
Syarat pertama yang harus dilakukan untuk mengambil sampel secara acak adalah memperoleh atau membuat kerangka sampel atau dikenal dengan nama“sampling frame”. Yang dimaksud dengan kerangka sampling adalah daftar yang berisikan setiap elemen populasi yang bisa diambil sebagai sampel. Elemen populasi bisa berupa data tentang orang/binatang, tentang kejadian, tempat, atau juga benda.
Misalnya, Jika populasi penelitian adalah siswa sekolah “X”, maka peneliti harus bisa memiliki daftar semua siswa yang ada di sekolah “X” tersebut selengkapnya. Nama, NIS, jenis kelamin, alamat, usia, dan informasi lain yang berguna bagi penelitiannya.. Dari daftar ini, peneliti akan bisa secara pasti mengetahui jumlah populasinya (N).
Di samping sampling frame, peneliti juga harus mempunyai alat yang bisa dijadikan penentu sampel. Dari sekian elemen populasi, elemen mana saja yang bisa dipilih menjadi sampel?. Alat yang umumnya digunakan adalah Tabel Angka Random, kalkulator, atau undian. Pemilihan sampel secara acak bisa dilakukan melalui sistem undian jika elemen populasinya tidak begitu banyak. Tetapi jika sudah ratusan, cara undian bisa mengganggu konsep “acak” atau “random” itu sendiri.
Berikut dijabarkan teknik sampling yang masukdalam kategori
probability/random sampling :
1. Simple Random Sampling atau Sampel Acak Sederhana
mengambil sampel secara acak sederhana. Dengan demikian setiap unsur populasi harus mempunyai kesempatan sama untuk bisa dipilih menjadi sampel.
Prosedur penggunaan teknik ini adalah:
1. Susun “sampling frame” (kerangka sampel), 2. Tetapkan jumlah sampel yang akan diambil, 3. Tentukan alat pemilihan sampel, lalu
4. Pilih sampel sampai dengan jumlah terpenuhi.
2. Stratified Random Sampling atau Sampel Acak Terstratifikasi
Karena unsur populasi berkarakteristik heterogen, dan heterogenitas tersebut mempunyai arti yang signifikan pada pencapaian tujuan penelitian, maka peneliti dapat mengambil sampel dengan cara ini. Misalnya, seorang peneliti ingin mengetahui sikap manajer terhadap satu kebijakan perusahaan.Dia menduga bahwa manajer tingkat atas cenderung positif sikapnya terhadap kebijakan perusahaan tadi.Agar dapat menguji dugaannya tersebut maka sampelnya harus terdiri atas paling tidak para manajer tingkat atas, menengah, dan bawah. Dengan teknik pemilihan sampel secara random distratifikasikan, maka dia akan memperoleh manajer di ketiga tingkatan tersebut, yaitu tingkat manajer atas, manajer menengah dan manajer bawah. Dari setiap tingkat tersebut dipilih sampel secara acak.
Prosedur penggunaan teknik ini adalah:
1. Siapkan “sampling frame” (kerangka sampel),
2. Bagi sampling frame tersebut berdasarkan strata yang dikehendaki, 3. Tentukan jumlah sampel dalam setiap stratum, lalu
4. Pilih sampel dari setiap stratum secara acak.
Pada saat menentukan jumlah sampel dalam setiap tingkatan, peneliti dapat menentukan secara “proposional”, maupun secara “tidak proposional”.
tersebut. Misalnya, untuk tingkatan manajer tingkat atas (I) terdapat 15 manajer, tingkat menengah ada 45 manajer (II), dan manajer tingkat bawah (III) ada 100 manajer. Artinya jumlah seluruh manajer adalah 160. Kalau jumlah sampel yang akan diambil seluruhnya 100 manajer, maka untuktingkatan I diambil (15:160)x100 = 9 manajer, tingkatan II = 28 manajer, dan tingkatan 3 = 63 manajer.
Jumlah dalam setiaptingkatan tidak proposional. Hal ini terjadi jika jumlah unsur atau elemen di salah satu atau beberapa tingkatan sangat sedikit. Misalnya saja, kalau dalam tingkatan manajer kelas atas (I) hanya ada 4 manajer, maka peneliti bisa mengambil semua manajer dalam tingkatan tersebut , dan untuk manajer tingkat menengah (II) ditambah 5, sedangkan manajer tingat bawah (III), tetap 63 orang.
3. Cluster Sampling atau Sampel Gugus
Teknik ini biasa juga diterjemahkan dengan cara pengambilan sampel berdasarkan gugus. Berbeda dengan teknik pengambilan sampel acak terstratifikasi, di mana setiap unsur dalam satu stratum memiliki karakteristik yang homogen (stratum A : laki-laki semua, stratum B : perempuan semua), maka dalam sampel gugus, setiap gugus boleh mengandung unsur yang karakteristiknya berbeda-beda atau heterogen. Misalnya, dalam satu organisasi terdapat 100 departemen.Dalam setiap departemen terdapat banyak pegawai dengan karakteristik berbeda pula. Beda jenis kelaminnya, beda tingkat pendidikannya, beda tingkat pendapatnya, beda tingat manajerialnya, dan perbedaan-perbedaan lainnya. Jika peneliti bermaksud mengetahui tingkat penerimaan para pegawai terhadap suatu strategi yang segera diterapkan perusahaan, maka peneliti dapat menggunakan cluster sampling untuk mencegah terpilihnya sampel hanya dari satu atau dua departemen saja.Prosedur :
1. Susun sampling frame berdasarkan gugus – Dalam kasus di atas, elemennya ada 100 departemen.
2. Tentukan berapa gugus yang akan diambil sebagai sampel 3. Pilih gugus sebagai sampel dengan cara acak
4. Systematic Sampling atau Sampel Sistematis
Jika peneliti dihadapkan pada ukuran populasi yang banyak dan tidak memiliki alat pengambil data secara random, cara pengambilan sampel sistematis dapat digunakan. Cara ini menuntut kepada peneliti untuk memilih unsur populasi secara sistematis, yaitu unsur populasi yang bisa dijadikan sampel adalah yang “keberapa”.Misal, setiap unsur populasi yang ke-tiga, yang bisa dijadikan sampel. Soal “keberapa”-nya satu unsur populasi bisa dijadikan sampel tergantung pada ukuran populasi dan ukuran sampel.Contoh, dalam satu populasi terdapat 5000 rumah. Sampel yang akan diambil adalah 250 rumah dengan demikian interval di antara sampel kesatu, kedua, dan seterusnya adalah 25. Prosedurnya :
1. Susun sampling frame
2. Tetapkan jumlah sampel yang ingin diambil 3. Tentukan K (kelas interval)
4. Tentukan angka atau nomor awal di antara kelas interval tersebut secara acak atau random – biasanya melalui cara undian saja.
5. Mulailah mengambil sampel dimulai dari angka atau nomor awal yang terpilih.
6. Pilihlah sebagai sampel angka atau nomor interval berikutnya
5. Area Sampling atau Sampel Wilayah
Teknik ini dipakai ketika peneliti dihadapkan pada situasi bahwa populasi penelitiannya tersebar di berbagai wilayah. Misalnya, seorang marketing manajer sebuah stasiun TV ingin mengetahui tingkat penerimaan masyarakat kota Medan atas sebuah mata tayangan, teknik pengambilan sampel dengan area sampling sangat tepat. Prosedurnya :
1. Susun sampling frame yang menggambarkan peta wilayah (Medan). 2. Tentukan wilayah yang akan dijadikan sampel, kecamatan atau
kelurahan?
3. Tentukan berapa wilayah yang akan dijadikan sampel penelitiannya. 4. Pilih beberapa wilayah untuk dijadikan sampel dengan cara acak atau
5. Kalau ternyata masih terlampau banyak responden yang harus diambil datanya, bagi lagi wilayah yang terpilih ke dalam sub wilayah.
2.10 Nonprobability/Nonrandom Sampling
Selanjutnya, teknik pengambilan sampel yang dimana sampelnya tidak diambil secra acak, disebut nonprobability random sampling. Yang dimana artinya tidak semua unsur atau elemen populasi mempunyai kesempatan sama untuk bisa dipilih menjadi sampel. Unsur populasi yang terpilih menjadi sampel bisa disebabkan karena kebetulan atau karena faktor lain yang sebelumnya sudah direncanakan oleh peneliti.
1. Convenience Sampling atau sampel yang dipilih dengan pertimbangan kemudahan.
Dalam memilih sampel, peneliti tidak mempunyai pertimbangan lain kecuali berdasarkan kemudahan saja. Seseorang diambil sebagai sampel karena kebetulan orang tadi ada di situ atau kebetulan dia mengenal orang tersebut. Oleh karena itu ada beberapa penulis menggunakan istilah accidental sampling – tidak disengaja – atau juga captive sample (man-on-the-street) Jenis sampel ini sangat baik jika dimanfaatkan untuk penelitian penjajagan, yang kemudian diikuti oleh penelitian lanjutan yang sampelnya diambil secara acak (random). Beberapa kasus penelitian yang menggunakan jenis sampel ini, hasilnya ternyata kurang obyektif.
2. Purposive Sampling
Sesuai dengan namanya, sampel diambil dengan maksud atau tujuan tertentu.Seseorang atau sesuatu diambil sebagai sampel karena peneliti menganggap bahwa seseorang atau sesuatu tersebut memiliki informasi yang diperlukan bagi penelitiannya. Dua jenis sampel ini dikenal dengan nama judgement dan quota sampling.
Judgment Sampling
oleh suatu perusahaan, maka manajer produksi merupakan orang yang terbaik untuk bisa memberikan informasi. Jadi, judment samplingumumnya memilih sesuatu atau seseorang menjadi sampel karena mereka mempunyai “information rich”.
Dalam program pengembangan produk (product development), biasanya yang dijadikan sampel adalah karyawannya sendiri, dengan pertimbangan bahwa kalau karyawan sendiri tidak puas terhadap produk baru yang akan dipasarkan, maka jangan terlalu berharap pasar akan menerima produk itu dengan baik. (Cooper dan Emory, 1992).
Quota Sampling
Teknik sampel ini adalah bentuk dari sampel distratifikasikan secara proposional, namun tidak dipilih secara acak melainkan secara kebetulan saja.
Misalnya, di sebuah kantor terdapat pegawai laki-laki 60% dan perempuan 40% . Jika seorang peneliti ingin mewawancari 30 orang pegawai dari kedua jenis kelamin tadi maka dia harus mengambil sampel pegawai laki-laki sebanyak 18 orang sedangkan pegawai perempuan 12 orang.Sekali lagi, teknik pengambilan ketiga puluh sampel tadi tidak dilakukan secara acak, melainkan secara kebetulan saja.
3. Snowball Sampling – Sampel Bola Salju