Kumpulan Rumus Cepat Matematika SMA

http://meetabied.wordpress.com

SMAN 1 Bone-Bone, Luwu Utara, Sul-Sel

Bergaullah dengan para pemenang karena pemenang memberi pengaruh baik kepada Anda. Sedangkan pecundang dapat meracuni Anda. (John D. Rockefeller)

[

RUMUS CEPAT MATEMATIKA

]

================================================================================ Materi ini dapat disebarluaskan secara bebas, untuk tujuan bukan komersial, dengan atau tanpa

1Persamaan kuadrat yang akar-akarnya kebalikan dari akar-akar ax2+ bx + c = 0 Adalah :

cx2 +bx +a = 0

(Kunchi : posisi a dan c di tukar )

1Jika akar-akar yang diketahui x1 dan x2 maka, kebalikan

akar-akarnya berbentuk :

2 1 x 1 dan 1 x r Missal akar-akar 2x2 -3x + 5 = 0

x1 dan x2 . maka Persamaan

baruakar-akarnya

1 1

x dan ₂

1

x

r α = 1 1

x dan β = ₂

1

x

a +β =

1

1

x + ₂

1

x = _{1 2}

2 1 .x x x x + = 5 3 = -= -c b a c a b

a . β =

1

1

x . 2

1 x = 2 1. 1 x

x = 5

2

= c a

r Gunakan Rumus : x2 –(a +β)x + a .β = 0

x2 -5 3 x + 5 2 = 0

5x2 -3x + 2 = 0 1. UMPTN 1991

Persamaan kuadrat yang akar-akarnya kebalikan dari akar-akar persamaan 2x2-3x + 5 = 0 adalah..

A. 2x2 -5x + 3 = 0 B. 2x2 + 3x + 5 = 0 C. 3x2 -2x + 5 = 0 D. 3x2 -5x + 2 = 0 E. 5x2 -3x + 2 = 0

@

Perhatikan terobosannya

2x -3x +5 = 0 2

5x -3x +2 = 0 2

di tuker ..aja..OK !

1 Persamaan kuadrat yang akar-akarnya BERLAWANAN dari akar-akar ax2+ bx + c = 0 adalah : ax2 -bx +c = 0

(Kunchi : Tanda b berubah)

1 Jika akar-akar yang diketahui x1 dan x2 maka, Lawan akar-akarnya berbntuk –x1 dan -x2

r Missal akar-akar :

5x2 -8x + 6 = 0 , x1 dan x2 . maka Persamaan baru akar-akarnya –x1 dan –x2

r α = -x1dan β = -x2

a

+β = -x1 –x2

= -(x1 + x2)

= -

5 8

-= =

-a b a

b

a

. β = -x1 .(-x2) = x1 .x2

=

5 6

= a c

r Gunakan Rumus : x2 –(

a

+β)x +

a

.β = 0

x2

-5 8

-x +

5 6

= 0

5x2 + 8x + 6 = 0

2. Prediksi UAN/SPMB

Persamaan kuadrat yang akarnya berlawanan dengan akar-akar persamaan 5x2-8x + 6 = 0 adalah..

A. 2x2 -5x + 3 = 0 B. 2x2 + 3x + 5 = 0 C. 5x2 -6x + 8 = 0 D. 5x2 + 8x + 6 = 0

E.

5x2 -8x -6 = 0

@

Perhatikan terobosannya :

5x -8x +6 = 0 2

5x +8x +6 = 0 2 berubah tanda...!

1Persamaan kuadrat yang akar-akarnya n kali (artinya : nx1 dan nx2) akar-akar persamaan ax2+ bx + c = 0 adalah : ax2 +n.bx +n2.c = 0

@

Tiga kali, maksudnya : 3x1 dan 3x2

r Missal akar-akar : x2 + px + q = 0

x1 dan x2 . maka Persamaan baru akar-akarnya 3x1 dan 3x2

r Misal : α = 3x1dan β = 3x2

a

+β = 3x1 + 3x2

= 3(x1 + x2) =

3. p p

a b

3 1 3

-= -=

-a

. β = 3x1 .3x2 = 9( x1 .x2)

= 9. q q

a c

9 1 9

= =

r Gunakan Rumus : x2 –(

a

+β)x +

a

.β = 0 x2 –(-3p)x + 9q= 0 x2 + 3px + 9q = 0

Jawaban : E 3. UMPTN 2001/B

Persamaan kuadrat yang masing-masing akarnya tiga kali dari akar-akar persamaan kuadrat x2 + px+ q = 0 adalah….

A. 2x2+ 3px + 9q = 0 B. 2x2-3px + 18q = 0 C. x2-3px+ 9q = 0 D. x2+ 3px -9q = 0 E. x2+ 3px + 9q = 0

@

Perhatikan terobosannya

x +px +q =0

2

n = 3

3

3

2

kalikan

@

Persamaan kuadrat yang akar-akarnya k lebihnya (x1 +k) dan (x2 +k) dari akar-akar persamaan ax2+bx +c = 0 adalah :

a(x-k)2 +b(x-k) +c = 0

@

Dua lebih besar, maksudnya : x1+2 dan x2 +2

r Missal akar-akar : 3x2 _{-12x +2 = 0 adalah} x1 dan x2 . maka Persamaan baru akar-akarnya x1+2 dan x2+2

r α = x1+2 dan β = x2+2

a +β = x1+2 +x2+2 = (x1 +x2) +4 =

8 4 3 12

4=-- + =

+

-a b

a . β = (x1+2)(x2+2) = (x1.x2) +2(x1+x2) +4

= +2(- )+4 a b a c

=

3 38 4 3 24

3 2

= + +

r Gunakan Rumus : x2 –(a+β)x + a.β = 0

x2 –8x + 3 38

= 0

3x2 _{-24x +38 = 0}

Jawaban : A 4. UMPTN 1997

Persamaan kuadrat yang akarnya dua lebih besar dari akar-akar persamaan kuadrat 3x2 -12x+ 2= 0 adalah….

A. 3x2-24x+ 38= 0 B. 3x2+ 24x+ 38= 0 C. 3x2-24x-38= 0 D.3x2-24x+ 24= 0 E. 3x2-24x-24= 0

@

Perhatikan terobosannya :

3(x -2)2 -12(x -2) +2 = 0

3(x2 -4x +4) -12x +24 +2 = 0

@

akar-akar

a 1 - dan a 1

-Ditulis :

-

x 1

Berlawanan

Berkebalikan

r Persamaan 2x2 -3x + 5 = 0

a

+β =

2 3 2 3 = -= -a b

a

. β =

2 5

=

a c

J = Jumlah = a 1 -b 1 = 5 3 2 5 2 3 . ÷÷_ø=- = -ö çç è æ +

-b

a

b

a

K = Kali = ( b 1 - )( a 1 - ) = b a. 1 = 5 2 = c a

r Gunakan Rumus : x2 –Jx + K = 0

x2 + 5 3

x + 5 2

= 0

5x2 + 3x + 2 = 0

Jawaban : C 5. PREDIKSI UAN/SPMB

Persamaan kuadrat 2x2 -3x+ 5= 0 akar-akarnya

a

dan β, maka

persamaan kuadrat baru yang akar-akarnya

a 1 - dan

b

1 - adalah…...

A. x2-24x+ 3 = 0 B. x2+ 24x+ 3 = 0 C. 5x2+ 3x + 2 = 0 D. 5x2-3x + 2 = 0 E. 5x2-2x-2 = 0

@

Perhatikan terobosannya :

2x2 -3x +5 = 0

Berkebalikan :

5x2 -3x +2 = 0

Berlawanan :

1 ax2 + bx + c = 0

D

³

0

à

syarat kedua akarnya Nyata,

D = b2 -4.a.c

1

³

0 ,artinya :bil.kecil _“atau_” bil.besar

1Persamaan kuadrat : x2 + (m -2)x + 9 = 0 a = 1

b = m -2 c = 9

mempunyai dua akar nyata, maka D ≥ 0

b2-4ac ≥ 0 (m -2)2 -4.1.9

³

0

m2 -4m -32

³

0 (m -8)(m + 4)

³

0

Pembuat nol : m = 8 atau m = -4 Garis Bilangan :

Jadi : m

£

-4 atau m

³

8

Jawaban : A

6. EBTANAS 2002/P1/No.1

Persamaan kuadrat x2 + (m -2)x + 9 = 0 akar-akarnya nyata. Nilai m yang memenuhi adalah…

A. m

£

-4 atau m

³

8 B. m

£

-8 atau m

³

4 C. m

£

-4 atau m

³

10 D. -4

£

m

£

8

E. -8

£

m

£

4

1x2 + (m -2)x + 9 = 0 D ≥ 0

Þ

b2-4ac ≥ 0 (m -2)2 -4.1.9

³

0

m2 -4m -32

³

0 (m -8)(m + 4)

³

0

Karena Pertidaksamaannya

≥ 0, maka :

Jadi : m ≤ -4 atau m ≥ 8

+

-

+

+

1 ax2 + bx + c = 0

D = 0 _à syarat kedua akar- nya Nyata dan sama

1 Jumlah akar-akarnya :

a

b

x

x

₁

+

₂

=

-1 (k + 2)x2 -(2k -1)x + k -1 = 0 a = k+ 2

b = -(2k-1) c = k-1 D = 0 , syarat

b

2

-4.a.c = 0

(

2k-1)2-4(k + 2)(k -1) = 0 4k2 -4k + 1 -4k2-4k + 8 = 0

ð

k = 8 9

7. EBTANAS 2003/P2/No.1

Persamaan kuadrat (k + 2)x2 -(2k -1)x + k -1 = 0 akar-akarnya nyata dan sama. Jumlah kedua akar persamaan tersebut adalah…

A.

8 9

B.

9 8

D.

5 2

C.

2 5

E.

5 1

1

5 2 25 10

1 1

1 1 2

8 9 4 9 2

1 = =

+ -= +

-= -= +

k k a b x

x

1 Jika akar-akar x1 dan x2 , maka yang dimaksud “ Jumlah Kebalikan “ adalah

c b x x₁ + ₂ =

-1 1 1 3x2-9x + 4= 0, missal

akar-akarnya x1 dan x2 maka :

4

9

4

3

3

9

3

4

3

9

.

1

1

2 1

2 1

2 1

=

´

=

-=

-=

+

=

+

a

c

a

b

x

x

x

x

x

x

JAWABAN : D

8. EBTANAS 1995

Jumlah kebalikan akar-akar persamaan 3x2-9x + 4= 0 adalah….

A. -₉4

B. -₄3

C. -₄9

D. ₄9 E. ¾

1

3x

2

-9x +4 = 0

4 9 4

9 1

1

2 1

= -=

-= +

c b

1 Jumlah Kuadrat 2 2 2 2 2 1 2 a ac b x

x + =

-1 x2- (2m + 4)x + 8m = 0 x1 + x2 = 2m + 4 x1x2 = 8m

1 Jika akar-akar x1 dan x2 , maka yang dimaksud “ Jumlah kuadrat “ adalah x1

2 + x2

2

= (x1 + x2) 2

-2x1x2

1 x1 2

+ x2 2

= 52 (x1 + x2)

2

-2x1x2 = 52 (2m + 4)2 -2(8m) = 52 4m2 + 16m + 16 -16m = 52 4m2 = 36

m2 = 9

m = 3 atau m = -3

JAWABAN : B 9. PREDIKSI UAN/SPMB

Bila jumlah kuadrat akar-akar persamaan :

1 Jika Persamaan : ax2 + bx + c = 0,

mempunyai perban -dingan m : n, maka ;

2 2

) (

) . (

n m a

n m b c

+ =

1 Persamaan x2 -8x + k = 0 x1 : x2 = 3 : 1 atau x1 = 3x2 …….(i)

@

₁+ ₂ =- =8

a b x x

3x2+ x2 = 8

4x2 = 8 berarti x2 = 2

@

x2 = 2 substitusi ke (i) x1 = 3.2 = 6

@

k

a c x x₁. ₂ = =

6.2 = k berarti k = 12

JAWABAN : B

10. EBTANAS 2000

Persamaan x2 -8x + k = 0 mempunyai akar-akar yang berbanding seperti 3 : 1, harga k adalah…

A. 10 B. 12 C. 16 D. 8 E. -8

1

x

2

-8x +k = 0

.Perbandingan 3 : 1

12 16

3 . 64

) 1 3 .( 1

) 1 . 3 .( ) 8 (

2 2

1 Jika akar-akar persamaan ax2 +bx +c = 0, x1 dan x2 maka :

a D x

x₁ - ₂ = atau

1 a ac b x x 4 2 2 1 -=

-1 2x2 -6x –p = 0 x1– x2 = 5 x1+ x2 = 3

x1.x2 =

2 p -8 16 2 9 25 ) 2 ( 2 3 25 2 ) ( 25 ) 2 .( 2 5 2 ) ( 2 2 1 2 2 1 2 2 2 2 2 2 2 1 2 2 2 1 1 1 = = + + = + -= + -+ = -+ = + -= -p p p p p p p x x x x p x x x x x x x x

1 p2 -2p = 64 -2.8 = 64 -16 = 48

JAWABAN : C 11. PREDIKSI UAN/SPMB

Akar-akar persamaan 2x2 -6x –p = 0 adalah x1 dan x2, jika x1– x2 = 5, maka nilai p2 -2p adalah…

A. 42 B. 46 C. 48 D. 64 E. 72 1

1 2x2 -6x –p = 0 x1 –x2 = 5

p

p

8 36 10

5 ( 6) ₂4.2( )

2

+ =

= - - -

100= 36 + 8p ,berarti p = 8 p2 -2p = 64 -2.8

1 Jika ax2 + bx + c = 0, Kedua akarnya berlainan maka : D > 0 atau b2 -4ac > 0

1 ≥ 0

> 0, artinya terpisah Jadi : kecil “ atau” besar

1 x2 + ax + a = 0 kedua akar berlainan, syarat D > 0 atau : b2 -4ac > 0

a2 -4a > 0 a(a -4) > 0

Karena > 0 artinya terpisah.

Jadi : a < 0 atau a > 4 Mudeh……. .!

JAWABAN : C 12. PREDIKSI UAN/SPMB

Supaya persamaan x2 + ax + a = 0 mempunyai dua akar berlainan, harga a harus memenuhi…

A. a

£

0 atau a

³

4 B. 0

£

a

£

4

1 Jika akar-akar : ax2 + bx + c = 0, tidak sama tandanya , maka :

( i ) x1 .x2 < 0 dan ( ii ) D > 0

1 x2 -2ax + a + 2 = 0

berlainan tanda, syaratnya : ( i ) x1 .x2 < 0

a + 2 < 0 , berarti a < -2 ( ii ) D > 0

4a2-4.1.(a + 2) > 0 4a2 -4a -8 > 0

a2 –a -2 > 0 (a -2)(a + 1) > 0

a < -1 atau a > 2

Jadi : a < -2

JAWABAN : E

13. PREDIKSI SPMB

Jika akar-akar persamaan kuadrat x2 -2ax + a -2 = 0 tidak sama tandanya, maka….

A. a < -1 atau a > 2 B. -1 < a < 2 C. -2 < a < 2 D. -2 < a < 1 E. a < -2

-2

-1 2

(i)

1 Supaya kedua akar ax2+ bx + c = 0 imajiner atau tidak real ,maka : D < 0

1 D = b2-4ac < 0

≤ 0 , artinya terpadu

Jadi :

kecil “ tengahnya” besar

1 x2+ (m + 1)x + 2m -1 = 0

D < 0

(m + 1)2 -4.1.(2m -1) < 0 m2 + 2m + 1 -8m + 4 < 0

m2 -6m + 5 < 0

(m -1)(m -5) < 0 < 0, artinya terpadu Jadi : 1 < m < 5

kecil besar

tengahnya

JAWABAN : E 14. PREDIKSI UAN/SPMB

Agar supaya kedua akar dari x2+ (m + 1)x + 2m -1= 0 tidak real, maka haruslah…

A. m < 1 atau m > 5 B. m

£

1 atau m

³

5 C. m > 1

1 Jika akar-akarPersamaan ax2 + bx + c = 0, mempu-

nyai perbandingan m : n, maka

2 2

) (

) . (

n m a

n m b c

+ =

1 x2 + px + q = 0, akar-akarnya dua kali akar yang lain, artinya : x1 = 2x2

1 p

a b x

x₁+ ₂ =- =

-2x2 + x2 = -p

3x2 = -p atau x2 =

-3

p

1 q

a c x x₁. ₂= =

2x2.x2 = q

2(-3

p

)(-3

p ) = q

q p

=

9 2 2

2p2 = 9q

JAWABAN : C

15. PREDIKSI SPMB

Jika salah satu akar x2 + px + q = 0 adalah dua kali akar yang lain, maka antara p dan q terdapat hubungan…

A. p = 2q2 B. p2 = 2q C. 2p2 = 9q D. 9p2 = 2q E. p2 = 4q

1

1 x2 +px +q = 0 x1 = 2x2 atau

x1 : x2 = 2 : 1

1 ₂

2

) 1 2 .( 1

) 1 . 2 (

+

= p

q

1 ax2 + bx + c = 0, maka

a c x x₁. ₂ = 1 Persamaan ax2 + 5x -12 = 0

salah satu akarnya x1 = 2, maka : a(2)2 + 5.2 -12 = 0 4a + 10 -12 = 0

a =

2 1

1 x1.x2 = -2 1 12

e

_2x

2 = -24

x2 = -12

JAWABAN : A 16. PREDIKSI UAN/SPMB

Jika salah satu akar persamaan ax2+ 5x -12 = 0 adalah 2, maka …. A. a = ½ , akar yang lain -12

1 Jika akar-akar :

ax2 + bx + c = 0, x1 dan x2 maka Persamaan baru yang akar-akarnya x1

2 dan x2

2

adalah :

a2x2 –(b2-2ac)x + c2 = 0 1 x2 -5x + 2 = 0, akar p dan

q

p + q = a b - = 5

p.q = a c

= 2

missal akar-akar baru

a

dan β

1

a

= p2dan β = q2

a

+β = p2 + q2 = (p + q)2 -2pq = 25-2.2 = 21

a

.β = p2 .q2 = (p.q)2 = 22 = 4

1 Gunakan Rumus :

x2 –(

a

+β)x +

a

.β = 0 x2 -21x + 4 = 0

JAWABAN : B

17. Persamaan kuadrat x2 -5x + 2 = 0 mempunyai akar p dan q. Persamaan kuadrat dengan akarr-akar p2 dan q2 adalah…

A. x2 + 21x + 4 = 0 B. x2 -21x + 4 = 0 C. x2 -21x -4 = 0 D. x2 + x -4 = 0 E. x2 + 25x + 4 = 0

1 x2 -5x + 2 = 0 a = 1, b = -5, c = 2

1 Selisih akar-akar persa-maan ax2 + bx + c = 0

adalah :

a D x x₁- ₂ =

atau 2 2 2 1 ) ( a D x

x - =

1 x2-nx + 24 = 0 x1+ x2 = n x1.x2= 24

diketahui x1-x2 = 5

11 121 96 25 48 48 25 48 24 . 2 25 48 2 ) ( 25 24 . 2 5 2 ) ( 2 2 2 2 2 1 2 2 1 2 2 2 2 2 2 2 1 2 2 2 1 1 1 ± = = -= -= -= -+ = -+ = + -= -n n n n n x x x x x x x x x x x x

1 Jumlah akar-akar : x1+ x2 = n =

!

11

JAWABAN : A

18. PREDIKSI UAN/SPMB

Jika selisih akar-akar persamaan x2-nx + 24 = 0 sama dengan 5, maka jumlah akar-akar persamaan adalah….

A. 11 atau -11 B. 9 atau -9 C. 7 atau -8 D. 7 atau -7 E. 6 atau -6

1 x2-nx + 24 = 0

2 2 2 1 24 . 1 . 4 5 = n

25 = n2 -96 n2 = 121 n =

!

11

1 Ingat... “ Nilai Max/min “ arahkan pikiran anda ke “TURUNAN = 0” 1 Ingat juga :

2 2 2 2 2 1 2 a ac b x

x + =

-1 x2+ kx+ k = 0 x1 + x2 = -k x1.x2 = k

1 Misal : z = x₁2 +x₂2

k k k k a c a b x x x x x x z 2 1 2 ) 1 ( 2 ) ( . 2 ) ( 2 2 2 2 1 2 2 1 2 2 2 1 -= -= -= -+ = + =

1 z’ = 2k -2 0 = 2k -2

e

k = 1

JAWABAN : E 19. PREDIKSI UAN/SPMB

Jika x1 dan x2 akar-akar persamaan x 2

+ kx+ k= 0 maka x1 2

+ x2 2

mencapai nilai minimum untuk k sama dengan…. A. -1

B. 0 C. ½ D. 2 E. 1

1

x

2

+ kx+ k = 0

k

k

k

k

a

ac

b

x

x

z

2

1

.

1

.

2

2

2 2 2 2 2 2 2 2 1

-=

-=

-=

+

=

1 z’ = 2k -2

1 ax2+ bx + c = 0, akar-akar mempunyai perbandingan :

n

a

= m

b

, maka :

2 2

) .(

) . (

n m a

n m b c

+ =

1

x

2

+ 4x+ a-4= 0

,

akar-akarnya mempunyai perbandingan :

a

= 3β

1 + =- =-4

a b

b

a

3β +β = -4

4β = -4 atau β = -1

4 . = =a

-a c

b

a

3β.β = a -4 3(-1)(-1) = a - 4 3 = a -4 , berarti a = 7

JAWABAN : D

20. PREDIKSI UAN/SPMB

a

dan

b

adalah akar-akar persamaan kuadrat :

x2+ 4x+ a-4= 0, jika

a

= 3

b

, maka nilai a yang memenuhi adalah…. A. 1

B. 4 C. 6 D. 7 E. 8

1 x2+4x+a-4=0

7 4 3

3 16

16 . 3

) 3 1 .( 1

) 3 . 1 ( 4 4

2 2

= + =

= = + =

-a a

p Jumlah akar-akar = 0, maksudnya adalah : x1 + x2 = 0, berarti :

-a b

= 0

Sehingga b = 0

@

x2+ (2p-3)x + 4p2-25 = 0 diketahui : x1 + x2 = 0

-a b

= 0

- 0

1 3 2p- ₌

, berarti :

2p -3 = 0 atau p =

2 3

@

untuk p =

2 3

substitusi keper

samaan kuadrat , di dapat : x2 + 0.x + 4(3/2)2-25 = 0

x2 + 9 -25 = 0 x2 = 16 x =

!

4

JAWABAN : D 21. PREDIKSI UAN/SPMB

Jika jumlah kedua akar persamaan :

x2+ (2p-3)x + 4p2-25 = 0, sama dengan nol, maka akar-akar itu adalah….

A. 3/2 dan – 3/2 B. 5/2 dan – 5/2 C. 3 dan 3 D. 4 dan -4 E. 5 dan -5

1

x2+ (2p-3)x + 4p2-25 = 0 b = 0 (syarat jumlah = 0) 2p -3 = 0

e

p = 3/2 x2 + 0.x+ 4(3/2)2-25 = 0 x2 + 9 -25 = 0

p Jika akar-akar persaman x1 dan x2 ,maka akar-akar yang n lebih besar

maksudnya x1+ n dan x2+ n

p Persamaan kuadrat yang akar-akarnya n lebih besar (x1+ n dan x2+ n) dari akar-akar persamaan :

ax2 + bx + c = 0 adalah : a(x-n)2 + b(x-n) + c = 0

13x2 -12x + 2 = 0

x1 +x2 = 4

3 12₌

-=

-a b

x1.x2 =

3 2

= a c

1Persamaan baru yg akar-akarnya dua lebih besar, artinya : x1 + 2 dan x2 + 2 missal

a = x1 + 2 dan β = x2 + 2 a+β = x1 + x2 + 4

= 4 + 4 = 8 a .β = (x1 + 2)( x2 + 2)

= x1.x2 + 2(x1+ x2) + 4

=

3 2

+ 2.4 + 4 = 12+

3 2

=

3 38

1Gunakan Rumus : x2 –(a +β)x +a.β = 0

x2 -8x +

3 38

= 0 --- kali 3

3x2 -24x + 38 = 0

JAWABAN : A 22. PREDIKSI UAN/SPMB

Persamaan kuadrat yang akarnya dua lebih besar dari akar-akar persamaan :

3x2 -12x + 2 = 0 adalah….. A. 3x2 -24x + 38 = 0 B. 3x2 + 24x + 38 = 0 C. 3x2 -24x -38 = 0 D. 3x2 -24x + 24 = 0 E. 3x2 -24x -24 = 0

1 Perhatikan terobosannya

n = 2 à 3x2 12x +2 = 0 3(x -2)2-12(x -2) +2 = 0 3(x24x+4) -12x+24 +2 = 03x212x +12 -12x + 26= 0

1 Salah satu akar ax2+ bx+ c = 0 adalah k lebih besar dari akar yang lain, maksudnya :

x1 = x2 + k, di dapat :

D = a2k2

1

x

2

+ax -4 = 0

x1 +x2 = a a a b -= -= -1

x1.x2 = 4

1 4₌

-= a c

diketahui salah satu akarnya 5 lebih besardari akar yang lain,maksudnya x1 = x2 +5 1x1 +x2 = -a

x2 +5 +x2 = -a

2x2 = -a -5 sehingga

2 5 2 -= a

x berarti :

2 5 5 2 5 1 + -= +

-= a a

x

1x1.x2 = -4

3 9 16 25 4 2 ) 5 ( . 2 ) 5 ( 2 2 ± == -= -= + -a a a a a

JAWABAN : C

23. PREDIKSI UAN/SPMB

Salah satu akar persamaan x2+ ax -4 = 0 adalah lima lebih besar dari akar yang lain. Nilai a adalah….

A. -1 atau 1 B. -2 atau 2 C. -3 atau 3 D. -4 atau 4 E. -5 atau 5

1Perhatikan terobosannya x2+ ax -4 = 0

2 (a +b)2=a2 +2ab +b2

2 (a -b)2 = a2 -2ab +b2 = (a +b)2-4ab

2 x2 +ax -4 = 0 x1+x2 = -a

x1.x2 = -4

2 x1 2

-2x1x2 +x2 2

= 8a (x1+x2)

2

-4x1x2 = 8a

a2 -4.(-4) = 8a a2 +16 = 8a a2 -8a +16 = 0 (a -4)(a -4) = 0 a = 4

JAWABAN : B

24.PREDIKSI UAN/SPMB

Akar persamaan x2+ ax -4 = 0 adalah x1 dan x2, jika x1 2

-2x1x2 + x2 2

= 8a, maka nilai a adalah….

1 Ingat...! 2 2 2 2 2 1

2

a

ac

b

x

x

+

=

-2 x2 -5x + k + 3 = 0

x1 + x2 = 5

1 5₌ -= -a b

x1.x2 = 3

1 3

+ = +

=k k

a c

2 x1 2

+ x2 2

= 13 (x1+ x2)

2

-2x1.x2 = 13 52 -2(k + 3) = 13 25 -2k -6 = 13 2k = 19 -13 2k = 6 k = 3

JAWABAN : B

25. PREDIKSI UAN/SPMB

Jika x1 dan x2 adalah akar-akar persamaan kuadrat : x2 -5x + k + 3 = 0, dan x1

2 + x2

2

= 13, maka k adalah…. A. 0

B. 3 C. 6 D. 9 E. 18

1

x

2

-5x + k + 3 = 0

x

12

+ x

22

= 13

13 2 2 2 = -a ac b 13 1 ) 3 k .( 1 . 2 25 2 = +

1 Ingat....!

3 3 3 2 3 1

3

a abc b

x

x + =- +

atau

) ( 3 )

( _{1 2} 3 _{1 2 1 2}

3 2 3

1 x x x xx x x

x + = + - +

Stasioner

e

TURUNAN = NOL

1 x2 –(a -1)x + a = 0 x1 + x2 = - =a-1

a b

x1.x2 = a a a c

= =

1

1 missal :

z = x1 3

+ x2 3

+ 3x1x2 = (x1+ x2)

3

-3x1x2(x1+ x2)+ 3x1x2 = (a -1)3-3a(a -1) + 3a = (a -1)3 -3a2 + 6a z’ = 3(a -1)2-6a + 6 = 3(a2-2a+ 1) -6a + 6 = 3a2 -12a + 9 0 = 3a2-12a + 9 a2 -4a + 3 = 0 (a -3)(a -1) = 0 a = 3 atau a = 1

JAWABAN : B

26. PREDIKSI UAN/SPMB

Jika x1 dan x2 merupakan akar persamaan : x2 –(a -1)x + a = 0. Nilai stasioner dari x1

3

+ 3x1x2 + x2 3

dicapai untuk a = ….

A. 1 dan 2 B. 1 dan 3 C. 3 dan 2 D. -1

1 Jika kedua akar : ax2+ bx + c = 0 saling berkebalikan, maka : a = c

1 p2x2-4px + 1 = 0 kedua akarnya saling berkebalikan, artinya :

2 1

1

x

x = atau

x1 .x2 = 1

1 1 1 1

1

2 2

± ==

= =

p p p a c

1 Jadi p = -1 atau p = 1

JAWABAN : E

27. PREDIKSI UAN/SPMB

Kedua akar persamaan p2x2-4px + 1 = 0 berkebalikan, maka nilai p adalah….

A. -1 atau 2 B. -1 atau -2 C. 1 atau -2 D. 1 atau 2 E. -1 atau 1

1

p

2

x

2

-4px +1 = 0

a = c

p

2

= 1

1 Persamaan kuadrat

Baru : x2 + Jx + K = 0 J = Jumlah akar-akarnya K = Hasil kali akar-akarnya

1

x2 + 6x -12 = 0

x2 –(

.

)

.

₁

.

₂

0

2 3 1 3 2 1 2 3 1

3

+

+

x

x

x

+

+

x

x

=

x x x

x

x2 –(

.

)

(

).

₁

.

₂

0

2 . 1

) 2 1 ( 3 2 1 2 . 1

) 2 1 (

3 +

+

+

+

=

x

x

x

x

x

x x

x x x

x x x

x2 –(3(-

)

c b ₊

a

c_{)x+ 3(-}

)

a b _{= 0}

x2 –( 2

3_{-12)x -18= 0 ….Kalikan 2} x2 + 21x -36 = 0

28. Akar-akar persamaan x2 + 6x -12 = 0 adalah x1 dan x2. Persamaan

baru yang akar-akarnya

2 1 x

3 x

3 ₊

dan x1.x2 adalah….

1

x

2

+

(

x

12

+

x

22

)

x

+

4

=

0

a = 1

b = x₁2 +x₂2

c = 4

1 ₂

2 2 2 2 1

2

a ac b x

x + =

-1 x2+(x₁2 +x₂2)x+4=0 akar-akarnya u dan v

u+v = -u.v , artinya :

4 ) ( ₁2 + ₂2 =

-- x x

4 2 2 2 1 +x =

x

1 x2 +6x +c = 0, 4 2 2 2 1 +x =

x

16 32 2

4 2 36

4 1

. 1 . 2 36

2

== =

-=

-c c

c c

1 x13x2+x1x23=x1.x2(x12+x12)

= c. 4 = 4c = 4.16 = 64

JAWABAN : E

29. SPMB 2003//420-IPA/No.11

Akar-akar persamaan kuadrat x2 + 6x + c = 0 adalah x1 dan x2.

Akar-akar persamaan kuadrat

x

2

+

(

x

₁2

+

x

₂2

)

x

+

4

=

0

adalah u dan v.Jika u+ v = -u.v, maka

x

₁3

x

₂

+

x

₁

x

₂3= ….

1 ax2 +bx +c = 0, tidak mempunyai akar real artinya : b2 -4ac < 0

O

2x(mx -4) = x

2

-8

2mx

2

-8x = x

2

-8 atau

(1-2m)x

2

+8x -8 = 0

D < 0 (syarat )

b

2

-4ac < 0

8

2

-4(1-2m)(-8) < 0

64 +32(1-2m) < 0

2 + 1 -2m <0

3 < 2m

m >

2

3

.

berarti m bulat adalah :

2,3,4,5,…..

Jadi m bulat terkecil adalah : 2

Jawaban : D

30. UAN 2003/P-1/No.1

Bilangan bulat m terkecil yang memenuhi persamaan 2x(mx -4) = x2 -8 agar tidak mempunyai akar real adalah…. A. -2

1 Persamaan kuadrat, dapat di susun menggunakan rumus : x2 –Jx +K = 0

dengan :

J = Jumlah akar K = hasil kali akar

1 Diketahui akar-akarnya 5 dan -2, berarti : x1 = 5 dan x2 = -2

1 x1 + x2 = 5 + (-2) = 3 x1 .x2 = 5.(-2) = -10

1 Persamaan kuadrat yang

akar-akarnya x1 dan x2 rumusnya adalah : x2 –(x1+ x2)x + x1.x2 = 0 x2 -3x -10 = 0

JAWABAN : E

31. UAN 2004/P-1/No.1

Persamaan kuadrat yang akar-akarnya 5 dan -2 adalah… A. x2 + 7x + 10 = 0

B. x2 -7x + 10 = 0 C. x2 + 3x + 10 = 0 D. x2 + 3x -10 = 0 E. x2 -3x -10 = 0

1 Akar-akar 5 dan -2, maka : x2 –Jx +K = 0

1 Fungsi kuadrat : F(x) = ax2 + bx + c mem- Punyai nilai max/min

a D x f 4 )

( _max/min

-=

1 Soal yang berkaitan dengan nilai

maksimum atau minimum diselesaikan dengan :

“Turunan = 0”

1 Pandang h(t)=10t-t2

sebagai fungsi kuadrat

dalam t. maka :

a = -1

b = 10

c = 0

1 Tinggi maksimum, dida- pat dengan rumus :

25 4 0 100 ) 1 ( 4 0 ). 1 .( 4 10 4 4 4 ) ( 2 2 max = -= -= -= -= a ac b a D t h

JAWABAN : B

1. UAN 2004/P-1/No.2

Tinggi h meter dari suatu peluru yang ditembakan vertical ke atas dalam waktu t detik dinyatakan sebagai

h

(

t

)

=

10

t

-

t

2. Tinggi maksimum peluru tersebut adalah…

A. 15 meter B. 25 meter C. 50 meter D. 75 meter E. 100 meter

1 h(t)=10t -t2

5 2 10 0 2 10 ) ( ' = -= -= t t t t h 25 25 50 5 5 . 10 ) 5

( = - 2= - =

1

1 Nilai minimum dari f(x) = ax2+ bx + c adalah

c

b

a

f

a b a b a

b

=

-

+

-

+

-

)

(

)

(

)

(

_{2 2} 2 ₂

1 f(x) = 2x2-8x + p a = 2

b = -8 c = p

Nilai maksimum = 12,

20 8 12 8 12 1 8 8 8 64 12 2 . 4 . 2 . 4 ) 8 ( 12 4 4 12 4 ) ( 2 2 max = + = + -= + -= -= -= -= -= p p p p p a ac b a D x f

JAWABAN : D

2.

Nilai minimum fungsi yang ditentukan oleh rumus f(x) = 2x2-8x + p adalah 20. Nilai f(2) adalah…. A. -28

B. -20 C. 12 D. 20 E. 28

1 f(x) = 2x2-8x + p

2 2 . 2 ) 8 (

2 = =

=- -

-a b x

1 20 = 2(2)2-8(2) + p 20 = -8 + p → p = 28

§ Titik Puncaknya :

÷ ø ö ç è æ -= ÷ ø ö ç è æ -+ = ÷ ÷ ø ö ç ç è æ -= ÷ ø ö ç è æ -4 9 , 2 1 4 8 1 , 2 1 1 . 4 ) 2 .( 1 . 4 ) 1 ( , 2 1 4 , 2 2 a D a b 1 f(x) = x2 –x –2

·Titik potong dengan sumbu X, yaitu y = 0

x2 –x –2 = 0

(x + 1)(x –2) = 0 di dapat x = -1 atau x = 2, maka koordinat titik potongnya dengan sumbu X adalah (-1,0) dan (2,0)

·Titik potong dengan sumbu Y, yaitu x = 0

Maka y = 02-0-2 = -2

Jadi titik potongnya dengan sumbu Y adalah (0, -2).

·Puncak : _÷

ø ö ç è æ -a D a b 4 , 2 Dari fungsi di atas : a = 1

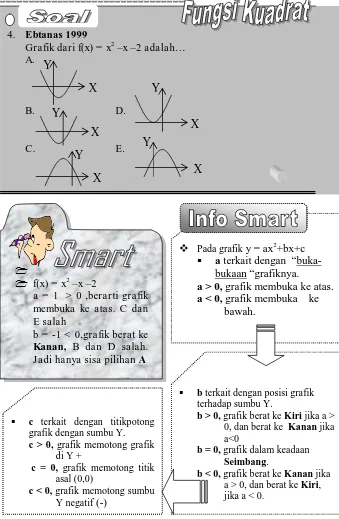
b = -1 c = -2 3. Ebtanas 1999

Grafik dari f(x) = x2 –x –2 adalah… A.

B. D.

C. E.

-v Pada grafik y = ax2+bx+c § a terkait dengan

“buka-bukaan “grafiknya.

a > 0, grafik membuka ke atas. a < 0, grafik membuka ke

bawah. 1

1 f(x) = x2 –x –2

a = 1 > 0 ,berarti grafik membuka ke atas. C dan E salah

b = -1 < 0,grafik berat ke Kanan, B dan D salah. Jadi hanya sisa pilihan A 4. Ebtanas 1999

Grafik dari f(x) = x2 –x –2 adalah… A.

B. D.

C. E.

Y

X

Y

X

Y

X

Y

X

Y

X

§ b terkait dengan posisi grafik

terhadap sumbu Y.

b > 0, grafik berat ke Kiri jika a >

0, dan berat ke Kanan jika a<0

b = 0, grafik dalam keadaan Seimbang.

b < 0, grafik berat ke Kanan jika

a > 0, dan berat ke Kiri, jika a < 0.

§ c terkait dengan titikpotong

grafik dengan sumbu Y.

c > 0, grafik memotong grafik

di Y +

c = 0, grafik memotong titik

asal (0,0)

c < 0, grafik memotong sumbu

@

Garis y = mx +n

@

Parabol y = ax2 +bx c, maka : D = (m-b)2 -4a(c –n)

@

Memotong di dua titik artinya :

(m-b)2 -4a(c –n) > 0

@

> 0 artinya “terpisah” oleh

atau

1 Garis y = x- 10 memotong y = x2 –ax + 6, didua titik. Berarti :

x –10 = x2 –ax + 6 x2 –ax –x + 6 + 10 = 0 x2-(a + 1)x + 16 = 0

1 Memotong di dua titik, maka D > 0

(a + 1)2 -4.1.16 > 0 a2 + 2a -63 > 0 (a + 9)(a -7) > 0 Uji ke garis bilangan : Missal nilai a = 0

(0 + 9)(0 –7) = -63 (negatif)

Padahal nilai a > 0 atau positif Jadi : a < -9 atau a > 7

JAWABAN : C

5. Garis y = x -10 memotong parabol y = x2 –ax + 6 di dua titik berlainan jika…..

A. a

≥

-9

B. a

≤

-9 atau a

≥

7 C. a < -9 atau a > 7

D. -9

≤

a

≤

7 E. -9 < a < 7

@

y = x- 10, y = x2 –ax +6

@

(m-b)2 -4a(c –n) > 0 (1 +a)2-4.1(6 +10) >0 (1 +a)2 –64 > 0 (1 +a+8)(1 +a-8) >0 (a +9)(a –7) > 0 Jadi : a < -9 atau a > 7

+

-

+

v y = a(x –p)2 + q q = nilai max/min untuk x = p

v Mempunyai nilai a untuk x = b , maksudnya y = a , x = b

v Misal fungsi kuadrat : y = ax2 + bx + c

x = 1, merupakan sumbu simetri, rumusnya

a b x

2

-= atau 1 =

a b

2

-2a = -b atau -2a + b = 0 …(i)

v Grafik melalui (1 ,2) berarti : 2 = a + b + c atau

a+ b + c = 2..(ii)

v Grafik melalui (2 ,3) berarti : 3 = 4a + 2b + c atau

4a+ 2b+ c= 3 …(iii)

v Pers(iii)-Pers(ii) di dapat: 3a + b = 1 ….(iv)

v Pers (iv)-pers(i) di dapat :

a = 1, substitusi ke pers (i) di dapat b = -2

untuk a = 1 dan b = -2 substitusi kepersamaan (ii) di dapat : c = 3

v Substitusikan nilai-nilai a,b dan c ke persamaan umum di dapat : y = x2 –2x + 3

JAWABAN : B

6. Fungsi kuadrat yang mempunyai nilai minimum 2 untuk x = 1 dan mempunyai nilai 3 untuk x = 2 adalah….

A. y = x2 -2x + 1 B. y = x2 -2x + 3 C. y = x2 + 2x -1 D. y = x2 + 2x + 1 E. y = x2 + 2x + 3

v

v y = a(x –p)2 + q

y = a(x -1)

2

+ 2

y = 3 untuk x = 2

3 = a(2 -1)

2

+ 2

didapat a = 1

v

Nilai minimum 2 untuk x = 1,artinya puncaknya di (1, 2) dan grafik pasti melalui puncak.

v

Nilai 3 untuk x = 2,artinya grafik tersebut melalui tutik (2 ,3)

v Misal fungsi kuadrat : y = ax2 + bx + c

x = 1, merupakan sumbu simetri, rumusnya

a b x

2

-= atau 1 =

a b

2

-2a = -b atau -2a + b = 0 …(i)

v Grafik melalui (1 ,2) berarti : 2 = a + b + c atau

a+ b + c = 2..(ii)

v Grafik melalui (2 ,3) berarti : 3 = 4a + 2b + c atau

4a+ 2b+ c= 3 …(iii)

v Pers(iii)-Pers(ii) di dapat: 3a + b = 1 ….(iv)

v Pers (iv)-pers(i) di dapat : a = 1, substitusi ke pers (i) di dapat b = -2

untuk a = 1 dan b = -2 substitusi kepersamaan (ii) di dapat : c = 3

v Substitusikan nilai-nilai a,b dan c ke persamaan umum di dapat: y = x2 –2x + 3

JAWABAN : B

7. Prediksi UAN/SPMB

Fungsi kuadrat yang mempunyai nilai minimum 2 untuk x = 1 dan mempunyai nilai 3 untuk x = 2 adalah….

A. y = x2 -2x + 1 B. y = x2 -2x + 3 C. y = x2 + 2x -1 D. y = x2 + 2x + 1 E. y = x2 + 2x + 3

1 Grafik melalui (1 ,2), uji x = 1 harus di dapat nilai y = 2 pada pilihan

1 Pilihan A :

y = 12 –2.1+ 1 = 0

¹

2 berarti pilihan A salah

1 Pilihan B

1 Ada garis : y = mx + n Parabol : y = ax2 + bx + c maka :

D = (b –m)2 -4.a(c –n) 1 Garis y = x + n akan

menyinggung parabola :

y = 2x2 _{+3x –5 , berarti :}

x + n = 2x2 _{+3x –5}

2x2 _{+3x –x –5 –n =0}

2x2 _{+2x –5 –n =0}

a = 2, b= 2 dan c = -5-n 1 Menyinggung,maka D = 0

b2_{-4ac = 0}

22 _{–4.2(-5-n) = 0}

4 –8(-5-n) = 0 4 +40 +8n =0 8n = -44

5 , 5

8 44

-=

-= n

JAWABAN : D

8. Prediksi UAN/SPMB

Garis y = x + n akan menyinggung parabola : y = 2x2 + 3x -5, jika nilai n sama dengan… A. 4,5

B. -4,5 C. 5,5 D. -5,5 E. 6,5

1

1 y = x +n , menyinggung parabol :

1 y =2x2+3x -5 (3 -1)2-4.2(-5-n) = 0 4 +40 +8n = 0

1 F(x) = ax2 + bx + c Nilai tertinggi atau nilai

terendah = a

ac b

4 4

2

-Perhatikan rumusnya SAMA

Gunakan info smart :

1

F(x) = ax

2

+ 4x + a

a = a, b = 4 dan c = a

Nilai tertinggi =

a

ac b

4 4

2

-a a a

4 . . 4 16 3

-=

16 -4a

2

= -12a

a

2

-3a -4 = 0

(a -4)(a + 1) = 0

a = -1 (sebab nilai

tertinggi/max , a < 0)

2 ) 1 ( 2

4 2 =- - =

-=

a b x

JAWABAN : D 9. Prediksi UAN/SPMB

Nilai tertinggi fungsi f(x) = ax2+ 4x+ a ialah 3, sumbu simetrinya adalah x = ….

1 y = ax2 +bx +c

Puncak _÷÷

ø ö çç è æ -- a ac b a b 4 4 , 2 2 1 y = x2 –kx + 11

a = 1, b = -k dan c = 11

Puncak _÷÷ ø ö çç è æ -- a ac b a b 4 4 , 2 2 ÷÷ ø ö çç è æ -= ÷÷ ø ö çç è æ -4 44 , 2 1 . 4 11 . 1 . 4 ) ( , 1 . 2 2 2 k k k k disini : 2 k x= dan

4 44 2 -=k y

diSusi-susi ke y = 6x-5

4 44 2 -k = 6. 2 k

-5 = 3k -5

k2 -44 = -4(3k -5) k2 + 12k -64 = 0 (k -4)(k + 16) = 0 k = 4 atau k= -16

1 untuk k = 4 Maka Puncak nya :

)

7

,

2

(

4

44

16

,

2

4

4

44

,

2

2

=

÷

ø

ö

ç

è

æ

-=

÷÷

ø

ö

çç

è

æ

-k

k

JAWABAN : A 10. Prediksi UAN/SPMB

Garis y = 6x -5 memotong kurva y = x2-kx + 11 di titik puncak P. Koordinat titik P adalah…..

A. (2, 7) B. (1, -1) C. (-2, -17) D. (-1, -11) E. (2, 13)

1

1 Perhatikan , kita asum sikan semua pilihan A –E adalah Puncak Parabola. Dan Puncak tersebut melalui garis

y = 6x-5

1 Uji pilihan A. Ganti x = 2 harus di dapat y = 7.

1 y = ax2 +bx +c Nilai max/min =

a

ac

b

4

4

2

-1 y = ax2 +bx +c

maksimum , berarti a negative.

Gunakan info smart :

1

y = 2ax

2

-4x + 3a

Nilai maksimum = 1

1

2

.

4

3

.

2

.

4

16

=

-a

a

a

16 -24a

2

= -8a

3a

2

–a -2 = 0

(3a + 2)(a -1) = 0

a = -2/3 (ambil nilai a <

0)

1

27a

2

-9a =

)

3 2 ( 9 9 4 .

27 -

= 12 + 6 = 18

JAWABAN : E

11. Prediksi UAN/SPMB

Jika fungsi kuadrat y = 2ax2-4x + 3a mempunyai nilai maksimum 1, maka 27a2-9a = ...

1 Sumbu simetri x = p Persamaman umum : y = a(x –p)2 + q Nilai maks/min = q

Gunakan info smart :

1 Fungsi y = a(x -1)2 + q x = 1 melalui (2,5) 5 = a + q ... (i) melalui (7,40) 40 = 36a + q .... (ii)

1 Dari (i) dan (ii) didapat :

) ( 40 36

5

-þ ý ü = +

= +

q a

q a

-35a = -35 , a = 1 substitusi ke pers (i)

berarti q = 4

1 Karena a = 1 > 0 berarti minimum , dan q = 4 Jadi Nilai ekstrimnya : minimum = 4

JAWABAN : C 12. Prediksi UAN/SPMB

Fungsi y = f(x) yang grafiknya melalui titik (2,5) dan (7,40) serta mempunyai sumbu simetri x = 1, mempunyai nilai ekstrim…..

1 Y = ax2 + bx + c Absis titik balik :

a b x

2

-=

Ordinat titik balik :

a ac b y

4 4

2

-=

Gunakan info smart :

1

y = -x

2

–(p -2)x + (p -4)

Ordinat = y = 6

4

16 4 4 4

) 1 ( 4

) 4 )( 1 ( 4 ) 2 (

2 2

6

6

-+ +

-=

=

p p p

p p

6 =

₄12

2

-p

à

p

2

-36 = 0

p

2

= 36,maka p = 6

Absis =

p_--₂2

=

6_--₂2

=

-

2

JAWABAN : B 13. Prediksi UAN/SPMB

Ordinat titik balik maksimum grafik fungsi :

y = -x2-(p -2)x + (p -4) adalah 6. Absis titik balik maksimum adalah… A. -4

1 y = ax2 +bx +c Sumbu Simetri :

a

b

x

2

-=

Nilai max:

a

ac

b

y

4

4

2

-=

gunakan Info Smart :

1 y = ax2+ 6x + (a + 1) Sumbu simetri :

3 =

a

2

6

-6a = -6

à

a = -1

1 Nilai max

=

)

1

(

4

)

1

1

)(

1

.(

4

36

-+

-= 9

Jawaban : D

14. Jika fungsi kuadrat y = ax2+ 6x + (a + 1) mempunyai sumbu simetri x = 3, maka nilai maksimum fungsi itu adalah…

1 Ada garis : y = mx +n 1 Ada parabol :

y = ax2 +bx +c

Berpotongan di dua titik, maka :

(b –m)2 -4a(c –n) > 0 1 Titik potong antara :

y = mx -14 dan

y = 2x2 +5x -12 adalah : mx -14 = 2x2 +5x -12 2x2 +5x –mx -12 +14 = 0 2x2 +(5 –m)x +2 = 0 1 D > 0 (syarat berpotongan)

b2 -4.a.c > 0 (5-m)2 -4.2.2 > 0 25 -10m +m2 -16 > 0 m2 -10m +9 > 0 (m -1)(m -9) > 0 Pembuat nol : m = 1 atau m = 9

1 Gunakan garis bilangan : + - +

1 9

Arah positif :

Jadi : m < 1 atau m > 9

Jawaban : C

15. Grafik fungsi kuadrat y = 2x2 + 5x -12 dan fungsi linier y = mx -14 berpotongan pada dua titik jika….

A. m < 9 B. 1 < m < 9

C. m > 9 atau m < 1 D. m > 1

E. m < -9 atau m > -1

1

y = mx -14

y = 2x

2

+5x -12

1

Berpotongan di dua

titik :

(5 –m)2 -4.2(-12 +14) > 0

1 Persamaan garis melalui (a,b) sejajar Ax+ By + C = 0 adalah :

Ax + By = Aa + Bb

Gunakan info smart :

1 Persamaan garis yang sejajar dengan 2x + y = 15 melalui titik (4,-6) adalah : 2x + y = 2(4) + (-6) = 2

2x + y = 2 y = -2x + 2

1 Titik potong garis y = -2x + 2

Dengan parabol y = 6 + x – x2 adalah :

6 + x –x2 = -2x + 2 x2 -3x -4 = 0 (x -4)(x + 1) = 0 x = -1 atau x = 4 untuk x = -1, di dapat : y = -2(-1) + 2 = 4

jadi memotong di (4,-6) dan di (-1,4)

Jawaban : C

16. Garis yang sejajar dengan garis 2x + y = 15 memotong kurva y = 6 + x –x2 di titik (4,-6) dan ..

A. (-4,14) B. (1, 4) C. (-1, 4) D. (2, 4) E. (1, 6)

1 Asumsikan y = 6 + x –x2 melalui semua titik pada pilihan, uji :

A. (-4,14)ð14= 6-4+ 16 = 18(S) B. (1, 4)_ð 4 = 6+ 1-1= 6(S) C. (-1,4)_ð 4 = 6-1-1 = 4 (B)

1 Pers.Kuadrat dengan puncak P(p, q) adalah

y = a(x –p)2 + q

1 f(x) = ax2+ bx + c sumbu simetrinya :

a 2

b x=

-Gunakan info smart :

1

f(x) = x

2

+4x +3

2

1

.

2

4

2

=

-=

-=

a

b

x

f(-2) = (-2)2 +4(-2) +3 = -1 Puncaknya : (-2, -1)

1 P(-2,-1) → y = a(x +2)2 -1 Mel (-1 ,3) → 3 = a(-1 +2)2 -1 → a = 4

1 Jadi y = 4(x +2)2 -1 = 4(x2+4x +4) -1 = 4x2 +16x +15

Jawab : C

17. Fungsi kuadrat yang grafiknya melalui titik (-1 ,3) dan titik terendahnya sama dengan puncak grafik f(x) = x2 + 4x + 3 adalah…. A. y = 4x2 + x + 3

B. y = x2 –x -3 C. y = 4x2 + 16x + 15 D. y = 4x2 + 15x + 16 E. y = x2 + 16x + 18

1 Substitusikan aja titik (-1, 3) kepilihan, yang mana yg cocok. Ke A : 3 = 4 -1 +3 = 6 (tdk cocok) B : 3 = 1 +1 -3 = -1 (tdk cocok) C : 3 = 4 -16 +15 = 3 (cocok)

1 -2 tidak terletak pada : 0 < x < 1

jadi -2 disubstitusikan ke x2 + 1

1 -4 tidak terletak pada : 0 < x < 1

jadi -4 disubstitusikan ke x2 + 1

1 ½ terletak pada 0 < x < 1 jadi ½ disubstitusikan ke 2x -1

1 3 tidak terletak pada : 0 < x < 1

jadi 3 disubstitusikan ke x2 + 1

Gunakan info smart :

1 F(-2) = (-2)2 + 1 = 5 F(-4) = (-4)2 + 1 = 17 F( ½ ) = 2. ½ -1 = 0 F(3) = 32 + 1 = 10

1 F(-2).f(-4) + f( ½ ).f(3) 5. 17 + 0.10 = 85 + 0 = 85

Jawaban : C

18. Misalkan :

î

í

ì

+

<

<

-=

lain

yang

untuk x

1

x

1

x

0

untuk

1

2

)

(

x

₂

x

f

maka f(-2).f(-4) + f( ½ ).f(3) = …. A. 52

O

Nilai maksimum 3 untuk x = 1, artinya Puncak di (1 ,3)

O

Gunakan rumus : y = a(x –p)2 + q

Dengan p = 4 dan q = 3

Gunakan iinfo smart :

O

y = a(x –p)2 + q

y = a(x -1)2 + 3, melalui titik (3 ,1)

1 = a(3-1)2 + 3

-2 = 4a , maka a = - ½

O

Kepersamaan awal :

y = - ½ (x -1)2 + 3, memotong sumbu Y, berarti :

x = 0 ,maka

y = - ½ (0 -1)2 + 3 = ₂5

O

Jadi titik potongnya : (0 , ₂5)

Jawaban : C

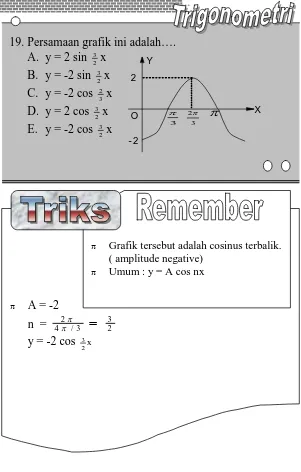
19. UAN 2003/P-1/No.2

Fungsi kuadrat yang mempunyai nilai maksimum 3 untuk x = 1 dan grafiknya melalui titik (3 ,1), memotong sumbu Y di titik….

B. (0, ₂7 ₎

C. (0 ,3) D. (0 , ₂5 ₎

O

Nilai maksimum 5 untuk x = 2, artinya Puncak di (2 ,5)

O

Gunakan rumus : y = a(x –p)2 _+q

Dengan p = 2 dan q = 5

Gunakan info smart :

O

f(x) = a(x –p)

2

+ q

f(4) = a(4 -2)

2

+ 5,

3 = 4a + 5 maka a =

-

₂1

O

Kepersamaan awal :

f(x) =

-

₂1

(x -2)

2

+ 5

=

-

₂1 _(x2

-4x+ 4) + 5

=

-

₂1 _x2

+ 2x + 3 20. UAN 2002/P-1/No.5

Suatu Fungsi kuadrat f(x) mempunyai nilai maksimum 5 untuk x = 2 sedang f(4) = 3. Fungsi kuadrat tersebut adalah…...

A. f(x) =

-

₂1 x2 + 2x + 3

B. f(x) =

-

₂1 x2 -2x + 3

C. f(x) =

-

₂1 x2 -2x -3

1

þ ý ü £ <

0 0

è KECIL “ tengahnya” BESAR (Terpadu)

1

þ ý ü ³ >

0 0

è BESAR “ atau “KECIL (Terpisah)

1 x2 -2x -3 £ 0

(x -3)(x +1) £ 0

1

Pembuat Nol : x = 3 atau x = -1

Garis bilangan :

Uji x = 0 , (0-3)(0+ 1)= -3(-)

-1

3

-

+

+

x = 0

@

Jadi : -1 £ x £ 3

1. Himpunan penyelesaian dari pertidaksamaan : x2_{£ 2x +3 adalah….}

A. {x|x < -2 atau x > 3} B. {x|x £ -2 atau x ³ 3} C. {x| -2< x > 3}

D. {x| -1 £ x £ 3} E. {x| -3 £ x £ 2}

@

Perhatikan terobosannya Jawaban : D

0

)

3

x

)(

1

x

(

0

3

x

2

x

2

£

-+

£

-besar

kecil

3

x

1

£

£

p Pada garis bilangan : Jumlah Suku ganjil : tanda “ Selang seling - + - “

Jumlah Suku genap: tanda “ Tetap “ : - - atau + +

1

(3 –x)(x -2)(4 –x)2

³

0

Pembuat Nol :

(3 –x)(x -2)(4 –x)2 = 0 3 – x = 0 , x = 3 x – 2 = 0 , x = 2

4 – x = 0 , x = 4 (ada 2 buah)

Garis bilangan :

2 3 4

-

+

-

-Uji x = 0

ð

(3-0)(0-2)(4-0)2 = -

x = 2,5

ð

(3-2,5)(2,5-2)(4-2,5)2= + x = 3,5

ð

(3-3,5)(3,5-2)(4-3,5)2= - x = 5

ð

(3-5)(5-2)(4-5)2= -

Padahal yang diminta soal ≥ 0 (positif)

Jadi : {x| 2 £ x £ 3}

2. Himpunan penyelesaian dari pertidaksamaan : (3 –x)(x -2)(4 –x)2_{³ 0 adalah….}

A. {x|x £ -2 atau 3 £ x £ 4} B. {x|x £ -2 atau x ³ 3} C. {x| 2 £ x £ 3}

D. {x|x £ -2 atau x ³ 4} E. {x|x < -2 atau x > 3}

@

Perhatikan terobosannya (3 –x)(x -2)(4 –x)2 = 0

2 3 4

-

+

-

(genap) Uji x = 0 (hanya satu titik) (3-0)(0-2)(4-0)2 = -

Jadi : 2

£

x

£

3

@

Perhatikan terobosannya

0

2 2

9-x

£

x

§ 9-x2 artinya x ≠ 3, maka pilihan B dan D pasti salah

(karena memuat x = 3)

§ x = 4

ð

0 7 16 16 9 16 £ -= - (B)

Jadi A pasti salah (karena tidak memuat 4)

§ x = 0

ð

0

0 9

0

=

- ≤ 0 (B)

Jadi C juga salah, berarti Jawaban benar A

1 0 9 2 2 £ -x x

Perhatikan ruas kanan sudah 0, Maka langsung dikerjakan dengan cara memfaktorkan suku-sukunya :

0 ) 3 )( 3 ( . _£

-+x x

x x

x = 0 (atas, ada dua suku ; genap) 3 + x = 0 , x = -3

3 –x = 0 , x = 3 Garis bilangan :

-3 0 ₃

-

+

+

-(genap)

Uji x = -4

ð

=

--16 9

16

x = -2

ð

=+ -4 9

4

x = 1

ð

=+

-1 9

1

x = 4

ð

= --16 9

16

Jadi : x < -3 atau x = 0 atau x > 3

3. Himpunan penyelesaian pertidaksamaan : 0 9 2 2 £ -x x adalah…..

A. {x| -3 < x < 3} B. {x| -3 £ x £ 3} C. {x|x < -3 atau x > 3}

D. {x|x £ -3 atau x ³ 3 atau x = 0} E. {x|x < -3 atau x = 0 atau x > 3}

Jawaban : E

p

Penyebut pecahan tidak

boleh ada “ = “

1 0 6 1 2 2 2 £ -+ -x x x x 0 ) 2 )( 3 ( ) 1 )( 1 ( £ + -x x x x

x -1 = 0, x = 1 (suku genap) x -3 = 0, x = 3

x + 2 = 0, x = -2

Uji x = -3

ð

=+

6 16

x = 0

ð

= --6

1

x = 2

ð

=

--4 1 . 1

x = 4

ð

= --6

9

-2

1

3

+

-

-

+

(genap)

Jadi : -2 < x < 3

Perhatikan tanda pertidaksa maan (sama atau tidak)

4. Himpunan penyelesaian pertidaksamaan :

0

6

1

2

2 2

£

-+

-x

x

x

x

untuk x

Î R adalah….

A. {x|x < -1 atau x < -2} B. {x|x £ 1 atau x > -2} C. {x|x > 3 atau x < -2} D. {x| -2 < x < 3} E. {x|x £ 3 atau x ³ -2}

@

Perhatikan terobosannya x2 -2x + 1 = (x -1)2 , ini nilainya selalu positif untuk setiap harga x, supaya hasil ≤ 0 (negative) maka :

x2 –x -6 harus < 0 atau (x -3)(x + 2) < 0 Jadi : -2 < x < 3

1

2x –a >

x₂-1

+

ax₃ Pertidaksamaan > , syarat > 5 Maka ambil x = 5

Options A.: ) ( 3 12 2 5 2 10 2 5 S a x + = -þ ý ü = = Options B ) ( 7 7 3 15 2 4 3 10 3 5 benar a x = + = -þ ý ü = =

Jadi pilihan B benar.

@

2x –a >

x₂-1

+

ax₃

a a x a a x a ax x ax x a x ax x a x ax x a x 2 9 3 6 3 6 ) 2 9 ( 3 6 2 9 2 3 3 6 12 2 ) 1 ( 3 ) 2 ( 6 3 2 1 2 -> -> -> -+ -> -+ -> -+ ->

-Padahal x > 5 (diketahui)

3 48 16 10 45 3 6 5 2 9 3 6 = = -= -= -a a a a a a

5. Pertidaksamaan 2x –a >

3 2

1 ax x- ₊

mempunyai penyelesaian x > 5.

Nilai a adalah…. A. 2

B. 3 C. 4 D. 5 E. 6

1

6

5

3

2

+

>

-

x x

coba x = 0

ð

6 0 5 3 0 2 + > - (S)

Jadi pilihan yang memuat x = 0 pasti bukan jawaban. Jadi B, D dan E salah.

Coba x = 4

ð

6 4 5 3 4 2 + > -11 5

2> (benar)

Jadi pilihannya harus memuat 4. Pilihan C salah(sebab C tidak memuat x = 4)

Kesimpulan Jawaban A

1

6

5

3

2

+

>

-

x

x

0 ) 6 )( 3 ( ) 9 ( 3 0 ) 6 )( 3 ( 3 27 0 ) 6 )( 3 ( ) 3 ( 5 ) 6 ( 2 0 6 5 3 2 > + -> + -> + -+ > + -x x x x x x x x x x x x

9-x = 0, x = 9 x -3 = 0, x = 3 x + 6 = 0, x = -6

titik-titik tersebut jadikan titik terminal dan uji x = 0 misalnya untuk mendapatkan tanda(-) atau (+ ) :

+

-

+

-6 3 9

Jadi : x < -6 atau 3 < x < 9

6. Jika

6

5

3

2

+

>

-

x

x

, maka ….

A. x < -6 atau 3 < x < 9 B. -6 < x < 3 atau x > 9 C. x < -6 atau x > 9 D. -6 < x < 9 atau x g 3 E. -3 < x < 9

Jawaban : A

1

2

1

8

3

4

3

+

³

-

x

x

x

(kali 16)

4 8 2

8 6 4

8 6 12 16

) 2 1 8 3 ( 16 ) 4 3 ( 16

-£

³

-+ ³

+ ³

-+ ³

-x x

x x

x x x

x x

x

Perhatikan perubahan tanda, saat membagi dengan bilangan negative (8 : -2)

Jadi nilai terbesar x adalah : -4

7. Nilai terbesar x agar

2 1 8 3 4

3

³

+

-

x x

x

adalah….

A. 1 B. -1 C. -2 D. -3 E. -4

1|x -2|2 > 4|x -2| + 12

coba x = 0

ð

|0 -2|2 > 4|0 -2| + 12 4 > 8+ 12 (salah) berarti A dan B salah (karena memuat x = 0)

coba x = 7

ð

|7 -2|2 > 4|7 -2| + 12 25 > 20+ 12 (salah) berarti E salah (karena memuat x = 7)

coba x = -3

ð

|-3 -2|2 > 4|-3 -2| + 12 25 > 20+ 12 (salah) berarti C salah (karena memuat x = -3)

Kesimpulan : Jawaban benar : D

Catatan :

Setiap akhir pengujian, sebaiknya pilihan yang salah dicoret agar mudah menguji titik uji yang lain.

1|x -2|2 > 4|x -2| + 12 misal : y = |x -2| y2 -4y -12 > 0

(y + 2)(y -6) > 0 (terpisah “ atau” )

y < -2 atau y > 6

1y < -2

à

|x -2| < -2 (tak ada tuh.)

y > 6

à

|x -2| > 6 (x -2)2 > 62 x2 -4x + 4 -36 > 0 x2 -4x -32 > 0 (x – 8)(x + 4) > 0, terpisah

Jadi : x < -4 atau x > 8

8. Nilai x yang memenuhi ketaksamaan : |x -2|2 > 4|x -2| +12 adalah…

A. -4 < x < 8 B. -2 < x < 6 C. x < -2 atau x > 8 D. x < -4 atau x > 8 E. x < -2 atau x > 6

1|x + 3| ≤ |2x| baca dari kanan, karena koefisien x nya lebih besar dari koefisien x sebelah kiri. Jadi :

3

2

x

³

x

+

+

-3x +3=0 x = -1

x -3=0 x = 3

Jadi : x < -1 atau x > 3

1|x + 3| ≤ |2x|

kuadratkan : (x + 3)2≤ (2x)2

(x + 3)(x + 3) ≤ 4x2 x2 + 3x + 3x + 9 ≤ 4x2 3x2 -6x -9 ≥ 0

x2 -2x -3 ≥ 0

(x -3)(x + 1) ≥ 0 (terpisah) x ≤ -1 atau x ≥ 3

9. Nilai-nilai x yang memenuhi |x +3| £ |2x| adalah… A. x £ -1 atau x ³ 3

B. x £ -1 atau x ³ 1 C. x £ -3 atau x ³ -1 D. x £ 1 atau x ³ 3

E. x £ -3 atau x ³ 1

1 3 5 x

1 x 2

£ +

coba x = 0

ð

3

5 ` 0

1 0

£ +

3 5 1_£

(benar)

berarti B, C dan E salah (karena tidak memuat x = 0)

coba x = -16

ð

3

5 16

1 16 _£

+

-3 11 17

£ (benar)

berarti D salah (karenatidak memuat x = -16)

Kesimpulan : Jawaban benar : A

1 3

5 x

1 x 2

£ +

(kali silang)

| 2x -1 | £ | 3x +15 |

--- kuadratkan (2x-1)2

£

(3x + 15)2

4x2-4x + 1

£

9x2+ 90x + 225 5x2+ 94x + 224

³

0

(5x + 14)(x + 16)

³

0

-16 -14

5

+

-

+

Jadi : x

£

-16 atau x

³

5 14

-10. Pertaksamaan 3 5 x

1 x 2

£ +

-mempunyai penyelesaan …..

A. x £ -16 atau x ³ -14/5 B. x £ -14/5 atau x > 16 C. x £ -14/5

D. x ³ -14/5

E. -16 £ x £ -14/5

1 2 x x 10 x 3 x 2 2 + -+ bernilai positif, artinya : 0 2 10 3 2 2 > + -+ x x x x maka : 0 2 ) 2 )( 5 (

2 _{- +} >

-+ x x x x

Uji x = -6

+ = = + + -44 8 2 6 36 10 18 36

Uji x = 0

-= -= + + -2 10 2 0 0 10 0 0

Uji x = 3

+ = = + -+ 8 8 2 3 9 10 9 9 -5 2 +

-

+

Ø 0, artinya daerah +

Ø Jadi : x < -5 atau x > 2

11. Agar pecahan

2 x x 10 x 3 x 2 2 + -+

bernilai positif , maka x anggota

himpunan…..

A. {x|x < -5 atau x > 2} B. {x| -5 < x < 2} C. {x|x £ -5} D. {x| x < 2 } E. {x| -5 £ x £ 2}

@

Perhatikan terobosannya

@

x2-x + 2 _à definite positif (selalu bernilai positif untuk setiap x)

@

Supaya 2 x x 10 x 3 x 2 2 + -+ bernilai

positif maka : x2 + 3x -10 positif,sebab + : + = +

@

Jadi : x2 + 3x -10 > 0 (x + 5)(x -2) > 0à besar nol (penyelesaian terpisah) Maka : x < -5 atau x > 2

1 2 4 3 14 7 3 2 2 ³ -+ -+ x x x x

coba x =2

ð 2 4 6 4 14 14 12 ³ -+ -+ 2 6 12_³ (benar)

berarti A dan D salah (karena tidak memuat x = 2)

coba x = - 4

ð 2 0 6 4 12 16 14 28 48 ³ = -(Sal

ah, penyebut tidak boleh 0) berarti C salah

coba x = - 11

ð 2 84 272 4 33 121 14 77 363 ³ =

-(Benar,) E salah, sebab tidak memuat x = -11

Kesimpulan : Jawaban benar : B

@

2 4 3 14 7 3 2 2 ³ -+ -+ x x x x 0 4 3 ) 4 3 ( 2 14 7 3 2 2 2 ³ -+ -+ -+ x x x x x x 0 4 3 6 2 2 ³ -+ -+ x x x x 0 ) 1 )( 4 ( ) 2 )( 3 ( _³ -+ -+ x x x x

Setelah melakukan pengujian, untuk x = 0, di dapat + , selanjutnya bagian daerah yang lain diberi tanda selang seling (sebab semua merupakan suku ganjil)

-4 -3 1 2

+

-

+

-

+

+

+

+

Jadi : x < -4 atau -3 £ x < 1 atau x ³ 2 12. Nilai-nilai x yang memenuhi 3 2 ₃7 14₄

2

2

³

-+ -+ x x x x adalah…. A. x < -4

B. x < -4 atau -3 £ x < 1 atau x ³ 2 C. x £ -4 atau -3 £ x < 1 atau x ³ 2 D. -10 £ x < -4 atau -3 £ x < 1

1 0 7 3 3 2 > -+ x x Pertidaksamaannya sudah mateng, maka langsung uji titik :

x = 0

ð

=

-= -+ 7 3 7 0 . 3 3 0 . 2

Selanjutnya beri tanda daerah yang lain, selang seling.

2 3 -3 7

-+

+

> 0, artinya daerah positif (+ )

Jadi : x <

2 3

- atau x >

3 7

13. Himpunan penyelesaian pertidaksamaan : 0

7 3 3 2 _> -+ x x adalah….

A. {x|x < -₂3 _{atau x >} 3 7 _}

B. {x|x < -₂3 _{dan x >} 3 7 _}

C. {x| -₂3 _{< x <} 3 7 _}

D. {x| ₃7 _{> x >} -2 3 _}

E. {x|x < -₃2 _{atau x >} 2 3 _}

@

Perhatikan terobosannya

0 7 3 3 2 _> -+ x

x _{Uji demngan}

mencoba nilai :

x = 0_ð =

-+ 7 0 3 0 (Salah)

berarti : C dan D salah

x = 1

4 5 7 1 . 3 3 1 . 2 -= -+ (salah)

berarti E salah (sebab memuat 1)

B Salah menggunakan kata hubung dan.

p

f

(

x

)

<

c

,maka : ( i ) kuadratkan (ii) f(x) ≥ 0

@

Penyelesaian : Irisan ( i) dan ( ii)

@

x

2

-

3

x

<

2

à Kuadratkan : x2 _{-3x < 4}

à x2 _{-3x -4 < 0}

(x -4)(x +1) < 0

@

syarat : x2 -3x ³ 0 x(x -3) ³ 0

- 1 4

0 3

Jadi : -1 < x £ 0 atau 3 £ x < 4

14. Himpunan penyelesaian pertidaksamaan x2 -3x<2adalah…. A. {x| -1 £ x £ 0 atau 3 £ x £ 4}

B. {x| -1 < x £ 0 atau 3 £ x < 4} C. {x| 0 £ x £ 3}

D. {x| -1 < x < 4} E. {x|x < -1 atau x > 4}

@

Perhatikan terobosannya

zdasdfhhhhhhhhhhhh

p

<

®

-

<

0

bd

bc

ad

d

c

b

a

p 0 bd bc ad d c b a > -® >

@

3

5

2

1

-+

<

-+

x

x

x

x

0 ) 3 )( 2 ( 7 5 0 ) 3 )( 2 ( 10 3 3 2 0 ) 3 )( 2 ( ) 5 )( 2 ( ) 3 )( 1 ( 2 2 < -+ -< -+ -< -+ -+ x x x x x x x x x x x x x x x

-

+

-2

3

5 7

Jadi : 2

5 7_{< <}

x atau x > 3 15. Harga x dari pertidaksamaan

3

5

2

1

-+

<

-+

x

x

x

x

adalah….

A. x < -1/6 atau 2 < x < 3 B. x > 1/3 atau – ¼ < x < 0 C. x > ½ atau 0 < x < ¼ D. x > 3 atau 7/5 < x < 2 E. x < 1 atau 2 < x < 3

@

1

4

)

4

2

)(

1

(

2

+

<

+

-x

x

x

Uji nilai :

x = 0

ð

1 1

4 4 . 1 < -= (B)

berarti A dan B salah (karena pilihan trs tidak memuat x = 0)

x = 3

ð

1

13 20 4 9 10 . 2 < =

+ (S)

berarti D salah (karena D memuat x = 3)

x = -5

ð

1

29 36 4 25 ) 6 .( 6 < = + (S)

berarti C salah (karena C memuat x = -5)

Jadi pilihan benar : E

1

x

2

+4 selalu positif

untuk semua nilai x,

makanya disebut Definite

positif

@

1

4

)

4

2

)(

1

(

2

+

<

+

-x

x

x

0

4

)

4

(

4

2

2

2 2 2

<

+

+

-+

x

x

x

x

0 8 2 2 < + -+ x x

berarti : x

2

+2x -8 : (-)

x

2

+2x -8 < 0

(x +4)(x -2) < 0

@

Jadi : -4 < x < 2

16. Himpunan penyelesaian pertaksamaan :

1

4

)

4

2

)(

1

(

2

+

<

+

-x

x

x

adalah… A. {x|x > 2} B. {x|x < -4} C. {x|x < 2} D. {x|x > -4} E. {x|-4 < x < 2}

1Perhatikan ujung daerah penyelesaian pada gambar tertutup, berarti

pertidaksamaannya memuat tanda SAMA

1Perhatikan pula, daerah yang diarsir, menyatu. Maka pertidaksamaannya KECIL. Jadi :

(x + 1)(x -5)

£

0 x2 -5x + x -5

£

0 x2 -4x -5

£

0

17. Grafik yang diperlihatkan pada gambar berikut :

-1 5 _{adalah penyelesaian dari pertidaksamaan ..} A. x2 -4x – 5 £ 0

B. x2 -4x + 5 £ 0 C. x2 +x – 5 ³ 0 D. x2 -4x – 5 < 0 E. x2 -4x – 5 > 0

1

a > b berarti a –b > 0

c > d berarti c –d > 0 +

a + c > b + d

1

a –b > 0

c –d > 0 kalikan :

(a –b)(c –d) > 0

ac –ad –bc + bd > 0

ac + bd > ad + bc

Jadi jawaban benar : B

18. Jika a, b, c dan d bilangan real dengan a > b dan c > d, maka berlakulah….

A. ac > bd dan ac + bd < ad + bc B. a + c > b + d dan ac + bd > ad + bc C. ad > bc dan ac –bd > ad -bc D. a + d > b + c dan ac –bd = ad + bd E. a –d > b –c dan ac –bd = ad -bd

1

2 6 x x 16 x 5 x 3 2 2 ³ -+ -+

Dengan mencoba nilai x = 0

ð

2 3 8 6 0 0 16 0 0 > = -+ -+ (B)

berarti pilihan harus memuat nol. Jadi : B, dan C salah.

x = 2

ð

2 0 6 6 2 4 16 10 12 > = -+ -+ (S)

berarti pilihan harus tidak memuat 2. Jadi : D, dan E salah.

Jadi pilihan yg tersisa hanya A

1

2 6 x x 16 x 5 x 3 2 2 ³ -+ -+ 0 ) 2 x )( 3 x ( ) 1 x )( 4 x ( 0 6 x x 4 x 3 x 0 6 x x 12 x 2 x 2 16 x 5 x 3 0 6 x x ) 6 x x ( 2 6 x x 16 x 5 x 3 2 2 2 2 2 2 2 2 2 ³ -+ -+ ³ -+ -+ ³ -+ + -+ ³ -+ -+ -+ -+

Uji x = 0ð =+

-) 2 ( 3 ) 1 ( 4

-4

-3

1

2

bawah bawah

+

+

+

-

+

-

+

+

Jadi : x

£

-4 atau -3 < x

£

1 atau x > 2

Jawaban benar : A

19. Nilai x yang memenuhi pertidaksamaan 2

6 x x 16 x 5 x 3 2 2 ³ -+ -+ adalah…

A. x

£

-4 atau -3 < x

£

1 atau x > 2 B. x

£

-4 atau -2

£

x

£

-1 atau x

³

2 C. x

£

-4 atau -2 < x

£

-1 atau x > 2 D. x

³

-4 atau -2

£

x

£

-1 atau x > 2

1

x2 -4x+4-|2x+3|³0 Coba nilai :

x = 0

ð

Ö

4-3= 2-3= -1

³

0 (salah) berarti pilihan yg memuat nol, salah. Jadi : C, D dan E salah

x = -4

ð

Ö

36 -5= 6 -5= -5

³

0 (B) berarti penyelesaian harus memuat x = 4. Jadi A salah.

Maka jawaban yang tersisa hanya pilihan B

1

x2 -4x+4-|2x+3|³0

| 3 x 2 | 4 x 4

x2 - + ³ +

Kedua ruas dikuadratkan x2 -4x + 4

³

(2x + 3)2 x2 -4x + 4

³

4x2 + 12x + 9 3x2 + 16x + 5

£

0

(3x + 1)(x + 5)

£

0 …(i)

1

Syarat di bawah akar

harus positif.

x2 -4x + 4

³

0

(x -2)(x -2)

³

0 , ini berlaku saja untuk setiap harga x Berarti penyelesaiannya adalah (i), yakni :

-5

£

x

£

-3 1

(ingat :

£

0, terpadu)

20. Jika x2 -4x+4-|2x+3|³0maka…

A. -3

£

x

£

-5 1