Irvan Dedy Bimbingan Belajar SMA Dwiwarna
LOGIKA MATEMATIKA
1. Pernyataan
Pernyataan adalah kalimat yang bernilai benar atau salah tetapi tidak sekaligus benar dan salah.
Pernyataan dilambangkan dengan huruf kecil, misalnya p, q, r dan seterusnya. Pernyataan dibedakan menjadi:
1. Pernyataan Tunggal, yaitu penrnyataan yang mengandung satu gagasan. 2. Pernyataan Majemuk, yaitu pernyataan yang mengandung dua gagasan atau
lebih. Dapat pula dikatakan bahwa pernyataan majemuk adalah gabungan dua atau lebih pernyataan tunggal yang dihubungkan dengan kata gabungan logika.
2. Pernyataan Berkuantor
2.1 Pernyataan Berkuantor Universal (umum)
Pernyataan berkuantor universal adalah pernyataan yang memuat kata semua atau setiap.
Notasi: p dibaca semua/setiap.
Contoh:
1) Semua siswa ingin lulus ujian 2) Setiap bilangan genap habis dibagi 2
2.2 Pernyataan Berkuantor Eksistensial (Khusus)
Pernyataan berkontur eksistensial adalah pernyataan yang memuat kata ada atau beberapa.
Notasi: p dibaca ada /beberapa p.
Contoh:
(1). Ada ikan bernafas dengan paru-paru (2). Beberapa siswa hari ini tidak hadir
3. Pernyataan Majemuk
3.1 Konjungsi
Konjungsi dari dua pernyataan tunggal p dan q adalah “p dan q” yang dibaca “p dan q”
Tabel kebenaran Konjungsi:
p q p q B
B S S
B S B S
B S S S
Irvan Dedy Bimbingan Belajar SMA Dwiwarna
abel Kebenaran Disjungsi: T
Tabel Kebenaran Implikasi:
Implikasi (Pernyataan Bersyarat)
Implikasi dari dua pernyataan tunggal p dan q adalah “p
1) jika p maka q 3) p syarat cukup bagi q Ekivalensi (Biimplikasi)
Eki alensi dari dua pernyata 1) p jika dan hanya jika q
Tabel Kebenaran Ekivalensi:
p q p q
nyataan p ditulis ~p dan dibaca:
i alnya benar. Selain dari itu p q bernilai salah.
eadaan, kecuali apabila p benar dan q salah.
tunggalnya sama selain dari itu salah.
Negasi dari Pernyataan Tunggal Negasi dari per
Dari tabel dapat disimpulkan bahwa: p q bernila benar apabila salah satu pernyataan tungg
Dari tabel dapat disimpulkan bahwa: p q bernilai benar untuk semua k
Irvan Dedy Bimbingan Belajar SMA Dwiwarna
1) Tidak p
2) Bukan p
3) Tidak benar p
Tabel kebenaran:
p ~p
B
S B
S
4.2 n B
h y
~p : ada x tidak y ~p : semua x tidak y
Contoh 1)
2)
anjil 3)
negatif
4) 7
~p : semua x berlaku x 7
4.3 Negasi dari Pernyataan Majemuk
4.3.1 N si
~(p q) ~p ~q
4.3.2 Negasi dari Diskonjugasi
~(p q) ~p ~q
4.3.3 Negasi dai Implikasi
~(p q) p ~q
4.3.4 N
(q p)]
p ~q q ~p
. Variasi Pernyataan Bersyarat
tiga buah pernyataan bersyarat lainnya yaitu n kontraposisi.
Negasi dari Pernyataa erkuantor
p : semua x adala p : ada x adalah y
:
p : Semua siswa hadir di kelas ini ~p : Ada siswa tidak hadir di kelas ini p : Semua bilangan prima adalah ganjil ~p : Ada bilangan prima yang tidak g p : Ada bilangan prima yang negatif ~p : Semua bilangan prima tidak p : Ada harga x sehingga x <
egasi dari Konjuga
egasi dari Ekivalensi
~(p q) ~[(p q)
~(p q) (q p)
5
Dari implikasi p q dapat dibuat
invers, konvers, da
Irvan Dedy Bimbingan Belajar SMA Dwiwarna
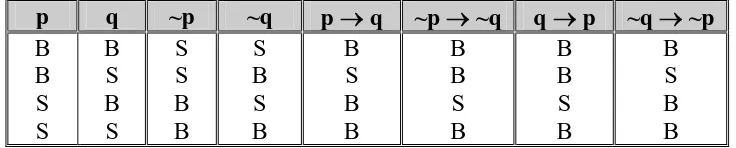
Invers : ~ p ~q Kontraposisi : ~q ~p
Tabel kebenaran
p q ~p ~q p q ~p ~q q p ~q ~p
1) dengan kontraposisi:
2) gan konvers
~p ~q q p
sukses
Kontraposisi: Jika kamu tidak sukses, maka kamu tidak rajin
. Tautologi dan Kontradiksi
pernyataan yang selalu benar
Contoh : p ~p
Dari tabel terlihat bahwa: Implikasi ekivalen
p q ~q ~p
Invers ekivalen den
Contoh:
Implikasi : Jika kamu rajin belajar, maka kamu sukses Invers : Jika kamu tidak rajin, maka kamu tidak
Konvers : Jika kamu sukses, maka kamu rajin
6
7. Sifat operasi Logika
7.1 Sifat Id
(2). p p p
ifat Komutatif
(1). p q q p
ifat Assosiatif
(1). p (q r) (p q) r
7.4 S
(2). p (q r) (p q) r
7.5 S d
(2). (4). p k k
k : kontradiksi
7.6 Sifat Komplemen
(5). ~k = t
. Penarikan Kesimpulan
8.1
p q … premis 1
ifat Distributif
(1). p (q r) (p q) r
ifat I entitas
(1). p t t (3). p t p
p k p
t : tautologi
(1). p ~p t (4). ~t = k
(2). p ~p k
ifat Idempoten
(1). p~(p q) ~p ~q
ifat Implikasi
8
odus Tollens
kesimpulan