BUKU AJAR
METODE ELEMEN HINGGA
JURUSAN TEKNIK MESIN FAKULTAS TEKNIK
1.1. Definisi Umum
Truss adalah struktur yang terdiri atas batang-batang lurus yang disambung pada titik perpotongan dengan sambungan tanpa momen (pin). Pembebanan pada batang / struktur truss hanya terdapat pada sambungannya saja (berupa gaya-gaya aksial saja). Tegangan yang diakibatkan oleh gaya-gaya aksial disebut tegangan primer. Sambungan llas atau keling selama ditata dengan hati-hati dimana sumbu-sumbu batang bertemu pada satu titik dapat dianggap sebagai batang truss karena tegangan sekunder akibat proses pengelasan tidak terlalu berpengaruh pada tegangan primer.
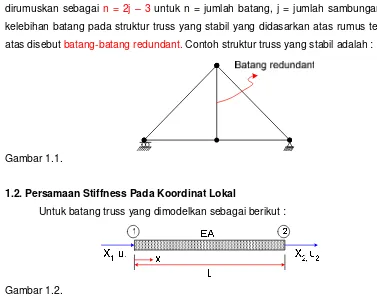
Struktur truss akan stabil jika tersusun atas konstruksi-konstruksi dasar berbentuk segitiga dimana jumlah batang yang diperlukan dalam menyusun struktur stabil tersebut dirumuskan sebagai n = 2j – 3 untuk n = jumlah batang, j = jumlah sambungan. Setiap kelebihan batang pada struktur truss yang stabil yang didasarkan atas rumus tersebut di atas disebut batang-batang redundant. Contoh struktur truss yang stabil adalah :
Gambar 1.1.
1.2. Persamaan Stiffness Pada Koordinat Lokal
Untuk batang truss yang dimodelkan sebagai berikut :
Gambar 1.2.
u2 merupakan pergeseran titik 2 akibat gaya X2. Kedua pergeseran tersebut dinamakan derajat kebebasan batang.
Jika EA dianggap berharga konstan (batang uniform/serba sama) maka pergeseran tiap titik yang berjarak x dari nodal 1 dapat ditentukan. Jika diasumsikan pergeseran aksial akibat gaya X di sepanjang batang mengikuti rumus linier, diperoleh :
x
a
a
x
u
(
)
=
1+
2 1)dalam hal ini a1 dan a2 adalah konstanta yang ditentukan nilainya berdasarkan kondisi batas berikut :
Pada x = 0, u (x) = u (0) = u1 = a1
Pada x = L, u (x) = u (L) = u2 = a1 + a2 L maka
L u u
a 2 1
2
− =
Jika nilai a1 dan a2 dikembalikan pada persamaan 1) maka akan diperoleh persamaan berikut :
L u u u x
u 2 1
1
)
( = + −
jika diubah dalam variabel u1 dan u2 akan menjadi :
2 2 1
1( ) ( )
)
(x f x u f x u
u = + 2)
Dimana
L x x
f1( )=1− dan
L x x
f2( )= dinamakan fungsi bentuk. Untuk kondisi tegangan uniaksial, regangan yang terjadi didefinisikan sebagai :
x u x
x u x x u
x ∂
∂ = ∆
− ∆ + ∈=
→ ∆
) ( ) ( lim
0 3)
∆x adalah pertambahan panjang x yang sangat kecil. Jika persamaan 2) disubstitusikan pada persamaan 3) akan diperoleh ∈ = a1 atau :
2 ' 2 1 '
1(x)u f (x)u
f +
∈=
dx f x
f'( )=∂ 4)
Mengacu pada teori statika, gaya-gaya aksial dirumuskan sebagai :
x u EA A E A S
∂ ∂ = ∈ =
=
σ
] ) ( )
(
[f1' x u1 f2' x u2 EA
S = + 5)
Dan energi regangan dinyatakan sebagai :
+ =
=
L L
dx u x f u x f EA dx EA S U
0 0
2 2 ' 2 1 ' 1 2
] ) ( )
( [ 2
Dengan menggunakan Teorema Castigliano akan diperoleh gaya-gaya batang sebagai berikut :
+ =
∂ ∂ =
L
dx f u f u f EA u U X
0
' 1 2 ' 2 1 ' 1 1
1 [ ]
= +
L L
u dx f f EA u
dx f f EA
0
2 ' 2 ' 1 0
1 ' 1 '
1 ) ( )
(
+ =
L L
u dx f f EA u
dx f f EA X
0
2 ' 2 ' 2 0
1 ' 1 ' 2
2 ( ) ( ) 7)
Dalam bentuk matriks dapat ditulis menjadi {X} = [k] {u} atau :
=
2 1
22 21
12 11
2 1
u u
k k
k k
X X
8)
Matriks [k] disebut matriks stiffness (matriks kekakuan) dengan koefisien-koefisien
=
L
j i
ij EA f x f x dx
k
0
' '
) ( )
( i = 1, 2 j = 1, 2 9)
Jika fungsi-fungsi bentuk pada persamaan 1) dimasukkan pada persamaan 9) akan diperoleh nilai matriks [k] sebagai berikut :
−
−
=
2 1
2 1
1
1
1
1
u
u
L
EA
X
X
Catatan : Persoalan-persoalan elemen hingga pada umumnya bertujuan menentukan nilai {X} dan {u} sedangkan nilai [k] biasanya telah tersedia / diketahui.
Latihan Soal 1.1 :
Coba rumuskan nilai [k] jika pergeseran titik pada batang truss mengikuti pola : a. polinomial u (x) = a1x + a2x2 + a3 !
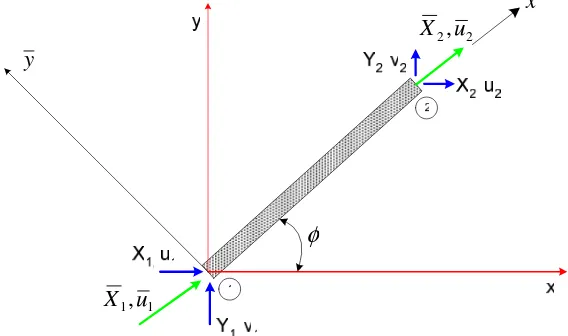
1.3. Persamaan Stiffness Pada Sumbu Dengan Orientasi Sembarang
Perhatikan gambar 3 berikut ini :
x
y
φ
2 2
,
u
X
1 1
,
u
X
y
x
,
Gambar 1.3.Penurunan rumus untuk mentransformasikan sumbu lokal ke sumbu global diawali dengan memperhatikan hubungan bahwa di nodal 1 dan 2 berlaku :
φ
φ
sin
cos
1 11
u
v
u
=
+
φ
φ
sincos 2
2
2 u v
u = + 10)
Jika digunakan λ = cos φ dan µ = sin φ maka, dalam bentuk matriks, akan diperoleh persamaan :
=
2 2 1 1
2
1 0 0
0 0
v u v u
u u
µ
λ
µ
λ
11)
Persamaan energi dalam U (x) akan menjadi : )
( 1 1 2 2
2
1 X u X u
U = +
=
2 1
2 1 2 1
u u
X
X T
12)
Dalam persamaan koordinat lokal, {x} = [k] {u} menjadi :
− − =
2 1
2 1
1 1
1 1
u u
L EA X
X
Persamaan 11) dan 13) disubstitusikan pada persamaan 12), menjadi
− −
− −
− −
− −
=
2 2 1 1
2 2
2 2
2 2
2 2
2 2 1 1
2
v u v u
v u v u
L EA U
T
µ
λµ
µ
λµ
λµ
λ
λµ
λ
µ
λµ
µ
λµ
λµ
λ
λµ
λ
14)
Maka persamaan kekakuan {x} = [k] {u} menjadi :
− −
− −
− −
− −
=
∂ ∂
∂ ∂
∂ ∂
∂ ∂
=
2 2 1 1
2 2
2 2
2 2
2 2
2 2 1 1
} {
v u v u
L EA
v U
u U
v U
u U
X
µ
λµ
µ
λµ
λµ
λ
λµ
λ
µ
λµ
µ
λµ
λµ
λ
λµ
λ
15)
Jadi matriks
− −
− −
− −
− −
2 2
2 2
2 2
2 2
µ
λµ
µ
λµ
λµ
λ
λµ
λ
µ
λµ
µ
λµ
λµ
λ
λµ
λ
L EA
adalah matriks [k] yang dicari.
Contoh Soal :
Gambar 1.4.
Struktur truss 3 batang dengan panjang L (2 m) membentuk konstruksi segitiga sama sisi dan memiliki rigiditas aksial EA se-besar 4 N. Jika beban P sese-besar 10 N diaplikasikan, tentukan semua gaya batang dan pergeseran titik ujung yang terjadi karenanya !
Jawab :
1. Gambar diagram benda bebas dari konstruksi tersebut adalah :
2. Nilai sinus dan cosinus tiap batang adalah :
3. Maka mengacu pada persamaan 15), persamaan di tiap elemen adalah :
a. elemen 1-2 :
4. Proses penggabungan persamaan elemen menjadi persamaan struktur.
Karena X1, Y1, .... Y3 adalah gaya-gaya nodal, bukan gaya batang. Jadi gaya-gaya batang diperoleh dari penjumlahan gaya-gaya-gaya-gaya nodal pada posisi yang bersesuaian.
[ ]
Sehingga didapat :
−
sebagai berikut :
a. u1 = v2 = u3 = v3 = 0 (jenis tumpuan jepit dan arah tegak lurus tumpuan rol tidak terjadi pergeseran) b. P2 = 0 (pada arah gerak tumpuan rol tidak terdapat beban luar)
c. P3 = P (pada arah gerak tumpuan rol terdapat beban luar P)
Dengan memberikan harga pada variabel-variabel {P} dan {D} yang diketahui maka dapat dilihat bahwa :
a. pada posisi baris 2 dan 3, elemen {P} diketahui nilainya, elemen {D} tidak diketahui b. pada posisi baris 1, 4, 5, dan 6, elemen {P} tidak diketahui nilainya, elemen {D} diketahui
Maka untuk memudahkan perhitungan dilakukan transformasi matriks dengan urutan langkah sebagai berikut :
a. Geser elemen baris 2 dan 3 matriks {P} ke posisi baris 1 dan 2 sehingga urutan baris matriks {P} berubah menjadi 2, 3, 1, 4, 5, 6.
[ ]
c. Geser kolom 2 dan 3 matriks [K] hasil pergeseran baris, ke posisi kolom 1 dan 2, sehingga urutan kolom matriks [K] menjadi 2, 3, 1, 4, 5, 6. Matriks yang dihasilkan adalah :
Matriks hasil transformasi adalah :
=
penyederhanaan hitungan.6. Untuk menyelesaikan persamaan matriks di atas, mengacu pada hukum perkalian
matriks, didapat persamaan berikut :
a. A = (I x C) + (II x D) b. B = (III x C) + (IV x D)
a. =
2 1
5 0
0 3 4 0
u v
L EA
P yang diselesaikan menjadi :
=
[ ]
− = =1 0 5 4 0 3 0
0 5 15
4 0
1 2 2 2
1
EA PL P
EA L P
K u
v
x
b.
− −
−
=
− − −
− −
=
− − −
− −
=
3 1 3 4
5 1 0
3 3
1 3
3 0
4 3
5 4 4 3
3 1 3
3 0
4 3
4 2
1
6 5 4 1
P EA
PL L EA u
v
L EA
P P P P
Dengan demikian semua variabel yang tidak diketahui telah ditemukan. Nilai negatif pada gaya-gaya batang P menunjukkan arah pembebanan yang berbeda dengan asumsi awal. Maka diagram benda bebas yang sebenarnya adalah :
Gambar 1.6. Latihan Soal 1.2 :
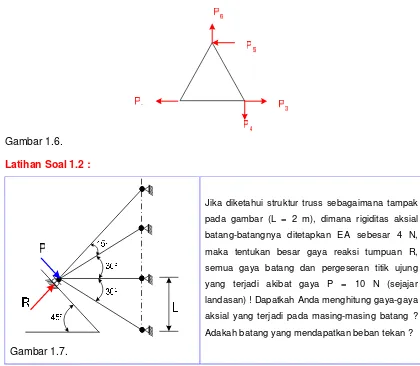
Gambar 1.7.
Jika diketahui struktur truss sebagaimana tampak pada gambar (L = 2 m), dimana rigiditas aksial
batang-batangnya ditetapkan EA sebesar 4 N, maka tentukan besar gaya reaksi tumpuan R, semua gaya batang dan pergeseran titik ujung yang terjadi akibat gaya P = 10 N (sejajar
landasan) ! Dapatkah Anda menghitung gaya-gaya aksial yang terjadi pada masing-masing batang ?
2.1. Definisi Umum
Beam adalah batang lurus ditumpu di dua atau lebih titik, mendapatkan pembebanan tunggal, merata maupun beban kombinasi (termasuk beban momen) dimana defleksi yang terjadi terdiri atas defleksi linier berarah tegak lurus sumbu aksial dan puntiran.
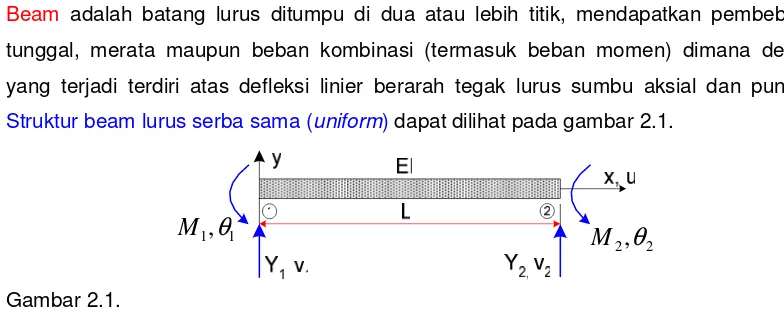
Struktur beam lurus serba sama (uniform) dapat dilihat pada gambar 2.1.
1 1
,
θ
M
2 2
,
θ
M
Gambar 2.1.
Pada batang dimaksud, sumbu longitudinal terletak pada sumbu x sedangkan sumbu transversal adalah sumbu y. Batang memiliki konstanta momen inersia I, modulus elastisitas E dan panjang L. Batang dianggap memiliki 2 derajat kebebasan pada setiap titik nodal yaitu defleksi transversal v akibat gaya transversal Y dan slope (sudut rotasi) θ
yang merupakan turunan v terhadap x (∂v/∂x) akibat momen bending M. Tidak terjadi pergeseran pada arah x.
Berdasarkan analisis statika struktur, defleksi yang terjadi pada beam untuk daerah tanpa pembebanan dinyatakan sebagai :
0
4 4
= ∂ ∂ x
v
16) yang menghasilkan penyelesaian :
3 4 2 3 2 1
)
(x a a x a x a x
v = + + + 17)
Pada kondisi batas berlaku : x = 0 → v = v 1 = a1
x
v ∂
∂ / = θ1 = a2
x = L → v = v 2 = a1 + a2L +a3L2 + a4L3
x
v ∂
∂ / = θ2 = a2 + 2a3L + 3a4L2
Dalam bentuk matriks dapat ditulis sebagai berikut : =
4 3 2 1
2 3 2
2 2 1 1
3 2 1 0 1
0 0 1 0
0 0 0 1
a a a a
L L
L L L v
v
Atau
− − −
− =
2 2 1 1
2 2
2 3
3
4 3 2 1
2 2
3 2 3
0 0 0
0 0 0 1
θ
θ
v v
L L
L L L L
L L
L
a a a a
18)
Jika nilai matriks {a} pada persamaan 18) dikembalikan pada persamaan 17) maka akan didapat :
( )
x f1(x)v1 f2(x)θ
1 f3(x)v2 f4(x)θ
2v = + + + 19)
Dimana :
( ) ( )
2 3 1(x) 1 3xL 2 xLf = − +
( )
( )
23 2
2(x) x 2 xL x L
f = − +
( ) ( )
2 3 3(x) 3 xL 2 xLf = −
( ) ( )
23 2
4(x) x L x L
f =− + →→→→adalah fungsi-fungsi bentuk defleksi.
Untuk menentukan matriks konstanta (matriks stiffness), diketahui bahwa dari Teorema Castigliano untuk beam berlaku persamaan :
(
∂ ∂)
=
L
dx x v EI
U
0
2 2 2
2 ; Yi =∂U∂vi
Maka dengan mengikuti prosedur sebagaimana pada struktur truss akan diperoleh persamaan berikut :
−
− −
−
− −
=
2 2 1 1
2 2
2 2
2 2
2 2
1 1
4 6
2 6
12 2
12
2 6
4 6
6 12 6
12
θ
θ
v v
L L
L L
L L
L L
L L L
L
L EI
M Y M
Y
{F} = [K] {q} 20)
Catatan :
1. Perlu diketahui bahwa dalam kondisi tanpa tumpuan (seperti pada gambar 2.1.) beam harus berada dalam keseimbangan dibawah 4 gaya nodal dan 4 defleksi. Jadi :
a. ΣF = 0 → Y1 = -Y2
2. Karena pada matriks [K] baris 1 = - baris 3 maka matriks [K] singular, artinya [K]-1 tidak bernilai (tidak eksis), jadi tidak ada penyelesaian. Secara fisik hal ini tidak benar karena tidak pernah terjadi beam tanpa tumpuan. Maka dapat dipastikan bahwa ada setidaknya 1 tumpuan pada ujung-ujung struktur beam.
Contoh : Jika ujung 1 ditumpu dengan tumpuan jepit, maka v1 = θ1 = 0 sehingga persamaannya menjadi =
2 2 2
2 2
4 L 6
-L 6 -L 12
θ
v
L EI M
Y
Contoh Soal 2.1. :
Gambar 2.2.
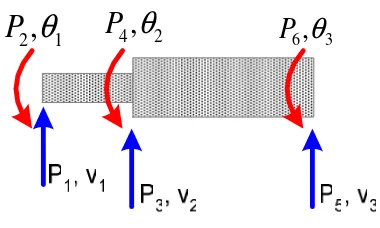
Diketahui struktur beam sebagaimana tampak pada gambar 2.2. Tentukanlah
gaya-gaya internal dan mo-men nodal pada titik-titik
nodal !
Jawab :
1. Gambar diagram benda bebas dari konstruksi tersebut adalah :
1 2
,
θ
P
P
4,θ
2P
6,
θ
3Gambar 2.3.
2. Maka mengacu pada persamaan 20), persamaan di tiap elemen adalah :
a. elemen 1-2 :
−
− −
−
− −
=
2 2 1 1
2 2
2 2
2 2
2 2
1 1
4 6
2 6
12 2
12
2 6
4 6
6 12 6
12
θ
θ
v v
L L
L L
L L
L L
L L L
L
L EI
M Y M
b. elemen 2-3 :
3. Proses penggabungan persamaan elemen menjadi persamaan struktur.
−
sebagai berikut :
0
Maka untuk memudahkan perhitungan dilakukan transformasi matriks dengan urutan langkah sebagai berikut :
a. Geser elemen baris 3, 4 dan 6 matriks {P} ke posisi baris 1, 2 dan 3 sehingga urutan baris matriks {P} berubah menjadi 3, 4, 6, 1, 2, 5. Lakukan hal yang sama untuk matriks {q}.
b. Geser elemen baris 3, 4 dan 6 matriks [K] ke posisi baris 1, 2 dan 3 sehingga urutan baris matriks [K] berubah menjadi 3, 4, 6, 1, 2, 5
c. Geser elemen kolom 3, 4 dan 6 matriks [K] hasil pergeseran b) ke posisi baris 1, 2 dan 3.
Matriks hasil transformasi adalah :
Garis merah adalah garis batas partisi matriks yang akan digunakan untuk melakukan penyederhanaan hitungan.
5. Untuk menyelesaikan persamaan matriks di atas, mengacu pada hukum perkalian
matriks, didapat persamaan berikut :
− − =
−
3 2 2
3 3
3 3 15
4 2
2 8 0
2
θ
θ
v
L EI PL
P
L L
L L L
Atau
− − =
−
− −
− −
=
L L EI PL PL
P
L L
L
L L
L
L L
EI L v
9 33 10 276
0 111
39 30
39 51
18
30 18
28 276
3
2 2
2 2
3
3 2 2
θ
θ
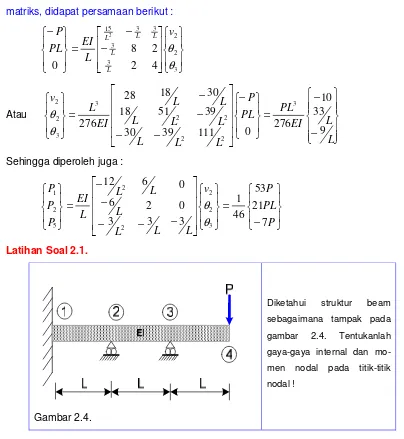
Sehingga diperoleh juga :
− = −
− −
− −
=
P PL
P v
L L L
L
L L
L EI
P P P
7 21
53 46
1 3
3 3
0 2 6
0 6
12
3 2 2
2 2
5 2 1
θ
θ
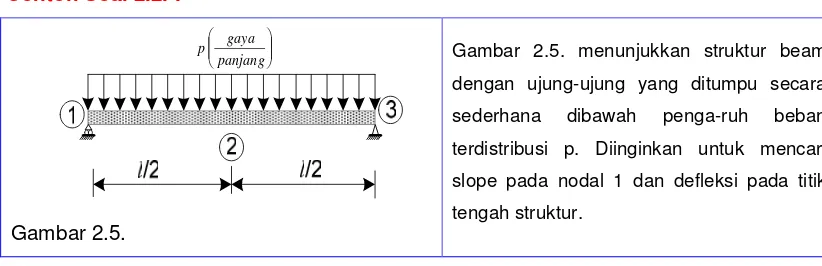
Latihan Soal 2.1.
Gambar 2.4.
Diketahui struktur beam sebagaimana tampak pada gambar 2.4. Tentukanlah gaya-gaya internal dan
2.2. Beam Dengan Beban Merata
Pada sub bab sebelumnya, pembebanan terpusat pada titik-titik nodal. Pada kondisi struktur yang sebenarnya, pembebanan tidak hanya merupakan beban-beban terpusat namun terdistribusi di seluruh batang. Dalam hal ini beban yang terdistribusi ditransformasikan menjadi beban terpusat sehingga dapat diaplikasikan pada titik nodal. Salah satu metode yang digunakan untuk keperluan tersebut adalah Metode Beban - Kerja Ekuivalen. Pada metode ini kerja yang dihasilkan oleh beban nodal yang tidak diketahui dibuat sama dengan kerja yang dihasilkan oleh beban terdistribusi. Metode ini sangat mudah dilakukan khususnya jika beban terdistribusi dapat dimodelkan dalam bentuk persamaan matematis.
Umpamakan suatu elemen beam, kerja yang dilakukan oleh beban nodal tapi tidak diketahui nilainya dinyatakan dalam bentuk :
[
]
=
2 2 1 1
2 2 1 1 2 1
θ
θ
v v
M Y M Y
W 21)
Di sisi lain, kerja yang dilakukan oleh beban terdistribusi dapat diperoleh dengan cara :
=
L
dx x v x p W
0 2
1 ( ) ( ) 22)
Dimana fungsi defleksi v (x) dinyatakan dalam persamaan 19) dengan bentuk matriks :
[
]
=
2 2 1 1
4 3
2
1( ) ( ) ( ) ( )
) (
θ
θ
v v
x f x f x f x f x
v 23)
Persamaan 21) disamakan dengan persamaan 22) menjadi :
=
L L L L
dx x f x p
dx x f x p
dx x f x p
dx x f x p
M Y M
Y
0
4 0
3 0
2 0
1
2 2
1 1
) ( ) (
) ( ) (
) ( ) (
) ( ) (
atau secara umum : =
L
i i p x f x dx
F
0
) ( )
( 24)
terdistribusi dengan fungsi bentuknya. Definisi ini dapat digeneralisasi untuk tipe-tipe elemen lainnya seperti elemen plate dan shell. Karena beban yang ditemukan diperoleh secara konsisten sesuai fungsi bentuk yang bersesuaian maka beban-beban tersebut dinamakan Beban-beban Konsisten.
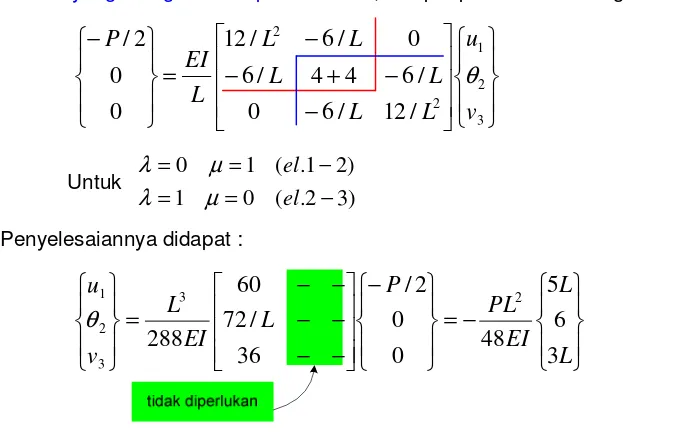
Contoh Soal 2.2. :
panjang gaya p
Gambar 2.5.
Gambar 2.5. menunjukkan struktur beam dengan ujung-ujung yang ditumpu secara
sederhana dibawah penga-ruh beban terdistribusi p. Diinginkan untuk mencari slope pada nodal 1 dan defleksi pada titik
tengah struktur.
Jawab :
Struktur di atas merupakan struktur yang simetri, karenanya dapat dimodelkan sebagai beam separuh dan analisis dilakukan terhadap beam dengan panjang l/2. Dengan kondisi batas beam diperoleh v1 =
θ
2 =0sehingga persamaan elemen menjadi :− − =
2 1 96 24
24 8
2 1
3 2
2
v EI
Y M
l l
l
l
θ
25)
Beban ekuivalen kerja akibat beban terdistribusi –p (tanda – karena p mengarah ke bawah) dapat dicari dengan menggunakan persamaan 24) :
48 4
4
2 2
/
0
2 3 2
1
pl dx l x l
x x p M
l
− = +
− − =
4 16
12
2 /
0
3
2
pl dx l x l
x p Y
l
− = −
− =
Sehingga persamaan 25) dapat diselesaikan menjadi :
− −
= − − =
16 51
1 24
4 48 1
3 3 12 24
3 2
2 3
2 1
EI pl pl
pl
l l l EI l v
θ
3.1. Definisi Umum
Frame terjadi pada saat elemen beam dimiringkan dalam bidang datar. Dalam hal ini beban yang bekerja meliputi gaya aksial, gaya geser dan momen bending. Pada kondisi ini di setiap titik nodal terdapat 3 derajat kebebasan yaitu u, v yang mengikuti sumbu x, y
dan sudut rotasi θ. Gaya-gaya yang bekerja sesuai masing-masing derajat kebebasan tersebut secara berurutan adalah X, Y dan momen bending M. Elemen berorientasi sembarang dengan sudut φ berarah bjj terhadap sumbu global horisontal. Konstanta elemen meliputi modulus elastisitas E, luas penampang lintang A, momen inersia I dan panjang L. Struktur frame dimaksud dapat dilihat pada gambar 3.1.
φ
1 1,θ M
2 2,θ M
Gambar 3.1.
Matriks stiffness untuk frame diperoleh melalui penggabungan matriks stiffness elemen truss dan beam. Dalam hal ini matriks stifness truss 2x2 dan beam 4x4 diekspansikan menjadi 6x6, kemudian ditransformasikan ke global koordinat. Jadi matriks yang diperoleh adalah sebagai berikut :
−
− −
−
− − −
−
=
2 2 1 1 2 1
2 2
2 3
2 3
2 2
2 3
2 3
2 2
1 1
2 1
4 6
2 6
0 0
6 12
6 12
0 0
2 6
4 6
0 0
6 12 6
12 0 0
0 0
0 0
0 0
0 0
θ θ
v v u u
L EI L
EI L
EI L
EI L
EI L
EI L
EI L
EI
L EI L
EI L
EI L
EI L
EI L
EI L
EI L
EI L
EA L
EA L
EA L
EA
M Y M Y X X
Jika diurutkan sesuai nodalnya, persamaan 26) menjadi :
Matriks transformasi koordinatnya adalah :
−
Maka matriks [K] hasil transformasinya adalah :
[ ]
Dalam hal ini R = (A / I), yaitu perbandingan luas area dan momen inersia.
Contoh Soal 3.1. :
Gambar 3.2.
Gambar 3.2. menunjukkan struktur frame persegi yang dikenai gaya berpasangan P. Jika diasumsikan
bahwa batang-batang frame tidak bisa meregang dan sudut-sudut putar kanan pada sambungan dijaga konstan,
tentukan bentuk defleksi, diagram gaya geser dan diagram momen bending !
Jawab :
Struktur frame yang diacu merupakan struktur yang simetri baik dalam arah vertikal maupun horisontal. Jadi, hanya seperempat bagian struktur saja yang dijadikan model dengan 2 elemen, yaitu elemen 1-2 dan 2-3. Karena batang frame tidak dapat meregang maka defleksi aksial tidak terjadi, sehingga didapat kondisi batas :
a. akibat simetrisitas : v1 =
θ
1=v2 =u3 =θ
3 =0 b. akibat sifat tak teregang : u2 = 0Sebagai hasilnya, mengacu pada persamaan 29) dengan mengeliminasi komponen matriks yang menghasilkan perkalian nol, didapat persamaan sebagai berikut :
−
−
+
−
−
=
−
3 2 1
2 2
/
12
/
6
0
/
6
4
4
/
6
0
/
6
/
12
0
0
2
/
v
u
L
L
L
L
L
L
L
EI
P
θ
Untuk
) 3 2 . ( 0 1
) 2 1 . ( 1 0
− =
=
− =
=
el el
µ
λ
µ
λ
Penyelesaiannya didapat :
−
=
−
−
−
−
−
−
−
=
L
L
EI
PL
P
L
EI
L
v
u
3
6
5
48
0
0
2
/
36
/
72
60
288
2 3
3 2 1
θ
Gaya geser internal diperoleh dengan mensubstitusikan nilai persamaan a) pada persamaan 29). Jadi untuk elemen 1-2 akan diperoleh :
−
Untuk elemen 2-3 diperoleh :−
perhitungan sama dengan nol, padahal seharusnya masing-masing bernilai –P/2 dan P/2. Hal ini disebabkan karena asumsi batang tidak teregang mengakibatkan u2 = 0.2
θ
2
θ v2
1 u
Gambar 3.3.
Latihan Soal 3.1. :