MODEL SIS (SUSCEPTIBLE INFECTED SUSCEPTIBLE) PADA PENULARAN DUA PENYAKIT ENDEMIK YAYA SUKARYA

MODEL SIS (SUSCEPTIBLE INFECTED SUSCEPTIBLE)

PADA PENULARAN DUA PENYAKIT ENDEMIK

YAYA SUKARYA

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

2009

ABSTRACT

YAYA SUKARYA. SIS (Susceptible Infected Susceptible) Model for a spread of a two Disease Endemic. Supervised by PAIAN SIANTURI and N. K. KUTHA ARDANA.

SIS (Susceptible Infected Susceptible) model is an epidemiology model, obtained via SIR (Susceptible Infected Removed) model, in which individuals have no immunity might reinfected again after they get recovered of a disease.

In this paper, we studied the SIS model for a spread of two endemic diseases in a population. The three types of equilibrium points were obtained via stability analysis, the first point called the disease free equilibrium point and the other two points were considered as endemic equilibrium points. The stability of equilibrium SIS model depend on reproduction basic number (R0). If

0 1

R < then disease free equilibrium is stable. For the endemic equilibrium, if R0> then the 1 endemic equilibrium is stable.

Based on simulations performed, there were three types behavior of solutions obtained; that is when only major, only minor or both diseases were present. The stability of population infected by major disease was proportional to the effective transmission rate with which individual become infected with the major disease.

ABSTRAK

YAYA SUKARYA. Model SIS (Susceptible Infected Susceptible) pada Penularan dua Penyakit Endemik. Dibimbing oleh PAIAN SIANTURI dan N. K. KUTHA ARDANA.

Model SIS (Susceptible Infected Susceptible) merupakan salah satu model epidemiologi yang diperoleh dari model SIR (Susceptible Infected Removed), ketika individu tidak mempunyai kekebalan tubuh setelah terserang penyakit dan menyebabkan individu tersebut menjadi rentan kembali setelah sembuh dari penyakit.

Dalam tulisan ini dipelajari model SIS pada penularan dua penyakit endemik dalam suatu populasi. Dari analisis kestabilan diperoleh tiga titik tetap yaitu satu titik tetap tanpa penyakit dan dua titik tetap endemik. Analisis kestabilan titik tetap tersebut bergantung pada bilangan reproduksi dasar (R0). Titik tetap tanpa penyakit berada dalam kestabilan ketika R0< . Untuk 1 titik tetap endemik, berada dalam kestabilan ketika R0> . 1

Dari simulasi numerik yang dilakukan terhadap model dua penyakit endemik diperoleh tiga tipe perilaku model yaitu ketika hanya penyakit utama yang muncul, ketika hanya penyakit tambahan yang muncul atau kedua penyakit (co-infected) yang muncul. Kondisi kestabilan populasi individu yang terinfeksi oleh penyakit utama berbanding lurus dengan laju penularan efektif individu menjadi terinfeksi oleh penyakit utama.

MODEL SIS (SUSCEPTIBLE INFECTED SUSCEPTIBLE)

PADA PENULARAN DUA PENYAKIT ENDEMIK

YAYA SUKARYA

Skripsi

sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains pada

Departemen Matematika

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

2009

Judul Skripsi

: Model SIS (Susceptible Infected Susceptible) pada Penularan

dua Penyakit Endemik

Nama

: Yaya Sukarya

NRP :

G54104005

Disetujui

Dr. Paian Sianturi

Pembimbing I

Ir. N. K. Kutha Ardana, M.Sc.

Pembimbing II

Diketahui

Dr. drh. Hasim, DEA

Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam

RIWAYAT HIDUP

Penulis dilahirkan di Subang pada tanggal 21 Desember 1986 sebagai anak kedua dari tiga bersaudara, dari pasangan Anda dan A’ah Komariah.

Tahun 1998 penulis lulus dari SD Negeri Pamanukan Sebrang I. Tahun 2001 penulis lulus dari SLTP Negeri 1 Pamanukan. Tahun 2004 penulis lulus dari SMA Negeri 1 Subang dan pada tahun yang sama lulus seleksi masuk IPB melalui jalur Ujian Saringan Masuk IPB (USMI). Penulis memilih Jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.

Selama mengikuti kegiatan perkuliahan, penulis aktif diberbagai kegiatan mahasiswa yaitu sebagai staf Departemen Lingkar Muslim Matematika (LIMIT) Gugus Mahasiswa Matematika (Gumatika) IPB (2005/2006), staf Divisi Relasi Serambi Ruhiyah Mahasiswa FMIPA (2006/2007). Penulis juga aktif sebagai panitia pada beberapa acara antara lain Kajian Ilmu Pengetahuan Al Qur’an dan Sunnah (KIPAS) tahun 2007, Masa Perkenalan Departemen (2005 & 2006), Matematika RIA Nasional (2006), Pesta Sains Nasional (2006), Musyawarah Wilayah (Muswil) III IKAHIMATIKA (2006).

PRAKATA

Puji dan syukur penulis panjatkan kepada Allah SWT yang telah melimpahkan rahmat dan karunia-Nya sehingga penulis dapat menyelesaikan karya ilmiah ini. Penyusunan karya ilmiah ini tidak terlepas dari bantuan berbagai pihak. Oleh karena itu, dalam kesempatan ini penulis mengucapkan terima kasih yang sebesar-besarnya kepada:

1. Dr. Paian Sianturi selaku dosen pembimbing I.

2. Ir. N. K. Kutha Ardana, M.Sc selaku dosen pembimbing II.

3. Drs. Ali Kusnanto, M.Sc selaku dosen penguji dan moderator seminar. 4. Semua dosen Departemen Matematika.

5. Bu Ade, Bu Susi, Mas Yono, Mas Bono, Mas Deni, Mas Heri. 6. Keluarga tercinta: Ayah, Ibu, Kakak dan Adik.

7. Ibrahim Amin, Nidia Rosita dan Nur Armi selaku pembahas.

8. Teman-teman Math 41: Rangga, bang Idris, Triyadi, Iboy, Ujang, Great, Fariz, Fredrick, Mahnur, Majid, Mora, Aji, Jali, Dika, Dee-dee, Lia Y, Lia M, Mahar, Mukti, Nurjanah, Mba Syifa, Darwisah, Eli, Rofah, Niken, Mariam, dan semuanya yang tidak dapat disebutkan satu per satu.

9. Teman-teman Math 39, 40, 42 dan semuanya yang tidak dapat disebutkan satu per satu. 10. Temen-temen kost-an : Pondok 55, PPM Al Inayah, Wisma Savana.

11. Semua pihak yang telah membantu yang tidak dapat penulis sebutkan satu per satu. Semoga karya ilmiah ini bermanfaat bagi semuanya.

Bogor, September 2009

DAFTAR ISI

Halaman

DAFTAR GAMBAR ... viii

DAFTAR LAMPIRAN ... viii

I PENDAHULUAN 1.1 Latar Belakang ... 1 1.2 Tujuan ... 1 II LANDASAN TEORI ... 1 III PEMBAHASAN 3.1 Perumusan Model ... 4 3.2 Titik Tetap ... 6

3.3 Analisis Kestabilan Titik Tetap ... 6

3.3.1 Kestabilan Sistem di Titik Tetap E0 ... 6

3.3.2 Kestabilan Sistem di Titik Tetap E1 ... 7

3.3.3 Kestabilan Sistem di Titik Tetap E2... 8

3.4 Analisis Kualitatif... ... 9

IV SIMPULAN ... 13

DAFTAR PUSTAKA ... 14

DAFTAR GAMBAR

halaman

1 Diagram alur untuk penularan dua penyakit endemik ... 4

2 Kurva solusi p( )α dan ( )qα terhadap α dengan β=0.3 ... 10

3 Kurva solusi ( )pα dan ( )qα terhadap α dengan β =0.5 ... 10

4 Kurva solusi ( )pα dan ( )qα terhadap α dengan β =0.7 ... 10

5 Kurva solusi ( )pα dan ( )qα terhadap α dengan β =0.8 ... 10

6 Dinamika populasi dari keempat model terhadap t dengan α=0.52 dan β=0.75 ... 11

7 Dinamika populasi dari keempat model terhadap t dengan α=0.6 dan β=0.4 ... 11

8 Dinamika populasi dari keempat model terhadap t dengan α =0.8 dan β =0.8 ... 11

9 Dinamika populasi dari keempat model terhadap t dengan α =0.9 dan β =0.9 ... 11

DAFTAR LAMPIRAN

halaman

1 Pembuktian teorema 1 dan teorema 2 ... 16

2 Penurunan persamaan (6)-(9) ... 17

3 Mencari titik tetap ... 18

4 Matriks Jacobi untuk persamaan (18) ... 21

5 Penurunan persamaan (24) dan persamaan (26) ... 22

6 Penurunan persamaan (32) ... 23

7 Program analisis kestabilan dengan metode Routh-Hurwizt Criterion untuk titik tetap E 1

... 23

8 Program analisis kestabilan dengan metode Routh-Hurwizt Criterion untuk titik tetap E 2

... 24

9 Program untuk menentukan gambar kurva solusi ( )pα dan ( )qα terhadap α ... 25

I PENDAHULUAN

1.1 Latar Belakang

Sejak dikenalkannya model SIR (Susceptible Infected Removed) oleh Kermack dan McKendrick pada tahun 1927 untuk penyebaran penyakit, persamaan diferensial secara luas digunakan dalam matematika epidemiologi. Banyak model matematika yang dibangun untuk mempelajari penularan penyakit, mengevaluasi atau menilai penularan dari suatu epidemik, dan banyak lagi yang penting lainnya. Untuk memahami mekanisme dari epidemik untuk mencegah atau meminimumkan penularan suatu penyakit, diantaranya dengan karantina dan perlakuan lainnya.

Dalam karya ilmiah ini akan dibahas suatu model SIS (Susceptible Infected

Susceptible) dari penularan dua penyakit

endemik dalam suatu populasi. Model SIS ini sendiri diperoleh dari model SIR (Susceptible

Infected Removed), dengan mengganti R

(Removed) menjadi S (Susceptible), ketika individu tidak memiliki kekebalan tubuh setelah datangnya penyakit, yang menyebabkan individu tersebut menjadi rentan kembali setelah sembuh dari penyakit. Model ini menjelaskan gambaran secara

umum dari dua penyakit endemik dan analisis dari dinamika populasi agar menambah pemahaman dari kelakuan atau perilaku sifat dalam sistem tersebut. Dalam hal ini adanya hubungan antara penyakit utama dan penyakit tambahan dengan munculnya suatu ( )pα dan

( )

qα yang harus dipenuhi ketika salah satu

dari dua penyakit endemik tersebut muncul dengan α sebagai parameter kontrol. Kestabilan titik tetap dan analisis kestabilan titik tetap dari model tersebut dilakukan dengan menggunakan software Mathematica

6 dan berdasarkan parameter dari Blyuss &

Kyrychko (2005). 1.2 Tujuan

Tujuan penulisan karya ilmiah ini adalah : 1. Mempelajari model matematika dari

sistem penularan dua penyakit endemik dalam suatu populasi.

2. Menganalisis kestabilan titik tetap yang diperoleh.

3. Menganalisis perilaku solusi model.

II LANDASAN TEORI

Pada bab ini akan diberikan teori yang menjadi landasan pengerjaan karya ilmiah ini. Berikut ini adalah definisi-definisi mengenai istilah yang digunakan.

Sistem Persamaan Diferensial Definisi 1 (Persamaan Diferensial Linear Orde 1)

Suatu persamaan yang dinyatakan sebagai , ) ( ) ( n x t g x t a x+ = ∈ℜ

(1)

Disebut persamaan diferensial (PD) linear orde 1. Jika g(t)=0, PD disebut PD linear homogen dan jika g(t)≠0, PD disebut PD linear takhomogen.

[Tu, 1994] Definisi 2 (Sistem Persamaan Diferensial Mandiri)

Suatu sistem persamaan diferensial (SPD) dinyatakan sebagai

dx ( ) , n

x f x x

dt = = ∈ℜ (2)

dengan f fungsi kontinu bernilai real dari x dan mempunyai turunan parsial kontinu. SPD tersebut disebut SPD mandiri (autonomous) jika tidak memuat waktu )(t secara eksplisit di dalamnya.

[Tu, 1994] Kestabilan di Sekitar Titik Tetap Definisi 3 (Titik Tetap)

Diberikan SPD . ) (_{x x} n f x dt dx_{= = ∈ℜ}

Titik _{x disebut titik tetap jika} *

0 ) (_x* ₌

f .Titik tetap disebut juga titik kritis

atau titik keseimbangan. Untuk selanjutnya akan digunakan istilah titik tetap.

Definisi 4 (Titik Tetap Stabil) Misalkan *

x adalah titik tetap SPD mandiri dan x

( )

t adalah sebuah solusi SPD mandiri

dengan nilai awal x

( )

0 =x dengan 0 * 0≠

x x . Titik *

x dikatakan titik tetap stabil jika untuk sebarang radius ε > terdapat 0 r> 0 sedemikan sehingga jika posisi awal x 0

memenuhi * 0− <r x x maka solusi x

( )

t memenuhi

( )

* t − <ε x x , untuk setiap t> . 0 [Verhulst, 1990] Definisi 5 (Titik Tetap Stabil Asimtotik Lokal)

Titik x dikatakan titik tetap stabil asimtotik *

lokal jika titik_{x stabil dan terdapat} *

0 >

ε sedemikian sehingga jika *− ₀ <ε

x x maka limx(t) x* t = ∞ → , dengan x0=x(0).

[Szidarovszky & Bahill, 1998] Definisi 6 (Titik Tetap Stabil Asimtotik Global)

Titik x dikatakan titik tetap stabil asimtotik *

global jika titikx stabil dan * x0∈Ω⊆ℜn, * ) ( limxt x t = ∞ → , dengan x0=x(0).

[Szidarovszky & Bahill, 1998] Definisi 7 (Titik Tetap Tak Stabil)

Misalkan *

x adalah titik tetap sebuah SPD mandiri dan x

( )

t adalah sebuah solusi SPD

mandiri dengan nilai awal x

( )

0 =x dengan 0 *

0≠

x x . Titik x dikatakan titik tetap tak * stabil jika terdapat radius ε > dengan ciri 0 sebagai berikut : untuk sebarang r> 0 terdapat posisi awal x memenuhi 0

* 0− <r

x x , berakibat solusi x

( )

t memenuhi

( )

*

t − ≥ε

x x , untuk paling sedikit satu 0

t> .

[Verhulst, 1990] Definisi 8 (Nilai Eigen dan Vektor Eigen) Diberikan matriks koefisien konstan A

Berukuran n x n, dan SPD homogen berikut 0

, (0) , n

R

= + = ∈

x Ax b x x x (3)

Suatu vektor tak nol x dalam ruang n

R

disebut vektor eigen dari A jika untuk suatu skalar λ berlaku

λ =

Ax x (4)

Nilai skalar λ dinamakan nilai eigen dari A. Untuk mencari nilai λ dari matriks A , maka Persamaan (4) dapat ditulis kembali sebagai

(

A- Iλ

)

x=0 (5)

dengan I matrik identitas. Persamaan (5) mempunyai solusi tak nol jika dan hanya jika

(

)

( ) det - I I 0

pλ = Aλ = A−λ = (6)

Persamaan (6) disebut persamaan karakteristik dari matriks A.

[Anton, 1995] Definisi 9 (Pelinearan)

Diberikan SPD tak linear

( ) , n d f R dt = = ∈ x x x x (7)

Dengan menggunakan perluasan Taylor pada titik-titik tetapnya, maka diperoleh

( ) x ϕ = + x A x (8) dengan * * * 1 1 1 1 ( ) ( ) n n n n Df Df f f f f = = = = ∂ ∂ ⎡ ⎤ ⎢_{∂ ∂} ⎥ ⎢ ⎥ ⎢ ⎥ = ⎢_{∂ ∂} ⎥ ⎢ ⎥ ⎢∂ ∂ ⎥ ⎣ ⎦ X X X X A x x x x x x … … dan fungsi ( )ϕ x memenuhi

0 lim ( ) 0 x→ ϕ x =

.

Akibatnya persamaan differensial (7) dapat dihampiri oleh persamaan

=

x Ax (9)

Persamaan (9) disebut pelinearan dari persamaan diferensial (7).

[Tu, 1994]

Analisis Kestabilan Titik Tetap Definisi 10 (Kestabilan Titik Tetap) Diberikan SPD sebarang

( ) , n.

dx

x f x x

dt = = ∈ℜ

Tentukan titik tetap _{x yang memenuhi} *

. 0 ) (x* =

f Penentuan kestabilan titik tetap

didapat dengan melihat nilai-nilai eigennya, yaitu : λ dimana i i=1,2, ,n yang diperoleh

dari persamaan karakteristik (5).

Secara umum kestabilan titik tetap mempunyai tiga perilaku :

a. Re(λi)<0untuk setiap i.

b. Terdapat Re( ) 0λ = untuk sebarang j i dan Re(λi)<0untuk setiap i≠ .j II. Tak stabil, jika terdapat paling sedikit satu i

dimana Re(λ_i)>0.

III. Sadel, jika perkalian dua buah nilai eigen real sembarang adalah negatif (λ λ < i j 0 untuk i dan j sembarang).

[Grimshaw, 1990] Kriteria Kestabilan

Kondisi Routh Hurwitz

Misalkan a1,a2, ,ak bilangan-bilangan real, aj=0jika j> . Semua nilai eigen dari k persamaan karakteristik 1 2 1 1 2 1 ( ) k k ... + 0 k k k pλ =λ +aλ − + a₋λ +a₋λ +a =

mempunyai bagian real yang negatif jika dan hanya jika determinan dari matriks i× ,i untuk setiap i=1,2, ,k, determinan dari

matriks i× ,i ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ₋ − − i i i i a a a a a a a a a a a M 0 0 0 0 1 3 2 3 1 2 2 4 2 1 2 5 3 1 adalah positif. [Fisher, 1990] Sehingga menurut kondisi Routh-Hurwitz, untuk suatu k , k=2, 3, 4 disebutkan bahwa titik tetap _x* _{stabil jika dan hanya jika (untuk}

4 , 3 , 2 = k ), , 0 , 0 ; 2 1> 2> = a a k , , 0 , 0 ; 3 a1 a3 a1a2 a3 k= > > > . , 0 , 0 , 0 ; 4 a1 a3 a4 a1a2a3 a32 a12a4 k= > > > > + [Tu, 1994] Untuk kasusk=3dan k= , kondisi Routh-4 Hurwitz disajikan pada teorema 1 dan 2

berikut.

Teorema 1

Misalkan A,B,C bilangan real. Bagian real

dari setiap nilai eigen persamaan karakteristik 0 )

( = 3+A 2+B +C=

pλ λ λ λ

adalah negatif jika dan hanya jika ,A C

bernilai positif dan AB>C. Bukti : [lampiran 1] Teorema 2

Misalkan A B C dan , , D bilangan real.

Bagian real dari setiap nilai eigen persamaan karakteristik

4 3 2

( ) 0

pλ =λ +Aλ +Bλ +Cλ+ = D

adalah negatif jika dan hanya jika , ,A C D

bernilai positif dan 2 2 _.

ABC>C +A D

Bukti : [lampiran 2]

Definisi 11 (Bilangan Reproduksi Dasar (R )) 0

Bilangan Reproduksi Dasar (R0) adalah rata- rata banyaknya individu rentan yang terinfeksi secara langsung oleh individu lain yang sudah terinfeksi bila individu yang sudah terinfeksi tersebut masuk ke dalam populasi yang seluruhnya masih rentan.

Formula untuk menentukan bilangan reproduksi dasar (R0) adalah :

0

R = maks

{

R R R1, 2, 3

}

,

dengan R R1, 2, dan ,R menyatakan bilangan 3 reproduksi dasar masing-masing dari penyakit utama, penyakit tambahan, dan kedua-duanya. Kondisi yang akan timbul adalah salah satu di antara kemungkinan berikut :

1. Jika R0 < maka penyakit akan 1, menghilang.

2. Jika R0= maka penyakit akan menetap 1, (endemis),

3. Jika R0 > maka penyakit akan 1, meningkat menjadi wabah.

III PEMBAHASAN

3.1 Perumusan Model

Dalam penulisan karya ilmiah ini, model yang akan dibahas adalah suatu model SIS (Susceptible Infected Susceptible) dari penularan dua penyakit endemik dalam suatu populasi.

Model SIS merupakan suatu model penyebaran penyakit yang diperoleh dari model SIR (Susceptible Infected Removed) yang dibuat oleh Kermack dan McKendrick pada tahun 1927. Model SIS diperoleh dengan mengganti R (Removed) menjadi S (Susceptible), ketika individu tidak mempunyai kekebalan tubuh setelah terserang penyakit, artinya individu tersebut menjadi rentan kembali setelah sembuh dari penyakit.

Secara skematik, diagram alur model SIS pada penularan dua penyakit endemik dalam suatu populasi dapat dilihat pada gambar 1. Misalkan banyaknya populasi individu pada waktu t dinyatakan dengan N =N(t).

Populasi ini dibagi menjadi tiga kelas yaitu populasi individu rentan S=S(t), populasi individu terinfeksi oleh penyakit utamaI_D =I_D(t), populasi individu terinfeksi oleh penyakit tambahanId =Id(t),dan populasi individu terinfeksi oleh kedua

penyakit tersebut IdD =IdD(t).Total populasi dituliskanN =S+I_D+I_d +I_dD.

Konstruksi model matematika untuk model SIS pada penularan dua penyakit endemik dalam suatu populasi ini menggunakan asumsi:

1. Tiap individu setelah sembuh akan menjadi rentan kembali.

2. Recruitment (B) konstan.

3. Efisiensi dari penularan penyakit diasumsikan sama untuk individu yang rentan dan individu yang terinfeksi. 4. Peluang individu menjadi terinfeksi oleh

penyakit kedua adalah sama dengan peluang individu rentan menjadi individu terinfeksi oleh penyakit tersebut.

5. Peluang individu menjadi terinfeksi oleh penyakit utama setelah adanya interaksi dengan individu yang terinfeksi oleh kedua penyakit adalah α −

(

1 β

)

, peluang individu menjadi terinfeksi oleh penyakit tambahan setelah adanya interaksi dengan individu yang terinfeksi oleh kedua penyakit adalah β −

(

1 α

)

, dan peluang individu menjadi terinfeksi oleh kedua penyakit adalah αβ .

Gambar 1. Diagram alur untuk penularan dua penyakit endemik

S

I

d

I

dD

I

D B µ D r rd β α αβ rdD

(

β

)

α −1 β −

(

1 α

)

µ µ µ σ_D σd α α β β d D σ σ +

Setelah semua diasumsikan, model dapat dituliskan sebagai berikut:

(

)

(

)

(

)

(

)

(

)

(

)

(

)

1 1 , (1) 1 , (2) 1 dD D dD d dD D D d d dD dD D D dD D D D D d dD d dD d d d d dS S S S S S B S I I I I I r I r I r I dt N N N N N dI S S I I I r I I I dt N N N dI S S I I r I dt N N µ α β α β α β αβ α β α σ µ β β α β σ µ = − − − − − − − − + + + = − + − + + − + = − + − + + −

(

)

(

)

(

)

(

)

, (3) , (4) . d D dD dD D d dD d D D d dD dD dD D d dD I I I N dI I I I S I I r I I dt N N N N S I I I α α β α β σ σ µ αβ + = + + + − + + + + = + + + (5) dengan, N : total populasi,

S : populasi individu rentan,

D

I : populasi individu terinfeksi oleh

penyakit utama, d

I : populasi individu terinfeksi oleh

penyakit tambahan,

B : recruitment, B>0,

µ : Tingkat kematian alami, 0<µ≤1,

α : penularan efektif individu menjadi terinfeksi oleh penyakit utama, α >0,

β : penularan efektif individu menjadi terinfeksi oleh penyakit tambahan,

, 0 > β D

σ : tingkat kematian yang disebabkan oleh penyakit utama, 0<σ_D ≤1, d

σ : tingkat kematian yang disebabkan oleh penyakit tambahan,

0<σ_d ≤1, D

r : tingkat kesembuhan dari penyakit

utama, 0<r_D≤1, d

r : tingkat kesembuhan dari penyakit

tambahan, ,0<r_d ≤1 dD

r : tingkat kesembuhan dari kedua

penyakit, 0<r_dD≤1,

Selanjutnya digunakan penskalaan dengan mensubstitusikan persamaan (5) ke dalam sistem persaman (1)-(4), sehingga diperoleh sistem persamaan (6)-(9) sebagai berikut :

(

1

)

dD D d dD dS S B S I dt = −µ −α −β S+I +I +I D D d dD S I S I I I α − + + +

(

)

1 dD D d dD S I S I I I β α − − + + + d D d dD S I S I I I β − + + + dD D d dD S I S I I I αβ − + + + +r ID D+r Id d+r IdD dD, (6)

(

1

)

D dD D d dD dI S I dt =α −β S+I +I +I

(

)

D D D D D d dD S I r I S I I I α σ µ + − + + + + +

(

)

D , d dD D d dD I I I S I I I β − + + + + (7)

(

1

)

d dD D d dD dI S I dt =β −α S+I +I +I

(

)

d d d d D d dD S I r I S I I I β σ µ + − + + + + +

(

)

d , D dD D d dD I I I S I I I α − + + + + (8)

(

)

dD D d D d dD dI I I dt = α β+ S+I +I +I

(

)

dD d D D d dD I I I S I I I α β + + + + +

(

)

− σD+σd+ +µ rdD IdD + dD . D d dD S I S I I I αβ + + + (9)

Selanjutnya akan diturunkan titik tetap untuk sistem persamaan (6)-(9) yang kemudian akan dibahas analisis kestabilan disekitar titik tetap tersebut serta dinamika populasinya.

3.2 Titik Tetap

Analisis titik tetap pada SPD sering digunakan untuk menentukan suatu solusi yang tidak berubah terhadap waktu t. Perhatikan kembali persamaan (6)–(9), misalkan titik tetap persamaan tersebut dinotasikan dengan

(

*_, *_, *_, *

)

_.

D d dD

E= S I I I

Dengan demikian menurut definisi, titik tetap

E dapat diperoleh dengan menentukan

0, 0, 0, dID dId dan 0,dIdD

dS

dt = dt = dt = dt =

dari persamaan (6)-(9).

Titik tetap yang diperoleh adalah 0 ,0,0,0 B E µ ⎛ ⎞ = ⎜ ⎟ ⎝ ⎠ ,

(

)

1 , D, 0, 0 E = S I , dan

(

* *

)

2 ,0, d , 0 E = S I , dengan, (10) D N = +S I 2 ˆ _{, (11)} D D D D D B N r α σ µ αµ ασ σ σ = − + + − − 2 ( ) , (12) D D D D D D D r B S r µ σ σ µ αµ ασ σ σ + + = − + + − − 2 ( ) , (13) D D D D D D D D r B I r α µ σ σ µ αµ ασ σ σ − − − = − + + − − * * * ₍₁₄₎ d N =S +I * 2 , (15) d d d d d B N r β σ µ βµ βσ σ σ = − + + − − * 2 ( ) , (16) d d d d d d d r B S r µ σ σ µ βµ βσ σ σ + + = − + + − − * 2 ( ) , (17) d d d d d d d d r B I r β µ σ σ µ βµ βσ σ σ − − − = − + + − −

Penentuan titik tetap ini dapat dilihat di lampiran 4.

3.3 Analisis Kestabilan Titik Tetap

Pada bagian ini akan dianalisis kestabilan titik tetap dari sistem persamaan (6)-(9). Misalkan persamaan (6)–(9) dituliskan sebagai berikut :

(

, D, ,d dD

)

, dS A S I I I dt =

(

, , ,

)

, D D d dD dI B S I I I dt =

(

, , ,

)

, d D d dD dI C S I I I dt =

(

, , ,

)

. dD D d dD dI D S I I I dt =

Dari sistem persamaan di atas dapat diperoleh matriks Jacobi:

J D d dD D d dD D d dD D d dD A A A A S I I I B B B B S I I I C C C C S I I I D D D D S I I I ∂ ∂ ∂ ∂ ⎡ ⎤ ⎢_{∂ ∂ ∂ ∂} ⎥ ⎢ ⎥ ⎢∂ ∂ ∂ ∂ ⎥ ⎢_{∂ ∂ ∂ ∂} ⎥ ⎢ ⎥ =_{⎢ ⎥} ∂ ∂ ∂ ∂ ⎢_{∂ ∂ ∂ ∂} ⎥ ⎢ ⎥ ⎢_{∂ ∂ ∂ ∂} ⎥ ⎢ ⎥ ∂ ∂ ∂ ∂ ⎢ ⎥ ⎣ ⎦ 11 12 13 14 21 22 23 24 31 32 33 34 41 42 43 44 = α α α α α α α α α α α α α α α α ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ (18) dengan, J={ }α untuk ij i=1, 2,3, 4 dan j=1, 2,3, 4 (lihat lampiran 5).

3.3.1 Kestabilan Sistem di Titik Tetap

(

,0,0,0

)

0 µB

E =

Sistem persamaan diferensial pada titik tetap E akan menghasilkan matriks Jacobi 0 sebagai berikut : J0 ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = 44 43 42 41 34 33 32 31 24 23 22 21 14 13 12 11 α α α α α α α α α α α α α α α α (19) dengan, 11 α = − µ α = ₃₁ 0 12 rD α = − + α α = ₃₂ 0 13 rd α = − +β α33= −β (σd+ +µ rd) 14 rdD α = − − +α β αβ+ α₃₄=β

₍

1−α

₎

21 0 α = α₄₁=0 22 ( D rD) α = −α σ + +µ α = ₄₂ 0 23 0 α = α = 43 0 24 (1 ) α =α − β α44= −(σD+σd+ +µ rdD)+αβ Persamaan karakteristik dari matriks J0

diperoleh dari persamaan det (J0-λ I) 0=

11 12 13 14 22 24 33 34 44 0 0 det 0 0 0 0 0 0 α λ α α α α λ α α λ α α λ − ⎡ ⎤ ⎢ ₋ ⎥ ⎢ _{⎥ =} ⎢ − ⎥ ⎢ ₋ ⎥ ⎣ ⎦

(

α11−λ α

)(

22−λ α

)(

33−λ α

)(

44−λ

)

=0 (20) Persamaan (20) menghasilkan nilai eigen sebagai berikut : , 1 µ λ =− 2 ( D rD), λ = −α µ σ+ + 3 ( d rd), λ = −β µ σ+ + dan 4 ( d D rdD). λ =αβ− µ σ+ +σ + (21) Matriks J0 mempunyai empat nilai eigen yang

mempunyai nilai bilangan realnya negatif jika dan hanya jika

, , dan . D D d d d D dD r r r α µ σ β µ σ αβ µ σ σ < + + < + + < + + + (22)

Dengan mengekspresikan dalam bentuk , , 2 1 R R dan R dengan 3, 1 2 3 , , dan , D D d d D d dD R r R r R r α σ µ β σ µ αβ σ σ µ = + + = + + = + + + (23)

maka kita peroleh bahwa E0 adalah stabil

lokal asimtotik jika R₁<1,R₂<1,dan

3 1.

R < Dengan menggunakan definisi untuk

1

R dan R akan secara mudah diperoleh 3

bahwa jika (24) D d dD D D r r σ σ µ β σ µ + + + < + + (lihat lampiran 6) maka R1>R3 dan cukup mengikuti dinamika

pada R saja untuk memperoleh nilai terkecil 1

dari α yang mana E0 akan menjadi takstabil.

3.3.2 Kestabilan Sistem di Titik Tetap

(

)

1 , D,0,0

E = S I

Sistem persamaan diferensial pada titik tetap E , akan menghasilkan matriks Jacobi 1 sebagai berikut : J1 ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = 44 43 42 41 34 33 32 31 24 23 22 21 14 13 12 11 α α α α α α α α α α α α α α α α (25) dengan, 2 11 _{( )}2 D D I S I α α = − −µ + 2 12 _{( )}2 D D S r S I α α = − + + 13 2 ( ) ( ) D D d D SI S S I r S I α β α = − + + + 14 2 ( ) ( ) + ( ) D D dD D S S I S I r S I α α β αβ α = − − + + + + 2 21 _{( )}2 D D I S I α α = + 2 22 _{( )}2 ( D D) D S r S I α α = −σ + +µ + 2 23 2 ( ) ( ) D D D I SI S I β α β α =− − + + 2 24 2 ( ) ( ) ( ) D D D I S S S I S I α β α α = − + + + + 31 0 α = 32 0 α = 33 ( ) ( ) D d d D I S r S I α β α = − + − σ + +µ + 34 ( 1) ( D) S S I β α α = − − + 41 0 α = 42 0 α = 43 ( ) ( ) D D I S I α β α = + + 44 ( ) ( ) ( ) D D d dD D I S r S I α β α = + − σ +σ + +µ +

Persamaan karakteristik dari matriks J1

diperoleh dari persamaan det (J1 -λ I) 0= 11 12 13 14 21 22 23 24 33 34 43 44 det 0 0 0 0 0 α λ α α α α α λ α α α λ α α α λ − ⎡ ⎤ ⎢ ₋ ⎥ ⎢ _{⎥ =} ⎢ − ⎥ ⎢ ₋ ⎥ ⎣ ⎦ (26)

Kestabilan titik tetap E diperoleh 1 dengan mengamati nilai eigen matriks J1 pada

persamaan (26) yaitu : 4 3 2 1 1 1 1 0 A B C D λ + λ + λ + λ+ = dengan nilai 1

A, B1, C1 D1, ada pada lampiran 7.

Berdasarkan kriteria Routh Hurwitz,

titik tetap E1 stabil jika keempat syaratnya dipenuhi yakni :

1. A1> , kondisi ini terpenuhi jika 0 ,

D rD

α µ σ> + + (27)

dapat dituliskan sebagai R1> 1. 2. C1> , kondisi ini terpenuhi jika 0

1 2 1 3 1 1 1 1 0. p R R R R αβ _β⎛ ⎞ _α⎛ ⎞ αβ = − + _⎜ − +_{⎟ ⎜} − _⎟+ > ⎝ ⎠ ⎝ ⎠ (28) 3. D1> , kondisi ini terpenuhi jika 0

1 2 3 0, q=q +q +q > (29) disini,

(

)

1 2 2 2 1 3 2 3 3 1 2 , 1 1 1 1 , 1 1 . q R q R R R q R R R β α β α αβ αβ α _α β ⎛ ⎞ = −_⎜ + _⎟ ⎝ ⎠ ⎛ ⎛ ⎞ ⎞ = ⎜_⎜ + ⎜ − ⎟+ − ⎟_⎟ ⎝ ⎠ ⎝ ⎠ ⎛ ⎛ ⎞ ⎞ = ⎜_⎜ ⎜ − ⎟+ ⎟_⎟ ⎝ ⎠ ⎝ ⎠ 4. 2 1 1 1 1 1 0,A B C −C12−A D > kondisi ini

terpenuhi jika ketiga syarat sebelumnya terpenuhi.

(30) Jadi titik tetap E1 stabil jika keempat syarat tersebut terpenuhi. (lihat lampiran 9). 3.3.3 Kestabilan Sistem di Titik Tetap

(

* *

)

2 ,0, , 0d

E = S I

Sistem persamaan diferensial pada titik tetap E2, akan menghasilkan matriks

Jacobi sebagai berikut :

J2 ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = 44 43 42 41 34 33 32 31 24 23 22 21 14 13 12 11 α α α α α α α α α α α α α α α α (31) dengan, * 11 ₍ * * 2₎ d d I S I β α = − −µ + * * * * * 12 * * 2 ( ) ( ) d d D d S S I S I r S I α β α =− + + + + * 2 13 * * 2 ( ) ( ) d d S r S I β α = − + + * * * 14 * * * * 2 ( ) ( ) ( ) d dD d d S I S r S I S I β α β αβ α = − − + + + + + 21 0 α = * * 22 * * ( ) ( ) ( ) d D D d S I r S I α β α = − −σ + +µ + 23 0 α = * 24 * * (1 ) ( d) S S I α β α = − + * 2 31 * * 2 ( ) ( ) d d I S I β α = + * * * 2 32 * * 2 ( ) ( ) ( ) d d d S I I S I α β α α =− + − + * 2 33 * * 2 ( ) _{( )} ( ) d d d S r S I β α = − σ + +µ + * 2 * 2 * * 34 * * 2 ( ) ( 1)( ) ( 1) ( ) d d d I S S I S I α β α α β α = − + − + + + 41 0 α = * 42 * * ( ) ( ) d d I S I α β α = + + 43 0 α = * * 44 ₍ * *₎ ( ) d D d dD d S I r S I αβ α α = + − σ +σ + +µ +

Persamaan karakteristik dari matriks J2

diperoleh dari persamaan det (J2 -λ I) 0= 11 12 13 14 22 24 31 32 33 34 42 44 0 0 det 0 0 0 α λ α α α α λ α α α α λ α α α λ − ⎡ ⎤ ⎢ ₋ ⎥ ⎢ _{⎥ =} ⎢ − ⎥ ⎢ ₋ ⎥ ⎣ ⎦ (32) Kestabilan titik tetap E diperoleh 2 dengan mengamati nilai eigen matriks J2 pada

persamaan (32) yaitu : 4 3 2 2 2 2 2 0 A B C D λ + λ + λ + λ+ = dengan nilai 2

A, B2, C2 D2, ada pada lampiran 8. Berdasarkan kriteria Routh Hurwitz,

titik E2 stabil jika keempat syaratnya dipenuhi yakni :

1. A2> , kondisi ini terpenuhi jika : 0 ,

d rd

dapat dituliskan sebagai R2> 1. 2. C2> , kondisi ini terpenuhi jika 0

2 1 2 3 1 1 1 1 0. p R R R R αβ _{α β} αβ ∗_{= − +} ⎛ _{− +}⎞ ⎛ ₋ ⎞_{+ >} ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠ (34) 3. D2> , kondisi ini terpenuhi jika 0

1 2 3 0, q∗=q∗+q∗+q∗> (35) disini, 1 1 , q R α β ∗_{= −}⎛ ₊ ⎞ ⎜ ⎟ ⎝ ⎠

(

)

2 2 2 3 1 1 1 1 1 , q R R R α β αβ αβ ∗₌ ⎛_{⎜ +} ⎛ ₋ ⎞_{+ −} ⎞_⎟ ⎜ ⎟ ⎜ _{⎝ ⎠} ⎟ ⎝ ⎠ 3 3 2 2 1 1 . q R R R β _β α ∗₌ ⎛_⎜ ⎛ ₋ ⎞₊ ⎞_⎟ ⎜ ⎟ ⎜ _{⎝ ⎠} ⎟ ⎝ ⎠ 4. 2 2 2 2 2 2 0, A B C −C22−A D > kondisi ini

terpenuhi jika ketiga syarat sebelumnya terpenuhi.

(36) Jadi titik tetap E2 stabil jika keempat syarat tersebut terpenuhi. (lihat lampiran 10).

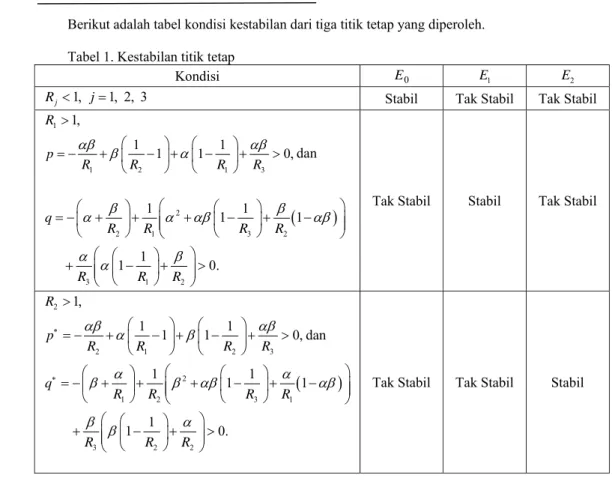
Berikut adalah tabel kondisi kestabilan dari tiga titik tetap yang diperoleh. Tabel 1. Kestabilan titik tetap

Kondisi E0 E1 E2

1, 1, 2, 3 j

R < j= Stabil Tak Stabil Tak Stabil

1 1, R > 1 2 1 3 1 1 1 1 0, p R R R R αβ _β⎛ ⎞ _α⎛ ⎞ αβ = − + ⎜ − +⎟ ⎜ − ⎟+ > ⎝ ⎠ ⎝ ⎠ dan

(

)

2 2 1 3 2 3 1 2 1 1 1 1 1 1 0. q R R R R R R R β β α α αβ αβ α _α β ⎛ ⎛ ⎞ ⎞ ⎛ ⎞ = −⎜ + ⎟+ ⎜_⎜ + ⎜ − ⎟+ − ⎟_⎟ ⎝ ⎠ ⎝ ⎝ ⎠ ⎠ ⎛ ⎛ ⎞ ⎞ + ⎜_⎜ ⎜ − ⎟+ ⎟_⎟> ⎝ ⎠ ⎝ ⎠

Tak Stabil Stabil Tak Stabil

2 1, R > 2 1 2 3 1 1 1 1 0, p R R R R αβ _{α β} αβ ∗_{= − +} ⎛ _{− +}⎞ ⎛ ₋ ⎞_{+ >} ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠ dan

(

)

2 1 2 3 1 3 2 2 1 1 1 1 1 1 0. q R R R R R R R α α β β αβ αβ β _β α ∗_{= −}⎛ ₊ ⎞₊ ⎛_{⎜ +} ⎛ ₋ ⎞_{+ −} ⎞_⎟ ⎜ ⎟ ⎜ ⎟ _{⎜ ⎟} ⎝ ⎠ ⎝ ⎝ ⎠ ⎠ ⎛ ⎛ ⎞ ⎞ + ⎜_⎜ ⎜ − ⎟+ ⎟_⎟> ⎝ ⎠ ⎝ ⎠

Tak Stabil Tak Stabil Stabil

Selanjutnya akan dibahas analisis kualitatif untuk mengetahui perilaku solusi model dan dinamika populasinya.

3.4 Analisis Kualitatif

Ilustrasi kondisi kestabilan sistem pada ketiga titik tetap dapat ditunjukkan dalam kurva solusi dan dinamika populasinya dengan menggunakan bantuan software

Mathematica 6.

Untuk itu diperlukan nilai-nilai parameter yang terdapat dalam persamaan (1)-(5). Parameter yang diberikan dalam tulisan ini diambil dari Blyuss & Kyrychko (2005).

a. Dengan menggunakan nilai-nilai parameter µ=0.01, σ_D =0.04, , 03 . 0 = d σ r_D =0.5, rd =0.8, dan 1,

B= kurva solusi ( )pα dan ( )qα

0.7

β= , dan β=0.8yang diilustrasikan

pada Gambar 2(a) - 2(d).

0.2 0.4 0.6 0.8 1 α -0.4 -0.2 0.2 0.4 0.6 0.8 1 p@αD,q@αD 0.2 0.4 0.6 0.8 1 α -0.4 -0.2 0.2 0.4 0.6 0.8 1 p@αD,q@αD (a) (b) 0.2 0.4 0.6 0.8 1 α -0.4 -0.2 0.2 0.4 0.6 0.8 1 p@αD,q@αD 0.2 0.4 0.6 0.8 1 α -0.4 -0.2 0.2 0.4 0.6 0.8 1 p@αD,q@αD (c) (d)

Gambar 2. (a)-(d) kurva solusi ( )pα dan ( )qα terhadap α dengan (a)β=0.3,(b)β=0.5,(c)

0.7,

β = dan (d) β=0.8

Keterangan : : kurva ( )pα

: kurva ( )qα

Pada Gambar 2(a) terlihat bahwa untuk nilai β =0.3,terlihat nilai α sekitar 0,6 pada gambar 2(a) atau tepatnya pada saat nilai α =0.55, keseimbangan titik tetap E0

menjadi takstabil dan keadaan endemik E1 muncul. Keadaan endemik E muncul ₁

ketika R1> dan kondisi ( ) 01 pα > dan ( ) 0

qα > dipenuhi.

Pada Gambar 2(b) terlihat bahwa untuk β yang lebih besar menjadi β =0.5, keadaan endemik E1 ini secara alami mulai tak stabil. Tetapi, menjadi tak stabil untuk

α lebih besar.

Pada Gambar 2(c) dan 2(d) terlihat bahwa untuk nilai β yang sama besar, garis endemik titik tetap E tak stabil untuk ₁

semua nilai α saat kondisi untuk kestabilan ( ) 0

pα > dan ( ) 0qα > tidak dipenuhi.

b. Dengan menggunakan nilai-nilai parameter µ=0.01, σ_D =0.04, σ_d =0.03, r_D =0.5, , 8 . 0 = d

r dan B= hubungan dinamika populasi antara 1, , N S _, N I_D , N Id IdD_, N diperoleh pada

saat (a) α=0.52 dan β=0.75; (b) α=0.6 dan 4β=0. ; (c) α=0.8 dan 8β=0. ; (d)

9 . 0 =

100 200 300 400 t 20 40 60 80 100 S,ID,Id,Id D 100 200 300 400 t 20 40 60 80 100 S,ID,Id,Id D 100 200 300 400 t 20 40 60 80 100 S,ID,Id,Id D 100 200 300 400 t 20 40 60 80 100 S,ID,Id,Id D (a) (b) (c) (d)

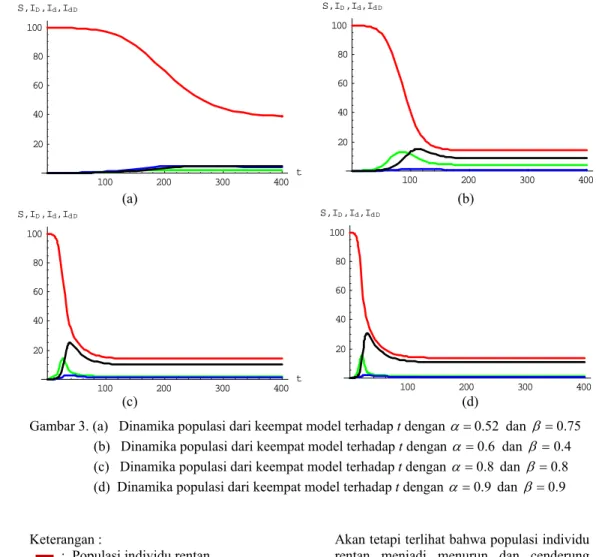
Gambar 3. (a) Dinamika populasi dari keempat model terhadap t dengan α=0.52 dan β=0.75

(b) Dinamika populasi dari keempat model terhadap t dengan α=0.6 dan β =0.4

(c) Dinamika populasi dari keempat model terhadap t dengan α =0.8 dan β =0.8

(d) Dinamika populasi dari keempat model terhadap t dengan α =0.9 dan β =0.9

Keterangan :

: Populasi individu rentan : Populasi individu terinfeksi oleh

penyakit utama

: Populasi individu terinfeksi oleh penyakit tambahan

: Populasi individu terinfeksi oleh kedua penyakit

Pada Gambar 3(a) terlihat bahwa secara biologis hanya populasi dari populasi individu rentan dapat bertahan hidup dan stabil. Sedangkan untuk populasi individu terinfeksi oleh penyakit utama, individu terinfeksi oleh penyakit tambahan dan individu terinfeksi oleh kedua penyakit banyaknya populasi akan menuju kepunahan.

Pada Gambar 3(b) terlihat bahwa ketika

αmeningkat menjadi α=0.6 dan β menurun menjadi β=0.4, secara biologis

populasi individu rentan, individu terinfeksi oleh penyaki utama dan individu terinfeksi oleh kedua penyakit dapat bertahan hidup.

Akan tetapi terlihat bahwa populasi individu rentan menjadi menurun dan cenderung takstabil dan menyebabkan titik tetap

0

E takstabil dan titik tetap E stabil mulai 1 terlihat. Populasi individu terinfeksi oleh penyakit utama meningkat dibandingkan sebelumnya dikarenakan nilai α yang

meningkat pula. Sedangkan Populasi individu terinfeksi oleh penyakit tambahan banyaknya populasi menurun dan cenderung akan menuju kepunahan.

Pada Gambar 3(c) terlihat bahwa ketika

αdan β meningkat menjadi α =0.8 dan

0.8

β = , secara biologis populasi dari

populasi individu terinfeksi oleh kedua penyakit meningkat dan menyebabkan titik tetap E menjadi takstabil dan keadaan co-1

infected mulai terlihat stabil. Sedangkan

untuk populasi individu rentan dan individu terinfeksi oleh penyakit utama dan individu terinfeksi oleh penyakit tambahan banyaknya populasi menurun dan akan menuju kepunahan.

Pada Gambar 3(d) terlihat bahwa ketika

αdan β meningkat menjadi α =0.9 dan

0.9

β= , secara biologis populasi individu

terinfeksi oleh kedua penyakit meningkat dan keadaan co-infected stabil. Sedangkan untuk populasi individu rentan dan individu terinfeksi oleh penyakit utama dan individu terinfeksi oleh penyakit tambahan banyaknya populasi menurun dan akan menuju kepunahan.

Dari ketiga titik tetap yang telah dibahas diatas, dengan mengambil contoh nilai parameter yang berbeda dapat diketahui bagaimana adanya saling keterikatan dari masing-masing titik tetap tersebut dalam menganalisis kestabilannya. Titik tetap E0

akan stabil jika R₁<1,R₂<1,dan R3< 1. Dalam hal ini, setelah mensubstitusikan semua nilai parameter dan α sebagai parameter kontrol, maka diperoleh bahwa ketika nilai α =0.55, titik tetap E₀ akan

menjadi tidak stabil dan titik tetap E akan 1

muncul untuk nilai α ≥0.55. Ini akan terjadi ketika salah satu R atau 1 R menjadi 3

lebih besar dari 1. Dengan menggunakan definisi untuk R dan ₁ R akan secara mudah ₃

diperoleh bahwa jika

D d dD D D r r σ σ µ β σ µ + + + < + +

maka R1>R3 dan cukup mengikuti

dinamika pada R saja untuk memperoleh ₁

nilai terkecil dari α yang mana E akan ₀

menjadi takstabil.

Dengan demikian titik tetap E akan 1 menjadi stabil pada saat titik tetap E0

menjadi tak stabil dan menghilang. Sedangkan untuk titik tetap E sama seperti 2 titik tetap E1, karena dalam hal ini β yang dijadikan parameter kontrol.

IV SIMPULAN

Dari analisis yang telah dilakukan terhadap model dua penyakit endemik diperoleh tiga tipe titik tetap, yaitu titik tetap tanpa penyakit E dan titik tetap endemik 0 E 1 dan E . 2

Analisis kestabilan titik tetap tersebut bergantung pada R ,₁ R dan₂ R yang masing-₃

masing menyatakan bilangan reproduksi dasar dari penyakit utama, penyakit tambahan dan keduanya. Titik tetap E berada dalam 0 kestabilan ketika bilangan reproduksi dasar kurang dari satu (R0< ) dan titik tetap 1 endemik E dan 1 E dalam kestabilan ketika 2

bilangan reproduksi dasar lebih dari satu (R0> ), 1 R0 = maks

{

R R R1, 2, 3

}

.

Dari simulasi yang telah dilakukan terhadap model dua penyakit endemik diperoleh tiga tipe perilaku model yaitu ketika hanya penyakit utama yang muncul,dan ketika hanya penyakit tambahan atau kedua penyakit (co-infected) yang muncul.

Kondisi kestabilan populasi individu yang terinfeksi oleh penyakit utama berbanding lurus dengan laju penularan efektif individu menjadi terinfeksi oleh penyakit utama (α ).

DAFTAR PUSTAKA

Anton H. 1995. Aljabar Linear Elementer. Edisi ke-5. Pantur Silaban & I Nyoman Susila, penerjemah. Jakarta: Erlangga. Blyuss KB, Kyrychko YN. 2005. On a basic

model of a two-disease epidemic.

Elsevier Applied Mathematics and Computation 160 :177–187.

Chavez CC, Feng Z, Huang W. 2002. On the

Computation of R0 and its role on

Global Stability. Berlin:

Springer-Verlag.

Fisher SD. 1990. Complex Variables. 2nd

edition. California: Wadsworth &

Brooks/Cole.

Grimshaw R. 1990. Nonlinear Ordinary

Differensial Equations. Oxford:

Blackwell Scientific Publications. Purcell EJ, Varberg D.1998. Kalkulus dan

Geometri Analisis. Jilid 2. Edisi ke-5. I

Nyoman Susila, Bana Kartasasmita dan Rawuh, penerjemah. Jakarta: Erlangga. Strogatz SH. 1994. Nonlinear Dynamics and

Chaos: with Application to Physics, Biology, Chemestry, and Engeneering.

Canada: Addison-Wesley Publishing Company.

Szidarovszky F, Bahill AT. 1998. Linear

System Theory. 2nd edition. Florida:

CRC Press.

Tu PNV. 1994. Dynamics Systems : An

Introduction with Application in Economics and Biology. New York:

Spinger-Verlag.

Verhulst F. 1990. Nonlinear Differential

Equation and Dynamics Systems.

Lampiran 1 Pembuktian Teorema 1

Teorema 1.

Misalkan , ,

A B C bilangan-bilangan real. Bagian real dari setiap nilai eigen

persamaan karakteristik 3 2

( ) 0

p λ =λ +Aλ +Bλ+ =C

adalah negatif jika dan hanya jika A C positif dan, ΑΒ >C

.

Bukti :

Dari persamaan _{( )} 3 2

p λ =λ +Aλ +Bλ+C

,

maka

0 1, 1 , 2 , 3 dan i 0 jika selainnya.

a = a =A a =B a =C a = i Berdasarkan kriteria Routh-Hurwitz, maka

bagian real dari setiap akar polinomial _{( )} 3 2

pλ =λ +Aλ +Bλ+C adalah negatif jika dan hanya

jika M1.M2.M3 positif, dimana :

1 = a1 = A= >A 0 M (1) 1 3 2 2 0 1 1 a a A C AB C a B = = = − > M (2) 1 3 2 3 2 1 3 0 0 1 0 1 0 0 0 0 a a A C a B ABC C a a A C = = = − > M (3)

Dari (1) maka diperoleh A>0 Dari (2) maka diperoleh AB C− > 0 Dari (3) maka diperoleh 2 ₀

ABC−C > yang dapat diubah dalam bentuk (C AB C- ) 0> , sehingga

dari (2) diperoleh nilai C> . 0

Dengan demikian diperoleh bahwa bagian real dari setiap akar polynomial 3 2

( )

p λ =λ +Aλ +Bλ+ adalah negatif jika dan hanya jikaC A>0

,

C> serta 0 AB>C

.

Terbukti ■

Lampiran 2 Pembuktian Teorema 2

Teorema 2. MisalkanA B C dan D bilangan-bilangan real. Bagian real dari setiap nilai eigen , ,

persamaan karakteristik

4 3 2

( ) 0

p λ =λ +Aλ +Bλ +Cλ+ =D

adalah negatif jika dan hanya jika A C dan D positif dan, ABC>C2+A D2

.

Bukti :

Dari persamaan _{( )} 4 3 2 _,

p λ =λ +Aλ +Bλ +Cλ+D

,

maka

0 1, 1 , 2 , 3 , = dan 4 i 0 jika selainnya.

a = a =A a =B a =C a D a = i Berdasarkan kriteria Routh-Hurwitz, maka bagian real dari setiap akar polinomial p( )λ =λ4+Aλ3+Bλ2+Cλ+D adalah

negatif jika dan hanya jika M1,M2 ,M3 ,M4 positif, dimana :

1 = a1 = A= >A 0

1 3 2 0 2 0 1 a a A C AB C a a B = = = − > M (2) 1 3 5 2 2 3 0 2 4 1 3 0 1 0 0 0 a a a A C a a a B D ABC A D C a a A C = = = − − > M (3) 1 3 5 7 0 2 4 6 2 2 4 1 3 5 0 2 4 0 0 1 0 ( 0 0 0 0 0 0 1 a a a a A C a a a a B D D ABC A D C a a a A C a a a B D = = = − − ) > M (4)

Dari (1) maka diperoleh A> 0 Dari (3) dan (4) diperoleh D> 0.

Dari (2) dan (3), maka dapat ditulis _{( )} 2 _,

C AB C− >A D karena A D2 > dan 0 AB C- > , sehingga 0

dari diperoleh nilai C> . 0

Persamaan (4) benar jika D> dan 0 ABC>C2+A D2 .

Dengan demikian diperoleh bahwa bagian real dari setiap akar polynomial 3 2

( )

p λ =λ +Aλ +Bλ+ adalah negatif jika dan hanya jikaC A>0

,

C> , 0 D> serta 0. 2 2

ABC>C +A D

.

Terbukti ■

Lampiran 3

Penurunan persamaan (6) – (9)

Subsitusikan persamaan (5) yaitu N= +S ID+Id+IdD,ke persamaan (1) – (4) berikut ini

(

1

)

_{dD D}

(

1

)

_{dD d dD} r_DI_D r_dI_d r_dDI_dD, N S I N S I N S I N S I N S I S B dt dS_{= −µ −α −β −α −β −α −β −αβ + + + (1)}

(

1

)

(

)

(

)

, N I I I I r N S I N S I dt dI D dD d D D D D dD D ₌α ₋β ₊α ₋ σ ₊µ_{+ −}β _{+ (2)}

(

1

)

(

)

(

)

, N I I I I r N S I N S I dt dI _d dD D d d d d dD d _{=β −α +β − σ +µ+ −α + (3)}

(

)

(

)

(

)

, N S I I r N I I I N I I dt dI dD dD dD d D dD D d d D dD _{= α+β + α +β − σ +σ +µ+ +αβ (4)}

sehingga diperoleh persamaan (6) – (9) sebagai berikut

(

1

)

(

1

)

, dD D dD D d dD D d dD D d dD d dD D D d d dD dD D d dD D d dD dS S S S B S I I I dt S I I I S I I I S I I I S S I I r I r I r I S I I I S I I I µ α β α β α β αβ = − − − − − − + + + + + + + + + − − + + + + + + + + + (6)

(

)

(

)

(

)

1 , D dD D D D D D d dD D d dD D d dD D d dD dI S S I I r I dt S I I I S I I I I I I S I I I α β α σ µ β = − + − + + + + + + + + − + + + + (7)

(

)

(

)

(

)

1 , d dD d d d d D d dD D d dD d D dD D d dD dI S S I I r I dt S I I I S I I I I I I S I I I β α β σ µ α = − + − + + + + + + + + − + + + +

(8)

(

)

(

)

(

)

. dD D d dD d D D d dD dD D d dD D d dD dD D d dD dI I I I I I r I dt S I I I S I I I S I S I I I α β α β σ σ µ αβ = + + + − + + + + + + + + + + + + + (9) Lampiran 4

Mencari titik tetap

Dengan mensubstitusikandS dID dId dIdD 0

dt = dt = dt = dt = , maka persamaan (6) – (9) menjadi

(

1

)

(

1

)

0, dD D dD D d dD D d dD D d dD d dD D D d d dD dD D d dD D d dD S S S B S I I I S I I I S I I I S I I I S S I I r I r I r I S I I I S I I I µ α β α β α β αβ − − − − − − + + + + + + + + + − − + + + = + + + + + + (10)

(

)

(

)

(

)

1 0, dD D D D D D d dD D d dD D d dD D d dD S S I I r I S I I I S I I I I I I S I I I α β α σ µ β − + − + + + + + + + + − + = + + + (11)

(

)

(

)

(

)

1 0, dD d d d d D d dD D d dD d D dD D d dD S S I I r I S I I I S I I I I I I S I I I β α β σ µ α − + − + + + + + + + + − + = + + + (12)

(

)

(

)

(

)

0. D d dD d D D d dD dD D d dD D d dD dD D d dD I I I I I r I S I I I S I I I S I S I I I α β α β σ σ µ αβ + + + − + + + + + + + + + + = + + + (13) ¾ Untuk kondisi S=0,solusi tidak ditemukan.

¾ Untuk kondisi S≠0,dan ID=0,Id =0, IdD=0(keadaan bebas penyakit) diperoleh .

B S

µ =

¾ Untuk kondisi S≠0,dan ID≠0,Id =0, IdD =0persamaan (10) – (13) menjadi

0, D D D D S B S I r I S I µ α − − + = + (14)

(

)

0, D D D D D S I r I S I α − σ + +µ = + (15)

(

)

( )( ) ( ) ( ) ( ) ( ) ( ) . ( ) D D D D D D D D D D D D D D D D D D D D D D D S I r I S I S S I r S S r I r r S I r I r S r α σ µ α σ µ α σ µ σ µ α σ µ σ µ σ µ α σ µ = + + + = + + + = + + + + + − − − = + + + + = − − −

Substitusikan S ke persamaan (14), sehingga diperoleh

( ) ( ) ( ) _0, ( ) ( ) ( ) ( ) ( ) ( ) 0, ( ) ( ) ( ) ( ) ( ( ) D D D D D D D D D D D D D D D D D D D d d D D D D D D D D D D D D D D D D D D D D D D D D I r I r r B I r I I r I r r r I r I r B I r I r I r I r I r I B I r σ µ σ µ α σ µ µ α _{σ µ α σ µ} α σ µ α σ µ σ µ σ µ µ α α σ µ σ µ α σ µ σ µ µ α α σ µ + + + + − − − − − + = + + + − − − − − − − − − + + + + − − + = − − − + + + − − − + + − − − − − ) 0, ( ) ( ) 0, ( ) ( ) ( ) , ( ) [ ( )]( ) ( ) [ ( ) ( )( )] ( ) ( ) ( D D D D D D D D D D D D D D D D D D D D D D D D D D D D D D D D D D D D D D D D D D r r I I I r B I r r I r I r B I r B I r I r B r I r I r B r I σ µ α σ µ µ σ µ α σ µ σ µ σ µ µ α σ µ σ µ α σ µ µ σ µ α σ µ σ µ α σ µ µ σ µ α σ µ σ + + _{+ =} + + − − + + + = − − − + + − + = − − − − + − − − = + + − − − − + − − − = + + − − − = 2 )( ) ( ) ( ) [( )( ) ( )] ( ) [( ) ( ) ( )] ( ) [( ) ] ( ) ( ) ( D D D D D D D D D D D D D D D D D D D D D D D D D D D D D D D D D D D D D D r I r B r r r I B r r r r I B r r I B r r I B I µ α σ µ µ σ µ α σ µ σ µ α σ µ µ σ µ α σ µ α σ µ σ α σ µ µ µ σ µ α σ µ α σ µ σ αµ α σ µ ασ σ µσ σ αµ + − − − + + + − − − = + − − − + + + − − − = − − − + − − − + + + − − − = − − − + − − − = − − − + = ₂ ) ( ) D D D D D D D r r α σ µ ασ σ µσ σ αµ − − − − − − +

Karena persamaan S yang diperoleh tadi masih dalam bentuk variabel I maka substitusikan D kembali persamaan I ke persamaan S sehingga diperoleh D

2 2 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) D D D D D D D D D D D D D D D D D D D D D D D I r S r B r r r S r B r S r σ µ α σ µ α σ µ _{σ µ} ασ σ µσ σ αµ α σ µ σ µ ασ σ µσ σ αµ + + = − − − − − − _{+ +} − − − + = − − − + + = − − − +

Sehingga diperoleh nilai titik tetap yaitu

1 2 ( ) ( ) ( , ,0,0), ( ) ( ) D D D D D D D D D D D D I r B r E r r σ µ α σ µ α σ µ ασ σ µσ σ αµ + + − − − = − − − − − − +

¾ Untuk kondisi S≠0,dan Id ≠0,ID=0, IdD =0persamaan (10) – (13) menjadi

0, d d d d S B S I r I S I µ β − − + = + (16)