AN ANALYSIS OF STUDENT LEARNING WITH DIGITAL TOOLS FOR
ALGEBRA FROM AN INSTRUMENTATION THEORY VIEW
Al Jupri
Department of Mathematics Education Faculty of Mathematics and Science Education
Indonesia University of Education
aljupri@upi.edu
Abstract
In this paper, we describe the relationship between the use of digital tools and student
conceptual understanding by interpreting students’ behavior from an instrumentation
theory perspective. The theoretical framework includes student difficulties in initial algebra learning and the instrumentation theory. The data included video registrations of a group of three seventh-grade students (12-13 year-old) using the Cover-up and the Balance Strategy applets for solving equations in one variable. The results revealed that the instrumentation theory provides an explicit relationship between techniques and schemes while solving the problems using digital tools. The techniques can be interpreted as observable procedural skills while using the digital tools and the schemes as conceptual understanding of the students, including their difficulties while solving the problems.
Keywords: algebra education, applets, digital technology, equations in one variable, instrumentation theory.
INTRODUCTION
Nowadays, Information and Communication Technology (ICT) plays an important role not only in daily life, but also in education, mathematics education, and algebra education in particular. Digital tools for learning mathematics, for instance, become more widespread and are used more frequently in the teaching and learning processes (e.g., Drijvers, & Barzel, 2012). The interest and the optimism in the potential of the digital tools for mathematics learning have grown and influenced educational stakeholders, such as mathematics educators, educational technology researchers, and teachers. Review studies in mathematics education reveal that the use of ICT affects positively on
mathematics achievemenet Li & Ma, and on students’ attitude towards
Concerning the above results, and in relation to the role of the use of technology toward student conceptual understanding and skills, several important pedagogical questions may rise: While using technology, digital tools in particular, what do students actually learn? (ow does technology influence students’ conceptual understanding and procedural skills? What is the relationship between the use of technological tools and students’ conceptual understanding and skills? e.g., Drijvers, & Barzel, . )n this paper, we would like to investigate the subtle relationship between the use of digital tools, the applets for algebra education in particular, and student conceptual understanding. Also, we would like to see this relationship by considering its impact on student written work in the paper-and-pencil environment.
To address this issue, the theoretical framework of this paper includes student difficulties in algebra learning and the instrumentation theory. Next, the research question and method are presented and elaborated. Then, in the results and discussion section we describe an analysis of two episodes of student learning with digital tools – the Cover-up and the Balance Strategy applets – for algebra. Conclusions section finishes the paper. THEORETICAL FRAMEWORK
Difficulties in Initial Algebra
Student conceptual understanding and skills in algebra can be analyzed in terms of difficulties emerged in the learning and teaching processes. Based on the literature review and explorative interview study, Jupri, Drijvers and Van den Heuvel-Panhuizen (2014) have identified five categories of difficulties in initial algebra. First, difficulties in applying arithmetical operations and properties in numerical and algebraic expressions include adding or subtracting like terms (e.g., Herscovics, & Linchevski, 1994; Linchevski, 1995); applying associative, commutative, distributive, and inverses properties; and applying priority rules of arithmetical operations (e.g., Booth, 1988; Warren, 2003). Second, difficulties in dealing with the notion of variable concern understanding it as a placeholder, a generalized number, an unknown, or a varying quantity (Booth, 1988; Herscovics, & Linchevski, 1994). Third, the difficulties in understanding algebraic expressions include the parsing obstacle, the expected answer obstacle, the lack of closure obstacle, and the gestalt view of algebraic expressions (Arcavi, 1994; Thomas, & Tall, 1991). Fourth, the difficulties in understanding the different meanings of the equal sign include difficulties to comprehend it as a sign that invites a calculation in arithmetic, and as a sign of equivalence in algebra (Herscovics, & Linchevski, 1994; Kieran, 1981). And the fifth, the difficulties in mathematization concern the difficulty in transforming the problem situation to the world of mathematics and vice versa, as well as in reorganizing the symbolic world of mathematics (Treffers, 1987; Van den Heuvel-Panhuizen, 2003).
Instrumentation Theory
the following terms play a key role: artefact, tool, technique, scheme, and instrument (e.g., Drijvers, Godino, Font, & Trouche, 2013; Trouche, & Drijvers, 2010).
An artefact is an object, a thing, either tangible or not. If an artefact is used to carry out a specific task, it is called a tool. In this study reported in this paper, the artefacts include the Cover-up applet and the Balance Strategy applet. If the Cover-up applet, for instance, is used for solving an equation, this applet can be seen as a tool, a digital tool for solving the equation (Trouche, 2004).
In order to be able to use a tool for solving a specific task, we need to apply a specific technique. According to Artigue (2002) a technique is a manner of solving a task using an
artefact. As such, the technique can be observed from the user’s behavior while using the
artefact for solving the task. The technique itself is based on the cognitive foundation, which is called a scheme. Vergnaud (1996) defines a scheme as an invariant organization of behavior for a given class of situations. The technique and the scheme share similar characteristics, but the main difference is that the scheme is invisible and the technique is observable. In other words, a technique is the observable manifestation of the invisible scheme (Drijvers, Godino, Font, & Trouche, 2013).
Based on the above description, an instrument is defined as a mixed entity of scheme, technique, artefact and task (Trouche, & Drijvers, 2010; Trouche, 2004). The process of the user developing an instrument, consisting of cognitive schemes and observable techniques for using a specific artefact for a specific class of tasks is called instrumental genesis. This combination of technical and conceptual aspects within the instrumentation scheme makes the theory of instrumentation is promising for investigating the relationship among digital tools use, student conceptual understanding, and written paper-and-pencil work (Drijvers, 2003).
RESEARCH QUESTION
To address the issue phrased in the Introduction, that is, to describe the subtle and complex relationship between the use of digital tools, the Cover-up and the Balance Strategy applets for algebra in particular, and student conceptual understanding and skills, we formulate the following research question:
Which relationships between techniques and understanding do students develop while using the Cover-up and the Balance Strategy applets for solving equations?
The problems addressed in the present study include equations in one variable of the form � = �, which is the main topic of the algebra lesson with the Cover-up applet; and linear equations in one variable of the form � = � , the main topic of the algebra lesson with the Balance Strategy applet.
METHOD
Strategy applet, on (linear) equations in one variable which is a part of the grade VII Indonesian mathematics curriculum (Depdiknas, 2007). The learning arrangements included the activities with the two applets which are embedded within the Digital Mathematics Environment (DME)1. The DME is a web-based environment providing: (i) interactive digital tools for mathematics learning; (ii) a design of open online tasks; (iii) immediate feedback for the tasks; (iv) access at any time and place, as long as technological infrastructure is met; and (v) a storage for student work (Boon, 2006; Drijvers, Boon, Doorman, Bokhove, & Tacoma, 2013).
Each lesson was lasted for 80 minutes, and consisted of the following three parts. First, a paper-and-pencil activity was done to introduce the concept of equation through posing problems and class discussion. Second, a whole class demonstration how to work with an applet was carried out and was followed by a group-based digital activity done by students under the teacher guidance. Third and final, an individual paper-and-pencil test was carried out.
The data reported in this paper included video registrations of one group of three male students (12-13 year-old), its corresponding student digital work, and written work. By applying the instrumentation theory lens and student difficulties in algebra as described in the Theoretical Framework section, an integrative qualitative analysis on these data, with the help of Atlas.ti software, was carried out to investigate the relationship between the use of the applets and the targeted conceptual understanding.
RESULTS AND DISCUSSION
This section presents the observation of two episodes of a group work of the three students: one episode from the Cover-up activity and another one from the Balance Strategy activity. For each episode, we first provide an analysis and its corresponding commentaries of a task carried out by the students in our observation. Next, we summarize the relationship between techniques and its corresponding schemes while solving the task. Then, we discuss student difficulties and understanding from the observation, including written student work from the individual paper-and-pencil test. The techniques can be interpreted as procedural skills and schemes as conceptual understanding of the students.
Relationship between Techniques and Understanding in the Cover-Up Activity
Table presents an observation of the group’s work on a task from the Cover-up activity.
The left column provides a description of the observation, and the right column provides commentaries which are based on the theoretical lens described in Section 2.
Table 1.
A case observation of the group’s work for a task taken from the Cover-up activity
Observation Commentary
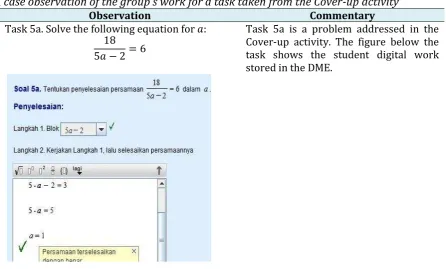
Task 5a. Solve the following equation for �:
8
Students in the group read the task out loud. They are thinking and reading the given first step, and choosing a part of the equation that should be covered firstly.
By reading the task, students are expected to realize that the equation is in the form of � = �, and to realize that
� =< numerical value > as the solution. In addition, they are expected to be able to see the structure of the algebraic expression in the left hand side as a division between 18 and � − . In this way, the students would understand that they should choose � − as the expression to be covered in the first step. Student 1: So, the equation means that 18 is
divided by "something" equals 6.
Student 2: Three, three, three, ... [He then tries to highlight � − with the mouse. However, he tries to highlight � − . Next, After Student3 has been successfully covering � − and assigning its value 3, i.e., by highlighting � − with the mouse, and typing 3, he forgets to press enter.]
[Student 3 presses enter and it is correct!] algebraic expression, and an expected answer obstacle in particular.
Student 1: a [should be covered from the equation
� − = .]
Student 1 seems not to understand that the easier part to cover for the equation
� − = is � than � directly. Student2 suggests that � is the easier part to cover and to assign a value.
Student1 and Student3 could not assign a proper value for �. This because they do
Student 1 & 2: No, no, it is 5. [Laughing. Student3 highlights � from the equation � − = , the applet automatically produces � = ⋯ in the line below. He then types 5 and presses enter. It is correct!]
Students 1 & 2: Now a, a, a [should be covered from the equation � = ].
Student 3: 5 times something ... Student 2: 5 times something equals 5 Studens 1 & 3: [So the value of a is] 1.
[Student 3 highlights � with the mouse, types 1 as a numerical value for it, and presses enter. ]
Student 3: Correct! Yes! how to proceed: choosing �, highlighting it, typing as its value, and pressing enter!
Figure 1. Written work by Student 2 (left) and Student 1 (right) after engaging in the Cover-up activity
Based on the conversations during the group work, we conjecture that Student 2 seemed to have a better understanding than the other two students in the group. We identified that Students 1 and 3 encountered difficulties in understanding algebraic expression (an expected answer obstacle), such as when viewing � − as − = , and in understanding the concept of variable as an unknown. The different mastery of understanding of the students is manifest in their written work, solving a similar task as in the digital group work, from the individual paper-and-pencil test after engaging the Cover-up activity as shown in Figure . The left part shows a correct Student ’s work and
the right part displays an incorrect Student ’s work, which is similar to Student ’s work.
Relationship between Techniques and Understanding in the Balance Strategy Activity
Table presents an observation of the group’s work on a task from the Balance Strategy activity. The left column provides a description of the observation, and the right column provides commentaries which are based on the theoretical lens described in Section 2. Table 2.
A case observation of the group’s work for a task taken from the Balance Strategy activity
Observation Commentary
Task 6. Solve the following equation for �:
8� + = � + 8
Students read the task together aloud. By reading the task, students are expected to realize that the equation is in the form of
� = � , and to realize that � =<
numerical value > is the solution. Student 1: [It must firstly be] subtracted by 3, ideas about the first step to do for solving the equation. The Student 1 suggests to subtract 3 from both sides of the equation, while Student 2 suggests to subtract � from both sides. Both ideas are correct.
Student follows Student ’s idea probably
because he realizes that either his or his friend idea is correct.
Observer: What is the next [step]? Students 1 & 2: Subtracted by 3.
Student 1: 3p = 18, eh no, 3p = 15 Student 3: [Types 3p = 15.]
Both Students 1 and 2 agree to subtract 3 from both sides of the equation � + =
8.
Initially, Student 1 forgets to subtract 3 from the right side, but then he realizes that he should do so.
Student 3: [He clicks the division button, types 3, and presses enter.]. Student1 that the equation must be divided by 3 and not by 3p.
new simpler equation and of pressing enter to check whether the new equation is correct or not.
Main possible difficulties that might emerge while solving the equation � = � include, for instance, choosing an appropriate operation to do to both sides of the equation, doing the same operations to both sides of the equation—such as forgeting to subtract from both sides of the equation � + = 8 as the case in our obervation, and arithmetical calculation mistakes. Of course there are other possible difficulties, such as applying a distributive property if the equation contains an algebraic expression with a bracket.
From the conversations, similar to the case of the Cover-up activity, we conjecture that Student 2 seemed to have a better understanding than the other two students in the group (at least better than Student 1, as Student 3 did not speak to much in the conversation). For instance, Student1 made mistakes when simplifying the result of subtracting 3 from both sides of the equation � + = 8, in which he initially thought � = 8 as the result; also Student 1 seemed to not sure what to divide for the equation � = , whether to divide by 3 or 3� to obtain the solution. This conjecture is strengthened by observing written student work shown in Figure 2. The left part shows a correct Student ’s work and the right part displays an incorrect Student ’s work, which is similar to Student ’s work.
Figure 2. Written work by Student 2 (left) and Student 1 (right) after engaging in the Balance Strategy activity
CONCLUSIONS
correspond to finding an appropriate operation—with a corresponding number or an expression, and to providing the result of the operation carried out to both sides of the equation. To establish these relationships, students should perceive the interplay between the techniques that they use and their cognitive schemes.
We showed that the two theoretical lenses, student difficulties in algebra and the intrumentation theory, are fruitful to analyze student work with digital tools. The first lens is fruitful to better understand student conceptual understanding in terms of encountered difficulties while solving equations.The instrumentation theory shows how the conceptual understanding (in terms of the schemes) and procedural skills (in terms of techniques) are linked to each other.
Acknowledgment
This study was funded by the Indonesia Ministry of Education project BERMUTU IDA CREDIT NO.4349-IND, LOAN NO.7476-IND DAN HIBAH TF090794. The author thanks Peter Boon for designing the Cover-up and the Balance Strategy applets, the teachers and students for their participation.
References
Arcavi, A. (1994). Symbol sense: Informal sense-making in formal mathematics. For the Learning of Mathematics, 14(3), 24–35.
Artigue, M. (2002). Learning mathematics in a CAS environment: The genesis of a reflection about instrumentation and the dialectics between technical and conceptual work. International Journal of Computers for Mathematical Learning, 7(3), 245–274.
Barkatsas, A., Kasimatis, K., & Gialamas, V. (2009). Learning secondary mathematics with technology: Exploring the complex interrelationship between students’ attitudes, engagement, gender and achievement. Computers & Education, 52(3), 562–570. Bokhove, C., & Drijvers, P. (2010). Symbol sense behavior in digital activities. For the
Learning of Mathematics, 30(3), 43–49.
Boon, P. (2006). Designing didactical tools and micro-worlds for mathematics education. In C. Hoyles, J. B. Lagrange, L. H. Son, & N. Sinclair, Proceedings of the 17th ICMI Study Conference; http://www.fi.uu.nl/isdde/documents/software_boon.pdf
Booth, L. R. . Children’s difficulties in beginning algebra. )n A.F. Coxford Ed. , The
ideas of algebra, K–12(1988 Yearbook) (pp. 20–32). Reston, VA: National Council of Teachers of Mathematics.
Departemen Pendidikan Nasional (2007). Naskah Akademik Kajian Kebijakan Kurikulum Mata Pelajaran TIK [An academic document for the curriculum of ICT subject.] Jakarta: Badan Penelitian dan Pengembangan Pusat Kurikulum.
Doorman, M., Drijvers, P., Gravemeijer, K., Boon, P., & Reed, H. (2012). Tool use and the development of the function concept: from repeated calculations to functional thinking. International Journal of Science and Mathematics Education, 10(6), 1243– 1267.
Drijvers, P. H. M. (2003). Learning algebra in a computer algebra environment: Design research on the understanding of the concept of parameter. Dissertation. Utrecht, the Netherlands: CD-B Press
Drijvers, P., Boon, P., Doorman, M., Bokhove, C., & Tacoma, S. (2013). Digital design: RME principles for designing online tasks. In C. Margolinas (Ed.), Proceedings of ICMI Study 22 Task Design in Mathematics Education (pp. 55–62). Clermont-Ferrand, France: ICMI.
Drijvers, P., Godino, J. D., Font, V., & Trouche, L. (2013). One episode, two lenses: A reflective analysis of student learning with computer algebra from instrumental and onto-semiotic perspectives. Educational Studies in Mathematics, 82(1), 23–49. DOI: 10.1007/s10649-012-9416-8
Ghosh, J. B. (2012). Learning mathematics in secondary school: The case of mathematical modeling enabled by technology. Regular lecture 12th ICME conference;
http://nime.hbcse.tifr.res.in/indian-participants-at-icme-2012/JonakiG_RL612Mathematicalmodellingenabledbytechnonlogy.pdf
Herscovics, N., & Linchevski, L. (1994). A cognitive gap between arithmetic and algebra. Educational Studies in Mathematics, 27(1), 59–78.
Jupri, A., Drijvers, P., & Van den Heuvel-Panhuizen, M. (2014). Difficulties in initial algebra learning in Indonesia. Mathematics Education Research Journal, 26(4), 683–710. DOI: 10.1007/s13394-013-0097-0.
Kieran, C. (1981). Concepts associated with the equality symbol. Educational Studies in Mathematics, 12(3), 317–326.
Linchevski, L. (1995). Algebra with numbers and arithmetic with letters: A definition of pre-algebra. Journal of Mathematical Behavior, 14(1), 113–120.
Li, Q., & Ma, X. (2010). A meta-analysis of the effects of computer technology on school
students’ mathematics learning. Educational Psychology Review, 22(3), 215–243.
Rakes, C. R., Valentine, J. C., McGatha, M. B., & Ronau, R. N. (2010). Methods of instructional improvement in algebra: A systematic review and meta-analysis. Review of Educational Research, 80(3), 372–400.
Tall, D., & Thomas, M. (1991). Encouraging versatile thinking in algebra using the computer. Educational Studies in Mathematics, 22(2), 125–147.
Treffers, A. (1987). Three dimensions. A model of goal and theory description in mathematics instruction-The Wiskobas project. Dordrecht, the Netherlands: Kluwer Academic Publishers.
Trouche, L. (2004). Managing complexity of human/machine interactions in computerized learning environments: Guiding students’ command process through instrumental orchestrations. International Journal of Computers for Mathematical Learning, 9, 281–307.
Trouche, L., & Drijvers, P. (2010). Handheld technology: Flashback into the future. ZDM, the International Journal on Mathematics Education, 42(7), 667–681.
Van den Heuvel-Panhuizen, M. (2003). The didactical use of models in realistic mathematics education: An example from a longitudinal trajectory on percentage. Educational Studies in Mathematics, 54(1), 9–35.
Vergnaud, G. (2009). The theory of conceptual fields. Human Development, 52, 83–94. Warren, E. (2003). The role of arithmetic structure in the transition from arithmetic to