i
MODEL MATEMATIS
UNTUK PENYEBARAN PENYAKIT TIDUR
MAKALAH
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains
Program Studi Matematika
Disusun oleh: Fransisca Ratri Susanti
NIM: 103114010
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA YOGYAKARTA
ii
A MATHEMATICAL MODEL FOR THE SPREAD
OF SLEEPING SICKNESS
A PAPER
Presented As Partial Fulfillment of the Requirements To Obtain the Sarjana Sains Degree of
Mathematics Study Program
Written by: Fransisca Ratri Susanti
Student ID: 103114010
MATHEMATICS STUDY PROGRAM MATHEMATICS DEPARTMENT FACULTY OF SCIENCE AND TECHNOLOGI
SANATA DHARMA UNIVERSITY YOGYAKARTA
iii
MAKALAH
MODEL MATEMATIS
UNTUK PENYEBARAN PENYAKIT TIDUR
Disusun oleh: Fransisca Ratri Susanti
NIM : 103114010
Telah disetujui oleh:
Dosen Pembimbing Makalah,
iv MAKALAH
MODEL MATEMATIS
UNTUK PENYEBARAN PENYAKIT TIDUR
Dipersiapkan dan ditulis oleh: Fransisca Ratri Susanti
103114010
Telah dipertahankan di depan Panitia Penguji pada tanggal 23 Juli 2014
dan dinyatakan telah memenuhi syarat
Susunan Panitia Penguji
Nama Lengkap Tanda Tangan
Ketua Ir. Ig. Aris Dwiatmoko, M.Sc.
……….
Sekretaris Sudi Mungkasi, S.Si., M.Math.Sc., Ph.D.
……….
Anggota Lusia Krismiyati Budiasih, S.Si., M.Si.
……….
Yogyakarta, 26 Agustus 2014 Fakultas Sains dan Teknologi Universitas Sanata Dharma Dekan,
v
HALAMAN PERSEMBAHAN
“Janganlah hendaknya kamu kuatir tentang apapun juga, tetapi
nyatakanlah dalam segala hal keinginanmu kepada Allah dalam
doa dan
permohonan dengan ucapan syukur.” (Filipi 4:6)
tugas akhir ini kupersembahkan kepada Keluarga, Sahabat, Teman dan Paguyuban yang telah memberi dukungan, semangat serta doa
vi
PERNYATAAN KEASLIAN KARYA
Saya menyatakan dengan sesungguhnya bahwa makalah yang saya tulis ini tidak memuat karya atau bagian karya orang lain, kecuali yang telah disebutkan dalam kutipan dan daftar pustaka, sebagaimana layaknya karya ilmiah.
Yogyakarta, 22 Juli 2014 Penulis,
vii ABTRAK
Penyakit tidur adalah penyakit yang disebabkan oleh parasit trypanomiasis yang dapat menginfeksi manusia melalui gigitan lalat tsetse. Penyebaran lalat tsetse dapat diilustrasikan dalam model matematika yang bergantung pada populasi lalat dan manusia dengan asumsi-asumsi tertentu. Model tersebut berupa suatu sistem persamaan diferensial dengan lima variabel, yang menyatakan banyaknya vektor pada masa inkubasi, banyaknya vektor terinfeksi, banyaknya vektor rentan, banyaknya manusia terinfeksi dan banyaknya manusia sembuh. Sistem persamaan diferensial dapat diselesaikan secara numeris dengan menggunakan metode Runge-Kutta.
Banyaknya vektor pada masa inkubasi dan terinfeksi mengalami penurunan dan stabil mendekati nol. Banyaknya vektor rentan mengalami kenaikan yang cukup tinggi dan konvergen menuju ke titik kritisnya. Banyaknya manusia terinfeksi dan banyaknya manusia sembuh pada awalnya mengalami kenaikan, namun pada waktu tertentu banyaknya manusia terinfeksi dan sembuh mengalami penurunan mendekati nol dan banyaknya manusia kembali pada kelompok rentan.
viii ABSTRACT
Sleeping sickness is a disease caused by a trypanomiasis parasite which can infectious human by the biting tsetse fly. The spread of tsetse fly can be illustrated in a mathematical model which dependent on the population of flies and humans with certain assumptions. The model is in the form of a system of differential equations with five variables, which specifies the number of incubating vectors, the number of infected vectors, the number of susceptible vectors, the number of infected humans and the number of removed humans. System of differential equations can be solved numerically using the Runge-Kutta method.
The number of incubating vectors and infected has decreased and stable approach to zero. The number of susceptible vectors has to high increase and converges toward the critical point. At the number of infected and the number of removed humans at the beginning increase, but at certain times the number of humans infected and removed decreased approach to zero and the number of humans return to the susceptible stage.
Keywords: spread sleeping sickness, system of differential equations,
ix
LEMBAR PERNYATAAN PERSETUJUAN
PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS
Yang bertandatangan di bawah ini, saya mahasiswa Universitas Sanata Dharma dengan:
Nama : Fransisca Ratri Susanti NIM : 103114010
Demi pengembangan ilmu pengetahuan, saya memberikan karya ilmiah saya kepada Perpustakaan Universitas Sanata Dharma dengan Judul:
MODEL MATEMATIS UNTUK PENYEBARAN PENYAKIT TIDUR
beserta perangkat yang diperlukan, bila ada. Dengan demikian, saya memberikan hak untuk menyimpan, mengalihkan ke dalam bentuk media lain, mengelolanya dalam bentuk pangkalan data, mendistribusikannya secara terbatas, dan mempublikasikannya di internet atau media lain untuk kepentingan akademis tanpa perlu meminta izin dari saya maupun memberikan royalti kepada saya selama tetap mencantumkan nama saya sebagai penulis kepada Perpustakaan Universitas Sanata Dharma.
Demikian pernyataan ini saya buat dengan sebenarnya.
Dibuat di Yogyakarta Pada tanggal 22 Juli 2014
Yang menyatakan,
x
KATA PENGANTAR
Puji dan Syukur kepada Tuhan Yang Maha Esa, atas segala berkat dan Rahmat-Nya yang diberikan, sehingga dapat menyelesaikan makalah ini.
Dalam menulis makalah ini, penulis menemukan banyak kesulitan, namun atas bantuan dan dukungan dari banyak pihak akhirnya penulis dapat menyelesaikan makalah ini. Oleh karena itu, penulis ingin mengucapkan terima kasih kepada:
1. Ibu Paulina Heruningsih Prima Rosa, S.Si., M.Sc., selaku Dekan Fakultas Sains dan Teknologi, Universitas Sanata Dharma.
2. Bapak Y.G. Hartono, S.Si., M.Sc., Ph.D., selaku Ketua Program Studi Matematika yang sudah membantu dalam proses menyusun makalah ini.
3. Ibu Lusia Krismiyati Budiasih, S.Si., M.Si., selaku dosen pembimbing makalah yang dengan sabar memberi bimbingan, meluangkan waktu dan pikiran dalam menyusun makalah ini.
4. Bapak Ir. Ig. Aris Dwiatmoko, M.Sc., selaku dosen pembimbing akademik sekaligus dosen penguji yang telah memberikan masukan dan saran atas topik untuk makalah ini.
xi
6. Bapak dan Ibu dosen Program Studi Matematika telah memberikan ilmu yang sangat bermanfaat bagi penulis.
7. Keluarga dan sahabat yang telah memberikan dukungan dalam segala hal.
8. Teman-teman seperjuangan Prodi Matematika angkatan 2010 dalam kebersamaan, semangat, doa dan segala bantuan kepada penulis.
9. Kakak-kakak dan adik-adik angkatan mahasiswa Matematika yang turut memberikan semangat, doa dan segala bantuan kepada penulis.
10.Semua pihak yang tidak dapat disebutkan satu per satu, yang telah berperan dalam penulisan makalah ini.
Yogyakarta, 22 Juli 2014
xii DAFTAR ISI
HALAMAN JUDUL ... i
HALAMAN JUDUL DALAM BAHASA INGGRIS ... ii
HALAMAN PERSETUJUAN PEMBIMBING ... iii
HALAMAN PENGESAHAN ... iv
HALAMAN PERSEMBAHAN ... v
PERNYATAAN KEASLIAN KARYA ... vi
ABSTRAK ... vii
ABSTRACT ... viii
PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH ... ix
KATA PENGANTAR ... x
DAFTAR ISI ... xii
DAFTAR TABEL ... xiv
DAFTAR GAMBAR ... xv
BAB I PENDAHULUAN ... 1
A. Latar Belakang ... 1
B. Rumusan Masalah ... 3
C. Batasan Masalah ... 4
D. Tujuan Penulisan ... 4
E. Manfaat Penulisan ... 4
F. Metode Penulisan ... 4
xiii
BAB II LANDASAN TEORI ... 7
A. Sistem Linear dan Matriks... 7
B. Sistem Persamaan Diferensial ... 16
C. Metode Runge kutta ... 40
BAB III MODEL PENYEBARAN PENYAKIT ... 44
A. Penyebaran Penyakit Tidur ... 44
B. Model Kompartemen ... 46
C. Model Matematika Tentang Gigitan Vektor ... 51
D. Dinamika Populasi Vektor ... 54
E. Dinamika Populasi Manusia ... 74
F. Analisis Dinamika Populasi Vektor dan Manusia ... 79
BAB IV PENUTUP ... 82
A. Kesimpulan ... 82
B. Saran ... 83
DAFTAR PUSTAKA ... 84
xiv DAFTAR TABEL
xv
DAFTAR GAMBAR
Gambar 1.1 Lalat Tsetse Tampak dari Atas ... 2
Gambar 1.2 Lalat Tsetse Tampak dari Samping ... 2
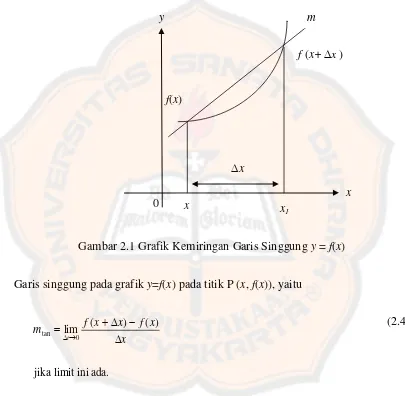
Gambar 2.1 Grafik Kemiringan Garis Singgung y=f(x) ... 16
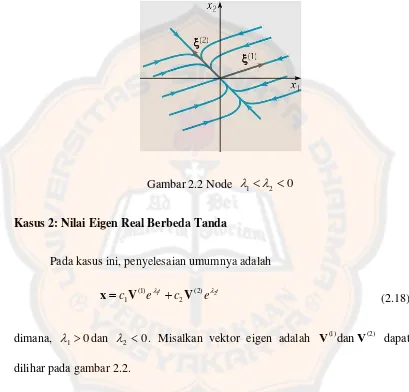
Gambar 2.2 Node 12 0 ... 27
Gambar 2.3 Titik Pelana 1 0, 2 0 ... 28
Gambar 2.4 Titik Star 12 0 ... 29
Gambar 2.5 Improper Node 12 0 ... 29
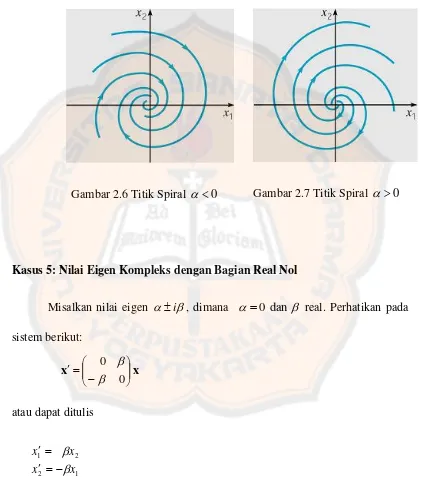
Gambar 2.6 Titik Spiral 0 ... 31
Gambar 2.7 Titik Spiral 0 ... 31
Gambar 2.8 Center 1 i,2 i ... 32
Gambar 2.9 Bidang fase x1 dan x2 ... 40
Gambar 3.1 Siklus Perpindahan Parasit: Manusia dan Lalat ... 46
Gambar 3.2 Model Kompartemen Vektor ... 49
Gambar 3.3 Model Kompartemen Vektor pada Model ... 50
Gambar 3.4 Model Kompartemen Manusia ... 50
Gambar 3.5 Bidang Fase ViVa ... 67
Gambar 3.6 Bidang Fase ViVs ... 67
Gambar 3.7 Bidang Fase VaVs ... 70
Gambar 3.8 Grafik Dinamika Populasi Vektor ... 73
xvi
1
BAB I
PENDAHULUAN
A. LATAR BELAKANG
Penyakit tidur adalah salah satu penyakit yang menyebar karena gigitan lalat. Penyakit tidur yang disebut juga dengan trypanosomiasis penularannya melalui gigitan lalat tsetse. Penyakit tidur menyebar di kawasan Afrika. Pada tahun 1996, diperkirakan bahwa antara 20.000 dan 25.000 orang meninggal akibat penyakit tersebut setiap tahunnya, dan risiko epidemi yang parah terus ada. Nama penyakit yang terdengar aneh itu tidak kalah bahayanya dengan penyakit lain, misal malaria dan AIDS. Penyakit ini dapat menyebabkan kematian jika tidak segera diobati, karena terjadi peradangan getah bening.
biasanya di bawah semak-semak, kayu, batu-batu besar dan menopang akar. Larva mengubur diri dan segera berubah menjadi pupa. Lalat muncul 22-60 hari kemudian, tergantung pada suhu. Lalat betina berkembang biak menghasilkan larva setiap 10 hari. Masa hidupnya sekitar 30 hingga 90 hari.
Gambar1.1 Lalat Tsetse Tampak dari Atas Sumber: Wikipedia.org 24 Oktober 2013
Gambar 1.2 Lalat Tsetse Tampak dari Samping Sumber: Encyclopedia Britannica 24 Oktober 2013
menjadi terinfeksi oleh lalat itu. Selain melalui lalat tsetse, penyakit tidur ini dapat menular melalui tranfusi darah.
Beberapa metode untuk pencegahan penyakit tidur, antara lain peningkatan mortalitas lalat yakni penyemprotan menggunakan insektisida, penjebakan, pengobatan dan isolasi individu yang terinfeksi. Hal ini dapat digunakan untuk upaya pencegahan, karena lalat memiliki harapan hidup lebih pendek dan memiliki waktu lebih sedikit untuk menginfeksi manusia.
Dari fenomena penyebaran parasit penyakit tidur dapat disusun strategi pengendalian penyebaran penyakit, sehingga perlu mempelajari model penyakit. Pengendalian penyebaran penyakit tidur dapat dimodelkan dengan model matematika. Model ini memiliki peran penting dalam penyebaran penyakit tidur untuk membantu menyelesaikan masalah tersebut dengan asumsi-asumsi tertentu. Model epidemik adalah model matematika yang dapat mengontrol dan mengetahui penyebaran penyakit pada suatu daerah tertentu dalam waktu singkat dan frekuensi meningkat. Model penyebaran penyakit tidur ini menggunakan model yang bersifat stokastik (probabilistik) karena tidak adanya informasi keadaan obyek pada masa mendatang secara pasti.
B. RUMUSAN MASALAH
2. Bagaimana ilustrasi model matematika penyebaran penyakit tidur dengan nilai parameter yang diberikan pada populasi lalat dan manusia?
C. BATASAN MASALAH
Pembatasan masalah dalam tulisan ini pada kestabilan penyebaran penyakit tidur terhadap dinamika populasi vektor dan manusia.
D. TUJUAN PENULISAN
Tujuan penulisan ini adalah untuk memahami prinsip persamaan diferensial dengan konsep dinamika populasi dalam memodelkan penyebaran penyakit tidur yang diilustrasikan dengan nilai-nilai parameter yang diberikan.
E. MANFAAT PENULISAN
Manfaat yang dapat diambil dari tulisan ini adalah untuk memperoleh pengetahuan tentang penyelesaian numerik permasalahan penyebaran penyakit tidur dengan model matematika.
F. METODE PENULISAN
G. SISTEMATIKA PENULISAN
BAB I PENDAHULUAN
A. Latar Belakang
B. Rumusan Masalah
C. Batasan Masalah
D. Tujuan Penulisan
E. Manfaat Penulisan
F. Metode Penulisan
G. Sistematika Penulisan
BAB II LANDASAN TEORI
A. Sistem Linear dan Matriks
B. Sistem Persamaan Diferensial
C. Metode Runge kutta
BAB III MODEL PENYEBARAN PENYAKIT
A. Sistem Linear dan Matriks
B. Model Kompartemen
D. Dinamika Populasi Vektor
E. Dinamika Populasi Manusia
F. Analisis Dinamika Populasi Vektor dan Manusia
BAB IV PENUTUP
A. Kesimpulan
B. Saran
DAFTAR PUSTAKA
7
BAB II
LANDASAN TEORI
A. SISTEM LINEAR DAN MATRIKS
Definisi 2.1 Sistem Persamaan Linear
Sistem persamaan linear adalah suatu himpunan berhingga dengan m persamaan
dalam n variabel x1,x2,...,xn.
Definisi 2.2 Penyelesaian Sistem persamaan Linear
Suatu bilangan terurut s1,s2,...,sn disebut penyelesaian dari sistem jika
n n s
x s x s
x1 1, 2 2,..., adalah penyelesaian setiap persamaan pada sistem.
Matriks adalah suatu susunan bilangan yang berbentuk persegi panjang. Cara menuliskan ukuran suatu matriks dengan m baris dan n kolom. Bentuk matriks A berukuran m x n dan elemen aij berada pada baris i dan kolom j dituliskan seperti di bawah ini:
i
a ... a ... a a
a ... a ... a a
a ... a ... a a
a ... a ... a a
j
mn mj
m m
in ij
i i
n j
21
n 1j
12 11
Baris Kolom
2 1
2 1
2 2
22
1
Definisi 2.3 Operasi Baris Elementer
Operasi Baris Elementer terhadap suatu matriks A adalah salah satu dari yang berikut:
Operasi I: Kalikan baris i dengan k 0
Ri kRi
Operasi II: Tukarkan baris i dengan baris j
Ri Rj
Operasi III: Gantilah baris j dengan jumlah antara baris itu sendiri dengan k kali baris i
Rj kRi Rj
Simbol-simbol di dalam tanda kurung di atas digunakan untuk menerangkan rincian penyederhanaan baris tertentu. Tanda panah menandakan penggantian, Rimenyatakan baris ke-i pada matriks yang sedang disederhakankan, sedangkan Rj menyatakan baris ke-j pada matris yang sama. Proses pengubahan suatu matriks menjadi matriks lain melalui pengolahan dasar baris disebut baris tereduksi.
Definisi 2.4 Matriks Eselon Baris tereduksi
Matriks Eselon Baris tereduksi ialah suatu matriks yang memenuhi keempat sifat berikut:
1)Jika suatu baris matriks mempunyai setidaknya satu elemen tidak nol, maka elemen tidak nol yang pertama (kepala baris) adalah 1.
3)Di dalam dua baris tidak nol yang berurutan, elemen 1 yang menjadi kepala baris di baris yang lebih bawah berada lebih ke kanan dibandingkan dengan kepala baris di baris yang lebih atas.
4)Jika di dalam suatu kolom terdapat kepala baris, elemen-elemen lain di dalam kolom itu nol semuanya.
Matriks yang demikian ini dikatakan berada dalam bentuk eselon baris.
Teorema 2.1
Setiap matriks ekuivalen baris dengan sebuah matriks tunggal yang berada dalam bentuk eselon baris tereduksi.
Contoh 2.1
Selesaikan sistem persamaan berikut dengan cara operasi baris elementer:
5 5 2
2 3
2 2
z y x
z y x
z y x
Penyelesaian:
Sistem persamaan tersebut bila dituliskan dalam bentuk matriks, yaitu:
5 5 1 2
2 3 1 1
2 2 1 1
1 1 1 0
0 5 0 0
2 2 1 1
Kemudian mengalikan baris ketiga dengan -1 (R3 (1)R3)dan dilanjutkan dengan penukaran baris 2 dan baris 3 (R2 R3), sehingga menghasilkan:
0 5 0 0
1 1 1 0
2 2 1 1
Dari hasil operasi baris elementer di atas diperoleh persamaan:
0 5z
1
2 2
z y
z y x
Dengan demikian, dapat diselesaikan dengan substitusi langkah mundur, sehingga diperoleh hasil x3,y1dan z0
Definisi 2.5 Minor Elemen
Jika A adalah suatu matriks n x n, maka sub-matriks berukuran (n-1) x (n-1) yang diperoleh dari matriks A, dengan cara menghapus baris baris ke-i dan kolom ke-j disebut dengan Minor Elemen (i, j) dari matriks A dan dilambangkan Mij atau Mij(A).
Definisi 2.6 Determinan Matriks
Misalkan suatu matriks A berukuan 2 x 2 atau
A maka determinan
matriks A sebagai berikut:
21
Misal matriks A berukuran 3 x 3, maka akan diperoleh determinan matriks dengan menggunakan persamaan (2.1), yaitu:
Dari persamaan (2.2) diperoleh:
Definisi 2.7 Invers Matriks
A adalah matriks persegi dan jika matriks B berukuran sama dapat dicari sedemikian sehingga AB = BA = I, maka A disebut invertible (dapat dibalik) dan B disebut invers dari A yang dilambangkan dengan A-1.
Contoh 2.3
Hitung invers matriks A berkut:
Penyelesaian :
Jika suatu matriks 2x2, misal
menggunakan rumus:
BA =
Karena AB = BA = I, maka berdasarkan definisi B adalah invers dari matriks A.
Teorema 2.2
Matriks A yang berukuran n x n punya invers jika dan hanya jika det(A)0
Definisi 2.8 Nilai Eigen dan Vektor Eigen
Misalkan A adalah sebuah matriks n x n. Sebuah matriks tak nol x berukuran n x 1 sedemikian sehingga Ax=λx disebut vektor eigen dari A, sedangkan skalar λ disebut nilai eigen dari A.
Contoh 2.4
Carilah nilai eigen dan vektor eigen dari matriks A.
Penyelesaian:
Pilih λ sedemikian sehingga det(A-I) = 0, jadi didapat:
Dengan demikian, diperoleh dua nilai eigen, yaitu 1 3 dan 2 7. Untuk mencari vektor eigen dari matriks A, akan diselesaikan dengan persamaan (A-I)x = 0 untuk 1= 3 dan 2 = -7.
i. Vektor eigen untuk 1= 3
Dengan operasi baris tereduksi, diperoleh:
diperoleh demikian,
Dengan
3 diperoleh
Dengan operasi baris tereduksi, diperoleh:
Jadi, didapatkan dua vektor eigen, yaitu:
adalah -7
untuk eigen vektor diperoleh
Jadi, diperoleh
B. SISTEM PERSAMAAN DIFERENSIAL
B.1 Turunan
Definisi 2.9 Kemiringan Garis Singgung
Gambar 2.1 Grafik Kemiringan Garis Singgung y = f(x)
Garis singgung pada grafik y=f(x) pada titik P (x, f(x)), yaitu
ada. ini limit jika
) ( ) ( lim
0 tan
x x f x x f m
t
(2.4)
Didefinisikan turunan sebagai berikut:
Definisi 2.10 Turunan
Turunan fungsi f adalah fungsi yang nilainya di setiap bilangan sebarang x di dalam daerah asal f didefinisikan oleh:
y
x 0
f(x)
x
f (x+x) m
x x f x x f x
f
x
) ( ) (
lim ) (
0 '
Asalkan limit ini ada, turunan fungsi f dilambangkan f '
(2.5)
Turunan berkaitan dengan laju perubahan suatu populasi. Berawal dari kecepatan yang merupakan laju perubahan jarak terhadap waktu. Perubahan dalam koordinat x, dapat dituliskan dengan cara sebagai berikut:
x x2 x1 (2.6)
Dimana Δ menunjukkan perubahan besaran, yang dihitung dengan mengurangkan nilai awal dari nilai akhir. Oleh karena itu, selang waktu dari
2 1ke t
t adalah
t t2 t1 (2.7)
Kecepatan rata-rata (v), yaitu perpindahan x dibagi selang waktu t dapat dinyatakan sebagai berikut:
1 2
1 2
t x t
t x x v
(2.8)
Kecepatan sesaat adalah limit dari kecepatan rata-rata untuk selang waktu mendekati nol. Kecepatan sesaat sama dengan besarnya perubahan sesaat dari posisi terhadap waktu, atau dapat dituliskan sebagai:
lim
0 dt
dx t x v
t
Limit dari untuk t0
t x
disebut sebagai turunan (derivative) dari x terhadap t
yang dituliskan sebagai
dt dx
.
B.2 Persamaan Diferensial
Definisi 2.11 Persamaan Diferensial
Persamaan diferensial adalah persamaan yang mengandung derivatif (turunan) satu atau beberapa fungsi yang tidak diketahui.
Persamaan diferensial diklasifikasikan menjadi dua kasus, yaitu Persamaan Diferensial Biasa dan Persamaan Diferensial Parsial.
Definisi 2.12 Persamaan Diferensial Biasa
Jika fungsi yang tidak diketahui tergantung pada satu variabel bebas saja maka persamaan diferensial yang terbentuk disebut dengan persamaan diferensial biasa.
Contoh 2.5
Sebagai contoh untuk persamaan diferensial biasa, yaitu:
450 5
. 0
2 . 0 8 . 9
p dt
dp
v dt
Definisi 2.13 Persamaan Diferensial Parsial
Jika fungsi yang tidak diketahui tergantung pada beberapa variabel bebas maka persamaan diferensial yang terbentuk disebut dengan persamaan diferensial parsial.
Contoh 2.6
Contoh yang khas dari persamaan diferensial parsial pada persamaan panas dan persamaan gelombang.
Klasifikasi Persamaan Diferensial Berdasarkan Orde
Persamaan diferensial memiliki orde (tingkat) dan derajat (pangkat) tertentu. Orde persamaan diferensial didefinisikan tingkat dari derivatif tertinggi yang muncul dalam persamaan diferensial. Sedangkan derajat suatu persamaan diferensial adalah pangkat turunan tertinggi dalam persamaan diferensial.
Klasifikasi Persamaan Diferensial Berdasarkan Kelinearan
Berdasarkan kelinearan ada dua sifat, yaitu linear dan non linear. Suatu persamaan diferensial dikatakan linear jika tidak ada perkalian antara
variabel-) , ( )
, (
yakni Gelombang, Persamaan
) , ( ) , (
yakni , panas Persamaan
2 2 2
2 2
2 2 2
t t x u x
t x u a
t t x u x
t x u
variabel tak bebas dan derivatif-derivatifnya. Dengan kata lain, semua koefisiennya adalah fungsi dari variabel-variabel bebas. Sedangkan sifat non linear bila dalam beberapa variabel tak bebas dikatakan tidak linear dalam variabel tersebut. Sebagai contoh:
Contoh 2.7
Persamaan Diferensial Linearitas
) cos( 2
4 '
''
x y
xy
y Linear
) cos( 2
4 '
''
x y
yy
y Tidak linear karena memuat yy'
) sin( 2
2
u v
u t v x
u
Linear pada v tetapi tidak linear
pada u karena memuat sin (u). Jadi persamaan tersebut tidak linear
) sin( 2
2
t xy
t y t
x
Linear pada setiap variabel tak
Klasifikasi Persamaan Diferensial Berdasarkan Homogenitas
Bentuk dari persamaan diferensial biasa dapat dinyatakan sebagai:
) ( ) ( )
(x y' q x y g x
p (2.10)
Persamaan diferensial dikatakan homogen bila g(x) =0. Persamaan diferensial dikatakan nonhomogen bila g(x) tersebut dapat berbentuk fungsi exponensial, trigonometri, ataupun fungsi polynomial dan g(x)0.
Definisi 2.14 Penyelesaian Persamaan Diferensial
Penyelesaian dari persamaan diferensial y(n) f(t,y',y'',...,y(n1))pada interval
t adalah suatu fungsi sedemikian sehingga '(t),''(t),...,n(t)ada dan memenuhi:
)] ( ),..., ( ), ( , [ )
(t f t t ' t n 1 t
n
(2.11)
Contoh 2.8
Selesaikan Persamaan Diferensial Orde 1 berikut:
ax dt
dx (2.12)
Persamaan (2.12) dapat ditulis sebagai:
a
dt xdx
maka kan diintegral ruas
kedua Bila
atau ln
diperoleh sehingga
c at x
c at
e K Ke
x dengan (2.13)
Jika diketahui nilai awal x(0) x0 dan bila disubstitusikan ke persamaan (2.13) dan diperoleh x0 K, sehingga persamaan (2.13) menjadi:
at
e x t x( ) 0
Jadi, penyelesaian Persamaan Diferensial Orde 1 adalah x(t)x0eat
Titik setimbang (equilibrium point) diperoleh jika ' 0 dt dx
x . Dalam
kasus x'ax ,a0 maka titik setimbangnya:
0 atau
0 0 '
x
a ax
B.3 Sistem Persamaan Diferensial
Definisi 2.15 Sistem Persamaan Diferensial
Sistem persamaan diferensial adalah suatu sistem yang memuat n persamaan diferensial dengan n buah fungsi yang tidak diketahui.
Definisi 2.16 Sistem Homogen
Sistem homogen dari n persamaan diferensial linear orde satu dengan koefisien real, secara umum dapat ditulis, sebagai:
(2.14)
Sistem persamaan (2.13) dapat ditulis sebagai x' = Ax, dengan
Sebuah sistem disimulasikan dengan orde 1 persamaan diferensial biasa
Definisi 2.17 Penyelesaian Sistem Persamaan Diferensial
Sistem Persamaan Diferensial x' = Ax, A matriks n x n memiliki penyelesaian pada I: <t < jika ada n fungsi yang terdiferensialkan pada I dan memenuhi sistem persamaan diferensial pada semua titik dalam I.
Definisi 2.18 Titik Setimbang (Equilibrium)
Diberikan sistem persamaan diferensial x' = Ax, titik setimbang (equilibrium) adalah suatu penyelesaian yang memenuhi x' = Ax =0
Definisi 2.19 Titik Kritis
Penyelesaian x dimana Ax=0, sedemikian sehingga titik berkorespondensi dengan penyelesaian konstan atau penyelesaian equilibrium dan disebut titik kritis.
Jika det(A)0 maka A-1 ada sehingga:
0
0
0 )x
(
) 0 ( ) (
0
1 -1
-1 -1
-
x x I
A A A
A Ax A Ax
Definisi 2.20 Kestabilan
Gangguan pada sistem tidak memberikan pengaruh terhadap kestabilan suatu sistem sehingga jika sistem tersebut stabil terhadap suatu gangguan maka sistem akan stabil untuk gangguan yang ada.
Titik kritis dikatakan stabil jika untuk semua 0ada 0 sedemikian sehingga setiap penyelesaian x(t) dimana t 0, memenuhi 0
) 0
( x ,
ada untuk semua t positif dan memenuhi 0
)
(t x untuk semua t0.
Titik kritis dikatakan stabil asmptotik jika stabil dan jika ada 0
0
sedemikian sehingga penyelesaian x(t)memenuhi 0 0
) 0
(
x
maka lim ( )x0
t
t .
Penyelesaian x0 dari Ax 0 dengan A adalah matriks berukuran 2 x 2, sesuai dengan penyelesaian kesetimbangan dan disebut dengan titik kritis. Misal A matriks non singular atau det(A)0,x0 adalah satu-satunya titik kritis
untuk sistem x' = Ax. Suatu penyelesaian dari x' = Ax adalah fungsi vektor x =
(t) yang memenuhi persamaan diferensial dan dapat dilihat sebagai representasi parametrik pada kurva x1x2. Kurva tersebut dapat dianggap sebagai trayektori
(lintasan) yang dilalui oleh partikel bergerak dengan laju perubahan
dt dx
yang
Definisi 2.21 Bidang Fase
Bidang x1x2 dari suatu sistem persamaan yang dinyatakan sebagai diferensial terhadap t.
Untuk menganalisis sistem x' = Ax harus mempertimbangkan beberapa kasus yang tergantung pada sifat dari nilai eigen dari A. Ada lima kasus untuk nilai eigen, yang diklarifikasikan sebagai berikut:
Kasus 1: Nilai Eigen Real Tidak Sama tetapi Tanda Sama
Pada kasus ini, penyelesaian umumnya adalah
(2.16)
dimana, 1dan 2 keduanya positif atau keduanya negatif. Misalkan 0
2 1
dan vektor eigen adalah V(1)dan V(2). Oleh karena itu, x 0 sebagai
t untuk semua penyelesaian, dengan mengabaikan nilai c1dan c2.
Jika penyelesaian dimulai dengan titik awal, pada garis melalui (1)
V maka 0
1
c dan penyelesaian tetap pada garis. Demikian pula, jika titik awal pada garis melalui (2)
V , penyelesaian dapat ditulis sebagai:
(2.17)
Karena 1-2 0untuk c2 0, c (1)e1 2t 1
V diabaikan, dan dibandingkan dengan c2V(2)untuk tmembesar.
t t
e c e
c 1 (2) 2 2
) 1 ( 1
V V
x
(2)
2 )
1 ( 1 )
2 ( 2 )
1 ( 1
2 1 2
2
1 V V V
V
Jadi, semua penyelesaian bersinggungan dengan (2)
V pada titik ktitis x = 0 kecuali untuk penyelesaiannya tepat pada garis yang melalui V(1). Jenis titik kritis ini disebut node atau nodal sink.
Gambar 2.2 Node 12 0
Kasus 2: Nilai Eigen Real Berbeda Tanda
Pada kasus ini, penyelesaian umumnya adalah
(2.18)
dimana, 10dan 2 0. Misalkan vektor eigen adalah V(1)dan V(2) dapat dilihar pada gambar 2.2.
Satu-satunya penyelesaian yang mendekati titik kritis pada titik asal adalah penyelesaian dimulai garis yang ditentukan oleh V(2). Jenis titik kritis ini disebut titik pelana.
t t
e c e
c 1 (2) 2 2
) 1 ( 1
V V
Gambar 2.3 Titik Pelana 1 0, 2 0
Kasus 3: Nilai Eigen Sama
Misalkan 1 2 . Ada dua subkasus tergantung memiliki dua vektor eigen atau bebas linear atau hanya satu, diklarifikasikan sebagai berikut:
a)Dua Eigen Vektor Bebas Linear
Pada kasus ini, penyelesaian umumnya adalah
(2.19)
Dengan demikian, setiap lintasan terletak pada garis yang melewati titik asal, seperti yang terlihat dalam gambar 2.4 di bawah ini. Titik kritis pada titik asal disebut node proper atau titik star.
t r
e c e
c1V(1) 2V(2)
Gambar 2.4 Titik Star 12 0
b)Satu Eigen Vektor Bebas Linear
Pada kasus ini, penyelesaian umumnya adalah
(2.20)
Ketika nilai eigen ganda hanya memiliki satu nilai eigen yang bebas linear, titik kritis disebut improper node atau degenerate node.
Gambar 2.5 Improper Node 12 0
t t
t
e te c e
cV V η
Kasus 4: Nilai Eigen Kompleks dengan Bagian Real Tak Nol
Misalkan nilai eigen i, dimana dan bilangan real dengan
0 dan
0
. Perhatikan pada sistem berikut:
atau dapat ditulis sebagai:
2 1 2
2 1 1
x x x
x x x
(2.21)
Koordinat polar r, dapat diberikan dengan:
Dengan mendiferensialkan persamaan di atas, diperoleh:
Mensubtitusikan ke persamaan (2.21), sehingga didapat:
penyelesaian diferensialnya adalah:
Persamaan ini adalah persamaan parametrik dalam koordinat polar dari lintasan solusi untuk sistem x' = Ax. Karena 0, berarti menurun saat t membesar, maka arah gerak lintasan searah jarum jam.Jika 0, maka r 0
x
x
1 2 2
2 2 1 2
tan
, x x
x x
r
21 1 2 2 1 2
2 2 1
1x x x , sec x x x x x
x r
r
r, r
) 0 ( ,
, 0 0
ce t
bila t , sedangkan jika 0 maka r . Jadi lintasan berbentuk spiral, yang mendekati titik asal tergantung pada tanda , dan titik kritis disebut titik spiral.
Gambar 2.6 Titik Spiral 0 Gambar 2.7 Titik Spiral 0
Kasus 5: Nilai Eigen Kompleks dengan Bagian Real Nol
Misalkan nilai eigen i, dimana 0 dan real. Perhatikan pada
sistem berikut:
atau dapat ditulis
1 2
2 1
x x
x x
Pada kasus 4 menggunakan koordinat polar r, , sehingga menyebabkan: x
x
0 0
0 ,
Dengan demikian, lintasan berbentuk lingkaran dengan pusat di titik asal yang melintasi searah jarum jam jika 0dan berlawanan jarum jam jika 0. Titik kritis disebut center.
Gambar 2.8 Center 1 i,2 i
Dari kelima kasus di atas dengan memeriksa gambar yang berkorespondensi dapat diamati bahwa:
1. Setelah waktu lama, masing-masing lintasan menunjukkan salah satu dari tiga jenis perilaku. Saat t, setiap lintasan mendekati titik kritis x=0, berulang kali melintasi kurva tertutup yang mengelilingi titik kritis atau menjadi tidak terbatas.
3. Dalam setiap kasus himpunan semua lintasan sedemikian sehingga salah satu dari tiga situasi terjadi, seperti berikut:
a. Semua lintasan mendekati titik kritis x=0, saat t . kasus ini terjadi jika nilai-nilai eigen adalah real dan negatif atau kompleks dengan bagian real negatif. Titik awal merupakan nodal sink atau spiral sink.
b. Semua lintasan tetap dibatasi tetapi tidak mendekati titik awal saat t. Kasus tersebut terjadi jika nilai eigen murni imajiner. Titik awal merupakan center.
c. Semua lintasan dan kemungkinan semua lintasan kecuali x=0 menjadi tidak terbatas saat t. Kasus ini terjadi jika salah satu nilai-nilai eigen positif atau nilai-nilai eigen memiliki bagian real positif. Titik awal ini merupakan nodal source, spiral source, atau titik pelana.
Sifat kestabilan dari sistem linear x' = Ax dengan det(A-I)0 dan
0 )
det(A dirangkum dalam tabel 2.1 berikut:
Tabel 2.1 Sifat Kestabilan
Nilai Eigen Tipe dari Titik Kritis Kestabilan
0 2 1
Node Tidak Stabil
0 2 1
Node Stabil Asimpotik
2
1 0
0 2 1
Proper atau improper
node
Tidak Stabil
0 2 1
Proper atau improper
node
Stabil Asimpotik
1, 2 i Titik Spiral
Tidak Stabil
Stabil Asimpotik 0
0
1 i , 2 i Center Stabil
Kestabilan suatu sistem persamaan diferensial dapat ditentukan dengan melihat bentuk bidang fasenya.
Contoh 2.9
Carilah penyelesaian umum dari sistem:
x
x
3 0
0 2 '
Dari matriks tersebut matriks koefisiennya adalah diagonal matriks. Jadi, bentuk skalar sistem di atas dapat ditulis sebagai berikut:
2 '
2 1 ' 1
3 2
x x
x x
Setiap persamaan meliputi hanya satu variabel tidak diketahui, jadi didapatkan penyelesaian seperti berikut:
t t
e c x
e c x
3 2 2
2 1 1
Dapat ditulis penyelesaian dalam bentuk vektor, yaitu
t t
t t
e c e c e
c e
c 3
2 2 1 3 2
2 1
1 0 0
1
x
Contoh di atas terdiri dari dua penyelesaian independen dari sistem yang diberikan dalam bentuk fungsi exponensial perkalian dengan vektor.
Langkah-Langkah Mencari Penyelesaian Umum
Dalam sistem persamaan diferensial akan dicari penyelesaian umumnya untuk mengetahui kestabilan pada bidang fase, dalam bentuk seperti pada persamaan (2.14). Berikut adalah langkah-langkah dalam mencari penyelesaian umum sistem persamaan diferensial:
1. Memisalkan penyelesaian dalam bentuk xVet, dimana dan vektor V harus ditentukan.
2. Mensubtitusikan xVetke x' Axsehingga diperoleh:
0
I)V -A
AV V
AV V
(
t t
3. Mencari vektor eigen untuk setiap nilai eigen
4. Mensubtitusikan vektor eigen yang diperoleh ke dalam pemisalan pada langkah (1)
Contoh 2.10
Carilah penyelesaian umum dari sistem persamaan berikut dan gambarkan bidang fasenya untuk memperlihatkan lintasan kestabilannya.
2 1 ' 2
2 1 ' 1
4x x x
x x x
Penyelesaian:
Sistem di atas dapat ditulis sebagai:
x
x
1 4
1 1 '
Sehingga diperoleh:
2 1 ;
1 4
1 1
x x x A
Akan dicari vektor dan nilai eigen dari A. Misalkan V adalah vektor eigen dan λ adalah nilai eigen dari A.
Misalkan x = Vert maka (A-λI)V = 0
0 0 1
4 1 1
2 1 v v
Penyelesaian untuk mencari nilai eigen dengan det(A-λI)=0
didapat λ1 = 3 dan λ2 = -1
i.Vektor eigen untuk λ1 = 3
Diselesaikan dengan operasi baris tereduksi didapat: ) vektor diperoleh
sehingga diperoleh
ii.Vektor eigen untuk λ2 = -1
Diselesaikan dengan operasi baris tereduksi didapat:
vektor diperoleh
2
Untuk penyelesaian persamaan x = Vert adalah
DiperolehDengan demikian, diperoleh penyelesaian umumnya adalah
Untuk mengambarkan bidang fasenya, akan dituliskan sebagai:
Gambar 2.9 Bidang fase x1 dan x2
Pada gambar 2.9 menunjukan bentuk bidang fase yang disebut bentuk titik pelana. Titik pelana selalu tidak stabil, bila t membesar akan menjauhi titik pusat (0,0) dan tampak pada titik (0,0) tidak stabil.
C. METODE RUNGE-KUTTA ORDE 4
Metode Runge-Kutta Orde 4 mempunyai skema sebagai berikut:
2 2
dengan,
Contoh 2.11
Selesaikan sistem persamaan diferensial berikut dengan menggunakan metode Runge-Kutta Orde 4, dengan asumsi
Penyelesaian:
kemudian langkah selanjutnya untuk
didapat:
t x1 x2
0 4 6
0.5 3 6.9
1.0 2.25 7.715
1.5 1.6875 8.44525
44
BAB III
MODEL PENYEBARAN PENYAKIT
Bab ini akan membahas mengenai dinamika populasi vektor dan manusia yang terjangkit penyakit tidur untuk memodelkan penyebaran penyakit tidur.
A. PENYEBARAN PENYAKIT TIDUR
Tsetse adalah carrier (pembawa) parasit Trypanosomiasis, Tsetse tidak menghasilkan racun dan tidak berbahaya sebelum lalat tersebut tertular parasit Trypanosomiasis. Lalat ini menghisap darah. Apabila darah korbannya telah
terinfeksi Trypanosomiasis maka Tsetse akan tertular parasit tersebut dan dapat menyebarkan ke korban-korban berikutnya yang dihisap darahnya, karena air liur dari lalat ini ikut masuk ke dalam lubang gigitan saat ia menghisap darah.
Parasit Trypanosomiasis, menyebabkan demam, migrain dan menimbulkan kantuk yang luar biasa. Korban dapat tertidur yang disebut dengan Sleeping Sickness), dan bila tidak segera disembuhkan maka korbannya tidak akan
pernah bangun lagi (meninggal). Binatang ataupun manusia dapat terinfeksi parasit ini dan juga dapat saling menularkan dengan perantara lalat tsetse.
1. Fase awal (Initial stage)
Ditandai dengan timbulnya reaksi inflamasi lokal pada daerah gigitan lalat tsetse. Reaksi inflamasi dapat berkembang menjadi bentuk parut ( primary chancre). Reaksi inflamasi ini biasanya mereda dalam waktu 1-2
minggu.
2. Fase penyebaran (Haemoflagellates stage)
Setelah fase awal mereda, parasit masuk ke dalam darah dan kelenjar getah bening (parasitemia). Gejala klinis yang sering muncul adalah demam yang tidak teratur, sakit kepala, nyeri pada otot dan persendian. Tanda klinis yang sering muncul antara lain: Lymphadenopati, lymphadenitis yang terjadi pada bagian posterior kelenjar cervical (Winterbotton’s sign), papula dan rash pada kulit. Pada fase ini juga terjadi proses infiltrasi perivascular oleh sel-sel endotel, sel limfoid dan sel plasma, hingga dapat menyebabkan terjadinya pelunakan jaringan iskemik dan perdarahan di bawah kulit (ptechial haemorhagic). Parasitemia yang berat (toksemia) dapat mengakibatkan
kematian pada penderita.
3. Fase kronik (Meningoencephalitic stage)
diikuti dengan infeksi sekunder oleh karena immunosupresi. Jumlah lekosit normal atau sedikit meningkat. Bila tercapai stadium tidur terakhir, penderita sulit dibangunkan atau mengalami kematian. Penyakit tidur ini juga diperberat oleh penyakit lain seperti malaria, disentri, pneumonia atau juga kelemahan tubuh.
B. MODEL KOMPARTEMEN
Perpindahan / penyebaran penyakit tidur dapat diilustrasikan pada gambar 3.1 berikut:
Gambar 3.1 Siklus Perpindahan Parasit: Manusia dan Lalat
Keterangan :
= Lalat yang terinfeksi = Manusia yang terinfeksi
= Lalat sehat = Manusia sehat
Pada gambar tersebut dapat diamati bahwa lalat tsetse yang terinfeksi oleh penyakit tidur akan menginfeksi manusia yang sehat. Manusia tersebut terkena parasit dan selanjutnya menjadi terinfeksi. Manusia yang sudah terinfeksi digigit oleh lalat sehat, sehingga lalat tersebut menjadi terinfeksi penyakit. Manusia yang terinfeksi penyakit dapat sembuh dari penyakit atau akan mati. Namun, dalam model ini diasumsikan bahwa setelah terinfeksi manusia akan sembuh. Dan lalat yang terinfeksi akan kembali menginfeksi manusia yang sehat. Siklus ini akan berlangsung secara terus-menerus.
Model ini memiliki dua variabel (dan karenanya dalam bahasa epidemiologi disebut model dua kompartemen), yakni lalat yang terinfeksi dan manusia yang terinfeksi. Banyaknya lalat dan manusia yang rentan (tidak terinfeksi) diketahui karena banyaknya lalat dan manusia keseluruhan diasumsikan konstan.
Misalkan V(t) adalah total banyaknya vektor pada waktu t, Vs(t) adalah terinfeks yang
vektor banyaknya
atau dapat ditulis sebagai
) adalah banyaknya manusia yang rentan terhadap penyakit, Ha(t) adalah banyaknya manusia yang terinfeksi penyakit, dan Hr(t) adalah banyaknya manusia sembuh, maka
terinfeks
manusia banyaknya
rentan manusia
banyaknya manusia
banyaknya
atau dapat ditulis sebagai:
Siklus penyebaran penyakit pada vektor diilustrasikan pada gambar sebagai berikut,
Gambar 3.2 Model Kompartemen Vektor
Vektor yang rentan akan memasuki masa inkubasi sekitar 25 hari dan vektor dapat mengalami kematian dengan laju m. Pada masa inkubasi, vektor juga dapat mengalami kematian dengan laju m, dan vektor akan kembali memasuki masa rentan dengan laju b, serta vektor akan memasuki tahap terinfeksi dengan laju q. Pada saat vektor masuk dalam tahap terinfeksi, vektor dapat mengalami kematian dengan laju m, dan vektor juga akan kembali memasuki masa rentan dengan laju b.
Namun, dalam model penyebaran penyakit tidur dalam makalah ini, pada vektor diasumsikan bahwa vektor yang berada pada tahap terinfeksi tidak kembali sembuh atau kembali ke masa rentan. Model ini juga diasumsikan bahwa vektor pada tahap rentan tidak masuk ke masa inkubasi. Serta model ini tidak
q
waktu m
waktu m
waktu
b
waktu b
waktu
m waktu
k(Vc – V(t)) Rentan
Vs (t)
Terinfeksi
Va (t) Inkubasi
mempertimbangkan banyaknya vektor yang mengalami migrasi, sehingga model kompartemen vektor menjadi seperti ditunjukkan dalam Gambar 3.3:
Gambar 3.3 Model Kompartemen Vektor pada Model
Sedangkan siklus penyebaran penyakit pada manusia diilustrasikan pada Gambar 3.4:
Gambar 3.4 Model Kompartemen Manusia
Setelah masa inkubasi manusia yang singkat yaitu sekitar 12 hari, manusia memasuki tahap terinfeksi penyakit, dimana manusia terinfeksi oleh parasit ketika
Terinfeksi
Ha (t)
Sembuh Hr (t)
Rentan Hs (t) b
waktu r1
r2 Inkubasi
Vi(t)
Rentan
Vs (t) b
waktu q
waktu m
waktu m
waktu Terinfeksi
digigit oleh vektor. Ketika manusia masuk tahap terinfeksi penyakit, manusia memasuki tahap sembuh dengan laju r1, dan kembali memasuki masa rentan
dengan laju b. Pada saat manusia masuk dalam tahap sembuh, manusia kembali memasuki masa rentan dengan laju r2. Ketika manusia kembali memasuki masa rentan, manusia dapat memasuki kembali ke tahap terinfeksi.
C. MODEL MATEMATIKA TENTANG GIGITAN VEKTOR
Vektor menggigit manusia rata-rata tiga hari sekali (Shier, 1999) sehingga dalam model ini akan mempertimbangkan model kontinu dimana unit waktu adalah tiga hari. Banyaknya vektor menggigit didekati dengan banyaknya manusia yang ditandai dengan timbulnya gejala-gejala penyakit. Pada model penyebaran penyakit tidur ini menggunakan simbol-simbol untuk menghitung suatu probabilitas, yaitu:
τ1 = Probabilitas vektor menggigit seorang manusia selama unit waktu (tiga hari).
τ2 = Probabilitas vektor rentan yang akhirnya menjadi terinfeksi setelah
menggigit seorang yang terinfeksi.
τ3 = Probabilitas seorang manusia rentan yang digigit oleh vektor terinfeksi dan
akhirnya menjadi terinfeksi.
manusia, kemungkinan vektor akan menggigit sebanyak 2 kali. Dari persamaan (3.2), diasumsikan bahwa banyaknya manusia yang mungkin digigit seekor vektor bergantung pada banyaknya manusia yang rentan dan terinfeksi sehingga dapat ditulis persamaan sebagai berikut:
) yang nilainya di antara 0 dan 1. Vektor menggigit manusia tiga hari sekali dengan probabilitas sebesar τ1. Banyaknya manusia yang terinfeksi didekati oleh
banyaknya vektor yang menginfeksi manusia. Banyaknya manusia terinfeksi yang mendapat pengobatan maka sistem kekebalan tubuh akan meningkat sehingga manusia menjadi sembuh. Probabilitas seorang manusia sembuh yang digigit oleh wA0 vektor adalah:
vektor banyaknya gigitan ve proporsi dan terinf digigit
yang
manusia banyaknya
terinfeksi dan tidak
digigit yang tetapi
digigit yang i terinfeks manusia mendapat
yang
Atau dapat dinyatakan sebagai:
Dari persamaan (3.4) populasi vektor samaran dapat didekati oleh banyaknya vektor menggigit yang mengakibatkan terinfeksi yaitu:
Banyaknya vektor yang menggigit seorang manusia terinfeksi didekati oleh banyaknya manusia yang terinfeksi. Probabilitas bahwa vektor menggigit seorang manusia yang terinfeksi yaitu:
menggigit vektor
banyaknya terinfeksi
dan tidak digigit
yang manusia banyaknya
penyakit i
terinfeks
manusia terinfeks manusia
menggigit yang
vektor banyaknya
i terinfeks manusia
seorang
menggigit yang
vektor banyaknya
( ) ( )
Banyaknya vektor yang menggigit seorang manusia rentan didekati oleh banyaknya manusia yang rentan. Probabilitas vektor menggigit seorang manusia yang rentan yaitu:
rentan
manusia
menggigit yang
vektor banyaknya
rentan manusia
seorang
menggigit yang
D. DINAMIKA POPULASI VEKTOR
1. Banyaknya vektor konstan
2. Vektor hanya menggigit manusia
3. Vektor menggigit manusia rata-rata 3 hari sekali
4. Vektor rentan terhadap penyakit
5. Vektor mempunyai masa inkubasi 25 hari
Untuk memahami dinamika populasi vektor, didefinisikan:
Vs(t) = banyaknya vektor yang rentan ( dapat terinfeksi penyakit )
Vi(t) = banyaknya vektor pada masa inkubasi
Va(t) = banyaknya vektor yang terinfeksi aktif
vektor p op ulasi total
vektor p op ulasi
besarny a
rentan vektor bany akny a
terinfeksi, vektor itu menjadi terinfeksi. Banyaknya vektor pada kelompok masa inkubasi dimisalkan V(t)b dengan b laju kelahiran vektor, vektor yang berisiko terinfeksi juga sebanyak V(t)b.
Perubahan banyaknya vektor pada suatu kelompok adalah banyaknya vektor yang masuk dalam kelompok tersebut dikurangi dengan banyaknya vektor yang keluar dari kelompok tersebut. Persamaan perubahan untuk banyaknya vektor pada masa inkubasi selama waktu t adalah
vektor bany akny a
rentan menjadi
inkubasi masa
p ada
vektor bany akny a
i terinfeks menjadi
inkubasi masa
p ada
vektor bany akny a
inkubasi masa
masuk
vektor bany akny a
inkubasi masa
dari keluar
vektor bany akny a inkubasi
masa masuk
vektor banyaknya i
terinfeks yang
terinfeks menjadi
Pada saatt0, laju perubahan banyaknya vektor pada masa inkubasi adalah
m
terinfeks tahap
vektor banyaknya perubahan
i terinfeks tahap
dari keluar
vektor banyaknya i
terinfeks tahap
ke masuk
vektor banyaknya
Pada saat t 0, laju perubahan banyaknya vektor yang terinfeksi adalah
dt
Persamaan perubahan untuk banyaknya vektor rentan adalah
rentan vektor bany akny a
rentan bany akny a
rentan bany akny a
rentan tahap ke keluar
vektor bany akny a rentan
tahap ke masuk
vektor bany akny a )
Dari persamaan (3.12) diperoleh:
= k V V t V t m
Pada saat t 0, laju perubahan banyaknya vektor rentan adalah
Bila faktor migrasi diabaikan maka persamaan (3.17) akan menjadi:
m diferensial, yaitu:
banyaknya manusia diasumsikan konstan sejumlah 300 manusia. Banyaknya manusia rentan, terinfeksi penyakit, dan sembuh masing-masing adalah 100 manusia, serta nilai-nilai parameter model yang digunakan dirangkum dalam Tabel 3.1 (Shier, 1999).
Tabel 3.1 Nilai Parameter untuk Ilustrasi
Parameter Deskripsi Nilai
H total banyaknya manusia 300
Hs banyaknya manusia rentan 100
Ha banyaknya manusia terinfeksi penyakit 100
Hr banyaknya manusia sembuh 100
τ1 probabilitas vektor menggigit seorang manusia 0.1
τ2 probabilitas vektor rentan menjadi terinfeksi 0.1
τ3 probabilitas seorang manusia rentan digigit oleh vektor terinfeksi
0.1
q laju perubahan vektor pada masa inkubasi masuk ke tahap terinfeksi
0.12 per hari
r1 laju perubahan manusia terinfeksi masuk ke tahap sembuh
r2 Laju perubahan manusia sembuh masuk ke tahap rentan
0.0075 per hari
b
laju kelahiran vektor
1/15 per hari
m
laju kematian vektor
1/15 per hari
A0 sekumpulan vektor 100
w proporsi gigitan vektor yang menyebabkan infeksi
0.5
Dari menggunakan nilai-nilai parameter tersebut didapat sistem persamaan diferensial dengan unit waktu 3 hari, sebagai berikut:
s a
i i
V V
V dt
dV
001 . 0 001 . 0 62 . 0 .
0
(3.19)
022 . 0 04 .
0 i a
a
V V
dt dV
(3.20)
s a
i s
V V
V dt
dV
001 . 0 022 . 0 022 .
0
(3.21)
Untuk menyelesaikan system persamaan di atas, misalkan:
Sehingga, sistem di atas dapat ditulis sebagai V'AV. Penyelesaian dari sistem tersebut diperoleh dengan mencari nilai eigen dan vektor eigen dari A. Misalkan B adalah vektor eigen dan λ adalah nilai eigen dari A, maka penyelesaian sistem persamaan diferensial tersebut adalah V = Bert .
Nilai eigen dan vektor eigen dari A diperoleh melalui (A-λI)B = 0, yaitu:
Nilai eigen merupakan penyelesaian dari det(A-λI)=0, yaitu
0
Dengan menggunakan perintah MATLAB diperoleh tiga nilai eigen, yaitu
λ1 = -0.063, λ2 = -0.022, dan λ3 = 0
Dari persamaan (3.22), dengan mensubtitusikan λ1 = -0.063 diperoleh:
Penyelesaian sistem di atas diperoleh dengan operasi baris elementer, terhadap matriks koefisien, sehingga didapat:
Dengan demikian,
Dari penyelesaian di atas, diperoleh persamaan:
ii.Vektor eigen untuk λ2 = -0.022
Dari persamaan (3.22), dengan mensubtitusikan λ2 = -0.022 diperoleh:
Penyelesaian sistem di atas diperoleh dengan operasi baris elementer, terhadap matriks koefisien, sehingga didapat:
Dengan demikian,
Dari penyelesaian di atas, diperoleh persamaan:
Dari persamaan (3.22), dengan mensubtitusikan λ3 = 0 diperoleh:
Penyelesaian sistem di atas diperoleh dengan operasi baris elementer, terhadap matriks koefisien, sehingga didapat:
Dengan demikian,
Dari penyelesaian di atas, diperoleh persamaan:
Misal b3 cmaka b1 0.0166cdan b2 0.0289c, sehingga diperoleh vektor
Dengan demikian, diperoleh penyelesaian umumnya adalah:
Dari persamaan (3.24) dapat dituliskan, sebagai berikut:
3
Dengan menggunakan perintah MATLAB diperoleh nilai konstanta, yaitu:
3424
Dengan demikian, penyelesaian khususnya dapat dituliskan, sebagai berikut:
064
Dalam dinamika populasi vektor terdapat tiga variabel, yaitu Vi,Va dan Vs, sehingga tidak mudah untuk mengilustrasikan dalam bidang fase. Dengan demikian, untuk menggambarkan sifat kestabilannya akan diamati dua variabel, yaitu ViVa,ViVs dan VaVs.
i. Bidang Fase untuk ViVa
Sistem persamaan diferensial untuk ViVa menjadi, sebagai berikut:
Gambar 3.5 Bidang Fase ViVa
ii.Bidang Fase untuk ViVs
Sistem persamaan diferensial untuk ViVsmenjadi, sebagai berikut:
s i
i
V V
dt dV
001 . 0 062 .
0
(3.30)
s i
s
V V
dt dV
001 . 0 022 .
0
(3.31)
iii.Bidang Fase untuk VaVs
Sistem persamaan diferensial untuk VaVs menjadi sebagai berikut:
022 .
0 a
a
V dt
dV
(3.32)
s a
s
V V
dt dV
001 . 0 022 .
0
(3.33)
Gambar 3.7 Bidang Fase VaVs
Titik setimbang untuk dinamika populasi vektor, yaitu ' 0 dt dV V .
Dengan demikian, titik setimbang untuk banyaknya vektor pada masa inkubasi, terinfeksi dan rentan adalah
0 001 . 0 001 . 0 062 .
0
i a s
i
V V
V dt
0 Penyelesaian Linear Homogen), bila dituliskan bentuk matriks, diperoleh sebagai berikut:
SPLH di atas dapat diselesaikan dengan operasi baris elementer, dan diperoleh:
Dari hasil operasi baris elementer di atas, didapat persamaan sebagai berikut:
0
Dengan demikian, persamaan (3.37) dan (3.38) dapat diperoleh:
c
Vi 0.0166 (3.39)
c
Va 0.0289 (3.40)
c
Vs (3.41)
Bila c124.65, dengan demikian persamaan (3.39), (3.40) dan (3.41) dapat diperoleh bahwa titik setimbang untuk ketiga kelompok vektor tersebut adalah:
65 . 124
602 . 3
069 . 2
s a i
V V V
Hasil Vi,Va,dan Vs yang diperoleh di atas merupakan titik kritis, berdasarkan definisi 2.20 tentang kestabilan bahwa: dinamika populasi vektor memiliki sifat stabil karena V(0)V* dan stabil asimptotik karena limV(t) V*
t .
Gambar 3.8 Grafik Dinamika Populasi Vektor