PENENTUAN DIMENSI METRIK GRAF HELM
SKRIPSI
Oleh :
DIAN FIRMAYASARI S
NIM : H 111 08 011
JURUSAN MATEMATIKAFAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS HASANUDDIN
MAKASSAR 2012
PENENTUAN DIMENSI METRIK GRAF HELM
SKRIPSI
Diajukan sebagai salah satu syarat untuk memperoleh gelar
Sarjana Sains pada
Program Studi Matematika Jurusan Matematika
Fakultas Matematika dan Ilmu Pengetahuan Alam
Universitas Hasanuddin
Makassar
Oleh :
DIAN FIRMAYASARI S
NIM : H 111 08 011
JURUSAN MATEMATIKAFAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS HASANUDDIN
MAKASSAR 2012
P E R N Y A T A A N
Saya yang bertanda tangan di bawah ini menyatakan dengan sesungguh-sungguhnya bahwa skripsi yang saya buat dengan judul :
PENENTUAN DIMENSI METRIK GRAF HELM
adalah benar-benar kerja saya sendiri, bukan hasil plagiat dan belum pernah dipublikasikan dalam bentuk apapun.
Makassar, 21 Mei 2012
DIAN FIRMAYASARI S H111 08 011
PENENTUAN DIMENSI METRIK GRAF HELM
SKRIPSI
Oleh :
DIAN FIRMAYASARI S
NIM : H 111 08 011
Telah Diperiksa dan Disetujui untuk Diuji : Tanggal : 21 Mei 2012
Pembimbing Utama
Dr. Nurdin, M.Si NIP. 19700807 200003 1 002
Pembimbing Pertama
Dr. Amir Kamal Amir, M.Sc NIP. 19680803 199202 1 001
JURUSAN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS HASANUDDIN
Pada hari ini, Senin, tanggal 21 Mei 2012, panitia ujian sidang sarjana menerima dengan baik skripsi yang berjudul :
PENENTUAN DIMENSI METRIK GRAF HELM
yang diajukan untuk memenuhi salah satu syarat guna memperoleh gelar Sarjana Sains pada Program Studi Matematika Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Hasanuddin.
Makassar, 21 Mei 2012
Susunan Panitia Ujian Sidang Sarjana Tanda Tangan 1. Ketua : Prof. Dr. Syamsuddin Toaha, M.Sc (………)
NIP. 19680114 199412 1 001
2. Sekretaris : Hendra, S.Si, M.Si (………) NIP. 19760102 200312 1 001
3. Anggota : Drs. Muhammad Zakir, M.Si (………) NIP. 19640217 199103 1 004
4. Anggota : Dr. Nurdin, M.Si (………)
(Ex. Officio) NIP. 19700807 200003 1 002
5. Anggota : Dr. Amir Kamal Amir, M.Sc (………)
KATA PENGANTAR
Alhamdulillahirobbil’alamiin, puji dan syukur penulis haturkan kehadirat Allah SWT yang telah melimpahkan rahmat dan hidayah-Nya, sehingga penulisan skripsi dengan judul “Penentuan Dimensi Metrik Graf Helm” dapat terselesaikan dengan baik . Salawat dan salam semoga tetap tercurah kepada Rasulullah SAW yang menjadi suri teladan bagi umat islam dalam menjalani hidup yang sesungguhnya.
Penulisan skripsi ini dapat terselesaikan berkat bantuan dan motivasi dari berbagai pihak. Oleh karena itu, penulis sampaikan terima kasih kepada:
1. Ayahanda Siala Rahman dan Ibunda St. Puji tercinta yang senantiasa memberikan kasih sayang, doa dan materi kepada penulis dalam menuntut ilmu.
2. Bapak Dr. Nurdin, M.Si dan Bapak Dr. Amir Kamal Amir, M.Sc yang dengan sabar meluangkan waktunya demi memberikan bimbingan, pengarahan, dan saran sehingga penulisan skripsi ini dapat terselesaikan. 3. Bapak Prof. Dr. Syamsuddin Toaha, M.Sc, Bapak Hendra, S.Si, M.Kom
dan Bapak Drs. Muhammad Zakir, M.Si selaku penguji sekaligus penasehat akademik, terima kasih atas saran dan kritiknya demi perbaikan skripsi penulis.
4. Seluruh dosen di Jurusan Matematika FMIPA Universitas Hasanuddin, yang telah mendidik, mengajarkan, membimbing, dan mencurahkan ilmu-ilmunya kepada penulis.
5. Kedua adikku Ardy dan Ria serta seluruh keluarga besarku yang selalu memberikan doa, semangat, dan kasih sayang tanpa batas.
6. Kedua sahabatku Uchi dan Anti yang selalu menemaniku baik suka maupun duka, memberikan doa dan semangat.
7. Teman-teman seperjuangan di jurusan matematika khususnya angkatan 2008, terima kasih atas rasa persaudaraan dan kebersamaan yang telah diberikan kepada penulis.
8. Warga Himatika FMIPA Unhas, terima kasih atas ilmu dan pengalaman yang telah diberikan kepada penulis baik melalui pengkaderan maupun kegiatan kampus lainnya.
9. Semua pihak yang tidak dapat disebutkan satu-persatu, yang telah membantu penulis dalam menyelesaikan penulisan skripsi ini.
Dengan segala kerendahan hati, penulis menerima kritik dan saran demi tercapainya kesempurnaan skripsi ini.
Semoga skripsi ini dapat bermanfaat bagi pembaca khususnya bagi penulis. Amin Ya Rabbal Alamin.
Makassar, 21 Mei 2012
ABSTRAK
Misalkan adalah graf terhubung dan adalah suatu sub himpunan titik pada graf terhubung . Himpunan disebut himpunan penentu pada jika untuk setiap titik pada graf memiliki representasi jarak yang berbeda terhadap .
Himpunan penentu dengan banyak anggota minimum disebut himpunan penentu minimum atau basis dari dan kardinalitas himpunan tersebut menyatakan dimensi metrik pada graf , dinotasikan dengan
Pada skripsi ini dibahas mengenai dimensi metrik graf helm yang dikontruksi dari graf roda . Berdasarkan hasil pembahasan diperoleh bahwa
⌊ ⌋ untuk dan
ABSTRACT
If is a connected graph and be a vertices subset on a connected graph . The set S is called resolving set for if every vertex on graph has distinct representation of . A resolving set containing a minimum number of vertices is called resolving set minimum or basis for and the cardinality of resolving set is the metric dimension on graph , denoted by
In the thesis discussed about metric dimension of helm graph constructed from graph wheel . Based on the discussion of the results obtained that ⌊ ⌋ for and
DAFTAR ISI
HALAMAN JUDUL . ... i
HALAMAN PENGAJUAN . ... ii
HALAMAN PERNYATAAN KEASLIAN TULISAN ... iii
HALAMAN PERSETUJUAN ... iv HALAMAN PENGESAHAN ... v KATA PENGANTAR ... vi ABSTRAK . ... viii ABSTACT ... ix DAFTAR ISI ... x
DAFTAR GAMBAR ... xii
DAFTAR LAMBANG . ... xiii
BAB I PENDAHULUAN 1.1 Latar Belakang ... 1 1.2 Rumusan Masalah ... 3 1.3 Batasan Masalah ... 3 1.4 Tujuan Penulisan ... 3 1.5 Manfaat Penulisan ... ……. 3
BAB II TINJAUAN PUSTAKA 2.1 Terminologi Graf ... 4
2.2 Graf Roda dan Graf Helm ... . 8
BAB III HASIL DAN PEMBAHASAN
3.1 Graf Helm ... 13 3.2 Dimensi Metrik Graf Helm ... 14 BAB IV PENUTUP
4.1 Kesimpulan ... 43 4.2 Saran ... 43 DAFTAR PUSTAKA ... 44
DAFTAR GAMBAR
Gambar 2.1 Graf dengan 6 titik ... 5
Gambar 2.2 Graf dengan 4 titik ... 6
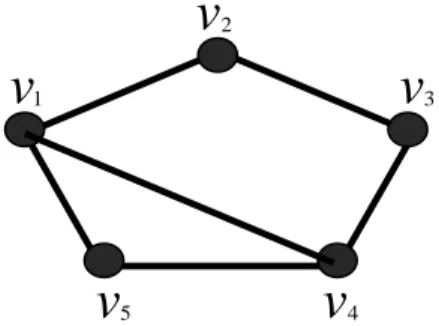
Gambar 2.3 Graf dengan 5 titik ... 7
Gambar 2.4 Graf dengan 4 titik ... 7
Gambar 2.5 Graf dengan 5 titik ... 8
Gambar 2.6 Graf ... 9
Gambar 2.7 Graf Roda ... 9
Gambar 2.8 Graf Helm ... 10
Gambar 2.9 Graf ... 11
Gambar 3.1 Graf Helm ... 13
Gambar 3.2 Graf Helm ... 16
Gambar 3.3 Graf Helm ... 19
Gambar 3.4 Graf Helm ... 20
DAFTAR LAMBANG
Lambang Keterangan
Pemakaian pertama kali pada halaman
Dimensi metrik graf 2
Jarak antara titik dan pada graf 2
Graf roda dengan titik 2 Graf helm dengan titik 2
⌊ ⌋ Bilangan bulat terbesar yang lebih kecil atau sama dengan 2
Himpunan sisi graf 4
Graf dengan himpunan titik dan himpunan sisi 4
Himpunan titik graf 4
Banyaknya anggota himpunan titik pada graf 4
Banyaknya anggota himpunan sisi pada graf 4
Derajat titik pada 6
Derajat titik yang minimum pada graf 6
Derajat titik yang maksimum pada graf 6 Graf lingkaran dengan titik 9
Representasi dari terhadap 10
sub himpunan titik pada graf 10
Kardinalitas 12
BAB I
PENDAHULUAN
Pada bab ini dibahas mengenai latar belakang masalah, rumusan masalah, batasan masalah, tujuan penulisan, manfaat penulisan, dan sistematika penulisan dari skripsi ini.
1.1 Latar Belakang
Ilmu matematika merupakan alat bantu untuk menyederhanakan penyajian dan pemahaman masalah. Dalam bahasa matematika, suatu masalah dapat menjadi sederhana untuk disajikan, dipahami, dianalisis, dan dipecahkan. Untuk keperluan tersebut, maka pertama dicari pokok masalahnya kemudian dibuat rumusan atau model matematikanya sehingga masalah lebih mudah dipecahkan.
Salah satu konsep dari disiplin ilmu matematika adalah teori graf. Teori graf pertama kali diperkenalkan oleh matematikawan Swiss bernama Leonhard Euler pada tahun 1736 ketika mendiskusikan mengenai persoalan jembatan Konigsberg Rusia. Cikal bakal dari teori graf dinyatakan dalam bentuk permainan atau teka-teki. Tetapi sekarang teori graf telah dapat memberikan kerangka dasar bagi banyak persoalan yang berhubungan dengan struktur dan hubungan antara suatu obyek diskrit dalam bentuk apapun. Graf menggambarkan struktur tersebut dalam beberapa objek yang dinyatakan dengan noktah, bulatan atau titik sedangkan hubungan antara objek dinyatakan dengan garis.
Seiring dengan kemajuan ilmu pengetahuan dan teknologi, akhir-akhir ini banyak sekali penelitian-penelitian terbaru tentang graf. Salah satu topik yang banyak dibicarakan adalah dimensi metrik. Dimensi metrik pada suatu graf pertama kali diperkenalkan oleh F. Harary dan R. A Melter (1976) pada jurnal berjudul on the metric dimension of a graph.
Untuk menentukan dimensi metrik graf ada beberapa konsep yang digunakan. Pertama adalah konsep jarak antara dua titik pada suatu graf. Misalkan
dan adalah titik-titik pada graf terhubung , maka jarak antara titik dan
pada graf adalah panjang lintasan terpendek antara dan pada , dinotasikan dengan . Konsep lainnya adalah himpunan penentu (resolving set). Suatu himpunan bagian dari himpunan titik disebut himpunan penentu pada jika setiap titik di mempunyai representasi yang berbeda terhadap . Himpunan penentu yang memiliki anggota (kardinalitas) yang minimum disebut himpunan
penentu minimum (minimum resolving set) dan anggota pada himpunan penentu
minimum disebut basis, sedangkan jumlah anggota dari basis tersebut disebut
dimensi metrik dari dan dinotasikan dengan .
Berdasarkan hasil penelitian beberapa peneliti terdahulu, dimensi metrik dari beberapa jenis graf sudah diketahui, diantaranya adalah graf roda dan graf lingkaran. Misalnya, Buczkowski dkk (2003) menemukan dimensi metrik graf roda dengan . Lebih jelasnya, jika dan dimensi metrik adalah ⌊ ⌋, sedangkan untuk dan dimensi metrik adalah .
Namun demikian, beberapa graf yang dikonstruksi dari graf roda belum ditemukan dimensi metriknya, misalnya graf helm (helm graph). Graf helm
adalah graf yang dikonstruksi dari graf roda dengan menambahkan sisi pendant pada setiap titik dari lingkaran luar graf roda.
1.2 Rumusan Masalah
Adapun rumusan masalah yang akan dibahas dalam penulisan skripsi ini adalah bagaimana menentukan dimensi metrik graf helm.
1.3 Batasan Masalah
Batasan masalah dalam penulisan skripsi ini dibatasi pada penentuan dimensi metrik graf helm hingga titik.
1.4 Tujuan Penulisan
Tujuan penulisan skripsi ini adalah menentukan dimensi metrik graf helm. 1.5 Manfaat Penulisan
Adapun manfaat yang diharapkan dalam penulisan skripsi ini adalah untuk menambah pemahaman tentang konsep teori graf khususnya dimensi metrik suatu graf.
BAB II
TINJAUAN PUSTAKA
Pada bab ini dibahas beberapa materi yang dijadikan landasan teori untuk memahami penentuan dimensi metrik suatu graf, khususnya graf helm. Materinya meliputi beberapa definisi, istilah-istilah dalam teori graf termasuk dimensi metrik. Adapun definisi, istilah-istilah, dan contoh yang dibahas pada bab ini umumnya dikutip dari referensi [1], [2], [3], [4], [5], [6], [7], dan [8].
2.1 Terminologi Graf
Pada sub bab ini dibahas beberapa definisi dan istilah-istilah dalam teori graf beserta contoh yang digunakan dalam penulisan skripsi ini.
Definisi 2.1 Graf adalah pasangan himpunan dengan adalah himpunan tidak kosong dan berhingga dari obyek-obyek yang disebut sebagai titik dan adalah himpunan (mungkin kosong) pasangan tidak terurut dari titik-titik berbeda di yang disebut sebagai sisi.
Himpunan titik di dinotasikan dengan dan himpunan sisi dinotasikan dengan Sedangkan banyaknya unsur di disebut order dari dan dilambangkan dengan dan banyaknya unsur di disebut ukuran dari dan dilambangkan dengan
Berdasarkan Definisi 2.1, didefinisikan graf sederhana adalah graf yang tidak mempunyai sisi ganda (multiple edges) dan loop. Dua buah sisi disebut
ganda pada suatu graf jika kedua sisi tersebut mempunyai titik ujung yang sama. Sedangkan yang disebut dengan loop adalah suatu sisi yang mempunyai titik ujung sama. Pada pembahasan skripsi ini, graf yang dibahas adalah graf sederhana.
Titik pada suatu graf dapat disimbolkan dengan huruf, seperti
atau bilangan asli, seperti atau gabungan keduanya, sedangkan sisi dapat disimbolkan dengan .
Contoh 2.1
Gambar 2.1. Graf G dengan 6 titik
Graf pada Gambar 2.1, memiliki himpunan titik dan himpunan sisi sebagai berikut : { } { } sehingga dan .
v
1v
3v
2v
4v
5v
6e
1e
2e
3e
4e
6e
5Definisi 2.2 Misal adalah graf dengan Jika adalah sisi pada maka dan disebut bertetangga (adjacent), sedangkan disebut terkait
(incident) dengan dan disebut terkait dengan
Contoh 2.2
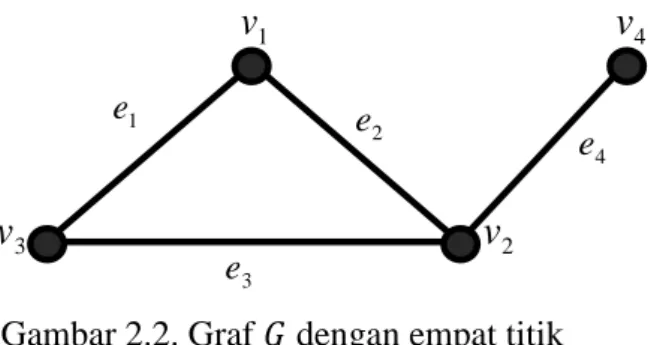
Gambar 2.2. Graf dengan empat titik
Pada Gambar 2.2 diketahui bahwa pasangan titik yang terhubung langsung
(adjacent) yaitu dan . Titik terkait langsung
(incident) dengan sisi dan sisi terkait langsung (incident) dengan titik
tetapi titik tidak terkait langsung (incident) dengan sisi , demikian juga sebaliknya, yaitu sisi tidak terkait langsung (incident) dengan titik
Definisi 2.3Derajat (degree) dari suatu titik pada graf adalah banyaknya sisi
yang terkait dengan titik dan dinotasikan dengan deg ).
Suatu titik yang berderajat 0 disebut titik terisolasi dan titik yang berderajat 1 disebut titik ujung. Derajat minimum titik di dinotasikan dengan dan derajat maksimum titik di dinotasikan dengan
2
v
1v
3v
4v
1 e 2 e 4 e 3 eContoh 2.3
Gambar 2.3. Graf dengan 5 titik Derajat titik-titik graf pada Gambar 2.3 adalah sebagai berikut :
. Dengan demikian, dipeoleh dan .
Definisi 2.4 Misal adalah graf dengan Lintasan dari titik ke
titik pada graf dinotasikan dengan adalah barisan selang-seling
antar titik dan sisi, , dimulai dengan titik
dan diakhiri dengan titik di mana untuk dan tidak
terdapat pengulangan titik dan sisi.
Contoh 2.4
Gambar 2.4. Graf dengan 4 titik
Graf pada Gambar 2.4, memiliki lintasan dengan barisan sisi yaitu
dan .
v
1v
2v
3v
5 1e
2e
3e
4e
5e
v
4 6 ev
1v
2v
4v
3Definisi 2.5 Misal adalah graf dengan . Graf disebut graf
terhubung (connected), jika setiap dua titik yang berbeda di terdapat suatu
lintasan dari ke
Definisi 2.6 Jarak (distance) antara titik dan pada graf , dinotasikan
dengan , adalah panjang lintasan terpendek antara dan pada .
Contoh 2.5
Gambar 2.5. Graf dengan 5 titik Pada Gambar 2.5 diperoleh
2.2 Graf Roda dan Graf Helm
Pada sub bab ini dibahas tentang definisi graf roda dan graf helm serta beberapa definisi yang berkaitan dengan kedua graf tersebut.
Definisi 2.7 Graf lingkaran (cycle) adalah graf terhubung yang semua titiknya berderajat dua.
v
1v
2v
3Contoh 2.6
Gambar 2.6. Graf
Definisi 2.8 Graf roda (wheel) adalah graf terhubung yang dikonstruksi dari graf
lingkaran dinotasikan dengan dengan menambahkan satu titik sebagai
titik pusat dan n sisi sedemikian sehingga bertetangga dengan semua titik pada
lingkaran .
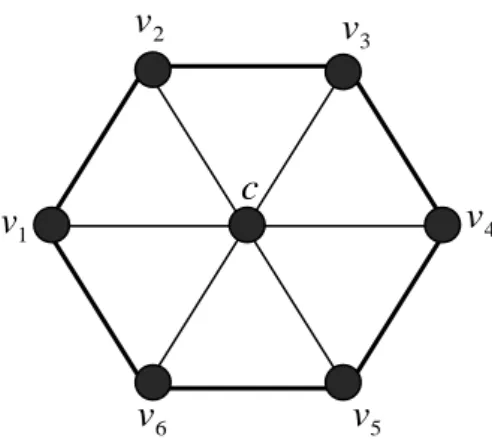
Contoh 2.7
Gambar 2.7. Graf Roda
Berdasarkan hasil penelitian Buczkowski dkk. pada tahun 2003, diperoleh dimensi metrik dari graf roda Wn. Dimensi metrik dari graf roda jika
dan adalah ⌊ ⌋. Untuk dan diperoleh dimensi metriknya .
1 v 5 v 4 v 3 v 6 v 2 v c 4 v 5 v 1 v v2 3 v 6 v
Definisi 2.9 Sisi pendant adalah sebuah sisi yang terkait (incident) dengan titik ujung (pendant) pada graf .
Definisi 2.10 Graf Helm adalah graf terhubung berorder dan
berukuran yang dikonstruksi dari graf roda dengan menambahkan sisi
pendant pada setiap titik pada lingkaran .
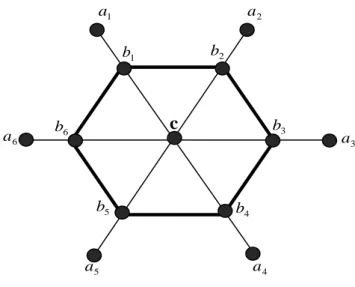
Contoh 2.8
Gambar 2.8. Graf Helm 2.3 Dimensi Metrik
Pada sub bab ini dibahas tentang istilah-istilah yang berkaitan dengan dimensi metrik dari suatu graf.
Misalkan adalah suatu graf terhubung sederhana, dan
.
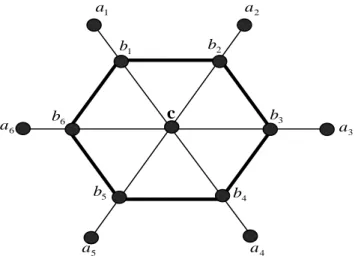
Definisi 2.11 Representasi dari terhadap adalah pasangan -tuple yaitu ( ) 1 a a2 4 a 3 a 5 a 6 a 1 b b2 3 b 4 b 5 b 6 b c
Definisi 2.12 Himpunan merupakan himpunan penentu pada graf jika titik-titik pada graf mempunyai representasi yang berbeda terhadap .
Definisi 2.13 Himpunan penentu yang memiliki anggota (kardinalitas) yang minimum disebut himpunan penentu (resolving set) minimum pada graf
Definisi 2.14 Anggota-anggota pada himpunan penentu minimum disebut basis. Definisi 2.15 Dimensi metrik dari dinotasikan dengan yang menyatakan jumlah anggota dari basis.
Contoh 2.9
Gambar 2.9. Graf
Misal dipilih { } , maka representasi titik-titik di adalah sebagai berikut : ( ) ( ) ( ) ( ) ( ) 1 v v2 3 v 4 v c
Karena representasi setiap titik di berbeda, maka merupakan himpunan penentu bagi Selain graf juga mempunyai himpunan penentu yang lain, yaitu { } merupakan himpunan penentu karena representasi
setiap titik di berbeda, yaitu :
( ) ( ) ( ) ( ) ( )
Akan tetapi jika dengan maka bukan himpunan penentu bagi . Karena setiap titik di mempunyai derajat lebih besar 3, maka setidaknya untuk setiap titik memiliki 3 titik tetangga.
Dengan demikian, merupakan himpunan penentu minimum bagi Jadi,
BAB III
HASIL DAN PEMBAHASAN
Pada bab ini dibahas tentang hasil penelitian penulis dan buktinya serta beberapa hasil peneliti lain yang terkait dengan kajian penulis.
Beberapa peneliti terdahulu menemukan dimensi metrik dari beberapa jenis graf, antara lain graf roda dan graf lingkaran. Berdasarkan hasil penelitian Buczkowski dkk, pada tahun 2003, dimensi metrik dari graf roda untuk
dan adalah ⌊ ⌋, sedangkan untuk dan adalah .
3.1 Graf Helm
Pada sub bab ini dibahas definisi himpunan titik dan himpunan sisi serta jarak setiap titik pada graf helm .
Contoh 3.1
Gambar 3.1 Graf Helm .
1 a a2 4 a 3 a 5 a 6 a 1 b b2 3 b 4 b 5 b 6 b c
Berdasarkan Gambar 3.1, diketahui himpunan titik dan himpunan sisi pada graf helm yaitu :
{ }
{ } { }
Berdasarkan definisi himpunan titik dan himpunan sisi graf helm
tersebut, diperoleh beberapa sifat yang terkait dengan jarak titik - titik pada graf helm sebagai berikut :
1. 2. 3. ( ) { 4. ( ) { 5. ( ) {
3.2 Dimensi Metrik Graf Helm
Pada sub bab ini dibahas tentang penentuan dimensi metrik graf helm beserta pembuktian dimensi metrik graf helm.
Lemma 1
Misalkan merupakan graf helm dengann 3, makadim( ) > 1.
Bukti:
Diketahui bahwa banyaknya titik pada adalah , di mana terdapat 1 titik berderajat , titik berderajat 1 dan titik berderajat 4.
Misal, dipilih { } dengan maka terdapat 3 kemungkinan, yaitu
dan
i. jika , maka bertetangga dengan titik lainnya,
sehingga Akibatnya,
(terdapat nilai representasi yang sama). ii. jika , maka untuk suatu ,
sehingga
Akibatnya, (terdapat nilai representasi
yang sama).
iii. jika , maka untuk suatu , ,
sehingga Akibatnya, (terdapat nilai representasi yang sama).
Dengan demikian, jika { } dengan maka bukan himpunan penentu. Akibatnya,
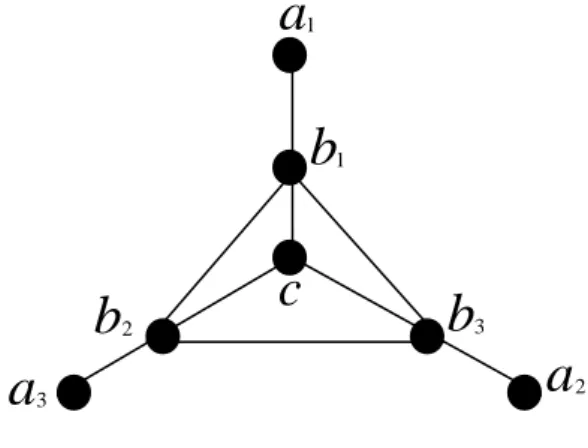
Teorema 1 Dimensi metrik graf helm adalah 3.
Bukti:
Graf helm digambarkan sebagai berikut :
Gambar 3.2. Graf helm
Berdasarkan Lemma 1 Selanjutnya akan ditunjukkan bahwa
dengan jalan akan dibuktikan bahwa jika maka bukan himpunan penentu. Untuk itu, dibuktikan 6 kasus berikut .
Kasus 1. Untuk { } diperoleh representasi titik dan terhadap adalah
( ) ( )
Karena maka { } bukan himpunan penentu bagi Karena posisi { } serupa dengan posisi { } dan
{ }, maka { } dan { } juga bukan himpunan penentu bagi
Kasus 2. Untuk { } diperoleh representasi titik dan terhadap adalah ( )
a
1b
1a
3a
2b
3b
2c
( )
Karena maka { } bukan himpunan penentu bagi Karena posisi { } serupa dengan posisi { } dan { } maka
{ } dan { } juga bukan himpunan penentu bagi
Kasus 3. Untuk { } diperoleh representasi titik dan terhadap adalah
( ) ( )
Karena maka { } bukan himpunan penentu bagi Karena posisi { } serupa dengan posisi { } dan { } maka
{ } dan { } juga bukan himpunan penentu bagi
Kasus 4. Untuk { } diperoleh representasi titik dan terhadap adalah
( ) ( )
Karena maka { } bukan himpunan penentu bagi Karena posisi { } serupa dengan posisi { } dan { }, maka
{ } dan { } juga bukan himpunan penentu bagi
Kasus 5. Untuk { } diperoleh representasi titik dan terhadap adalah
( ) ( )
Karena maka { } bukan himpunan penentu bagi Karena posisi { } serupa dengan posisi { } dan
{ }, maka { } dan { } juga bukan himpunan penentu bagi
Kasus 6. Untuk { } diperoleh representasi titik dan terhadap adalah
( ) ( )
Karena maka { } bukan himpunan penentu bagi Karena posisi { } serupa dengan posisi { }, { },
{ } { } dan { } maka { }, { }, { } { } dan
{ } juga bukan himpunan penentu bagi
Dengan demikian, untuk setiap dengan maka bukan himpunan penentu bagi . Akibatnya, .
Misal { } representasi semua titik pada graf adalah sebagai berikut ; ( ) ( ) ( ) ( ) ( ) ( ) ( )
Karena semua titik memiliki representasi yang berbeda maka
{ } merupakan himpunan penentu bagi
Dengan demikian,
Karena dan maka
Teorema 2. Dimensi metrik graf helm adalah 2.
Bukti :
Graf helm digambarkan sebagai berikut:
Gambar 3.3. Graf helm
Berdasarkan Lemma 1 atau Selanjutnya akan ditunjukkan bahwa
Misal dipilih { } representasi semua titik pada graf adalah sebagai berikut : ( ) ( ) ( ) ( ) ( )
a
1b
1c
b
2a
2b
4a
4a
3b
3( ) ( ) ( ) ( )
Karena semua titik pada graf mempunyai representasi yang berbeda relatif terhadap { }, maka { } merupakan himpunan penentu bagi Dengan demikian, Jadi,
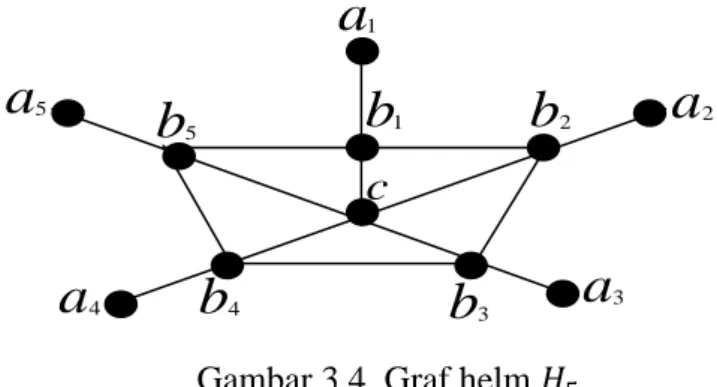
Teorema 3. Dimensi metrik graf helm adalah 2.
Bukti :
Graf helm digambarkan sebagai berikut :
Gambar 3.4. Graf helm
Berdasarkan Lemma 1 atau . Selanjutnya akan ditunjukkan bahwa
Misal dipilih { } representasi semua titik pada graf adalah sebagai berikut : ( ) ( )
a
1b
1c
b
2a
2a
3b
3b
4a
4b
5a
5( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
Karena semua titik pada graf mempunyai representasi yang berbeda relatif terhadap { }, maka { } merupakan himpunan penentu bagi Dengan demikian, Jadi,
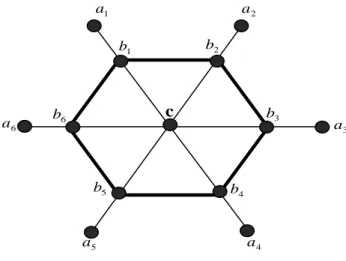
Teorema 4. Dimensi metrik graf helm adalah 3.
Bukti:
Gambar 3.5.Graf helm
1 a a2 4 a 3 a 5 a 6 a 1 b b2 3 b 4 b 5 b 6 b c
Berdasarkan Lemma 1 Selanjutnya akan ditunjukkan bahwa
dengan jalan akan dibuktikan bahwa jika maka bukan himpunan penentu. Untuk itu, dibuktikan 12 kasus berikut.
Kasus 1. Untuk { } diperoleh representasi titik dan terhadap adalah
( ) ( )
Karena maka { }
bukan himpunan penentu bagi Karena posisi { } serupa dengan
{ } { } { } { } dan { } maka { } { } { } { } dan { } juga bukan himpunan penentu bagi
Kasus 2. Untuk { } diperoleh representasi titik dan terhadap adalah
( ) ( )
Karena maka { } bukan himpunan penentu bagi Karena posisi { } serupa dengan posisi { } { } { } { } dan { } juga bukan himpunan penentu bagi
Kasus 3. Untuk { } diperoleh representasi titik dan terhadap adalah
( ) ( )
Karena maka { } bukan himpunan penentu bagi Karena posisi { } serupa dengan posisi { } dan
{ } maka { } dan { } juga bukan himpunan penentu bagi Kasus 4. Untuk { } diperoleh representasi titik dan terhadap adalah
( ) ( )
Karena maka { } bukan himpunan penentu bagi Karena posisi { } serupa dengan posisi { } { } { } { } dan { } maka { } { } { } { } { } juga bukan himpunan penentu bagi
Kasus 5. Untuk { } diperoleh representasi titik dan terhadap adalah
( ) ( )
Karena maka { } bukan himpunan penentu bagi Karena posisi { } serupa dengan posisi { } { } { } { } { } { } { } { } { } { } dan
{ } maka { } { } { } { } { } { } { } { } { } { } dan { } juga bukan himpunan penentu bagi Kasus 6. Untuk { } diperoleh representasi titik dan terhadap adalah
( )
Karena maka { } bukan himpunan penentu bagi Karena posisi { } serupa dengan posisi { } { } { } { } { } { } { } { } { } { } dan
{ } maka { } { } { } { } { } { } { } { } { } { } dan { } juga bukan himpunan penentu bagi Kasus 7. Untuk { } diperoleh representasi titik dan terhadap adalah
( ) ( )
Karena maka { } bukan himpunan penentu bagi Karena posisi { } serupa dengan posisi { } { } { } { } dan { } maka { } { } { } { } dan
{ } juga bukan himpunan penentu bagi
Kasus 8. Untuk { } diperoleh representasi titik dan terhadap adalah
( ) ( )
Karena maka { } bukan himpunan penentu bagi Karena posisi { } serupa dengan posisi { } { } { } { } dan { } maka { } { } { } { } dan { } juga bukan himpunan penentu bagi
Kasus 9. Untuk { } diperoleh representasi titik dan terhadap adalah
( ) ( )
Karena maka { } bukan himpunan penentu bagi Karena posisi { } serupa dengan posisi { } { } { } { } dan { } maka { } { } { } { } dan
{ } juga bukan himpunan penentu bagi
Kasus 10. Untuk { } diperoleh representasi titik dan terhadap
adalah
( )
( )
Karena maka { } bukan himpunan
penentu bagi Karena posisi { } serupa dengan posisi { } { } { } { } dan { } maka { } { } { } { } dan
{ } juga bukan himpunan penentu bagi
Kasus 11. Untuk { } diperoleh representasi titik dan terhadap adalah
( ) ( )
Karena maka { } bukan himpunan
{ } { } dan { } maka { } { } { } { } dan
{ } juga bukan himpunan penentu bagi
Kasus 12. Untuk { } diperoleh representasi titik dan terhadap
adalah
( )
( )
Karena maka { } bukan himpunan
penentu bagi Karena posisi { } serupa dengan posisi { } dan
{ } maka { } dan { } juga bukan himpunan penentu bagi
Dengan demikian, untuk setiap dengan maka bukan himpunan penentu bagi Akibatnya,
Misal { } representasi semua titik pada graf adalah sebagai
berikut: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
( )
( ) ( )
( )
Karena semua titik memiliki representasi yang berbeda terhadap { },
maka { } merupakan himpunan penentu bagi dengan demikian,
Karena dan maka
Selanjutnya akan ditunjukkan bahwa ⌊ ⌋ untuk
Untuk tujuan tersebut, pertama akan ditunjukkan bahwa dengan
⌊ ⌋ maka bukan himpunan penentu bagi
Untuk tujuan tersebut, beberapa lemma digunakan sebagai berikut : Lemma 2.
Misalkan dengan ⌊
⌋ dan { } maka bukan
himpunan penentu bagi
Bukti :
Ada dua kemungkinan :
I. Ada dua titik dan
II. Ada titik dan dan { }
Jika kemungkinan I yang benar, maka dan Dengan demikian,
Jika kemungkinan II yang benar, maka
{ } dan { }
Dengan demikian,
Hal ini menunjukkan bahwa bukan himpunan penentu bagi
Lemma 3.
Misalkan dengan ⌊ ⌋ dan { } maka bukan
himpunan penentu bagi
Bukti:
Ada dua kemungkinan :
I. Ada dua titik dan II. Ada titik dan
dan { }
Jika kemungkinan I yang benar, maka dan Dengan demikian,
Jika kemungkinan II yang benar, maka dan { }
Dengan demikian,
Hal ini menunjukkan bahwa bukan himpunan penentu bagi
Lemma 4.
Misalkan dengan dengan dan
Bukti:
Ada empat kemungkinan:
I. Ada dua titik yang mempunyai jarak lebih besar atau sama dengan dua ke titik-titik yang ada pada .
II. Ada dua titik yang memenuhi dua syarat berikut. a. Titik dan mempunyai jarak 1 ke salah satu titik yang ada
pada .
b. Titik dan mempunyai jarak lebih besar atau sama dengan dua ke semua titik yang ada pada kecuali titik yang disebut pada bagian a. III. Ada dua titik yang mempunyai jarak lebih besar
atau sama dengan tiga ke titik-titik yang ada pada .
IV. Ada dua titik yang memenuhi dua syarat berikut. a. Titik dan mempunyai jarak 2 ke salah satu titik yang ada pada .
b. Titik dan mempunyai jarak lebih besar atau sama dengan tiga ke semua titik yang ada pada kecuali titik yang disebut pada bagian a. Jika kemungkinan I yang benar, maka diperoleh dan Dengan argumentasi yang sama dengan sebelumnya, diperoleh juga dan
Jika kemungkinan II yang benar, tanpa mengurangi pembuktian pada bagian ini, dapat dimisalkan bahwa salah satu titik pada yang mempunyai jarak 1 ke dan
adalah atau .
- .Jika titik yang dimaksud adalah maka diperoleh , , { } dan , { }
Lebih lanjut, diperoleh juga ,
, { } dan , { }. Dengan demikian,
- Jika titik yang dimaksud adalah maka diperoleh ,
, { } dan , { }
Lebih lanjut, diperoleh juga , , { } dan , { } Dengan demikian,
Dengan demikian,
Jika kemungkinan III yang benar, maka diperoleh dan Dengan argumentasi yang sama dengan sebelumnya, diperoleh juga dan
Dengan demikian,
Jika kemungkinan IV yang benar, tanpa mengurangi pembuktian pada bagian ini, dapat dimisalkan bahwa salah satu titik pada yang mempunyai jarak 2 ke dan adalah atau .
, { } dan , { }
Lebih lanjut, diperoleh juga ,
, { } dan
, { }. Dengan demikian,
- Jika titik yang dimaksud adalah maka diperoleh ,
, { } dan , { }
Lebih lanjut, diperoleh juga , , { } dan , { }
Dengan demikian,
Hal ini menunjukkan bahwa bukan himpunan penentu bagi
Berdasarkan lemma 2, 3, dan 4, diperoleh teorema berikut.
Teorema 5. Misal dengan ⌊ ⌋ maka bukan himpunan
penentu bagi untuk
Teorema 6. Dim =⌊ ⌋ untuk
Bukti:
Berdasarkan teorema 5 diperoleh ⌊ ⌋ untuk
Untuk tujuan tersebut, pemilihan titik-titik di yang merupakan himpunan penentu bagi dengan ⌊ ⌋ akan dibagi menjadi dua bagian sebagai berikut:
1. Misal pilih { } ⌊ ⌋ berlaku untuk 4 kasus yakni , , , dan
maka diperoleh representasi titik-titik di terhadap sebagai berikut : dan , di mana angka masing-masing berada pada posisi ke.
dan , di mana angka masing-masing berada pada posisi ke.
dan , di mana angka masing-masing berada pada posisi ke- ,
dan , di mana angka masing-masing berada pada posisi ke- ,
di mana angka masing-masing berada pada posisi ke- dan ke- . dan , di mana angka masing-masing berada pada posisi ke.
dan , di mana angka masing-masing berada pada posisi ke.
dan , di mana angka masing-masing berada pada posisi ke- ,
dan , di mana angka masing-masing berada pada posisi ke- ,
dan , di mana angka 2 masing-masing berada pada posisi ke- dan ke-
.
Untuk lebih jelasnya, representasi titik-titik di terhadap akan dibagi menjadi 4 kasus berikut :
Kasus 1. Untuk
⌊ ⌋ representasi titik-titik di sebagai berikut:
Karena setiap titik pada graf dengan memiliki representasi yang berbeda terhadap { } dengan dan
⌊ ⌋, maka merupakan himpunan penentu bagi Jadi, ⌊ ⌋
Kasus 2. Untuk
Misal pilih { } dengan dan
⌊ ⌋ representasi titik-titik di sebagai berikut:
Karena setiap titik pada graf dengan memiliki representasi yang berbeda terhadap { } dengan
Jadi, ⌊ ⌋
Kasus 3. Untuk
Misal pilih { } dengan dan
⌊ ⌋ representasi titik-titik di sebagai berikut:
Karena setiap titik pada graf dengan memiliki representasi yang berbeda terhadap { } dengan dan
⌊ ⌋, maka merupakan himpunan penentu bagi Jadi, ⌊ ⌋
Kasus 4. Untuk
Misal pilih { } dengan dan
⌊ ⌋ representasi titik-titik di sebagai berikut:
Karena setiap titik pada graf dengan memiliki representasi yang berbeda terhadap { } dengan dan
⌊ ⌋, maka merupakan himpunan penentu bagi Jadi, ⌊ ⌋
2. Misal pilih { } dan ⌊ ⌋ berlaku untuk 1 kasus yakni , maka diperoleh representasi titik-titik di terhadap sebagai berikut :
dan , di mana angka masing-masing berada pada posisi ke- .
dan , di mana angka masing-masing berada pada posisi ke- .
di mana angka masing-masing berada pada posisi ke- .
dan , di mana angka masing-masing berada pada posisi ke- .
dan , di mana angka masing-masing berada pada posisi ke- dan ke-
dan , di mana angka masing-masing berada pada posisi ke-
dan , di mana angka masing-masing berada pada posisi -
dan , di mana angka masing-masing berada pada posisi ke- .
dan , di mana angka masing-masing berada pada posisi ke- .
dan , di mana angka masing-masing berada pada posisi ke- dan
ke-
Selanjutnya, untuk maka representasinya adalah
Karena setiap titik pada graf dengan memiliki representasi yang berbeda terhadap { } dan ⌊ ⌋
maka merupakan himpunan penentu bagi Jadi, ⌊ ⌋
Selain dengan cara mendaftarkan representasi semua titik seperti bukti diatas, representasi titik dapat juga ditinjau dari pembagian kasus-kasus sebagai berikut : Kasus 1. Untuk
Misal dipilih { } maka ⌊ ⌋
Akan ditunjukkan bahwa { } dan
⌊ ⌋ adalah himpunan penentu dari
Ambil dengan selanjutnya akan ditunjukkan bahwa
representasi dari dan terhadap berbeda. Pembuktian ini akan dibagi dalam beberapa kasus dan sub kasus.
A. atau
Jika maka ( ) dan ( ) untuk suatu Jadi, jika
maka
Jika maka ( ) dan ( ) untuk suatu Jadi, jika
maka
B. dan
B.1. atau
Jika maka ( ) untuk setiap Hal ini menunjukkan bahwa
Begitu pula jika maka ( ) untuk setiap Hal ini menunjukkan bahwa
B.2. dan
B.2.1. atau
Jika maka Jadi titik yang mungkin mempunyai representasi yang sama dengan adalah atau
karena Namun demikian,
tetapi begitu pula tetapi
. Oleh karena itu, representasi dan begitu pula representasi dan terhadap berbeda.
Jika maka Jadi titik yang mungkin mempunyai representasi yang sama dengan adalah atau
karena Namun demikian,
. Oleh karena itu, representasi dan begitu pula representasi dan terhadap berbeda.
B.2.2. dan
B.2.2.1. atau
Jika maka sehingga titik yang mungkin mempunyai representasi yang sama dengan terhadap adalah dan untuk setiap , dan
, karena Akan tetapi
dan
Oleh karena itu, . Pada sisi lain,
( ) untuk setiap , sedangkan ( )
atau untuk suatu dengan
Oleh karena itu, tidak mempunyai representasi yang sama dengan salah satu untuk dan
Dengan demikian,
Begitu pula, jika maka akan menunjukkan bahwa
B.2.2.2. dan
B.2.2.2.1. dan untuk dan genap.
Tanpa mengurangi berlaku umumnya pembuktian, bisa dimisalkan Karena genap, maka
sedangkan Jadi,
B.2.2.2.2. dan .
Jika ganjil maka , sehingga
tetapi Jika genap, maka dan
ganjil, sehingga
sedangkan
atau Jadi,
B.2.2.2.3. dan .
Jika genap, maka ganjil dan , sehingga tetapi
Oleh karena itu,
B.2.2.2.4. dan untuk dan ganjil.
Tanpa mengurangi berlaku umumnya pembuktian, bisa dimisalkan Karena ganjil, maka
genap sehingga Dapat dilihat bahwa
sedangkan
Jadi,
B.2.2.2.5. dan .
Jika genap maka , sehingga
tetapi Jika ganjil, maka dan
sedangkan
atau Jadi,
B.2.2.2.6. dan .
Jika ganjil, maka genap dan , sehingga tetapi
Oleh karena itu,
Dari keseluruhan kasus dan sub kasus terlihat bahwa untuk setiap
dengan diperoleh Akibatnya, adalah himpunan penentu bagi
Dengan cara yang serupa, hal ini dapat dilakukan untuk empat kasus lainnya, yaitu dan dengan
⌊ ⌋
Karena ⌊ ⌋ dan ⌊ ⌋ maka ⌊ ⌋
Teorema 7. ⌊ ⌋ untuk dan
Bukti:
Berdasarkan teorema 6 diperoleh ⌊ ⌋ serta hasil penelitian Buczkowski dkk, pada tahun 2003, diperoleh ⌊ ⌋ untuk dan
BAB IV
PENUTUP
4.1 Kesimpulan
Berdasarkan hasil yang diperoleh maka dapat disimpulkan bahwa dimensi metrik graf helm adalah
i.
ii. ⌊ ⌋
iii. ⌊ ⌋
4.2 Saran
Bagi yang ingin mengkaji tentang dimensi metrik suatu graf, penulis menyarankan untuk menggunakan program agar memudahkan pencarian dimensi metrik suatu graf tanpa harus mencoba satu persatu titik-titik pada graf tersebut. Selain itu, penulis berharap akan ada yang tertarik untuk mengembangkan graf helm.
DAFTAR PUSTAKA
[1] Buczkowski, P., Chartrand, G., Poisson, C., dan Zhang, P. (2003), ‘On k-
Dimensional Graphs and Their Bases’, Period. Math. Hungar. 46(1), 9-15.
[2] Chartrand, G. dan Lesniak, L. (1986). Graph and Digraph second Edition. California: Wadsworth. Inc.
[3] Chartrand, G., Eroh, L., Johnson, M. dan Oellermann, O. (2000a),
‘Resolvability in Graphs and the Metric Dimension of a Graph’, Discrete
Appl. Math. 105, 99-113.
[4] Chartrand, G. dan Zhang, P. (2005). Introduction to Graph Theory. McGraw-Hill Companies, Inc.
[5] Harary, F. (1969). Graph Teory. Wesley Publishing Company,Inc.
[6] Harary, F. dan Melter, R. (1976), ‘On the Metric Dimension of a Graph’, Ars
Combin. 2, 191 – 195.
[7] Ghofur, Abdul. (2008). Pewarnaan Titik Pada Graf Yang Berkaitan dengan
Sikel. Malang : UIN.Skripsi ,tidak diterbitkan.
[8] Robert F. Bailey and Peter J. Cameron. (2000). “Base size, metric dimension and other invariants of groups and graphs”.
http://www.math.uregina.ca/~bailey/papers/basesize_metdim.pdf. Diakses