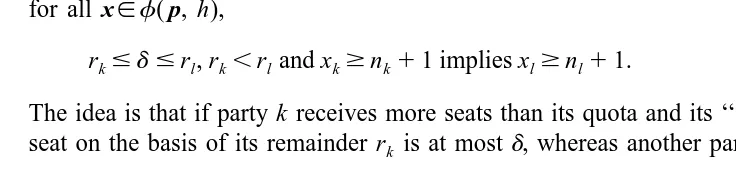Parametric methods of apportionment, rounding and
production
a ,* b
´ Michel Balinski , Victoriano Ramırez
a ´ ´
´
C.N.R.S. and Laboratoire d’Econometrie, Ecole Polytechnique, 1 rue Descartes, 75005 Paris, France b
´
Departamento de Matematica Aplicada, Universidad de Granada, Granada, Spain Received 10 November 1997; received in revised form 30 April 1998; accepted 30 May 1998
Abstract
The class of ‘‘parametric’’ methods of apportionment, of rounding, or for minimizing the variation of production rates in just-in-time production systems is characterized in several different
ways that depend on the underlying qualitative behavior of its solutions. 1999 Elsevier
Science B.V. All rights reserved.
Keywords: Apportionment; Rounding; Just-in-time production; Axiomatic characterization
JEL classification: C44; C69; C79; D71
1. Introduction
The motivation for studying parametric methods is threefold. To begin they play an important role in electoral systems. In Japan the debate on what method should be chosen to apportion the 512 seats of its Diet seems to have concentrated on parametric methods (Balinski, 1993; Oyama, 1991). In Spain the House of Representatives is elected by a system of proportional representation at the level of its provinces. Recent experience has shown that this has strongly and increasingly favored solidly implanted provincial political parties at the expense of the nation-wide parties of similar or smaller size – indeed, so much so that one party, the Catalonian CiU (Convergencia i Union) party, has held the balance of power since 1993, permitting the socialists (Partido
˜
Socialista Obrero Espanol) to govern from 1993 to 1996, and then permitting the right (Partido Popular) to govern since 1996. This has sparked a considerable debate on what should be done that is regularly nourished by electoral data. The data naturally evoked a
desirable property that a method of apportionment should have, which it turns out is met only by the class of parametric methods. More generally, political scientists have for years talked about the ‘‘thresholds’’ of votes that will assure a party of representation in a proportional representation system (see, Lijphart, 1994; Rae, 1971): an answer to this question leads to yet another characterization of parametric methods. This is the ‘‘apportionment’’ part of the title.
The term ‘‘rounding’’ refers to a second motivation. Given a list of real numbers the sum of their roundings may well differ from the rounding of their sum. For example, newspapers usually give the percentages of the votes won by each of a set of competing candidates along with the actual vote totals, and they often fail to add to 100%. Another current example comes with the introduction of the new common European Union currency, the ‘‘euro’’, expected to be introduced on January 1, 1999. There will be a period of transition in which financial transactions in banks will be given in the two currencies of a participating country, the old and the new: e.g., in France, the franc and
´ `
the euro (Ministere de l’Economie et des Finances, 1997). Sums of roundings will often differ from the rounding of the sum, and though each single problem represents practically nothing, the discrepancies summed over all problems could bring significant windfall gains (or losses) due to the sheer number of transactions. Two questions present themselves (Balinski, 1996). The first has been addressed elsewhere (Balinski and Rachev, 1993): if one accepts the idea that sums of percentages may differ from 100%, what ‘‘rule’’ of rounding should be used? The second is of concern here: if one insists that the sums must always be exactly 100%, what ‘‘method’’ should be used (Balinski and Rachev, 1997)? A particularly desirable property for methods of rounding distinguishes the class of parametric methods (called ‘‘stationary’’ in Balinski and Rachev, 1997) among the far wider class of ‘‘divisor’’ methods.
There is an extensive literature on minimizing the variation of production rates in ‘‘just-in-time’’ systems (e.g., Balinski and Shahidi, 1997; Bautista et al., 1996; Kubiak, 1993; Miltenburg, 1989; Steiner and Yeomans, 1993). In one guise – the ‘‘product rate variation’’ problem – it is formally equivalent to the problem of apportionment, though what constitutes a ‘‘good’’ solution must of course be evaluated in the context of the actual problem. A particularly appealing property, often discussed in the literature (when praising the qualities of a particular method or type of solution) – to wit, that an optimal sequence in the production of different products should eventually repeat or cycle – once again elects parametric methods as the only ones that meet the test. This is the third motivation, and the reason for the existence of the word ‘‘production’’ in the title.
The answer to the question, ‘‘why a parametric method?’’ depends on the inherent context of the problem to be treated, but several different fundamental properties, persuasive in different contexts, yield the same methods: they are the subject of this paper.
2. The problem
A problem is defined by any pair ( p, h), where p5( p )j .0, j[S, is a nonzero
isuSu5s. A solution for the problem ( p, h) is a vector of positive integers xdef 5(x )j $0,
j[S satisfying xS5oj[S xj5h.
A method f is a point to set mapping that assigns at least one solution to each problem.
In apportionment, p are the populations of s states or provinces (or the vote totals of political parties) and x the total number of seats each is to be allocated, which must sum to h. The goal is to find solutions that are as ‘‘fair’’ as possible, the unattainable ideal being proportionality.
In rounding, p are data that are to be rounded and x the roundings, whose sum must equal h (e.g. h5100%). The aim here is to find solutions that in some probabilistic sense best ‘‘represent’’ the vectors p.
In the product rate variation or PRV problem, p are the relative demands for s products to be produced (so pS51) and x the cumulative production through period h. Here it is assumed that producing one item of any product requires one period and that
Dp is integer valued for some integer D.0: what is wanted is the order of production in succeeding periods, so a solution is necessary for every value of h, 0#h#D. For the
PRV problem an order of production is sought that best maintains cumulative productions over the D periods that come ‘‘closest’’ to being proportional to the rates of production.
3. Divisor and parametric methods
There is a particularly rich history of methods in the context of apportionment (see Balinski and Young, 1982). Most, though not all, of the specific methods proposed or used belong to a class called ‘‘divisor’’ methods.
A divisor function d is any monotone real valued function defined over the nonnegative integers that satisfies d(k)[[k, k11] for all integers k, and for which there exists no pair of integers a$0 and b$1 with d(a)5a11 and d(b)5b. A d-rounding of
The divisor methodf based on d is
d
f ( p, h)5hx5(x ), jj [S: xj5[lp ] ,j d l .0 chosen so that xS5hj. (1) The seats of the U.S. House of Representatives have been apportioned by the divisor
]]]
method based on d(a)5
œ
a(a11) since 1940; and in 1840 the method based on1 ]
d(a)5a(a11) /(a12) was proposed (among others). An equivalent definition is the min –max condition
d
A parametric method is a divisor method f based on d(k)5k1d for all k, where
def d
0#d #1. It is denoted byf , and for convenience [z]d5[z] . Note that [k]d 05k or k11, and [k]15k or k21. (In terms of the more usual notation, where [z]2 and [z]1 denote the real number z rounded down and up, respectively, to the nearest integer: [z]15[z]2
and [z]05[z] .)1
Various specific parametric methods have been proposed or used for apportionment: ¨
J.Q. Adams suggestedd 50, Condorcet d 50.4, Webster and Sainte-Lagued 50.5, and Jefferson and d’Hondtd 51.
The lemma that follows is trivial to verify.
a b d
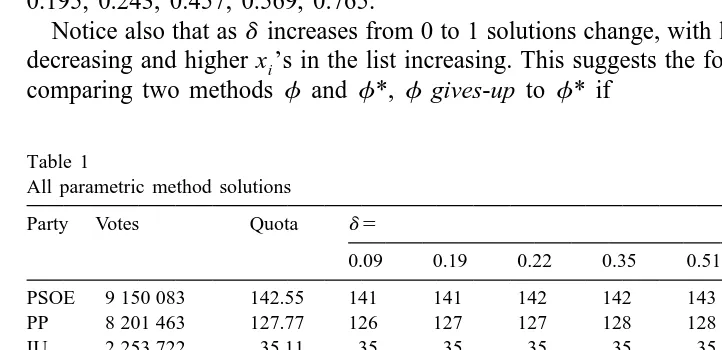
Lemma 1. If x[f ( p, h) and x[f ( p, h) then for alld, a #d #b, x[f ( p, h). Due to lemma 1, Table 1 gives all of the parametric method solutions for the problem ( p, h), where p is the vector of votes received by the respective parties in the 1993 Spanish elections and h5350 is the number of seats in its lower house. The quotas of a problem ( p, h) are given by the vector q5hp /p : it is the exact proportional vector thatS
sums to h. One representative value of d is given in every case; and each pair of adjacent columns are alternate solutions for some one intermediate value ofd. Thus, the
d
first solution in the table is the same for all methods f when 0#d #(1461987 / 7994587)5d1¯0.182872 . . . . Whend 5d1 there is a ‘‘tie’’, the first two solutions both belong, and so on, pair by pair for the remaining solutions of the table. The successive
23
approximate values of d where there is a tie (given to the closest 10 ) are: 0.183, 0.195, 0.243, 0.457, 0.569, 0.765.
Notice also that asd increases from 0 to 1 solutions change, with lower x ’s in the listi
decreasing and higher x ’s in the list increasing. This suggests the following concept: Ini
comparing two methods f andf*, f gives-up to f* if
Table 1
All parametric method solutions
Party Votes Quota d 5
0.09 0.19 0.22 0.35 0.51 0.66 0.88
PSOE 9 150 083 142.55 141 141 142 142 143 143 144
PP 8 201 463 127.77 126 127 127 128 128 129 129
Total 22 467 002 350 350 350 350 350 350 350 350
* *
x[f( p, h), x*[f*( p, h) and pi.p implies xj i#x or xi j$x .j
This definition is well known in the literature (see Balinski and Young, 1982 page 118): it formalizes the idea of one method favoring the bigger as versus the smaller parties. Think of ‘‘gives-up’’ in terms of seats being ‘‘given-up’’ by the smaller parties, as the method is changed fromf tof*, in favor of the bigger parties . . . that are further ‘‘up’’ on the list of parties!
In the context of parametric (as versus the more general divisor) methods this concept permits the characterization given in the following lemma.
a b
Lemma 2. A parametric method f gives-up to another parametric methodf if and only ifa ,b.
a b
Proof. Consider a problem ( p, h), with x[f ( p, h), x*[f ( p, h) and pi.p . Thenj p /(xi i211a)$p /(xj j1a), so a ,b implies p /(xi i211b).p /(xj j1b), meaning that
* *
either xi $x or xi j #x . However, ifj a .b it is easy to construct a problem ( p, h), with
a b
x[f ( p, h), x*[f ( p, h) and pi.p , for which p /(xj i i211a)$p /(xj j1a) and
* *
p /(xi i211b),p /(xj j1b), meaning that either xi #xi21 or xj $xj11. j
d
Thus, the parametric method f that is most favorable to the smaller parties is that with the smallestd, namelyd 50; and that most favorable to the bigger parties is that with the largestd, namelyd 51.
The well known method of Hamilton (sometimes called that of Hare), used for apportionment at various times in various countries including France, Israel, Mexico and the USA, stands, in view of its properties, in opposition to the class of divisor methods. It is easily described: (i) for each i set xi5[q ] ; (ii) then increase by 1 each x thati 2 i
belongs to a set of cardinality h2oi q[ ]i 2 having the largest remainders qi2[q ] .i 2
There may, of course, be several solutions (when some of the remainders are the same).
4. Properties of methods
The three most fundamental properties that a method for any of the three problems should enjoy are as follows. First, scale-invariancy:f( p, h)5f(lp, h) for everyl.0. The problem is the same no matter what scale is used in presenting it. Second,
exactness: if p is integer valued andoi pi5h then p is the unique solution,f( p, h)5p.
If there is no ‘‘problem’’ then there is no problem! Third, anonymity: solutions depend only on the values of the data, i.e., they are independent of the order in which the data is presented. Every method must realize these three demands. In particular, divisor methods as well as Hamilton’s method satisfy these properties.
Arguably the most important ‘‘nonobvious’’ property concerning methods is that they be ‘‘consistent’’. In all of the applications of problems ( p, h) the ‘‘ideal’’ solution is the proportional one. The fundamental underlying property of proportionality is that any part of a proportional solution is itself proportional. To make this precise, if J is some subset
¯
¯ ¯ ¯
and p(J ), and similarly for x, and write x5(x(J ), x(J )) and p5( p(J ), p(J )) (modulo a rearrangement of the order of the indices which, by anonymity, is of no consequence).
¯ ¯
A methodf is consistent if (x(J ), x(J ))[f(( p(J ), p(J )), h) implies x(J )[f( p(J ),
¯ ¯
x ) for all JJ ,S; and if also y(J )[f( p(J ), x ), then ( y(J ), x(J ))J [f(( p(J ), p(J )), h). Any part of a best apportionment, rounding or production schedule should itself be a best apportionment, rounding or production schedule. It is at once evident that every divisor method, so every parametric method, is consistent. On the other hand, simple examples show that Hamilton’s method is not consistent.
Indeed, consistency is a strong property. We begin by deducing several of its consequences.
A methodf is balanced if x[( p, h) and pi5p impliesj uxi2xju#1.
Lemma 3. A consistent, exact and anonymous method is balanced.
Proof. Suppose it were not so. There would then exist x[f( p, h) with (say) p15p25p
whose seats x , x differ by at least 2, (x , x )1 2 1 2 5(x1d, x),d $2.
Suppose d 52k. Then by consistency, (x12k, x)[f(( p, p), 2x12k), contradicting exactness. By the same reasoning, if x[f(( p, . . . , p), h) and x , x are of the samei j
parity, then xi5x . It may therefore be assumed thatj
If f is not balanced, (x12k11, x)[f(( p, p), 2x12k11) for some k$1. Consider
Then ay1(4k2a)z52k(2x12k11), so that a( y2z);2k (mod 4k). This equation always has the solutiona 52k. Moreover, ifa is a solution then so is 4k2a.
If a 52k, then y1z52x12k11. Applying consistency 2k times yields
Invoking consistency once more,
contradicting exactness.
which contradicts exactness. If, on the other hand,a .2k solves the modular equation, a similar construction leads again to a contradiction. j
A method f is increasing if x[f( p, h) implies there exists x9[f( p, h11) with
x9$x. Simple examples show that Hamilton’s method is not increasing: this is the
‘‘Alabama paradox’’.
Lemma 4. A consistent, balanced and anonymous method is increasing.
Proof. To begin note that since f is consistent it is increasing if and only if (x ,1
9 9 9
x )2 [f(( p , p ), h) and (x , x )1 2 1 2 [f(( p , p ), h1 2 11) implies xi$x for ii 51, 2.
9 9 9
Supposef is not increasing: say x1#x121, so that x2$x212. Consider ( y , y , y ,1 2 1
9 9 9
y )2 [f(( p , p , p , p ), 2h1 2 1 2 11).f balanced impliesuy12y1u#1 anduy22y2u#1, so it 9 9
may be assumed that y11y25h and y11y25h11. Two appeals to consistency yields 9 9
(x , x , x , x )1 2 1 2 [f(( p , p , p , p ), 2h1 2 1 2 11). But then by consistency once more (x ,2
9 9 9
x )2 [f(( p , p ), x2 2 21x ): this contradicts the fact that2 f is balanced becauseux22x2u$ 2. j
Lemma 5. If a method f is consistent, balanced and anonymous then (x , x )1 2 [f(( p ,1
p ), x2 11x ) implies2 , for any t$2.
Proof. Sincef is balanced it may be assumed that
(3)
where 0#s,t.
9 9 9 9 9 9
Suppose x 1x ±x 1x , say x 1x ,x 1x . Then sincef is increasing (x , x )#
1 2 1 2 1 2 1 2 1 2
9 9 9 9 9
(x , x ), so x1 2 1#x and if x1 2,x we have x2 211#x , implying x2 11tx25x11tx21s#
9 9
x11tx22t1s, and thus s$t, a contradiction. One concludes that x25x , x2 1,x , and1
¯ 9 9 ¯ 9
sincef is increasing, (x , x )1 2 [fs( p , p ), x1 2 11x2dfor every x1[[x , x ], in particular,1 1
9 9 9 9 9 9
(x111, x )2 [f(( p , p ), x1 2 11x211). But consistency and (3) imply that (x , x1 211)[
9 9
f(( p , p ), x1 2 11x211), so by consistency the first of these solutions may be substituted in (3) to obtain
Repeating one obtains
* 9 * 9 * 9
Corollary. If a methodf is consistent, balanced and anonymous then (x , x )1 2 [f(( p ,1 p ), x2 11x ) implies2
for any integers t , t1 2.0.
Nevertheless, consistency (together with anonymity, exactness and invariancy) is not sufficient to characterize the divisor methods, as shown by the following example. For all k$0 and integer, define
k or k11 if k,z,k11
izi5
H
k if z5k
and consider the method
c( p, h)5hx5(x ), jj [S: xj5ilpji,l .0 chosen so that xS5hj.
It is easy to verify that the methodc meets the properties of scale-invariancy, exactness and anonymity, and it is clearly consistent: but it is not a divisor method.
A method is responsive if
x[f( p, h) and pi.p implies xj i$x .j
Theorem 1 (Balinski and Young, 1982, 1977).fis a divisor method if and only if it is consistent, exact, anonymous, scale-invariant and responsive.
This theorem characterizes the class of divisor methods, and opens the door to a host of characterizations of individual methods, but how and why the parametric methods constitute a class of their own has remained an open question.
5. Cyclic characterization
In the contexts of production scheduling and of rounding a cyclic property seems to be particularly compelling. Suppose, for example, that the relative demands for two
7 18 7 18
] ] ] ]
products are p5(25, 25) and that a methodf yieldsf((25, 25), 5)5(1, 4). Observe that
7 18 ] ]
f((25, 25), 25);f((7, 18), 25)5(7, 18), the last by exactness, and it is evident that the
7 18 ] ]
same order of production should repeat, so it should be true that f((25, 25), 30)5(7, 18)1(1, 4)5(8, 22). And the same remark seems reasonable in the context of rounding. For apportionment, however, the property seems uninteresting: by the very nature of the problem, h is very small as compared with the large values of the vector p.
A method is cyclic if
x[f( p, h) and p integer implies x1p[f( p, h1p ).S
Theorem 2. A divisor method f is parametric if and only if it is cyclic.
Proof. To see that a parametric method is cyclic it suffices by (2) to note that
p p
Assume then thatf is a cyclic divisor method, say f . Suppose it is not parametric, so d(k)5k1d for all k satisfying 0#k,k* but d(k*)5k1d*, withd±d*, sayd .d*.
which is true for l large enough.
d d
f cyclic implies that (k*, k*(lp221)1lp )1 [f ((1, lp221), lp11k*lp ). But2
this is impossible because for large enough l the min–max condition (2) is violated:
lp221 lp221 1
A similar construction handles the cased*.d.j
In the PRV problem, the aim is that the cumulative productions at each period be approximately proportional to the rates of demand. By and large the approach found in the literature is to postulate a measure of disproportionality or of error and so turn the problem into a sequence of minimization problems, one for each period. Most papers impose a measure yielding solutions identical to those given by the method of Hamilton. But this leads to an unfortunate difficulty since Hamilton’s method is not increasing: it is possible for the cumulative production to decrease in going from one period to the next! Thus the main effort has been to devise heuristics or other involved algorithms to guarantee a feasible solution (which may or may not be cyclic). No attention has been given to the idea that perhaps another objective function would do better: indeed, there are infinite numbers of measures of disproportionality that one could use, but little to nothing on why one is better than another. Cyclicity is a powerful reason for choosing to minimize a measure of error whose solutions belong to parametric methods. The fact is
d
1 2
This makes it tempting to chose the parametric method based ond 51 / 2. In fact there is a persuasive reason for this choice: it is the unique parametric method for which the average cumulative production of each product i over the full cycle of D periods is exactly equal to one-half of its total demand Dp (see Balinski and Shahidi, 1997). Soi
1 / 2
f is the unique parametric method that achieves ‘‘proportionality’’ over the entire production cycle.
6. Remainder characterizations
In Spain’s Parliament each province (or state) is allocated a certain number of deputies, on the basis of its population, and within each province parties are allocated seats according to their vote totals within the province by the method of Jefferson
1
(known in Europe as the method of d’Hondt),f . For example, in the 1989 elections the results within the province of Barcelona, which elects 32 deputies, were as in Table 2. Lemma 2 shows that among the parametric methods – and this is true as well among the class of all divisor methods – the method of Jefferson (or d’Hondt) is the most favorable for the large parties, the least favorable for the small parties. In the interest of reducing this advantage, and so obtaining a more ‘‘equitable’’ apportionment, the idea of
1 / 2
¨
using Webster’s method (or Sainte-Lague’s), f , was considered. The example of Table 2 immediately fuelled the arguments against: why should the PP receive 4 seats ‘‘for’’ 3 and a remainder of 0.72 and the CDS 2 ‘‘for’’ 1 and a remainder of 0.60, whereas the CiU only receives 10 ‘‘for’’ 10 and a remainder of 0.74? This suggests two possible properties.
Letting qj5hp /pj S5nj1r , nj j$0 and integer, a methodfrespects remainders atd if for all x[f( p, h),
rk#d #r , rl k,r and xl k$nk11 implies xl$nl11.
The idea is that if party k receives more seats than its quota and its ‘‘claim’’ to an extra seat on the basis of its remainder r is at mostk d, whereas another party l’s ‘‘claim’’ on
the basis of r is at leastl d, then surely party l should also receive more than its quota. It is surprising that this property together with consistency, exactness and anonymity is
d
sufficient to characterize the parametric methodf , with no appeal to the more general and more difficult characterization of divisor methods.
Theorem 3. The unique consistent, exact and anonymous method that respects
d remainders atd is the parametric method f .
d
Since f respects remainders it must be balanced. To see this, suppose the contrary: for some positive p and positive integer x, either (a) (x11, x21)[f(( p, p), 2x), or (b)
Again it suffices to prove that f,f over all 2-dimensional problems. So suppose that for some 2-dimensional problem the statement is false, and let h* be the smallest h
d
where a difference is realized: (x , x )1 2 [f(( p , p ), h*1 2 21)>f (( p , p ), h*1 2 21) and
d
(x111, x )2 [f(( p , p ), h*), but (x1 2 111, x )2 [⁄ f (( p , p ), h*). This means that1 2 p /(x1 11d),p /(x2 21d), so p x1 22p x2 11e 5( p22p )1d withe .0.
Let t , t be positive integers chosen to satisfy the following inequalities1 2
A straightforward calculation shows that r1,d ,r , thus contradicting the fact that2 f respects remainders at d.j
The example of Table 2 invokes a second possible property. A methodfrespects the remainders of the large when for all x[f( p, h),
pi.p , rj i.r , and xj j.q implies xj i.q .i
In this case the concept of respecting remainders takes on a more ‘‘realistic’’ cast (if realism coincides with the weight of the bigger parties that might induce the choice of a method that satisfies the property): if some party receives more seats than its quota ‘‘for’’ a remainder of r, then only the bigger parties who have larger remainders are guaranteed to receive more seats than their quotas (see the CiU in Table 2).
d
Theorem 4. f respects the remainders of the large if and only ifd $12(1 /s).
Proof. Supposed $12(1 /s) and let i, j be a pair satisfying pi.p , rj i.r . If rj j,d,
qj [q ]j 21rj [q ]i 21rj [q ]i 21ri qi
]]]5]]]#]]],]]]5]]],
[q ]j 21d [q ]j 21d [q ]i 21d [q ]i 21d [q ]i 21d
d
showing that f gives [q ]i 211 seats to i before it gives [q ]j 211 seats to j.
˜ ˜
Otherwise, ri.rj.d. Let S5hk[S: rk$dj, and suppose S5S. This implies rS5s21,
˜ ¯ ¯
so rk5d 5121 /s for all k[S, a contradiction. Therefore, S,S and rS$sd .s21,
¯ ¯
s5uSu, so since r is integer valued, rS S$s. But thenok [q ]k d#h, so any apportionment
d ˜
of f must at least round-up every q , kk [S, and the condition is verified. d
On the other hand, ifd ,12(1 /s) thenf does not necessarily respect the remainders of the large. An example suffices to show this. Choose s$3 and e .0 to satisfy e ,minh(121 /s2d) /(112d), 1 /sj, and consider the problem ( q, h) where
d
is the vector of the quotas. r15121 /s1e .r25121 /s, but (1, . . . , 1)[f ( q, s) is the unique apportionment since
1 1 1 1 1
] ] ] ] ]
22 1e 12 12 12 2e 22 1e
s s s s s
]]].]]5 ? ? ? 5]].]]].]]].
d d d d 11d
This means state 1 receives its quota rounded-down, state 2 its quota rounded-up.j
7. Threshold characterizations
apportionment ( p, h), where p represents the votes of parties (as in the example of the previous section). The questions are these: when is a party assured of at least one deputy? and when is a party denied any representation whatsoever? An answer leads to yet other characterizations of parametric methods.
An inequality such as x#[z] is unambiguous when [z] has a unique value. But itd d may have two values: in this case (and in similar cases) take the inequality to mean that
x is less than or equal to both of the values.
Lemma 6. If x$0 is integer and z.0 is real,
x#[z] if and only if xd ,z112d
(and similarly x$[z] if and only if xd .z2d).
Proof. Let z5k1r, where k is integer and 0#r,1.
Suppose, first, thatd±0, 1. If r,d, [z]d5k and z112d 5k111r2d, with21,r2 d ,0. If r.d, [z]d5k11 and z112d 5k111r2d, with 0,r2d ,1. If r5d, [z]d5k
or k11 and z112d 5k11. In each case the statement is verified.
Ifd 50 and r.0, [z]05k11 and z112 5k1r11. Ifd 50 and r50, [z]05k or k11 and z112d 5k11. Again, the statement is verified.
Finally, ifd 51 and r.0, [z]15k and z112d 5k1r. Ifd 51 and r50, [z]15k or k21 and z112 5k. So the statement is verified in all cases. j
d
Theorems 5 and 6 below characterize parametric methodsf in terms of upper and lower bounds on the number of seats each single party i receives given as functions of its percentage of the vote, the number of seats to be distributed, the number of parties in competition and the value ofd[[0, 1]. The upper bound answers the question: when is the party denied any representation whatsoever (or is denied any given total number of seats). The lower bound answers the question: when is the party sure to have at least one seat (or is guaranteed any given total number of seats). And in the ‘‘gaps’’ in between there is a doubt. An example below illustrates how these theorems may be used. Since
d
both characterize the parametric methodf the bounds are the best possible (for some problem at least one inequality must be tight). On the other hand, there may be other upper and lower bound functions that do the job differently.
Theorem 5. The unique consistent and anonymous method f that satisfies pi
]
x[f( p, h) implies xi#
F
(h1ds)pG
for all i[S, (4)S d d
is the parametric method f .
Proof. Supposef is an anonymous and consistent method that satisfies the upper bound
¯
conditions (4), and let pi5p /p .i S d
f is clearly anonymous and consistent. Suppose it did not satisfy (4). Then by the
¯ ¯
¯p ¯p
1 i j
]]h1ds$]]]x 211d$]]x 1dall j[S, or xj1d $p (h¯j 1ds),
i j
with at least one inequality strict (when j5i ), so summing over j[S one deduces d
It remains to show thatf,f . Suppose the statement were true for all 2-dimensional problems (( p , p ), h). Consider x1 2 [f( p, h) for an arbitrary problem. Since f is
Therefore, to establish the theorem it is only necessary to show that f,f overall 2-dimensional problems. Suppose the contrary and let h* be the smallest h where a
d
difference is realized, so that f(( p , p ), h)1 2 ,f (( p , p ), h) for h1 2 ,h*, but not for h5h*. Since f is balanced and so increasing (lemma 4) it may be assumed that (x ,1
d
x )2 [f(( p , p ), h*1 2 21)>f (( p , p ), h*1 2 21) and (x , x1 211)[f(( p , p ), h*), but1 2 d
(x , x1 211)[⁄ f (( p , p ), h*). This means that p /(x1 2 1 11d).p /(x2 21d). By lemma 5
Butf satisfies the upper bound conditions (4), so
p2
Theorem 6. The unique consistent and anonymous method f that satisfies
pi
Proof. The argument parallels that for theorem 5. Let f be an anonymous, consistent
¯
method that satisfies the lower bound conditions (5), and pi5p /p .i S d
f is clearly anonymous and consistent. Suppose it did not satisfy (5). Then for some
¯ ¯
¯p ¯p
1 i j
]]]h2s1ds#]]x 1d#]]]x 211dall j[S, or xj211d #p (h¯j 2s1ds), i j
with at least one inequality strict (when j5i ), so summing over j[S one deduces d
The argument that shows it suffices to prove thatf,f over 2-dimensional problems is the same. So suppose that for some 2-dimensional problem the statement is false, and
d
and since f satisfies the lower bound conditions (5),
p1 p1
]]] ]]]]]]]
x1$
F
p 1tp (x11tx2211dt1d)G
or t,p (x 1d)2p (x 1d),1 2 d 1 2 2 1
a contradiction. j
These theorems generalize the following well known characterizations of the methods of Jefferson and of Adams (Balinski and Young, 1982). The unique anonymous, consistent method that satisfies: x[f( p, h) implies (i) xi$[hp /p ]i S 2 for all i[S is the
1 0
method of Jefferson,f ; and (ii) xi#[hp /p ]i S 1 for all i[S is the method of Adams,f . In these particular cases the result is independent of the number of parties s.
For more of an idea as to the use of these results, consider the example given at the beginning of Section 6: h532 seats are to be distributed among s55 political parties on the basis of their respective percentages of the votes, p /p . With what percentage of thei S
vote is a party guaranteed to obtain at least one seat, no matter how the remaining votes are distributed among the other parties, when the law of the land is the parametric
d
Similarly: with what percentage of the vote is a party guaranteed to obtain no seats, no matter how the remaining votes are distributed among the other parties, when the law of
d
p,1 / 69 or a party has less than 1.45%; and Jefferson when p,1 / 37 or a party has less than 2.70%. (All percentages are reported to the nearest 0.01%.)
When a party has a percentage of the vote that falls in the gap between 1.45% and 1.69% of the vote and h532 seats are to be distributed among s55 parties by the method of Webster the result is uncertain: it may receive either 0 or 1 seat (and similarly for other parametric methods and other gaps).
The interest of these characterizations is that they are sparse and simple: only anonymity and consistency together with the bounds are required, and the proofs are relatively straightforward (and much simpler than those required to characterize the more general class of divisor methods).
References
¨
Balinski, M.L., 1996. How should data be rounded? In: Ruschendorf, L., Schweizer, B., Taylor, M.D. (Eds.), Distributions with Fixed Marginals and Related Topics. Lecture Notes-Monograph Series, vol. 28. Institute of Mathematical Statistics, Hayward, CA, pp. 33–44.
Balinski, M., 1993. The problem with apportionment. Journal of the Operations Research Society of Japan 36, 134–148.
Balinski, M.L., Rachev, S.T., 1997. Rounding proportions: methods of rounding. Mathematical Scientist 22, 1–26.
Balinski, M.L., Rachev, S.T., 1993. Rounding proportions: rules of rounding. Numerical Functional Analysis and Optimization 14, 475–501.
Balinski, M., Shahidi, N., 1997. A simple approach to the product rate variation problem via axiomatics. To appear in Operations Research Letters.
Balinski, M.L., Young, H.P., 1982. Fair Representation: Meeting the Ideal of One Man, One Vote. Yale University Press, New Haven, CT.
Balinski, M.L., Young, H.P., 1977. On Huntington methods of apportionment. SIAM Journal on Applied Mathematics (Part C) 33, 607–618.
Bautista, J., Companys, R., Corominas, A., 1996. A note on the relation between the product rate variation (PRV) problem and the apportionment problem. Journal of the Operational Research Society 47, 1410– 1414.
Kubiak, W., 1993. Minimizing variation of production rates in just-in-time systems: a survey. European Journal of Operational Research 66, 259–271.
Lijphart, A., 1994. Electoral Systems and Party Systems. Oxford University Press, Oxford.
Miltenburg, J., 1989. Level schedules for mixed-model assembly lines in just-in-time production systems. Management Science 35, 192–207.
´
` `
Ministere de l’Economie et des Finances, mai 1997. Le passage a l’euro: les arrondis.
Oyama, T., 1991. On a parametric divisor method for the apportionment problem. Journal of the Operations Research Society of Japan 34, 187–221.
Rae, D.W., 1971. The Political Consequences of Electoral Laws, rev. ed. Yale University Press, New Haven. Steiner, G., Yeomans, S., 1993. Level schedules for mixed-model, just-in-time processes. Management Science