Penjumlahan dan Pengurangan Bilangan Pecahan

(1)

Penjumlahan dan Pengurangan

Bilangan Pecahan

egiatan

K

1.5

Pada kegiatan ini, kalian akan diajak untuk memahami operasi penjumlahan dan pengurangan pada bilangan pecahan. Sebelum melakukan kegiatan ini sebaiknya kalian mengingat kembali bahasan tentang pecahan senilai. Untuk mengawali kegiatan penjumlahan dan pengurangan, perhatikan masalah berikut.

Contoh_1.19

Nina membeli 1 4

kg buah jeruk.

Tetapi mengingat teman-temannya akan datang ke rumah, Ia membeli

lagi 3 4

kg buah jeruk. Berapa kg berat

jeruk keseluruhan?

Penyelesaian Alternatif

Pada contoh tersebut bisa kita buat bentuk matematikanya sebagai berikut.

1

4 + 3

4

= 1 3 4

+

= 4

4

= 1

Jadi, berat buah jeruk yang dibeli oleh Nina adalah 1 kg. Sumber: Kemdikbud

(2)

Contoh_1.20

Karena sedang mendapatkan nilai bagus di sekolah, As’ad membawa sebuah kue dan ingin berbagi kue yang ia miliki kepada Heri dan Sugeng. Heri diberi

1

4

bagian, sedangkan Sugeng mendapatkan 2 5

bagian. Berapa bagian yang

masih dimiliki oleh As’ad setelah diberikan kepada kedua temannya tersebut?

Sisa kue yang masih dimiliki As’ad sama dengan 1 kue utuh dikurangi 1 4

untuk Heri dan 2 5

untuk sugeng. Kita bisa membuat bentuk matematikanya

sebagai berikut.

1 2 1

4 5

 

−_ + _

  =

1 5 2 4 1

20 20

× ×

 

−_ + _

 

= 1 5 8

20 20

 

−_ + _

 

= 1 5 8

20

+

 

− _ _

= 1 13

20

−

= 1 20 13

20

× −

= 20 13

20

−

= 7

20

Jadi, sisa kue yang masih dimiliki As’ad adalah 7 20

(3)

Pada Contoh 1.19 penjumlahan dua bilangan pecahan tersebut sederhana, yaitu dengan cara menjumlahkan kedua pembilangnya, karena kedua penyebut bilangan tersebut sama-sama 4.

Pada Contoh 1.20 ada proses mengubah penyebut menjadi sama sebelum melakukan operasi penjumlahan maupun pengurangan. Karena penyebut berubah, maka pembilang pun ikut berubah agar menjadi pecahan yang ekuivalen.

Beberapa teman kalian mungkin sudah bisa memecahkan masalah tersebut, beberapa juga juga masih belum bisa. Untuk menambah pemahaman kalian tentang penjumlahan dan pengurangan bilangan pecahan mari ikuti kegiatan berikut.

Ayo

Kita Amati

Penjumlahan Bilangan Pecahan

Contoh_1.21

Tentukan hasil dari 3 2

3 1

+

Penjumlahan 3 2

3 1

+ dapat diilustrasikan menggunakan pita pecahan berikut.

3 2

+

3 1

=

3 3

(4)

Perhatikan bahwa 1 objek utuh (keseluruhan) pada pita pecahan di atas tersusun dari 3 bagian yang sama (sepertigaan).

Jadi 3 1

+ 3 2

= 3 3

= 1

3 3

bermakna 3 bagian dari 3 bagian yang sama dan berarti 1 objek utuh.

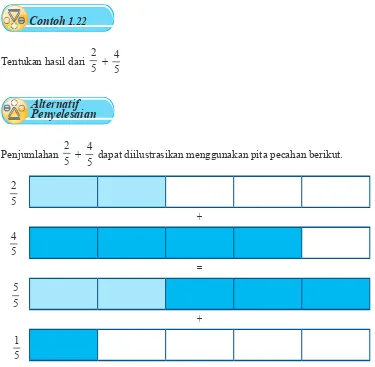
Contoh_1.22

+ 5 4

Penjumlahan 5 2

+ 5 4

dapat diilustrasikan menggunakan pita pecahan berikut.

Gambar 1.27 Pita pecahan +

=

+ 5

2

5 4

5 5

5 1

(5)

Jadi

bermakna 1 objek utuh dan 1 bagian dari 5 bagian yang sama dari 1 objek utuh.

•

5 6

bermakna 6 bagian dari 2 objek utuh (keseluruhan)

Contoh_1.23

Tentukan hasil dari 5

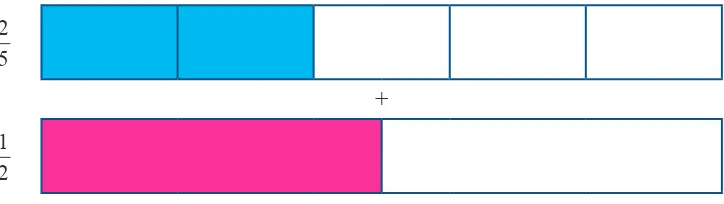
Penjumlahan 5 2

+ 2 1

tidak dapat langsung dijumlahkan karena kedua pecahan

tersebut memiliki bagian keseluruhan yang berbeda.

5 2

+

2 1

Gambar 1.28 Pita pecahan

Untuk menjumlahkan kedua pecahan tersebut kita harus mengubah menjadi

pecahan ekuivalen yang penyebutnya sama. Dalam hal ini 5 2

+ 2 1

dapat ditulis

4

ekuivalen dengan 5 2

, sedangkan 5

10 ekuivalen (senilai)

dengan 2 1

(6)

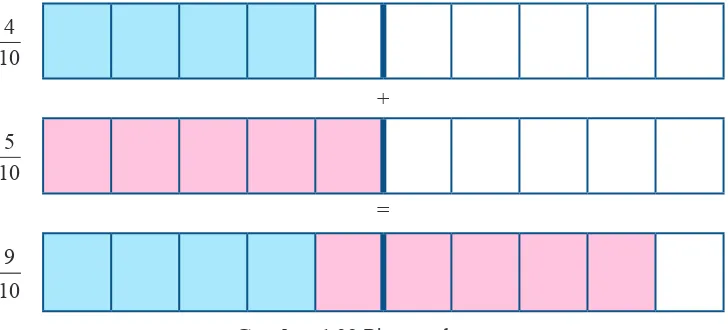
Gambar 1.29 Pita pecahan 10

4

+

10 5

=

9

10

Perhatikan bahwa 1 objek utuh (keseluruhan) pada pita pecahan ini tersusun dari 10 bagian yang sama (sepersepuluhan).

Jadi 5 2

+ 2 1

= 4

10 + 5

10 = 9

10 9

10 bermakna 9 bagian yang sama dari 1 objek utuh (10 bagian yang sama).

Contoh_1.24

− ₅2

Untuk menentukan hasil dari 2 1

− ₅2 kita harus menyamakan penyebutnya terlebih dahulu

2 1

−

5 2

(7)

Dalam hal ini 2 1

− ₅2 dapat ditulis 10

5

− ₁₀4 , karena 10

5

ekuivalen dengan

2 1

, sedangkan 10

4

ekuivalen dengan 5 2

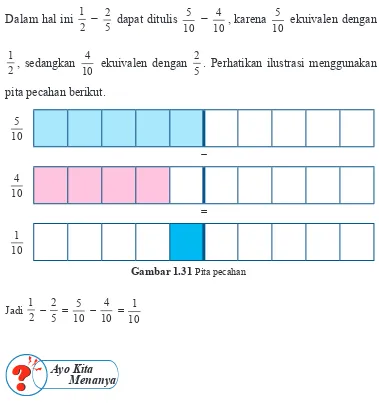
. Perhatikan ilustrasi menggunakan

pita pecahan berikut.

Gambar 1.31 Pita pecahan 10

5

−

10 4

=

10 1

Jadi 2 1

− 5 2

= 10

5 −

10 4

= 10

1

Ayo Kita Menanya

?

Buatlah pertanyaan yang berkaitan hal yang kalian amati. Sebaiknya pertanyaan kalian membuat kalian untuk menggali informasi lebih jauh tentang materi yang sedang kalian pelajari. Contoh pertanyaan:

1. Bagaimana menjumlahkan bilangan pecahan dengan penyebut berbeda?

2. Bagaimana mengurangkan bilangan pecahan dengan penyebut berbeda?

(8)

Ayo Kita

Menggali Informasi +

=₊

Perhatikan bilangan-bilangan berikut.

2

Bilangan-bilangan tersebut dapat dikelompokkan menjadi empat bilangan, yaitu:

1. Pecahan sejati: Pecahan yang pembilangnya kurang dari penyebut dan FPB dari pembilang dan penyebutnya adalah 1.

 Bilangan di atas yang termasuk bilangan pecahan sejati adalah 2

bukan bilangan pecahan sejati karena FPB dari

pembilang dan penyebutnya adalah 2.

 Seperti yang sudah dibahas sebelumnya pecahan 4 2

adalah pecahan

yang ekuivalen atau senilai dengan 2 1 .

 Bilangan pecahan dengan penyebut 100 disebut persen.  Bilangan pecahan dengan penyebut 100 disebut permil.

Misal:

2. Pecahan tidak sejati : Pecahan yang pembilangnya lebih dari penyebut.

Bilangan di atas yang termasuk bilangan pecahan tidak sejati adalah 5 6

(9)

3. Bilangan campuran

 Bilangan campuran yang dimaksud adalah campuran antara bilangan bulat dengan bilangan pecahan.

 Bilangan di atas yang termasuk bilangan campuran adalah 2

 Bilangan campuran bisa diubah menjadi bilangan pecahan dengan cara sebagai berikut

Secara umum, jika ada bilangan campuran c

b a

dengan a dan b adalah

bilangan bulat positif dan c adalah bilangan bulat.

Bisa diubah menjadi pecahan

c

4. Bilangan desimal

 Sistem bilangan desimal bilangan tersusun dari angka 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

 Bilangan yang termasuk bilangan desimal adalah 0,5; 1,25; dan 3.  Bilangan bulat juga termasuk ke dalam bilangan desimal.

(10)

Ayo Kita Menalar

1. Ubahlah bilangan berikut menjadi bilangan pecahan paling sederhana

a. 2,4

b. 75%

2. Urutkan bilangan berikut dari yang terkecil

a. 5 3

, 70%, 0,55, 500‰

b. 6 1

, 350‰, 30%, 0,25

3. Tentukan hasil dari

a. 5 4 1

+ 1 3 2

− 2 6 1

b. 7,5 − 25% + 1 5 2

4. Jika diketahui dua bilangan pecahan b a

dan d c

, dengan a, b, c, dan d

adalah bilangan bulat, b dan d ≠ 0.

a. Nyatakan hasil penjumlahan kedua bilangan pecahan tersebut. Jalaskan langkah kalian mendapatkan hasilnya

b. Nyatakan hasil pengurangan kedua bilangan pecahan tersebut. Jalaskan langkah kalian mendapatkan hasilnya

Ayo Kita Berbagi

(11)

Ayo Kita

!

?

!

?

Berlatih

1.5 A. Soal Pilihan Ganda

1. Sepertiga yang presentasi di awal suatu pertemuan adalah pria. Tidak ada orang yang meninggalkan ruang, 10 orang peserta pria dan 10 orang wanita datang ke pertemuan tersebut. Manakah di antara pernyataan berikut ini yang benar?

a. Lebih banyak peserta pria dari pada wanita dalam pertemuan tersebut. b. Banyak pria sama dengan banyak wanita dalam rapat tersebut. c. Lebih banyak peserta wanita dari pada pria dalam pertemuan tersebut. d. Informasi yang diberikan kurang untuk menyatakan jumlah peserta

pria dan wanita dalam rapat tersebut.

(Sumber: TIMSS 2003 8th-Grade Mathematics Items) 2. Dani mampu menyelesaikan balap lari dalam waktu 49,86 detik.

Sedangkan Sugi mampu menyelesaikan balap lari dalam waktu 52,30 detik. Berapa detik lebih lama, waktu yang dibutuhkan oleh Sugi dibandingkan Dani?

a. 2,44 detik b. 2,54 detik c. 3,56 detik d. 3,76 detik

3. Ketika suatu tol dibangun, rata-rata waktu yang dibutuhkan untuk berkendara dari kota A ke kota B menurun dari 25 menit menjadi 20 menit. Berapa persen penurunan waktu yang dibutuhkan untuk berkendara dari kota A ke kota B?

a. 4% b. 5% c. 20% d. 25%

(Sumber: TIMSS 2003 8th-Grade Mathematics Items) 4. Harga suatu barang, naik 20%. Jika harga sebelum kenaikan adalah

8.000 rupiah, maka harga setelah kenaikan adalah ...

(12)

5. Pada suatu seminar, 3 25

pesertanya adalah perempuan. Jika dinyatakan

dalam persen adalah ...

a. 12% b. 3% c. 0,3% d. 0,12%

(Sumber: TIMSS 2003 8th-Grade Mathematics Items)

B. Soal Uraian

1. Urutkan bilangan berikut dari yang terkecil.

a.

2. Tentukan hasil penjumlahan berikut.

a.

(13)

5. Ibu Sindy membeli dua ekor ayam. Satu ekor beratnya 1 4 1

kg dan

satu ekor lainnya beratnya 2 5 4

kg. Berapa kg berat kedua ekor ayam?

6. Ibu Sundari membeli 1 kg minyak goreng. Di tengah jalan, minyak goreng itu tumpah. Ternyata sisa minyak goreng yang tersisa adalah

3 1

kg. Berapa kg minyak goreng yang tumpah?

7. Setelah Pak Majid pensiun dari pegawai negeri, Ia membeli satu hektare tanah. Pada tanah itu, Ia menanami berbagai jenis bunga seluas

5 4

hektare dan di tanah yang masih kosong Ia mendirikan pondok

pesantren. Berapakah luas tanah tempat pondokan pesantren?

8. Dua karung beras masing-masing beratnya 20 10

Berapa kilogram berat kedua karung beras itu seluruhnya?

9. Mula-mula Ati membeli 4 3

liter minyak goreng. Kemudian, ia

membeli lagi 1 3 2

liter. Berapa liter jumlah minyak goreng yang dibeli

(14)

10. Tiga buah truk mengangkut kelapa sawit. Truk I memuat 4 3 2

ton, truk

II mengangkut 5 4 1

ton, dan truk III mengangkut 4 8 5

ton. Berapa

kuintal kelapa sawit yang dapat diangkut oleh ketiga truk itu?

11. Pak Sani dan 3 orang temannya harus menyelesaikan panen tomatnya dalam minggu ini, karena minggu depan Ia harus mempersiapkan pesta perkawinan putrinya. Agar panen dapat selesai, tiap-tiap mereka

berempat harus dapat memanen 5 3

petak tomat. Berapa petak

keseluruhan tomat?

12. Untuk keperluan menyambut hari Raya Idul Fitri, Bu Zubaidah berencana membuat kue nastar spesial. Berikut ini bahan-bahan yang dibutuhkan untuk membuat kue nastar spesial tersebut.

Bahan yang diperlukan:

• 4 butir kuning telur (125 gram

per butir)

• ½ kg tepung terigu • ½ kg mentega butter atau

margarin

• 100gram gula halus • 1 bungkus vanili (45 gram) • 100 gram keju Gouda/ chedar • 2 butir kuning telur untuk

olesan

• 1 potong kecil kayu manis • 50 gram kismis

Bahan selai nanas kue Nastar:

• 1 buah nanas (0,5 kg)

• 300 gram gula pasir

a. Tentukan total berat bahan seluruhnya yang dibutuhkan Bu Zubaidah untuk membuat kue nastar spesial tersebut.