A R I T M AT I K A
MODUL PEMBINAAN
O L E H
T I M P E M B I N A O L I M P I A D E K O M P U T E R I L M U K O M P U T E R U D A Y A N A
( D I S A J I K A N U N T U K P E S E R T A P E M B I N A A N B I D A N G K O M P U T E R – O S N 2 0 0 9 )
DA F T A R I S I
PENDAHULUAN ... 3
TEORI BILANGAN ... 4
DEVISIBILITAS (KETERBAGIAN) ... 4
BILANGAN PRIMA ... 6
FAKTOR PERSEKUTUAN TERBESAR ... 9
KELIPATAN PERSEKUTUAN TERKECIL ... 13
ARITMATIKA MODULAR ... 14
DIGIT TERAKHIR ... 15
DEFINISI REKURSIF ... 18
DERET ... 19
KOMBINATORIKA ... 22
KONSEP DASAR PENCACAHAN ... 23
PRINSIP PENJUMLAHAN(RULE OF SUM)... 23
PRINSIP PERKALIAN (RULE OF PRODUCT) ... 24
PERMUTASI DAN KOMBINASI ... 25
Permutasi ... 26
Permutasi dari n-objek yang terpilih ... 26
Permutasi sebanyak r dari n objek ... 27
Permutasi Keliling (Circular Permutation) ... 27
Permutasi sebanyak r dari n objek dengan pengembaliam objek yang terpilih .. 29
Permutasi sebanyak r dari n obyek yang tidak seluruhnya dapat dibedakan ... 29
Kombinasi ... 30
Kombinasi sebanyak r dari n objek yang berbeda. ... 32
TEOREMA BINOMIAL DAN MULTINOMIAL ... 35
PIGEONHOLE PRINCIPLE/PERINSIP SARANG MERPATI ... 40
PERINSIP INKLUSI DAN EKSLUSI ... 42
MEMBUAT MODEL ARITMATIKA/MATEMATIKA ... 46
KONTEKS MASALAH ... 48
BERPIKIR SECARA CERDAS ... 49
PENDAHULUAN
Secara umum materi uji tertulis terbagi atas tiga komponen utama: materi uji analitika dan logika, materi uji aritmattika dan materi uji algoritmika. Materi uji analitika dan logika bertujuan untuk menguji potensi akademis peserta namun sedapat mungkin memiliki relevansi yang tinggi dengan problem solving dan elemen penting dalam menguasai pemrograman computer.
Materi aritmatika sebenarnya sejalan dengan analitika dan logika di atas karena soal aritmatika di OSN bidang Informatika bukan sekedar menguji ketrampilan dalam hitung menghitung, tetapi lebih pada cara berpikir yang logis dan analitis namun dengan soal bertemakan aritmatika.
Sedangkan materi algoritmika bertujuan untuk menguji kemampuan peserta dalam memahami dan menyusun suatu algoritma. Aspek-aspek yang terkait dengan pengetahuan dan bahasa pemrograman direduksi seminimal mungkin ke tingkat pseudocode.
Materi Uji Aritmatika
Terdapat enam aspek analitis dalam persoalan aritmatika yang umumnya dijadikan sebagai materi uji pada OSN bidang informatika, yaitu:
1. Memahami sifat-sifat bilangan (Teori Bilangan); 2. Memahami formula rekursif (Sifat Rekursif); 3. Menentukan pola dari sebuah deret bilangan; 4. Eksplorasi dalam masalah kombinatorik;
5. Mampu membentuk model aritmatika/matematika serta melakukan deduksi/ induksi model;
TEORI BILANGAN
DEVISIBILITAS (KETERBAGIAN)
Untuk bilangan a dan b, a ≠ 0, kita katakan a membagi b jika b =ac untuk sebuah bilangan bulat c. Kita tunjukkan dengan menggunakan notasi a|b. Dapat juga dikatakan bahwa b terbagi oleh a. Berikut adalah sifat-sifat turunan dari a|b :
1. Jika a|b, b ≠ 0, maka |a| ≤ |b|
2. If a|b and a|c, maka a|αb+βc untuk sembarang bilangan bulat α dan β 3. Jika a|b dan a|b ± c maka a|c
4. a|a (refleksif)
5. Jika a|b dan b|c maka a|c (transitif) 6. Jika a|b dan b|a maka |a| = |b|
Teorema: untuk sembarang bilangan bulat positif a dan b akan ada sebuah pasangan unik (q,r) bilangan bulat positif yang memenuhi
b = aq + r, r < a
Hal ini juga dikenal dengan Algoritma Pembagian. Algoritma Pembagian dapat diperluas untuk bilang bulat lainnya sebagai berikut: untuk sembarang bilangan bulat a dan b, a ≠ 0, akan terdapat pasangan unik (q,r) bilangan bulat sehingga b = aq + r, 0 ≤ r < |a|.
Contoh Soal 1: Buktikan n5− 5n3 + 4n terbagi oleh 120!
Solusi: n5− 5n3 + 4n = n(n2-1)(n2-4)
= n(n-1)(n+1)(n-2)(n+2)
Lima produk persamaan diatas berturut-turut adalah: n – 2, n – 1, n, n + 1, n + 2. jika n {-2, -1, 0, 1, 2} kita dapat katakan bahwa n5− 5n3 + 4n = 0 terpenuhi. Maka untuk n ≤ 3 kita bisa nyatakan:
n5− 5n3 + 4n = n(n-1)(n+1)(n-2)(n+2)
= ⎟⎟
⎠ ⎞ ⎜⎜ ⎝ ⎛ +
= ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ +
5 2 ( 120 n
Untuk n ≤ -3, ambil n = -m, dimana m ≥ 3 akan diperoleh n5− 5n3 + 4n =
⎟⎟ ⎠ ⎞ ⎜⎜
⎝
⎛ +
−
5 2 ( 120 m
jadi berdasarkan persamaan diatas dapat dikatakan bahwa 120| n5− 5n3 + 4n.
Contoh Soal 2: temukan semua bilangan bulat positif n dimana bilangan yang diperoleh dengan menghilangkan digit terakhir n tersebut adalah sebuah pembagi dari n.
Solusi: Ambil b sebagai digit terakhir dari bilangan n dan ambil a sebagai bilangan yanng diperoleh dari menghilang digit terakhir. Maka n = 10a + b. Karena a adalah pembagi n, maka kita bisa nyatakan bahwa a membagi b. Semua bilangan n yang berakhir dengan 0 adalah solusinya. Untuk b ≠ 0 maka a adalah satu digit dan solusi yang mungkin untuk n adalah bilangan-bilangan berikut: 11, 12,. . . , 19, 22, 24, 26, 28, 33, 36, 39, 44, 48, 55, 66, 77, 88 atau 99.
Contoh Soal 3: Misalkan p > 2 adalah bilangan ganjil dan n adalah bilangan bulat positif. Buktikan bahwa
n n
n
p p
p
p
1
)
(
...
2
1
+
+
+
−
terbagi oleh p.Solusi: Misalkan n
p
k= dan perhatikan bahwa k adalah bilangan ganjil. Maka
] ) ( ... ) ( [
)
( − = −1− −2 − + + − −1
+ k k k k
k
d p d
p d d p d p
d . Dengan menjumlahkan
persamaan-persamaan tersebut dari d=1 sampai
2 1
−
= p
d , kita bisa menghasilkan
persamaan
n n
n p p
p
p
1
)
(
...
2
1
+
+
+
−
pada ruas kiri, yang ternyata terbukti bisa dibagi p (terlihat pada ruas kanan).Contoh Soal 4: Temukan semua bilangan bulat positif n yang untuk semua bilangan bulat ganjil a, jika a2 ≤n maka a|n
4 4 8
6 2 2
3 − a + a≤a + a+
a . Maka a3−7a2+4a−4≤0
atau
0 ) 1 ( 4 ) 7 (
2 − + − ≤
a a
a , solusinya adalah a = 1, 3 atau 5. Jika a = 1, maka 12 ≤n≤32 sehingga n∈{1,2,...,8}
Jika a = 3, maka 32 ≤n≤52 dan 1.3|n sehingga n∈{9,12,15,18,21,24} Jika a = 5, maka 52 ≤n≤72 dan 1.3.5|n sehingga n∈{30,45}. Karena itu n∈{1,2,3,4,5,6,7,89,12,15,18,21,24,30,45}
SOAL LATIHAN:
1. Tunjukkan bahwa untuk sembarang bilangan natural n, diantara n2 dan (n+1)2 bisa ditemukan tiga bilangan natural berbeda a, b dan c sehingga a2 + b2 bisa terbagi oleh c.
2. Temukan semua bilangan bulat positif n sehingga 3n−1+5n−1
bisa membagi n
n 5 3 +
BILANGAN PRIMA
Bilangan bulat p > 1 dikatakan prima jika tidak ada bilangan bulat lain d > 1 yang memenuhi d|p. Sembarang bilangan bulat n > 1 mempunya setidaknya satu pembagi prima. Jika n adalah bilangan prima maka pembagi primanya adalah n itu sendiri. Jika n bukan bilangan prima, misalkan a > 1 sebagai pembagi terkecilnya. Selanjutnya n = a.b, dimana 1 < a ≤ b. Jika a bukan bilangan prima maka akan ada a1 dan a2 sehingga a = a1.a2 dengan 1 < a1≤ a2 <a dan a1|n, ini merupakan kontradiksi dari minimalitas a.
Bilangan bulat n > 1 yang bukan merupakan bilangan prima disebut bilangan komposit. Jika n adalah komposit maka n memiliki sebuah pembagi prima yang tidak melebihi n. Sesungguhnya seperti yang telah ditunjukkan diatas, n = a.b, dimana 1 < a ≤ b dan a adalah pembagi terkecil dari n. Maka n > a2 sehingga a ≤ n.
Teorema 1:
Bukti: Asumsikan dengan kontradiksi bahwa hanya ada jumlah terbatas dari bilangan prima: p1 < p2 <...< pm. Misalkan sebuah bilangan P = p1p2...pm+1. Jika P adalah bilangan prima maka P> pm, ini merupakan kontradiksi terhadap maksimalitas dari
m
p . Di lain pihak, jika P adalah komposit maka dia akan memiliki pembagi prima p > 1 yang merupakan salah satu dari p1,p2,...,pm, kita misalkan pk. Ini diikuti dengan
1 ... | 1 2 m +
k p p p
p sedangkan karena pk salah satu dari p1,p2,...,pm, berarti m
k p p p
p | 1 2... ini mengarah ke pk |1. Ini merupakan kontradiksi.
Perhatikan: Bilangan prima terbesar yang diketahui adalah 232582657 – 1. Bilangan itu ditemukan pada 2006 dan memiliki 9808358 digit. Hasil fundamental dari aritmatika menghadapi tantangan terbesarnya, faktorisasi dari bilangan bulat.
Teorema 2:
(Teorema faktorisasi prima) Setiap bilangan bulat n > 1 mempunyai sebuah representasi unik sebagai produk dari bilangan-bilangan prima.
Bukti: Keberadaan presentasi tersebut dapat diperoleh dari cara berikut: Misalkan p1
adalah pembagi prima (faktor) dari n. Jika p1 = n, maka n = p1 adalah faktorisasi prima dari n. Jika p1 < n, maka n= p1r1 dimana r1 > 1. Jika r1 prima maka n= p1p2 dimana
2
p = r1, ini adalah foktorisasi yang diingin dari n (sesuai dengan teorema). Jika r1 adalah komposit maka r1 = p2r2 dimana p2 prima, r2 > 1 sehingga n= p1p2r2. Jika r2 prima maka n= p1p2p3 dimana r2 = p3, dan kita selesai. Jika r2 adalah komposit, maka kita lanjutkan algoritma ini sehingga memperoleh deret bilangan r1 >r2 >...≥1. Setelah
langkah yang terhingga, kita akan memperoleh rk=1 =1 sehingga n= p1p2...pk.
Untuk keunikannya, mari kita asumsikan ada setidaknya satu bilangan bulat positif n sehingga n= p1p2...pk =q1q2...qh dimana p1, p2, ..., pk, q1, q2, ..., qhadalah bilangan-bilangan prima. Terlihat jelas bahwa k≥2 dan h≥2. Misalkan n adalah bilangan minimal yang memenuhi syarat tersebut. Kita menyatakan bahwa pi ≠qj untuk setiap i = 1, 2, …, k, j = 1, 2, …, h. Jika, sebagai contoh, pk =qh = p, maka
1 1 1 1
/
'=n p= p pk− =q qh−
minimalitas n. Asumsikan bahwa p1 adalah faktor prima terkecil dari n dalam representasi diatas. Dengan menerapkan Algoritma Pembagian sebagai berikut:
1 1 1 1 pc r
q = +
2 2 1 2 p c r
q = +
K
h h
h pc r
q = 1 +
Dimana 1≤ri ≤ p1,i=1,K,h. Kita akan peroleh
) (
) )(
( 1 1 1 1 2 2 1
2
1q qh pc r pc r p ch rh
q
n= K = + + K +
Dengan memperluas persamaan ini kita akan memperoleh n= Ap1+r1r2Krh. Dengan mengetahui bahwa n'=r1r2Krh kita peroleh n= p1p2Kpk = Ap1+n'. Dari sini kita dapat ketahui bahwa p1|n' dan n'= p1s1s2Ksi, dimana s1,s2,K,si adalah bilangan prima.
Dari sudut lain, menggunakan faktorisasi dari r1,r2,K,rh kedalam bentuk prima, semua faktor dari ri < p1. Dari n'=r1r2Krh diikuti n’ sudah difaktorkan kedalam bentuk n'=t1t2Ktj dimana ts < p1, s = 1, 2, ..., j. Faktorisasi ini berbeda dari bentuk
i
s s s p
n'= 1 1 2K . Namun n’ < n, ini merupakan kontradiksi dari minimalitas n.
Dari teorema ditas dapat diturunkan bahwa untuk setiap bilangan bulat n > 1 bisa dituliskan secara unik dalam bentuk
k k
p
p
n
α1K
α1
=
Dimana p1, p2, ..., pk adalah bilangan-bilangan prima unik dan α1,α2,K,αk adalah bilangan bulat positif. Representasi ini disebut faktorisasi kanonikal (canonical factorization) dari n.
Contoh Soal 1 : Buktikan bahwa untuk sembarang bilangan bulat n > 1 bilangan
1
4 5+n +
Solusi: Kita peroleh n5+n4+1
=n5 +n4+n3−n3 −n2 −n+n2 +n+1
=n3(n2 +n+1)−n(n2 +n+1)+(n2+n+1)
=( 2 + +1)( 3 − +1)
n n n
n ,
hasil perkalian dari dua bilangan bulat diatas 1. Oleh karena itu n5+n4 +1
bukan bilangan prima.
Contoh Soal 2: Carilah semua bilangan prima a, b, c sehingga ab + bc + ac > abc. Solusi: Misalkan a≤b≤c. Jika a≥3 maka ab + bc + ac > 3bc, sebuah kontradiksi. Karena a adalah bilangan prima, maka ini mengarahkan ke a = 2. Pertidaksamaannya akan menjadi 2b + 2c + bc > 2bc, sehingga:
2 1 1 1+ >
b c
jika b≥5, maka c≥5 dan
5 2 5 1 5 1 1 1 2
1 < + < + =
c
b , ini salah. Jadi solusinya ada untuk
5
≤
b , yaitu:
1. b = 2 dan c bisa sembarang bilang prima 2. b = 3 dan c = 3 atau 5.
CONTOH SOAL:
1. Diberikan p, q dan r bilangan prima dan diberikan n sebuah bilangan bulat positif sehingga
2
r q
pn + n =
Buktikan bahwa n=1.
2. Buktikan pertidaksamaan Bonse p1p2Kpn > pn2+1 untuk n≥4, dimana
K
, 3 , 2 2
1 = p =
p adalah deret menaik dari bilangan-bilangan prima.
FAKTOR PERSEKUTUAN TERBESAR
bulat positif m dan n, elemen maksimal dari himpunan Dm∩Dn disebut faktor persekutuan terbesar (greatest common divisor) dari m dan n, kita menggunakan notasi fpb(m,n).
Pada kasus dimana Dm ∩Dn={1}, kita mengatakan bahwa fpb(m,n)=1 dan kita
nyatakan m dan n adalah relatif prima.
Hal berikut bisa diturunkan secara langsung dari definisi di atas: 1. Jika d = fpb(m,n), m = dm’, n = dn’ maka fpb(m’,n’)=1
2. Jika d = fpb(m,n), m = d’m’’, n = d’n’’ maka fpb(m’’,n’’) = 1 maka d’ = d 3. Jika d’ adalah faktor persekutuan dari m dan n maka d bisa membagi fpb(m,n) 4. Jika
k
k
p
p
m
α1K
α1
=
,k
k
p
p
n
β1K
β1
=
,k i
i i i
i,β ≥0,α +β ≥1, =1,2,K,
α , maka
) , min( )
, min( 1
1 1
)
,
(
k kk
p
p
n
m
fpb
=
α βK
α β .5. Jika m = nq + r maka fpb(m,n) = fpb(n,r)
Mari kita buktikan poin 5. Misalkan d = fpb(m,n) dan d’ = fpb(n,r). Karena d|m dan d|n diikuti d|r. Karena d|d’. Kebalikannya dari d’|n dan d’|r diikuti oleh d’|m, jadi d’|d. Oleh karena itu d = d’.
Sebuah algoritma yang berguna untuk menemukan faktor persekutuan terbesar dari dua bilangan bulat positif adalah Algoritma Euclidean. Ini berisi penerapan berulang dari Algoritma Pembagian:
n r r nq
m= 1+ 1,1≤ 1 <
1 2 2 2
1q r,1 r r
r
n= + ≤ <
1 1
2 − ,1 −
− = k k + k ≤ k < k
k r q r r r
r
0 , 1 1 1
1 = + + + + =
− k k k k
k rq r r
r
Rantai persamaan ini adalah terhingga karena n>r1 >r2 >K>rk.
Sisa bagi yang tidak nol, rk, adalah faktor persekutuan terbesar dari m dan n. Sebenarnya dengan menggunakan aturan 5) diatas kita dapatkan
k k
k r r
r fpb r r fpb r n fpb n m
fpb( , )= ( , 1)= (1, 2)=K= ( −1, )=
Proposisi 1: Untuk bilangan bulat positif m dan n, terdapat bilangan bulat a dan b sehingga am +bn = fpb(m,n).
Bukti: Dari Algoritma Euclidian bisa diperoleh
K
), 1
(
, 2 2 1 2
1
1 m nq r mq n q q
r = − =− + +
Secara umum ri =mαi−nβi,i=1,K,k. Karenari+1 =ri−1−riqi+1, sehingga
⎩ ⎨ ⎧ − = − = + − + + − + i i i i i i i i q q β β β α α α 1 1 1 1 1 1
i = 2, ..., k-1. Akhirnya, kita mendapatkan bahwa fpb(m,n)=rk =αkm+βkn.
Kita bisa mendefinikan faktor persekutuan terbesar dari beberapa bilangan bulat positif m1,m2,K,ms dengan memperhatikan:
) , ( , ), , ( ), ,
( 1 2 2 1 3 1 2
1 fpb m m d fpb d m ds fpb ds ms
d = = K − = −
Bilangan bulat d =ds−1 disebut faktor persekutuan terbesar dari m1,m2,K,msdan
dinotasikan sebagai fpb(m1,m2,K,ms)
Contoh Soal 1: Temukan faktor persekutuan terkecil dari bilangan-bilangan yang memenuhi =23n+36n+2 +56n+2
n
A .dimana n = 0, 1, ..., 1999. Solusi: Kita dapatkan A0 =1+9+25=35=5.7
Menggunakan kongruen mod 5 kita peroleh
) 5 (mod ) 1 ( 2 3
23 + 6 +2 ≡ 3 + − 3 +1
≡ n n n n
n
Sebaliknya, n n n n
A =8 +9.93 +25.253
n
n 3
3 4.4
2 . 2
1+ +
≡
n n 4.64 8
. 2 1+ +
≡
n n
1 . 4 1 . 2 1+ +
≡
) 7 (mod 0
≡
Oleh sebab 7 dapat membagi An, untuk semua bilangan bulat n≥0. Akibatnya, faktor persekutuan terbesar dari bilangan Ao,A1,K,A1999 adalah 7.
Contoh Soal 2: Temukan semua tripel bilangan bulat positif (a, b, c) sehingga 3
3 3 b c
a + + bisa dibagi a2b+b2c+c2a
Solusi: Biarkan g sebagai faktor persekutuan terbesar dari a dan b. Maka g3 bisa membagi a2b jadi g3 bisa membagi a3 +b3+c3dan g bisa membagi c. Dengan ini, fpb dari setiap pasangan (dua bilangan) dari a, b, c adalah fpb untuk ketiganya.
Biarkan (l,m,n) = (a/g, b/g, c/g). Maka (l, m, n) adalah tripel yang memenuhi kondisi permasalahan, dan l, m, n merupakan pasangan-pasangan relatif prima. Karena l2, m2 dan n2 semuanya bisa membagi l3+m3+n3, sekarang kita mempunyai
3 3 3 2 2 2
|l m n n
m
l + +
Asumsikan tanpa kehilangan arti umumnya bahwa l≥m≥n. Kita akan mempunyai 3
3 3 3 2 2
2m n l m n 3l
l ≤ + + ≤
dan karena itu, m2n2/3≤l
. Karena l2 |(m3+n3)
, kita juga mempunyai 3
3 3 2 4
4n /9 l m n 3m
m ≤ ≤ + ≤
Jika n≥2 maka m≤2.9/24 <2≤n
Jika m≥2 maka l>m karena l dan m relatif prima, jadi m2n2 ≤l3 +m3+1<2l3,
dan l>m2/2, sehingga
1
3 2
4 <l ≤m +
m ,
dan m≤4. Tidaklah sulit untuk melihat bahwa satu-satunya solusi adalah (3, 2, 1).
KELIPATAN PERSEKUTUAN TERKECIL
Berlawanan dengan himpunan Dk yang sudah kita pelajari di sub bahasan sebelumnya, Mk adalah himpunan terhingga bilangan bulat. Untuk bilangan bulat positif s dan t, elemen terkecil dari himpunan Ms∩Mt disebut kelipatan persekutuan terkecil dari s dan t dan dinotasikan sebagai kpk(s,t).
Berikut adalah turunan langsung dari definisi tersebut: 1. Jika m = kpk(s,t), m = ss’ = tt’, maka fpb(s’,t’) = 1.
2. Jika m’ adalah kelipatan persekutuan dari s dan t dan m’ = ss’ = tt’, fpb(s’,t’)=1, maka m’=m
3. Jika m’ adalah kelipatan persekutuan dari s dan t maka m|m’.
4. Jika p k
k p
p
p
s
α1K
α1
=
dan p kk p
p
p
t
β1K
β1
=
, αi,βi ≥0,αi +βi ≥1, i= 1, ..., k, maka
) max( )
max( 1
1 1
) ,
( k k
k
p p
t s
kpk = αβ K αβ
Hal berikut menunjukkan hubungan antara fpb dengan kpk.
5. Untuk setiap bilangan bulat positif m dan n akan memenuhi hubungan berikut:
) , ( ). ,
(m n kpk m n fpb
ARITMATIKA MODULAR
Untuk bilangan bulat a, b dan n, dimana n ≠ 0. Kita katakan a dan b adalah modulo kongruen n jika n|a-b. Kita notasikan dengan a ≡ b (mod n). Relasi ≡ pada himpunan Z bilangan bulat disebut relasi kongruen. Jika m tidak bisa membagi a – b, maka kita katakan bilangan bulat a dan b bukan modulo kongruen n. Berikut pernyataan yang bisa diturunkan dari hal ini:
1. a ≡ a (mod n) (reflektif)
2. jika a ≡ b (mod n) dan b ≡ c (mod n), maka a ≡ c (mod n) (transitif) 3. jika a ≡ b (mod n) maka b ≡ a (mod n)
4. Jika a ≡ b (mod n) dan c ≡ d (mod n) maka a+c ≡ b+d (mod n) dan a – c ≡ b – d (mod n)
5. Jika a ≡ b (mod n) maka untuk sembarang bilangan bulat k, ka ≡ kb (mod n) 6. Jika a ≡ b (mod n) dan c ≡ d (mod n) maka ac ≡ bd (mod n)
Teorema 1: Untuk a, b, n bilangan bulat, n≠0 sehingga a=nq1+r1, b=nq2+r2, 1
0≤r ,rs ≤|n|. Maka a≡b(modn) jika dan hanya jika r1 =r2.
Bukti: Karena a−b=n(q1−q2)+(r1−r2), ini menghasilkan n|a-b jika dan hanya
jika n|r1−r2. Dengan memperhatikan bahwa |r1−r2 |<|n|, kita akan peroleh n|r1−r2 jika dan hanya jika r1 =r2.
Contoh Soal: Temukan sebuah bilangan bulat n dengan 100 ≤ n ≤ 1997 sehingga n membagi 2n +2
Solusi: Perhatikan bahwa 2 mebagi 2n +2
untuk semua n. Selain itu 2 juga membagi
2 2n +
jika dan hanya jika n ≡ 6 (mod 10), dan 43 membagi 2n +2
DIGIT TERAKHIR
Misalkan anan-1....a0 adalah representasi desimal dari bilangan bulat positif N. Digit terakhir N adalah l(N) = a0 dan untuk k ≥ 2, k digit terakhir adalah lk(N) = ak-1 ... a0. Konsep sederhana ini muncul dalam berbagai situasi. Sangat berguna mengetahui digit terakhir dari kn, dimana untuk k = 2, 3, ..., 9:
Dan jelas bahwa jika l(N)=0 maka ln(Nn) = 0...0 (0 sebanyak n) dan jika l(N) = 1 maka l(Nn) = 1 untuk semua n ≥ 2.
Contoh Soal 1: Apakah digit terakhir dari (. . . (((77)7)7) . . .7)? Ada 1001 buah 7 dalam formula tersebut.
Solusi: Digit terakhir dari bilangan desimal adalah sisa modulo 10. Sekarang 72 = 49 ≡ -1 (mod 10). Sehingga 77 = (72)3.7 ≡ -7 (mod 10) dan
(77)7≡ (-7)7≡ -(77) ≡ -(-7) ≡ 7 (mod 10)
Melanjutkan proses tersebut kita akan melihat bahwa ((77)7)7) ≡ 7 (mod 10) dan secara umum (…(((77)7)7)….7) ≡ ± 7 (mod 10), dimana tandanya + jika jumlah kemunculan 7 adalah ganjil dan – jika kemunculan 7 adalah genap. Jadi untuk pertanyaan diatas jawabannya adalah 7
Solusi: Dengan mengubah n=1,2,3…dst, perhitungan 2n menghasilkan deret 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, dst. Amati angka terakhir dari setiap bilangan, kita mendapatkan perulangan dari 6 – 2 – 4 – 8 pada n mod 4 = 0, 1, 2, 3. Jadi jika n=2003, diperoleh 2003 mod 4 = 3, yaitu memiliki digit terakhir 8.
Contoh Soal 3: Ketiga digit awal dari hasil perkalian 22002 x 52005 jika dijumlahkan adalah?
Solusi: Ini juga tidak mungkin dihitung manual. Perhatikan bilangan dasarnya 2 dan 5 yang jika dikalikan menjadi 10. Karena setiap pasang faktor 2 dan 5 menghasilkan 10 berarti hanya menambah 0 di digit terkanan. Ada 2002 pasang faktorfaktor tersebutg sehingga 22002 x 52005 = 53 x 102002= 125 102002. Penjumlahan tiga digit awal 1+2+5=8
Contoh Soal4: Hitunglah (80! x 38!) /(77! x 40!).
Solusi: Menggunakan sifat sbb untuk a dan b bulat positif, a > b, maka a!/b! = a.(a – 1).(a – 2)…(b + 1). Maka
(80! x 38!) /(77! x 40!) = (80!/77!) / (40!/38!) = (80x79x78) / (40x39) = (80/40) x (78/39) x 79 = 2 x 2 x 79 = 316 yang dapat dihitung tanpa kalkulator.
Contoh Soal 5: Jika n dan p adalah dua bilangan bulat, dan n + p berharga ganjil, manakah dari berikut ini bil ganjil?
(A) n – p + 1 (B) np
(E) (p – n)(n – p)
Solusi : A bukan, karena (n+p) adalah ganjil maka dari n dan p salah satu ganjil dan yang lain genap. Selisih antara n dan p pasti ganjil sehingga jika ditambah 1 menjadi genap. B bukan karena perkalian antara suatu bilangan genap dengan bilangan apapun akan menjadi genap.
DEFINISI REKURSIF
Definisi rekursif adalah bagaiman membangun sesuatu dari versi sederhana dari hal yang sama. Definisi rekursif mempunyai dua bagian :
1. Kasus basis (base case) yang tidak tergantung dengan apapun
2. Kasus Kombinasi yang bergantung pada kasus yang lebih sederhana.
Sebagai contoh kita ambil definisi rekursif dari faktorial:
⎩ ⎨ ⎧
> − = =
0 ), 1 ( .
0 , 1 ) (
x x fac x
x x
fac
Kasus basis dari contoh diatas adalah fac(x)=1 untuk x=0 dan kasus kombinasinya adalah f(x) = x.fac(x-1) untuk x >0
Contoh lain adalah deret Fibonacci, yang telah disinggung di bab sebelumnya. Misalkan kita memiliki fungsi fib(n) yang mengembalikan bilangan fibonacci ke-n. Maka dengan cara rekursif dapat kita definisikan bahwa:
⎪ ⎩ ⎪ ⎨ ⎧
> − +
− =
= =
1 ), 2 ( ) 1 (
1 , 1
0 , 0 ) (
n n fib n
fib n n
n fib
Untuk fungsi diatas kasus basisnya ada dua yaitu fib(n) = 0 untuk n=0, dan fib(n) = 1 untuk n=1. Sedangkan kasus kombinasinya adalah fib(n) = fib(n-1) + fib(n-2), n > 1.
Cara tradisional untuk mendefinisikan fungsi Fibonacci adalah dengan menggunakan
∑
dan sudah dianggap sebagai definisi informal dari fungsi Fibonacci.Contoh Soal 1: Jika didefinisikan f(n)=n.f(n-1) untuk setiap n > 0 dan f(0)=1 maka berapakah
Solusi: Fungsi ini adalah fungsi faktorial yang definisikan secara rekursif. Yaitu sama dengan contoh diatas (fungsi fac). Jadi f(10) = 10!, f(7)= 7! Dan f(6) = 6!
Sehingga, 10!/7! = (10.9.8.7.6.5.4.3.2.1)/(7.6.5.4.3.2.1) = 10.9.8 dan (10.9.8) /(6.5.4.3.2.1) = 1
Contoh Soal 2: Jika suatu fungsi didefinisikan f(x, y) = x2-y2 untuk x dan y dua bilangan real.
Maka f(3, f(3, 4)) adalah?
Solusi: f(x, y) = x2-y2 maka f(3, f(3,4) = f(3, 3.3-4.4)
= f(3, -7)
= 3.3 + (-7)(-7)
= 9 - 49
= -40
SOAL LATIHAN:
Jika
⎪ ⎩ ⎪ ⎨ ⎧
> ∈
+ ∈ = =
1 , ),
1 3 (
), 2 / (
1 , 1 ) (
n ganjil n
n f
genap n
n f
n
n
f untuk n bilangan bulat positif n > 0. Berapakah
DERET
Ada dua macam deret yang sering menjadi topik, yaitu deret aritmatika dan deret geometri. Kedua deret ini berbeda dalam hal definisi suku berikutnya terhadap suku sebelumnya.
Deret aritmatika adalah deret bilangan yang selisih suku-suku bersebelahan selalu tetap. Contohnya deret bilangan bulat: ..., -3, -2, -1, 0, 1, 2, 3, .... Misalkan Un melambangkan suku ke n dari deret aritmatika, maka Un-Un-1 =b atau beda antar sukunya. Suku pertama dari deret ini U1 kita misalkan a. Maka akan berlaku hal berikut:
Un = a + (n-1)b
Misalkan Sn adalah jumlah n suku pertama, U1+U2+U3+ ... + Un, berlaku
2 ) (a Un n
Sn= +
dengan kata lain
2
) ) 1 ( 2
( a n b n
Sn= + −
Pembuktian untuk formula Sn ini sudah kita lakukan pada bab sebelumnya.
Selanjutnya kita akan membahas mengenai deret geometri. Deret geometri adalah deret bilangan dimana hasil bagi suku-suku bersebelahan selalu tetap. Contoh deret geometri adalah sebagai berikut: 1, 2, 4, 8, ... Un/Un-1 selalu menghasilkan 2, hal ini kita sebut sebagai rasio r. Maka akan berlaku
Un = arn-1, dan
1 ) 1 (
− − =
r r a Sn
Contoh Soal 1: 12. Diberikan dua deret bilangan
R: 1, 2, 3, 4, 5, 6
S: 2, 5, 8, 11,14, 17
Tunjukkan persamaan yang menunjukkan hubungan antara R dan S?
Solusi: Kita dapat lihat deret tersebut adalah deret aritmatika. Mari kita lihat masing-masing
deret mulai dari deret R. ar = 1 dan br =1, maka Unr = ar +(n-1)br = 1 + (n-1).1 = n.
Sedangkan untuk deret S. as = 2 dan bs = 3, maka Uns = as + (n-1)bs = 2 + (n-1)3 = 3n-1.
KOMBINATORIKA
Kombinatorial adalah cabang matematika untuk menghitung jumlah penyusunan objek-objek tanpa harus mengenumerasi semua kemungkinan susunannya. Kombinatorial merupakan bahasan yang penting dalam matematika diskrit. Blaise Pascal (1623-1662) adalah seorang bangsawan Perancis yang membaktikan seluruh hidupnya untuk matematika, bahkan bisa disebut matematikawan terbaik pada jamannya. Pada usia 17 tahun ia sudah menulis essai tentang kerucut. Belum sampai usia 20 tahun ia menjadi salah seorang yang pertama menemukan perhitungandalam mekanika. Ia meninggal di usia 39 tahun, tetapi sebelumnya telah bekerja sama dengan Pierre de Fermat meletakkan dasar-dasar probabilitas. Dari konsep-konsep kombinatorik Paskal menyusun segitiga Pascal yang digunakan untuk menghitung banyaknya cara memilih r unsur dari n unsur yang ada. Selain itu, Pascal juga tertarik pada probabilitas dari kejadian-kejadian yang jarang muncul. Menjelang akhir hidupnya ia berharap dapat mencari tahu probabilitas dari kejadian-kejadian semacam ini. Sekarang kita menggunakan probabilitas yang Pascal kembangkan untuk mempelajari keajaiban-keajaiban yang jarang muncul dari berbagai macam kejadian, seperti kecelakaan, kerusakan mesin, dan kerusakan akibat cuaca buruk. Meskipun sebagai manusia kita tidak tahu pasti apa yang akan terjadi nanti namun ahli-ahli statistika dapat mengestimasi kemungkinan dari kejadian-kejadian tertentu yang akan terjadi menggunakan probabilitas (teori peluang/kemungkinan). Banyak dari para ahli matematika yang pertama kali mengembangkan teori probabilitas sebenarnya adalah orang-orang yang menyukai judi. Mereka berharap bahwa pemahaman mengenai probabilitas dapat meningkatkan peluang mereka untuk memenangkan permainan yang mereka lakukan.
didasarkan kepada peluang yang mungkin terjadi diluar jangkauan kita. Matematika dapat digunakan untuk memprediksi peluang yang mungkin dari kejadian-kejadian tersebut. Mungkin juga ahli-ahli ekonomi menggunakan statistika untuk membantu mereka memprediksikan perubahan-perubahan dalam pasar-pasar uang atau bursa saham, yang dapat menyebabkan perolehan ataupun kehilangan uang dalam jumlah yang sangat besar. Inilah yang menyebabkan konsep kombinatorika penting dalam penalaran matematika.
KONSEP DASAR PENCACAHAN
Dalam kehidupan sehari-hari kita sering dihadapkan dengan masalah penghitungan. Misalnya ada berapa cara yang dapat dilakukan pada saat memasukan sebuah kelereng ke dalam sebuah kantung, begitu pula apabila memasukan beberapa kelereng ke dalam beberapa kantung, berapa cara memilih wakil dari bebarapa kelompok mahasiswa dan masih banyak lagi kasus yang lain. Salah satu prinsip dasar yang mendasari perkembangan probabilitas terutama yang terkait dengan masalah penghitungan adalah konsep dasar pencacahan. Ada dua perinsip dasar pada konsep dasar pencacahan yaitu prinsip penjumlahan dan prinsip perkalian
PRINSIP PENJUMLAHAN (RULE OF SUM)
Apabila kita mempunyai dua buah himpunan yang tidak memiliki unsur bersama, maka jumlah anggota dari dua himpunan ini adalah jumlah dari banyak anggota dari masing-masing himpunan.
Definisi 5.1.
Jika ada sebanyak m cara untuk memilih benda jenis A dan ada n cara untuk memilih benda jenis B, maka total ada sebanyak n+m cara untuk memilih benda jenis A atau benda jenis B dengan A∩B =φ. Perinsip ini disebut sebagai Perinsip Penjumlahan.
Secara umum apabila dalam suatu pelaksanaan tugas diperoleh hal berikut:
- Jika tugas I dilaksanakan dengan m1 cara
Dengan syarat tugas yang diberikan harus disjoint (saling asing), maka seluruh tugas dapat dilaksanakan dengan m1 +m2 +...+mk.
Contoh 5.2.
Misalkan ada tujuh kuliah yang berbeda yang ditawarkan di pagi hari dan lima kuliah yang berbeda yang ditawarkan di siang hari. Maka ada sebanyak 7+5=12 pilihan bagi mahasiswa yang akan mengambil hanya satu kuliah saja.
PRINSIP PERKALIAN (RULE OF PRODUCT)
Apabila dalam suatu prosedur (urutan pengerjaan) yang dapat dilakukan dalam dua langkah yang saling lepas (tidak bergantung). Jika langkah pertama ada sebanyak m cara dan langkah kedua dapat dilakukan dengan n cara maka prosedur tersebut dapat dilakukan dengan m×n cara.
Definisi 5.3.
Jika ada m cara untuk memilih benda jenis A dan untuk setiap pilihan tersebut ada n cara untuk memilih benda jenis B, maka total ada sebanyak m×n cara untuk memilih satu benda jenis A dan satu jenis benda B. Perinsip ini disebut Perinsip Perkalian.
Secara umum apabila diberikan suatu langkah yang terdiri dari beberapa tugas misalkan saja sampai sebanyak k tugas dengan ketentuan berikut:
- Jika tugas I dilaksanakan dengan m1 cara
- Jika tugas II dilaksanakan dengan m2 cara
M M
- Jika tugas ke k dilaksanakan dengan mk cara
Dengan pelaksanaan yang saling lepas antara tugas satu dan tugas yang lain, maka pasangan tugas dalam suatu langkah dapat dilaksanakan dengan m1×m2×...×mk cara.
Contoh 5.4.
macam hidangan (terdiri dari 1 makanan dan 1 minuman) yang dapat disusun adalah sebagai berikut:
9 Langkah pertama, kita memilih makanan yang bisa di lakukan dalam 4 cara
9 Langkah kedua, kita memilih minuman yang bisa dilakukan dalam 3 cara,
Sehingga banyaknya macam hiadangan adalah sebanyak 4×3=12 cara.
PERMUTASI DAN KOMBINASI
Secara garis besar persoalan pencacahan dapat dikelompokkan sebagai berikut:
a. Pencacahan pola terurut dari beberapa benda, dalam hal ini susunan (urutan) dari benda tersebut sangat diperhatikan, jadi ab≠ba.
b. Pencacahan pola yang tak terurut dari beberapa benda, dalam hal ini susunan (urutan) dari benda tersebut tidak diperhatikan, jadi ab=ba.
Berdasarkan cara pengambilan, kelompok ini terbagi lagi ke dalam dua bagian yaitu:
- Pengambilan dengan pemgembalian/pengulangan.
- Pengambilan tanpa pengembalian/tanpa pengulangan
PERMUTASI
Dalam berapa cara tiga buah buku A, B, C yang berbeda dapat disusun secara teratur di atas sebuah meja? Cara yang paling sederhana untuk menjawab pertanyaan ini adalah dengan mencatat semua susunan yang mungkin dapat dibuat dengan bantuan metode ruang. Persoalan yang dihadapi sebetulnya sama saja dengan mengisikan 3 ruang kosong dengan buku A, B, C. Ketiga ruang tersebut dapat digambarkan sebagai berikut.
3 2 1
Bawah tengah atas
Jika ruang pertama diisi dengan salah satu dari ketiga buku A, B, C maka akan terdapat tiga kemungkinan cara untuk mengisinya. Ini berarti untuk yang paling bawah kita dapat mengisi dengan memilih satu diantara tiga buah buku. Setelah meletakkan satu buku pada lokasi paling bawah maka kita hanya dapat mengisi ruang kedua dengan dua cara saja, karena hanya sisa dua buku saja yang dapat digunakan untuk mengisi ruang kedua. Karena dua buku sudah diletakkan maka untuk pengisian ruang ke tiga masih tersisa satu buku saja. Menggunakan prinsip perkalian maka hasilnya ketiga ruang tersebut dapat diisi dengan
6 1 2
3× × = cara. Dari contoh tersebut penyusunan secara teratur berarti penyusunan atau pengaturan suatu kelompok objek dalam suatu urutan (order) tertentu. Urutan penyusunan atau pemilihan merupakan ciri khas dari masalah permutasi.
Definisi 5.6.
Permutasi sejumlah objek adalah penyusunan objek tersebut dalam suatu urutan tertentu. Berikut akan dibicarakan terlebih dahulu permutasi dari n objek yang berbeda tanpa pengembalian objek yang telah terpilih.
PERMUTASI DARI n-OBJEK YANG TERPILIH
Dari contoh penyusunan buku diperoleh cara menyusun tiga buah buku yang berbeda adalah 3×2×1=6 cara, secara umum untuk n objek berbeda dapat dipermutasikan dalam
! ) 1 )( 2 )( 3 )...( 2 )( 1
(n n n
Definis 5.7.
Bila n menyatakan bilangan bulat positif maka hasil penggandaan bilangan tersebut dari 1 sampai dengan n dinamakan n faktorial dan dilambangkan dengan n!.
Teorema 5.8.
Permutasi dari keseluruhan n objek yang berbeda adalah jumlah cara penyusunan dari suatu kelompok yang terdiri dari n obyek yang berbeda kedalam sebanyak n ruang, secara keseluruhan menjadi n! dan dilambangkan sebagai P(n,n)=n!
PERMUTASI SEBANYAK r DARI n OBJEK Definisi 5.9.
Pengaturan atau penyusunan sebanyak r obyek yang diambil dari suatu kelompok obyek yang terdiri dari n obyek yang berbeda dinamakan permutasi sebanyak r dari n objek yang berbeda dimana r≤n dan secara simbolis permutasi tersebut dinotasikan sebagai P(n,r).
Teorema 5.10.
Jumlah permutasi sebanyak r dari n objek yang berbeda dimana r≤n dan pengambilan r tanpa pengulangan adalah
)! (
! )
, (
r n
n r
n P
−
= .
Contoh 5.11.
Dari 7 orang anak akan disusun suatu perangkat kelas yang terdiri dari ketua, sekretaris dan bendahara. Berapa cara yang dapat dilakukan untuk memilih perangkat kelas tersebut? Persoalan ini dapat diselesaikan dengan permutasi. Dari soal diketahui n=7 dan r =3. Jadi banyaknya cara memilih perangkat kelas adalah 210
! 4
! 7 )! 3 7 (
! 7 ) 3 , 7
( = =
− =
P cara.
PERMUTASI KELILING (CIRCULAR PERMUTATION) Definisi 5.12.
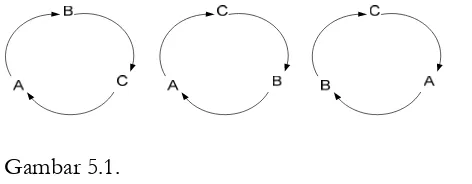
Bila suatu kelompok objek disusun secara teratur dalam sebuah lingkaran maka permutasi objek yang bersangkutan sebetulnya hanya mempersoalkan kedudukan relatif obyek-oyek bila melintasi lingkaran dalam syarat tertentu. Penyusunan obyek A, B, C dalam susunan melingkar berikut dianggap sama.
Gambar 5.1.
Dalam persoalan tentang permutasi keliling, hal yang terpenting adalah kedudukan objek yang tertentu relatif terhadap objek yang lain. Untuk mencari jumlah permutasi dalam susunan keliling tersebut kita harus berusaha menentukan terlebih dahulu kedudukan salah satu objek secara tetap. Kemudian dilanjutkan menghitung jumlah permutasi dari obyek yang lain seperti apabila obyek tersebut tersusun berjajar.
Teorema 5.13.
Permutasi keliling dari n obyek apabila n obyek tersebut disusun dalam sebuah lingkaran dapat disusun secara teratur dalam (n−1)! cara.
Teorema 5.14.
Permutasi keliling r dari n obyek apabila r obyek tersebut disusun dalam sebuah lingkaran dapat disusun secara teratur dalam
)! (
! )
, (
r n r
n r
n P
−
= cara.
Contoh 5.15.
Ada 4 orang yang akan duduk di dalam tiga buah bangku yang disusun melingkar di taman. Ada berapa macam cara posisi duduk yang dapat dilakukan apabila disyaratkan bahwa jika penempatan yang diperoleh dari penempatan lain dengan memindahkan seseorang r
sembarang. Untuk menempatkan 2 dari 3 orang sisanya kita bisa mengurutkan mereka kemudian meletakkannya dalam urutan searah jarum jam dari A. Untuk menempatkan 2 dari 3 orang dapat diperoleh dengan sebanyak C(3,2) = 3 cara. Berarti ada 3 posisi yang sama (identik). Sedangkan untuk memilih 3 diantara 4 orang dapat dilakukan dengan sebanyak P(4,3) = 24 cara. Jadi banyaknya cara duduk melingkar yang dapat dilakukan oleh keempat orang tersebut adalah 8
3 ) 3 , 4 ( =
P
cara.
PERMUTASI SEBANYAK r DARI n OBJEK DENGAN PENGEMBALIAM OBJEK YANG TERPILIH
Teorema 5.16.
Permutasi sebanyak r dari n objek dengan pengembaliam objek yang terpilih adalah jumlah permutasi dari suatu kelompok yang terdiri dari n obyek dan yang diambil sekaligus sebanyak r dengan pengembalian objek yang telah terpilih dilambangkan dengan
r
n r n
R( , )= dengan ketentuan r≤n dan merupakan bilangan bulat positif.
PERMUTASI SEBANYAK r DARI n OBYEK YANG TIDAK SELURUHNYA DAPAT DIBEDAKAN
Secara intuitif jumlah pemilihan obyek yang dapat dibedakan tentunya lebih banyak dari pada jumlah pemilihan dimana terdapat beberapa himpunan obyek yang sama (tidak dapat dibedakan). Misalnya kumpulan
{
a,a,a}
terdiri dari 3 unsur yang tidak dapat dibedakan hanya dapat dipermutasikan dalam 1 cara saja. Sedangkan apabila kita bedakan unsur himpunan tersebut menjadi{
a1,a2,a3}
maka jumlah permutasinya akan menjadi sebanyak 3!= 6. Jadi apabila dibandingkan maka jumlah permutasinya berkurang hingga 1/6 dari jumlah semula apabila himpunan
{
a1,a2,a3}
diubah sedemikian hingga menjadi{
a,a,a}
sehinggatidak bisa dibedakan dari anggota himpunan yang satu dengan anggota himpunan yang lain.
Teorema 5.17.
Jika terdapat suatu kelompok yang terdiri dari n obyek dimana n1 merupakan kumpulan
objek yang sama, n2 merupakan kumpulan objek yang sama, dan seterusnya hingga nk
permutasi dari n obyek yang meliputi seluruh obyek di atas adalah sebanyak
! ! !
!
2 1 2
1 k n n nk
n n
n n
n
L L ⎟⎟⎠=
⎞ ⎜⎜
⎝ ⎛
Contoh 5.18.
Dalam berapa carakah kata “MISSISSIPPI” dapat dipermutasikan? MISSISSIPPI tersusun dari 4 huruf yang terdiri dari 1M, 4I, 4S dan 2P. Dengan sendirinya diperoleh n1 =
1, n2 = 4, n3 = 4, n4 = 2, dan n = 11. Jadi permutasi 11 huruf di atas diperoleh:
34650 !
2 ! 4 ! 4 ! 1
! 11 2
4 4 1
11
= =
⎟⎟ ⎠ ⎞ ⎜⎜
⎝ ⎛
cara .
KOMBINASI
Perbedaan dasar antara permutasi dan kombinasi terletak pada diperhatikan atau tidaknya suatu urutan dalam pemilihan serangkaian obyek. Permutasi memberikan tekanan pada urutan pemilihan sedangkan kombinasi tidak memperhatikan urutan pemilihan.
Definisi 5.19.
Kombinasi dari sejumlah objek merupakan cara pemilihan objek yang bersangkutan tanpa memperhatikan urutan objek itu sendiri. Susunan ABC, BAC, ACB, BCA, CAB dan CBA dianggap sama.
Contoh 5.20.
Terdapat empat mata kuliah yang ditawarkan kepada Andi. Karena IP-nya kecil, Andi hanya bisa mengambil dua dari empat mata kuliah yang ditawarkan. Ada berapa cara pemilihan yang dapat dilakukan oleh Andi?
Cara 1:
Misalkan empat mata kuliah tersebut diberi nama M1, M2, M3 dan M4. Dapat
dibentuk pasangan sebagai berikut:
1
M
, M2
1
M
, 3
M 1
M
2
M , M1 2
M , M3 2
M , M4 M
3 M
,M4
M
4
M , M3
Jelas terdapat sebanyak 4×3 pasangan dari urutan ini. Tapi karena adanya pasangan yang sama muncul dua kali maka diperoleh banyaknya pemilihan adalah 6
2 3 4× =
cara.
Cara 2:
Dibentuk pasangan sebagai berikut:
3 , , , 4 1 3 1 2 1 ⎪ ⎭ ⎪ ⎬ ⎫ M M M M M M 2 , , 4 2 3 2 ⎭ ⎬ ⎫ M M M M
M3,M4
}
1Pasangan ini dapat ditulis sebagai 4 3 6
2 1 1 2 3 2 6 = × × = + + = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛
cara. Jika diperluas
maka diperoleh ( 1) 2
1 2⎟⎟⎠= −
⎞ ⎜⎜ ⎝ ⎛ n n n
cara. Untuk pengambilan tiga mata kuliah diperoleh daftar
sebagai berikut: 3 1 2 2 3 , , , , 4 2 1 4 3 1 3 2 1 = + = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎪⎭ ⎪ ⎬ ⎫ M M M M M M M M M .
Jadi banyaknya pasangan berurutan yang diawali dengan M1 adalah 3 buah yaitu
}
12 2 , 3 4 2 ⎟⎟=
Jadi banyaknya pasangan berurutan yang diawali dengan M2 adalah 1 buah. Jadi 4 2 2 2 3 3 4 = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ .
Secara umum maka diperoleh persamaan
⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − + + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 1 1 1 1 3 1 2 1 1 r r r r r n r n r n r n L
Inilah yang disebut pemilihan sebanyak k dari n obyek yang berbeda.
KOMBINASI SEBANYAK r DARI n OBJEK YANG BERBEDA. Definisi 5.21.
Pemilihan suatu kelompok terdiri dari r obyek yang mungkin dipilih dari suatu kelompok yang terdiri dari n obyek berbeda tanpa memperhatikan urutan pengambilan dengan 0<r<ndisebut kombinasi r dari n obyek dan dinotasikan C(n,r)atau ⎟⎟
⎠ ⎞ ⎜⎜ ⎝ ⎛ r n .
Misalkan r merupakan bilangan bulat non negatif. Dengan suatu kombinasi-r himpunan S dengan n anggota, dimaksud sebagai suatu pemilihan tak terurut dari r obyek dari n anggota S. Dengan kata lain, suatu kombinasi-r dari S merupakan himpunan bagian dari S dengan r anggota. Jika S =
{
a,b,c,d}
maka{
a,b,c}
,{
a,b,d}
,{
a,c,d}
,{
b,c,d}
merupakan empat kombinasi-3 dari S. Notasi C(n,r) menunjukkan jumlah kombinasi-r himpunan dengan n anggota. Sehingga jika r >n maka C(n,r)=0!. Jika0
=
n , dan r merupakan bilangan bulat positif, maka C(0,r)=0. Untuk alasan kemudahan lebih lanjut dibuat suatu kesepakatan bahwa C(0,0)=1.
Teorema 5.22.
Kombinasi sebanyak r dari n obyek yang berbeda adalah jumlah kombinasi dari n obyek yang berbeda dan yang dipilih sekaligus sebanyak r adalah
Tiap kombinasi dari n obyek yang berbeda dan yang diambil sekaligus sebanyak r akan menciptakan sebanyak r! permutasi karena tiap kelompok yang terdiri dari r obyek tersebut dapat dipermutasikan diantara mereka sendiri dalam r! cara. Oleh karena itu diperoleh bahwa r!
r n
⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛
=P(n,r). Jadi
)! ( !
! !
) , (
r n r
n r
r n P r n
− = =
⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛
, dengan 0<r<n.
Contoh 5.23.
Diberikan himpunan bilangan H= {1, 2, 3, 4, …, 300}, ada berapa cara memilih 3 bilangan diantara anggota himpunan tersebut sehingga jumlahnya habis dibagi tiga.
Solusi
Bentuk himpunan-himpunan bagian Hn dengan anggota-anggotanya jika dibagi tiga
akan bersisa sebanyak n bilangan. Diperoleh :
0
H = {3, 6, 9, 12, 15, …, 300}
1
H = {1, 4, 7, 10, 13, …. 298}
2
H = {2, 5, 8, 11, 14, …, 299}
Pengambilan 3 bilangan yang jumlahnya habis dibagi tiga dapat dilakukan dengan cara :
- pilih 3 diantara anggota-anggota H0 diperoleh sebanyak ⎟⎟
⎠ ⎞ ⎜⎜ ⎝ ⎛
3 100
cara
- pilih 3 diantara anggota-anggota H1 diperoleh sebanyak
⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛
3 100
cara
- pilih 3 diantara anggota-anggota H2 diperoleh sebanyak ⎟⎟
⎠ ⎞ ⎜⎜ ⎝ ⎛
3 100
cara
- pilih 1 anggota H0 diperoleh sebanyak ⎟⎟
⎠ ⎞ ⎜⎜ ⎝ ⎛
1 100
pilih 1 anggota H1 diperoleh sebanyak ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 1 100
cara, pilih 1 anggota H2 diperoleh
sebanyak ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 1 100 cara.
Karena terjadi bersama-sama dengan menggunakan prinsip perkalian diperoleh
pengambilan sebanyak ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 1 100 ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 1 100 ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 1 100 = 3 1 100 ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ cara.
Jadi total cara memilih tiga bilangan sehingga jumlahnya habis dibagi tiga adalah
⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 3 100 + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 3 100 + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 3 100 + 3 1 100 ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛
= 3 ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 3 100 + 3 1 100 ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛
= 1498501000 cara.
Teorema 52.24.
Untuk setiap n≥r berlaku ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ r n n r n
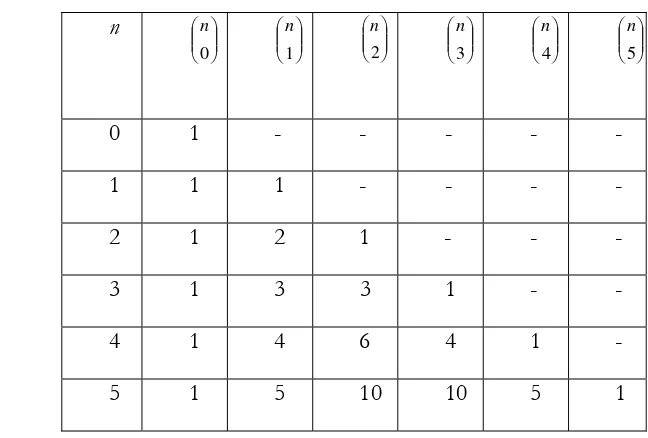
. Hal ini dapat dilihat pada tabel kombinatorial
berikut: Tabel 5.1. n ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 0 n ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 1 n ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 2 n ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 3 n ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 4 n ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 5 n
0 1 - - - 1 1 1 - - - - 2 1 2 1 - - - 3 1 3 3 1 - - 4 1 4 6 4 1 -
Pada baris ke-3 : 3 2 3 2 3 3 1 3 = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛
. Pada baris ke-5 : 10
3 5 2 5 5 2 5 = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ . Teorema 5.25.
Andaikan n dan r adalah dua bilangan bulat yang memenuhi 1≤r≤(n−1) maka berlaku
bahwa : ⎟⎟
⎠ ⎞ ⎜⎜ ⎝ ⎛ − − + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 1 1 1 r n r n r n .
TEOREMA BINOMIAL DAN MULTINOMIAL
Teorema Binomial
Sebelum kita membahas tentang Teorema Binomial, akan diperkenalkan dulu tentang Koefisien Binomial. Koefisien Binomial disusun berdasarkan definisi kombinatorik. Hasil susunan dari kombinatorik yang bersesuaian dalam tingkat orde tertentu dalam koefisien binomial akan menyusun segitiga Pascal. Selanjutnya konsep segitiga Pascal tersebut dipakai untuk menyelesaikan kasus yang lebih kompleks. Dari teorema-teorema dalam sub bab kombinasi sebelumnya diperoleh tabel berikut:
n ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 0 n ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 1 n ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 2 n ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 3 n ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 4 n ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 5 n ……
0 1 - - - …….
1 1 1 - - - - ……..
2 1 2 1 - - - ……..
3 1 3 3 1 - - …….. 4 1 4 6 4 1 - ……..
5 1 5 10 10 5 1 …….
M M M M M M M M
Pasangan ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ r
n ini disebut koefisien binomial. Pasangan ⎟
⎠ ⎞ ⎜ ⎝ ⎛n
n = 1 n = 2 n = 3 n = 4 n = 5
Batas dari segitiga itu terdiri dari bilangan-bilangan 1 dan nilai-nilai di dalamnya merupakan hasil penjumlahan dari dua bilangan diantasnya, identitas yang dihasilkan dari suatu proses penghitungan tersebut identitas kombinatorial, dan argumen yang mengarah pada pembentukannya disebut argumen kombinatorial. Untuk selanjutnya akan dibahas tentang Teorema Binomial.
Teorema 5.26. (Teorema Binomial)
Jika n adalah bilangan bulat positif, maka untuk setiap a dan b dipenuhi persamaan
(
)
∑
=
−
⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ =
+ n
k
k k n n
b a k n b
a
0
.
Contoh 5.27.
Jabarkan
(
3x−2y)
4dengan menggunakan teorema binomial.Jawaban : sesuai dengan teorema binomial, kita ambil a=3x, b=−2y dan n=4, maka kita dapatkan :
1 1
1 1
1 1
1 1
1 1
2
3 3
4 6 4
5 10 10 5
(
) (
4)
42
3x− y = a+b
( ) (
)
( ) (
)
( ) (
)
( ) (
)
( ) (
)
(
)
( )
( )( )
( )
4 3 2 2 3 4 4 4 3 3 2 2 2 2 3 3 4 4 4 0 3 1 2 2 1 3 0 4 4 0 3 1 2 2 1 3 0 4 16 96 216 216 81 2 2 3 . 4 2 3 . 6 2 3 . 4 3 2 3 4 4 2 3 3 4 2 3 2 4 2 3 1 4 2 3 0 4 4 4 3 4 2 4 1 4 0 4 y xy y x y x x y y x y x y x x y x y x y x y x y x b a b a b a b a b a + − + − = − + − + − + − + = − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = Contoh 5.28.Carilah koefisien dari a5b4dalam penjabaran
(
a+b)
9.Solusi : suku yang melibatkan a5b4 muncul dalam teorema binomial dengan mengambil 9
=
n dan k =4 5 4 126 5 4
4 9 b a b a b a k
n n k k
= ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ −
Sehinga koefisien dari a5b4 adalah 126.
Bertikut persamaan-persamaan yang merupakan hasil pengembangan teorema Binomial.
1.
∑
= = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ n k n k n 0 2 2. ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + 1 1 k n k n k ndengan 1≤k ≤n
3. ... 2 1
2 ... 4 2 0 − = + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ n k n n n n
4. ... 2 1
1 2 ... 5 3 1 − = + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ n k n n n n
5.
∑
⎟⎠ ⎞ ⎜ ⎝ ⎛ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛
n n n
n r
6. ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ⎟ ⎠ ⎞ ⎜ ⎝
⎛0 1 2 +1
1 .... n n r r r r
r yang bersekawan dengan
⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ⎟ ⎠ ⎞ ⎜ ⎝
⎛ +1 +2 + + +1
.... 2 1 0 r n r n n n n r r Teorema Multinomial
Berapa banyak bilangan yang terdiri dari 10 digit dapat dibuat dengan menggunakan bilangan 4,4,4,4,3,3,3,2,2,1? Banyaknya cara menempatkan 10 bilangan ke dalam 10 tempat dapat dilakukan dengan 10! cara. Akan tetapi bilangan-bilangan tersebut dapat dikelompokkan ke dalam 4 golongan yaitu bilangan 4 ada 4 buah, bilangan 3 ada 3 buah, bilangan 2 ada 2 buah dan bilangan 1 ada 1 buah. Karena urutan bilangan yang sama dalam satu golongan memiliki nilai yang sama maka 10! harus dibagi dengan banyaknya cara penempatan bilangan 4,3,2 dan 1. diperoleh 12.600
! 1 ! 2 ! 3 ! 4 ! 10 =
cara. Cara lain yang dapat di tempuh adalah dengan menggunakan kombinasi yang diperumum yaitu:
- Meletakkan 4 bilangan ke dalam 10 kotak dapat ditempuh dalam ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 4 10 cara.
- Meletakkan 3 bilangan ke dalam 6 kotak yang tersisa dapat ditempuh dalam ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 3 6 cara.
- Meletakkan 2 bilangan ke dalam 3 kotak yang tersisa dapat ditempuh dalam ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 2 3 cara.
- Meletakkan 1 bilangan ke dalam 1 kotak yang tersisa dapat ditempuh dalam ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 1 1 cara.
Karena kejadian terjadi bersama-sama maka cara mengatur 10 angka tersebut ke dalam 10 digit adalah ⎟⎟
⎠ ⎞ ⎜⎜ ⎝ ⎛ 4 10 ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 3 6 ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 2 3 ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 1 1
= 12.600
! 1 ! 2 ! 3 ! 4 ! 10 =
. Secara umum jika r ≥2 dan
r
k k k k
banyaknya cara meletakkan InI bilangan ke dalam r kotak adalah
! !.... !
! .... 1 2 2
1 r k k kr
n k k k n = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ .
Bentuk inilah yang di kenal sebagai Koefisien Multinomial. Ekspansi binomial dapat diperumum menjadi ekspansi multinomial yaitu:
(
)
(
) (
)
r i r r k r k k n k k k k k k r r r n r a a a k k k n a a a a a a a a a a a a ... ... . ... ... ... ... 2 2 1 2 1 2 1 ... 0 ..., 1 2
kali n sebanyak 3 2 1 3 2 1 3 2 1
∑
= + + + ≥ ⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ = + + + + + + + + = + + + + 4 4 4 4 4 4 4 4 4 3 4 4 4 4 4 4 4 4 4 2 1Sifat Koefisien Multinomial adalah
⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − + + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ 1 .... 1 ... ,.... 1 1 .... , 1 1
.... 1 2 1 2 1 2
2
1 r r r k k kr
n k k k n k k k n k k k n Contoh 5.29.
Tentukan koefisienx2 y3z pada ekspansi (x−2y+3z)6.
Jawaban Dari soal diketahui n=6, k1 =2, k2 =3, k3 =1 sedangkan koefisien x=1,
) 2 (−
=
y , dan z =3. Koefisien dari x2y3z pada ekspansi (x−2y+3z)6 adalah
( ) ( ) ( )
( 24) ( 1440)! 1 !. 3 !. 2 ! 6 3 2 1 1 3 2
6 2 − 3 1= − = −
⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ .
Teorema 5.30. (Teorema Multinomial)
Untuk n suatu bilangan bulat positif, maka untuk setiap bilangan real
t
X X X X
X1, 2, 3, 4,...., akan berlaku :
n t X X X X
X .... )
( 1 + 2 + 3 + 4 + +
nt n n n t n Xt X X X n n
n1 2.... 1 1 2 2 3 3....
∑
⎟ ⎠ ⎞ ⎜ ⎝ ⎛= dengan syarat
n n n
n
Contoh 5.31.
1. Expansikan bentuk (X1+X2 +X3 +X4 +X5)7 sehingga anda dapat menentukan koefisien (X12X3X43X5)
Solusi : koefisien ( 5) 3 4 3 2
1 X X X
X adalah 420
! 1 ! 3 ! 1 ! 0 ! 2
! 7 1
3 1 0 2
7
= =
⎟⎟ ⎠ ⎞ ⎜⎜
⎝ ⎛
2. Bila yang diekspansikan
(
2X1 −3X2 +5X3)
6 maka tentukan koefisien2 3 2 3 1 X X
X .
Solusi: koefisiennya =
( ) ( ) ( )
2 3 5 36000 21 3
6 3 − 1 2 =−
⎟⎟ ⎠ ⎞ ⎜⎜
⎝ ⎛
2. Tentukan koefisienx2 y3z pada ekspansi (x−2y+3z)6.
Solusi:
Dari soal diketahui n = 6, k1 = 2, k2 = 3, k3 = 1 sedangkan koefisien x = 1, y = (-2) , dan
z = 3. Koefisien dari x2 y3z pada ekspansi (x−2y+3z)6 adalah
( ) ( ) ( )
( 24) ( 1440)! 1 !. 3 !. 2
! 6 3
2 1 1 3 2
6 2 − 3 1= − = −
⎟⎟ ⎠ ⎞ ⎜⎜
⎝ ⎛
.
PIGEONHOLE PRINCIPLE/PERINSIP SARANG MERPATI
Teorema 5.32.
Jika n di dalam bilangan asli N dan n + 1 atau lebih obyek didistribusikan ke dalam n
himpunan maka paling sedikit satu diantara himpunantersebut pasti terdiri dari paling sedikit dua obyek.
Generalisasi dari teorema tersebut adalah:
Jika k dan n adalah bilangan asli dan sejumlah kn + 1 obyek akan didistribusikan ke dalam n himpunan maka paling sedikit satu diantara himpunan tersebut pasti memuat paling sedikit k + 1 obyek.
Contoh 5.33.
Jika ada 367 orang disuatu ruangan maka paling sedikit dua diantaranya memiliki tanggal dan bulan kelahiran yang sama.
Contoh 2.34.
Jika 51 surat didistribusikan ke dalam 5 kotak surat maka paling sedikit satu diantara kotak surat tersebut pasti memuat paling sedikit sejumlah k + 1 = 10 +1 = 11 surat.
Berikut akan diberikan beberapa contoh permasalahan yang dapat diselesaikan dengan menggunakan prinsip pigeonhole.
Contoh 5.35.
Seorang pemain catur handal mempunyai waktu 11 minggu untuk mengikuti turnamen. Sebagai persiapan ia ingin berlatih setiap hari dengan memainkan sedikitnya 1 permainan catur (gim), tetapi tidak ingin lebih dari 12 kali gim dalam seminggu. Buktikan bahwa ia pernah melakukan permainan sebanyak tepat 21 kali gim dalam beberapa hari berturutan.
Solusi:
Tulis a1 sebagai jumlah gim yang dimainkan pada hari pertama, a2 sebagai jumlah gim
yang dimainkan pada hari pertama dan kedua, a3 jumlah gim yang dimainkan sampai dengan
(77 hari). Berdasarkan syarat bahwa setiap munggu tidak boleh lebih dari 12 gim maka diperoleh a77 ≤12×11=132. Jadi kita memiliki barisan
132 ...
1≤a1 <a2 <a3 <a4 < <a77 ≤
dan diperoleh pula
153 21 ...
21 21
21 21
22≤a1+ <a2+ <a3+ <a4 + < <a77 + ≤
Angka 21 diperoleh dari yang diberikan. Bilangan
21 ,...
21 ,
21 ,
... 77 1 2 77 ,
4 , 3 , 2 ,
1a a a a a + a + a + a
adalah 154 bilangan bulat yang terletak di antara 1 dan 153. Oleh karena itu ada dua bilangan yang sama. Dua bilangan yang sama ini pasti dalam bentuk ai =aj+21 untuk
suatu j<i. Oleh karena itu pada hari ke j+1 sampai hari ke i, ahli catur bermain sebanyak 21 kali permainan
PERINSIP INKLUSI DAN EKSLUSI
Berapa banyak anggota di dalam gabungan dua buah himpunan A dan B? Gabungan antara dua buah himpunan menghasilkan himpunan baru yang elemen-elemennya berasal dari himpunan A dan B. Himpunan A dan himpunan B memiliki kemungkinan elemen-elemen yang sama. Banyaknya elemen-elemen bersama antara A dan B adalah A∩B . Setiap unsur yang sama tidak dihitung dua kali, sekali pada A dan sekali pada B, meski dianggap satu elemen di dalam A∪B . Karena itu,jumlah elemen hasil penggabungan seharusnya adalah jumlah elemen di masing-masing himpunan dikkurangi dengan jumlah elemen di dalam irisannya, atau ada berapa anggota dalam gabungan dua himpunan hingga?
Prinsip ink