31
MODEL EPIDEMIK DUA PENYAKIT DALAM SATU POPULASI Yuni Yulida, Faisal, Dewi Anggraini
Program Studi Matematika FMIPA Unlam Universitas Lambung Mangkurat
Jl. Jend. A. Yani km. 35,8 Kampus Unlam Banjarbaru Email: y_yulida@yahoo.com
ABSTRAK
Pada tulisan ini disajikan model epidemik penyebaran dua penyakit dalam satu populasi. Selanjutnya, model tersebut diselidiki eksistensi dan kestabilan titik ekuilibrium bebas penyakit dan endemiknya.
Kata kunci: Model epidemic, titik ekuilibrium, analisis kestabilan
ABSTRACT
This paper considers a epidemic model for a spread of two diseases in a population. From the model we study existence and stability of two equilibrium states: an infectious free equilibrium and an endemic equilibrium.
Key words:Epidemic model, equilibrium state, stability analysis 1. PENDAHULUAN
Model epidemik SIR pertama kali diperkenalkan oleh Kermack &
Mckendrick pada tahun 1927 dalam buku “ A Contribution to the Mathematical
Theory of Epidemics”. Model ini disusun secara deterministik untuk
menggambarkan sifat penyebaran penyakit yang berbentuk persamaan diferensial. Banyak model-model matematika yang telah dikembangkan, bertujuan untuk mempelajari penularan penyakit, untuk mengevaluasi penyebaran dari epidemik, dapat mencegah adanya penyakit atau untuk meminimalisir penyebaran penyakit. Dalam kurun waktu yang panjang, memahami perilaku penyakit akan membantu untuk mengetahui apakah epidemik akan menghilang atau tetap berada dalam suatu populasi[2].
Terdapat banyak model-model matematik yang menjelaskan perilaku suatu penyakit. Ada juga yang memberikan model dengan dua penyakit seperti AIDS dan kencing nanah atau menjelaskan dua virus dalam satu penyakit berada dalam suatu populasi, misalnya influenza dan tobercolusis[2]. Dalam hal ini berarti kemungkinan individu dalam suatu populasi dapat terjangkit dua penyakit sekaligus.
Model matematika yang dibahas adalah model matematika dua penyakit yang berada dalam satu populasi. Kemudian akan diselidiki titik ekuilibrium dan kestabilannya.
32
2. TINJAUN PUSTAKA
2.1 Sistem Persamaan Diferensial, Titik Ekuilibrium dan Kestabilannya Diberikan sistem persamaan diferensial sebagai berikut:
𝒙′= 𝒇(𝒙) (1)
dengan 𝒙 = 𝑥1, 𝑥2, … , 𝑥𝑛 𝑇∈ 𝐸 ⊂ ℝ𝑛, 𝒇 = 𝑓1, 𝑓2, … , 𝑓𝑛 𝑇 dan kondisi awal 𝑥 𝑡0 = 𝑥0 = 𝑥10, 𝑥20, … , 𝑥𝑛0 ∈ 𝐸. Notasi 𝑥 𝑡 = 𝑥(𝑥0, 𝑡) menyatakan
solusi Sistem (1) yang melalui 𝑥0. Selanjutnya, diberikan definisi titik ekuilibrium
Sistem (1) sebagai berikut. Definisi 1 [7]
Titik𝒙 ∈ ℝ𝑛 disebut titik ekuilibrium Sistem (1) jika 𝒇 𝒙 = 0.
Definisi 2 [9]
Titikekuilibrium 𝒙 ∈ ℝ𝑛 pada Sistem (1) dikatakan:
a) Stabil jika untuk setiap 0 terdapat 0 sedemikian sehingga untuk
setiap solusi Sistem (2.3) x(t) yang memenuhi 𝒙 𝑡0 − 𝒙 < 𝛿 maka berakibat 𝒙 𝑡 − 𝒙 < 𝜀 untuk setiap tt0.
b) Stabil asimtotik jika titik ekuilibrium 𝒙 ∈ ℝ𝑛 stabil dan terdapat bilangan
0 0
sehingga untuk setiap solusi Sistem (2.3) x(t) yang memenuhi
𝒙 𝑡0 − 𝒙 < 𝛿0 maka berakibat lim ( ) ˆ t x t x.
c) Tidak stabil jika titik ekuilibrium 𝒙 ∈ ℝ𝑛 tidak memenuhi (a).
Diberikan sistem persamaan diferensial homogen sebagai berikut:
𝒙′= 𝐴𝒙 (2)
dengan𝒙 = 𝑥1, 𝑥2, … , 𝑥𝑛 𝑇 ∈ 𝐸 ⊂ ℝ𝑛 dan 𝐴 matriks ukuran 𝑛 × 𝑛.
Berikut ini diberikan sistem persamaan diferensial yang linier
𝒙′ = 𝒇(𝒙) (3)
dengan 𝒙 ∈ 𝐸 ⊂ ℝ𝑛 , 𝒇 = 𝑓1, 𝑓2, … , 𝑓𝑛 𝑇dan 𝒇 ∶ 𝐸 ⊂ ℝ𝑛 → ℝ𝑛 fungsi kontinu pada 𝐸. Sistem (3) disebut sistem persamaan diferensial nonlinear jika terdapat
fungsi fi pada Sistem (3) yang nonlinear dan tidak dapat dinyatakan dalam
bentuk Sistem (2). Definisi 3[5]
Diberikan fungsi 𝒇 = 𝑓1, 𝑓2, … , 𝑓𝑛 𝑇 pada Sistem (3) dengan 𝑓𝑖 ∈ 𝐶′ 𝐸 ,
𝑖 = 1, 2, … , 𝑛.Matriks 𝐽 𝒇 𝒙 = 𝜕𝑓1(𝑥) 𝜕𝑥1 𝜕𝑓1(𝑥) 𝜕𝑥2 𝜕𝑓2(𝑥) 𝜕𝑥1 𝜕𝑓2(𝑥) 𝜕𝑥2 … 𝜕𝑓1(𝑥) 𝜕𝑥𝑛 … 𝜕𝑓2(𝑥) 𝜕𝑥𝑛 ⋮ ⋮ 𝜕𝑓𝑛(𝑥) 𝜕𝑥1 𝜕𝑓𝑛(𝑥) 𝜕𝑥2 ⋮ ⋮ … 𝜕𝑓𝑛(𝑥) 𝜕𝑥𝑛 (4)
33
Definisi 4 [7]
Diberikan matriks Jacobian 𝐽 𝒇 𝒙 pada (4). Sistem linier 𝒙′ = 𝐽 𝒇 𝒙 𝒙 disebut linierisasi Sistem (3) di sekitar titik 𝒙 .
Sifat kestabilan lokal titik ekuilibrium ˆx dapat diketahui, asalkan titik tersebut hiperbolik. Berikut diberikan definisi titik ekuilibrium hiperbolik..
Definisi 5 [7]
Titik ekuilibrium 𝒙 disebut titik ekuilibrium hiperbolik dari Sistem (3) jika tidak ada nilai eigen dari 𝐽 𝒇 𝒙 yang mempunyai bagian real nol.
Teorema 6 (6)
Diberikan matriks Jacobian 𝐽 𝒇 𝒙 dari Sistem (3) dengan nilai eigen . a) Jika semua bagian real nilai eigen matriks 𝐽 𝒇 𝒙 berharga negatif, maka titik ekuilibrium xˆ dari Sistem (3) stabil asimtotik lokal.
b) Jika terdapat paling sedikit satu nilai eigen matriks 𝐽 𝒇 𝒙 yang bagian realnya positif, maka titik ekuilibrium xˆ dari Sistem (3) tidak stabil
2.2. Teorema Routh-Hurwitz
Berdasarkan Teorema 6, untuk menganalisis sifat kestabilan lokal diperlukan perhitungan untuk menentukan nilai-nilai eigen dari matriks Jacobian di titik ekuilibrium. Sebagai alternatif untuk menentukan bagian riil dari nilai eigen bernilai negatif atau positif digunakan Teorema Routh-Hurwitz.
Diberikan polinomial berikut
1
0 1
( ) n n n
P z a z a z a . (5)
Definisi 7 [3]
Diberikan polinomial (5), dengan a0 positif dan ak bilangan real, k=1,2,3, …,n.
Matriks Hurwitz untuk persamaan (5) didefinisikan sebagai matriks bujur sangkar berukuran n yang berbentuk sebagai berikut
1 0 3 2 1 0 5 4 3 2 2 1 0 0 0 0 0 0 0 0 . 0 0 0 0 0 0 0 0 0 n n n a a a a a a a a a a H a a a (6)
Determinan Hurwitz tingkat ke-k, dinotasikan dengan k;k 1, 2,...,n, yang dibentuk dari matriks Hurwitz (6), didefinisikan sebagai berikut.
34 1 a1 , 1 0 2 3 2 , a a a a 3 13 02 1 5 4 3 0 ,..., a a a a a a a a 1 0 3 2 1 0 5 4 3 2 2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 n n n n a a a a a a a a a a a a a . Teorema 8 [4]
Pembuat nol dari Polinomial (5)mempunyai bagian real negatif jika dan hanya
1 0, 2 0, 3 0, , n 0
. (7)
2.3. Model Epidemik SIR klasik
Model epidemik SIR klasik menggambarkan penyebaran suatu penyakit.
Pada model epidemik SIR klasik ini, populasi diasumsikan dibagi menjadi tiga
kelompok populasi yaitu Suceptible (S) adalah kelompok individu yang sehat
tetapi rentan terhadap penyakit, Infected (I) adalah kelompok individu yang sakit
dan dapat sembuh dari penyakit dan Recovered (R) yaitu kelompok individu yang
telah sembuh dan kebal terhadap penyakit. Total populasi N diasumsikan
konstan karena tidak terdapat kelahiran, kematian ataupun migrasi. Jadi
N=S+I+R.
Berikut model epidemik SIR klasik dalam bentuk persamaan diferensial 𝑑𝑆 𝑑𝑡 = −𝛼𝑆𝐼, 𝑑𝐼 𝑑𝑡 = 𝛼𝑆𝐼 − 𝛽𝐼 dan 𝑑𝑅 𝑑𝑡 = 𝛽𝐼.
Individu pada kelompok Susceptible dapat terinfeksi penyakit melalui kontak
dengan laju infeksi 𝛼. Individu pada kelompok Infected dapat sembuh dari
penyakit dengan laju kesembuhan 𝛽. 2.4 Rasio Reproduksi Numbers
Untuk mengetahui tingkat penyebaran suatu penyakit diperlukan suatu parameter tertentu. Parameter yang biasa digunakan dalam masalah penyebaran
penyakit adalah Rasio Reproduksi Numbers atau Basic Reproduksi Numbers.
Rasio Reproduksi merupakan rasio yang menunjukkan jumlah individu
susceptible yang dapat menderita penyakit yang diakibatkan oleh satu individu
infected.
Rasio Reproduksi Number (R0) untuk Model Epidemik SIR klasik dapat ditentukan dari laju pertumbuhan Infected. Penyakit akan menyebar jika laju
pertumbuhan Infected terhadap waktu lebih dari nol dan penyakit tidak akan
menyebar jika laju pertumbuhan Infected (kelompok yang terinfeksi) terhadap
waktu kurang dari nol. Selanjutnya, Rasio Reproduksi Number untuk Model
Epidemik SIR klasik adalah 𝑅0 =𝛼𝑆𝛽. Jadi Penyakit akan menyebar jika 𝑅0 < 1
35
3. METODE PENELITIAN
Metode yang digunakan dalam penelitian ini adalah studi literatur. Adapun prosedur pada penelitian ini adalah mempelajari materi yang berhubungan dengan model penyebaran penyakit (model SIR), Sistem Persamaan Diferensial Linear dan nonlinear serta kestabilan lokal suatu titik ekuilibrium, membuat asumsi-asumsi pada populasi manusia, mendefinisikan parameter yang digunakan pada model. Setelah itu, membuat diagram transfer model penyebaran penyakit berdasarkan asumsi-asumsi. Dari diagram transfer tersebut diperoleh model epidemik dua penyakit dalam suatu populasi. Selanjutnya menentukan titik-titik ekuilibrium model tersebut serta menganalisis sifat kestabilan lokal titik-titik ekuilibrium
4. HASIL DAN PEMBAHASAN
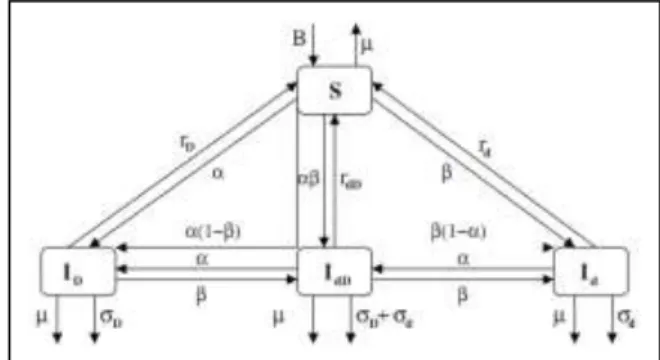
Model epidemik dua penyakit dalam suatu populasi dibentuk berdasarkan model SIR. Model SIR ini direduksi menjadi model SIS dengan asumsi individu yang telah sembuh dari sakit tidak mempunyai kekebalan, sehingga individu tersebut akan menjadi rentan kembali. Dalam populasi diasumsikan terdapat dua
penyakit misalnya penyakit 1 dan penyakit 2. Jumlah populasi manusia pada saat t
dilambangkan dengan N(t), yang kemudian dibagi menjadi 4 (empat) subpopulasi
yaitu Susceptible (S=S(t)) yaitu jumlah individu yang rentan terhadap penyakit pada saat t, Infected 1(𝐼𝐷 = 𝐼𝐷(𝑡)) yaitu jumlah individu yang terinfeksi penyakit 1 pada saat, Infected 2 (𝐼𝑑 = 𝐼𝑑(𝑡)) yaitu jumlah individu yang terinfeksi penyakit
2 pada saat t dan Infected 12 dilambangkan dengan (𝐼𝑑𝐷 = 𝐼𝑑𝐷(𝑡)) yaitu jumlah
individu yang terinfeksi penyakit 1 dan penyakit 2 secara bersamaan pada saat .
Jadi jumlah populasi manusia dapat dinyatakan sebagai
( ) ( ) D( ) d( ) dD( )
N t S t I t I t I t .
Asumsi-asumsi yang digunakan untuk membentuk model ini adalah setiap individu dapat terinfeksi oleh satu atau dua penyakit sekaligus, tidak terdapat kekebalan tubuh (artinya individu sembuh dari satu penyakit bisa terinfeksi penyakit lain atau penyakit yang sama), semua individu yang menyebabkan
populasi bertambah masuk ke subpopulasi Suceptibles, kedua penyakit dapat
menyebabkan kematian, peluang individu yang Infected menjadi Infected dengan
penyakit lain adalah sama dengan peluang individu yang Suceptible menjadi
Infected dengan penyakit itu.
Berikut ini parameter-parameter yang digunakan dalam model Simbol Keterangan
B Banyaknya pertambahan populasi (migrasi dan kelahiran)
𝜇 Laju kematian alami
𝛼 Laju penularan infected 1 (penyakit 1)
𝛽 Laju penularan infected 2 (penyakit 2)
𝜎𝐷 Laju kematian akibat infected 1(penyakit 1)
36
𝑟𝐷 Laju kesembuhan dari infected 1 (penyakit 1)
𝑟𝑑 Laju kesembuhan dari infected 2 (penyakit 2)
𝑟𝑑𝐷 Laju kesembuhan dari infected 12 (penyakit 1 dan 2 secara
bersama).
Selanjutnya dapat didefinisikan bahwa peluang individu menjadi infected 1
dan 2 berturut-turut 𝛼(1 − 𝛽) dan 𝛽(1 − 𝛼). Sedangkan peluang individu menjadi
infected 12 adalah 𝛼𝛽. Laju kematian untuk infected 12 adalah penjumlahan dari
laju kematian karena infected 1 dan infected 2 yaitu (𝜎𝐷+ 𝜎𝑑). Berdasarkan
asumsi-asumsi dan pemaparan di atas berikut diberikan diagram alir model epidemik
Gambar 1. Diagram alir model epidemik dua penyakit
Dari Gambar 1 dapat dituliskan model dalam bentuk sistem persamaan diferensial nonlinear sebagai berikut
𝑑𝑆 𝑑𝑡 = 𝐵 − 𝜇𝑆 − 𝛼 1 − 𝛽 𝐼𝑑𝐷 𝑆 𝑁− 𝛼𝐼𝐷 𝑆 𝑁− 𝛽 1 − 𝛼 𝐼𝑑𝐷 𝑆 𝑁− 𝛽𝐼𝑑 𝑆 𝑁 −𝛼𝛽𝐼𝑑𝐷 𝑆 𝑁+ 𝑟𝐷𝐼𝐷+ 𝑟𝑑𝐼𝑑+ 𝑟𝑑𝐷𝐼𝑑𝐷 (8a) 𝑑𝐼𝐷 𝑑𝑡 = 𝛼 1 − 𝛽 𝐼𝑑𝐷 𝑆 𝑁+ 𝛼𝐼𝐷 𝑆 𝑁− 𝜎𝐷+ 𝜇 + 𝑟𝐷 𝐼𝐷− 𝛽𝐼𝑑𝐷 𝐼𝐷 𝑁 − 𝛽𝐼𝑑 𝐼𝑑 𝑁 (8b) 𝑑𝐼𝑑 𝑑𝑡 = 𝛽 1 − 𝛼 𝐼𝑑𝐷 𝑆 𝑁+ 𝛽𝐼𝑑 𝑆 𝑁− 𝜎𝑑 + 𝜇 + 𝑟𝑑 𝐼𝑑 − 𝛼𝐼𝑑𝐷 𝐼𝑑 𝑁 − 𝛼𝐼𝐷 𝐼𝑑 𝑁 (8c) 𝑑𝐼𝑑𝐷 𝑑𝑡 = (𝛼+𝛽)𝐼𝐷 𝐼𝑑 𝑁 + 𝛼𝐼𝑑 + 𝛽𝐼𝐷 𝐼𝑑𝐷 𝑁 + 𝛼𝛽𝐼𝑑𝐷 𝑆 𝑁 − 𝜎𝐷+ 𝜎𝑑 + 𝜇 + 𝑟𝑑𝐷 𝐼𝑑𝐷. (8d)
4.1Rasio Reproduksi Number pada Model
Rasio Reproduksi Number Untuk penyakit 1, ditinjau Persamaan (8b), yaitu 𝑑𝐼𝑑𝑡𝐷 > 0, karena hanya memperhatikan penyakit 1 saja maka diperoleh
𝛼𝐼𝐷 𝑆 𝑁− 𝜎𝐷+ 𝜇 + 𝑟𝐷 𝐼𝐷 > 0 𝛼 𝑆 𝑁> 𝜎𝐷+ 𝜇 + 𝑟𝐷 𝛼 𝜎𝐷+ 𝜇 + 𝑟𝐷 𝑆 𝑁> 1.
Penyakit akan menyebar bergantung pada parameter 𝜎 𝛼
𝐷+𝜇 +𝑟𝐷. Misalkan parameter
tersebut ditulis 𝑅1 = 𝜎 𝛼
𝐷+𝜇+𝑟𝐷 sebagai Rasio reproduksi number untuk penyakit 1.
37 𝑅2 = 𝜎 𝛽
𝑑+𝜇+𝑟𝑑, sebagai Rasio reproduksi number untuk penyakit 2. Selanjutnya
yang berhubungan dengan penyakit 12 pada Persamaan (8d), Rasio reproduksi
numbernya adalah 𝑅3 = 𝜎 𝛼𝛽
𝐷+𝜎𝑑+𝜇+𝑟𝑑𝐷.
4.2 Titik Ekuilibrium dan Kestabilan Model
Titik ekuilibrium pada model terdiri dari dua jenis, yaitu titik ekuilibrium bebas penyakit dan titik ekuilibrium endemik. Titik ekuilibrium bebas penyakit terjadi jika populasi terbebas dari penyakit, sedangkan titik ekuilibrium endemik terjadi ketika terdapat penyakit di dalam populasi (satu atau dua sekaligus). Titik ekuilibrium disimbolkan dengan 𝐸𝑖 = 𝑆, 𝐼𝐷, 𝐼𝑑, 𝐼𝑑𝐷 ,
Titik ekuilibrium berdasarkan Definisi 1 harus memenuhi:
𝐵 − 𝜇𝑆 − 𝛼 1 − 𝛽 𝐼𝑑𝐷𝑁𝑆− 𝛼𝐼𝐷𝑁𝑆 − 𝛽 1 − 𝛼 𝐼𝑑𝐷𝑁𝑆 − 𝛽𝐼𝑑 𝑁𝑆− 𝛼𝛽𝐼𝑑𝐷𝑁𝑆+ 𝑟𝐷𝐼𝐷 +𝑟𝑑𝐼𝑑 + 𝑟𝑑𝐷𝐼𝑑𝐷 = 0 (9a) 𝛼 1 − 𝛽 𝐼𝑑𝐷𝑁𝑆+ 𝛼𝐼𝐷𝑁𝑆 − 𝜎𝐷+ 𝜇 + 𝑟𝐷 𝐼𝐷− 𝛽 𝐼𝑑 + 𝐼𝑑𝐷 𝐼𝑁𝐷 = 0 (9b) 𝛽 1 − 𝛼 𝐼𝑑𝐷 𝑆 𝑁+ 𝛽𝐼𝑑 𝑆 𝑁− 𝜎𝑑+ 𝜇 + 𝑟𝑑 𝐼𝑑− 𝛼 𝐼𝐷+ 𝐼𝑑𝐷 𝐼𝑑 𝑁 = 0 (9c) 𝛼 + 𝛽 𝐼𝐷𝐼𝑑 𝑁 + 𝛼𝐼𝑑 + 𝛽𝐼𝐷 𝐼𝑑𝐷 𝑁 − 𝜎𝐷+ 𝜎𝑑+ 𝜇 + 𝑟𝑑𝐷 𝐼𝑑𝐷 + 𝛼𝛽𝐼𝑑𝐷 𝑆 𝑁= 0 (9d)
4.2.1 Titik Ekuilibrium Model
Titik ekuilibrium bebas penyakit tercapai jika 𝐼𝑑 = 𝐼𝐷 = 𝐼𝑑𝐷 = 0, jika
disubstitusi ke Persamaan (9) maka diperoleh 𝑆 =𝐵𝜇 . Jadi diperoleh titik
ekuilibrium bebas penyakit, yaitu 𝐸1 = 𝐵𝜇, 0,0,0 . Pada model ini, titik ekulibrium endemik adalah
1. Jika penyakit 1 eksis (𝐼𝐷 ≠ 0) dan tidak terdapat penyakit yang lain, maka titik
ekuilibriumnya adalah 𝐸2 = 𝑆 , 𝐼 𝐷, 0,0 dengan 𝑁 = 𝑆 + 𝐼 𝐷,
𝑆 = 𝐵 𝜎𝐷+𝜇+𝑟𝐷
−𝜎𝐷𝑟𝐷−𝜎𝐷2+𝛼𝜎𝐷+𝛼𝜇 −𝜇 𝜎𝐷 dan 𝐼 𝐷 =
𝐵 𝛼−𝜎𝐷−𝜇−𝑟𝐷
−𝜎𝐷𝑟𝐷−𝜎𝐷2+𝛼𝜎𝐷+𝛼𝜇 −𝜇𝜎𝐷, asalkan 𝑅1> 1.
2. Jika penyakit 2 eksis (𝐼𝑑 ≠ 0) dan tidak terdapat penyakit yang lain, maka titik
ekuilibriumnya adalah 𝐸3 = 𝑆 , 0, 𝐼 𝑑, 0 dengan 𝑁 = 𝑆 + 𝐼 𝑑,
𝑆 = 𝐵 𝜎𝑑+𝜇+𝑟𝑑
−𝜎𝑑𝑟𝑑−𝜎𝑑2+𝛽𝜎𝑑+𝛽𝜇 −𝜇𝜎𝑑 dan 𝐼 𝑑 =
𝐵 𝛽−𝜎𝑑−𝜇−𝑟𝑑
−𝜎𝑑𝑟𝑑−𝜎𝑑2+𝛽𝜎𝑑+𝛽𝜇 −𝜇𝜎𝑑, asalkan 𝑅2> 1.
3. Penyakit 1 dan 2 eksis (𝐼𝐷 ≠ 0, 𝐼𝑑 ≠ 0 dan 𝐼𝑑𝐷 ≠ 0), peneliti terkendala dalam
penyelesaian sistem persamaan (9), ini dapat dijadikan bahan dikusi untuk penelitian lanjutan.
4.2.2 Kestabilan Model
38 𝐽 = −𝜇 − 𝛼𝐼𝐷 𝑁− 𝛽 − 𝛼𝛽 + 𝛼 𝐼𝑑𝐷 𝑁 − 𝛽 𝐼𝑑 𝑁 −𝛼 𝑆 𝑁+ 𝑟𝐷 𝛼 1 − 𝛽 𝐼𝑑𝐷 𝑁 + 𝛼 𝐼𝐷 𝑁 𝛼 𝑆 𝑁− 𝜎𝐷+ 𝜇 + 𝑟𝐷 − 𝛽 𝐼𝑑+𝐼𝑑𝐷 𝑁 𝛽 1 − 𝛼 𝐼𝑑𝐷+ 𝛽 𝐼𝑑 𝑁 𝛼𝛽𝐼𝑑𝐷 −𝛼𝐼𝑑 𝑁 𝛼 + 𝛽 𝐼𝑑 𝑁+ 𝛽 𝐼𝑑𝐷 𝑁 −𝛽𝑁𝑆+ 𝑟𝑑 − 𝛼 + 𝛽 − 𝛼𝛽 𝑁𝑆+ 𝑟𝑑𝐷 −𝛽𝐼𝐷 𝑁 𝛼 1 − 𝛽 𝑆 𝑁− 𝛽 𝐼𝐷 𝑁 𝛽𝑁𝑆− 𝜎𝐷+ 𝜇 + 𝑟𝐷 − 𝛼𝐼𝐷+𝐼𝑁𝑑𝐷 𝛼 + 𝛽 𝐼𝐷 𝑁+ 𝛼 𝐼𝑑𝐷 𝑁 𝛽 1 − 𝛼 𝑁𝑆− 𝛼𝐼𝑑 𝑁 𝛼𝐼𝑑 𝑁+ 𝛽 𝐼𝐷 𝑁+ 𝛼𝛽 𝑆 𝑁− 𝜎𝐷+ 𝜎𝑑+ 𝜇 + 𝑟𝑑𝐷 .
4.2.2.1 Kestabilan titik ekuilibrium Bebas Penyakit
Matriks Jacobian di titik ekuilibrium bebas penyakit diperoleh
𝐽 𝐸1 = −𝜇 −𝛼 + 𝑟𝐷 0 𝛼 − (𝜎𝐷+ 𝜇 + 𝜎𝑑) −𝛽 + 𝑟𝑑 − 𝛼 + 𝛽 − 𝛼𝛽 + 𝑟𝑑𝐷 0 𝛼 1 − 𝛽 0 0 0 0 𝛽 − 𝜎𝐷+ 𝜇 + 𝑟𝐷 𝛽 1 − 𝛼 0 𝛼𝛽𝑆 𝑁− 𝜎𝐷+ 𝜎𝑑+ 𝜇 + 𝑟𝑑𝐷
Dari Matriks 𝐽 𝐸1 diperoleh persamaan karakteristik sebagai berikut
𝐽 𝐸1 − 𝜆𝐼 = 0 −𝜇 − 𝜆 𝛼 − 𝜎𝐷+ 𝜇 + 𝜎𝑑 − 𝜆 𝛽 − 𝜎𝐷+ 𝜇 + 𝑟𝐷 − 𝜆
𝛼𝛽 − 𝜎𝐷+ 𝜎𝑑+ 𝜇 + 𝑟𝑑𝐷 − 𝜆 =0 (10) Dari Persamaan (10) diperoleh
𝜆1= −𝜇 < 0 𝜆2= 𝛼 − 𝜎𝐷+ 𝜇 + 𝜎𝑑 < 0, jika 𝛼 < 𝜎𝐷+ 𝜇 + 𝜎𝑑 𝜎 𝛼 𝐷+𝜇 +𝜎𝑑 < 1 𝑅1< 1. 𝜆3= 𝛽 − 𝜎𝐷+ 𝜇 + 𝑟𝐷 < 0, jika 𝛽 < 𝜎𝐷+ 𝜇 + 𝑟𝐷 𝜎 𝛽 𝐷+𝜇 +𝑟𝐷 < 1 𝑅2< 1. 𝜆4= 𝛼𝛽 − 𝜎𝐷+ 𝜎𝑑+ 𝜇 + 𝑟𝑑𝐷 < 0, jika 𝛼𝛽 < 𝜎𝐷+ 𝜎𝑑+ 𝜇 + 𝑟𝑑𝐷 𝛼𝛽 𝜎𝐷+ 𝜎𝑑+ 𝜇 + 𝑟𝑑𝐷 < 1 𝑅3< 1.
Berdasarkan Definisi 5 titik ekuilibrium bebas penyakit adalah titik ekuilibrium hiperbolik, sehingga analisis kestabilannya dapat dijelaskan. Berdasarkan Teorema 6 dapat disimpulkan bahwa titik ekuilibrium bebas penyakit 𝐸1 stabil asimtotik lokal asalkan 𝑅𝑗 < 1, 𝑗 = 1, 2, 3 dan tidak stabil jika 𝑅𝑗 > 1, 𝑗 = 1, 2, 3.
4.2.2.1 Kestabilan titik ekuilibrium Endemik
Matriks Jacobian untuk Model (8) di titik ekuilibrium 𝐸2 = 𝑆 , 𝐼 𝐷, 0,0 adalah sebagai berikut
39 𝐽 𝐸2 = −𝜇 − 𝛼𝐼 𝐷 𝑁 −𝛼 𝑆 𝑁 + 𝑟𝐷 −𝛽 𝑆 𝑁 + 𝑟𝑑 𝛼𝐼 𝐷 𝑁 𝛼 𝑆 𝑁 − 𝜎𝐷+ 𝜇 + 𝑟𝐷 −𝛽 𝐼 𝐷 𝑁 0 0 0 𝛽𝑆 𝑁 − 𝜎𝐷+ 𝜇 + 𝑟𝐷 − 𝛼 𝐼 𝐷 𝑁 0 𝛼 + 𝛽 𝐼 𝐷 𝑁 − 𝛼 + 𝛽 − 𝛼𝛽 𝑆 𝑁 + 𝑟𝑑𝐷 𝛼 1 − 𝛽 𝑆 𝑁 − 𝛽 𝐼 𝐷 𝑁 𝛽 1 − 𝛼 𝑆 𝑁 𝛽𝐼 𝐷 𝑁 + 𝛼𝛽 𝑆 𝑁 − 𝜎𝐷+ 𝜎𝑑+ 𝜇 + 𝑟𝑑𝐷
Dari Matriks 𝐽 𝐸2 diperoleh persamaan karakteristik sebagai berikut
𝐽 𝐸2 − 𝜆𝐼 = 0 𝛽𝑆 𝑁 − 𝜎𝐷+ 𝜇 + 𝑟𝐷 − 𝛼 𝐼 𝐷 𝑁 − 𝜆 𝛽 𝐼 𝐷 𝑁 + 𝛼𝛽 𝑆 𝑁 − 𝜎𝐷+ 𝜎𝑑+ 𝜇 + 𝑟𝑑𝐷 − 𝜆 − 𝛼 + 𝛽 𝐼 𝐷 𝑁 𝛽 1 − 𝛼 𝑆 𝑁 −𝜇 − 𝛼 𝐼 𝐷 𝑁 − 𝜆 𝛼 𝑆 𝑁 − 𝜎𝐷+ 𝜇 + 𝑟𝐷 − 𝜆 − 𝛼𝐼 𝐷 𝑁 −𝛼 𝑆 𝑁 + 𝑟𝐷 = 0 Jadi diperoleh 𝛽𝑆 𝑁 − 𝜎𝐷+ 𝜇 + 𝑟𝐷 − 𝛼 𝐼 𝐷 𝑁 − 𝜆 𝛽 𝐼 𝐷 𝑁 + 𝛼𝛽 𝑆 𝑁 − 𝜎𝐷+ 𝜎𝑑+ 𝜇 + 𝑟𝑑𝐷 − 𝜆 – 𝛼 + 𝛽 𝐼 𝐷 𝑁 𝛽 1 − 𝛼 𝑆 𝑁 = 0 (11) atau −𝜇 − 𝛼𝐼 𝐷 𝑁 − 𝜆 𝛼 𝑆 𝑁 − 𝜎𝐷+ 𝜇 + 𝑟𝐷 − 𝜆 − 𝛼 𝐼 𝐷 𝑁 −𝛼 𝑆 𝑁 + 𝑟𝐷 = 0. (12) Dari Persamaan (12) dapat ditulis menjadi
𝜆2+ 𝜆 −𝛼𝑆 𝑁 + 𝛼 𝐼 𝐷 𝑁 + 𝜎𝐷 + 2𝜇 + 𝑟𝐷 + −𝜇𝛼𝑁 𝑆 − 𝛼2 𝑆 𝐼 𝐷 𝑁 𝑁+ 𝜇 𝜎𝐷+ 𝜇 + 𝑟𝐷 + 𝛼 2 𝐼 𝐷 𝑁 𝑆 𝑁 − 𝛼 𝐼 𝐷 𝑁 𝑟𝐷+ 𝛼 𝜎𝐷+ 𝜇 + 𝑟𝐷 𝐼 𝐷 𝑁 = 0 atau 𝑎0𝜆2+ 𝑎 1𝜆 + 𝑎2 = 0 (13) dengan𝑎0= 1, 𝑎1= 𝛼 − 𝜎𝐷− 𝑟𝐷,dan𝑎2 = 𝑟𝐷 𝛼 − 𝜎𝐷− 𝜇 − 𝑟𝐷 .
40 Selanjutnya untuk mengetahui bagian real dari nilai eigen bernilai negatif atau bukan, Persamaan (13) berdasarkan Definisi 7 dapat dibentuk matriks Hurwizt sebagai berikut 𝐻 = 𝑎𝑎1 𝑎0
3 𝑎2 =
𝑎1 1
0 𝑎2
Selanjutnya berdasarkan Teorema 8 bagian real dari nilai eigen akan bernilai negatif jika ∆1= 𝑎1 >0 dan ∆2= 𝑎01 𝑎1
2 >0.
1. ∆1= 𝑎1 =𝑎1= 𝛼 − 𝜎𝐷 − 𝑟𝐷>0 jika 𝛼 > 𝜎𝐷+ 𝑟𝐷 (karena 𝑅1 >1). 2. ∆2= 𝑎01 𝑎1
2 =𝑎1𝑎2>0.
Untuk membuktikan 𝑎1𝑎2>0, karena 𝑎1 > 0, akan dibuktikan bahwa 𝑎2 > 0. Nilai 𝑎2 = 𝑟𝐷 𝛼 − 𝜎𝐷− 𝜇 − 𝑟𝐷 > 0 jika 𝑅1 > 1.
Jadi diperoleh bahwa ∆1 >0 dan ∆2 >0 asalkan 𝑅1 > 1.
Karena ∆1 >0 dan ∆2 >0 maka bagian real dari nilai eigennya bernilai negatif. Selanjutnya menentukan bagian real dari nilai eigen yang dapat diperoleh dari Persamaan (11) 𝛽𝑆 𝑁 − 𝜎𝐷+ 𝜇 + 𝑟𝐷 − 𝛼 𝐼 𝐷 𝑁 − 𝜆 𝛽 𝐼 𝐷 𝑁 + 𝛼𝛽 𝑆 𝑁 − 𝜎𝐷+ 𝜎𝑑+ 𝜇 + 𝑟𝑑𝐷 − 𝜆 – 𝛼 + 𝛽 𝐼 𝐷 𝑁 𝛽 1 − 𝛼 𝑆 𝑁 = 0 𝑎0𝜆2+ 𝑎 1𝜆 + 𝑎2= 0, dengan 𝑎0 = 1 𝑎1= −𝛽 𝑆 𝑁 + 𝜎𝐷+ 𝜇 + 𝑟𝐷 + 𝛼 𝐼 𝐷 𝑁 − 𝛽 𝐼 𝐷 𝑁 − 𝛼𝛽 𝑆 𝑁 + 𝜎𝐷+ 𝜎𝑑+ 𝜇 + 𝑟𝑑𝐷 = −𝜷𝜶 𝜎𝐷+ 𝜇 + 𝑟𝐷 + 𝜎𝐷+ 𝜇 + 𝑟𝐷 + 𝛼 − 𝜎𝐷− 𝜇 − 𝑟𝐷 −𝛽𝛼 𝛼 − 𝜎𝐷− 𝜇 − 𝑟𝐷 − 𝛽 𝜎𝐷+ 𝜇 + 𝑟𝐷 + 𝜎𝐷+ 𝜎𝑑+ 𝜇 + 𝑟𝑑𝐷 = 𝛼 𝑅𝛽 2 + 𝛼 − 𝛼 𝑅1− 𝛽 − 𝛼𝛽 𝑅1+ 𝛼𝛽 𝑅3 = 𝛼(1 −𝑅1 1) + 𝛽( 1 𝑅2 − 1) + 𝛼𝛽 𝑅3− 𝛼𝛽 𝑅1. 𝑎2= 𝛽2 𝑆 𝑁 𝐼 𝑁 𝐷+ 𝛼𝛽2 𝑁 𝑆 2 − 𝛽 𝜎𝐷+ 𝜎𝑑+ 𝜇 + 𝑟𝑑𝐷 𝑁 𝑆 − 𝛽 𝜎𝐷+ 𝜇 + 𝑟𝐷 𝐼 𝑁 𝐷 −𝛼𝛽 𝜎𝐷+ 𝜇 + 𝑟𝐷 𝑆 𝑁 + 𝜎𝐷+ 𝜇 + 𝑟𝐷 𝜎𝐷+ 𝜎𝑑+ 𝜇 + 𝑟𝑑𝐷 − 𝛼 + 𝛽 𝛽 1 − 𝛼 𝑆 𝑁 𝐼 𝐷 𝑁 = − 𝛼 +𝑅𝛽 2 + 1 𝑅2 𝛼 2+ 𝛼𝛽 1 − 1 𝑅3 + 𝛽 𝑅2 1 − 𝛼𝛽 + 𝛼 𝑅3 𝛼 1 − 1 𝑅1 + 𝛽 𝑅2 .
Berdasarkan Kreteria Routh Hurwizt titik ekuilibrium 𝐸2 = 𝑆 , 𝐼 𝐷, 0,0 bagian real dari nilai eigennya benilai negatif jika
𝑓 = 𝛼(1 −𝑅1 1) + 𝛽( 1 𝑅2 − 1) + 𝛼𝛽 𝑅3 − 𝛼𝛽 𝑅1 > 0 dan 𝑔 = − 𝛼 + 𝛽 𝑅2 + 1 𝑅2 𝛼 2+ 𝛼𝛽 1 − 1 𝑅3 + 𝛽 𝑅2 1 − 𝛼𝛽 + 𝛼 𝑅3 𝛼 1 − 1 𝑅1 + 𝛽 𝑅2 > 0.
41
Jadi Titik ekuilibrium endemik E2 pada Sistem (8) ada jika R1 > 1 dan Stabil asimtotik lokal jika 𝑓 > 0 dan 𝑔 > 0 terpenuhi.
Selanjutnya untuk menentukan kestabilan 𝐸3 = 𝑆 , 0, 𝐼 𝑑, 0 analog dengan
𝐸2 = 𝑆 , 𝐼 𝐷, 0,0 , diperoleh kesimpulan bahwa titik ekuilibrium endemik 𝐸3 = 𝑆 , 0, 𝐼 𝑑, 0 ada (eksis) jika𝑅2> 1 danstabil asimtotik lokal jika memenuhi = 𝛽(1 −𝑅1 2) + 𝛼( 1 𝑅1 − 1) + 𝛼𝛽 𝑅3 − 𝛼𝛽 𝑅2 > 0, dan 𝑖 = − 𝛽 + 𝛼 𝑅1 + 1 𝑅1 𝛽 2+ 𝛼𝛽 1 − 1 𝑅3 + 𝛼 𝑅1 1 − 𝛼𝛽 + 𝛽 𝑅3 𝛽 1 − 1 𝑅2 + 𝛼 𝑅1 > 0.
Sebagai bahan diskusi lanjutan adalah untuk titik ekuilibrium endemik penuh, bifurkasi dan simulasi numeriknya.
5. KESIMPULAN
Kesimpulan yang diperoleh, yaitu:
1. Titik Ekulibrium yang diperoleh dari model adalah
a. 1.Titik ekuilibrium bebas penyakit 𝐸1= 𝐵𝜇, 0,0,0
b. Titik Ekuilibrium endemik 𝐸2 = 𝑆 , 𝐼 𝐷, 0,0 dengan 𝑁 = 𝑆 + 𝐼 𝐷 dan 𝑆 = 𝐵 𝜎𝐷+𝜇+𝑟𝐷
−𝜎𝐷𝑟𝐷−𝜎𝐷2+𝛼𝜎𝐷+𝛼𝜇−𝜇𝜎𝐷, 𝐼 𝐷 =
𝐵 𝛼−𝜎𝐷−𝜇−𝑟𝐷
−𝜎𝐷𝑟𝐷−𝜎𝐷2+𝛼𝜎𝐷+𝛼𝜇−𝜇𝜎𝐷 asalkan 𝑅1 > 1.
c. Titik Ekuilibrium endemik 𝐸3= 𝑆 , 0, 𝐼 𝑑, 0 dengan 𝑁 = 𝑆 +𝐼𝑑 dan 𝑆 = 𝐵 𝜎𝑑+𝜇+𝑟𝑑
−𝜎𝑑𝑟𝑑−𝜎𝑑2+𝛽𝜎𝑑+𝛽𝜇−𝜇𝜎𝑑, 𝐼𝑑 =
𝐵 𝛽−𝜎𝑑−𝜇−𝑟𝑑
−𝜎𝑑𝑟𝑑−𝜎𝑑2+𝛽𝜎𝑑+𝛽𝜇−𝜇𝜎𝑑asalkan 𝑅2>
2. Kestabilan titik ekuilibrium
a. Titik ekuilibrium bebas penyakit 𝐸1= 𝐵𝜇, 0,0,0 pada Model (8) ini Stabil
asimtotik lokal jika 𝑅j < 1, 𝑗 = 1, 2, 3 dan tidak stabil jika
𝑅j > 1, 𝑗 = 1, 2, 3stabil asimtotik lokal
b. Titik Ekuilibrium endemik 𝐸2 = 𝑆 , 𝐼 𝐷, 0,0 pada Model (8) ini Stabil asimtotik lokal jika 𝑓 > 0 dan 𝑔 > 0 terpenuhi
c. Titik Ekuilibrium endemik 𝐸3= 𝑆 , 0, 𝐼 𝑑, 0 pada Model (8) ini Stabil asimtotik lokal jika > 0 dan 𝑖 > 0 terpenuhi .
6. DAFTAR PUSTAKA
[1] Anton, H. dan Rorres,C., 2004, Aljabar Linear Elementer Versi Aplikasi,
Edisi Kedelapan, alih bahasa oleh Indriasari, R. dan Harmaen I., Erlangga, Jakarta.
[2] Blyuss, B.K. & Kyrychko N.Y., 2005, On a Basic Model of a Two-Disease
Epidemic, Applied Mathematics and Computation, 160 hal 177-187.
[3] Gantmacher, F.R., 1959, The Theory of Matrices, Chelsea Publishing
Company, New York.
[4] Hanh, W., 1967, Stability of Motion, Springer- Verlag, New York.
[5] Kocak, H. & Hole, J.K, 1991, Dynamic and Bifurcation, Springer-Verlag,
42
[6] Olsder, G. J., 1994, Mathematical System Theory, Delftse Uitgevers
Maatschappij, Netherlands.
[7] Perko, L., 1991, Differential Equations and Dynamical Systems,
Springer-Verlag, New York.
[8] Verhulst, F., 1990, Nonlinear Differential Equations and Dynamical
Systems, Springer-Verlag, Berlin.
[9] Wiggins, S., 1990, Introduction to Applied Nonlinear Dynamical Systems