BAB 3 Getaran Bebas SDOF

Getaran (Vibration)

Dalam kehidupan sehari-hari terdapat banyak benda yang bergetar.

Garpu tala,

Senar gitar yang sering anda mainkan,

Sound system,

Ingat juga ketika anda tertawa terpingkal-pingkal tubuh anda juga bergetar

Getaran (Vibration)

Getaran adalah gerakan bolak-balik dalam suatu interval waktu tertentu.

Getaran dan gelombang merupakan dua hal yang saling

berkaitan. Baik itu gelombang air laut, gelombang gempa bumi, gelombang suara yang merambat di udara; semuanya bersumber pada getaran. Dengan kata lain, getaran adalah penyebab

Getaran Bebas (Free Vibration)

Persamaan gerak secara umum :

)

(

t

p

ku

u

c

u

m





+



+

=

Kecepatan dan perpindahan saat t=0 :

0 0

,

(

0

)

)

0

(

u

u

u

u

=



=



Sehingga persamaan gerak dapat ditulis :

)

(

2

2 2

t

p

k

u

u

u

_{n n} n

dimana

n n

cr

k

m

c

ω

ω

2

2

=

=

cr

c

c

=

ζ

dan

k c

n adalah frekuensi alami sudut tak teredam (rad/s), adalah faktor redaman

Getaran bebas system SDOF

Respon total :

)

(

)

(

)

(

t

u

t

u

t

u

=

_p

+

_c

Di dalam istilah matematika, penyelesaian umum dari persamaan diferensial terdiri dari penyelesaian sesungguhnya up(t) dan

penyelesaian komplemen/pelengkap u_c(t). u_p(t) = forced motion related p(t)

u_c(t) = natural motion P(t) m

u

K

I

Getaran bebas system SDOF

Untuk getaran bebas

→

P(t)=0:

0

=

+

+

c

u

ku

u

m







0

2

+

2

=

+

u

u

u

n

n

ω

ζω





Solusi umum, untuk menyelesaikan persamaan diatas :

t

s

e

C

u

=

Maka….

Getaran bebas system SDOF

0

)

2

(

s

2

+

ζω

n

s

+

ω

n

2

C

e

s

t

=

Supaya dapat valid untuk semua nilai t , kita harus mengeset :

0

2

2

2

=

+

+

n

s

n

s

ζω

ω

Getaran bebas system SDOF

SDOF Tak Teredam

(Undamped)

Persamaan gerakan untuk sistem "Undamped SDOF" adalah

0

=

+

ku

u

m





u

+

2

u

=

0

n

ω



atau

dan persamaan karakteristik yang sesuai adalah

0

2 2

=

+

_n

s

ω

akar dari persamaan diatas adalah

1

-i

dimana

2 ,

1

=

±

i

n

=

Sehingga penyelesaian umum :

t i t

ei

n n

e

C

C

u

=

₁ ω

+

₂ − ω

dengan memperkenalkan persamaan Euler

θ

θ

θ

cos

sin

i

e

±

i

=

±

kita dapat menulis ulang persamaan dalam bentuk fungsi trigonometri, yaitu

t

A

t

A

u

n

n

ω

ω

sin

cos

2

1

+

dimana A₁ dan A₂ adalah konstanta real, ditentukan dari kondisi awal perpindahan dan kecepatan,

jadi

t

u

t

u

u

n n n

ω

ω

ω

sin

cos

0 0

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

=



adalah respon getaran bebas d a r i s i s t e m " u n d a m p e d SDOF".

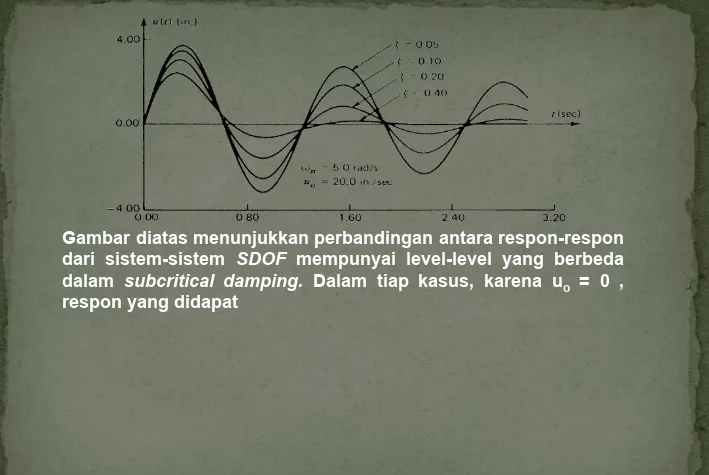
Pertama-tama dengan mempertimbangkan kasus dari sebuah sistem yang menggantikan dari posisinya yang seimbang dengan jumlah u_o dan dibebaskan. Kemudian ů_{(0) = 0 , jadi}

Dapat dilihat bahwa respon merupakan gerakan harmonik sederhana dengan amplitudo uo, dan periode dari "undamped natural"

t

u

u

n

ω

cos

0

=

(s)

2

n n

T

ω

π

=

dan sebuah frekuensi dari "undamped natural"

(Hz)

2

1

π

ω

_n

n n

T

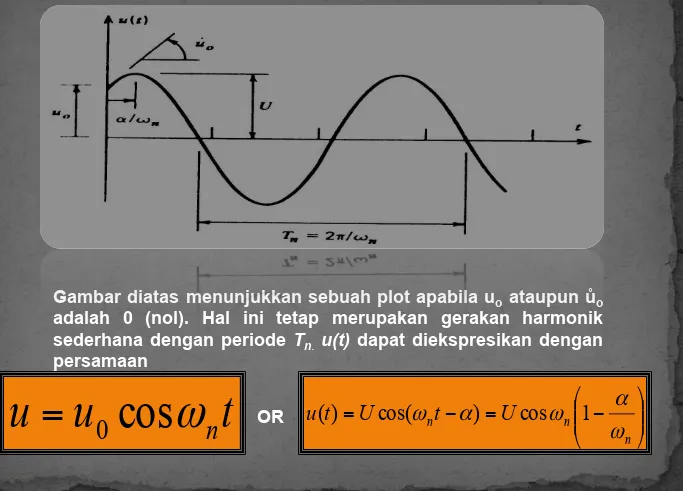
Gambar diatas menunjukkan sebuah plot apabila u_o ataupun ů

o

adalah 0 (nol). Hal ini tetap merupakan gerakan harmonik sederhana dengan periode T_n. u(t) dapat diekspresikan dengan persamaan

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

=

−

=

n n

n

t

U

U

t

u

ω

α

ω

α

ω

)

cos

1

cos(

)

(

t

u

u

n

ω

cos

0

F(t)

W8x24

200 lb/ft

15 ft

Model Struktur :

E = 30.106 _psi

I = 82,5 in4

W = 200 x 25 = 5000 lb

g = 386 in/dt2

Contoh

F(t)

W8x24

200 lb/ft

15 ft

F(t)

Model SDOF

Model Matematis

F(t)

m

K

y

FBD

f

s

m

F(t)

Penyelesaian :

( )

t

F

fs

I

+

=

fs m F(t)

I

( )

t

F

y

k

y

m

.





+

.

=

( )

(

)

(

)

sps f dt rad m k in dt lb g W m in lb L I E K n n 46 . 4 5000 386 . 185 , 10 2 1 2 / 786 . 0 5000 386 . 185 , 10 / . 95 . 12 386 5000 / 185 , 10 12 . 15 5 , 82 . 2 10 . 30 . 12 2 12 2 3 6 3 = = = = = = = = = = = =

π

π

ω

ω

( )

t

F

y

y

+

10

.

185

=

95

.

t

u

t

u

t

u

n n n

ω

ω

ω

sin

cos

)

(

₀ 0

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

=



t

u

t

u

t

u

sin

₀

.

786

786

.

0

786

.

0

cos

)

(

₀ 0

⎟

⎠

⎞

⎜

⎝

⎛

+

=



Latihan

Jika:  Simpangan  awal            

               Kecepatan  awal    

 Gaya  luar  F(t)  

Gambarkan  Respons  Struktur!!  

( )

0

=

0

,

001

ft

y

( )

0

=

0

,

1

ft/dt

0

=

+

+

c

u

ku

u

m







u

+

2

u

+

2

u

=

0

n

n

ω

ζω





Persamaan gerakan untuk sistem "Undamped SDOF" adalah

atau

dan persamaan karakteristik yang sesuai adalah

0

2

2

2

=

+

+

n

s

n

s

ζω

ω

dimana akar-akarnya , s₁ dan s₂ diberikan oleh

1

2 2

,

1

=

−

ζω

n

±

ω

n

ζ

−

Besarnya faktor "damping" ( ζ ) , dapat digunakan untuk membedakan 3 kasus, yaitu:

Ø  underdamped (0 < ζ < 1)

Ø  critically damped ( ζ = 1 )

Kasus

Underdamped

( 0 <

ζ

< 1)

1

2 2

,

1

=

−

ζω

n

±

ω

n

ζ

−

s

( 0 <

ζ

< 1)

d

n

i

s

=

−

ζω

±

ω

2 , 1

Lebih mudah bila menulis persamaan diatas dalam bentuk

dimana ω_d adalah frekuensi alami " damped circular " yang diberikan oleh

ζ

ω

ω

_d

=

_n

1

−

yang sesuai dengan periode damped , T_d , yang diberikan oleh

d d

T

ω

π

2

Dengan bantuan dari formula Euler, penyelesaian umum, u (t), dapat ditulis dalam bentuk

)

sin

cos

(

)

(

t

e

A

₁

t

A

₂

t

u

d d t n

ω

ω

ζω

+

=

−

dan juga, uo dan ů_{o digunakan untuk mengevaluasi A}

1 dan A2 ,

dengan hasil:

⎥

⎦

⎤

⎢

⎣

⎡

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

+

=

−

cos

sin

)

)

(

t

e

u

₀

t

u

0

u

0

t

u

d d n d t n

ω

ω

ζω

ω

ζω



Atau dapat ditulis dalam bentuk

)

cos(

)

(

t

=

Ue

−ζω

ω

t

−

α

u

d t

Walaupun nilai dari ζ mempunyai efek pada frekuensi , ω_d , efek yang paling berat dari damping adalah pada angka pada saat gerakan menyusut, yaitu pada waktu e-ζωdt_.

Ø 

Kasus critically damped (

ζ

= 1 )

Ketika  ζ=1  maka  persamaan  

1

2 2

,

1

=

−

ζω

n

±

ω

n

ζ

−

s

menjadi  

n

s

=

−

ζω

2 , 1

maka respon dari sistem redaman kritis adalah:

Solusinya  menjadi:  

t n

e

t

C

C

t

u

(

)

=

(

+

)

−ζω

2 1 t o n o o n

e

t

u

u

u

t

Eksperimen Penentuan dari

Frekuensi Alami Dasar dan

Faktor

Damping

dari sebuah

sistem SDOF

Faktor damping , ζ , umumnya diukur, dan bila diinginkan, nilai efektif dari c dapat dihitung dari persamaan

Frekuensi alami undamped dari sebuah sistem SDOF sederhana dapat ditentukan dari pengukuran statis.

Main Menu

cr

Contoh

Tentukan frekuensi alami dari sebuah sistem pegas sederhana dengan menggunakan pengukuran statis defleksi.

Penyelesaian :

k

L

o

k

w

u

_st

fs=ku

_st

ω_n2 _{= k/m}

keseimbangan berat dari massa yang tergantung pada pegas ditunjukkan pada

∑

=

↓

+

F

0

atau

0

=

−

f

_s

W

dari persamaan gaya yang menyebabkan perpanjangan pada pegas

st s

ku

f

=

2 1

3

4

persamaan 3 dan 4 digabungkan mendapat

st s

mg

ku

f

=

=

5

k L_{o k}

w

u_st

fs=ku_st

jadi, dari persamaan 1 dan 5

st n

u

g

=

2

ω

6

apabila the damping dalam sistem kecil ( ζ < 0.2 ), persamaan

menunjukkan bahwa ω_d kurang lebih sama dengan ω_n. Contoh selanjutnya menunjukkan bagaimana sebuah eksperimen getaran bebas dapat digunakan untuk menentukan frekuensi alami dari sebuah sistem SDOF.

1

2

−

Contoh

Frekuensi  natural  dari  balok  kantilever  dengan  massa  

lumped  (terpusat)  bergerak  dinamis.  Massa  bergerak  

dengan  amplitudo  A  =  1  in  kemudian  dilepaskan.  Gerakan  

yang  terjadi  ditunjukkan  gambar  di  bawah  yang  

Penyelesaian :

Pada titik a, beban telah bergerak 1¼ putaran

Hz

putaran

125

.

3

4

.

0

25

.

1

=

≈

s

f

_n

rad/s

6

.

19

)

125

.

3

)(

28

.

6

(

2

=

=

=



n

n

π

f

ω

s

f

T

n

n

0

.

32

Terdapat dua metode yang hampir sama untuk m e n e n t u k a n t h e d a m p i n g f a c t o r, ζ, d e n g a n menggunakan rekaman melemahnya getaran bebas dari sebuah sistem SDOF : metoda logarithmic decrement dan metoda setengah amplitudo. Keduanya berdasarkan pada persamaan,

)

cos(

)

(

t

=

Ue

−ζω

ω

t

−

α

u

d t

Dalam metoda logarithmic decrement , amplitudo gerakan, u_P, pada per mulaan dari putaran dan amplitudonya, u_Q, pada akhir putaran , dihitung.

Pada akhir dari periode (misal satu putaran ) nilai dari cos (ω_dt - α ) kembali pada nilai yang didapat pada permulaan dari putaran.

Karena itu, didapat persamaan

d nT

Q P

e

u

u

_ζω

=

the logarithmic decrement δ dijelaskan sebagai berikut :

d n Q

P

T

u

u

ζω

δ

=

⎟

⎟

⎠

⎞

⎜

⎜

⎝

⎛

dimana T_d adalah periode natural damped , dijelaskan sebagai berikut :

2

1

2

2

ζ

ω

π

ω

π

−

=

=

n d d

T

jadi, kita mendapatkan

2

1

2

ζ

πζ

ζω

δ

−

=

=

_n

T

_d

Untuk damping kecil ( ζ < 0.2 ) , perkiraannya :

πζ

δ

=

2

dapat diterima, memungkinkan faktor damping untuk

didapat dari persamaan :

Prosedur yang sama juga diterapkan pada metoda setengah amplitudo, dimana hasilnya merupakan

perhitungan yang sederhana untuk faktor damping.

Metoda setengah amplitudo ber dasar kan pada

amplitudo dari envelope curve (kurva envelope).

t

n

Ue

t

u

ˆ

(

)

=

−

ζω

2

ˆ

ˆ

P

R

u

u

=

Titik-titik tersebut adalah N periode damped yang

terpisah, dimana N tidak harus sebuah bilangan bulat.

Kemudian,

2

ˆ

ˆ

=

=

n

NT

d

R

P

e

u

u

ζω

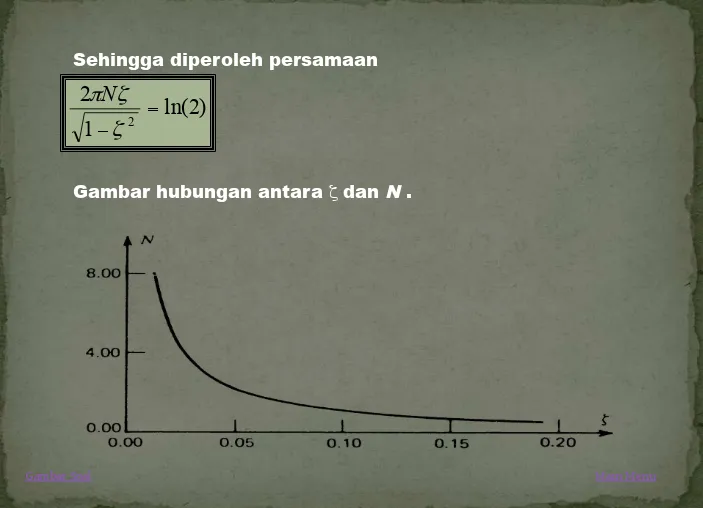
Sehingga diperoleh persamaan

)

2

ln(

1

2

2

=

−

ζ

ζ

π

N

Gambar hubungan antara ζ dan N .

Main  Menu  

Tetapi, untuk nilai damping yang kecil, ζ2 _{<< 1,}

menghasilkan:

)

2

ln(

2

π

N

ζ

=



atau

N

11

.

0

=



ζ

Contoh

Sebuah sistem bergetar terdiri dari berat W = 10 lb dan pegas

dengan kekakuan K = 20 lb/in. Akibat redaman viskous (liat)

sehingga terjadi amplitudo puncak 1,0 dan 0,85.

a). Frekuensi natural tak teredam (ωn)

b). Pengurangan logaritmis c). Rasio redaman(ζ)

d). Koefisien redaman(c)

e). Frekuensi natural redaman (ωn)

Penyelesaian :

a). Frekuensi natural tak teredam (ωn)

m K n =

ω

₂ in/sec 386 lb 10 = = g W m

K = 20 lb/in ,

sec rad 78 , 27 386 10 20 = = n

ω 4,42 sps

2 78 , 27

2 = =

= π π ω f atau

b). Pengurangan logaritmis

2 1

ln

y

y

=

δ

y1 = 1,00

y2 = 0,85

165

,

0

85

,

0

0

,

1

ln

=

=

δ

c). Rasio redaman(ζ)

π

δ

ζ

2

=

0

,

026

d). Koefisien redaman(c)

cr

c

c

=

ζ

c

=

2

k

⋅

m

=

2

10

⋅

20

386

cr

cr

c

c

=

ζ

⋅

(

)

⎟

⎠

⎞

⎜

⎝

⎛

⋅

=

386

20

10

2

026

,

0

in

dt

lb

⋅

=

0

,

037

e). Frekuensi natural redaman (ωD)

,

1

ζ

2

ω

ω

_D

=

−

rad/det

77

.

27

)

026

.

0

(

1

78

.

27

−

2

=

=

D

Contoh

Penyelesaian :

049

.

0

25

.

2

11

.

0

=

=

ζ

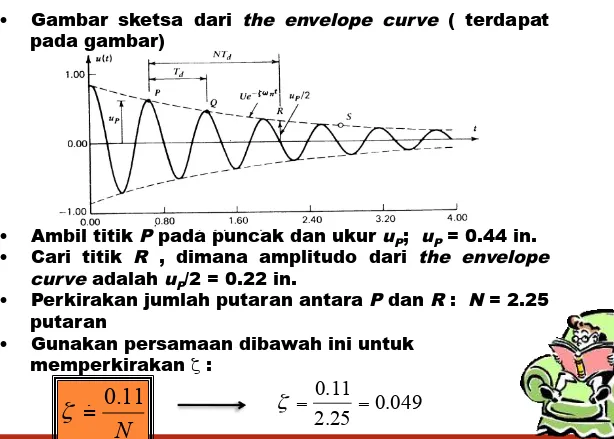
• Gambar sketsa dari the envelope curve ( terdapat pada gambar)

• Ambil titik P pada puncak dan ukur u_P; u_P = 0.44 in. • Cari titik R , dimana amplitudo dari the envelope

curve adalah u_P/2 = 0.22 in.

• Perkirakan jumlah putaran antara P dan R : N = 2.25 putaran

• Gunakan persamaan dibawah ini untuk memperkirakan ζ :

N

11

.

0

=



Level dari damping dari sebuah sistem juga tercer min dalam jumlah yang disebut time constant, τ.

Yang ar tinya waktu yang diper lukan bagi amplitudo untuk berkurang dengan faktor 1 / e. Dengan perlakuan yang sama ketika formula setengah amplitudo didapat, persamaan untuk time constant bisa didapat.

atau,

e

e

n

=

τ

ζω

dengan mengeliminasi logaritma pada kedua sisi, kita dapatkan

1

=

τ

ζω

n

kemudian, time constant , τ, diberikan sebagai :

πζ

ζω

τ

2

1

n

n

T

=

=

Getaran Bebas dari sebuah sistem

SDOF dengan

Coloumb

Damping

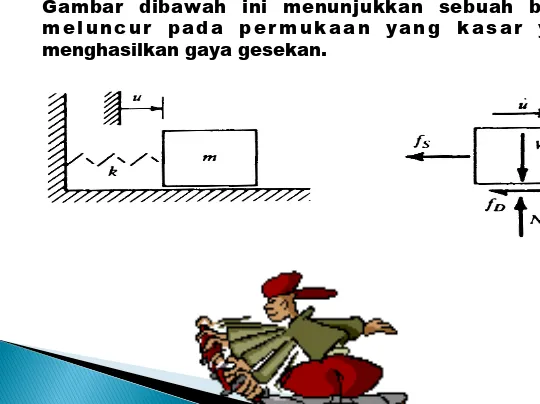
Gambar dibawah ini menunjukkan sebuah benda m e l u n c u r p a d a p e r m u k a a n y a n g k a s a r y a n g menghasilkan gaya gesekan.

mg

N

f

_D

=

µ

_k

=

µ

_k

dimana

µ_k adalah koefisien gesekan kinetik, atau koefisien gesekan luncur.

Gaya gesek selalu berlawanan dengan gerakan, yakni ber lawanan gaya yaitu u. Dengan m e n g g u n a k a n h u k u m N e w t o n I I , k i t a mendapatkan

u

m

f

f

_s

−

_D

=





−

tapi

f_s = ku dan

)

sgn(

u

mg

f

D

=

µ

k



Gerakan hasil di plot dalam gambar diatas. Catatan pada gambar, bahwa sistem coulomb-damped berlaku seperti sistem undamped SDOF yang posisi seimbangnya berubah di akhir pada setiap setengah putaran.