BAB 3
METODE PENELITIAN
Pada bab ini, akan dijelaskan metode-metode yang penulis gunakan dalam
penelitian ini. Adapun metode yang akan digunakan dalam penelitian ini adalah
Metode Simpleks dan Metode Branch and Bound.
3.1. Metode Simpleks
Metode simpleks adalah prosedur pemecahan program linier yang lebih efisien
daripada metode grafik. Meskipun problem program linier dapat diselesaikan
secara grafik, akan tetapi hampir seluruh problem program linier sesungguhnya
tidak dapat diselesaikan dengan cara ini, karena pada umumnya program linier
mempunyai lebih dari 3 variabel.
Oleh karena itu, George Dantzig pada tahun 1947 mengajukan satu
metode yang paling berhasil untuk meyelesaikan problem program linier yang
disebut Metode Simpleks.
Secara umum, bentuk umum dari program linier dapat dimodelkan sebagai
berikut.
Maksimumkan: z = c1x1 + c2x2 + … + cnxn Kendala :
xn ≥ 0, n = 1, 2, 3, …
Minimumkan : z = c1x1 + c2x2+ … + cnxn Kendala :
xn ≥ 0, n = 1, 2, 3, …
Prosedur (tahap proses) untuk menyelesaikan program linier dengan
menggunakan metode simpleks adalah sebagai berikut:
Tahap 1. Merumuskan problema ke dalam model simpleks.
Tahap 2. Menyusun tabel simpleks iterasi awal.
Tahap 3. Mengecek nilai optimal tabel simpleks dengan cara sebagai berikut:
a. Kalau sudah optimal, tafsirkan hasil penyelesaian.
b. Kalau belum optimal, teruskan penyelesaian pada tahap berikutnya.
Tahap 4. Mengidentifikasi variabel yang akan masuk dalam tabel.
Tahap 5. Mengidentifikasi variabel yang akan dikeluarkan dalam tabel.
Tahap 6. Menyusun tabel simpleks baru.
Tahap 7. Mengecek nilai optimal tabel simpleks baru tersebut:
a. Kalau sudah optimal, tafsirkan hasil penyelesaian.
b. Kalau belum optimal, kembali kepada prosedur tahap 4.
Tahap 1. Perumusan Model Simpleks
Untuk menyusun rumusan program linier ke dalam model matematika simpleks,
kita harus mengubah bentuk tanda ketidaksamaan kendala ke dalam bentuk tanda
memenuhi persyaratan yang dikehendaki pada persamaan kendala tersebut).
Bentuk ini biasanya dikatakan sebagai bentuk standar, sehingga bentuk standarnya
dapat dirumuskan sebagai berikut: (Asumsikan untuk permasalahan maksimasi).
Maksimumkan: z = c1x1 + c2x2 + … + cnxn Kendala :
xn ≥ 0, n = 1, 2, 3, …
si ≥ 0, i = 1, 2, 3, …
Pada permasalahan dalam penelitian ini, tanda ketidaksamaan kendala
adalah lebih kecil atau sama dengan (≤), diubah menjadi tanda sama dengan (=)
dengan syarat menambah variabel slack pada sisi bagian kiri persamaan kendala.
Mengapa harus ditambah dengan variabel slack? Jawabannya ialah agar
persamaan garis kendala memenuhi persyaratan penyelesaian pada daerah
kelayakan.
Tahap 2. Menyusun Tabel Simpleks
Ada beberapa macam format tabel simpleks dewasa ini. Salah satu format yang
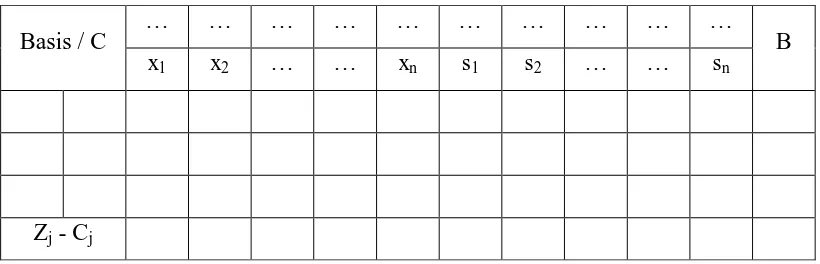
Tabel 3.1. Format Tabel Simpleks
Basis / C … … … B
x1 x2 … … xn s1 s2 … … sn
Zj - Cj
Penjelasan tabel simplek di atas:
1. C = Nilai kontribusi setiap variabel basis dalam proses iterasi.
2. Basis = Variabel basis dalam proses iterasi (nilainya tidak sama dengan nol).
3. B = Nilai variabel basis dalam proses iterasi.
4. Cj – Zj = Nilai kontribusi dalam problema meminimalkan dari setiap variabel
dalam proses iterasi.
Tahap 3. Pengecekan Optimalisasi Tabel Simpleks Iterasi Awal
Pengecekan apakah tabel simplek pada iterasi awal telah atau belum optimal
dilakukan dengan cara melihat nilai Zj - Cj masing-masing variabel fungsi tujuan.
Apabila Zj - Cj untuk semua variabel bernilai nol atau positif, maka penyelesaian
problema tersebut telah optimal. Apabila tidak, maka dilakukan tahap proses
selanjutnya.
Tahap 4. Identifikasi Variabel yang Akan Masuk (Incoming Variable)
Untuk menentukan variabel yang mana akan masuk dalam pertimbangan untuk
diproses pada iterasi berikutnya adalah variabel keputusan (variabel non-basis)
nonbasis ini memiliki nilai terbesar yang dapat ditingkatkan dalam proses iterasi
selanjutnya.
Tahap 5. Identifikasi Variabel yang Akan Keluar (Outgoing Variable)
Dengan adanya variabel yang masuk kedalam tabel simpleks, maka salah satu dari
variabel basis harus keluar dari tabel simpleks tersebut agar diperoleh peningkatan
nilai tujuan maksimum. Cara mengidentifikasi variabel yang akan keluar adalah
dengan mencari hasil bagi antara nilai solusi dan nilai substitusi marjinal yang
terkecil dan bilangan tersebut bernilai non-negatif.
Tahap 6. Penyusunan Tabel Simpleks Iterasi Pertama
Untuk menyusun tabel simpleks iterasi pertama, kita harus mencari koefisien
elemen pivot dari tabel simpleks sebelumnya. Koefisien elemen pivot dapat dicari
dengan cara menghubungkan kolom pivot dengan baris pivot sedemikian rupa
sehingga titik potong kedua pivot ini menunjukkan koefisien, yang disebut elemen
pivot.
Koefisien-koefisien baris pivot yang baru dicari dengan menggunakan
rumus sebagai berikut:
Nilai Baris Pivot Baru = Nilai Baris Pivot Lama : Elemen Pivot
Untuk menghitung nilai baris baru lainnya, dilakukan dengan
menggunakan rumus sebagai berikut:
Tahap 7. Pengecekan Optimalisasi Tabel Simpleks Iterasi Pertama
Pengecekan apakah tabel simpleks pada iterasi pertama telah atau belum optimal.
Apabila Zj - Cj untuk semua variabel bernilai nol atau negatif, maka penyelesaian
problema tersebut telah optimal. Apabila tidak, maka kembali pada prosedur
Tahap 4.
3.2. Metode Branch and Bound
Metode Branch and Bound mula-mula dipakai dan dikembangkan oleh Land and
Doig (1960) untuk menyelesaikan program integer yang kemudian dimodifikasi
oleh Dakin (1965) dan telah dengan sukses menerapkannya di dalam kitab
undang-undang hukum dagang banyak orang dalam memecahkan persoalan
program integer (Sidabutar, 2008).
Metode ini telah menjadi kode komputer standar untuk program integer,
dan penerapan-penerapan dalam praktek tampaknya menyarankan bahwa metode
ini lebih efisien dibanding dengan pendekatan Gomory. Teknik ini dapat
diterapkan baik untuk masalah pure programming maupun mixed programming.
Secara umum, bentuk umum dari program integer adalah sebagai berikut.
Maksimumkan:
∑
dengan kendala:
Dengan demikian, penjabaran bentuk umum dari fungsi tujuan dan fungsi
kendala program integer adalah sebagai berikut.
Asumsikan fungsi tujuan program integer adalah sebagai berikut.
Maksimumkan:
z = c1x1 + c2x2 + … + cnxn
maka,
( ) =
= ∑ ; j = 1, 2, …, n
Selanjutnya, asumsikan fungsi kendala program integer adalah sebagai berikut.
maka,
∑ ; i =1, 2, …, m
Langkah-langkah Metode Branch and Bound
Asumsikan suatu masalah program integer.
Maksimumkan
Kendala dimana S0 = {x | Ax = b, x ≥ 0, dan integer}.
Ide umum dari metode branch and bound adalah pertama untuk menyelesaikan problema sebagai model kontinu, yakni menyelesaikan program integer sebagai
program linier:
Maksimumkan
Kendala dimana T0 = {x | Ax = b, x ≥ 0}.
Andaikan bahwa xr merupakan peubah yang berkendala integer yang mempunyai
nilai optimum kontimu xr* yang pecahan. Hasil dari tidak
memuat solusi integer yang layak. Sebagai akibatnya nilai integer layak dari xr
harus memenuhi salah satu dari dua kondisi berikut yakni:
atau
Kedua kondisi ini bilamana diaplikasikan untuk model yang kontinu maka
hasilnya merupakan dua problema saling lepas (mutually exclusive) dengan
himpunan kendala sebagai berikut:
(i) { }
(ii) { }
dan bilamana kendala-kendala integernya dimasukkan, maka diperoleh himpunan:
S1 = {x|Ax = b, , x ≥ 0, dan integer} dan
S2 = {x|Ax = b, , x ≥ 0, dan integer}
Sebenarnya bentuk ini merupakan pemisahan dari S0, yakni ,
. Solusi optimal x* dari problema yang diberikan, harus berada di salah satu S1 atau S2 dan harus juga merupakan solusi optimal dari salah satu subproblema berikut:
(i) Maksimumkan z = c.x kendala
Subproblema-subproblema ini dapat lagi diselesaikan dengan mengulangi
proses yang sama dengan merelaksasi kendala integernya dan mencabangkan
kembali bila solusi optimal mempunyai komponen yang bernilai pecahan atau
tidak integer. Proses percabangan ini akan membangun pohon keputusan, dengan
setiap node k dari pohon keputusan tersebut berhubungan dengan sebuah subproblema: Maksimumkan z = c.x kendala . Jika solusi optimal yang berhubungan dengan program linier tersebut layak (memenuhi) atau mempunyai
komponen-komponen bulat, maka solusi ini dicatat dan nilai objektifnya
merupakan batas bawah untuk nilai optimum. Dalam kasus seperti ini tidak perlu
dilakukan percabangan lebih jauh lagi dari subproblema ini dan node yang
demikian difathom atau dipangkas. Node yang belum terfathom disimpan dalam
master list. Pada beberapa node, nilai optimal (nilai integer terbesar yang lebih
kecil atau sama dengan nilai optimum jika fungsi objektif mempunyai
koefisien-koefisien integer) ̅̅̅ dari program linier yang bersangkutan merupakan sebuah
batas atas untuk nilai optimum dari semua turunannya. Jika batas atas tersebut
lebih kecil dari batas bawah terbaik yang ada, maka subproblema ini tidak
dicabangkan lagi. Proses Branch and Bound diteruskan sampai setiap
subproblema berhenti karena salah satu dari dua alasan berikut, yakni
(i) Sebuah solusi integer, atau
(ii)Batas atas lebih kecil dari batas bawah yang ada sekarang (Bangun, 2004).
Berdasarkan uraian di atas, maka prosedur atau langkah-langkah metode
Branch and Bound untuk masalah maksimasi adalah sebagai berikut.
1. Selesaikan masalah program linier dengan metode simpleks.
2. Teliti solusi optimumnya. Apabila variabel keputusan yang diharapkan
merupakan bilangan integer, maka solusi optimum integer telah tercapai.
Apabila satu atau lebih variabel keputusan yang diharapkan ternyata bukan
3. Jadikan solusi pada penyelesaian langkah 1 menjadi batas atas dan untuk batas
bawahnya merupakan solusi yang variabel keputusannya telah diintegerkan
(rounded – down).
4. Pilih variabel yang mempunyai nilai pecahan terbesar (artinya bilangan
desimal terbesar dari masing-masing variabel untuk dijadikan pencabangan ke
dalam sub-sub masalah). Tujuannya adalah untuk menghilangkan solusi yang
tidak memenuhi persyaratan integer dalam masalah itu. Pencabangan itu
dilakukan secara mutually exclusive untuk memenuhi persyaratan integer dengan jaminan tidak ada solusi fisibel (layak) yang diikutsertakan.
5. Untuk setiap sub-masalah, nilai optimum fungsi tujuan ditetapkan sebagai
batas atas. Solusi optimum yang diintegerkan menjadi batas bawah (solusi
yang sebelumnya tidak integer kemudian diintegerkan). Sub-sub masalah yang
memiliki batas atas kurang dari batas bawah yang ada, tidak diikutsertakan
pada analisa selanjutnya. Suatu solusi integer fisibel (layak) adalah sama baik
atau lebih baik dari batas atas untuk setiap sub masalah yang dicari. Jika solusi
yang demikian terjadi, suatu sub masalah dengan batas atas terbaik dipilih
untuk dicabangkan. Kembali ke langkah 4 (Winston, 2004).
Perhitungan dalam Metode Branch and Bound
Satu kerugian dasar dari metode Branch and Bound adalah bahwa metode ini mengharuskan pemecahan program linier yang lengkap di setiap node. Dalam
masalah besar, hal ini dapat sangat memakan waktu, terutama ketika satu-satunya
informasi yang diperlukan di node tersebut adalah nilai tujuan optimumnya. Hal ini diperjelas dengan menyadari bahwa sebuah batas yang “baik” diperoleh, “banyak” node dapat disingkirkan dengan diketahui nilai tujuan optimum mereka.
Hal di atas mengarah pada pengembangan sebuah prosedur di mana kita
Gagasannya adalah “mengestimasi” sebuah batas atas (asumsikan masalah maksimasi) dari nilai tujuan optimum di setiap node. Jika batas atas ini menjadi
lebih kecil daripada nilai tujuan yang berkaitan dengan pemecahan integer terbaik
yang tersedia, node tersebut disingkirkan. Keuntungan utamanya adalah bahwa
batas atas tersebut dapat diestimasi dengan cepat dengan perhitungan minimal.
Gagasan umum ini mengestimasi penalti (yaitu, penurunan nilai tujuan) yang
dihasilkan dari pemberlakuan kondisi dan . Ini dapat
dicapai dengan menambahkan setiap batasan ini ke tabel optimum di node
tersebut.
Walaupun metode Branch and Bound memiliki kekurangan, dapat dikatakan bahwa sampai sekarang, ini adalah metode yang paling efektif dalam
memecahkan program-program integer dengan ukuran praktis. Pada kenyataannya,
semua program komersial yang tersedia didasari oleh metode Branch and Bound.
Tetapi, ini tidak berarti bahwa setiap program integer dapat dipecahkan dengan