Materi Kalkulus 2 (Integral)

Definisi :

Misal f fungsi yang didefinisikan pada [a,b], f dikatakan terintegralkan pada [a,b]

jika



 



n i i i P

x

x

f

1 0

)

(

lim

ada, selanjutnya



b a

dx

x

f

(

)

disebut Integral Tentu (Integral Riemann) f dari a ke b, dan didefinisikan



b a

dx

x

f

(

)

=



 



n i i i P

x

x

f

1 0

)

(

lim

Teorema :

Jika fungsi f kontinu pada selang , - dan F suatu anti turunan dari fungsi f pada selang itu,maka :

∫ ( )

F(b)-F(a)

Bukti : Jika P = * + adalah partisi sebarang dari selang, -, maka :

F(b)-F(a) = F( )-F( )+F( )- F( )+. . .+F( )-F( )=∑ , ( ) (

)-Menurut teorema nilai rata-rata yang diterapkan pada fungsi F pada selang

,

-

kita peroleh

F(

) (

)

=F(

) . (

)

=f(

) .

dengan

.

Jadi

F(b) –F(a) =

∑

(

)

Ruas kiri adalah suatu konstanta,sedangkan ruas kanan adalah jumlah Riemann fungsi f pada selang , -. Jika kedua ruas kita ambil limitnya untuk | | ,kita peroleh

1. Sifat Penambahan Selang Teorema :

Jika f terintegralkan pada suatu selang yang mengandung tiga titik a, b dan c, maka

dx

x

f

c a



(

)

=

f

x

dx

b a



(

)

+

f

x

dx

c b



(

)

bagaimanapun urutan a, b dan c.

Contoh :

1.



x

dx





x

dx





x

dx

2 1 2 1 0 2 2 0 2

_2.

_

_x

_dx

_

_

_x

_dx

_

2

_

_x

_dx

3 2 3 0 2 2 0 2

3.



x

dx



x

dx



x

dx

 





2 1 2 1 0 2 2 0 2 2. Sifat Simetri Teorema :

Jika f fungsi genap

[f(-x) = f(x)] ,

maka

f

x

dx

a a





)

(

= 2

f

x

dx

a



0

)

(

dan

Jika f fungsi ganjil

[f(-x) = - f(x)],

maka

f

x

dx

a a





)

(

= 0.

Contoh:

1.

∫

∫

( )

⁄

2.

∫

( )

Sifat yang lainnya :

Jika fungsi f dan g kontinyu pada selang , - dan k suatu konstanta, maka

1.

∫ ( )

2.

∫ ( )

∫ ( )

5.

∫ , ( ) ( )-

=

∫ ( )

∫ ( )

6.

∫ ( )

≥0 jika f(x)≥0 pada

,

-7.

∫ ( )

≤

∫ ( )

jika f(x)≤g(x) pada

,

-8.

∫ ( )

+

∫ ( )

=

∫ ( )

Bukti : kita buktikan sifat sebagai berikut

1.

∫ ( )

( ) ( )

2.

∫ ( )

( ) ( ) ( ) ( ) ∫ ( )

Bukti no. 4 :

∫, ( ) ( )-

| |

∑, ( ) ( )-

| |

∑ ( )

| |

∑ ( )

∫ ( )

∫ ( )

Contoh soal :

1.

∫ ( )

( ) ( )

2.

∫ ( )

( ) ( ) ( ) ( ) ∫ ( )

3.

∫ ,

-

∫

∫

1



 Jawab :

dx

x

dx

x

dx

x

x







  







2 1 2 2 1 2 1 2

₎

₄

₆

6

4

(

= 4 2 1 3 2 1 2

3

6

2

 



































_x

_x

= 4











 













 

3

1

3

8

6

2

1

2

4

=  12

MENCARI LUAS DAERAH DENGAN TEKNIK INTEGRASI

Perhatikan grafik fungsi dibawah ini!



Fungsi f(x) pada selang [a,b], bagi selang [a,b] menjadi n partisi



Panjang a =

x

0

<

x

1

<

x

2

< …<

x

n-1

<

x

n



Panjang partisi ∆

x

i

=

x

i

- x

i-1



∑

( )

CONTOH 1

Luas daerah dibawah kurva f(x) dapat dicari melalui limit jumlah Riemann sebagai berikut.

Partisikan selang [-1,4] menjadi n bagian!

P = { x_0, x_1, x_2, …, xi-_1, x_i, …, x_n-1, x_n }

Panjang selang dapat ditentukan : ( )

Ambil titik sampel x_i di selang [x_i-1, x_i]

Nilai titik untuk i = 0, 1, 2, …, n adalah :

x0 = -1 ( ) … ( ) ( ) Jadi : f (xi) = xi + 3 , . /- . / Sehingga : ∫ ( ) ∑ ( ) ∆ x 0 1 2 3 4 5 6 7 8 -2 -1 0 1 2 3 4 5 6 f(x) = x+3

( ) ( ) ∑ . ( )/ . ( )/ . )/ CONTOH 2

Cari luas yang dibatasi oleh kurva f(x)=x2 - 2x dan g(x)=6x - x2 dengan selang [0,4] JAWAB : P = { x_0, x_1, x_2, …, xi-_1, x_i, …, x_n-1, x_n } ∆x = = x₀ = 0 x1 = 0 + ∆xi = 0 + x2 = 0 + 2∆x = 0 + 2 . / … x i = 0 + i . ∆ x = 0 + i . / -2 -1 0 1 2 3 4 5 6 7 8 9 10 0 1 2 3 4 5 6 7 x y f(x)=x2 - 2x g(x)=6x - x2

Jadi : f (x_i) = x2 - 2x = . / . /- 2. / = g(x_i ) = 6x-x2 = 6 . /- . / . / = . / . / ∑ , (xi ) – g(xi )] . ∆ x ∑ ,( ) ( )] . ∑ ( ) . ∑ ∑ = . ( )( )/ ( ) = . )/ = = =

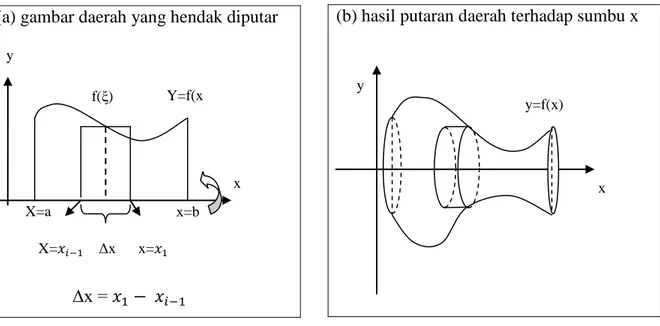
VOLUME BENDA PUTAR

Suatu bidang datar jika diputar mengelilingi suatu garis tertentu akan menghasilkan benda yang dapat dihitung volumenya. Ada dua metode untuk menghitungnya, yaitu metode cakram dan metode kulit silinder.

A.

Metode cakram

Diketahui suatu bidang datar yang dibatasi oleh grafik fungsi f(x), sumbu x, garis x = a, dan x = b, seperti tampak pada gambar 1. Jika luasan tersebut diputar mengelilingi sumbu x maka akan didapatkan suatu benda yang dapat dihitung volumenya (gambar 1 (b)). Jika suatu

y Y=f(x ) f(ξ) X=a x=b x y

suatu silinder dengan jari-jari alasnya f(ξ) dan tinginya Δx.

Gambar 1. Volume benda Putar dengan Menggunakan Metode Cakram

(c) hasil putaran pias terhadap sumbu x

Volume silinder (hasil putaran pias terhadap sumbu x) tersebut adalah

Selanjutnya, volume benda secara keseluruhan dapat didekati dengan menjumlahkan volume silinder yang diperoleh dari seluruh interval, yaitu,

Jumlahan ini akan semakin mendekati volume benda sesungguhnya jika diambil nilai limitnya seperti pada saat mencari luas datar.

(a) gambar daerah yang hendak diputar

Δx =

(b) hasil putaran daerah terhadap sumbu x

X= Δx x= X= 1 Δx x= 1 y=f(x) x f( ) Δx ( ( )) ∑ ( ( ))

X = 2 Y =

x y

dari daerah yang dibatasi oleh grafik fungsi f(x), sumbu x, garis x = a, x = b, dan diputar mengelilingi sumbu x sebagai berikut.

Contoh 1

Hitung volume benda yang terjadi jika daerah pada kuadran 1 yang dibatasi oleh kurva y = dan garis x = 2 diputar mengelilingi sumbu x.

Jawab:

Daerah pada kuadran 1 yang dibatasi oleh kurva y = , sumbu x dan garis x = 2

Hitung volume dengan menggunakan persamaan: ∫ ( ( )) = ∫ ( ) = π∫ = ( ) =

∫ ( ( ))

y Y=f(x ) f(ξ) X=a x=b x y x f(ξ) g(ξ) x=a x=b y=g(x) y=f(x) g(ξ) x=g(y) y = d y = y = y = c _x y y f(ξ) y=

Rumus Volume Benda Putar Menggunakan Metode Cakram:

Daerah dibatasi oleh

Sumbu

putar Gambar daerah Rumus

Y = f(x) Sumbu x Garis x = a Garis x = b Sumbu x V = ∫ ( ( )) Y=f(x) Y=g(x) Garis x=a Garis x=b Sumbu x V = ∫ 0( ( )) ( ( )) 1 x=g(y) sumbu x garis y=c garis y=d Sumbu y y= V = ∫ ( ( )) x=g(y) x=h(y) garis y=c garis y=d Sumbu y V = ∫ 0( ( )) ( ( )) 1 Contoh 2

Hitung volume benda putar dari daerah yang dibatasi y = dan y = x jika diputar pada sumbu y. X= Δx x= X= x= x=h(y) x=g(y) g( ) y=d y= y=c

o

Jawab:

Tentukan titik potong kedua kurva tersebut:

Jadi titik potongnya adalah (0,0) dan (1,1) Hitung volume dengan persamaan:

V = π∫ .(√ ) ( ) / = π ∫ ( )

= π . / = π (. / )

= satuan volume

B. Metode Kulit Silinder

Metode cakram dapat dipakai jika sumbu putarnya tegak lurus dengan piasnya. Jika pengambilan piasnya sejajar dengan sumbu putar, maka dipergunakan metode kulit silinder.

Jika luasan diputar terhadap sumbu y, maka akan tersebut suatu benda yang berlubang di tengahnya. Jika pias pada interval ke-i diputar mengelilingi sumbu y, maka akan terbentuk suatu silinder yang tingginya f( ) dan berlubang di tengahnya.

Daerah yang dibatasi y = dan y = x y x y= y=x ( )

Akan dihitung adalah volume silinder yang diarsir (gambar 2 (c)) dan itu sama artinya dengan menghitung volume silinder yang berjari-jari dikurangi dengan volume silinder yang berjari-jari atau

. π ( ) (ξ) ( ) ( ) = π f( )(( ) ( ) )

= π f( ) (( ) ( )) (( ) ( )) Jika adalah titik tengah dari dan , maka

ξ

Sehingga π (ξ) ξ Δ , maka

∫

π

( )

Contoh 1

Hitung volume benda jika daerahnya dibatasi dengan y= dan x=2 dan diputar mengelilingi sumbu y.

Jawab:

Hitung volume dengan

menggunakan persamaan: . ∫ π = 2π ∫ = , = ( ) = 8π satuan volume Daerah yang dibatasi y = , sumbu x dan garis x = 2

x x=2

y= y

y Y=f(x ) f(ξ) X=a x=b x y x f(ξ) g(ξ) x=a x=b y=g(x) y=f(x) g(ξ) x=g(y) y = d y = y = y = c _x y h( ) y= y y=g(x) x

Rumus Volume Benda Putar dengan Metode Kulit Silinder

Daerah dibatasi oleh

Sumbu

putar Gambar daerah rumus

y = f(x) Sumbu x Garis x = a Garis x = b Sumbu y V = ∫ ( ) y=f(x) y=g(x) Garis x=a Garis x=b Sumbu y V = ∫ ( ( ) ( )) x=g(y) sumbu y garis y=c garis y=d Sumbu x y= V = ∫ ( ) x=g(y) x=h(y) garis y=c garis y=d Sumbu x V = ∫ ( ( ) ( )) Contoh 2

Hitunglah volume benda putar pada gambar dibawah ini jika diputar mengelilingi sumbu x. X= x= X= x= y x=h(y) x=g(y) g( ) y=d y= y=c

O

Hitung volume dengan menggunakan persamaan: . π ∫ (√ ) = 2π ∫ ( ⁄ ) = 2π . ⁄ / = 2π (. / ) = π satuan volume

C. Menghitung Volume Benda dengan Metode Penampang Melintang

Selain untuk menghitung volume benda putar, integral juga dapat dipakai untuk menghitung volume yang sudah diketahui bentuk penampang melintangnya. Mula-mula ditentukan letak sumbu-sumbu koordinat pada benda tersebut sedemikian hingga luas penampangnya dapat dicari. Kemudian benda tersebut dibagi dalam n subinterval yang sama besar. Volume benda dalam satu subinterval dapat dipandang sama dengan volume silinder yang luas alasnya A(x) (luas penampang benda tersebut) dan tingginya Δx, yaitu ( ) .

Volume benda secara keseluruhan adalah limit dari jumlahan volume seluruh subinterval, yaitu

Contoh 1

Tentukan berapa volume gelas yang terlukis di bawah ini, jika tinggi bagian yang dapat menampung air 16 cm. Bentuk luar gelas tersebut dianggap parabola dengan persamaan x = .

Daerah yang dibatasi y = dan y = x

x y=x y= y A

V =

∫ ( )

O

y

x

y

Jawab:

Mula-mula ditentukan terlebih dahulu luas penampang benda tersebut. Oleh karena penampangnya berupa lingkaran, maka luasnya sama dengan π kali kuadrat dari jari-jari lingkaran dari gambar di bawah terlihat bahwa panjang jari-jari lingkaran tersebut adalah y sehingga ( ) π ( ) π dan ∫ π = . / = (( ) ) = 128 π satuan volume

MENENTUKAN PANJANG KURVA TEKNIK INTEGRASI

Jika diketahui suatu fungsi f(x) maka akan dihitung panjang grafik fungsi tersebut dari x = a sampai x = b. Interval a ≤ x ≤ b dibagi menjadi n subinterval. Karena subinterval sangat kecil maka potongan – potongan kurva (ΔS) dapat dianggap sebagai suatu garis lurus (ΔW) sedemikian sehingga ΔS ≈ ΔW .

Sehingga dapat diterapkan Teorema Phytagoras, yaitu ( ) = ( ) + ( )

Atau

ΔS = √( ) ( )

Jika ruas kanan persamaan tersebut dikalikan dengan bentuk diperoleh ΔS = √( ) ( )

= √( ) ( ) ( ) . Δx = √ ( ) Δx

Untuk menghitung panjang seluruh kurva, sama artinya dengan menjumlahkan potongan – potongan kurva tersebut. Jadi, panjang kurva y = f(x) dari x = a sampai x = b adalah

S =

∫ √ (

)

dx atau S =

∫ √ ( ( ))

dx

Rumus Panjang Kurva

Kurva Rumus

y = f(x) dari x = a sampai x = b

S = ∫ √ ( ) dx atau S = ∫ √ ( ( )) dx

x = (y) dari y = c sampai y = d

S = ∫ √ ( ) dy atau S = ∫ √ ( ( )) dy { _{( )} ( ) Dari t = a sampai t = b S =∫ √( ) ( ) dt Contoh 1

Carilah panjang ruas garis dari A(0, 1) ke B(13) dengan persamaan garis y = x + 1 ? Penyelesaian:

persamaan garisnya y = x + 1, sehingga = dan mengerjakan berdasar rumus nomer satu pada tabel,

S = ∫ √ ( ) = ∫ √ ( ) dx

= ∫ √ dx = ∫ √ dx =∫ √ dx

= ∫ = ⟦ ⟧ = 13 Contoh 2

Hitung panjang kurva x = , y = , untuk 0 ≤ x ≥ 1! Penyelesaian: = dan = 2t sehingga( ) = dan ( ) =

S =∫ √( ) ( ) dt = ∫ √ dt = ∫ √ dt

= ( ) - = ( √ )

INTEGRAL PARSIAL

Ialah metode untuk memecahkan permasalahan integral dengan menggunakan subtitusi ganda.Metode ini di dasar pada pengintegralan rumus untuk turunan hasil kali 2 fungsi.

Secara umum: Y = U.V Y' = U'V +V'U = .V + .U Dy = du.V +dv.U ∫ = ∫( ) y =∫ ∫ y-∫ =u.v-∫

Dengan x adalah variabel di setiap fungsi y.u dan v

A. Integral Parsial Sederhana

 Integral Parsial Sederhana Tak Tentu 1) ∫ =……… Misal = u =v du =dx dv =cosx dx v=∫ =sinx ∫ uv –∫ =x sinx –∫ =x sinx + cosx + c 2) ∫ =………… Misal : u =lnx dv=dx du= dx v = x

= x lnx - ∫ dx = x lnx - ∫ = x lnx – x + C 3) ∫ = ……….. U = arc sinx dv = dx du = √ ∫ ∫ = x arc sinx – ∫ √ = x arc sinx - ∫ _√ =x arc sinx – √ + C

 Integral Parsial Sederhana dengan Batas (Tentu) ∫ = (uv) - ∫ Contoh : 1) ∫ =……. Misal : u = x dv=cosx dx du = dx v =sin x ∫ π = (uv) -∫ =(x sinx ) - ∫ = = + cos - cos =0-1-1 =-2 2) ∫ = x ln x - x = e ln e – 1 ln 1 – (e-1) =e-o-e+1 =1

3) ∫ ⁄ = x arc sin x ⁄ – √ ⁄

= arc sin – (√ ( ) - √ ) = ( ) – √ + 1

= - √ + 1 B. Integral Parsial Berulang

 Integral Parsial Berulang Tak Tentu 1) ∫ sinx dx =….

Misal :u= dv=sinx dx du=2x dx v=-cosx

∫ sinx dx = u.v - ∫

=- cosx +∫ ( ) =- cosx +2∫

=- cosx +2(x sinx –∫ ) =- cosx +2x sinx +2 cosx +C

2) ∫ sinx dx =…. Misal: u = dv = sinx dx du = v = -cosx ∫ sinx dx = uv – ∫ = - cosx -∫ ( ) dx = - cosx +∫ cosx dx  ∫ cosx dx = … Misal :u = dv = cosx du = dx v = sinx ∫ cosx dx = uv –∫ = sinx –∫ dx ∫ ∫

= - cosx + sinx –∫ dx 2∫ sinx dx = sinx - cosx

∫ sinx dx = sinx - cosx +C

3) ∫ x dx =…… Misal : u = sec x dv = x dx du = sec x tg x dx v = tg x ∫ x dx = uv – ∫ = sec x tg x –∫ ( ) dx =sec x tg x - ∫ x sec x = sec x tg x – ∫( x-1) sec x dx = sec x tg x - ∫ x + ∫ 2∫ x dx = sec x tg x + ∫ dx ∫ x dx = sec x tg x + in I sec x – tg x I +C

 Integral Parsial Berulang Dengan Batas(Tentu) Contoh : 1) ∫ ⁄ sinx dx = … Misal : u = dv = sin x dx du = 2x dx v = -cosx ∫ ⁄ sinx dx = (uv )I - ∫ = - I ⁄ + 2 x sin x I ⁄ + 2 cos I ⁄

= -( ₎) cos( ) + cos0 + 2( ) sin ( ) - 2 (0) sin o + 2 cos ( )-2 cos 0 =0+0+o+ -0+0-2

= -2 2) ∫ sinx dx = …

=0 - 0 + + = ( + 1 )

INTEGRAL FUNGSI TRIGONOMETRI

Trigonometri Aturan Integral

∫ ∫ ∫ ∫ ∫ ∫ Identitas Trigonometri

Untuk Sudut Rangkap

( ) ( )

Pengubahan dari bentuk perkalian menjadi bentuk penjumlahan

1. ( ) ( ) 2. ( ) ( ) 3. ( ) ( ) 4. ( ) ( ) Contoh Soal ∫( ) ∫( )

∫ ∫( ) Pembahasan ∫( ) ∫ ∫ ∫( ) ∫ ∫ ∫ ∫( ) ∫( ) ∫ ∫ ∫ ( ( ) ( )) ∫( ) ( ( )) ( ) ∫ √ √ ∫ ( ) ∫( ) ( )

INTEGRAL SUBSTITUSI TRIGONOMETRI

A.

Substitusi Fungsi Trigonometri

Metode Substitusi Trigonometri dapat digunakan untuk mengitung integral dengan bentuk integran adalah : √ , √ , √ dengan a,b adalah konstanta,maka gunakan substitusi Trigonometri yang merujuk kepada Rumus Trigonometri/Identitas Phytagoras:

a) √ gunakan substitusi atau Maka : √ = √ = √ = √ = Atau √ = √ = √ = √ =

b) √ gunakan substitusi atau Maka : √ = √ = √ = √ = Atau √ = √ = √ = √ =

c) √ gunakan substitusi atau Maka :

√ = √ = √ = √ = Atau √ = √ = √ = √ =

Sehingga didapatkan differensialnya berturut-turut sebagai berikut : a) atau ,

b) atau ,

c) atau . Oleh karena itu diperoleh :

√ = dengan - /2 /2

√ = dengan - / 2 / 2

√ = dengan 0 / 2 atau

3 / 2

Agar lebih mudah maka gunakan tabel berikut :

Bentuk Integran Gunakan Substitusi Integran Rasional Differensialnya √ Atau Atau Atau √ Atau Atau Atau √ Atau Atau Atau

Contoh Soal:

1.

∫

√

=

Misal :

∫

√

=

∫

√

=

∫

√

=

∫

=

∫

=

+ c

2.

∫

( ) ⁄

=

Misal :

∫

( ) ⁄

=

∫

( ) ⁄

=

∫

( )

=

∫

( )

=

∫

( )

=

∫

=

∫

=

| |

=

⟨

√

⟨

Ingat : √

Substitusi Dengan

Bila suatu integral, integrannya merupakan fungsi dari atau maka integral tersebut diselesaikan dengan substitusi

Perhatikan :

√

√

z

√

Sehingga : 1. Sin x = 2. Cos x = cos2 Contoh soal : 1. Diselesaikan ∫ Substitusi Ingat sin x = Sehingga : ∫ ∫ = ∫ = ∫_{( )} = ∫_{( )} = 2 ⟨ ⟨ = 2. Diselesaikan ∫ Substitusi Ingat : cos x = Sehingga : ∫ ∫ = ∫ = ∫ = ∫ (√ ) dz = 2

=

√

√

INTEGRAL SUBSTITUSI BENTUK KUADRAT

 Bila diketahui f(x) = (2x-5)4 maka:

(2x-5) disebut bilangan pokok / bilangan dasar 4 disebut pangkat / eksponen

Tampak diatas bahwa pangkatnya lebih dari 1 dan bilangan pokoknya terdiri dari 2 buah suku yang merupakan persamaan linier maka untuk menentukan integral fungsi aljabar bentuk diatas, menggunakan rumus sebagai berikut :

Contoh Soal : Selesaikanlah ! a.





3x2



5dx







 





x



c c x c x            6 6 1 5 2 3 18 1 2 3 6 3 1 2 3 1 5 3 1 b.





_

_





   3 2 3 2 3 4 3 3 4 3 x dx x dx



























x



c c x c x c x c x dx x                            



3 3 1 3 1 3 1 3 3 3 2 3 2 3 4 4 9 3 4 4 9 3 4 3 4 3 3 4 3 1 4 3 3 4 3 3 3 2 4 3 3 4 3

Kadang-kadang suatu integral dapat dicari dengan melakukan substitusi sederhana menggunakan rumus sebagai berikut:



    c x n a du axn n 1 1



    c u n du un n 1 1 1





_

_





      c b ax n a dx b ax n n 1 1 1

Contoh Soal : a.





4x2 6x



10



16x12



dx → misalkan u



4x2 6x



4 du d



4x2 6



dx du8x6dx



x x



c c u du u      



11 2 11 10 6 4 11 1 11 1 .

 Interagran berbentuk p



axb



q dengan p dan q bilangan bulat

Akar dapat dihilangkan dengan substitusi z  p axb atau ax + b = zp. Jadi a dx = p . z p-1 dz Contoh : 1.



_x.3 ₁_xdx Jawab Subsitusi 3 3 3 1 1 1 z x x z x z      





 

dz z dx dz z dx z d x d z x 2 2 3 3 3 3 1 1         Maka :



 







x_.3₁xdx  ₁z3 z₃z2 dz









 x  x c c z z c z z dz z z dz z z                  _              3 7 3 4 7 4 7 4 6 3 3 3 1 . 7 3 1 . 4 3 7 3 4 3 7 1 4 1 3 3 1 3

Jadi :











x 3 x dx  3 x 4  3 x 7 c 1 . 7 3 1 . 4 3 1 . 2.



x dx x 1 Jawab: Subsitusi :





 

dz z dx z d x d z x z x x z x z 2 1 1 1 1 1 2 2 2 2            Maka :





   z zdx z dx x x 2 . 1 1 2







x



x c c z z dx z dx z             _     





1 2 1 3 2 2 3 2 2 2 2 1 3 3 2 2 Maka :



x



x c dx x x      



1 2 1 3 2 1 3  .Integran berbentuk p q a cx b ax        

dengan p dan q bilangan bulat. Akar dapat dihilangkan dengan substitusi :

z = p q a cx b ax         Contoh : 1.







_{ } dx x x x 3 2 2 2 2 2 Jawab: 1) Substitusi. p q a cx b ax         ke dalam 2

2) Cari x dalam notasi 2 3) Cari dx dalam notasi 2

Subsitusi





                           1 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 z z d dx z z x z x x z x x z z x x z x x z x x z 1 2 2 2 2 ₃ 3      z z x









1 4 1 2 2 2 2 1 2 2 1 1 2 3 3 3 3 3 3 3 3 3              z z z z z z z z z 2 1 1 v u v v u dx 





  















dz z x dz z z z z z dz z z z z z 2 3 2 2 3 5 2 2 5 2 3 3 3 3 2 1 12 1 6 6 6 6 1 2 2 3 1 6                u = 2 – 2 2z3 → u1 = -6z2 v = z3 + 1 → v1 = 3z2

Maka :













  



c x x c z c z c z dz z dz z dz z dz z z dz z z z z dz z z z z z dx x x x                                                          















3 2 2 2 3 1 3 3 3 6 3 2 3 2 3 3 2 3 2 3 2 2 3 3 3 2 2 2 4 3 4 3 2 1 2 3 3 1 1 2 3 2 3 1 2 3 1 16 24 16 24 1 4 1 24 1 12 . . 4 2 2 2 2 2 Jadi :







             c x x dx x x x 3 2 3 2 2 2 4 3 2 2 2 2

 Integran memuat akar-akar yang tidak sempurna senama, misalnya :



3 1



x x

dx

Akar-akar menjadi senama, substitusi 6

x z 

Angka 6 pada pangkat diperoleh dengan cara mencari KPK dari akar pangkat yang ada, yaitu 3 dan 2.

 Dari z6 x z6  x

,

 6z5dzdx  2 3 6 6 z z z x     3 2 6 3 6 3 _x  _z _z  _z Maka :















_  1 6 1 3 2 5 3 _{z z} dz z x x dx

 





 

 

x arc tag

 

x c c z tg arc z c z tg arc z dz z dz z z z dz z z dz z z                                   









6 6 2 2 2 2 2 2 2 2 . 6 6 . 6 6 . 6 1 1 1 6 1 1 1 1 6 1 1 1 6 1 6 Jadi :



  

 



    x arc tag x c x x dx _{6 6} 3 6 6 . 1 Kesimpulan : 1. p





q p





b ax Z b ax    2. p p d cx b ax Z q d cx b ax             3. p _f

 

_{x ,}q _f

 

_x _Z r _f

 

_x

INTEGRAL FUNGSI RASIONAL

Bentuk

∫

( )

( )

dikatakan integral fungsi pecah rasional bila M(x) dan N(x) merupakan bentuk polinomial (suku banyak). Yang dimaksud dengan derajat dari M(x) dan N(x) adalah pangkat tertinggi untuk x yang koefisiennya bukan bilangan nol, sehingga dapat ditulis ditulis : ) ( ) ( ) ( x N x M x

F  , M(x) dan N(x) fungsi –fungsi Polinom dengan N(x) ≠ 0 atau dapat dituliskan menjadi :

( )

Yang perlu diperhatikan dalam integral fungsi rasional adalah : 1. Jika M(x) dx = dN(x), maka untuk ∫ ( )

( )

adalah

∫ ( ) _{( )} ∫ ( ) _{( )} | ( )| , Contoh : ∫ Perhatikan d( ) = 2x dx Sehingga ∫ = ∫ ( ) | |

2. Jika pangkat M(x) pangkat N(x) atau n m, maka dilakukan pembagian terlebih dahulu, sehingga didapatkan bentuk : ( )

( )

( )

( ) ( )

Dengan P(x) merupakan hasil bagi M(x) oleh N(x) dan ( ) adalah sisa pembagian dengan pangkat Q(x) < pangkat N(x), sehingga :

∫ ( ) ( ) ∫ [ ( ) ( ) ( )] =

∫ ( ) ∫

( ) ( )

3. Jika pangkat M(x) < pangkat N(x) atau n < m, maka penyelesaian integral tersebut bergantung pada faktor-faktor dari N(x).

Setiap suku banyak dengan koefisien real dapat dinyatakan sebagai perkalian dari faktor-faktor linear dan kuadrat sedemikian sehingga tiap-tiap faktor mempunyai koefisien real.

Fungsi Rasional dibedakan atas :

a. Jika derajat dari M(x) lebih kecil daripada derajat N(x), maka F(x) disebut fungsi rasional sebenarnya (properrational function)

b. Jika derajat dari M(x) lebih besar daripada derajat N(x), maka F(x) disebut fungsi rasional tak sebenarnya (improper rational function).

Suatu fungsi rasional tak sebenarnya selalu dapat dinyatakan sebagai penjumlahan dari Suatu polinom dan suatu fungsi yang sebenarnya dengan melakukan operasi pembagian biasa. Misalnya :

( )

( )

Permasalahan mengintegralkan fungsi rasional terletak pada bagaimana

mengintegralkan fungsi rasional sebenarnya. Suatu fakta, bahwa fungsi rasional sebenarnya dapat ditulis sebagai jumlah dari fungsi rasional sebenarnya yang lebih sederhana (partial fraction), dimana penyebutnya berbentuk ( ) , dengan n bilangan bulat positif. Bentuk dari pecahan sederhana tersebut tergantung pada faktor N(x), penyebut fungsi tersebut. Contoh :

1

3

1

2

1

1

5

2

_











x

x

x

x

Ada 4 kasus dari pemfaktoran penyebut N(x) yaitu : 1. Faktor linear tidak berulang

Bentuk N(x) adalah :

N(x) =

(

)(

) (

)

Dengan bentuk N(x) tersebut, maka F(x) dapat dibentuk seperti berikut : F(x) = ( ) ( ) =

Contoh : Tentukan



  dx x x 9 1 2 Jawab : faktorkan penyebut : maka ) 3 )( 3 ( 9 2    x x x

   

( 3)( 3) ) 3 ( ) 3 ( 3 3 9 1 2             x x x B x A x B x A x x

samakan koefisien ruas kiri dan ruas kanan substitusi B ke persamaan A + B = 1 A + = 1 A = 1 - A = Sehingga : ∫ ∫( ) ∫( ) ∫_{( )} ∫_{( )} | | | |

2. Faktor Linear yang Berulang

Jika pada N(x) terdapat (ax + b) berulang sebanyak m kali, misalnya N(x) = ( ) Maka : F(x) = ( )

( ) Contoh : Tentukan Jawab : Samakan penyebut : Maka



AB

 

x 3A3B



 A + B =1 -3A + 3B =1 3A +3B=3 _{-3A+3B=1 +} 6B=4 B =



  

1 2 2 1 x x dx  





2

 

1

 

2

 

2





1



1 2 2 _    _    x C x B x A x x



 





2

 

1



) 2 ( ) 1 ( ) 1 )( 2 ( 1 2 1 2 2 2 _{ }          x x x C x B x x A x x 2       

dieliminasi

Substitusi C ke persamaan A + C = 0, maka diperoleh

Kemudian substitusi A dan C ke persamaan A + B + 4C = 0, maka diperoleh sehingga diperoleh hasil :

3. Faktor kuadrat tidak berulang

Dalam kasus ini N(x) berbentuk :

N(x) = ( )( ) ( ) Maka : F(x) =

Contoh : ∫ ( )( ) Jawab : ( )( ) ( ) ( ) ( ) ( )( ) ( )( ) Jadi : x2+ x + 6 = A(x2 + 4) + (Bx + C)(x + 2) = Ax2 + 4A + Bx2 + Cx + 2Bx + 2C = (A + B)x2 + (2B + C)x + 4A + 2C Maka : A + B = 1 2B + C = 1 4A + 2C = 6 A+C=0 A+B+4C=0

-2A-B+4C=1 A+B+4C=0 -2A-B+4C=1 + -A+8C=1 A+C=0 -A+8C=1 + 9C=1

C=1/9

A=-1/9

B=-1/3

C= A= B

=



 















dx x dx x dx x dx x x









 _        1 1 9 1 2 1 3 1 2 1 9 1 1 2 1 2 2 C x x x         ln| 1| 9 1 ) 2 ( 3 1 | 2 | ln 9 1

Samakan koefisien ruas kiri dan ruas kanan dengan eliminasi ⟨ ⟨ ⟨ ⟨ Substitusi : 2B + C = 1 A + B = 1 2B + 1 = 1 A + 0 = 1 2B = 0 A = 1 B = 0 Maka didapat ∫ ( )( ) ∫( ) ∫ ( )

=

∫

( )

∫

( )

= | | . /

4. Faktor kuadrat berulang Dalam kasus ini N(x) berbentuk : N(x) = Maka : Contoh : Jawab : Maka :





p i i ix b x c a 2 



_{ }

_

_

_

_

_

p i i i p p p i i i p p i i i i i i a x b x c B x A c x b x a B x A c x b x a B x A c x b x a B x A x F                    _ 2 1 2 1 1 2 2 2 2 2 1 1 ... ) (

 





6 15 22 3 2 2 2 2 x x x x dx    



 



₂



2

 



2

  

₂ 2 2 2 2 3 2 3 22 15 6             x E Dx x C x B x A x x x x









 

 



₂



2 2 2 2 2 3 ) 3 )( ( 3 2 ) ( 2            x x x E Dx x x C x B x A

Dengan menyamakan koefisien ruas kiri dan ruas kanan maka diperoleh :

1. Substitusi persamaan 1 ke persamaan 3 dan 5

 4A+2B+3C+D=6 (3)

(6)

 4A+6C+3E=22 (5)

(7)

2. Substitusi persamaan 2 ke persamaan 4 dan 6

 6B+2C+3D+E=-15 (4) (8)  (6) (9)

3. Substitusi persamaan 2 dan 8 ke persamaan 7 (7)

(10)

4. Substitusi persamaan 9 kepersamaan 10 (10) 7 1            4 3 2 2 ) 3 2 4 ( ) 3 ( ) ( 22 15 6x x A B x B C x A B C D x (6B2C3DE)x(4A6C3E) A+B=0 ( ) 3B+C=0 (2) 4A+2B+3C+D=6 (3) 6B+2C+3D+E=-15 (4) 4A+6C+3E=22 (5)

5. Substitusi B ke persamaan 1, 2, dan 9 6. Substitusi D ke persamaan 8 Maka didapat :

INTEGRAL FUNGSI RASIONAL BENTUK SINUS DAN

COSINUS

Bila integran merupakan fungsi rasional yang memuat suku-suku dari sin dan cos maka akan lebih mudah bila dikerjakan menggunakan substitusi, yaitu z = tan ( x/2) ,- < x <

.

Integral fungsi rasional dalam sin x dan cos x atau keduanya penyelesaiannya dapat melakukan perubahan bentuk berikut:

√ √





























 _          dx x x dx x x dx x dx x x x x 2 2 2 2 2 2 2 5 2 3 3 1 2 3 22 15 6









 _       dx x x x dx dx x x x dx 2 2 2 2 ) 2 ( 2 2 5 2 3 2 2 2 1 3 . ) 2 ( 2 5 2 tan 2 3 ) 2 ln( 2 1 | 3 | ln 2 1 ₂ C x x x x               





























 _          2 2 2 2 2 2 2 2 3 2 3 22 15 6 x E Dx dx x C x B dx x A dx x x x x √

Jika ketiga harga diatas digantikan dalam rumus sudut ganda didapat: √ √ ( √ ) (√ )

Bila maka adalah: ( √ ) Contoh soal: 1.

∫

Dengan mengganti

dan , didapat: ∫ ∫ ∫ ∫ ( )

Dimisalkan: Jadi: ∫ ( ) . / 2. Hitunglah

∫

Jawab: Dengan substitusi

,

, dan

kita peroleh: ∫

∫ ∫ ∫ ( )( ) ∫ ( )( ) ∫( ) ( ) Jadi ( ) ( ) ( )  A+B = 0  3A+B = 2 3A-A = 2 2A = 2 A = 1  B = -A B = -1 ∫ ( ) ∫ ( )

∫ ( ) ∫ ( ) ( ) ( )

INTEGRAL TAK WAJAR

Untuk fungdi F yang terintegralkn Riemann pada selang [a,b] definisi integral tentu :

dx x f b a



( )

Disebut integral tak wajar jika :

a. Salah atau kedua batas integralnya tak hingga

b. Integral f(x) mempunyai satu atau lebih titik ketidakkontinuan dalam interval a ≤ x ≤ b atau batas integralnya berhingga.

Integral tak wajar mempuyai 2 bentuk :

1. Integral tak wajar pada selang hingga

Integral tak wajar jika integran f(x) memiliki satu atau lebih titik ketidak kontinuan dalam interval a ≤ x ≤ b yang merupakan daerah integrasinya. Integral tak wajar b f x dx

a



( ) dapat memiliki integran f(x) diskontinu pada x = a, atau f(x) diskontinu dibatas atau x = b atau f(x) diskontinu disembarang titik x = c, dimana c terletak dalam interval [a,b].

Untuk integral tak wajar pada selang hingga, terdapat tiga definisi yaitu : a. Integral tak wajar dari fungsi f pada [a,b] dengan x = a maka :





   b a b t a t dx x f dx x f( ) lim ( ) 0 ... Rumus 1 Contoh : Hitung dx x



5 _ 2 2 1 Jawab : dx x dx x t





 _  _  5 2 2 5 2 2 1 lim 2 1





5 2 2 2 2 lim _t t x   _





5 2 2 2 2 lim _t t x   _



3 2



2 lim 2    _  t t

3

2



Jadi nilai dari dx x



5 _

2 2

1

adalah



2

3

dan konvergen

b. Integral tak wajar dari fungsi f pada [a,b] dengan x = b, maka



 



 b a t b a t dx x f dx x f( ) lim ( ) 0 ... Rumus 2 Selesaikan dx x



3 _ 0 3 1 Jawab :



x

 

d x



dx x t t        





lim 3 3 3 1 2 1 3 0 0 3 0 0





t t t x   



                  _ 3 0 3 0 2 1 0 3 . 1 1 2 1 1 lim 0





t t t       _   _ 3 0 2 1 0 3 2 lim 0









_            _{ }       _{ }   _  2 1 2 1 0 0 3 3 3 2 lim 0 t t                  _  2 ( ) 3 lim 2 1 00 t t

 

_   _   2 0 2 3 1

3

2



Jadi nilai dari dx x



3 _

0 3

1

c. Integral tak wajar dari fungsi f pada [a,b] dengan x = c, maka









        b t c t c a t b a t c a t dx x f dx x f dx x f( ) lim ( ) lim ( ) 0 0 ... Rumus 3 Dengan catatan a < c < b Contoh :

Selidiki kekonvergenan integral tak wajar



 

5

3 x 1

dx

Jawab :

Bentuk ini merupakan bentuk integral tak wajar karen fungsi

1 1 ) (  x x f kontinu

pada himpunan (-3,1)  (1,5) dengan 

  ₁ 1 lim 1 _x x

. Integral tak wajar ari fungsi f pada selang [-3,5] adalah :







 _      5 1 1 3 5 3 1 1 x 1 dx x dx x dx





       5 1 1 3 1 t 1 t x dx x dx





























        5 1 5 1 1 3 1 3

2

1

1

2

t t t _t

x

x



 

_





        5 1 1 3 2 4 4 2 t t t t 8 4 4   

Jadi integral tak wajar dari fungsi selang [-3,5] konvergen ke 8

Integral tak wajar tersebut disebut konvergen atau divergen sesuai integral tersebut ada atau tidak setelah digunakan proses limit.

2. Integral tak wajar pada selang tak hingga

Integral tak wajar pada selang tak hingga ada 3 definisi yaitu :

a. Integral tak wajar dari fungsi f pada [a,∞] didefinisikan sebagai





    t t f x dx dx x f( ) lim ( ) ... Rumus 4

Contoh

Tentukan apakah integral





1 x

dx

konvergen atau divergen Jawab





_    t t x dx x dx 1 0 1 lim



   t t _x dx 1 lim

 

t t Inx 1 lim   



1



lim Int In t     Int t lim   Jadi



 1 x dx adalah divergen

b. Integral tak wajar dari fungsi f pada [a,∞] didefinisikan sebagai





   b b t t f x dx dx x f( ) lim ( ) ... Rumus 5 Contoh : Diketahui ( ) ₃1 x x

f  kontinu pada selang [-∞,-1] Tentukan integral tak wajar dari fungsi F

Jawab :





       1 1 3 lim 3 1 t t _x dx x 1 1 2 1 2 3 lim    



_              t t t x            2 1 1 lim t t  

c. Integral tak wajar dari fungsi f pada [-∞,∞] di definisikan sebagai







       c c dx x f dx x f dx x f( ) ( ) ( )





       t c t c t f(x)dx lim f(x)dx lim ... Rumus 6 Contoh Tentukan dx x



    2 1 1 Jawab





 _    t t _x dx dx x ₀ 2 0 2 lim ₁ 1 1





t t x 0 1 tan lim    



tan tan 0



lim 1 1     t t t t 1 tan lim     2  





 _     0 2 0 2 1 lim 1 1 t t _x dx dx x



₁



0 tan lim t t x    



t



t 1 1 tan 0 tan lim               2 0  2   Jadi 2 2 1 1 2   _  



   dx x





konvergen

INTEGRAL TAK WAJAR UNTUK INTEGRAN TAK

TERDEFINISI

Dalam makalah ini kami akan membahas integral tak wajar jika integran f(x) memiliki satu atau lebih titik ketidakkontinuan dalam interval a ≤ x ≤ b yang merupakan daerah integrasinya.

Integral tak wajar b f x dx a



( ) dapat memiliki integran f(x) diskontinu pada x = a, atau f(x) diskontinu dibatas atau x = b atau f(x) diskontinu disembarang titik x = c, dimana c terletak dalam interval [a,b].

Untuk integral tak wajar pada selang hingga, terdapat tiga definisi yaitu :

1.

x = a, maka





    b a b t a t dx x f dx x f( ) lim ( ) 0

2.

x = b, maka





   b a t b a t f x dx dx x f( ) lim ( ) 0

3.

x = c, maka









         b t c t c a t b a t c a t f x dx f x dx dx x f( ) lim ( ) lim ( ) 0 0

dengan catatan a < c < b.

Jika f(x) memiliki beberapa titik diskontinu misalnya di x = c dan x = d dalam interval (a,b), maka integral dapat dihitung sebagai berikut:

∫ ( )

=

∫

( )

+

∫

( )

+

∫

( )

Integral tak wajar tersebut konvergen atau divergen sesuai integral tersebut ada atau tidak setelah digunakan proses limit.

Contoh soal:

1.

Hitung

dx x



5 _ 2 2 1

Jawab :

dx x dx x t





 _  _  5 2 2 5 2 2 1 lim 2 1





5 2 2 lim x  





5 2 2 2 2 lim t t x   _



3 2



2 lim 2    _  t t

3

2



Jadi nilai dari

dx

x



5 _

2 2

1

adalah



2

3

dan konvergen.

2.

Selesaikan

dx x



3 _ 0 3 1

Jawab :



x

 

d x



dx x t t        





lim 3 3 3 1 2 1 3 0 0 3 0 0





t t t x   



                  _ 3 0 3 0 2 1 0 3 . 1 1 2 1 1 lim 0





t t t       _   _ 3 0 2 1 0 3 2 lim 0









_            _{ }       _{ }   _  2 1 2 1 0 2 3 3 3 0 lim 0 t t                  _  2 ( ) 3 lim 2 1 00 t t

 

_   _   2 0 2 3 1

3

2



Jadi nilai dari

dx

x



3 _

0 3

1

adalah



2

3

dan konvergen.

Jawab :

Integral ini tak wajar karena integran f(x) =

diskontinu di x = 0, batas

bawah. Maka:

∫

=

∫

, -

( )

= lim (0 . (∞))

= + ∞ ( integral divergen)