Implementasi model Arima-Garch menggunakan metode maximum likelihood: Studi kasus harga saham Jakarta Islamic Index

IMPLEMENTASI MODEL ARIMA-GARCH MENGGUNAKAN METODE MAXIMUM LIKELIHOOD (Studi Kasus: Harga Saham Jakarta Islamic Index). SKRIPSI. OLEH NIKSIE GRETA SANCHIA NIM. 16610081. JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI UNIVERSITAS ISLAM NEGERI MAULANA MALIK IBRAHIM MALANG 2020.

IMPLEMENTASI MODEL ARIMA-GARCH MENGGUNAKAN METODE MAXIMUM LIKELIHOOD (Studi Kasus: Harga Saham Jakarta Islamic Index). SKRIPSI. Diajukan kepada Fakultas Sains dan Teknologi Universitas Islam Negeri Maulana Malik Ibrahim Malang Untuk Memenuhi Salah Satu Persyaratan dalam Memperoleh Gelar Sarajana Matematika (S.Mat). Oleh NIKSIE GRETA SANCHIA NIM. 16610081. FAKULTAS SAINS DAN TEKNOLOGI UNIVERSITAS ISLAM NEGERI MAULANA MALIK IBRAHIM MALANG 2020.

IMPLEMENTASI MODEL ARIMA-GARCH MENGGUNAKAN METODE MAXIMUM LIKELIHOOD (Studi Kasus: Harga Saham Jakarta Islamic Index). SKRIPSI. Oleh NIKSIE GRETA SANCHIA NIM. 16610081. Telah Diperiksa dan Disetujui untuk Diuji Tanggal 12 Mei 2020. Pembimbing I,. Pembimbing II,. Abdul Aziz, M.Si NIP. 19760318 200604 1 002. Muhammad Khudzaifah, M.Si NIDT. 1990511 20160811 057. Mengetahui, Ketua Jurusan Matematika. Dr. Usman Pagalay, M.Si NIP. 19650414 200312 1 001. iii.

IMPLEMENTASI MODEL ARIMA-GARCH MENGGUNAKAN METODE MAXIMUM LIKELIHOOD (Studi Kasus: Harga Saham Jakarta Islamic Index). SKRIPSI. Oleh NIKSIE GRETA SANCHIA NIM. 16610081. Telah Dipertahankan di Depan Dewan Penguji Skripsi dan Dinyatakan Diterima Sebagai Salah Satu Persyaratan untuk Memperoleh Gelar Sarjana Matematika (S.Mat) Tanggal 12 Mei 2020. Penguji Utama. : Dr. Sri Harini, M.Si. ……………...... Ketua Penguji. : Angga Dwi Mulyanto, M.Si. ……………...... Sekretaris Penguji. : Abdul Aziz, M.Si. ………………... Anggota Penguji. : Muhammad Khudzaifah, M.Si. ……………...... Mengetahui, Ketua Jurusan Matematika. Dr. Usman Pagalay, M.Si NIP. 19650414 200312 1 001.

HALAMAN PERNYATAAN KEASLIAN TULISAN. Saya yang bertanda tangan di bawah ini: Nama. : Niksie Greta Sanchia. NIM. : 16610081. Jurusan. : Matematika. Fakultas. : Sains dan Teknologi. Judul Skripsi. :Implementasi Model ARIMA-GARCH menggunakan Metode Maximum Likelihood (Studi Kasus: Harga Saham Jakarta Islamic Index). Menyatakan dengan sebenarnya bahwa skripsi yang saya tulis ini benar-benar merupakan hasil karya sendiri, bukan merupakan pengambilan data, tulisan, atau pikiran orang lain yang saya akui sebagai hasil tulisan atau pikiran saya sendiri, kecuali dengan mencantumkan sumber cuplikan pada daftar rujukan. Apabila di kemudian hari terbukti atau dapat dibuktikan skripsi ini hasil jiplakan, maka saya bersedia menerima sanksi atas perbuatan tersebut.. Malang, 10 Mei 2020 Yang membuat pernyataan,. Niksie Greta Sanchia NIM. 16610081.

MOTO. “Jika orang lain bisa, maka aku juga pasti bisa” “Raihlah cita-citamu setinggi langit, tetapi rendahkanlah hatimu serendah mutiara dasar laut” “Where there’s a will there’s a way, Live must go on”.

PERSEMBAHAN. Skripsi ini penulis persembahkan untuk:. Ayahanda Teguh, dukungan dan arahan darinya menjadi semangat bagi penulis. Ibunda tercinta Rista, do’a darinya menghadirkan keselamatan, keterlindungan, dan kelancaran bagi penulis. Mas Sandika dan adik Nevil tersayang, serta seluruh keluarga yang telah memberi dukungan kepada penulis..

KATA PENGANTAR. Assalamua’alaikum Warahmatullahi Wabarakatuh Puji Syukur kehadirat Allah SWT, yang telah melimpahkan rahmat dan hidayah-Nya, sehingga penulis mampu menyelesaikan penyusunan skripsi ini sebagai salah satu syarat untuk memperoleh gelar sarjana dalam bidang Matematika di Fakultas Sains dan Teknologi, Universitas Islam Negeri Maulana Malik Ibrahim Malang. Pada dasarnya penulisan skripsi ini tidak lepas dari bantuan dan dorongan berbagai pihak. Oleh karena itu pada kesempatan ini penulis ingin menyampaikan ucapan terimakasih yang sebesar-besarnya kepada : 1. Prof. Dr. H. Abd. Haris, M.Ag selaku rektor Universitas Islam Negeri Maulana Malik Ibrahim Malang. 2. Dr. Sri Harini, M.Si selaku dekan Fakultas Sains dan Teknologi Universitas Islam Negeri Maulana Malik Ibrahim Malang. 3. Dr. Usman Pagalay, M.Pd selaku ketua Jurusan Matematika Universitas Islam Negeri Maulana Malik Ibrahim Malang. 4. Abdul Aziz, M.Si selaku dosen pembimbing I yang selalu memberikan arahan, nasihat dan motivasi kepada penulis. 5. M. Khudzaifah, M.Si selaku dosen pembimbing II yang telah memberikan saran dan bantuan dalam penulisan skripsi ini.. viii.

6. Segenap sivitas akademika Jurusan Matematika, Fakultas Sains dan Teknologi, Universitas Islam Negeri Maulana Malik Ibrahim Malang terutama seluruh dosen, terimakasih atas segala ilmu dan bimbinganya 7. Ayah dan ibu serta adik tersayang yang selalu mendo’akan dan memberikan dukungan, kasih sayang, serta motivasi kepada penulis sehingga dapat menyelesaikan skripsi ini. 8. Teman-teman mahasiswa angkatan 2016 yang telah banyak membantu penulis dan memberikan dukungan dalam menyusun skripsi sampai selesai. 9. Serta semua pihak yang telah membantu terselesainya skripsi ini yang tidak dapat penulis sebut satu persatu. Penulis menyadari masih banyak kesalahan dalam penulisan skripsi ini, baik dalam teknik penyajian materi maupun pembahasan. Oleh sebab itu, kritik dan saran yang bersifat membangun sangat penulis harapkan. Semoga skripsi ini bermanfaat dan dapat memberikan ilmu bagi para pembaca.. Malang, 10 Mei 2020. Penulis. ix.

DAFTAR ISI. HALAMAN JUDUL HALAMAN PENGAJUAN HALAMAN PERSETUJUAN HALAMAN PENGESAHAN HALAMAN PERNYATAAN KEASLIAN TULISAN HALAMAN MOTTO HALAMAN PERSEMBAHAN KATA PENGANTAR ........................................................................................ viii DAFTAR ISI .......................................................................................................... x DAFTAR GAMBAR ........................................................................................... xii DAFTAR SIMBOL ............................................................................................ xiv ABSTRAK ......................................................................................................... xvii ABSTRACT ...................................................................................................... xviii ‫ ملخص‬..................................................................................................................... xix BAB I PENDAHULUAN 1.1 Latar Belakang ........................................................................................ 1 1.2 Rumusan Masalah................................................................................... 4 1.3 Tujuan ..................................................................................................... 4 1.4 Manfaat Penelitian .................................................................................. 5 1.5 Batasan Masalah ..................................................................................... 5 1.6 Sistematika Penulisan ............................................................................. 5 BAB II KAJIAN PUSTAKA 2.1 Deret Waktu (Time Series) ..................................................................... 7 2.1.1 Pengertian Deret Waktu.............................................................. 7 2.1.2 Autocorrelation Function (ACF) ................................................ 7 2.1.3 Parsial Autocorrelation Function (PACF) ................................. 9 2.1.4 Kestasioneran............................................................................ 10 2.1.5 Differencing .............................................................................. 16 2.1.6 Proses White Noise................................................................... 19 2.1.7 Model Time Series Stasioner .................................................... 20 2.1.8 Model Time Series Nonstasioner .............................................. 23 2.1.9 Model ARCH dan GARCH ...................................................... 24 2.2 Uji Hipotesa .......................................................................................... 26 2.2.1 Uji Stasioneritas........................................................................ 26 2.2.2 Uji Normalitas .......................................................................... 27 2.2.3 Uji Heteroskedastisitas ............................................................. 28 x.

2.2.4 Uji Signifikansi Parameter........................................................ 29 2.3 Saham dan Volatilitas ........................................................................... 30 2.3.1 Saham ....................................................................................... 30 2.3.2 Volatilitas.................................................................................. 31 2.4 Estimasi Parameter ............................................................................... 32 2.4.1 Metode Maximum Likelihood .................................................. 32 2.4.2 Iterasi Newton-Raphson ............................................................ 34 2.5 Ayat Al-Qur’an tentang Jual Beli ......................................................... 35 BAB III METODE PENELITIAN 3.1 Pendekatan Penelitian ........................................................................... 37 3.2 Jenis dan Sumber Data ......................................................................... 37 3.3 Variabel Penelitian ............................................................................... 37 3.4 Analisis Data......................................................................................... 37 3.5 Diagram Alir Analisis Data .................................................................. 39 BAB IV HASIL DAN PEMBAHASAN 4.1 Implementasi Model ARIMA-GARCH menggunakan Metode Maximum Likelihood ............................................................................ 41 4.1.1 Deskripsi Data .......................................................................... 41 4.1.2 Uji Hipotesa Data ..................................................................... 42 4.1.3 Pemodelan ARIMA .................................................................. 45 4.1.4 Pemodelan ARIMA-GARCH ................................................... 48 4.1.5 Evaluasi Model ARIMA-GARCH ........................................... 52 4.2 Peramalan Model ARIMA-GARCH .................................................... 53 BAB V PENUTUP 5.1 Kesimpulan ........................................................................................... 55 5.2 Saran ..................................................................................................... 55 DAFTAR RUJUKAN ......................................................................................... 57 LAMPIRAN RIWAYAT HIDUP. xi.

DAFTAR GAMBAR. Gambar 2.1. Plot Data Time Series Stasioner dalam Rata-rata ...................... 11. Gambar 2.2. Plot Data Time Series Stasioner dalam Variansi ....................... 11. Gambar 2.3. Plot Data Time Series Stasioner dalam Rata-rata dan Variansi . 12. Gambar 2.4. Plot Data Stasioner Kuat ............................................................ 13. Gambar 2.5. Plot Data Stasioner Lemah ......................................................... 14. Gambar 2.6. Plot Stasioner Hasil Uji Stasioneritas dengan ACF ................... 15. Gambar 2.7. Plot Tidak Stasioner Hasil Uji Stasioneritas dengan ACF ......... 16. Gambar 2.8. Plot Data Sebelum Differencing ................................................ 17. Gambar 2.9. Plot Data Setelah Differencing................................................... 17. Gambar 2.10. Plot Data bersifat White Noise ................................................... 20. Gambar 4.1. Statistik Deskriptif Data dengan Bantuan Minitab .................... 41. Gambar 4.2. Plot Data Harga Saham JII dengan Bantuan Minitab ................ 41. Gambar 4.3. Uji Stasioner Data Harga Saham JII dengan Bantuan Eviews ... 42. Gambar 4.4. Plot Data Log Return dengan Bantuan Minitab ......................... 43. Gambar 4.5. Uji Stasioneritas Data Log Return dengan Bantuan Eviews ...... 44. Gambar 4 6. Uji Normalitas Data Log Return dengan Bantuan Minitab ...... 45. Gambar 4.7. Correlogram Log Return dengan Bantuan Eviews .................... 45. Gambar 4.8. Estimasi Model ARIMA(1,1,1) dengan Bantuan Eviews .......... 46. Gambar 4.9. Uji Heteroskedastisitas Model ARIMA(1,1,1) dengan Bantuan Eviews ........................................................................................ 48. Gambar 4.10. Uji Autokorelasi Residual dengan Bantuan Eviews .................. 48. Gambar 4.11. Estimasi Model ARIMA(1,1,1)-GARCH (0,2) dengan Bantuan Eviews ........................................................................................ 49. Gambar 4.12. Uji Heteroskedastisitas Model ARIMA-GARCH dengan Bantuan. xii.

Eviews. 51. Gambar 4.13. Uji Autokorelasi Model ARIMA-GARCH dengan Bantuan Eviews ........................................................................................ 51. Gambar 4.14. Uji Normalitas Model ARIMA-GARCH dengan Bantuan Eviews ........................................................................................ 52. Gambar 4.15. Grafik Perbandingan Harga Saham dan Hasil Peramalan dengan Bantuan Excel ............................................................................ 53. xiii.

DAFTAR SIMBOL Simbol-simbol yang digunakan dalam skripsi ini memiliki makna sebagai berikut: : Nilai variansi varaibel acak t. : Periode/waktu. r. : Return. n . : Banyaknya pengamatan : Rata-rata variabel acak : Variabel acak untuk t  0, 1, 2,.... Zt. : Estimasi variabel acak untuk t  0, 1, 2,... : Hasil differencing pertama dari : Hasil differencing kedua dari : Variabel acak untuk t  0, 1, 2,... pada saat k. ̂. : Estimasi variabel acak t  0, 1, 2,... pada saat k. d. : Orde differencing. B. : Operator shift mundur : Nilai error. k. : Selang waktu, : Nilai fungsi autokovariansi (koefisien kovariansi) pada saat k. k. : Nilai fungsi autokorelasi (koefisien korelasi) pada saat k. Pk. : Nilai fungsi autokorelasi parsial pada saat k. Zt. : Simpangan data terhadap rata-ratanya : Parameter AR untuk koefisien variabel ke-  t  i  , : Orde AR : Parameter MA untuk koefisien variabel ke-  t  i  , : Orde MA : Parameter AR untuk koefisien variabel ke-  t  p . xiv.

: Parameter MA untuk koefisien variabel ke-  t  p . 0. : Parameter konsanta rata-rata. wt. : White noise. ht. : Nilai standar deviasi error. ht2. : Nilai variansi error : Variansi pada saat t. . : Parameter ARCH : Orde ARCH : Parameter ARCH. m,s. : Orde GARCH. ,. : Parameter GARCH. SE. : Nilai standar error. DF. : Nilai uji Dickey Fuller. ̂. : Penduga dari koefisien  : Skewness. TOL. : Nilai TOL. VIF. : Nilai VIF. ST. : Harga saham pada waktu ke-t : Kurtosis : Koefisien determinasi : Distribusi chi-square : Komponen deterministik : Komponen stokastik : Proses Wiener. T. : Periode. r. : Return. S. : Harga saham. K. : Harga ketentuan. C. : Opsi beli. P. : Opsi jual xv.

s. : Standar deviasi ̅. : Rata-rata return : Vektor (acak) 1 n : Matrik (acak) n   u  1 : Vektor parameter  u  1 1 : Vektor : Matrik transpos : Vektor parameter transpos : Fungsi likelihood : Fungsi log-likelihood. ̂. : Vektor parameter Maximum Likelihood : Harga opsi jual dengan Black Scholes. xvi.

ABSTRAK Sanchia, Niksie Greta. 2020. Implementasi Model ARIMA-GARCH menggunakan Metode Maximum Likelihood (Studi Kasus: Harga Saham Jakarta Islamic Index). Skripsi. Jurusan Matematika, Fakultas Sains dan Teknologi, Universitas Islam Negeri Maulana Malik Ibrahim Malang. Pembimbing: (I) Abdul Aziz, M.Si (II) Muhammad Khudzaifah, M.Si Kata kunci: ARIMA, GARCH, Harga Saham, Maximum Likelihood, Return Penelitian ini membahas implementasi model ARIMA-GARCH menggunakan metode Maximum Likelihood pada data harga saham Jakarta Islamic Index. Pemodelan ARIMA-GARCH diawali dengan transformasi data harga saham menjadi data log return kemudian dilakukan uji stasioneritas dan uji normalitas. Kemudian estimasi model menggunakan metode maximum likelihood dengan iterasi Newton Raphson. Setelah dilakukan estimasi, didapatkan model ARIMA(1,1,1)-GARCH(0,2) sebagai model signifikan. Kemudian model tersebut digunakan untuk meramalkan harga saham beberapa periode ke depan. Hasil peramalan menyatakan bahwa plot data prediksi hampir mengikuti pola data aktual. Hal tersebut menunjukkan bahwa model ARIMA(1,1,1)-GARCH(0,2) dapat memberikan hasil peramalan yang baik.. xvii.

ABSTRACT Sanchia, Niksie Greta. 2020. Implementation of ARIMA-GARCH Model with Maximum Likelihood Method (Case Study: Stock Price of Jakarta Index Islamic). Thesis. Department of Mathematics, Faculty of Science and Technology, State Islamic University of Maulana Malik Ibrahim Malang. Advisors: (I) Abdul Aziz, M.Si (II) Muhammad Khudzaifah, M.Si Keywords: ARIMA, GARCH, Stock Price, Maximum Likelihood, Return This thesis discusses the implementation of the ARIMA-GARCH model using the Maximum Likelihood method on the Jakarta Islamic Index stock price data. ARIMA-GARCH modeling begins with the transformation of stock price data into log return data then a stationarity and normality test is performed. Further, the model estimation using the maximum likelihood method with Newton Raphson iteration. After estimation, ARIMA (1,1,1)-GARCH (0,2) model is obtained as a significant model. Eventually model is used to forecast stock prices in the next few periods. Forecasting results state that the prediction data plot almost follows the actual data pattern. This shows that the ARIMA (1,1,1) GARCH (0,2) model can provide good forecasting results.. xviii.

‫ملخص‬. ‫سانشيا ‪ ،‬نيكسي جريتا‪.٠٢٠٢ .‬تنفيذ نموذج (‪ (ARIMA-GARCH‬بأقصى قدر‬. ‫‪Maximum‬‬. ‫‪( Likelihood‬دراسة حالة‪ :‬سعر سهم مؤشر جاكرتا اإلسالمي)‪ .‬البحث العلمي‪ .‬شعبة‬ ‫الرياضيات ‪ ،‬كلية العلوم والتكنولوجيا ‪ ،‬جامعة موالنا مالك إبراهيم اإلسالمية الحكومية ماالنج‪.‬‬ ‫‪ .١‬المشرف األول‪ ،‬عبد العزيز ‪ ،‬الماجستير ‪ .٠‬المشرف الثاني‪ ،‬محمد خديفة ‪ ،‬الماجستير‬. ‫الكلمات الرئيسية‪ ، GARCH ،ARIMA :‬سعر السهم ‪ ، Maximum Likelihood ،‬عائد‬. ‫يناقش هذا البحث تطبيق نموذج ‪ ARIMA-GARCH‬باستخدام طريقة ‪ Maximum Likelihood‬في‬ ‫بيانات أسعار أسهم في مؤشر جاكرتا اإلسالمي‪ .‬تبدأ نمذجة ‪ ARIMA-GARCH‬بتحويل بيانات أسعار‬ ‫األسهم إلى بيانات إرجاع السجل ثم يتم إجراء اختبار االستقرارية والحالة الطبيعية‪ .‬ثم قام بتقدير النموذج‬ ‫باستخدام طريقة ‪ Maximum Likelihood‬مع تكرار ‪ .Newton Raphson‬بعد التقدير ‪ ،‬يتم الحصول‬ ‫على نموذ )‪ARIMA (1,1,1)-GARCH (0,2‬‬. ‫نموذجا هاما‪ .‬ثم يتم استخدام النموذج للتنبؤ بأسعار‬. ‫األسهم في الفترات القليلة القادمة‪ .‬تشير نتائج التنبؤ إلى أن مخطط بيانات التنبؤ يتبع نمط البيانات الفعلي‬ ‫تقريبا‪ .‬يوضح هذا أن نموذج )‪ ARIMA (1,1,1)-GARCH (0,2‬يمكن أن يوفر نتائج تنبؤ جيدا‪.‬‬. ‫‪xix‬‬.

BAB I PENDAHULUAN 1.1 Latar Belakang Matematika merupakan ilmu yang banyak digunakan sebagai alat bantu memecahkan masalah dalam berbagai bidang ilmu yang lain. Salah satu cabang ilmu matematika yang sedang berkembang dan berperan dalam menjawab masalah-masalah dalam kehidupan adalah ilmu statistika (Saefuddin, dkk, 2009). Banyak teori-teori dari ilmu statistik yang dapat diterapkan pada semua bidang kehidupan. Salah satu teori statistik yang biasa digunakan adalah pemodelan deret berkala (time series) (Sudjana, 2005). Penerapan analisis deret berkala (time series) salah satunya adalah pada bidang ekonomi dan keuangan. Misalnya, untuk menggambarkan pergerakan harga opsi. Mawby (2007) mendefinisikan opsi sebagai salah satu bentuk investasi yang sangat populer karena kontrak pada opsi memungkinkan seseorang untuk mengendalikan resiko dan dapat berpotensi menghilangkannya. Harga opsi dipengaruhi oleh harga saham. Model runtun waktu yang dikembangkan oleh Box-Jenkins yaitu diantaranya, model Autoregressive (AR), Moving Average (MA), Autoregressive Moving Average (ARMA), dan model Autoregressive Integrated Moving Average (ARIMA). Model-model tersebut berdasarkan asumsi bahwa datanya stasioner dan variansinya tetap atau konstan (homoskedastik). Model ARIMA tidak relevan jika. dihadapkan. pada. data. dengan. variansinya. yang. tidak. konstan. (heteroskedastik). Untuk itu dibutuhkan model yang dapat digunakan untuk dihadapkan pada data dengan kondisi heteroskedastik. Model yang dapat 1.

2. digunakan untuk memodelkan data yang bersifat heteroskedastik adalah Autoregressive Conditional Heteroscedastic (ARCH). Model ARCH pertama kali dikenalkan oleh Engle (1982). Model ARCH menggambarkan perubahan variansi yang dipengaruhi oleh beberapa data sebelumnya. Pada tahun 1986, Bollerslev memperkenalkan model Generallized Autoregressive Conditional Heteroscedastic (GARCH) sebagai pengembangan dari model ARCH. Model GARCH merupakan model yang lebih sederhana dengan banyaknya parameter yang lebih sedikit dibandingkan model ARCH berderajat tinggi (Surya & Hariadi, 2002) . Metode yang dapat digunakan digunakan dalam model ARIMA-GARCH, yaitu metode least square, metode maximum likelihood, dan metode quasimaximum likelihood. Metode maximum likelihood pertama kali diperkenalkan oleh R. A. Fisher pada tahun 1922. Maximum likelihood digunakan untuk menentukan parameter yang memaksimalkan kemungkinan dari data sampel. Pada penelitian ini, peneliti menggunakan jenis penelitian studi kasus pada harga saham. Saham merupakan salah satu jenis investasi yang banyak digunakan untuk meningkatkan pendapatan. Seseorang berinvestasi sama halnya dengan menabung. Sebagaimana Allah berfirman dalam al-Qur’an surat al-Kahfi ayat 82 yang berkaitan dengan menabung: “Dan adapun dinding rumah itu adalah milik dua anak yatim di kota itu, yang dibawahnya tersimpan harta bagi mereka berdua, dan ayahnya seorang yang saleh. Maka Tuhanmu menghendaki agar jeduanya sampai dewasa dan keduanya mengeluarkan simpananya itu sebagai rahmat dari Tuhanmu….”. Dalam tafsir Ibnu Katsir, ayat di atas terdapat dalil yang menyatakan bahwa orang yang shalih akan senantiasa dipelihara keturunanya. Selain itu, juga mencangkup berkah ibadah yang dilakukan bagi anak keturunanya di dunia dan di.

3. akhirat melalui syafa’at bagi mereka. Derajat mereka akan ditinggikan ke derajat paling tinggi di surga supaya hatinya merasa senang terhadap mereka. Ayat di atas juga menjelaskan bahwa tersimpan harta bagi mereka anak yatim di balik dinding rumah mereka. Harta tersebut simpanan sampai mereka dewasa kelak sebagai rahmat dari Allah SWT. Fitriyah (2012), meneliti tentang pemodelan harga saham menggunakan model ARIMA-GARCH. Penelitian tersebut menghasilkan bahwa model ARIMA-GARCH terbukti dapat menghilangkan masalah heteroskedastisitas dan dapat memodelkan ragam sisanya, selain itu model tersebut juga dapat memberikan peramalan yang baik. Penelitian terkait juga dilakukan oleh Khoirunnisa. Elok. (2014). yang. meneliti. tentang. penerapan. metode. ARCH/GARCH pada pemodelan harga penutupan saham di Bursa Efek Indonesia periode. 2005-2013.. Penelitian. tersebut. menghasilkan. bahwa. model. ARCH/GARCH terbukti dapat mengatasi masalah heteroskedastisitas dengan baik. Penelitian selanjutnya dilakukan oleh Bunga Lety (2015) yang meneliti tentang pemodelan dan peramalan penutupan harga saham PT.Telkom dengan metode ARCH/GARCH. Penelitian tersebut menghasilkan bahwa model ARCH/GARCH dapat memodelkan dan meramalkan harga saham dengan baik. Penelitian selanjutnya dilakukan oleh Yolanda, dkk (2017). Dalam penelitian tersebut dilakukan penerapan model ARIMA-GARCH untuk memprediksi harga saham Bank BRI. Penelitian tersebut menghasilkan bahwa model ARIMAGARCH dapat dikatakan baik untuk memodelkan dan memprediksi harga saham Bank BRI..

4. Berdasarkan hasil dari beberapa penelitian di atas, yaitu Fitriyah (2012) dan Yolanda, dkk (2017) menggunakan penerapan model ARIMA-GARCH untuk memodelkan dan meramalkan harga saham, Khoirunnisa Elok (2014) dan Bunga Lety (2015) menggunakan penerapan model ARCH/GARCH pada pemodelan harga saham. Sehingga, peneliti tertarik untuk mengimplementasi model ARIMAGARCH menggunakan metode Maximum Likelihood pada data harga saham Jakarta Islamic Index (JII). Alasan (Fitriyah, 2012)Sehingga investor syariah akan memilih saham yang tergabung dalam JII karena dianggap sebagai yang terbaik. 1.2 Rumusan Masalah Berdasarkan latar belakang di atas, maka rumusan masalah dari penelitian ini adalah sebagai berikut: 1. Bagaimana. implementasi. model. ARIMA-GARCH. menggunakan. metode Maximum Likelihood pada penentuan harga saham JII? 2. Bagaimana peramalan harga saham JII menggunakan model ARIMAGARCH? 1.3 Tujuan Berdasarkan rumusan masalah di atas, maka tujuan dari penelitian ini adalah sebagai berikut: 1. Untuk. mengetahui. hasil. implementasi. model. menggunakan metode Maximum Likelihood. ARIMA-GARCH. pada penentuan harga. saham JII. 2. Untuk mengetahui hasil peramalan harga saham JII menggunakan model.

5. ARIMA-GARCH. 1.4 Manfaat Penelitian Beberapa manfaat yang dapat diperoleh dari penilitian ini adalah: 1. Penelitian ini dapat memberikan tambahan wawasan dan pengetahuan mengenai pemodelan ARIMA-GARCH menggunakan metode Maximum Likelihood pada penentuan harga saham dan peramalannya. 2. Penelitian ini dapat dijadikan sebagai pengembangan kurikulum dan silabus di bidang mata kuliah ekonometri.. 1.5 Batasan Masalah Agar tidak terjadi perluasan atau pengembangan masalah dalam penelitian ini, maka diperlukan adanya batasan masalah yaitu: 1. Error berdistribusi normal 2. Estimasi parameter model ARIMA-GARCH menggunakan metode Maximum Likelihood dengan iterasi Newton-Raphson.. 1.6 Sistematika Penulisan Sistematika penulisan yang digunakan dalam penulisan skripsi adalah sebagai berikut: Bab I Pendahuluan Pada bab ini akan diuraikan mengenai latar belakang, rumusan masalah, tujuan penelitian, manfaat penelitian, batasan masalah, metode penelitian dan sistematika penulisan..

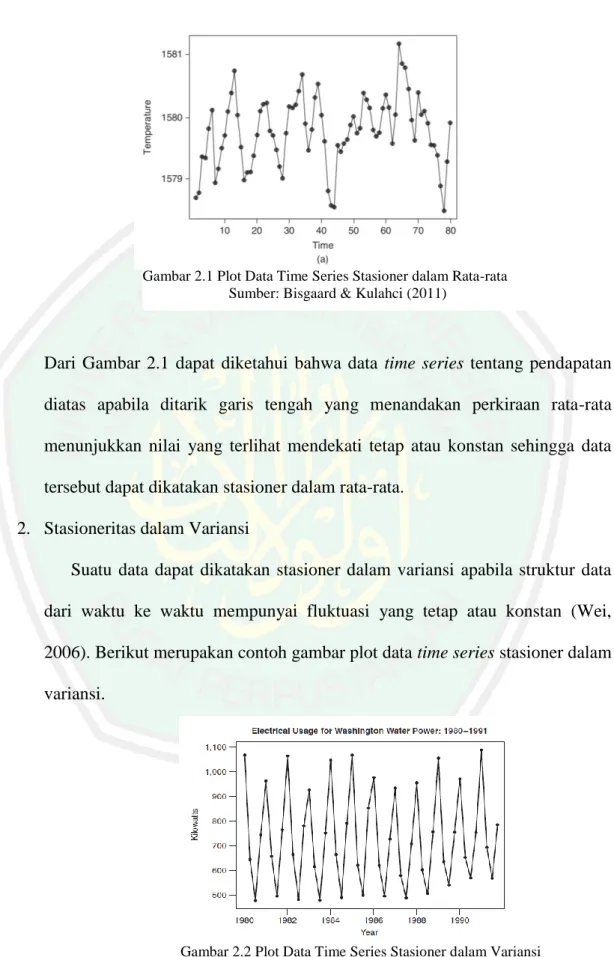
6. Bab II Kajian Pustaka Pada bab ini akan dijelaskan mengenai teori-teori yang mendasari pembahasan diantaranya; deret waktu (time series), autocorrelation fuction (ACF) , partial autocorrelation fuction (PACF), kestasioneran, differencing, proses white noise, model Autoregressive (AR), Moving Average (MA), Autoregressive Moving Average (ARMA), dan model Autoregressive Integrated Moving Average (ARIMA), ARCH dan GARCH, uji hipotesa, saham dan volatilitas, dan metode Maximum Likelihood. Bab III Metode Penelitian Pada bab ini akan dijelaskan mengenai pendekatan penelitian, sumber data, variabel penelitian, dan analisis data. Bab IV Hasil dan Pembahasan Pada bab ini merupakan inti dari skripsi yang menjelaskan tentang pembahasan hasil implementasi model ARIMA-GARCH menggunakan metode Maximum Likelihood pada penentuan harga saham. Bab V Penutup Pada bab ini disajikan mengenai kesimpulan dan saran dari hasil pembahasan..

BAB II KAJIAN PUSTAKA 2.1 Deret Waktu (Time Series) 2.1.1 Pengertian Deret Waktu Deret waktu adalah serangkaian pengamatan yang diambil berdasarkan urutan waktu dan antara pengamatan yang berdekatan dan saling berkorelasi, sehingga dikatakan bahwa pada deret waktu, tiap pengamatan yang di ambil dari variabel berkorelasi dengan variabel itu sendiri pada waktu sebelumnya (Wei, 2006). Deret waktu memiliki aplikasi dalam berbagai bidang. Contoh deret waktu dalam bidang ekonomi antara lain pergerakan harga saham, jumlah ekspor setiap bulan, dan keuntungan perusahaan. Dalam deret waktu (time series) perlu memperhatikan pola pergerakan data. Pola pergerakan data atau nilai variabel dapat diikuti dengan adanya data deret waktu, sehingga data deret waktu dapat digunakan sebagai dasar untuk pembuatan keputusan pada saat ini, peramalan keadaan perdagangan dan ekonomi pada masa yang akan datang, perencanaan kegiatan untuk masa depan (Spiegel & Stephens, 2017). 2.1.2 Autocorrelation Function (ACF) Korelasi merupakan hubungan linier antara dua variabel (Reykov & George, 2013), sedangkan autokorelasi merupakan suatu kondisi dimana terdapat hubungan antara nilai-nilai suatu deret waktu yang sama pada waktu yang berbeda (Makridakis, MeGee, & Wheel, 1999). Pada ACF, k merupakan ukuran korelasi antara dua nilai Z t dan Zt  k dengan koefisien korelasi pada lag-k. Rata-rata. 7.

8. kedua nilai tersebut konstan yang dapat dinyatakan dengan:. E  Zt   E  Zt k   . (2.1). dan memiliki variansi konstan sebagai berikut var  Z t   var  Z t  k   E  Z t      Z2 2. (2.2). Fungsi autokovariansi antara Z t dan Zt  k adalah sebagai berikut: cov  Z t , Z t  k   E  Z t    Z t  k       k. (2.3). Sehingga fungsi autokorelasi antara Z t dan Zt  k adalah:. cov  Zt , Zt  k . corr  Zt , Zt  k  . var  Zt  var  Zt  k  cov  Zt , Zt k . . . var  Zt  var  Zt  cov  Zt , Zt  k  var  Zt . E  Z t    Z t  k    . . E  Zt   . . E  Zt    E  Zt k    E  Zt   . n. . 2. n.   Z t     Z t  k    t 1. t 1. n. Z t 1.  k. dimana: Zt. 2. : variabel acak untuk t  0, 1, 2,.... t.  . 2. (2.4).

9. : selang waktu, : variabel acak untuk t  0, 1, 2,... pada lag ke k. k. : nilai fungsi autokorelasi (koefisien korelasi) pada lag ke k. k. : nilai fungsi autokovariansi pada lag ke k. . : rata-rata variabel acak. 2.1.3 Parsial Autocorrelation Function (PACF) PACF menunjukkan korelasi antara variabel pada saat saat. dan variabel pada. dengan mengeluarkan seluruh pengaruh antara variabel pada saat. variabel pada saat. dan. (Ariedianto, 2012). Menurut Wei (2006), Variansi antara. dan ̂ dapat dirumuskan sebagai berikut:. .  . var Zt  Zˆt  E Zt  Zˆt sedangkan variansi antara. dan ̂. . . 2.  E  t . 2. (2.5). dapat dirumuskan sebagai berikut:.  . var Zt k  Zˆt k  E Zt k  Zˆt k. . 2.  E  t k . 2. (2.6). dan fungsi autokovarian dapat dirumuskan sebagai berikut:. . . . .    Z. cov  Zt  Zˆt , Zt  k  Zˆt k   E  Zt  Zˆt     . t k.  .  Zˆt k    .  E   t     t  k    .  E  t    E  t k   . (2.7). Sehingga fungsi autokorelasi parsial dapat dirumuskan sebagai berikut:. . . . corr  Z t  Zˆt , Z t  k  Zˆt  k    . . . cov Z t  Zˆt , Z t  k  Zˆt  k. . var Z t  Zˆt. . . . var Z t  k  Zˆt  k. .

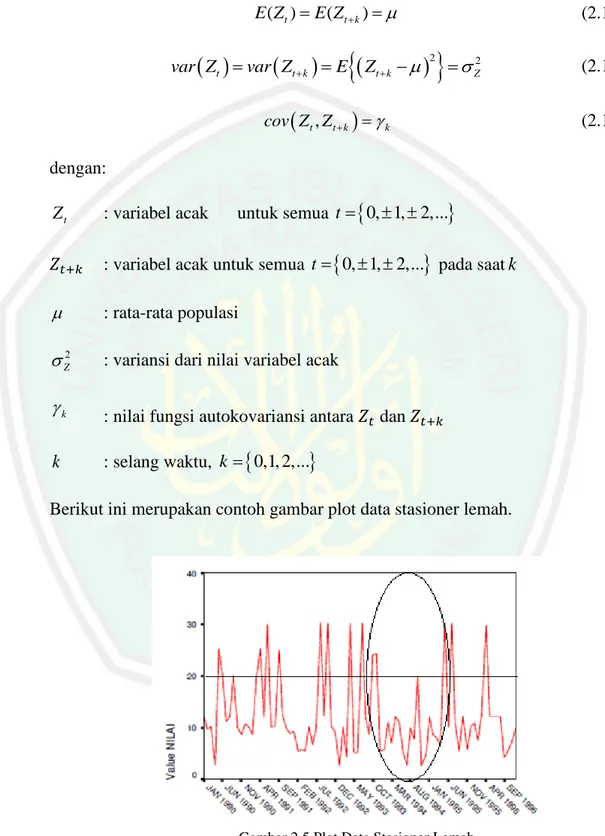
10. . E  t    E  t k    E  t  n. .   t 1. n. 2. E  t k . 2. n. t.      t  k   .   t . t 1. 2. t 1. n.    t 1. 2. t k.  Pk. (2.8). dimana: Zt. : variabel acak untuk t  0, 1, 2,.... Zt. : estimasi variabel acak untuk t  0, 1, 2,... : variabel acak t  0, 1, 2,... pada lag ke k. ̂. : estimasi variabel acak t  0, 1, 2,... pada lag ke k. . : nilai error. k. : selang waktu,. Pk. : nilai fungsi autokorelasi parsial pada lag ke k. . : rata-rata variabel acak. 2.1.4 Kestasioneran Data time series dapat dikatakan stasioner apabila tidak terjadi kenaikan atau penurunan secara tajam pada data. Stasioneritas dapat dibagi menjadi tiga, yaitu sebagai berikut: 1. Stasioneritas dalam Rata-rata Suatu data dapat dikatakan stasioner dalam rata-rata apabila fluktuasi data berada di sekitar suatu nilai rata-rata yang konstan, tidak tergantung pada waktu dan variansi dari fluktuasi tersebut (Wei, 2006). Berikut merupakan.

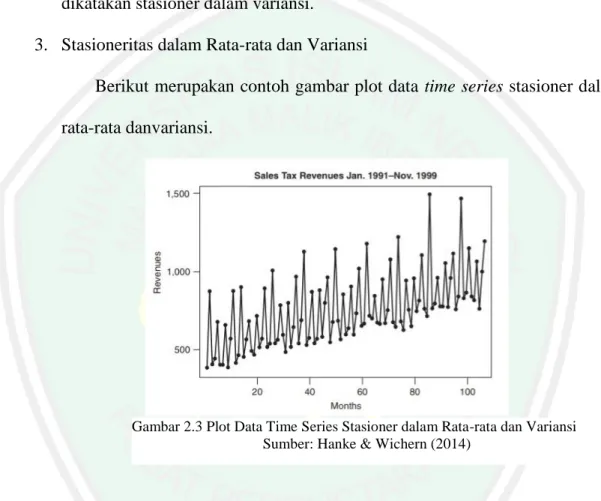
11. contoh gambar plot data time series stasioner dalam rata-rata.. Gambar 2.1 Plot Data Time Series Stasioner dalam Rata-rata Sumber: Bisgaard & Kulahci (2011). Dari Gambar 2.1 dapat diketahui bahwa data time series tentang pendapatan diatas apabila ditarik garis tengah yang menandakan perkiraan rata-rata menunjukkan nilai yang terlihat mendekati tetap atau konstan sehingga data tersebut dapat dikatakan stasioner dalam rata-rata. 2. Stasioneritas dalam Variansi Suatu data dapat dikatakan stasioner dalam variansi apabila struktur data dari waktu ke waktu mempunyai fluktuasi yang tetap atau konstan (Wei, 2006). Berikut merupakan contoh gambar plot data time series stasioner dalam variansi.. Gambar 2.2 Plot Data Time Series Stasioner dalam Variansi Sumber: Hanke & Wichern (2014).

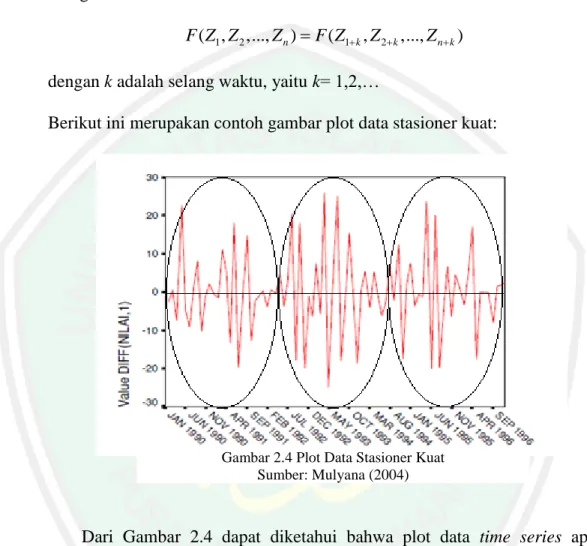
12. Dari Gambar 2.2 dapat diketahui bahwa data time series tentang pendapatan pajak penjualan diatas apabila ditarik garis lurus menaik pada tengah-tengah plot yang menandakan perkiraan rata-rata menunjukkan nilai yang terlihat berubah-ubah dan simpangan setiap data terhadap rata-ratanya menunjukkan nilai yang terlihat mendekati tetap atau konstan sehingga data tersebut dapat dikatakan stasioner dalam variansi. 3. Stasioneritas dalam Rata-rata dan Variansi Berikut merupakan contoh gambar plot data time series stasioner dalam rata-rata danvariansi.. Gambar 2.3 Plot Data Time Series Stasioner dalam Rata-rata dan Variansi Sumber: Hanke & Wichern (2014). Dari gambar 2.3 dapat diketahui bahwa data time series tentang penggunaan listrik diatas apabila ditarik garis tengah yang menandakan perkiraan rata-rata menunjukkan nilai yang konstan dan simpangan setiap data terhadap rataratanya menunjukkan nilai yang terlihat mendekati tetap atau konstan sehingga data tersebut dapat dikatakan stasioner dalam rata-rata dan variansi. Menurut Mulyana (2014), stasioneritas terbagi menjadi dua, yaitu: 1. Stasioneritas kuat (strictly stasionarity).

13. Suatu data dapat dikatakan stasioner kuat apabila distribusi gabungan dari variabel acak Zt , t  1, 2,..., n sama dengan distribusi gabungan dari variabel acak Zt  k dengan t  1, 2,..., n dan untuk semua lag k atau dapat dituliskan sebagai berikut: F ( Z1 , Z 2 ,..., Z n )  F ( Z1 k , Z 2 k ,..., Z n k ). (2.9). dengan k adalah selang waktu, yaitu k= 1,2,… Berikut ini merupakan contoh gambar plot data stasioner kuat:. Gambar 2.4 Plot Data Stasioner Kuat Sumber: Mulyana (2004). Dari Gambar 2.4 dapat diketahui bahwa plot data time series apabila diambil sampel dimanapun nilai tengah atau perkiraan rata-ratanya konstan, sehingga dapat dikatakan stasioner kuat. 2. Stasioneritas lemah (weakly stasionarity) Suatu data deret waktu dikatakan satsioner lemah apabila memiliki ratarata konstan dan autokovariansinya merupakan fungsi dari lag. Menurut Effendi & Setiawan (2014), stasioneritas lemah dapat diartikan sebagai kondisi.

14. dimana rata-rata, variansi, dan autokovariansi konstan pada suatu waktu dapat dinyatakan sebagai berikut: E (Zt )  E (Zt  k )  . . var  Zt   var  Zt  k   E  Zt  k   . (2.10) 2.  . 2 Z. cov  Z t , Z t  k    k. dengan: Zt. : variabel acak. untuk semua t  0,  1,  2,.... : variabel acak untuk semua t  0,  1,  2,... pada saat k. . : rata-rata populasi.  Z2. : variansi dari nilai variabel acak. k. : nilai fungsi autokovariansi antara. k. : selang waktu, k  0,1, 2,.... dan. Berikut ini merupakan contoh gambar plot data stasioner lemah.. Gambar 2.5 Plot Data Stasioner Lemah Sumber: Mulyana (2004). (2.11) (2.12).

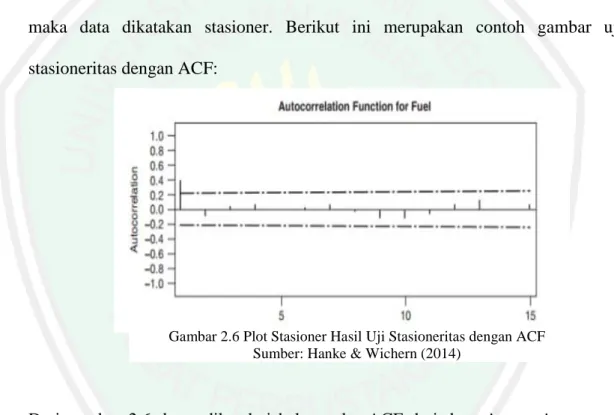
15. Dari Gambar 2.5 dapat diketahui bahwa plot data time series apabila diambil suatu sampel acak, garis tengahnya tidak mewakili rata-rata setiap data sehingga dapat dikatakan stasioner lemah. Menurut Ekananda (2015), terdapat tiga cara yang dapat digunakan untuk menguji kestasioneran. Cara yang pertama dapat menggunakan analisis grafis, yaitu dengan membuat plot dari deret data yang dimiliki. Kemudian cara yang ke dua dapat dilihat dari Autocorrelation Function (ACF) atau correlogram, yaitu apabila gambar correlogram mendekati nol mulai dari lag ke-2 atau lag ke-3 maka data dikatakan stasioner. Berikut ini merupakan contoh gambar uji stasioneritas dengan ACF:. Gambar 2.6 Plot Stasioner Hasil Uji Stasioneritas dengan ACF Sumber: Hanke & Wichern (2014). Dari gambar 2.6 dapat diketahui bahwa plot ACF dari data time series tentang bahan bakar menunjukkan nilai fungsi autokorelasi yang mendekati nol diantara garis interval pada saat lag ke-2, sehingga data tersebut dapat dikatakan stasioner. Sedangkan suatu data dapat dikatakan tidak stasioner apabila gambar correlogram mendekati nol pada lag yang cukup panjang, misalkan pada lag ke-15 atau bahkan lebih. Berikut ini merupakan contoh visualisasi correlogram suatu data yang tidak stasioner:.

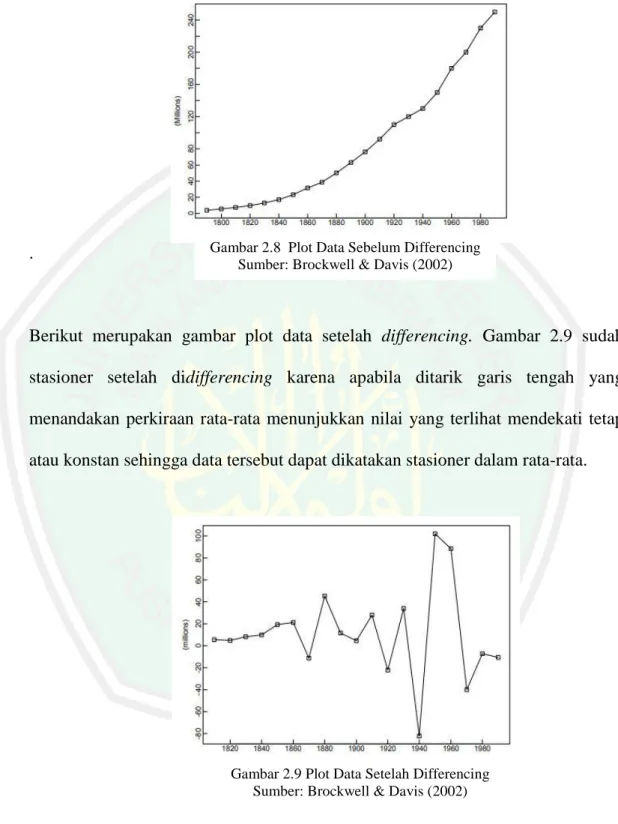
16. Gambar 2.7 Plot Tidak Stasioner Hasil Uji Stasioneritas dengan ACF Sumber: Mulyana (2004). Dari gambar 2.7 dapat diketahui bahwa plot ACF dari data time series di bawah ini menunjukkan nilai fungsi autokorelasi (ACF) yang melebihi garis interval saat lag pertama hingga lag ke-16 dan bergerak perlahan mendekati nol, karena pergerakan nilai ACF mendekati nol membutuhkan lag yang cukup panjang sehingga data tersebut dapat dikatakan tidak stasioner. 2.1.5 Differencing Differencing dilakukan untuk menstasionerkan data yang non stasioner. Operator shift mundur (backward shift) sangat tepat dalam menggambarkan proses differencing (Makridakis, MeGee, & Wheel, 1999). Berikut merupakan gambar plot data tidak stasioner kemudian dilakukan proses differencing sehingga plot data menunjukkan stasioner. Dari gambar 2.8 dapat diketahui bahwa data time series tentang populasi penduduk U.S.A pada 1790-1990 diatas jika ditarik garis tengah yang menandakan perkiraan rata-rata menunjukkan nilai yang terlihat tidak mendekati tetap atau konstan begitu juga simpangan setiap data terhadap rata-ratanya menunjukkan nilai yang terlihat tidak mendekati tetap atau konstan..

17. sehingga data tersebut dapat dikatakan tidak stasioner dalam rata-rata dan variansi. .. Gambar 2.8 Plot Data Sebelum Differencing Sumber: Brockwell & Davis (2002). Berikut merupakan gambar plot data setelah differencing. Gambar 2.9 sudah stasioner setelah didifferencing karena apabila ditarik garis tengah yang menandakan perkiraan rata-rata menunjukkan nilai yang terlihat mendekati tetap atau konstan sehingga data tersebut dapat dikatakan stasioner dalam rata-rata.. Gambar 2.9 Plot Data Setelah Differencing Sumber: Brockwell & Davis (2002). Menurut Makridakis, MeGee, dan Wheel (1999), dapat dituliskan sebagai berikut:. proses differencing.

18. Z 't  Zt  Zt 1. (2.13). dimana Z 't merupakan differencing pertama dari Z t . Selain itu, notasi yang dipasang pada Z t digunakan untuk menggeser data satu periode ke belakang yang dinotasikan dengan B yang merupakan operator mundur (backward shift) dapat dituliskan sebagai berikut:. BZ t  Z t 1. (2.14). Pada persamaan tersebut, notasi B yang dipasang pada X t memiliki efek menggeser data satu periode ke belakang. Opersasi shift mundur tersebut dapat menggambarkan proses differencing. Sebagai contoh, apabila suatu deret waktu tidak stasioner, maka data tersebut dapat dibuat lebih mendekati stasioner dengan melakukan differencing pertama dari deret data dan differencing pertama dituliskan sebagai berikut (Makridakis, dkk, 1999):. Zt'  Zt  Zt 1. (2.15). dengan Z t' merupakan nilai variabel Z pada waktu t setelah differencing. Dengan menggunakan backward shift, persamaan (2.15) dapat ditulis menjadi: Zt'  Zt  BZt. (2.16). Zt'  1  B  Z t. (2.17). atau. Differencing pertama pada persamaan (2.17) dinyatakan oleh 1  B  . Differencing orde kedua, yaitu differencing pertama dari differencing pertama sebelumnya. Jika differencing orde kedua harus dihitung, maka.

19. Z t''  Z t'  Z t'1.   Z t  Z t 1    Z t 1  Z t  2   Z t  2Z t 1  Z t  2. . .  1  2 B  B 2 Zt  1  B  Z t 2. (2.18). Differencing orde kedua pada persamaan (2.18) dinotasikan oleh 1  B  . Secara 2. umum, differencing orde ke-d dapat dinotasikan dengan Z td  1  B  Zt , d  1 d. (2.19). dimana:. Ztd. : differencing orde ke-d. d. : orde differencing. 2.1.6 Proses White Noise White noise merupakan suatu bentuk variabel acak yang tidak saling berkorelasi dari distribusi tertentu. Menurut Wei (2006), proses white noise ditentukan dengan rata-rata yang konstan:. E  Zt     0. (2.20). Proses ini juga memiliki varians konstan: var ( Zt )   2. (2.21). cov  Zt , Zt  k    k  0. (2.22). dan kovarian. dimana: Zt. : variabel acak. Zt  k. : variabel acak pada saat k.

20. t. : waktu. k. : selang waktu/lag. . : rata-rata variabel acak. 2. : variansi dari variabel acak : nilai fungsi autokovariansi antara. dan. , k  0. Berikut ini merupakan contoh gambar yang menunjukkan bahwa data bersifat white noise.. Gambar 2.10 Plot Data bersifat White Noise Sumber: Brockwell & Davis (2002). Dari gambar 2.10 menunjukkan data yang bersifat white noise karena membentuk seperti plot data stasioner, tidak mengandung unsur trend, hanya saja jarak antardata pada plot white noise lebih rapat daripada plot data stasioner. 2.1.7 Model Time Series Stasioner Model time series stasioner dapat dibagi menjadi tiga, yaitu: 1.. Model Autoregressive (AR) Autoregressive. merupakan. suatu. bentuk. regresi. yang. tidak. menghubungkan variabel tak bebas, melainkan menghubungkan nilai-nilai sebelumnya pada selang waktu yang bermacam-macam. Jadi model.

21. Autoregressive akan menyatakan ramalan sebagai fungsi nilai-nilai sebelumnya dari deret waktu tertentu (Makridakis, MeGee, & Wheel, 1999). Model Autoregressive (AR) dengan orde p dinotasikan dengan AR(p). Menurut Wei (2006), model AR(p), dapat dituliskan sebagai berikut:. Zt  1Zt 1  ...   p Zt  p   t. (2.23). Karena Zt  Zt   maka, persamaan (2.23) dapat ditulis dalam bentuk sebagai berikut: Zt    1 (Zt 1   )  ...   p (Zt  p   )   t.  1Zt 1  1  ...   p Zt  p   p    t Zt    1  ...   p   1Zt 1  ...   p Zt  p   t p   (1  1  ...   p )  1Zt 1  ...   p Zt  p   t   (1  (1  ...   p ))  1Zt 1  ...   p Zt  p   t.  0  1Zt 1  ...   p Zt  p   t. (2.24). dimana: Zt. : selisih antara variabel acak pada saat t dan rata-rata populasi. Zt. : nilai variabel acak pada saat t. . : rata-rata populasi : koefisien regresi pada proses AR orde ke- , : konstanta rata-rata : nilai error pada saat t. t. : waktu : orde AR 2. Model Moving Average (MA) Moving Average (MA) adalah nilai time series pada waktu t yang.

22. dipengaruhi oleh unsur kesalahan pada saat ini dan unsur kesalahan terbobot pada masa lalu (Makridakis, MeGee, & Wheel, 1999). Model moving average dengan orde q dinotasikan dengan MA(q). Menurut Wei (2006), model moving average dapat didefinisikan sebagai berikut:. Zt   t  1 t 1  ...  q t q. (2.25). Karena Zt  Zt   dan diasumsikan bahwa   0 , maka persamaan (2.25) dapat ditulis dalam bentuk sebagai berikut: Zt     t  1 t 1  ...  q t q Zt  0   t  1 t 1  ...  q t q. Zt  0   t  1 t 1  ...  q t q. (2.26). dimana: Zt. : selisih antara variabel acak pada saat t dan rata-rata populasi. Zt. : nilai variabel acak pada saat t. . : rata-rata populasi : koefisien regresi pada proses MA orde ke- , : nilai error pada saat t. t. : waktu : orde MA. 3. Model Autoregressive Moving Average (ARMA) Model AR dan MA dapat dikombinasikan untuk menghasilkan berbagai macam model yang merupakan gabungan dari model Autoregressive (AR) dan Moving Average (MA). Menurut Wei (2006), bentuk persamaan ARMA adalah sebagai berikut:.

23. Zt  1Zt 1  ...   p Zt  p   t  1 t 1  ...  q t q. (2.27). Karena Zt  Zt   , maka persamaan (2.27) dapat ditulis dalam bentuk sebagai berikut: Zt    1 (Zt 1   )  ...   p (Zt  p   )   t  1 t 1  ...  q t q  1Zt 1  1  ...   p Zt  p   p    t  1 t 1  ...  q t q Zt    1   p   1Zt 1  ...   p Zt  p   t  1 t 1  ...  q t q.   (1  1  ...   p )  1Zt 1  ...   p Zt  p   t  1 t 1  ...  q t q (2.28). dimana: Zt. : selisih antara variabel acak pada saat t dan rata-rata populasi. Zt. : nilai variabel acak pada saat t : koefisien regresi pada proses AR orde ke- , : nilai error pada saat t. t. : waktu : orde AR : koefisien regresi pada proses MA orde ke- , : orde MA. 2.1.8 Model Time Series Nonstasioner Salah satu model deret waktu nonstasioner adalah model Autoregressive Integrated Moving Average (ARIMA). ARIMA merupakan hasil modifikasi model ARMA (p,q) dengan memasukkan operator differencing karena merupakan syarat untuk menstasionerkan data, dalam notasi operator shift mundur. Menurut Wei (2006), bentuk persamaan ARIMA. adalah sebagai berikut:.

24. Zt  Zt d  1Zt 1  1Zt 1d  ...   p Zt  p   p Zt  pd  0  1 t 1  ...  q t q. Zt  Zt d  1 (Zt 1  Zt 1d )  ...   p (Zt  p  Zt  pd )  0  1 t 1  ...  q t q (2.29) atau dapat disederhanakan dengan bentuk berikut ini: p. q. i 1. j 1. Z t  Z t  d  0   1 ( Z t 1  Z t 1 d )    j t  j. (2.30). dimana: Zt. : variabel acak pada saat t : koefisien regresi pada proses AR orde ke- , : orde AR : koefisien regresi pada proses MA orde ke- , : orde MA : nilai error pada saat t. t. : waktu. d. : orde differencing. 2.1.9. Model ARCH dan GARCH Pada umumnya pemodelan data time series harus memenuhi asumsi varian. konstan (homoskedastisitas). Namun data time series pada sektor keuangan sangat tinggi volatilitasnya. Hal ini ditunjukkan oleh pergerakan varian yang tidak konstan (heteroskedastisitas). Untuk mengatasi masalah tersebut, maka digunakan model Autoregressive Conditional Heteroscedastic (ARCH) yang diperkenalkan oleh Engle (1982). Menurut Wei (2006) model ARCH berikut:. dapat didefinisikan sebagai.

25.  t  ht wt. (2.31). ht2  0  1 t21   m t2m. (2.32). dimana: : variabel acak white noise : variansi error pada saat t : standar deviasi error : parameter ARCH : error pada saat t : orde ARCH dengan. dan Selanjutnya,. untuk model. Generallized. Autoregressive. Conditional. Heteroscedastic (GARCH) dikembangkan oleh Bollerslev tahun 1986 yang merupakan model pengembangan dari model ARCH(m) untuk mengatasi orde yang lebih tinggi. Menurut Wei (2006), bentuk umum model GARCH(m,s) dapat didefinisikan sebagai berikut: ht2  0  1 t21   m t2m  1ht21  s ht2s. dimana: : variansi error pada saat t : error pada saat t , m,s. : parameter GARCH : orde GARCH. (2.33).

26. 2.2 Uji Hipotesa 2.2.1 Uji Stasioneritas Salah satu cara yang dapat digunakan untuk mengetahui data bersifat stasioner atau tidak yaitu dengan membuat plot antara nilai pengamatan terhadap waktu. Selain itu menurut Saludin (2017), uji stasioneritas juga dapat dilakukan dengan uji akar unit. Untuk memperoleh gambaran uji akar unit, akan ditunjukkan pada persamaan AR(1) berikut ini: Zt   Zt 1   t. (2.34). Hipotesis yang digunakan: H 0 : ADF  1 (data memiliki akar unit/ data bersifat stasioner) H1 : ADF  1 (data tidak memiliki akar unit/ data bersifat tidak stasioner). Statistik uji:. ADF .  SE ( ). (2.35). 2 n. (2.36). dengan,. SE  dimana: DF. : Uji Dickey Fuller. . : penduga dari koefisien . . : parameter AR. SE. : nilai standar error. 2. : variansi. n. : banyaknya pengamatan.

27. Keputusan : H 0 ditolak jika statistik uji DF lebih kecil daripada nilai kritis Kesimpulan : Jika H 0 ditolak maka data bersifat stasioner 2.2.2 Uji Normalitas Uji normalitas digunakan untuk menguji apakah suatu data berdistribusi normal atau tidak. Uji normalitas dapat digunakan untuk mengukur data berskala ordinal, interval, atau rasio. Menurut Rosadi (2012), salah satu pengujian normalitas data, yaitu menggunakan pendekatan grafik. Selain itu, normalitas juga dapat diketahui dengan membandingkan nilai Jarque Bera (JB) dan nilai Chi Square tabel (Ansofino, 2016). Hipotesis yang digunakan: H 0 :   0 (error berdistribusi normal) H1 :   0 (error tidak berdistribusi normal). Statistik uji:.  K  3 n JB   Sk2  u 2  4. 2.    . dan untuk estimasi skewness dan kurtosis digunakan statistik. (2.37). dan. yang. didefinisikan sebagai berikut:. 1 n 3  Zl     l 1 Sk  n 3/2 2 1 n   l 1  Zl     n . (2.38). 1 n 4  Zl     i 1 Ku  n 2 2 1 n Z      l 1  l n . (2.39). dan.

28. dimana: : variabel acak untuk semua t  0, 1, 2,... : nilai ekspektasi variabel acak (rata-rata variabel acak) : skewness : kurtosis Keputusan : Jika JB hitung > Chi Square tabel maka H0 ditolak. Kesimpulan : Jika H 0 ditolak, maka error tidak berdistribusi normal. 2.2.3 Uji Heteroskedastisitas Tujuan dari uji heteroskedastisitas adalah untuk menguji apakah dalam sebuah model regresi terjadi ketidaksamaan varians atau residual dari satu pengamatan ke pengamatan yang lain. Menurut Sarjono dan Julianita (2013), deteksi heteroskedastisitas dapat dilakukan dengan metode scatter plot dengan memplotkan nilai ZPRED (nilai prediksi) dengan SRESID (nilai residualnya). Model yang baik didapatkan jika tidak terdapat pola tertentu pada grafik, seperti mengumpul di tengah, menyempit kemudian melebar atau sebaliknya melebar kemudian menyempit. Selain itu, menurut Effendi & Setiawan (2014), cara untuk menguji heteroskedastisitas yaitu dengan menggunakan metode White. Proses pengujian dengan metode White pada model adalah dengan melakukan regresi tambahan sebagai berikut:.  i2  1  2 X 2i  3 X 3i  4 X 22i  5 X 32i  6 X 2i X 3i   i dimana. (2.40). merupakan nilai error dari persamaan struktural. Hasil regresi ini. bertujuan untuk mendapatkan nilai. yang akan digunakan dalam pengujian.

29. hipotesis. Hipotesis yang digunakan: H 0 :  t2   2 (homoskedastisitas) H1 :  t2   2 (heteroskedastisitas). Statistik uji:.  2  n.R 2. (2.41). dengan,. R2. Yˆ  Y  . Y  Y . 2. 2. (2.42). dimana: : banyaknya pengamatan : koefisien determinasi : distribusi chi-square Yˆ. : variabel terikat estimasi. Y. : variabel terikat. Y. : variabel terikat rata-rata. Keputusan : Jika  2 hitung >  2tabel maka H0 ditolak. Kesimpulan : Jika H0 ditolak maka ada heteroskedastisitas di dalam model. 2.2.4 Uji Signifikansi Parameter Uji signifikansi parameter merupakan uji yang dilakukan setelah estimasi nilai-nilai parameter dari model ARIMA yang ditetapkan sementara. Uji signifikansi parameter berguna untuk mengetahui signifikan atau tidaknya suatu parameter. Menurut Aswi & Sukarna (2006), pengujian ini dilakukan dengan cara.

30. sebagai berikut: Hipotesis yang digunakan: H 0 :   0 (parameter  tidak signifikan dalam model) H1 :   0 (parameter  signifikan dalam model). Statistik Uji: thitung . ˆ. . SE ˆ. (2.43). dimana:. ˆ. : nilai estimasi parameter. SE. : standart error. Keputusan: Tolak H 0 jika thitung  t dengan dimana  adalah taraf signifikansi. 2. Kesimpulan: Tolak H 0 artinya parameter pada model telah signifikan. 2.3 Saham dan Volatilitas 2.3.1. Saham Saham adalah salah satu bentuk investasi yang paling banyak diminati. karena memberi keuntungan yang menarik. Saham berwujud selembar kertas yang menerangkan bahwa pemilik kertas adalah pemilik perusahaan yang menerbitkan surat berharga tersebut. Porsi kepemilikan ditentukan oleh seberapa besar penyertaan yang ditanamkan di perusahaan tersebut (Darmadji & Hendi, 2006). Perubahan harga saham tidak dapat ditentukan secara pasti. Menurut Hull (2012), perubahan harga saham dapat dimodelkan menggunakan persamaan differensial stokastik sebagai berikut: dST   ST dt   ST dWT. (2.44).

31. dengan: : komponen deterministik : komponen stokastik : proses Wiener 2.3.2. Volatilitas Volatilitas adalah salah satu pengukuran statistik untuk fluktuasi harga. selama periode waktu tertentu. Volatilitas juga dapat didefinisikan sebagai ukuran dalam presentase yang menyatakan seberapa besar kemungkinan harga saham dapat bergerak naik atau turun dalam suatu periode tertentu (Karnadjaja, dkk, 2007). Dalam saham, volatilitas sangat penting untuk dipahami oleh para investor. Volatilitas digunakan para investor untuk meminimalisir resiko yang akan dihadapi. Semakin tinggi niali volatilitas dari suatu saham, maka semakin tinggi ketidakpastian dari return saham yang akan diperoleh. Menurut Ekananda (2015), perhitungan besarnya volatilitas dapat dinyatakan sebagai berikut:.  S  rt  ln  t   St 1 . (2.45). dimana: r. : return. t. : waktu. S. : harga saham. dan perhitungan standar deviasi dari return dapat dinyatakan sebagai berikut (Hull, 2012):. 1 n 2 s  rt  r   n  1 i 1. (2.46).

32. dimana: s. : standar deviasi. n. : banyaknya pengamatan. r. : return ̅. : rata-rata return. 2.4 Estimasi Parameter 2.4.1 Metode Maximum Likelihood Maximum Likelihood atau metode kemungkinan maksimum adalah teknik yang sangat luas dipakasi dalam penaksiran suatu parameter distribusi data dan tetap dominan dipakai dalam pengembangan uji-uji yang baru (Lehmann, 1986). Menurut Aziz (2010), metode maximum likelihood dirumuskan sebagai berikut: Misalkan X i' vektor 1 k , i  1,, n., maka yi  X i'    i , i  1,..., m., sehingga yi ~ N  X i'  ,  2  . Fungsi distribusi peluang dari yi jika diberikan X i ,  dan  2. adalah.  1  y  X '  2  1 i f  yi | X i ,  ,    exp    i    2   2    2. (2.47). karena yi ,, yn saling bebas, diperoleh:. f  yi ,, yn    2 Pandang fungsi likelihood berikut:. n 2 2. .  1 n  y  X '  2  i exp     i    2 i 1     . (2.48).

33 n  '  1  l   ,  2 |X , y    2 2  2 exp   2  y  X    y  X     2 . (2.49). maka fungsi log-likelihood-nya adalah. n 1 ' L  ln l   ln  2 2   2  y  X    y  X   2 2 n 1   ln  2 2   2  y '  ' X ' y  X   2 2 n 1  ln  2 2   2  yy  yX     X y   ' X ' X   2 2. . n 1 '  ln  2 2   2 yy   yX     ' X ' y   ' X ' X  2 2. . n 1   ln  2 2   2  yy   ' X ' y   ' X ' y   ' X ' X   2 2 n 1   ln  2 2   2  yy   ' X ' y   ' X ' y   ' X ' X   2 2. n 1   ln  2 2   2  yy  2  X y    X X   2 2 sehingga, L 1   2  2 X y  X X     X X   2. . . 1. 1 2.  2 X y  X X     X X  ' '. 2 2.  2 X y  2 X X   '. 2. (2.50).

34. . 1. 2.  X y  X X  . (2.51). dengan menyamakan hasil turunan ini dengan nol diperoleh. ˆml   X X  X ' Y 1. (2.52). 2.4.2 Iterasi Newton-Raphson Fungsi distribusi peluang (pdf) dari yt diberikan oleh X t ,  ,  2 adalah sebagai berikut (Aziz, 2010):. f  yt | X t ,  ,  2  .  1 2 exp   2  yt  f  X t ,     2 2  2  1. (2.53). Fungsi likelihood dari  dan  2 diberikan oleh yt dan X t adalah n   1 2 l      2 2  2 exp   2  yt  f  X t ,      2 . (2.54). Fungsi log-likelihood dari  dan  2 diberikan oleh yt dan X t adalah. L     ln  l     n    1 2   ln   2 2  2 exp   2  yt  f  X t ,       2   n    1  '  ln   2 2  2 exp   2  yt  f  X t ,     yt  f  X t ,      (2.55)  2  . Aprokmasi L    di sekitar  1 dengan deret Taylor 2, yaitu (Aziz, 2010):.  . L     L  1 . 2 L 1 1 1 '  L |        | 1    1 1  '  2  ' . .  . . . . (2.56). sehingga diperoleh. L     L  2 L   ' | 1   |    1 '  1      '. . . (2.57).

35. karena '.  L  L | 1  ' | 1       sehingga. (2.58). L    L 2 L  | 1  |    1 '  (1)   . . . (2.59). Menyamakan dengan nol akan diperoleh. L 2 L | 1  |   2   1  0 '  1  . . . (2.60). atau 1. .  2. . 1.  2 L  L  | | 1 '  1     . (2.61). Pada umumnya diperoleh iterasi sebagai berikut: 1. .  n 1. .  n. .  n. .  n.  2 L  L  | | n '   n      1.  1 2 L   1 L   2 |  2 | n  '   n    2    2   1.  2 L   L   | | n  '   n        . (2.62). Iterasi inilah yang dikenal sebagai iterasi Newton-Raphson. 2.5 Ayat Al-Qur’an tentang Jual Beli Dalam Al-Qur’an, sikap jual beli telah disinggung dalam surat Al-Baqarah ayat 282 berikut: “Dan persaksikanlah apabila kamu berjual beli, dan janganlah penulis dan saksi saling sulit menyulitkan. Jika kamu lakukan (yang demikian), maka sesunguhnya hal itu adalah suatu kefasikan pada dirimu. Dan bertakwalah kepada Allah, Allah mengajarmu, dan Allah maha mengetahui segala sesuatu.”. Dalam tafsir Ibnu Katsir, menjelaskan dalam ayat tersebut bahwa bagi.

36. orang yang ingin melakukan transaksi jual beli atau bermuamalah tidak secara tunai dalam kurun waktu yang ditentukan, hendaknya untuk menuliskannya, agar lebih dapat menjaga jumlah dan batas waktu dalam muamalah, serta lebih menguatkan bagi saksi. Ketika seseorang bermuamalah dan membuat surat perjanjian, orang tersebut harus berlaku adil dan benar serta tidak boleh berpihak kepada salah seorang dalam penulisanya tersebut dan tidak boleh juga sesorang menulis kecuali apa yang telah disepakati tanpa menambah atau menguranginya. Ayat di atas mengajarkan sesorang untuk tidak saling menyusahkan ketika ingin bermuamalah atau transaksi jual beli. Ketika salah seorang tidak mengerti mengenai tulis-menulis dalam bermuamalah, hendaklah mengajarinya agar orang tersebut mengerti dan mengamalkanya dalam bermuamalah..

BAB III METODE PENELITIAN 3.1 Pendekatan Penelitian Dalam penelitian ini, peneliti menggunakan pendekatan deskriptif kuantitatif dan studi literatur. Data yang digunakan dalam penelitian ini merupakan data yang diukur dalam suatu skala numerik, yaitu data harga saham (closing price). Studi literatur pada penelitian ini merupakan suatu metode penelitian yang dijadikan sumber dalam pemecahan masalah dengan kajian kepustakaan. 3.2 Jenis dan Sumber Data Jenis data yang digunakan dalam penelitian ini adalah data sekunder. Data sekunder yang digunakan dalam penelitian ini bersumber dari internet yaitu data harga saham harian Jakarta Islamic Index (JII) periode Januari 2019-Februari 2020.. Data-data. tersebut. diperoleh. peneliti. dari. sumber. website. https://finance.yahoo.com/quote/%5EJKII/history?period1=1546300800&period2 =1582848000&interval=1d&filter=history&frequency=1d pada tanggal 25 April 2020. 3.3 Variabel Penelitian Variabel yang digunakan pada penelitian ini yaitu harga saham harian dari Jakarta Islamic Index (JII) sebagai variabel independent. 3.4 Analisis Data Adapun langkah-langkah yang digunakan untuk implementasi model ARIMA-GARCH menggunakan metode Maximum Likelihood pada data harga 37.

38. saham Jakarta Islamic Index periode Januari 2019-Februari 2020, yaitu sebagai berikut: a. Transformasi data ke dalam bentuk log return b. Melakukan uji stasioneritas dan uji normalitas c. Identifikasi model ARIMA berdasarkan grafik ACF dan PACF d. Menentukan estimasi model ARIMA dengan metode Maximum Likelihood menggunakan iterasi Newton Raphson e. Melakukan uji signifikansi parameter pada hasil estimasi model ARIMA f. Melakukan uji heteroskedastisitas dan uji autokorelasi pada hasil estimasi model ARIMA g. Identifikasi model GARCH dengan model ARIMA h. Menentukan. model. ARIMA-GARCH. dengan. metode. Maximum. Likelihood menggunakan iterasi Newton Raphson. i. Melakukan uji signifikansi parameter pada hasil estimasi model ARMAGARCH j. Melakukan uji normalitas, uji heteroskedastisitas, uji autokorelasi pada hasil estimasi model ARIMA-GARCH k. Mengembalikan model kedalam bentuk harga saham, kemudian meramalkan harga saham dengan model ARIMA-GARCH.

39. 3.5 Diagram Alir Analisis Data. Mulai. Deskripsi Data. Transformasi. Tidak. Normalitas Data Ya. Differencing. Tidak. Stasioneritas Data Ya. ACF dan PACF. Identifikasi Model ARIMA. Estimasi Model ARIMA. White Noise. Signifikan Tidak. Ya. Diperoleh Model ARIMA. Tidak. Uji Heteroskedastisitas Ya. A Gambar 3.1 Flowchart Analisis Data.

40. A. Identifikasi Model GARCH. Estimasi Model ARIMA-GARCH Uji Signifikansi Parameter. Normal. White Noise Tidak. Homoskedastisitas Ya. Evaluasi Model ARIMA-GARCH. Peramalan. Selesai Gambar 3.2 Lanjutan Flowchart Analisis Data (A).

BAB IV HASIL DAN PEMBAHASAN 4.1 Implementasi Model ARIMA-GARCH menggunakan Metode Maximum Likelihood 4.1.1 Deskripsi Data Analisis statistik deskriptif dari data harga saham JII dapat dilihat pada gambar berikut:. Gambar 4.1Statistik Deskriptif Data dengan Bantuan Minitab. Dari gambar 4.1 dapat diketahui bahwa terdapat 284 data harga saham. Rata-rata harga saham JII periode Januari 2019-Februari 2020 sebesar Rp.683,990, median sebesar Rp.690,01, nilai maximum sebesar Rp.727,01, nilai minimum sebesar Rp.565,01, dan standar deviasi sebesar Rp.26,13. Untuk mengetahui perubahan harga saham tersebut, dapat dilihat pada gambar plot data sebagai berikut:. Gambar 4.2 Plot Data Harga Saham JII dengan Bantuan Minitab. 41.

42. Pada gambar 4.2 menunjukkan pergerakan harga saham untuk periode 1 Januari 2019-31 Februari 2020 (284 data). Dari plot data tersebut terlihat bahwa data mengalami penurunan dan penigkatan setiap minggunya, dengan kata lain fluktuasi data tidak berada di sekitar nilai rata-rata yang konstan. 4.1.2 Uji Hipotesa Data Sebelum dilakukan proses pemodelan dan estimasi, data harga saham terlebih dahulu harus memenuhi beberapa uji hipotesis berikut ini: a. Uji Stasioneritas Untuk mengetahui stasioneritas harga saham, maka dilakukan uji Augmented Dickey-Fuller (ADF) dengan menggunakan hipotesis sebagai berikut:. H 0 : ADF  1 (data bersifat stasioner). H1 : ADF  1 (data bersifat tidak stasioner) Dengan kriteria uji yaitu tolak H 0 jika ADF  t atau niali probabilitas > taraf signifikan 5% maka didapatkan hasil sebagai berikut:. Gambar 4.3 Uji Stasioner Data Harga Saham JII dengan Bantuan Eviews. Berdasarkan output diatas dapat dilihat nilai t-statistic uji ADF sebesar 0,086526 dan nilai probabilitas ADF sebesar 0,9624. Dengan menggunakan taraf signifikan.

43. sebesar   5% , nilai probabilitas ADF tersebut lebih besar dibandingkan dengan taraf signifikan atau nilai t statistic  0, 086526  t  2,871546 yang berarti. H 0 ditolak. Hal tersebut menunjukkan bahwa data harga saham bersifat tidak stasioner. Untuk mengubah data tidak stasioner menjadi data yang stasioner dapat dilakukan dengan menstransformasikan data ke dalam bentuk log return seperti pada persamaan (2.45). Hasil transformasi dapat dilihat pada plot data dibawah ini:. Gambar 4.4 Plot Data Log Return dengan Bantuan Minitab. Plot data return harga saham dari JII pada gambar di atas menunjukkan bahwa rata-rata data berada pada satu nilai konstan yaitu nol. Nilai return bernilai positif jika terjadi kenaikan harga saham dan bernilai negatif jika harga saham mengalami penurunan. Untuk memastikan apakah data log return sudah stasioner, maka dilakukan uji ADF dengan hasil sebagai berikut:.

44. Gambar 4.5 Uji Stasioneritas Data Log Return dengan Bantuan Eviews. Berdasarkan Gambar 4.5 di atas dapat dilihat nilai t-statistic uji ADF sebesar 15,88868 dan nilai kritis dengan tingkat 5% sebesar -2,871546. Sehingga nilai tstatistic uji ADF lebih kecil daripada nilai kritis yang berarti terima H 0 . Hal tersebut menunjukkan bahwa log return bersifat stasioner b. Uji Normalitas Uji normalitas bertujuan untuk mengetahui apakah data berdistribusi normal atau tidak berdistribusi normal. Uji normalitas pada log return menggunakan uji Jarque Bera dengan hipotesis sebagai berikut:. H 0 : JB  2 (data berdistribusi normal) H1 : JB  2 (data tidak berdistribusi normal) Dengan kriteria uji yaitu terima H 0 jika nilai Jarque Bera < 2 atau nilai probabilitas > taraf signifikan 5%, maka didapatkan hasil sebagai berikut:.

45. 35. Series: RETURN Sample 1 284 Observations 283. 30 25 20 15 10. Mean Median Maximum Minimum Std. Dev. Skewness Kurtosis. -0.000680 -0.000149 0.024064 -0.030450 0.010353 -0.186881 3.020919. Jarque-Bera Probability. 1.652434 0.437702. 5 0 -0.03. -0.02. -0.01. 0.00. 0.01. 0.02. Gambar 4 6 Uji Normalitas Data Log Return dengan Bantuan Minitab. Pada Gambar 4.6 terlihat bahwa nilai Jarque-Bera sebesar 1.652434 < 2 dan nilai p-value sebesar 0.437702 > 0.05 maka artinya terima H 0 yang berarti bahwa data log return saham JII berdistribusi normal. 4.1.3 Pemodelan ARIMA a. Identifikasi Model ARIMA Identifikasi model ARIMA pada data deret waktu dapat dilihat dari plot Autocorrelation Function (ACF) dan Partial Autocorrelation Function (PACF) data log return sebagai berikut:. Gambar 4.7 Correlogram Log Return dengan Bantuan Eviews.

46. Dari Gambar 4.7 dapat dilihat koefisien korelasi ACF dan PACF pada lag pertama telah melebihi batas interval, dan nilai probabilitas dari lag pertama sampai lag ke-sepuluh lebih kecil dari 0,05, maka hal ini menunjukkan bahwa model ARIMA (1,1,1) merupakan model yang teridentifikasi menjadi model yang akan diestimasi. b. Estimasi Model ARIMA Untuk mengetahui model ARIMA yang signifikan dapat dilihat dari nilai probabilitas < 0,05. Setelah dilakukan estimasi menggunakan metode Maximum Likelihood dengan iterasi Newton Raphson sebanyak 500 kali pada model ARIMA, didapatkan model signifikan dan terbaik yaitu model ARIMA(1,1,1) dengan output sebagai berikut:. Gambar 4.8 Estimasi Model ARIMA(1,1,1) dengan Bantuan Eviews. Dari Gambar 4.8 tersebut dapat dilihat bahwa nilai probabilitas < 0.05 yang menunjukkan bahwa model ARIMA (1,1,1) signifikan, sehingga model ARIMA (1,1,1) dapat dijadikan model yang tepat. c. Uji Parameter.

47. Setelah mendapatkan model ARIMA, perlu diuji apakah parameter dari hasil estimasi telah signifikan atau tidak. Hipotesis dari uji signifikansi parameter adalah sebagai berikut:. H 0 :   0 (parameter  tidak signifikan dalam model). H1 :   0 (parameter  signifikan dalam model) Dengan kriteria uji yaitu tolak H 0 jika thitung  t atau nilai probabilitas < 2. taraf signifikan 5%. Berdasarkan gambar 4.6, hasil uji signifikansi parameter menunjukkan bahwa probabilitas AR(1) dan MA(1) < 0.05. Artinya H 0 ditolak. Maka dapat disimpulkan bahwa model ARIMA(1,1,1) merupakan model yang signifikan. Selanjutnya, dilakukan uji heteroskedastisitas untuk mengetahui apakah model ARIMA yang didapatkan memiliki varians error yang konstan atau tidak. Jika model menghasilkan varians error yang tidak konstan artinya model tersebut memiliki masalah heteroskedastisitas. Uji heteroskedastisitas pada model ARIMA (1,1,1) menggunakan metode White dengan hipotesis sebagai berikut:. H0 :  t2   2 (data tidak bersifat heteroskedastisitas) H1 :  t2   2 (data bersifat heteroskedastisitas) Dengan kriteria uji yaitu tolak H 0 jika nilai probabilitas dari Chi Squre < taraf signifikan 5%, maka didapatkan hasil sebagai berikut:.

48. Gambar 4.9 Uji Heteroskedastisitas Model ARIMA(1,1,1) dengan Bantuan Eviews. Dari gambar 4.9 dapat dilihat bahwa nilai probability chi-square sebesar 0.0000 < 0.05. Artinya H 0 ditolak. Hal tersebut menunjukkan bahwa varians error mengandung heteroskedastisitas. Maka dapat dikatakan bahwa data tersebut mengikuti model ARCH/GARCH. Selanjutnya, untuk mengetahui bahwa error bersifat white noise pada model. ARIMA(1,1,1),. maka. dilakukan. uji. autokorelasi. menggunakan. correlogram. Didapatkan hasil uji autokorelasi sebagai berikut:. Gambar 4.10 Uji Autokorelasi Residual dengan Bantuan Eviews. Berdasarkan Gambar 4.10 diatas, dapat dilihat bahwa nilai probabilitas dari lag pertama sampai dengan lag ke-10 menunjukkan nilai yang lebih dari taraf signifikan 5% . Artinya, error tidak memiliki gejala autokorelasi atau bersifat white noise. 4.1.4 Pemodelan ARIMA-GARCH a. Estimasi Model ARIMA-GARCH.

49. Dalam estimasi model GARCH digunakan metode Maximum Likelihood dengan iterasi Newton Raphson. Untuk membangun kemungkinan suatu model GARCH diperlukan iterasi sebanyak 500 kali untuk mendapatkan model yang tepat. Untuk mengetahui model GARCH yang signifikan dapat dilihat dari nilai probabilitas < 0,05. Dengan bantuan software Eviews didapatkan hasil estimasi model ARIMA(1,1,1)-GARCH (0,2) dengan output sebagai berikut:. Gambar 4.11 Estimasi Model ARIMA(1,1,1)-GARCH (0,2) dengan Bantuan Eviews. Dari Gambar 4.11 tersebut dapat dilihat bahwa nilai probabilitas < 0.05 yang menunjukkan bahwa model GARCH (0,2) signifikan. Sehingga, model ARIMA(1,1,1)-GARCH (0,2) dapat dituliskan sebagai berikut:. Zt  Zt 1  0,853702(Zt 1  Zt 2 )  0,843128 t 1   t dimana. t. ,. N (0, ht2 ). Berdasarkan model di atas dapat diketahui bahwa model berawal dari hasil differencing orde 1 dari log harga saham (selisih log harga saham sekarang.

50. dengan log harga saham sebelumnya) atau sama dengan log return. Kemudian akan sama dengan kombinasi linier dari log harga saham sebelumnya dengan koefisien sebesar 0,853702 dan error sebelumnya dengan koefisien sebesar 0,843128. Untuk persamaan variansi error yaitu kombinasi linier dari error-error sebelumnya dan variansi-variansi error sebelumnya dapat dimodelkan sebagai berikut: ht2  0, 000000117  1,996413ht21  0,997518ht22. Berdasarkan model tersebut dapat diketahui bahwa nilai koefisien (  0 ) sebesar 0,000000117, nilai parameter orde pertama ( 1 ) dari variansi-variansi sebelumnya adalah 1,996413, sedangkan untuk nilai parameter orde kedua ( 2 ) adalah 0,997518. b. Uji Parameter Setelah mendapatkan model ARIMA-GARCH, perlu diuji apakah parameter dari hasil estimasi telah signifikan atau tidak. Berdasarkan gambar 4.9, hasil uji signifikansi parameter menunjukkan bahwa probabilitas < 0.05. Artinya. H 0 ditolak. Maka dapat disimpulkan bahwa model ARIMA(1,1,1)-GARCH(0,2) merupakan model yang signifikan. Selanjutnya, dilakukan untuk mengetahui apakah model ARIMA(1,1,1)GARCH(0,2) menghasilkan varians error yang tidak konstan, maka dilakukan uji heteroskedastisitas. kembali. heteroskedastisitas sebagai berikut:. dengan. ARCH-LM.. Didapatkan. uji.

51. Gambar 4.12 Uji Heteroskedastisitas Model ARIMA-GARCH dengan Bantuan Eviews. Dari Gambar 4.12 dapat dilihat bahwa nilai probability chi-square sebesar 0.8162 > 0.05, artinya. H 0 diterima. Hal tersebut menunjukkan bahwa model. ARIMA(1,1,1)-GARCH(0,2) sudah tidak terdapat masalah heteroskedastisitas. Selanjutnya. adalah. uji. autokorelasi. menggunakan. correlogram.. Didapatkan hasil uji autokorelasi sebagai berikut:. Gambar 4.13 Uji Autokorelasi Model ARIMA-GARCH dengan Bantuan Eviews. Berdasarkan Gambar 4.13 diatas, dapat dilihat bahwa nilai probabilitas dari lag pertama sampai dengan lag ke-10 menunjukkan nilai yang lebih dari taraf signifikan 5% . Artinya, model tidak memilik gejala autokorelasi atau bersifat white noise. Setelah uji heteroskedastisitas dan uji autokorelasi, langkah selanjutnya adalah uji normalitas residual untuk mengetahui bahwa error berdistribusi normal atau tidak melalui uji Jarque Bera. Didapatkan hasil uji sebagai berikut:.

52. Gambar 4.14 Uji Normalitas Model ARIMA-GARCH dengan Bantuan Eviews. Berdasarkan Gambar 4.14 dapat dilihat bahwa nilai Jarque-Bera sebesar 0,420045 dan nilai probabilitasnya sebesar 0,810566. Dengan menggunakan taraf signifikan 5%, maka nilai probabilitas lebih besar dibandingkan dengan nilai signifikan. Hal tersebut berarti bahwa model ARIMA(1,1,1,)-GARCH(0,2) berdistribusi normal. 4.1.5 Evaluasi Model ARIMA-GARCH Setelah model memenuhi semua kriteria uji, maka selanjutnya adalah mengembalikan model ARIMA(1,1,1)-GARCH(0,2) ke dalam bentuk harga saham sebagai berikut:. Zt  Zt 1  0,853702(Zt 1  Zt 2 )  0,843128 t 1   t Diketahui bahwa Zt merupakan log dari selisih harga saham sekarang dengan harga saham sebelumnya. Misal wt  Zt  Zt 1 maka diperoleh:. wt  0,853702( Zt 1  Zt 2 )  0,843128 t 1   t Misalakan St adalah harga saham pada waktu ke-t, maka:. St  St 1  exp(wt ) St  St 1  exp(wt ).