MAKALAH
RELASI ANTARA DUA HIMPUNAN
Disusun Oleh : Kelompok 3
1. Yuanda Ramadan Sobbirin 14601040011 2. Muhammad Ade Safitri 14601040012
3. Arman 14601040013
4. Pipit Marselaningsih 14601040015 5. Indah Lestari 14601040016
PENDIDIKAN MATEMATIKA
KATA PENGANTAR
Puji dan syukur kami panjatkan kehadirat Allah SWT karena atas berkat, rahmat dan karunia-Nya kami dapat menyelesaikan makalah pengantar dasar kimia kami yang berjudul “Relasi Antara Dua Himpunan” dengan tepat waktu. Adapun yang nanti akan kami bahas di dalam makalah ini adalah tentang pengertian antara dua himpunan, cara menyatakan relasi antara dua himpunan, banyaknya relasi antara dua himpunan, macam relasi, dan relasi ekivalen dan partisi.
Tak lupa kami ucapkan terima kasih yang sebanyak-banyaknya terutama kepada Ibu Nurmala R., M.Pd selaku dosen pembimbing mata kuliah Pengantar Dasar Matematika beserta teman-teman dan rekan sekalian yang turut terlibat secara langsung maupun tidak langsung dalam terselesainya makalah ini.
Kami menyadari makalah ini masih jauh dari kesempurnaan. Oleh sebab itu, diharapkan kritik dan saran pembaca demi kesempurnaan makalah kami untuk kedepannya. Mudah-mudahan makalah ini bermanfaat bagi kita semua terutama bagi mahasiswa yang mempelajari materi ini.
Tarakan, 6 April 2015
DAFTAR ISI
2.1 Pengertian Relasi Antara Dua Himpunan
... 3
2.2 Cara Menyatakan Relasi Antara Dua Himpunan
... 6
2.3 Banyaknya Relasi Antara Dua Himpunan
BAB III PENUTUP 3.1 Kesimpulan
... 27
3.2 Kritik dan Saran
... `27
DAFTAR PUSTAKA
... 28
LAMPIRAN
BAB 1 PENDAHULUAN
1.1 Latar Belakang
Matematika sebagai ilmu sains dapat berbentuk ilmu terapan jika diimplementasikan pada cabang ilmu lain. Relasi adalah salah satu bagian dari pengantar dasar matematika. Dimana relasi merupakan suatu hubungan. Dalam kehidupan sehari-hari pasti ada suatu hubungan yang terjadi. Misal “sekumpulan anak-anak kecil yang sedang bermain dan setiap anak memegang balon berbagai warna”. Dari ini dapat diberikan pengertian bahwa anak-anak kecil yang mempunyai hubungan dengan balon berbagai warna yang mereka pegang. Sebelumnya telah dipelajari materi tentang himpunan. Himpunan adalah sekumpulan benda atau obyek yang dididefinisikan dengan jelas. Disini terdapat dua himpunan, yang pertama adalah himpunan anak-anak kecil dan yang kedua adalah himpunan balon berbagai warna.
Relasi digunakan untuk menyatakan suatu hubungan antara dua himpunan. Relasi merupakan teori dasar dalam pembahasan pengantar dasar matematika. Maka perlu untuk membahas relasi. Baik dari definisi relasi antara dua himpunan ,cara menyatakan relasi antara dua himpunan, banyaknya relasi antara dua himpunan, macam-macam relasi, dan hubungan relasi ekivalen dan partisi.
1.2 Rumusan Masalah
1.2.1 Apa Pengertian Relasi Antara Dua Himpunan?
1.2.2 Bagaimana Cara Menyatakan Relasi Antara Dua Himpunan? 1.2.3 Bagaimana Banyaknya Relasi Antara Dua Himpunan?
1.2.4 Apa Macam Relasi?
1.2.5 Bagaimana Relasi Ekivalen dan Partisi?
1.3 Tujuan Penulisan
1.3.1 Mengetahui Pengertian Relasi Antara Dua Himpunan
1.3.2 Mengetahui Cara Menyatakan Relasi Antara Dua Himpunan 1.3.3 Mengetahui Banyaknya Relasi Antara Dua Himpunan
1.3.4 Mengetahui Macam Relasi
1.3.5 Mengetahui Relasi Ekivalen dan Partisi
1.4 Manfaat Penulisan
1.4.1 Agar kita tahu Pengertian Relasi Antara Dua Himpunan
1.4.2 Agar kita tahu Cara Menyatakan Relasi Antara Dua Himpunan 1.4.3 Agar kita tahu Banyaknya Relasi Antara Dua Himpunan 1.4.4 Agar kita tahu Macam Relasi
BAB 2 PEMBAHASAN
2.1 Pengertian Relasi Antara Dua Himpunan
Relasi adalah hubungan antara dua elemen himpunan. Hubungan ini bersifat abstrak, dan tidak perlu memiliki arti apapun baik secara konkrit maupun secara matematis.
Relasi merupakan hubungan antara anggota suatu himpunan (domain) dengan himpunan lainnya (kodomain), baik himpunan yang sama maupun himpunan yang berbeda.
Definisi : Jika terdapat himpunan A dan himpunan B (A bisa sama dengan B), maka relasi R dari A ke B adalah dari A×B.
Contoh 1
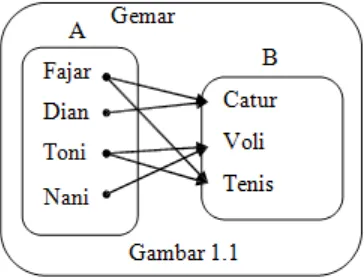
Misalnya ada empat anak yaitu Fajar, Dian, Toni, dan Nani ditanya apakah mereka gemar bermain catur, voli, atau tenis. Jawaban mereka:
Fajar dan Dian gemar bermain catur, Toni dan Nani gemar bermain voli, Fajar dan Toni gemar bermain tenis
Perhatikanlah bahwa sebenarnya ada dua himpunan : 1. Himpunan anak
A = {Fajar, Dian, Toni, Nani} 2. Himpunan permainan
Kedua himpunan A dan B dihubungkan dengan hubungan gemar bermain. Hubungan gemar bermain dari himpunan A ke himpunan B dapat digambar sebagai berikut.
Gambar 1.1 menunjukkan suatu cara untuk menyatakan hubungan atau relasi dari himpunan A ke himpunan B. Hubungan itu adalah gemar bermain. Gambar 1.1 disebut diagram panah. Perhatikanlah bahwa suatu relasi mempunyai arah pada diagram panah ditunjukkan dengan anak panah.
Dari uraian di atas dapat disimpulkan bahwa :
A B Cinta•
Dina• Dani
•
Nina•• Soto • Mie • Bakso Contoh 2
Diketahui: Cinta dan Dina suka makan Soto Nina dan Dani suka makan Mie Dani suka makan Bakso
Penyelesaiannya: Terdapat 2 himpunan yaitu: A = Himpunan siswa
A = {Cinta, Dina, Dani, Nina} B = Himpunan Makanan B = {Soto, Mie, Bakso}
Contoh 3
Dikelas 8 SMP terdapat 4 orang siswa yang lebih menyukai pelajaran tertentu. berikut ke-4 anak tersebut :
Buyung menyukai pelajaran IPS dan Kesenian
Doni menyukai pelajaran ketrampilan dan olah raga
Vita menyukai pelajaran IPA, dan
Putri lebih menyukai pelajaran matematika dan bahasa inggris
2.2 Cara Menyatakan Relasi Antara Dua Himpunan
Diketahui himpunan A = {2,3,4,5}, B = {4,5,6} dengan relasi faktor dari himpunan A ke himpunan B maka kita dapat menyatakan relasi tersebut dengan tiga cara yaitu:
1) Dengan diagram panah
2) Dengan himpunan pasangan berurutan
Perhatikanlah gambar 1.2. 2→6 ini berarti 2 faktor dari 6 dan dapat ditulis dengan pasangan berurutan (2,6). Jika relasi faktor dari himpunan A ke himpunan B dinyatakan dengan R, maka jelas 2 berelasi R dengan 6 atau dapat ditulis dengan 2R6 atau (2,6) ∈ R. Dengan cara yang sama dapat dituliskan 2R4 atau (2,4) ∈ R, 3R6 atau (3,6) ∈ R, tetapi 2 tidak berelasi dengan 5 atau dapat ditulis 2 R 5 atau (2,5) ∉ R. Dengan demikian relasi R tersebut merupakan himpunan pasangan berurutan yaitu: Tetapi pengganti "x" dengan "2" dan "y" dengan "5" didapat pernyataan yang salah, sehingga (2,5) bukan penyelesaian dari kalimat terbuka x faktor dari y. Jika relasi faktor dari himpunan A ke himpunan B dinyatakan dengan R maka himpunan semua pasangan berurutan (x,y) yang menghasilkan pernyataan yang benar yaitu himpunan penyelesaian kalimat terbuka
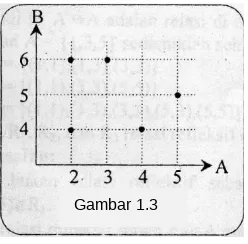
3) Dengan grafik Cartesius
Koordinat titik-titik pada gambar 1.3 menyatakan anggota-anggota pasangan berurutan dari relasi R (faktor dari).
Contoh 1
Diketahui M = {0,2 4,6,8}, N = {0,1,2,3,4,5}.
R: M→N adalah relasi dari M ke N dinyatakan dengan kalimat terbuka x dua kali y dengan X ∈ M, y ∈ N. Nyatakanlah relasi tersebut:
a. dengan diagram panah
b. dengan himpunan pasangan berurutan c. dengan grafik Cartesius
Penyelesaian:
a. dengan diagram panah
R = {(0,0),(2,1),(4,2),(6,3),(8,4)}
c. dengan grafik Cartesius
Contoh 2
Dikelas 8 SMP belajar matematika terdapat 4 orang siswa yang lebih menyukai pelajaran tertentu. berikut ke-4 anak tersebut :
Buyung menyukai pelajaran IPS dan Kesenian
Doni menyukai pelajaran ketrampilan dan olah raga
Vita menyukai pelajaran IPA, dan
Putri lebih menyukai pelajaran matematika dan bahasa ingris
Jawab :
Untuk mempermudah menjawab persoalan diatas gunakanlah permisalan seperti : Himpunan A = {Buyung, Doni, Vita, Putri}, Himpunan B = {IPS, kesenian, keterampilan, olahraga, matematika, IPA, bahasa Inggris}, dan “pelajaran yang disukai” adalah relasi yang menghubungkan himpunan A ke B.
Diagram panah
Diagram Cartesius
Himpunan pasangan berurutan
Contoh 3
Ani gemar makan Bakso dan Nasi goreng Irfan gemar makan Mie Ayam
Arman gemar makan Nasi Goreng, dan Coto Ahmad gemar makan Ikan bakar
Ade gemar makan Bakso
Dari penyataan di atas kita dapat menentukan dua himpunan yaitu
A = (Ani, Irfan, Arman, Ahmad, Erwin)
B = (Bakso, Nasi goreng, Mie ayam, Coto, Ikan Bakar)
Dari kedua himpunan di atas dihubungkan dengan relasi himpunan A dan himpunan B yaitu “gemar makan”.
Diagram Cartesius
Himpunan Pasangan Berurutan
Himpunan pasangan berurutan adalah {(Ani,Bakso), (Ani,NasiGoreng), (Irfan,MieAyam), (Arman,Nasi Goreng), (Arman,Coto),
2.3 Banyaknya Relasi Antara Dua Himpunan
Jika R: A→B adalah relasi dari A ke B. n(A) = 3, dan n(B) = 2 maka banyaknya relasi R tersebut dapat dijelaskan sebagai berikut. Misalkan A = {1,3,5} maka n(A) = 3,
B = {a,b} maka n(B) = 2
AxB = {(1,a),(1,b),(3,a),(3,b),(5,a),(5,b)) maka n(AxB) = 6 = 3x2.
Jika R1 = {(1,a)} jelas R1 (AxB) dan R1 relasi dari A ke B. Jika R2 = {(1,a),(2,b)} jelas R2 (AxB) dan R2 relasi dari A ke B.; Jika R0 = {} jelas R0 (AxB) dan R0 bukan relasi dari A ke B. Jika R6 = {(1,a),(1,b),(3,a),(3,b),(5,a),(5,b)} jelas R6 (AxB) dan
R6 relasi dari A ke B.
Dari uraian di atas dapat dikatakan bahwa: 1. Jika R relasi dari A ke B maka R ⊂ (AxB)
Diketahui R: M→N adalah relasi dari M ke N. Jika n(M)=4 dan n(N)=3, hitunglah banyaknya relasi R tersebut.
Penyelesaian: n(M)=4 dan n(N)=3.
Banyaknya relasi R ada = 24x3 - 1 = 4095
Contoh 2
Jika A = {bilangan prima kurang dari 5} dan B = {huruf vokal}, hitunglah banyaknya relasi tersebut
Penyelesaian: A = {2, 3}, n(A) = 2
B = {a, e, i, o, u}, n(B) = 5
Banyaknya relasi R ada = 22x5 - 1 = 1023
Contoh 3
Jika A = {x|–2 < x < 2, x є Z} dan B = {x | x bilangan prima < 6}, hitunglah banyaknya relasi
Penyelesaian:
A = {x|–2 < x < 2, x є Z} = {-1, 0, 1}, n(A) = 3 B = {x | x bilangan prima < 6} = {2, 3, 5}, n(A) = 3
2.4 Macam-macam Relasi
Diketahui B = {2, 4, 5}. Pada B didefinisikan relasi
R2 = {(x,y) │x kelipatan y, x, y ∈ B}.
Maka R2 = {(2,2), (4,4), (5,5), (4,2)}. Relasi R2 tersebut bersifat
refleksif.
Contoh 3
Diketahui B = {2, 4, 5}. Pada B didefinisikan relasi
R3 = {(x,y│x + y < 10, x, y ∈ A}.
Maka R3 ={(2,2), (2,4), (2,5), (4,2), (4,4), (4,5), (5,2), (5,4)}. Relasi
R3 tersebut tidak bersifat refleksif. Misalkan R suatu relasi di dalam himpunan A maka R disebut relasi refleksif jika dan hanya jika
b. Relasi Simetris Definisi 1.2
Dari definisi 1.2 dapat disimpulkan suatu relasi R di dalam himpunan A disebut bukan relasi simetris jika (a,b) ∈ R dan (b,a) ∉ R.
Contoh 1
Diketahui A = {1, 2, 3}. Pada A didefinisikan relasi
R1 = {(1,1) , (1,2) , (2,2) , (2,1) , (3,3)}. Relasi R1 tersebut
bersifat simetris.
Contoh 2
Diketahui B = {2, 4, 5}. Pada B didefinisikan relasi
R2 = { (x,y) │ x kelipatan y , x, y ∈ Z }
R2= {(2,2) , (4,4) , (5,5) , (4,2)}. Relasi R2 tersebut tidak bersifat
simetris karena (4,2) ∈ R2 tetapi (2,4) ∉ R2. Misalkan R suatu relasi di dalam
Contoh 3
Diketahui R: A→A adalah relasi di dalam himpunan A dengan A = {1,3,5} sedemikian sehingga:
R1 = {(1,1),(1,3),(3,3),(3,1),(3,5)} R2 = {(1,1),(3,3),(3,5),(5,5),(5,3)} R3 = {(1,1),(3,3),(5,5)}
Apakah R1, R2, R3 relasi simetris atau bukan? Penyelesaian:
R1 bukan relasi simetris sebab (3,5) ∈ R1 tetapi (5,3) ∉ R1.
c. Relasi Transitif Definisi 1.3
Dari definisi 1.3 dapat disimpulkan suatu relasi R di dalam himpunan A disebut bukan relasi transitif jika (a,b) ∈ R dan (b,c)
∈ R tetapi (a,c) ∉ R.
Contoh 1
Diketahui A = {1, 2, 3}.
Pada A didefinisikan relasi R1 = {(1,1) , (1,2) , (2,2) , (2,1) ,
(3,3)} Relasi R1 tersebut bersifat transitif.
Contoh 2
Relasi R2 = {(1,1) , (1,2) , (2,2) , (2,3) , (3,3) , (3,2)} yang didefinisikan pada himpunan A = {1, 2, 3} tidak bersifat transitif, karena terdapat (1,2) ∈ R2 dan (2,3) ∈ R2, tetapi (1,3) ∉
R2.
Contoh 3
Misalkan R suatu relasi di dalam himpunan A maka R disebut
relasi transitif jika (a,b) R dan
Apakah R1, R2, dan R3 relasi transitif atau bukan? Penyelesaian :
a) R1 bukan relasi transitif sebab
(3,1) R1 dan (1,3) R, tetapi (3,3) ∉ R1. b) R2 relasi transitif sebab
(1,3) R2 dan (3,1) R2 maka (1,1) R2;
Relasi R1 tersebut bersifat refleksif, simetris dan transitif. Oleh
karena itu relasi R1 merupakan relasi ekivalen. Misalkan R suatu relasi di dalam
himpunan A maka R disebut relasi ekivalen jika berlaku syarat:
a. Refleksi a ∈ A maka (a,a) R
b. Simetris artinya jika (a,b) R maka
berarti (b,a) R;dan
Contoh 2
Diketahui B = {2, 4, 5}. Pada B didefinisikan relasi
R2 = { (x,y)│x kelipatan y , x, y ∈ Z } maka
R2 = {(2,2), (4,4), (5,5), (4,2)}. Relasi R2 tersebut tidak bersifat
simetris, oleh karena itu relasi tersebut bukan relasi ekivalen.
Contoh 3
Diketahui himpunan A = {0, 2, 4}, relasi R di dalam himpunan A dengan R = {(0,0), (2,2), (4,4)} berlaku syarat refleksif, simetris, dan transitif. Oleh karena itu R merupakan relasi ekivalen.
2.5 Relasi Ekivalen dan Partisi a. Partisi Himpunan
Pengertian partisi himpunan dapat dijelaskan melalui contoh sebagai berikut. Misalkan A = {1,2,3,4,...,10}, A1={1,2,3}, A2 = {4,5,6,7}, A3 ={8,9,10}.
Koleksi himpunan A = {A1, A2, A3} mempunyai dua sifat yaitu: 1). A1 ∪ A2 ∪ A3 = A
2). A1 ∩ A2 = ∅ , A1 ∩ A3 = ∅ , A2 ∩ A3 = .
Contoh 1
Diketahui N = {x l x bilangan asli}. N1={1,5,9,17,...}, N2={2,6,10,14,...}, N3={3,7,11,15,...), N4=(4,8,12,16,...). Apakah koleksi (N1, N2, N3, N4) partisi dari N.
Penyelesaian:
Koleksi {N1, N2, N3, N4} mempunyai sifat: 1. N1 ∪ N2 ∪ N3 ∪ N4 = N
2. N1 ∩ N2 = , N1 ∩ N3 = , N1 ∩
N4 = .
N2 ∩ N3 = , N2 ∩ N4 = , dan N3
∩ N4 =
Jadi koleksi {N1, N2, N3, N4} merupakan partisi dari N.
Contoh 2
Diketahui N = {x l x bilangan kelipatan 2}. B1={2,6,10,...}, B2={4,16,18,...}, dan B3={8,12,14,...)
Apakah koleksi (B1, B2, B3) partisi dari B. Penyelesaian:
Koleksi {B1, B2, B3} mempunyai sifat: 1. B1 ∪ B2 ∪ B3 = B
Contoh 3
Diketahui N = {x l x bilangan prima}. N1={3,7,19,...}, N2={2,5,23,...}, N3={11,13,17,...), N4=(29,31,37,...). Apakah koleksi (N1, N2, N3, N4) partisi dari N.
Penyelesaian:
Koleksi {N1, N2, N3, N4} mempunyai sifat: 1. N1 ∪ N2 ∪ N3 ∪ N4 = N
2. N1 ∩ N2 = , N1 ∩ N3 = , N1 ∩
N4 = .
N2 ∩ N3 = , N2 ∩ N4 = , dan N3
∩ N4 =
Jadi koleksi {N1, N2, N3, N4} merupakan partisi dari N.
b. Hubungan Partisi dan Relasi Ekivalen
Sebelum dibicarakan hubungan antara partisi dan relasi ekivalen, maka pada uraian berikut akan dibicarakan a kongruen b modulo m.
Definisi 1.5
Misalkan a dan b bilangan asli, m bilangan asli, maka dikatakan a kongruen b modulo m ditulis a
Contoh 1
Untuk m=3, maka: 4 kongruen 1 modulo 3
Ditulis 4 1 (mod.3) sebab 4-1= 1(3) 10 kongruen 1 modulo 3
Ditulis 10 ≅ 1 (mod.3) sebab 10-1 = 3 (3) 20 kongruen 2 modulo 3
Ditulis 20 2 (mod.3) sebab 20-2 = 6 (3)
2 tidak kongruen 7 modulo 3 ditulis 2 7 (mod.3) sebab 2-7 k(3)
dengan k bilangan bulat.
Contoh 2
Diketahui N = himpunan bilangan asli. R:N→N adalah relasi di dalam himpunan N yang didefinisikan dengan
a kongruen b modulo m. Buktikan R relasi ekivalen. Bukti:
3. Jika a ≅ b (mod.m) dan b ≅ c (mod. m) maka:
a-b = k1(m)
b-c = k2(m)
a-c = (k1 + k2)(m) a-c = k(m)
Jadi a ≅ c (mod.m) (sifat transitif).
Jadi R relasi ekivalen.
Contoh 3
Diketahui N = himpunan bilangan asli. R relasi di dalam himpunan N yang didefinisikan dengan “a ≅ b (mod.3)” dengan a,b ∈ N. Tunjukkan bahwa N dipecah menjadi partisi.
N6 = {3,6,9,...}.
Ternyata N1=N4= {1,4,7,…} N2=N5= {2,5,8,…} N3=N6= {3,6,9,…}
Perhatikan koleksi (N1, N2, N3). Jelas bahwa : 2. N1 ∪ N2 ∪ N3 = N
3. N1 ∩ N2 = ∅, N1 ∩ N3 ¿∅, N2 ∩ N3 ¿∅ Jadi N dipecah menjadi partisi.
Contoh 4
Diketahui N = himpunan bilangan asli. N1 = {1,3,5,7,...} dan N2={2,4,6,8,...}. R relasi di dalam himpunan N.
a. Apakah koleksi {N1,N2} partisi dari N?
b. Tentukan relasi R yang memecah N menjadi partisi {N1,N2} Penyelesaian:
a. N1 N2= N dan N1 N2 = .
Jadi koleksi {N1,N2} partisi dari N.
b. N1 = {1,3,5,7,…} = {x|x ≅ 1 (mod. 2)} N2 = (2,4,6.8,...) = {x|x ≅ 2 (mod. 2)}
Jadi relasi R yang memecah N menjadi partisi {N1,N2} adalah
BAB 3 PENUTUP
3.1 Kesimpulan
Berdasarkan penjelasan di atas, kami menyimpulkan bahwa suatu hubungan atau relasi dari himpunan A ke himpunan B adalah pemasangan anggota- anggota A dengan anggota- anggota B. Cara menyatakan relasi antara dua himpunan ada tiga, yaitu dengan diagram panah, dengan himpunan pasangan berurutan, dan dengan grafik Cartesius. Sedangkan untuk mengetahui banyaknya relasi antara dua himpunan adalah jika R: A→B adalah relasi dari A ke B dan
n(A) = k, n(B) = l maka banyaknya relasi R = 2kxl. Macam dari relasi, antara lain relasi refleksif, relasi simetris, relasi transitif, relasi ekivalen, dan relasi partisi.
Hubungan antara relasi ekivalen dan partisi adalah jika diketahui R relasi di dalam himpunan N dan R relasi ekivalen maka himpunan N terpecah menjadi partisi; dan jika himpunan N dipecah menjadi partisi maka relasi R adalah relasi ekivalen.
3.2 Saran
DAFTAR PUSTAKA
Sugiarto dan Isti Hidayah. 2011. Bahan Ajar Pengantar Dasar Matematika (PDM). Semarang : Universitas Negeri Semarang.
Situs Web
http://relasidanfungsi.weebly.com/macam-macam-penyajian-relasi.html
https://www.google.co.id/url?
sa=t&rct=j&q=&esrc=s&source=web&cd=4&cad=rja&uact=8&ved=0CC8Q FjAD&url=http%3A%2F%2Fdina_indarti.staff.gunadarma.ac.id
%2FDownloads%2Ffiles