BAB I PENDAHULUAN
1.1 Latar Belakang
Ilmu ukur tanah merupakan bagian pendahuluan dari ilmu yang luas yang dinamakan Ilmu Geodesi (Wongsotjitro, 2013: 11). Ilmu Ukur Tanah terfokus pada pengukuran-pengukuran bentuk permukaan bumi untuk dipindahkan ke bidang datar dan mempelajari masalah kulit bumi yang berupa situasi atas permukaan kulit bumi, perbedaan ketinggian, jarak, dan luas. Ilmu geodesi ini sangat bagi pekerjaan perencanaan yang membutukan data-data koordinat dan ketinggian titik di lapangan. Berdasarkan ketelitian pengukurannya, ilmu geodesi diklasifikasikan menjadi dua bagian yaitu
a. Geodetic Surveying, yaitu survei yang memperhitungkan kelengkungan bumi atau kondisi sebenarnya. Biasanya digunakan dalam pengukuran daerah yang luas dengan menggunakan bidang hitung berupa bidang lengkung (bola/ellipsoid).
b. Plane Surveying, yaitu survei yang mengabaikan kelengkungan bumi dan mengasumsikan bumi sebagai bidang datar. Plane Surveying digunakan untuk pengukuran daerah yang tidak luas dengan menggunakan bidang hitung berupa bidang datar.
Pengukuran adalah sebuah teknik pengambilan data yang dapat memberikan nilai panjang, tinggi dan arah relatif dari sebuah objek ke objek lainnya. Pengukuran terletak di antara ilmu geodesi dan ilmu pemetaan. Hasil penelitian geodesi dipakai sebagai dasar referensi pengukuran, kemudian hasil pengelolaan data pengukuran digunakan untuk sebagai dasar pembuatan peta. Suatu bidang tanah yang diukur wajib dipasang dan ditetapkan tanda-tanda batasnya.
Ilmu Ukur Tanah merupakan salah satu mata kuliah Program Studi Teknik Sipil Universitas Bakrie pada semester II. Dalam praktikum mata kuliah Ilmu Ukur Tanah, teknik yang digunakan yaitu Plane Surveying, di mana bumi diasumsikan sebagai bidang datar, sehingga dapat ditentukan posisi titik-titik di permukaan bumi yang kemudian disajikan dalam bentuk peta. Adapun tujuan diadakannya praktikum Ilmu Ukur Tanah ini yaitu agar mahasiswa berlatih melakukan pekerjaan-pekerjaan survei, sehingga mahasiswa dapat melihat gambaran mengenai survei lapangan dan dapat menerapkannya di lapangan dalam konteks yang sebenarnya setelah lulus dari bangku kuliah serta dapat melatih mahasiswa melakukan pemetaan situasi teritris, yang pada umumnya diperlukan sebagai peta acuan dalam perencanaan teknis ataupun keperluan lainnya.
1.2 Tujuan Praktikum
Adapun tujuan praktikum Ilmu Ukur Tanah ini yaitu
1. Agar mahasiswa mengetahui dan mampu mengoperasikan theodolit manual ataupun digital (Total Station).
2. Mengetahui hasil pengukuran pada suatu poligon. 3. Dapat mengetahui bentuk permukaan suatu daerah.
4. Agar mahasiswa dapat menyatakan definisi Ilmu Ukur Tanah dan penggambarannya serta dapat menerangkan prinsip dan penggunaanya. 5. Untuk memudahkan membuat peta situasi.
1.3 Waktu dan Tempat Praktikum
Adapun praktikum Ilmu Ukur Tanah dilaksanakan pada hari : Senin, Kamis, dan Kamis
tanggal : 15 April 2013, 30 May 2013, dan 6 Juni 2013 waktu : Pukul 10.00 – Selesai WIB
lokasi : Taman Firdaus, GOR Soemantri, Jl. HR. Rasuna Said, Kuningan, Jakarta Selatan
1.4 Alat dan Perlengkapan
a. Total Station (Theodolit Digital)
Total station adalah alat ukur sudut dan jarak yang terintegrasi dalam satu unit alat. Total station juga sudah dilengkapi dengan processor sehingga dapat menghitung jarak datar, koordinat, dan beda tinggi secara langsung tanpa perlu kalkulator lagi.
Gambar 1.1. Total Station
Prism Pole (Prisma Terget) adalat yang menjadi taget bidikan oleh total station untuk memastikan keberadaan dan kebenaran posisi titik target yang dimaskud. Biasanya dipadukan dengan Statif atau pun Jaloon.
Gambar 1.2. Prims Pole
c. Patok
Patok ini berfungsi sebagai suatu tanda di lapangan untuk titik utama dalam pengukuran.
Gambar 1.3. Patok
d. Meteran
Meteran sering disebut pita ukur atau tape karena umumnya tersaji dalam bentuk pita dengan panjang tertentu. Sering juga disebut rol meter karena umumnya pita ukur ini pada keadaan tidak dipakai atau disimpan dalam bentuk gulungan atau rol. Kegunaan utama meteran mengukur jarak atau panjang. Dalam praktikum poligon sendiri, meteran digunakan untuk mengukur tinggi total station pada statif dari permukaan tanah.
Gambar 1.4. Meteran
e. Statif (Kaki Tiga)
Statif (kaki tiga) berfungsi sebagai penyangga waterpass dengan ketiga kakinya dapat menyangga penempatan alat yang pada masing-masing ujungnya runcing, agar masuk ke dalam tanah. Ketiga kaki statif
ini dapat diatur tinggi rendahnya sesuai dengan keadaan tanah tempat alat itu berdiri. Seperti tampak pada gambar dibawah ini :
Gambar 1.5. Statif/Tripod
f. Rambu Ukur
Rambu ukur mempunyai bentuk penampang segi empat panjang yang berukuran ± 3–4 cm, lebar ± 10 cm, panjang ± 300 cm, bahkan ada yang panjangnya mencapai 500 cm. Ujung atas dan bawahnya diberi sepatu besi. Bidang lebar dari bak ukur dilengkapi dengan ukuran milimeter dan diberi tanda pada bagian-bagiannya dengan cat yang mencolok. Bak ukur diberi cat hitam dan merah dengan dasar putih, maksudnya bila dilihat dari jauh tidak menjadi silau. Bak ukur ini berfungsi untuk pembacaan pengukuran tinggi tiap patok utama secara detail.
Gambar 1.6. Rambu Ukur /Rod
g. Jaloon
Jaloon adalah salah satu alat penyangga selain statif, yakni alat berdiri untuk prisma agar sasaran ke prisma oleh total station tepat.
Gambar 1.7. Jaloon
h. Alat Penunjang Lainnya
Alat penunjang seperti alat tulis, kalkulator, dan lainnya sangat dibutuhkan dalam pencatatan hasil pengukuran yang dilakukan.
Gambar 1.8. Alat Penunjang
BAB II KAJIAN TEORI
2.1 Teori poligon
Poligon adalah serangkaian garis lurus yang menghubungkan titik-titik yang terletak di permukaan bumi. Garis-garis lurus membentuk sudut-sudut pada titik-titik perpotongannya. Dengan menggunakan poligon dapat ditentukan secara sekaligus koordinat beberapa titik yang letaknya berurutan dan memanjang.
Pada ujung awal poligon diperlukan satu titik yang telah diketahui koordinat dan sudut jurusannya. Karena untuk menentukan koordinat titik yang lain diperlukan sudut mendatar dan jarak mendatar, maka pada pengukuran di lapangan data yang diambil adalah data sudut mendatar dan jarak mendatar di samping itu diperlukan juga penentuan sudut jurusan dan satu titik yang telah diketahui koordinatnya.
Berikut merupakan syarat-syarat pengukuran poligon yang harus dipenuhi terlebih dahulu. Di antaranya adalah :
1. Mempunyai koordinat awal dan akhir 2. Mempunyai azimuthawal dan akhir
Untuk mencapai ketelitian tertentu (yang dikehendaki) pada suatu poligon, perlu ditetapkan hal-hal berikut ini :
1. Jarak antara titik-titik poligon
2. Alat ukur sudut dan jarak yang digunakan 3. Jumlah seri pengukuran sudut
4. Ketelitian pengukuran jarak
5. Salah penutup sudut antara 2 pengamat matahari 6. Salah penutup koordinat
2.1.2. Pengukuran Poligon
A. Pengukuran Jarak Mendatar
Pengukuran jarak mendatar pada poligon dapat ditentukan dengan cara : mekanis (dengan menggunakan pita ukur) dan optis (seperti pada pengukuran sipat datar). pada bagian ini dijelaskan metode pengukuran jarak dengan menggunakan pita ukur. Pengukuran jarak dengan menggunakan pita ukur harus memperhatikanpermukaan tanah yang akan diukur.
Gambar 2.1 Pengukuran Jarak
Caranya :
Skala nol pita ukur diletakkan tepat berimpit di atas pusat anda titik A
Pita ukur ditarik dengan kuat agar keadaannya benar-benar lurus, tidak melengkung
Himpitkan skala pita ukur lainnya di atas pusat tanda titik B, maka bacaan skala inilah yang merupakan jarak antara titik A dan titik B
B. Pengukuran jarak pada tanah miring, seperti pada gambar
Gambar 2.2
Pengukuran Jarak pada Tanah Miring
Caranya :
Jika permukaan tanahnya relatif miring, maka pengukuran jarak dibagi dalam beberapa selang (pada gambar di atas bagi dua selang)
Skala nol diimpitkan di atas titik A (biasa dengan menggunakan bantuan unting-unting), tarik agar pita dalam keadaan datar sampai berimpit dengan titik 1, maka diperoleh d1
Dengan cara yang sama, jarak diukur dari titik 1 sampai titik B, hingga didapat d2
Maka : dAB = d1 + d2
C. Pengukuran Sudut Mendatar
Sudut adalah selisih antara dua arah yang berlainan. Yang dimaksud dengan arah atau jurusan adalah besarnya bacaan lingkaran horisontal alat ukur
sudut pada waktu teropong diarahkan ke jurusan tertentu. Seperti pada gambar
Gambar 2.3
Pengukuran Sudut Mendatar
Caranya :
Alat dirikan di titik P alalu diatur sesuai ketentuan
Target dipasang di titik A dan di tiik B
Alat dalam kedudukan “biasa” diarahkan ke target di titik A (arah pertama)
Atur tabung okuler dengamemutar sekrup yang ad pada okuler sehingga dapat melihat garis-garis diafragma (benang silang) denga jelas
Atur sekrup penjelas bayangan sehingga dapat melihat bayangan target di tiik A dengan terang dan jelas
Tepatkan benang silang diafragma pada target dengan memutar sekrup penggerak halus horisontal dan vertikal, baca dan catat skala lingkaran horisontalnya. Ulangi pembacaan tersebut minimal 3 kali, kemudian hitung rata-rata harga hasil bacaannya, catat sebagai L1 (B)
Teropong diputar searah jarum jam dan diarahkan ke target di titik B, dengancara yang sama seperti di atas, catat sebagai L2 (B)
Teropong dibalikkan dalam kedudukan “luar biasa” an diputar seearah jarum jam, dengan kedudukan tetap mengarah ke titikk B. dnegan cara yang sama seperti di atas, baca skala lingkarannya dan catat sebagai L2 (LB)
Putarlah teropong searah jarum jam ke titik A (tetap dalam kedudukan luar biasa), dengan menggunakan cara yang sam seperti di atas, bacalah skala lingkran horisontalnya dan catat sebagai L1 (LB)
Urutan pengukuran sudut seperti yang dijelaskan di atas adalah pengukuran sudut 1 seri.
D. Penentuan sudut jurusan awal dan koordinat awal 1. Sudut jurusan awal dapat ditentukan sebagai berikut
Bila di sekitar titik-titik kerangka dasar terdapat 2 titik triangulasi, sudut jurusan dihitung dari titik-titik triangulasi. Bila menggunakan sudut
jurusan awal ini, maka jaring titik-titik kerangka dasar harus disambungkan ke titik-titik triangulasi tersebut.
Bila tidak terdapt titik-titik triangulasi, sudut jurusan awal dapat ditentukan dari pengamatan astronomi (pengamatan matahari atau bintang) dari pengukuran menggunakan giro-theodolit yang berorientasi terhadap utara geografi atau dari pengukuran menggunakan theodolit kompas atau ditentukan sembarang.
2. Koordinat awal dapat ditentukan dalam sistem umum sebagai berikut :
Bila dikehendaki koordinat dalam sistem umum (sistem yang berlaku di wilayah negara) digunakan titik triangulasi (cukup satu titik saja). Dengan demikian kerangka dasar harus diikatkan ke titik triangulasi tersebut.
Bila diketahui koordinat dalam sistem umum tetapi tidak terdapat titik triangulasi, maka di salah satu titik kerangka dasar dilakukan pengukuran astronomis untuk menentukan lintang bujurnya. Dari lintang da bujur geografi ini dapat ditentukan koordinat (x,y) dalam sistem
Bila tidak terdapat titik triangulasi dan tidak dikehendaki koordinat dalam sistem umum, maka salah satu titik kerangka dasar dapat dipilih sebagai titik awal dengan koordinat sembarang (diusahakan pemilihan koordinat ini mempertimbangkan koordinat titik-titik yang lain agar bernilai positif). Sistem demikian sesitem koordinat setempat (lokal).
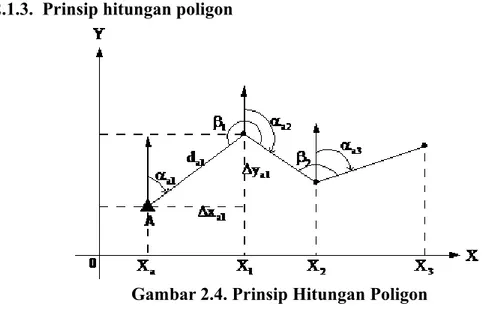
2.1.3. Prinsip hitungan poligon
Gambar 2.4. Prinsip Hitungan Poligon
Diketahui :
koordinat titik A sudut jurusan αA1
jarak datar dA1 sudut mendatar β1 dihitung : koordinat titik 1 (X1, Y1) koordinat titik 2 (X2, Y2) Tahapan hitungan :
Menghitung koordinat titik 1 :
X1 = XA + ∆XA1 Y1 = YA + ∆YA1
X1 = XA + dA1 Sin αA1 Y1 = YA + dA1 Cos αA1
Jika koordinat titik 1 diketahui, maka koordinat titik 2 dapat dihitung menggunakan koordinat titik 1, apabila d12 dan αA1 diketahui. d12 dapat diukur
dan biasanya sudut yang diukur dilapangan adalah sudut mendatar β1. α12 dapat
dihitung dari αA1 dan β1
α12 = {( αA1+ 180˚) + β1 } – 360˚
= αA1 + β1 - 180˚
maka koordinat titik 2 :
X2 = X1 + ∆X12 Y2 = Y1 + ∆Y12
X2 = X1 + d12 Sin α12 Y2 = Y2 + d12 Cos α12
Demikian pula untuk menghitung titik-titik selanjutnya dapat dilakukan secara brtahap dan berurutan menggunakan data koordinat titik sebelumnya. Sudut jurusan titik selanjutnya, dapat dihitung menggunakan α12 dan sudut
mendatar yang diukur di titik tersebut.
2.1.4 Rumus Urutan Koreksi Poligon
A. Kesalahan penutup sudut Total Error = X – X’
= (Σ sudut dalam ) – (n-2)180° Error = Total Error / n
Keterangan :
X = Jumlah Sudut Observasi X’ = Sudut sebenarnya n = Jumlah titik B. Adjusted ( ∆ X ) dan ( ∆ Y )
C-∆ Ymn = – ∑ ( ∆ Y ) / ∑d × dmn
Keterangan :
C-∆ Xmn = Koreksi absis
∑ ( ∆ X ) = Jumlah jarak ditinjau dari sumbu X (Departure) ∑d = Jumlah jarak
dmn = Panjang satu sisi
C-∆ Ymn = Koreksi ordinat
∑ ( ∆ Y ) = Jumlah jarak ditinjau dari sumbu Y (Departure) C. Toleransi
Toleransi pengukuran dalam polygon adalah: T = i √n
Dimana :
i = skala terkecil bacaan pada alat thedolit (ketelitiannya) n = jumlah titik yang diukur
2.3.3. Rumus Mencari Azimuth αBC = αAB + sudut B – 180° , atau αBC = αAB – sudut B + 180°
NB : Dalam penggunaannya tergantung keadaan D. Rumus Mencari Titik Koordinat
XB = XA + ∆ X AB
YB = YA + ∆ Y AB
Keterangan :
Xm = Absis titik m
∆ X AB = Jarak A ke B ditinjau dari sumbu X (Departure)
Ym = Latitude
∆ YAB =Jarak A ke B ditinjau dari sumbu Y (Latitude)
2.1.5. Macam-macam bentuk poligon
Poligon lepas adalah poligon yang hanya mempunyai satu titik ikat yaitu di awal dan untuk orientasi sudut jurusan awalnya sudah diketahui. Bentuk poligon lepas dapat dilihat pada gambar 2.8 di bawah ini.
Gambar 2.5 Bentuk Poligon Lepas
Poligon lepas memungkinkan terjadinya perambatan kesalahan yang disebabkan oleh pengukuran sudut mendatar dan jarak. Contoh : titik 1 telah mempunyai kesalahan akibat adanya pengukuran jarak, titik 2 akan mempunyai kesalahan juga yang lebih besardari titik 1 dan begitu seterusnya. Semakin panjang poligonnya, ketelitiannya akan semakin turun.
B. Poligon terikat
Pada poligon terikat diberikan satu titik ikat awal berikut jurusan awal dan juga titik ikat akhir atau sudut jurusan akhir.
a). Poligon dikontrol dengan sudut jurusan akhir
Titik awal diikatkan ke titik A dan untuk orientasi diberikan sudut jurusan awal, sedangkan titik terakhir diberikan sudut jurusan akhir. Akibat adanya sudut jurusan awal awal dan akhir, maka semua ukuran sudut yang sehadap dapat dikontrol.
Gambar 2.6
Poligon Terikat dan Dikontrol pada Sudut Jurusan Akhir
Diukur dilapangan :
Jarak datar d1, d2, d3, d4, dan d5
Sudut datar β1, β2, β3, β4
Setelah koordinat titik 1 dihitung dari koordinat titik A, untuk menghitung titik 2 diperlukan α12 dimana :
α12 = {( α0+ 180˚) + β1 } – 360˚
= α0 + β1 - 180˚
Untuk menghitung titik 3 diperlukan α23 dimana :
α23 = {( α12+ 180˚) + β2 } – 360˚
= αA1 + β2 - 180˚
= α0 + β1 + β2 – 360˚
Begitu juga selanjutnya :
α34 = {( α23+ 180˚) + β3 } – 360˚ = α23 + β3 - 180˚ = α0 + β1 + β2 + β3 – 540˚ Dan α45 = {( α34+ 180˚) + β4 } – 360˚ = α34 + β4 - 180˚ = α0 + β1 + β2 + β3 + β4 – 720˚ αa – α0 = β1 + β2 + β3 + β4 – 720˚ β1 + β2 + β3 + β4 = ( αa – α0 ) + 720˚ ∑ sudut diukur = ( αa – α0 ) + n. 180˚
Telah disebutkan sebelumnya bahwa sudut jurusan akhir (α45 = αa ) dan
sudut jurusan awa (α0) sudah diketahui. namun setiap pengukuran sudut
biasanya mengandung kesalahan, sehingga dapat dibentuk suatu persamaan dengan memberikan koreksi :
∑ sudut diukur + f(α) = ( αa – α0 ) + n. 180˚
Dimana f(α) adalah besarnya koreksi yang diberikan untuk pengukuran sudut. b) Poligon dikontrol dengan koordinat akhir
Koordinat titik awal dan sudut jurusan awal diketahui, kemudian titik akhir poligon diikatkan lagi pada satu titik yang telah diketahui koordinatnya
c) Poligon terkontrol dan terikat sempurna
Pada poligon ini, titik awalnya diikatkan pada satu titik yang ada koordinatnya (titik A) dan mempunyai sudut jurusan awal (α0). Selain itu pada
titik akhir diberikan sudut jurusan akhir (αa) dan diikatkan pada titik yang telah
mempunyai koordinat (titik B). dnegan adanya α0 dan αa, koordinat titik awal
dan titik akhir, maka hasil pengukurannya dapat dikontrol.
2.2 Teori Sipat Datar (Levelling)
2.2.1. Prinsip Penentuan Beda Tinggi dengan Sipat Datar
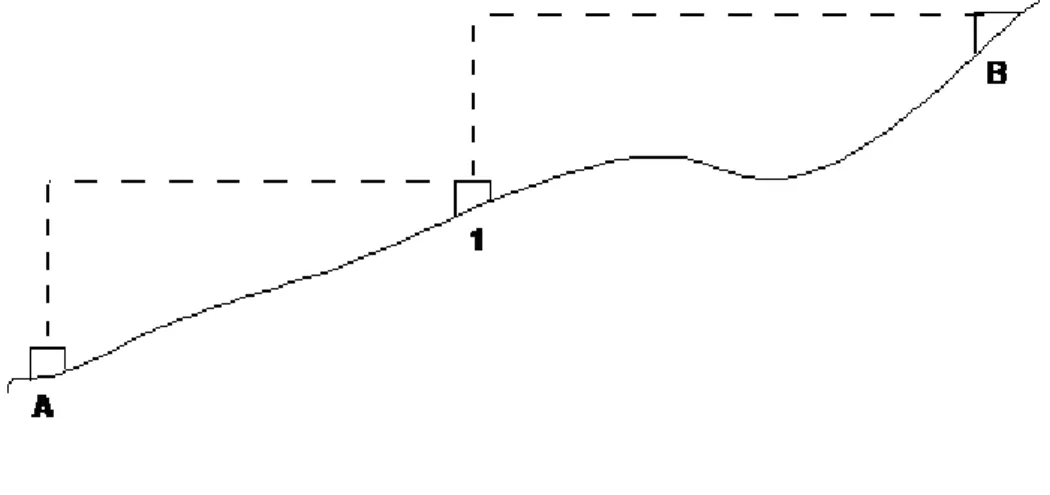
Beda tinggi didefinisikan sebagai perbedaan ketinggian antar dua titik atau lebih. Beda tinggi dapat diukur dengan cara sipat datar (Levelling), yang merupakan suatu metoda penentuan tinggi relatif dari beberapa titik di atas datum atau di bawah suatu bidang acuan tersebut sebagai referensi. Pada kenyataanya pengukuran beda tinggi adalah penentuan vertikal dari titik tersebut dengan garis penyipat datar alat yang ditempatkan di atas statif.
Dalam aplikasi praktis, levelling dilakukan dengan bantuan (alat ukur sipat datar) dan suatu baak ukur sebagimana diperlihatkan pada Gambar 2.7. tinggi titikA di atas datum adalah 1.500-0.750 = 0.750 m, dan tinggi titik C adalah 1.500-1.050 = 0.450 m di atas datum.
Datum merupakan bidang datar yang melalui titik B (patok B). Dalam istilah geodesi, datum ketinggian yang digunakan adalah berupa tinggi permukaan air laut rata-rata (mean sea level). Berdasarkan datum tersebut dapat dikembangkan jaringan levelling, sebagai titik kontrol ketinggian yang biasa disebut Bench Mark (BM). Sebagai acuan penentuan tinggi titik tersebut digunakan muka air laut rata-rata (MSL) atau tinggi lokal.
Gambar 2.7
Prinsip Pengukuran Beda Tinggi dengan Sipat Datar
2.2.2 Jenis Peralatan Sipat Datar
Berdasarkan Konstruksinya alat ukuyr penyipat datar dapat di bagi dalam empat macam utama :
a. Alat ukur penyipat datar dengan semua bagiannya tetap. Nivo tetap ditempatkan diatas teropong, sedang teropong hanya dapat diputar dengan sumbu ke satu sebagai sumber putar.
b. Alat ukur Penyipat datar yang mempunyai nivo reversi, dan ditempatkan pada teropong. Dengan demikian, teropong selain dapat diputar dengan sumbu ke satu sebagai sumbu putar, dapat pula diputar dengan suatu sumbu yang letak searah dengan garis bidik. Sumbu putar ini dinamakan sumbu mekanis teropong. Teropong dapat diangkat dari bagian bawah alat ukur penyipat datar.
c. Alat ukur penyipat datar dengan teropong yang mempunyai sumbu mekanis, tetapi nivo tidak diletakan pada teropong, melainkan ditempatkan di bawah, lepas dari teropong. Teropong dapat diangkat dari bagian bawah alat ukur penyipat datar.
d. Alat ukur penyipat datar dengan teropong yang dapat diangkat dari bagian bawah alat ukur penyipat datar dan dapat diletakkan di bagian bawah dengan landasan yang berbentuk persegi, sedang nivo ditempatkan di teropong.
2.2.3 Kesalahan-kesalahan dalam Levelling
A. Kesalahan Perorangan dan Alat
Adapun kesalahan dalam levelling karena human error yaitu
1. Kekeliruan dalam membaca angka pada rambu ukur dapat di atasi dengan membaca ketiga benang diafragma.
2. Kekeliruan penulis dalam mencatat data ukur.
3. Kesalahan pemegang rambu ketika menempatkan rambu di atas titik sasaran.
Sedangkan kesalahan dari alat meliputi :
1. Garis bidik tidak sejajar dengan garis nivo. Hal ini dapat dihindarkan dengan menempatkan alat di tengah-tengah rambu belakang dan rambu
muka (dp=dm) atau usahakan jumlah jarak rambu belakang = jumlah jarak muka.
2. Kesalahan karena garis nol skala dan kemiringan rambu. Misalnya letak garis nol sakal pada rambu A dan B tidak benar, maka hasil pembacaan pada rambu A harus dikoreksi Ka dan pada rambu B sebesar Kb. Misalnya dalam keadaan rambu tegak pembacaan akan menunjukkan angka a, sedangkan pembacaan pada waktu rambu miring sebesar α. Dari penelitian pengaruhmiringnya rambu tidak dapat dihilangkan sehingga untuk mendapatkan hasil beda tinggi yang lebih baik haruslah digunakan nivo rambu yang baik.
B. Kesalahan yang Bersumber pada Alam
Adapun beberapa kesalahan yang bersumber dari alam yaitu
1. Kesalahan karena melengkungnya sinar (refraksi). Dalam hal ini, sinar cahaya yang datang dari rambu ke alat penyipat datar karean melalui lapisan-lapisan udara yang berbeda baik kepadatan, tekanan maupun suhunya, maka sinar yang datang bukanlah lurus melainkan melengkung. 2. Kesalahan karena melengkungnya bumi.
3. Kesalahan karena masuknya Statif alat penyipat datar ke dalam tanah. Hal ini dapat memberi pengaruh pada hasil pengukuran. Pengaruh masuknya statif penyipat datar ke dalam tanah dapat dihilangkan dengan cara pengkuran sebagai berikut
- Baca rambu belakang, kemudian rambu muka, - Alat penyipat datar dipindah
- Baca rambu muka, kemudian rambu belakang.
4. Kesalahan karena panasnya sinar matahai dan geratan udara. Hal ini akan menimbulkan perubahan pada gelembung nivo sehingga akan mengakibatkana kesalahan pada hasil pengukuran. Oleh karena itu, untuk menghindari hal tersebut pada waktu pengukuran alat penyipat datar haris dilindungi dengan payung atau pengkuran dilakukan pada saat lapisan udara tenang yaitu waktu pagi dan sore.
2.3 Teori Kontur
2.3.1 Pengertian Kontur
Kontur adalah garis khayal yang menghubungkan titik-titik yang berketinggian sama dari permukaan laut.
Kontur memiliki sifat-sifat yaitu
2. Garis kontur berharga lebih rendah mengelilingi garis kontur yang lebih tinggi.
3. Garis kontur tidak berpotongan dan tidak bercabang
4. Kontur mempunyai interval tertentu (misalnya 1 m, 5 m, 25 m, dst.)
5. Rangkaian garis kontur yang rapat menandakan permukaan bumi yang curam/terjal, sebaliknya yang renggang menandakan permukaan bumi yang landai.
6. Rangkain garis kontur yang berbentuk huruf “U” menandakan punggungan gunung.
7. Rangkaian garis kontur yang berbentuk huruf “V” terbalik menandakan suatu lembah/jurang.
8. Kontur dapat mempunyai nilai positif (+), nol (0), atau pun negatif (-). 9. Pada jalan yang lurus dan menurun, maka kontur cembung ke arah turun. 10. Pasa sungai yang lurus dan menurun, maka kontur cekung ke arah turun. 11. Kontur tidak memotong bangunan atau melewati tungan di dalam bangunan.
2.3.2 Interval Kontur
Dalam penarikan antara kontur yang satu dengan kontur yang lain didasarkan pada besarnya perbedaan ketinggian antara ke dua buah kontur yang berdekatan dan perbedaan ketinggian tersebut disebut dengan „interval kontur“ (contour interval). Untuk menentukan besarnya interval kontur tersebut ada rumus umum yang digunakan yaitu :
Interval Kontur = 1/2000 x penyebut skala (dalam meter).
Contoh : Peta kontur yang dikehendaki skalanya 1 : 5.000, berarti interval konturnya : 1/2000 x 5.000 (m) = 2,5 m.
Dengan demikian kontur yang dibuat antara kontur yang satu dengan kontur yang lain yang berdekatan selisihnya 2,5 m. Sedangkan untuk menentukan
besaran angka kontur disesuaikan dengan ketinggian yang ada dan diambil angka yang utuh atau bulat, misalnya angka puluhan atau ratusan tergantung dari besarnya interval kontur yang dikehendaki. Misalnya interval kontur 2,5 m atau 5 m atau 25 m dan penyebaran titik ketinggian yang ada 74,35 sampai dengan 253,62 m, maka besarnya angka kontur untuk interval kontur 2,5 m maka besarnya garis kontur yang dibuat adalah : 75 m, 77,50 m, 80 m, 82,5 m, 85m, 87,5 m, 90 m dan seterusnya, sedangkan untuk interval konturnya 5 m, maka besarnya kontur yang dibuat adalah : 75 m, 80 m, 85 m, 90 m , 95 m, 100 m dan seterusnya, sedangkan untuk interval konturnya 25 m, maka besarnya kontur yang dibuat adalah : 75 m, 100 m, 125 m, 150 m, 175 m, 200 m dan seterusnya.
Cara penarikan kontur dilakukan dengan cara perkiraan (interpolasi) antara besarnya nilai titik-titik ketinggian yang ada dengan besarnya nilai kontur yang ditarik, artinya antara dua titik ketinggian dapat dilewati beberapa kontur, tetapi dapat juga tidak ada kontur yang melewati dua titik ketinggian atau lebih. Jadi semakin besar perbedaan angka ketinggian antara dua buah titik ketinggian tersebut, maka semakin banyak dan rapat kontur yang melalui kedua titik tersebut, yang berarti daerah tersebut lerengnya terjal, sebaliknya semakin kecil perbedaan angka ketinggian antara dua buah titik ketinggian tersebut, maka semakin sedikit dan jarang kontur yang ada, berarti daerah tersebut lerengnya landai atau datar. Dengan demikian, dari peta kontur tersebut, kita dapat membaca bentuk medan (relief) dari daerah yang digambarkan dari kontur tersebut, apakah daerah tersebut berlereng terjal (berbukit, bergunung), bergelombang, landai atau datar.
2.3.3. Penggunaan Kontur
Adapun kegunaan utama dari peta kontur yaitu
a. Memberikan profil permukaan (tinggi sampai dengan rendah) tanah. b. Menggambarkan potongan vertikal
c. Menempatkan proyek dan menggambarkan perpotongan dari permukaan-permukaan.
d. Membuat trase jalan raya/kereta api e. Membuat allignment saluran irigasi
2.3.4. Prosedur Pengambilan dan Pengolahan Data Kontur
Berikut prosedur yang dilakukan dalam pengambilan data hasil pengukuran kontur hingga prosedur peng-input-an data hasil pengukuran kontur :
1) Melakukan centering statif di titik yang telah diberi tanda dengan patok. Pastikan posisi titik di total station sejurus dengan patok
penanda. Kemudian hitung elevasi total station terhadap permukaan tanah.
2) Apabila total station telah di set dan siap untuk mengukur, siapkan 2 buah target yang masing-masing menempati daerah tertentu yang ingin diketahui bentuk kontur dan menjadikan variasi dalam data. Contohnya adalah pada samping jalan, gedung, tiang listrik, lampu, dan lain-lain
3) Setelah target berdiri tegak sempurna, arahkan total station ke target tersebut untuk menghitung jarak, sudut dan elevasinya. Sebelumnya, pada total station beri keterangan terlebih dahulu dimana target tersebut berada. Misalkan target berada di pinggiran jalan, untuk itu pada total station harus diberi keterangan ‘JLN’ baru kemudian diukur jaraknya.
4) Data tersebut akan tersimpan pada memori yang terdapat di dalam total station yang telah di-setting sebelumnya.
5) Ulangi langkah ke-3 dan ke-4 pada setiap tempat di sekitar lokasi pengambilan data, contohnya adalah jalan, pohon, tembok, pagar, dan lain-lain.
6) Setelah pengukuran dengan total station selesai dilakukan, masukkan data yang telah didapatkan tersebut ke dalam komputer. Caranya adalah dengan menggunakan aplikasi “Topcon Link” yang merupakan Operating System dari Total Station yang akan mentransfer data dari Total Station ke komputer. Kemudian masukkan data tersebut ke dalam microsoft excel.
7) Setelah data dimasukkan ke microsoft excel, perbaiki data sedemikian rupa, seperti merubah notasi sudutnya, dan lain-lain. Kemudian save data yang telah diolah dengan format .csv
8) Setelah di save, close microsoft excel. Kemudian buka aplikasi “Autocad Civil Design” dan import data microsoft excel yang telah di save dalam format .csv, maka akan muncul point-point pada layar di aplikasi “Autocad Civil Design” tersebut. Point-point yang terdapat pada layar tersebut, sesuai dengan data yang telah diperoleh saat pengambilan data kontur.
9) Point-point yang ada pada layar dihubungkan dengan layer yang berbeda-beda sesuai dengan keterangan yang terdapat pada point. Misalnya point-point jalan, maka buatlah layer dengan nama ‘Jalan’ dan dengan warna layer, misalnya merah. Setelah itu hubungkan tiap point-point jalan tersebut dengan menggunakan polyline. Cara seperti ini juga digunakan untuk point-point bangunan dan pagar.
10) Untuk mempermudah mengidentifikasi point, misalnya keterangan pohon, maka pada point-point pohon dapat diberikan simbol. Cara untuk memberikan simbol pohon misalnya dengan memilih menu utilities kemudian pilih submenu simbol manager , maka akan tersedia
jendela simbol manager, pilih ‘plant’ untuk memberikan simbol pohon, pilihlah model simbol yang diinginkan.
11) Setelah setiap point dihubungkan dan diberi simbol, kita masukkan 3D-Line pada layar cara Terrain > Edit Surface > Import 3D-Line. Setelah 3D-Line muncul pada layar, kita gunakan flip face untuk menyesuaikan 3D-Line dengan polyline.
12) Setelah itu, kita bisa memasukkan kontur pada layar dengan cara Terrain > Create Contour > Klik OK.
BAB III
DATA DAN PENGOLAHAN DATA 4.1 Data Hasil Pengukuran
4.1.1 Data Hasil Pengukuran Poligon
y
D C B
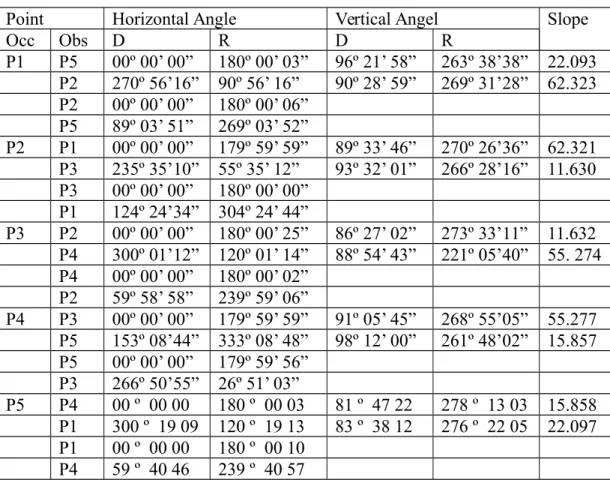
Tabel 4.1. Data Hasil Pengukuran Poligon
Point Horizontal Angle Vertical Angel Slope
Occ Obs D R D R P1 P5 00º 00’ 00” 180º 00’ 03” 96º 21’ 58” 263º 38’38” 22.093 P2 270º 56’16” 90º 56’ 16” 90º 28’ 59” 269º 31’28” 62.323 P2 00º 00’ 00” 180º 00’ 06” P5 89º 03’ 51” 269º 03’ 52” P2 P1 00º 00’ 00” 179º 59’ 59” 89º 33’ 46” 270º 26’36” 62.321 P3 235º 35’10” 55º 35’ 12” 93º 32’ 01” 266º 28’16” 11.630 P3 00º 00’ 00” 180º 00’ 00” P1 124º 24’34” 304º 24’ 44” P3 P2 00º 00’ 00” 180º 00’ 25” 86º 27’ 02” 273º 33’11” 11.632 P4 300º 01’12” 120º 01’ 14” 88º 54’ 43” 221º 05’40” 55. 274 P4 00º 00’ 00” 180º 00’ 02” P2 59º 58’ 58” 239º 59’ 06” P4 P3 00º 00’ 00” 179º 59’ 59” 91º 05’ 45” 268º 55’05” 55.277 P5 153º 08’44” 333º 08’ 48” 98º 12’ 00” 261º 48’02” 15.857 P5 00º 00’ 00” 179º 59’ 56” P3 266º 50’55” 26º 51’ 03” P5 P4 00 º 00 00 180 º 00 03 81 º 47 22 278 º 13 03 15.858 P1 300 º 19 09 120 º 19 13 83 º 38 12 276 º 22 05 22.097 P1 00 º 00 00 180 º 00 10 P4 59 º 40 46 239 º 40 57
Berikut merupakan sketsa poligon :
Keterangan : A = P1 B = P2 C = P3 D = P4 E = P5
4.1.2. Data Hasil Pengukuran Beda Tinggi (Levelling)
Berikut ini data hasil pengukuran beda tinggi (Levelling) :
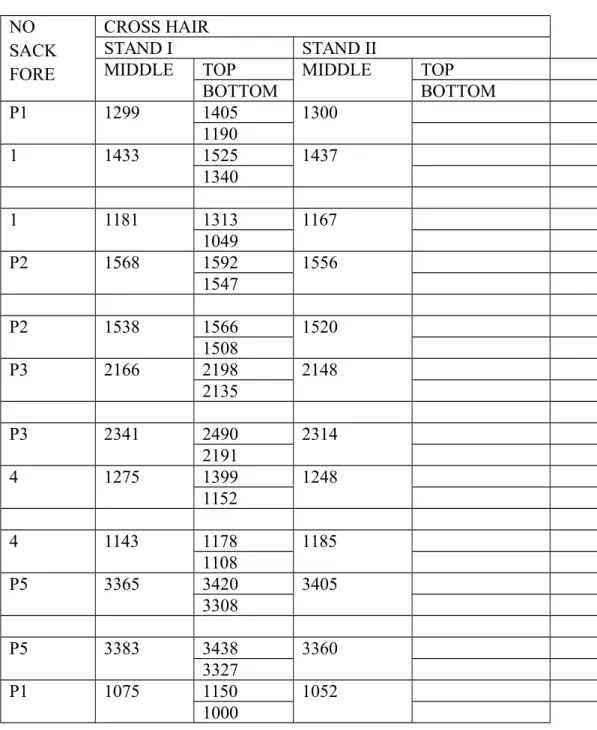
Tabel 4.2. Data Hasil Pengukuran Beda Tinggi (Levelling)
NO SACK FORE
CROSS HAIR
STAND I STAND II
MIDDLE TOP MIDDLE TOP
BOTTOM BOTTOM P1 1299 1405 1300 1190 1 1433 1525 1437 1340 1 1181 1313 1167 1049 P2 1568 1592 1556 1547 P2 1538 1566 1520 1508 P3 2166 2198 2148 2135 P3 2341 2490 2314 2191 4 1275 1399 1248 1152 4 1143 1178 1185 1108 P5 3365 3420 3405 3308 P5 3383 3438 3360 3327 P1 1075 1150 1052 1000
4.1.3. Data Hasil Pengukuran Kontur (Terlampir) 4.2 Pengolahan Data Hasil Praktikum
4.2.1 Pengolahan Data Hasil Praktikum Poligon
A. Koreksi Sudut Horisontal Contoh Perhitungan:
- Sudut Horisontal P1 ke P5 dan P2
Diketahui sudut hasil pengukuran ke P5 : Biasa = 00 00 00, Luar Biasa = 180 00 03, sehingga untuk mengetahui rata-rata sudut biasa dan luar biasanya, maka
Mean = (00 00 00 + 00 00 03)/2 = 00 00 03/2 = 00 00 1.5 (Cukup Second-nya yang diperhitungakan)
Diketahui sudut hasil pengukuran ke P2 : Biasa= 270 56 16, Luar Biasa= 90 56 16, sehingga untuk mengetahui rata-rata sudut
Mean = (00 00 16 + 00 00 16)/2 = 00 00 32/2 = 00 00 16
Selisih mean dari P5 dan P2 = 00 00 16-00 00 1.5 = 00 00 14.5
(Diselisihkan karena sudut Luar Biasa P5 lebih dari 180, jika kurang dari 180 maka dijumlahkan)
Sehingga didapatkan,
Sudut P5-P1-P2 = 270 56 00 + 00 00 14.5 = 270 56 14.5
- Sudut Horisontal P1 ke P2 dan P5(Backside)
Diketahui sudut hasil pengukuran ke P2 : Biasa = 00 00 00, Luar Biasa = 180 00 06, sehingga untuk mengetahui rata-rata sudut biasa dan luar biasanya, maka
Mean = (00 00 00 + 00 00 06)/2 = 00 00 06/2 = 00 00 03
Diketahui sudut hasil pengukuran ke P5 : Biasa = 89 03 51, Luar Biasa = 269 03 52, sehingga untuk mengetahui rata-rata sudut biasa dan luar biasa, maka
Mean = (00 00 51 + 00 00 52)/2 = 00 00 103/2 = 00 00 51.5
Selisih mean dari P2 dan P5 = 00 00 51.5-00 00 03 = 00 00 48.5
Sehingga didapatkan,
Sudut P2-P1-P5 = 89 03 00 + 00 00 48.5 = 89 03 48.5
Pengukuran Backside dilakukan agar memperoleh hasil koreksi sudut yang tepat untuk P5-P1-P2. Sehingga didapatkan,
Sudut P5-P1-P2 = 270 56 14.5 Sudut P2-P1-P2 = 89 03 48.5
_________ + Jumlah 360 00 03
Maka, Total eror = 360 00 03- 360 00 00 = 00 00 03
Eror = 00 00 03/2 = 00 00 1.5
Sehingga didapatkan sudut sebenarnya yaitu Sudut P5-P1-P2 = 270 00 14.5 – 00 00 1.5
= 270 00 13
Catatan : Apabila jumlah sudut (awal dan backside) kurang dari 360 maka hasil selisih dijumlahkan.
B. Koreksi Sudut Vertikal Contoh perhitungan :
- Sudut Vertikal P1 ke P5 dan P2
Diketahui sudut vertikal hasil pengukuran ke P5 : Biasa = 96 21 58, Luar Biasa = 263 38 38, sehingga untuk mengetahui rata-rata sudut biasa dan luar biasanya, maka
Mean = (00 00 58 – 00 00 38)/2 = 00 00 20/2 = 00 00 10
(Diselisihkan second-nya karena lebih dari 360, jika kurang dijumlahkan)
Sehingga didapatkan,
Sudut vertikal ke P5 = 96 21 00 + 00 00 10 = 96 21 10
Catatan : Jika jumlah sudut biasa dan luar biasa vertikal kurang dari 360, maka second-nya dijumlahkan dan hasil koreksinya tidak dibuat 00” lagi bagian second-nya, tetapi diselisihkan dengan second sudut biasa).
Diketahui sudut vertikal hasil pengukuran ke P2 : Biasa = 90 28 59, Luar Biasa = 269 31 28, sehingga untuk mengetahui rata-rata sudut biasa dan luar biasanya, maka
Mean = (00 00 59 – 00 00 28)/2 = 00 00 31/2 = 00 0015.5 Sehingga didapatkan,
Sudut Vertikal ke P2 = 90 28 00 – 00 00 15.5 = 90 28 15.5
C. Perhitungan Jarak Horisontal Contoh Perhitungan :
- Jarak Horisontal P1 ke P5 dan P2
Diketahui sudut vertikal P1 ke P5 yaitu 96 21 10 dan kemiringannya (slope) adalah 22.093 m, maka
Jarak Horisontal P1-P5 = 22.093 x Sin 96 21 10 = 21.957 m
Diketahui sudut vertikal P1 ke P5 yaitu 90 28 15.5 dan kemiringannya (slope) adalah 62.323 m, maka
Jarak horisontal P1-P2 = 62.323 x Sin 90 28 15.5 = 62.323 m
D. Perhitungan Jarak Vertikal (Beda tinggi) Contoh Perhitungan
- Jarak Vertikal P1 ke P5 dan P2
Diketahui sudut vertikal P1 ke P5 yaitu 96 21 10 dan kemiringannya (slope) adalah 22.093 m, tinggi P1 = 1.486 m, tinggi P5 = 1.343 m, maka
Jarak Vertikal P1-P5 = 22.093 x Cos 96 21 10 + (1.486-1.343) = -2.302 m
Diketahui sudut vertikal P1 ke P2 yaitu 90 28 15.5 dan kemiringannya (slope) adalah 62.323 m, tinggi P1 = 1.486 m, tinggi P2 = 1.486 m, maka
Jarak Vertikal P1-P2 = 62.323 x Cos 90 28 15.5 + (1.486-1.486) = -0.512
E. Perhitungan Luas Poligon
Tabel 4.3 Perhitungan Luas Poligon
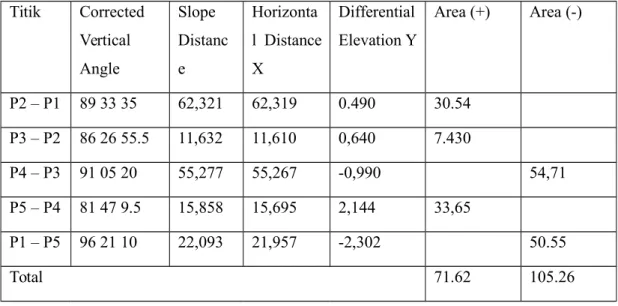
Titik Corrected Vertical Angle Slope Distanc e Horizonta l Distance X Differential Elevation Y Area (+) Area (-) P2 – P1 89 33 35 62,321 62,319 0.490 30.54 P3 – P2 86 26 55.5 11,632 11,610 0,640 7.430 P4 – P3 91 05 20 55,277 55,267 -0,990 54,71 P5 – P4 81 47 9.5 15,858 15,695 2,144 33,65 P1 – P5 96 21 10 22,093 21,957 -2,302 50.55 Total 71.62 105.26
4.2.2. Pengolahan Data Hasil Praktikum Levelling
1. Untuk titik P1 dan titik 1
Distance = distance titik awal+distance titik selanjutnya = 215 + 185
= 400 dm = 40 m
Height On the Pag = total diff elevation ∕ 2 = (134 + 137) / 2 = 135.5
= -0.1355 (disebabkan nilai elevasinya negatif) 2. Untuk titik 1 dan titik P2
Distance = distance titik awal+distance titik selanjutnya = 264 + 45
= 309 dm = 30.9 m
Height On the Pag = total diff elevation ∕ 2 = (390 + 389) / 2
= 389.5
= -0.388 (disebabkan nilai elevasinya negatif)
3. Untuk titik P2 dan titik P3
Distance = distance titik awal+distance titik selanjutnya = 58 +63
= 121 dm = 12.1 m
Height On the Pag = total diff elevation ∕ 2 = (628 + 628) / 2 = 628
= -0.628 (disebabkan nilai elevasinya negatif) 4. Untuk titik P3 dan titik 4
Distance = distance titik awal+distance titik selanjutnya = 299 + 247
= 546 dm = 54.6 m
Height On the Pag = total diff elevation ∕ 2 = (1066 + 1066 ) / 2 = 1066
= +1.066 (disebabkan nilai elevasinya positif) 5. Untuk titik 4 dan titik P5
Distance = distance titik awal+distance titik selanjutnya = 70 + 112
= 182 dm = 18.2 m
Height On the Pag = total diff elevation ∕ 2 = (2222 + 2220) / 2 = 2221
= -2.221 (disebabkan nilai elevasinya negatif) 6. Untuk titik P5 dan titik P1
Distance = distance titik awal+distance titik selanjutnya = 111 + 150
= 261 dm = 26.1 m
Height On the Pag = total diff elevation ∕ 2 = (2308 + 2308) / 2 = 2308
= +2.308 (disebabkan nilai elevasinya positif)
Kesalahan relatif keseluruhan
= -0.1355 + (-0.3895) + (-0.628) + 1.066 + (-2.221) + 2.308 = 0
Jadi kesalahan relatif yang dihasilkan dari pengambilan data-data percobaan yakni sebesar 0 (nol). Dengan kesalahan relatif sebesar 0 % menandakan pengolahan data tersebut nilainya sama dengan nilai presisi.
4.3.3. Pengolahan Data Hasil Praktikum Kontur
Pengolahan Data Hasil Praktikum Kontur tidak secara manual tetapi digital. Pengolahannya menggunakan Program MS. Excel dan aplikasi untuk mengubah data dalam bentuk koordinat agar dapat di plott di Autocad Civil Design 2009.
4.3 Tabel Hasil Pengolahan Data
4.3.1. Tabel Hasil Pengolahan Data Poligon (Terlampir) 4.3.2. Tabel Hasil Pengolahan Data Levelling
NO SAC K FOR CROSS HAIR DISTANCE (dm) DIFF ELEVATION HEIGHT ON THE PAG STAND 1 STAND 2 MIDDL TOP MIDDL + -BOTTO M
E E E P1 1299 1405 1300 215 134 -0.1355 1190 1 1433 1525 1437 185 137 1340 400 1 1181 1313 1167 264 390 -0.3895 1049 P2 1568 1592 1556 45 389 1547 309 P2 1538 1566 1520 58 628 -0.628 1508 P3 2166 2198 2148 63 628 2135 121 P3 2341 2490 2314 299 1066 +1.066 2191 4 1275 1399 1248 247 1066 1152 546 4 1143 1178 1185 70 2222 -2.221 1108 P5 3365 3420 3405 112 2220 3308 182 P5 3383 3438 3360 111 2308 +2.308 3327 P1 1075 1150 1052 150 2308 1000 261
Keterangan : Data yang diperoleh dari lapangan Data yang diolah
Total distance (dm)
BAB VI PENUTUP
4.1 Kesimpulan
Adapun kesimpulan dari praktikum Ilmu Ukur Tanah secara keseluruhan yaitu
Dalam Praktikum Poligon, jenis poligon yang diukur yaitu poligon tertutup. Adapun luas area poligon yatitu sekita 70 meter persegi
Levelling bertujuan untuk menghitung perbedaan ketinggian (elevasi) dari satu titik ke titik yang lain.
Data yang didapat mendekati presisi dikarenakan kesalahan relatif kurang dari 10%.
Kesalahan diakibatkan karena keadaan alam (cuaca yag panas) dan human error (kurang tepat membaca sumbu ukur).
Besarnya kesalahan relatif bergantung pada perbedaan ketinggian titik-titik tersebut dan tandanya (yang menunjukkan kedua titik tersebut naik atau turun).
Benang atas dan bawah dibutuhkan untuk membuktikan nilai dari besarnya ketinggian titik tersebut presisi atau mendekati benar yakni dengan merata-ratakan kedua nilai tersebut kemudian menyamakannya dengan nilai benang tengah.
Adanya data kontur yang sengaja disalahkan menyebabkan terjadinya kekacauan bentuk kontur
4.2 Saran
Adapun Saran oleh penulis agar data hasil praktikum bisa lebih baik sebagai berikut:
Sebaiknya alat yang akan digunakan harus dalam keadaan baik dan lengkap. Untuk itu, para praktikan harus memastikan alat dalam kondisi yang baik dan terkalibrasi secara benar untuk menghindari atu mengurang kesalahan yang bisa dibuat.
Untuk mendapatkan data yang akurat, sebaiknya para praktikan memastikan setiap saat alat dalam kondisi yang sesuai prosedur, contohnya kedudukan nivo yang harus berada di tengah.
Jangan lupa untuk mengambil sketsa lapangan agar dapat dicocokan dengan hasil yang diperoleh
Alat ukur harus selalu dijaga agar alat ukur tetap aman dan terkendali.
Perhatikan dengan cermat semua arahan yang diberikan asisten.
Koordinasikan selalu perkembangan proses praktikum dengan asisten, hal ini sangat berguna untuk mendeteksi kesalahan lebih awal.
Dalam pembacaan rambu gunakanlah kontrol dengan rumus Bt = ½ (Ba+Bb)
Sumber Buku :
Wongsotjiro, Soetomo. 2007. ILMU UKUR TANAH. Jakarta : KANISIUS. Sumber Internet : http://zulzulaidy.blogspot.com/2012/10/bab-i-pendahuluan-1.html http://lisabowo73.blogspot.com/2012/05/laporan-praktikum-ilmu-ukur-tanah-ii.html http://geojati.wordpress.com/2012/10/22/pemetaan-terestris-laporan/ http://download.spmabanjarbaru.sch.id/files/Alat%20Penyipat%20Datar.pdf http://squidybaflowbskey.blogspot.com/2011/06/total-station-20-judul-to-3-tgb-2.html#.UcwqdMif2xY http://learnmine.blogspot.com/2013/04/ilmu-ukur-tanah.html#axzz2XPwwh47I http://malemosau.blogspot.com/2011/03/ilmu-ukur-tanah-teknik-sipil.html * Diakses tanggal 19 Juni 2013